In this chapter, you learn about equations and how to solve them.
Equation Terminology
An equation is a statement of equality between two mathematical expressions. Equations may be true or false. For instance, the equation 9 + 7 = 16 is true, but the equation 9 + 7 = 20 is false. An equation has two sides. Whatever is on the left side of the equal sign is the left side (LS) of the equation, and whatever is on the right side of the equal sign is the right side (RS) of the equation.
A variable (or variables) might hold the place for numbers in an equation. For example, the equation
5x + 9 = 3x - 1
is an equation that has one variable, namely, x. Of course, you can have other letters (e.g., y, z, and A) that represent the variable in an equation.
Solving Equations
To solve an equation, proceed systematically to undo what has been done to the variable. In this discussion, for convenience, the variable is x.
The goal in solving an equation for the variable x is to get x by itself on only one side of the equation and with a coefficient of 1 (usually understood).
You solve an equation using the properties of real numbers and simple algebraic tools. An equation is like a balance scale. To keep the equation in balance, when you do something to one side of the equation, you must do the same thing to the other side of the equation.
 Tools for Solving Equations
Tools for Solving Equations
• Add the same number to both sides.
• Subtract the same number from both sides.
• Multiply both sides by the same nonzero number.
• Divide both sides by the same nonzero number.
You focus on the variable x while you work because what has been done to x determines the operation you choose to do. As you proceed step-by-step, you exploit the fact that addition and subtraction undo each other, and, similarly, multiplication and division undo one another. Here is a systematic approach.
 Solving an Equation for the Variable x
Solving an Equation for the Variable x
la. If fractions are involved, enclose numerators of more than one term in parentheses and then multiply each term on both sides of the equation by the least common multiple (LCM) of all the denominators.
lb. If the equation contains parentheses, remove them using the distributive property.
2. Combine like terms, if any, on each side of the equation.
3. If an xterm appears on both sides of the equation, add or subtract the x term so that, after you simplify, the x appears on only one side of the equation.
4. Undo addition or subtraction and then simplify. If a number is added to the x term, subtract that number from both sides of the equation. If a number is subtracted from the x term, add that number to both sides of the equation.
5. Divide both sides of the equation by the coefficient of x.
6. Check your work.
7. Check your answer.
Note: Steps la and lb are labeled this way because these two steps are interchangeable, depending on your judgment of which needs to be done first.
Solve the equation for x.
a. 5x + 9 = 3x - 1
b. 4(x - 6) = 40
c. −3x - 7 = 14
d. 3x - 2 = 7 - 2x
e. 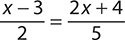
f. 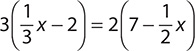
Solution
a. 5x + 9 = 3x - 1

Step 1. An x term appears on both sides of the equation, so subtract 3x from the RS to remove it from that side. To maintain balance, subtract 3x from the LS, too.
5x + 9 - 3x = 3x - 1 - 3x
Step 2. Simplify both sides by combining like variable terms.
2x + 9 = −1
Step 3. 9 is added to the x term, so subtract 9 from both sides.
2x + 9 - 9 = - 1 - 9
Step 4. Simplify both sides by combining constant terms.
2x = −10
Step 5. You want the coefficient of x to be 1, so divide both sides by 2.
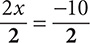
Step 6. Simplify.
x = −5
Step 7. Check your work by reviewing steps 1-6.
5x + 9 = 3x - 1
5x + 9 - 3x = 3x - 1 - 3x
Step 8. Check your answer by substituting −5 for x in the original equation, 5x + 9 = 3x - 1.
Substitute −5 for x on the LS of the equation: 5x + 9 = 5(-5) + 9 = −25 + 9 = −16. Similarly, on the RS, you have 3x - 1 = 3(-5) - 1 = - 15 - 1 = −16. Both sides equal −16, so −5 is the correct answer.
b. 4(x - 6) = 40

Step 1. Use the distributive property to remove parentheses.
4 · x - 4 · 6 = 40
4x - 24 = 40
Step 2. 24 is subtracted from the x term, so add 24 to both sides.
4x - 24 + 24 = 40 + 24
Step 3. Simplify both sides by combining constant terms.
4x = 64
Step 4. You want the coefficient of x to be 1, so divide both sides by 4.
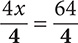
Step 5. Simplify.
x = 16
Step 6. Check your work by reviewing steps 1-5.
4(x - 6) = 40
4 · x - 4 · 6 = 40
4x - 24 = 40
4x - 24 + 24 = 40 + 24
4x = 64
x = 16
Step 7. Check your answer by substituting 16 for x in the original equation, 4(x - 6) = 40.
Substitute 16 for x on the LS of the equation: 4(x - 6) = 4(16 - 6) = 4(10) = 40. On the RS, you have 40 as well. Both sides equal 40, so 16 is the correct answer.
c. −3x - 7 = 14

Step 1. 7 is subtracted from the x term, so add 7 to both sides.
-3x - 7 + 7 = 14 + 7
Step 2. Simplify both sides by combining constant terms.
-3x = 21
Step 3. You want the coefficient of x to be 1, so divide both sides by −3.
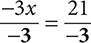
Step 4. Simplify.
x = -7
Step 5. Check your work by reviewing steps 1-4.

Step 6. Check your answer by substituting −7 for x in the original equation, −3x - 7 = 14.
Substitute −7 for x on the LS of the equation: −3x - 7 = −3(-7) - 7 = 21 - 7 = 14. On the RS, you have 14 as well. Both sides equal 14, so −7 is the correct answer.

Step 1. An x term appears on both sides of the equation, so add 2x to the RS to remove it from that side. To maintain balance, add 2x to the LS, too.
3x - 2 + 2x = 7 - 2x + 2x
Step 2. Simplify both sides by combining like variable terms.
5x - 2 = 7
Step 3. 2 is subtracted from the x term, so add 2 to both sides.
5x - 2 + 2 = 7 + 2
Step 4. Simplify both sides by combining constant terms.
5x = 9
Step 5. You want the coefficient of x to be 1, so divide both sides by 5.
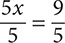
Step 6. Simplify.
x = 1.8
Step 7. Check your work by reviewing steps 1-6.
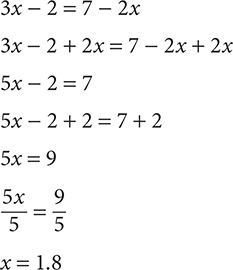
Step 8. Check your answer by substituting 1.8 for x in the original equation, 3x - 2 = 7 - 2x.
Substitute 1.8 for x on the LS of the equation: 3x - 2 = 3(1.8) - 2 = 5.4 - 2 = 3.4. Similarly, on the RS, you have 7 - 2x = 7 - 2(1.8) = 7 - 3.6 = 3.4. Both sides equal 3.4, so 1.8 is the correct answer.

Step 1. Eliminate fractions by multiplying both sides by 10, the least common multiple of 2 and 5. Write 10 as 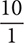 to avoid errors.
to avoid errors.
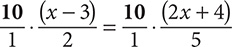
Step 2. Simplify
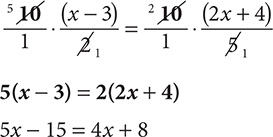
Step 3. An x term appears on both sides of the equation, so subtract 4x from the RS to remove it from that side. To maintain balance, subtract 4x from the LS, too.
5x - 15 - 4x = 4x + 8 - 4x
Step 4. Simplify both sides by combining variable terms.
x - 15 = 8
Step 5. 15 is subtracted from the x term, so add 15 to both sides.
x - 15 + 15 = 8 + 15
Step 6. Simplify both sides by combining constant terms.
x = 23
Step 7. Check your work by reviewing steps 1-6.
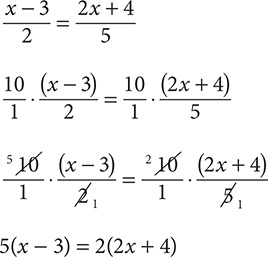
Step 8. Check your answer by using 23 for x in the original equation, 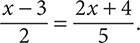 .
.
Put in 23 for x on the LS of the equation: 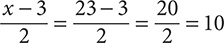 .
.
Similarly, on the RS, you have  .
.
Both sides equal 10, so 23 is the correct answer.
f. 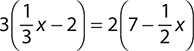

Step 1. Use the distributive property to remove parentheses.
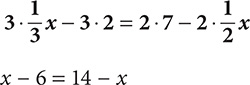
Step 2. An x term appears on both sides of the equation, so add x to the RS to remove it from that side. To maintain balance, add x to the LS, too.
x - 6 + x = 14 - x + x
Step 3. Simplify both sides by combining like variable terms.
2x - 6 = 14
Step 4. 6 is subtracted from the x term, so add 6 to both sides.
2x - 6 + 6 = 14 + 6
Step 5. Simplify both sides by combining constant terms.
2x = 20
Step 6. You want the coefficient of x to be 1, so divide both sides by 2.

Step 7. Simplify.
x = 10
Step 8. Check your work by reviewing steps 1-7.

Step 9. Check your answer by substituting 10 for x in the original equation, 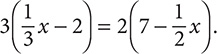
Substitute 10 for x on the LS of the equation: 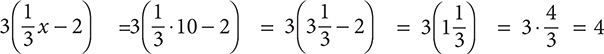 . Similarly, on the RS, you have
. Similarly, on the RS, you have 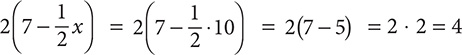 . Both sides equal 4, so 10 is the correct answer.
. Both sides equal 4, so 10 is the correct answer.
Translating and Solving Word Equations
Sometimes equations are expressed in words, with the word is (or equivalent word) indicating equality. The first step in learning to translate a word equation into mathematical symbols is to understand how addition, subtraction, multiplication, and division are expressed. Table 14.1 summarizes the most commonly used symbolism for the operations expressed as word phrases. The letter x is used in the table to represent an unknown number.
Translate the word equation into mathematical symbols and then solve it.
a. Fourteen plus five times a number x is four. Find x.
b. Four less than three times a number x is the product of two and the quantity x plus one. Find x.
Solution
a. Fourteen plus five times a number x is four. Find x.

Step 1. Replace the word is with the = symbol.
Fourteen plus five times a number x = four
Step 2. Translate the left side of the word equation into mathematical symbols.
“Fourteen plus five times a number x” is 14 + 5x
Step 3. Translate the right side of the word equation into mathematical symbols.
“four” is 4
Step 4. Write the symbolic equation and then solve for x.
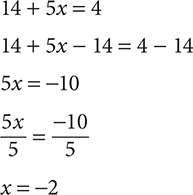
Step 5. Check your answer by substituting −2 for x in the word equation, “Fourteen plus five times a number x is four.” Substitute −2 for x on the LS of the word equation: “Fourteen plus five times a number x” = 14 + 5(-2) = 14 + −10 = 4. Similarly, on the RS, “four” = 4. Both sides equal 4, so −2 is the correct answer.
b. Four less than three times a number x is the product of two and the quantity x plus one. Find x.

Step 1. Replace the word is with the = symbol.
Four less than three times a number x = the product of two and the quantity x plus one
Step 2. Translate the left side of the word equation into mathematical symbols.
“Four less than three times a number x” is 3x - 4
Step 3. Translate the right side of the word equation quantity into mathematical symbols.
The product of two and the quantity x plus one” is 2(x + 1)
Step 4. Write the symbolic equation and then solve for x.
3x - 4 = 2(x + 1)
3x - 4 = 2 · x + 2 · 1
3x - 4 = 2x + 2
3x - 4 - 2x = 2x + 2 - 2x
x - 4 = 2
x - 4 + 4 = 2 + 4
x = 6
Step 5. Check your answer by substituting 6 for x in the verbal equation, “Four less than three times a number x is the product of two and the quantity x plus one.” Substitute 6 for x on the LS of the word equation: “Four less than three times a number x” = 4 less than 3(6) = 4 less than 18 = 14. Similarly, on the RS, “the product of two and the quantity x plus one” = the product of 2 and the quantity (6 + 1) = the product of 2 and 7 = 2(7) = 14. Both sides equal 14, so 6 is the correct answer.
Writing Equations to Solve Percent Problems
In Chapter 9, you solved percent problems using proportion concepts. You also can solve percent problems by writing and solving equations. The relationship among the elements of a percent problem is given by the formula
P = RB
where R is the rate, B is the base, and P is the percentage. The secret to solving percent problems is being able to identify the three elements correctly. Start with R and B because they are usually easier to find. R is the percent in the problem and will have a % symbol or the word percent attached. B is the whole on which the rate is based and very often is the amount that immediately follows % of or percent of. The percentage is the portion of B that is determined by R. It is the other amount in the problem, and when the problem statement contains the word is, P is near is. The value of two elements will be given in the problem, and you will be solving for the third element. After you identify the three elements, write an equation using the formula P = RB and then solve it.
Problem
Write an equation and then solve it.
a. What is 25% of 70?
b. Fifty is 40% of what number?
c. What percent of 150 is 30?
d. A student scored 60 out of 80 questions. What is the student’s percent grade?
e. A toy is on sale for $13. This sale price is 80% of the regular price of the toy. What is the regular price?
Solution
a. What is 25% of 70?

Step 1. Identify R, B, and P.
R = 25% = 0.25, B = 70, P = ?
Step 2. Write an equation and then solve it.
P = RB
P = (0.25)(70)
P = 17.5
Step 3. State the answer.
17.5 is 25% of 70.
b. Fifty is 40% of what number?

Step 1. Identify R, B, and P.
R = 40% = 0.4, B = ?, P = 50
Step 2. Write an equation and then solve it.
P = RB
50 = (0.4)B
(0.4)B = 50 Note: For convenience, switch sides, so that the variable B is on the LS.
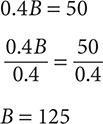
Step 3. State the answer.
50 is 40% of 125.
c. What percent of 150 is 30?

Step 1. Identify R, B, and P.
R = ?, B = 150, P = 30
Step 2. Write an equation and then solve it.
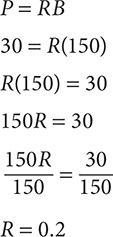
Step 3. Change 0.2 to a percent.
R = 0.2 = 20%
Step 4. State the answer.
30 is 20% of 150.
d. A student scored 60 out of 80 questions. What is the student’s percent grade?

Step 1. Identify R, B, and P.
R = ?, B = 80, P = 60
Step 2. Write an equation and then solve it.
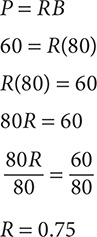
Step 3. Change 0.75 to a percent.
R = 0.75 = 75%
Step 4. State the answer.
The student’s percent grade is 75%.
e. A toy is on sale for $13. This sale price is 80% of the regular price of the toy. What is the regular price?

Step 1. Identify R, B, and P.
R = 80% = 0.8, B = ?, P = $13
Step 2. Write an equation and then solve it.
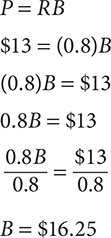
Step 3. State the answer.
The regular price of the toy is $16.25.
 Exercise 14
Exercise 14
For 1-4, solve the equation for x.
1. x - 7 = 11
2. 6x - 3 = 13
3. x + 3(x - 2) = 2x - 4
5. Translate the word equation into a symbolic equation and then solve for x: Two more than three times a number x is four less than six times the number x.
For 6-10, write an equation and then solve it.
6. What is 35% of 500?
7. Ninety is 60% of what number?
8. What percent of $144 is $21.60?
9. A student scored 70 out of 80 questions. What is the student’s percent grade?
10. A shirt is on sale for $76. This sale price is 80% of the regular price of the shirt. What is the regular price?
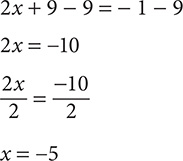


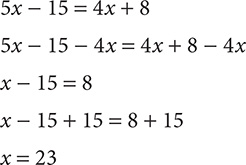

 on your calculator. The fraction bar indicates division.
on your calculator. The fraction bar indicates division.