Numbers and operations
Roots and radicals
Exponents
Order of operations
Scientific notation
Sets
Counting techniques
Basic probability
Graphical representation of data
Descriptive measures of data
This arithmetic review includes the following topics:
Numbers and operations
Roots and radicals
Exponents
Order of operations
Scientific notation
Sets
Counting techniques
Basic probability
Graphical representation of data
Descriptive measures of data
The counting numbers (or natural numbers) are the numbers 1, 2, 3, and so on. The whole numbers are the numbers 0, 1, 2, 3, and so on. Whole numbers that are greater than 1 are either prime or composite. A prime number is a whole number greater than 1 that has exactly two distinct whole number factors: itself and 1. The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. The whole numbers greater than 1 that are not prime are the composite numbers. They are the numbers that have more than two distinct whole number factors. The number 1 is neither prime nor composite.
The integers are either positive (1, 2, 3, …) or negative (… –3, –2, –1) or zero. Note: The three dots indicate that the pattern continues without end. On the number line, positive numbers are located to the right of zero and negative numbers are to the left of zero. Zero is neither positive nor negative:
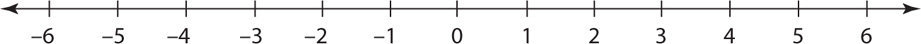
Integers that divide evenly by 2 are even. The even integers are …–6, –4, –2, 0, 2, 4, 6,.… Integers that do not divide evenly by 2 are odd. The odd integers are … –5, –3, –1, 1, 3, 5,.… Tip: Notice that 0 is an even integer.
Decimals are written using a base-10 place-value system. The value of a decimal number is determined by the placement of the decimal point in the number. A place-value diagram for some of the positional values of the decimal system is shown here.
The fraction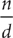 
is composed of three parts. The line between n and d is the fraction bar. The number above the fraction bar is the numerator, and the number below the fraction bar is the denominator. The fraction 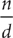means n ÷ d. Tip: The denominator of a fraction can never be zero, because division by zero is undefined. The reciprocal of the fraction 
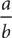is the fraction 
, provided a ≠ 0 and b ≠ 0.
In proper fractions (such as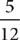 
), the numerator is less than the denominator. In improper fractions (such as 
and 
), the numerator is greater than or equal to the denominator. The value of an improper fraction is greater than or equal to one. A mixed number (such as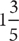 
) is the sum of a whole number and a fraction. Change an improper fraction to a mixed number or a whole number by performing the indicated division. If there is a remainder, write it as the numerator of a fraction that has the divisor as the denominator, for example:
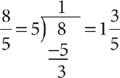
Change a mixed number to an improper fraction by multiplying the whole number part by the denominator of the fractional part. Then add the numerator of the fractional part to the resulting product. Place the resulting sum over the denominator of the fractional part, for example:
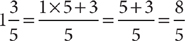
If both the numerator and denominator of a fraction are multiplied or divided by the same nonzero number, the value of the fraction is unchanged. The resulting fraction is equivalent to the original fraction. For example, 
and 
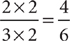are equivalent fractions. Similarly, 
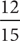and 
are equivalent fractions.
To write two fractions as equivalent fractions with the same denominator, use the least common multiple as the common denominator. A multiple of a number is the product of the number and any counting number. The least common multiple (or LCM) of two numbers is the least counting number that is a multiple of both numbers. List multiples of the greater number, in order. Stop when you first list a multiple that is also a multiple of the other number. This multiple will be the LCM of the two numbers. For instance, to write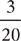 
and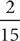 
as fractions with the same denominator, find the LCM (20, 15). List the multiples of 20, in order: 20, 40, 60. Stop. The number 60 is the first multiple of 20 that is also a multiple of 15, so 60 is the LCM (20, 15). Thus,
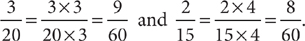
When the only common factor between the numerator and denominator of a fraction is one, the fraction is in lowest terms. Reduce a fraction to lowest terms by dividing the numerator and denominator by their greatest common factor. The greatest common factor (or GCF) of two numbers is the largest factor common to the two numbers. Tip: The GCF is always positive. For example, reduce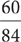 
by dividing its numerator and denominator by the GCF of 60 and 84. List the positive factors of 60 in pairs:
List the positive factors of 84 in pairs:
Examination of the two lists shows GCF (60, 84) is 12. Thus,
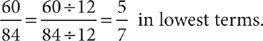
To obtain the equivalent decimal representation of a fraction, such as 
, perform the indicated division. Divide the numerator by the denominator. Insert a decimal point in the numerator and one or more zeros (as needed) to the right of the decimal point to complete the division:
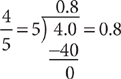
Percent means “per hundred.” The % sign stands for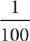 
or 0.01. To change a percent to an equivalent fraction, substitute multiplying by 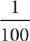for the percent sign. For example, 
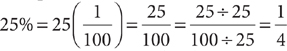. To change a percent to an equivalent decimal, substitute multiplying by 0.01 for the percent sign. For example, 25% = 25(0.01) = 0.25.
All of the counting numbers, whole numbers, integers, fractions, decimals, and percents are rational numbers. The rational numbers are numbers that can be expressed as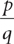 
, where p and q are integers (q ≠ 0). In other words, a rational number is a number that can be expressed as a quotient of an integer divided by an integer other than zero. Tip: Zero is excluded as a denominator for 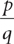because division by zero is undefined, so 
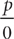has no meaning no matter what number you put in the place of p.
The decimal representations of rational numbers terminate or repeat a block of digits. For instance,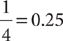 
is a rational number whose decimal representation terminates, and 
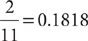… is a rational number whose decimal representation repeats the block of digits “18.” In most problems, you can round repeating decimals to a certain number of decimal places. For instance, rounded to two decimal places, 
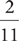is approximately 0.18.
The irrational numbers are numbers whose decimal representations neither terminate nor repeat. These numbers cannot be expressed as the quotient of two integers. For instance, the positive number that multiplies by itself to give 2 is an irrational number called “the positive square root of 2.” You use the square root symbol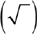 
to show the positive square root of 2 like this: 
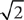. You cannot express 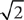as the quotient of two integers, nor can you express it precisely in decimal form. Its decimal equivalent continues on and on without a pattern of any kind. No matter how far you go with decimal places, you can only approximate 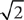. For instance, rounded to three decimal places, 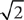is approximately 1.414. There are infinitely many square roots and other roots as well that are irrational.
The real numbers are all the rational and irrational numbers put together. All numbers used on the GMAT are real numbers. The relationship of the various sets of numbers included in the real numbers is shown here.
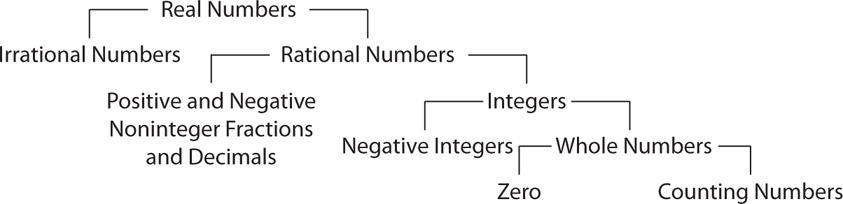
Real numbers are sometimes called signed numbers because they are positive, negative, or zero. Positive numbers lie to the right of zero on the number line and negative numbers lie to the left of zero. Zero is neither positive nor negative. It has no sign.
The absolute value of a real number is its distance from zero on the number line. The absolute value of a nonzero real number is positive. The absolute value of zero is zero. For example, the absolute value of –3.4 is 3.4, written as |–3.4| = 3.4.
Every real number has an opposite. If a real number is positive, its opposite is negative. If a real number is negative, its opposite is positive. For example, the numbers 
and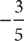 
are opposites. Zero is its own opposite. A number and its opposite have the same absolute value. For instance,
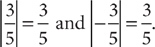
Addition, subtraction, multiplication, and division are the four basic arithmetic operations. Following are rules that you will find useful for completing basic operations:
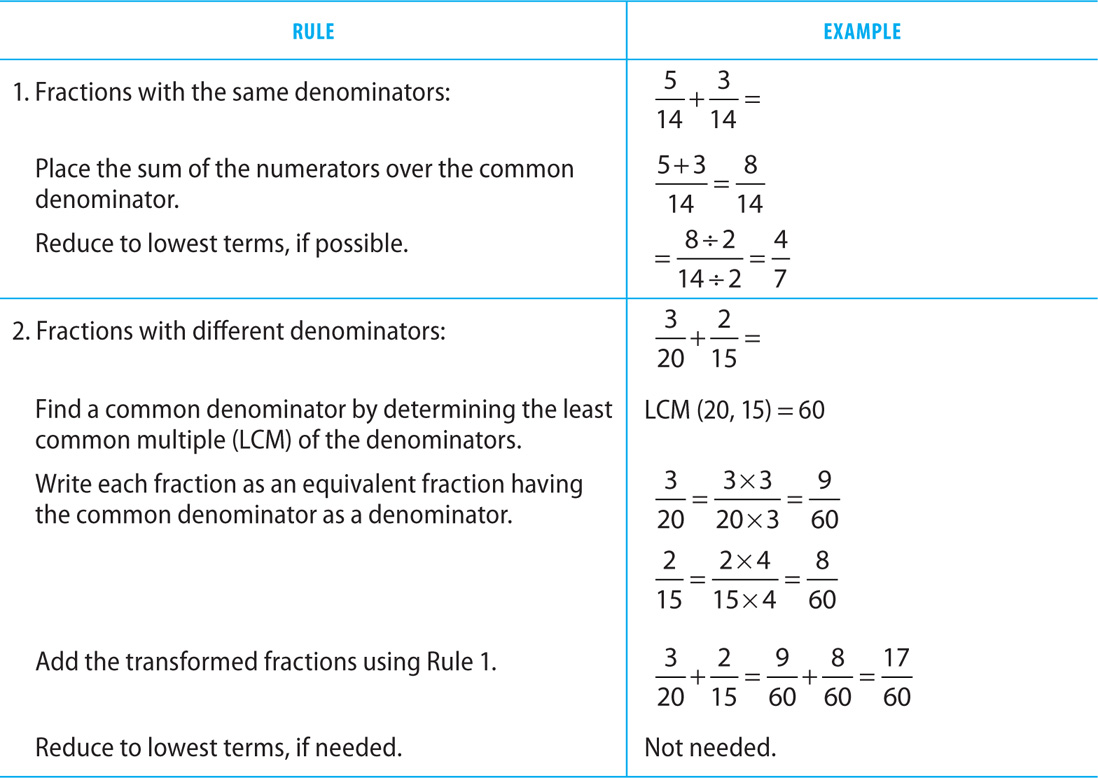
Adding Fractions
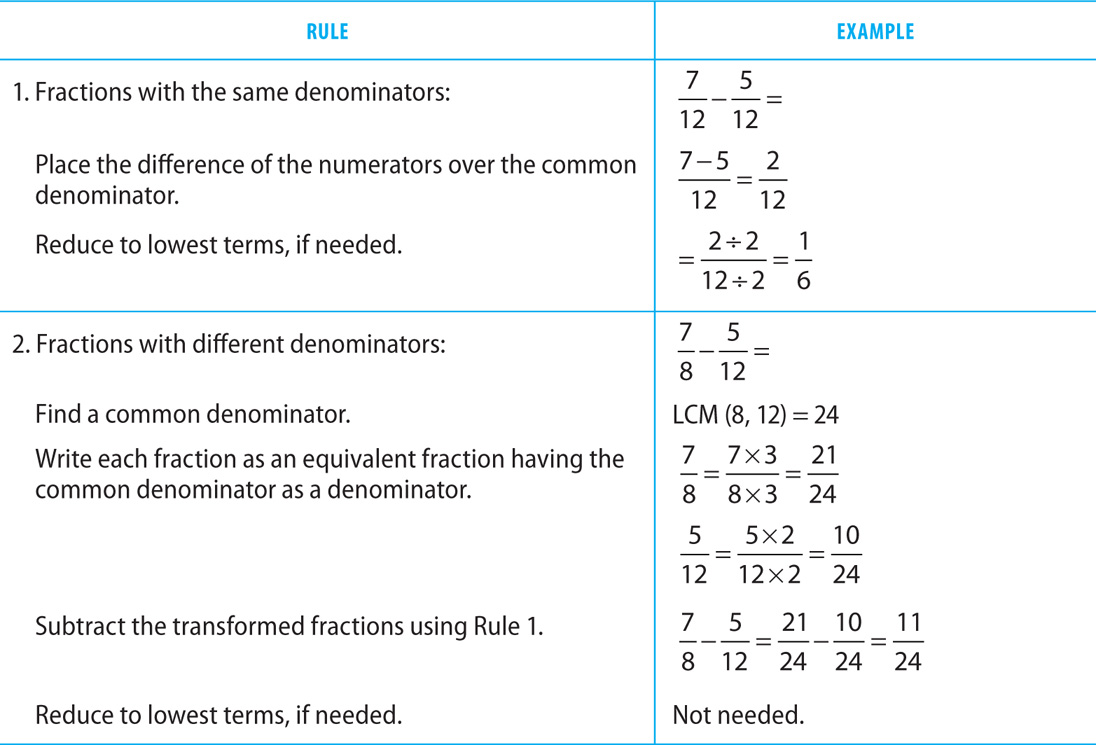
Subtracting Fractions
The process of multiplying fractions can be simplified by dividing out common factors, if any, before doing any multiplication. For example, 
. Also, remember you do not have to find a common denominator when multiplying fractions.
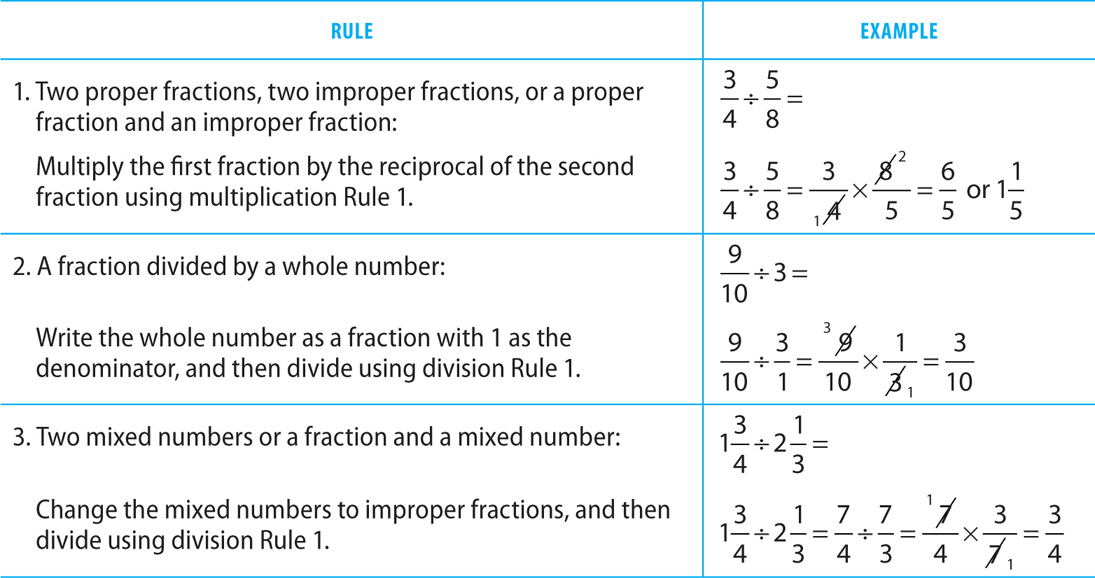
Dividing Fractions
Subtracting Decimals
Multiplying Decimals
Dividing Decimals
Adding and Subtracting Real Numbers
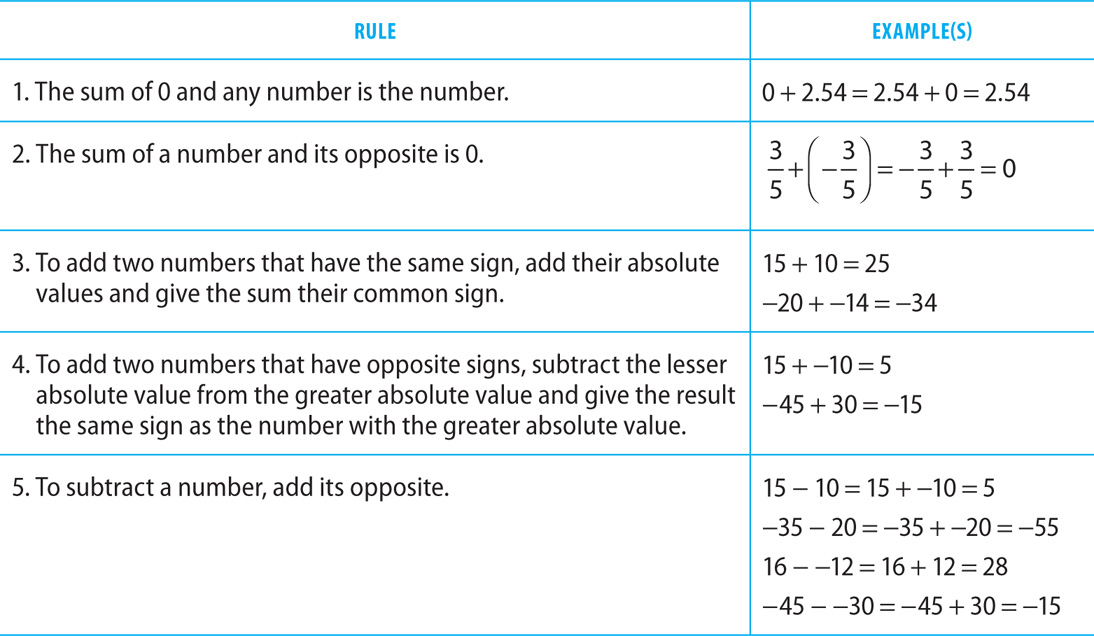
Multiplying and Dividing Real Numbers
The following 11 properties hold for the operations of addition and multiplication for all real numbers a, b, and c:
Closure Property of Addition: (a + b) is a real number. This property guarantees that the sum of any two real numbers is always a real number.
Closure Property of Multiplication: (a·b) is a real number. This property guarantees that the product of any two real numbers is always a real number.
Commutative Property of Addition: a + b = b + a. This property allows you to reverse the order of the numbers when you add, without changing the sum.
Commutative Property of Multiplication: a·b = b·a. This property allows you to reverse the order of the numbers when you multiply, without changing the product.
Associative Property of Addition: (a + b) + c = a + (b + c). This property says that when you have three numbers to add together, the final sum will be the same regardless of the way you group the numbers (two at a time) to perform the addition.
Associative Property of Multiplication: (ab)c = a(bc). This property says that when you have three numbers to multiply together, the final product will be the same regardless of the way you group the numbers (two at a time) to perform the multiplication.
Additive Identity Property: There exists a real number 0, called the additive identity, such that a + 0 = a and 0 + a = a. This property guarantees that you have a real number, namely 0, for which its sum with any real number is the number itself.
Multiplicative Identity Property: There exists a real number 1, called the multiplicative identity, such that a·1 = a and 1·a = a. This property guarantees that you have a real number, namely 1, for which its product with any real number is the number itself.
Additive Inverse Property: For every real number a, there is a real number called its additive inverse, denoted –a, such that a + –a = 0 and –a + a = 0. This property guarantees that every real number has an additive inverse (its opposite) that is a real number whose sum with the number is 0.
Multiplicative Inverse Property: For every nonzero real number a, there is a real number called its multiplicative inverse, denoted a–1 or 
, such that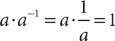 
and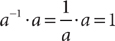 
. This property guarantees that every real number, except zero, has a multiplicative inverse (its reciprocal) whose product with the number is 1.
Distributive Property: a(b + c) = a·b + a·c and (b + c)a = b·a + c·a. This property says that when you have a number times a sum (or a sum times a number), you can either add first and then multiply, or multiply first and then add. Either way, the final answer is the same.
Every positive number has two square roots that are equal in absolute value, but opposite in sign. Zero has only one square root, namely 0. For instance, 4 and –4 are the two square roots of 16. The positive square root is the principal square root. The square root radical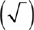 
always denotes the principal square root. Thus, 
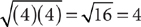and 
. Tip: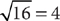 
, not –4 or ±4. You indicate the negative square root of 16 as 
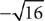. Thus, 
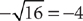. To be well-prepared for the GMAT, you should memorize the following 20 principal square roots:
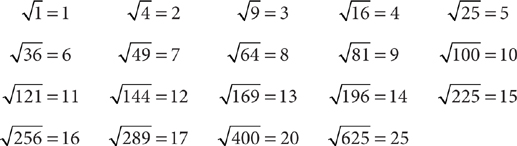
Every real number has one real cube root, called its principal cube root. For example, because 4 × 4 × 4 = 64, 4 is the principal cube root of 64. Likewise, because (–4)(–4)(–4) = –64, –4 is the principal cube root of –64. As you can see, the principal cube root of a positive number is positive, and the principal cube root of a negative number is negative. You use the cube root radical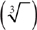 
to designate the principal cube root. The small number 3 in the radical indicates that the cube root is desired. This number is the index of the radical. Thus, 
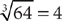and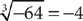 
.
Here is a list of principal cube roots of some positive perfect cubes.
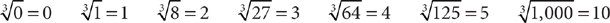
For the GMAT, it would be a good idea for you to know these roots.
In general, the index of the radical tells you which root to find. Tip: The index for the square root radical is understood to be 2. Here are examples of higher roots.
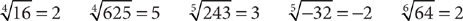
The number under the radical is the radicand. Here are some points to keep in mind:
If the index is even and the radicand is positive, the principal root is positive.
If the index is even and the radicand is negative, there is no real root.
If the index is odd and the radicand is positive, the principal root is positive.
If the index is odd and the radicand is negative, the principal root is negative.
An exponent is a small raised number written to the upper right of a quantity, which is called the base for the exponent. In the exponential expression bn, b is the base and n is the exponent: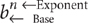 
. The act of doing what the exponent indicates is exponentiation.
Let m and n be positive integers. Here are types of exponents and their meanings.
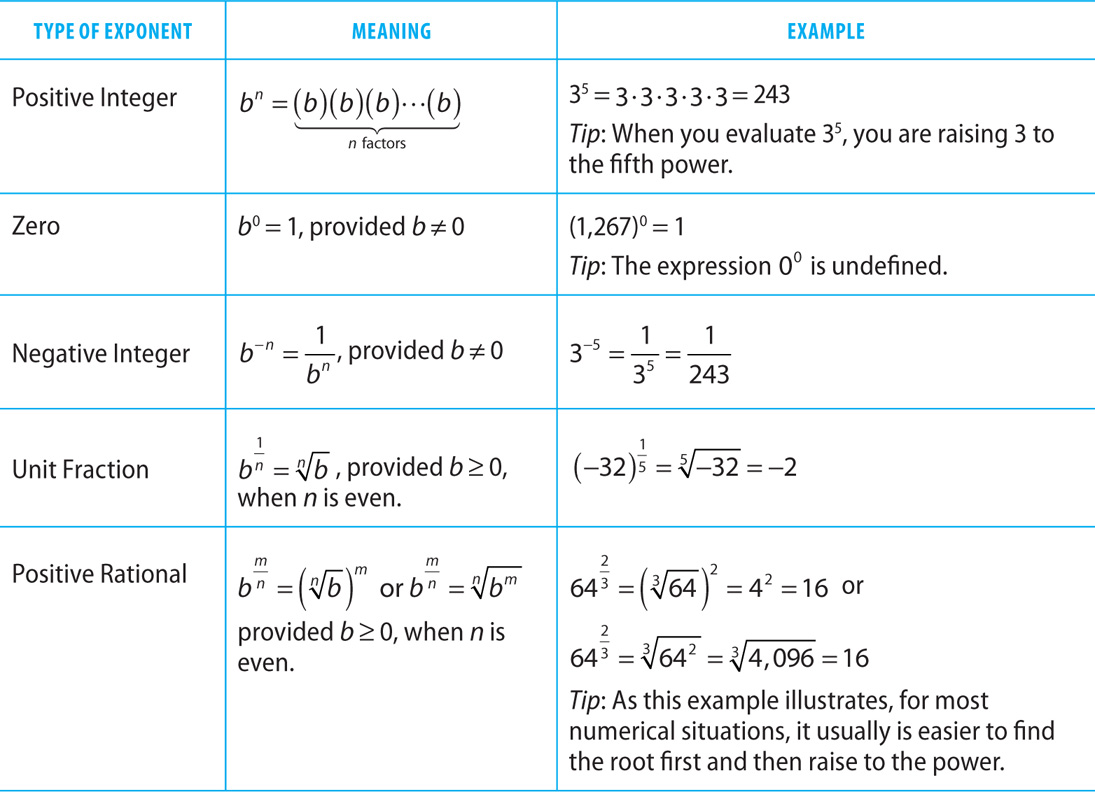
The following rules for exponents hold.
An exponent applies only to the base to which it is attached:
(–5)2 = (–5)(–5) = 25, but –52 = –(5·5) = –25
Which number is the exponent and which is the base makes a difference in the value of an exponential expression:
25 ≠ 52; 25= 2 × 2 × 2 × 2 × 2 = 32, but 52 = 5 × 5 = 25.
Exponentiation does not distribute over addition (or subtraction):
(4 + 1)3 ≠ 43 + 13; (4 + 1)3 = (5)3 = 125, but 43 + 13 = 64 + 1 = 65.
A negative number raised to an even power yields a positive product:
(–3)4 = (–3)(–3)(–3)(–3) = 81.
A negative number raised to an odd power yields a negative product:
(–3)5 = (–3)(–3)(–3)(–3)(–3) = –243.
A negative exponent tells you to write a reciprocal; it does not tell you to make your answer negative:
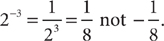
Grouping symbols such as parentheses ( ), brackets [ ], and curly braces { } are used to keep things together that belong together. Fraction bars, absolute value bars, and radicals also are grouping symbols. When you are performing computations, perform operations in grouping symbols first. It is very important that you do so when you have addition or subtraction inside the grouping symbol. For instance, (5 – 3)3 ≠ 53 – 33; (5 – 3)3 = 23 = 8, but 53 – 33 = 125 – 27 = 98. When you no longer need the grouping symbol, omit it.
Follow the order of operations when you evaluate numerical expressions:
1. Do computations inside Parentheses (or other grouping symbols). If there is more than one operation inside the grouping symbol, follow the order of operations given here to do the computations inside the parentheses. If there are grouping symbols within grouping symbols, start with the innermost grouping symbols.
2. Evaluate Exponential expressions (also, evaluate absolute value, square root, and other root expressions).
3. Multiply and Divide in the order in which they occur from left to right.
4. Add and Subtract in the order in which they occur from left to right.
Try the mnemonic “Please Excuse My Dear Aunt Sally”—abbreviated as PEMDAS—to help you remember the order of operations. The first letters stand for “Parentheses, Exponentiation, Multiplication, Division, Addition, and Subtraction.” Example:
Evaluate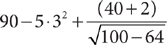 
.
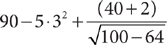First, compute inside grouping symbols.
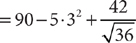Next, evaluate exponents and roots.
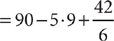Then, multiply and divide from left to right.
= 90 – 45 + 7 Finally, add and subtract from left to right.
= 52
A number expressed in scientific notation is written as a product of two factors. The first factor is a decimal number greater than or equal to 1, but less than 10. The second factor is a power of 10. The product of the two factors equals the original number. Any decimal number can be expressed in scientific notation:
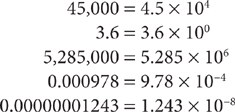
A set is a collection of objects. Sets are usually named with uppercase letters, such as A and B. The set’s objects are its elements or members. In the roster notation for sets, the set’s elements, separated by commas, are listed between curly braces. For instance, the set P, consisting of the first ten prime numbers, is P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}. You write 11 ∈ P to mean 11 is an element of P. The set that contains no elements is the empty set, denoted ∅. The number of elements in set A is its cardinality, denoted |A| (also, #A). For instance, if A = {2, 3, 5}, |A| = 3.
Two sets are equal if and only if they contain exactly the same elements, without regard to the order in which the elements are listed in the two sets or whether elements are repeated. For instance, {2, 3, 5} = {2, 5, 3} = {2, 2, 3, 3, 5, 5}.
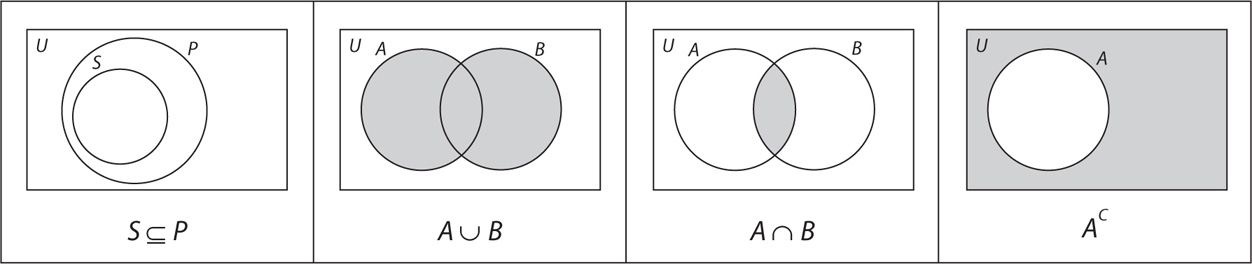
Set A is a subset of set B, written A ⊆ B, if every element of A is an element of B. For example, {2, 5} ⊆ {2, 3, 5}. In a discussion, the universal set (often denoted U) contains all the sets under consideration as subsets.
The union of two sets A and B, denoted A ∪ B, is the set of all elements that are in A or in B or in both. Tip: The word or in this definition is inclusive; that is, or means “one or the other, or possibly both at the same time.” For example, if A = {2, 3, 5} and B = {3, 5, 7, 11}, then A ∪ B = {2, 3, 5, 7, 11}. Tip: When you form the union of two sets, do not list an element more than once, because it is unnecessary to do so.
The intersection of two sets A and B, denoted A ∩ B, is the set of all elements that are common to both sets. For instance, if A = {2, 3, 5} and B = {3, 5, 7, 11}, then A ∩ B = {3, 5}.
Disjoint sets have no elements in common. Their intersection is the empty set. For instance, if A = {2, 3, 5} and C = {7, 11, 13, 17}, then A ∩ C = ∅ and A and C are disjoint.
The complement of set A, denoted AC (also,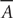 
or ~A), is the set of all elements in the universal set U that are not in A. For instance, if U = {1, 2, 3, 4, 5, 6, 7, 8, 9} and A = {2, 3, 5}, then AC = {1, 4, 6, 7, 8, 9}.
Venn diagrams visually depict set relationships. In a Venn diagram, circles represent sets—with the exception that the universal set is represented by a rectangular region, enclosing everything else in the diagram. Shading depicts the results of relationships. Here are examples.
The product rule for counting: For a sequence of k tasks, if a first task can be done in any one of n1 different ways, and for each of these ways, a subsequent second task can be done in any one of n2 different ways, and for each of these ways, a subsequent third task can be done in any one of n3 different ways, and so on to the kth task, which can be done in any one of nk different ways, then the total number of different ways the sequence of k tasks can be done is n1 × n2 × n3 × ··· × nk. Here are examples:
The number of 3-digit codes that are possible using the digits 1 through 5, if repetitions of digits are allowed, is 5 × 5 × 5 = 125 (because you have 5 ways to pick each of the 3 digits).
The number of 3-digit codes that are possible using the digits 1 through 5, if repetitions of digits are not allowed, is 5 × 4 × 3 = 60 (because once a particular digit is selected, it is no longer available to be picked).
The number of different ways to arrange the three letters in the word cat, if repetitions of letters is not allowed, is 3 × 2 × 1 = 6.
A permutation is an ordered arrangement of distinct objects in which repetition of objects is not allowed and different orderings of the same objects are counted as different outcomes. For instance, cat, cta, act, atc, tca, and tac are the six permutations of the letters in the word cat. For instance, cat and act are different permutations. Through a direct application of the product rule for counting, the number of permutations of n distinct objects is n!, where n! = (n)(n – 1)(n – 2) ··· (3)(2)(1). Read n! as “n factorial.”
A combination is an arrangement of distinct objects in which repetition of objects is not allowed and different orderings of the same items are considered to be the same arrangement. That is, when the order in which you make a selection for an arrangement of objects does not determine different outcomes, the arrangement is a combination of the objects. There is only one combination of n distinct objects because all the different ways you can arrange the n objects are not counted as different combinations. For example, there is only one combination of the three letters in the word cat. The six arrangements, cat, cta, act, atc, tca, and tac, are considered to be the same.
When you select r objects from n distinct objects without repetition, the number of combinations is nCr, where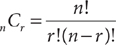 
. Tip: The notation nCr also is written as 
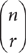. For example, the number of ways to put five people in pairs is
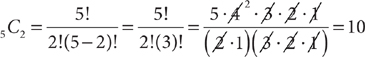
For combinations involving relatively small numbers like those given in this example, you might prefer to figure out the answer by listing the different combinations. Designate the people as A, B, C, D, and E. Then systematically list all of the 10 ways to match them two at a time: AB, AC, AD, AE, BC, BD, BE, CD, CE, and DE. Be careful when listing the combinations. You might overcount or undercount. Remember, AB and BA, AC and CA, and so forth are not different combinations. In general, using the combination formula saves time and is an accurate way to obtain the answer.
A random experiment is a chance process that gives a single result that cannot be determined beforehand. For example, tossing a standard six-sided die and observing the up face is a random experiment. Tip: A standard six-sided die is a balanced cube for which each of the six faces has one, two, three, four, five, or six dots on it.
An outcome is a single result from a random experiment. When you toss a standard six-sided die, the six possible outcomes are 1, 2, 3, 4, 5, or 6, where “1” means “one dot on the up face,” “2” means “two dots on the up face,” and so forth.
An event is a collection of one or more outcomes. For instance, when you toss a standard die, the event E that the die shows a number less than 3 consists of the outcomes 1 and 2. Tip: Uppercase letters represent events. The probability of an event is the likelihood the event will occur. Outcomes are equally likely if each outcome is as likely to occur as any other outcome. When you toss a standard die, 1, 2, 3, 4, 5, and 6 are equally likely outcomes.
An event is certain to occur if and only if the probability of the event is 1. For example, when you toss a standard six-sided die, the probability a whole number of dots will show on the up face is 1. An event is impossible if and only if the probability of the event is 0. For example, the probability the die will show seven dots on the up face is 0. The probability of any event is a number between 0 and 1, inclusive. Thus, the lowest probability you can have is 0, and the highest probability you can have is 1. All other probabilities fall between 0 and 1. The closer the probability of an event is to 1, the more likely the event is to occur; and the closer the probability of an event is to zero, the less likely the event is to occur.
A compound event is a combination of two or more events. The event A ∩ B (read as “A intersection B”) is the event consisting of all outcomes that A and B have in common. The event A ∪ B (read as “A union B”) is the event consisting of all outcomes that are in A only, B only, or in their intersection. Specifically, if an outcome is in A ∪ B, it is in at least one of the events A or B. The event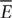 
(read as “complement of E”) is the set of outcomes that are not in E. It is the event that E does not occur. Tip: 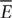is also known as the opposite of the event E. For example, suppose the possible outcomes for a random experiment are 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Let event A consist of outcomes 2, 3, 5, and 7, and event B consist of outcomes 3, 5, 7, 9. Then event A ∩ B consists of outcomes 3, 5, and 7; event A ∪ B consists of outcomes 2, 3, 5, 7, and 9; and event 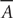consists of outcomes 1, 4, 6, 8, 9, 10.
Two events are mutually exclusive if they have no outcomes in common, meaning the two events are disjoint. They cannot occur at the same time. The occurrence of one prevents the occurrence of the other. For instance, when you toss a standard die, the event M that the die shows an even number (2, 4, or 6) and the event N that the die shows an odd number (1, 3, or 5) are mutually exclusive.
If all outcomes are equally likely, the probability of an event E, denoted P(E), is
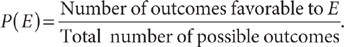
For example, for the die-tossing experiment, and the event E that the die shows a number less than 3,
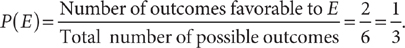
The probability of the complement of an event E is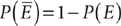 
; and, conversely, 
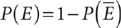. For example, if 
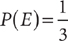, then 
.
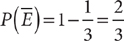For two events A and B, the event A ∪ B is the event that A occurs or B occurs or that both occur simultaneously on one trial of an experiment.
The Addition Rule states that P(A ∪ B) = P(A) + P(B) – P(A ∩ B). Tip: Keep in mind that this rule applies to one trial of an experiment. For example, given the following probabilities for tomorrow’s weather: P(rain) = 0.7, P(temperature below 32°F) = 0.3, and P(rain and temperature below 32°F) = 0.15, then P(rain or temperature below 32°F) = 0.7 + 0.3 – 0.15 = 0.85.
In many situations, you must calculate the probabilities used in the addition rule. For example, you toss a standard six-sided die one time. Let event A be the outcome is even, and event B be the outcome is greater than 4. Then:
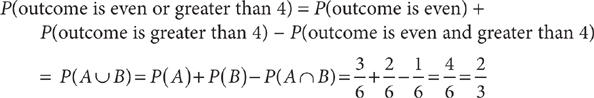
When you can determine the possible outcomes, an efficient way to find P(A ∪ B) is to sum the number of outcomes favorable to A and the number of outcomes favorable to B, being sure to add in such a way that no outcome is counted twice, and then divide by the total number of possible outcomes. Applying this strategy to the previous example, there are 3 outcomes that are even (namely, 2, 4, and 6) and 1 outcome greater than 4 that is not even (namely, 5). So, there are 3 + 1 = 4 distinct outcomes favorable to the event “outcome is even or greater than 4,” Thus, P(outcome is even or greater than 4)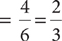 
.
When two events A and B are mutually exclusive, P(A ∩ B) = 0. So, for mutually exclusive events, P(A ∪ B) = P(A) + P(B). If you toss a standard six-sided die:
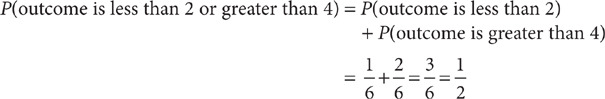
P(B | A) (read as “Probability B given A”) is the conditional probability of event B, given that event A has already occurred. For P(B | A), you must compute the probability of event B by taking into account that the event A has already occurred. For example, suppose that you randomly draw two marbles, one after the other, from a box containing 10 red marbles and 5 blue marbles. Then the probability of drawing a blue marble on the second draw given that a red marble was drawn without replacement on the first draw is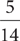 
(because after the red marble is drawn without replacement, there are 9 red marbles and 5 blue marbles in the box.) Tip: Without replacement means an object is NOT put back before the next object is selected. On the other hand, the probability of drawing a blue marble on the second draw given that a red marble was drawn with replacement on the first draw is 
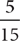(because after the red marble is drawn and then replaced, there are 10 red marbles and 5 blue marbles in the box.) Tip: With replacement means an object is put back before the next object is selected.
Two events A and B are independent if P(B) = P(B|A) and P(A) = P(A|B). In other words, A and B are independent if the occurrence of one does not affect the probability of the occurrence of the other. For instance, if you randomly draw two marbles, one after the other, from a box containing 10 red marbles and 5 blue marbles, the event of drawing a red marble with replacement on the first draw and the event of drawing a blue marble on the second draw are independent events. If events A and B are not independent, they are dependent. For example, if you randomly draw two marbles, one after the other, from a box containing 10 red marbles and 5 blue marbles, the event of drawing a red marble without replacement on the first draw and the event of drawing a blue marble on the second draw are dependent.
The multiplication rule says that for two events A and B, the probability that event A occurs on the first trial and event B occurs on the second trial of an experiment is P(A)P(B | A). This rule is used to find the probability of two events that occur in sequence. Tip: Keep in mind that this rule applies to two trials of an experiment. An efficient way to find the probability that event A occurs on the first trial and event B occurs on the second trial is to multiply the probability of event A times the probability of event B, where you have determined the probability of B by taking into account that the event A has already occurred. For example, suppose you draw two marbles, one after the other, without looking, from a box containing 10 red marbles and 5 blue marbles. Tip: A draw “without looking” is a random selection. The probability of drawing a red marble on the first draw without replacement and a blue marble on the second draw is
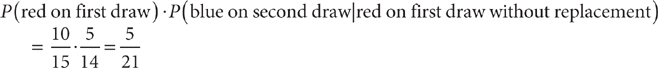
When two events A and B are independent, the probability that event A occurs on the first trial and event B occurs on the second trial of an experiment is P(A) P(B). For example, the probability of getting two heads on two flips of a coin is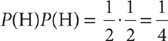 
(because each flip of the coin is independent of the other).
For the GMAT, be prepared to read and interpret information from frequency or relative frequency tables, pictographs, circle graphs, dot plots, stem-and-leaf plots, line graphs, bar graphs, and histograms.
A frequency table shows the frequency of each value in the data set. A relative frequency table shows the frequency as a proportion or percentage of the whole data set. Here is an example.
Exam 1 Grade Distribution of 20 Students
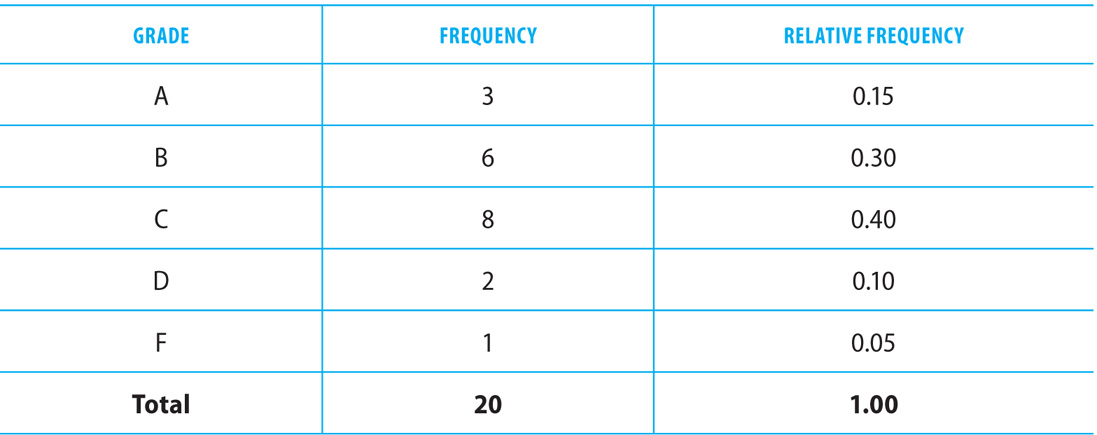
According to the table, 0.40 + 0.30 + 0.15 = 0.85 or 85% of the students made a C or better on Exam 1.
A pictograph represents data with symbols (or images). Each symbol, its meaning, and the quantity it represents are given on the graph. To read a pictograph, multiply the number of symbols in a row by the quantity it represents. If a fraction of a symbol is shown, approximate the fraction and use it accordingly. Here is an example.
Responses of 200 Women to the Question “Do You Have a Sibling?”
According to the graph, 15 × 10 = 150 women responded “Yes” to the survey question.
A circle graph (or pie chart) displays the relationships of different categories of data as portions of a whole, represented by a circle. The portions are labeled to show the categories for the graph. Percentages show the amount of the graph that corresponds to each category. Here is an example.
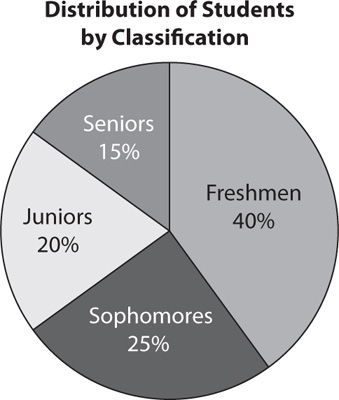
According to the graph 40% + 25% = 65% of the students are freshmen or sophomores.
A dot plot (or line plot) shows the frequency of data values on a number line. Dots (or other similar symbols) are placed above each value corresponding to the number of times that particular value occurs in the data set. Tip: A useful feature of dot plots is that they show all the data values. Here is an example.
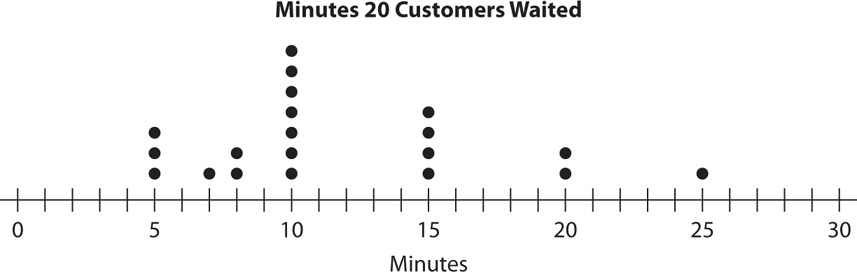
The dot plot shows three customers waited more than 15 minutes.
A stem-and-leaf plot visually displays data values, separated into two parts: a stem and a leaf. For a particular data value, the leaf is usually the last digit, and the stem is the remaining digits. A legend explains what is represented by the stem and leaf so that the reader can interpret the information in the plot; for example, 5|7 = 57. Tip: A feature of a stem-and-leaf plot is that the original data are retained and displayed in the plot. Here is an example.
According to the graph, five presidents were 54 years of age at the time of their inauguration.
A line graph shows plotted points that represent data. Consecutive points are connected with line segments. The slant of the line between points shows trends in the data. A line that slants upward from left to right indicates an increase. A line that slants downward from left to right indicates a decrease. A horizontal line (no slant) means the data remain constant. Line graphs are commonly used to show change over time. Here is an example.
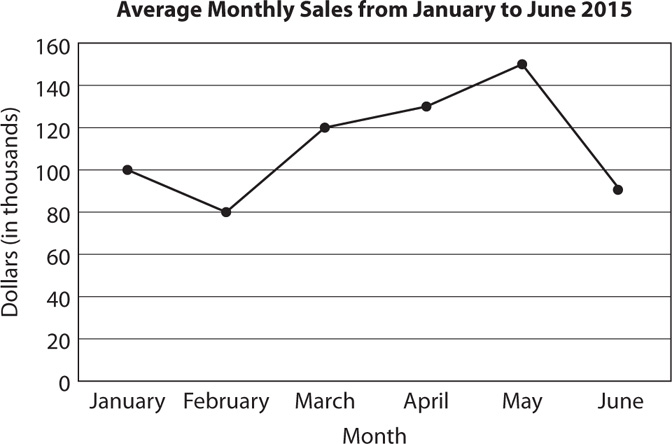
The line graph shows an upward trend in average monthly sales from February to May.
A bar graph uses rectangular bars to represent frequencies, percentages, or amounts. The bars represent different categories that are labeled at the base of the bars. To read a bar graph, examine the scale to determine the units and the amount corresponding to each category. Here is an example.
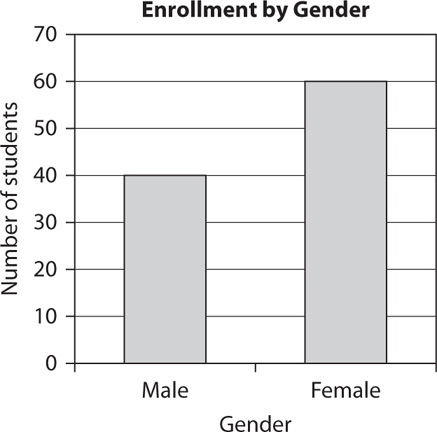
According to the graph, 40 males and 60 females are enrolled.
A histogram summarizes data by displaying frequencies or relative frequencies of the data within intervals. The intervals are of equal length and cover from the lowest to the highest data value. The left and right endpoints for the intervals are selected so that each data value clearly falls within one and only one interval. The frequency or relative frequency of occurrence of the data values within an interval is represented by a rectangular (or vertical) column. The bars in a histogram are side by side (usually) with no space in between. Here is an example.
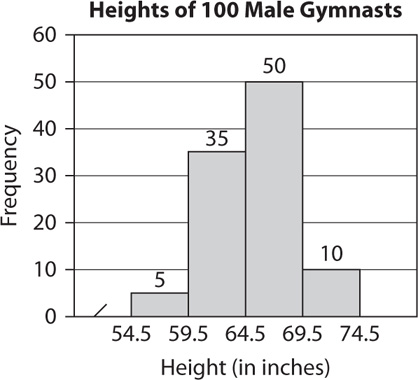
The mean of a data set is the arithmetic average of the data values:
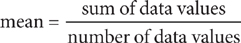
For example, the mean of 25, 43, 40, 60, and 12 is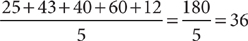 
.
The median is the middle value or the arithmetic average of the two middle values in an ordered set of data. Fifty percent of the data values fall at or below the median and 50% fall at or above the median. To find the median, put the data values in order from least to greatest (or greatest to least), and then locate the middle value. If there is no single middle value, compute the average of the two middle values. For example, after putting the data values in order, the median of 12, 25, 40, 43, 60 is 40. For –7, –7, 1, 8, 16, 22, the median is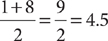 
. Tip: When finding a median, remember to put the numbers in order first.
In an ordered data set of n values, the median is in the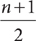 
position. For example, in the dot plot shown, the median is in the 
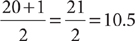position, meaning it is halfway between the 10th and 11th data values.
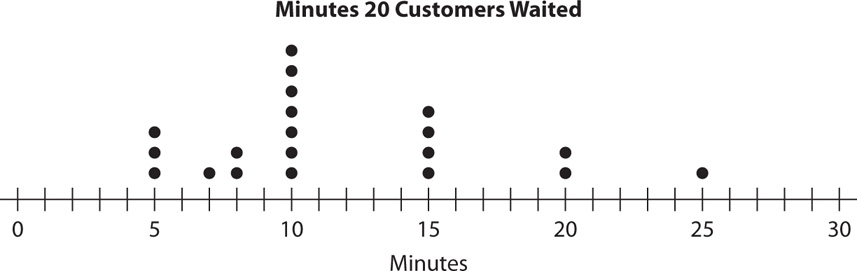
The 10th and 11th data values are both 10 minutes, so the median for the data shown in the dot plot is 10 minutes.
The mode is the data value (or values) that occurs with the greatest frequency in a data set. For example, the mode of 30, 40, 50, 50, 60, and 70 is 50. Tip: A data set in which each data value occurs the same number of times has no mode.
The range gives the spread between the greatest and least values of the data set. It is the difference between the maximum value and the minimum value in the data set. Thus, range = maximum value – minimum value. For example, the range of 6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, and 8.5 is 9.3 – 6.7 = 2.6.
The mean absolute deviation (MAD) quantifies the degree to which the data values vary from their mean. It is the average distance between each data value and the mean of the data values. The MAD for 30, 40, 50, 60, and 70 (which has a mean of 50) is
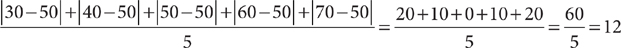
Like the MAD, the variance and standard deviation are measures of the variability of a set of data values about the mean. If there is no variability in a data set, each data value equals the mean, so both the variance and standard deviation for the data set are zero. The more the data values vary from the mean, the greater are the variance and standard deviation.
You compute the variance by subtracting the mean from each data value, squaring each difference, and then summing up the squared differences and dividing by the number, n, of data values. The standard deviation is the square root of the variance. Note: When the data set is a sample from a population, you divide by n – 1 instead of n. Questions about variance or standard deviation on the GMAT might require you to examine two (or more) data sets with equal means and decide which has the greater (or lesser) variance or standard deviation. For example, the data set 30, 40, 50, 60, and 70 (which has a mean of 50) has a greater variance and standard deviation than does the data set 35, 47, 50, 53, 65 (which also has a mean of 50). The data in the second data set are clustered more tightly around the mean.
Directions: Select the best answer choice.
1. Which expression is equivalent to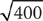 
?
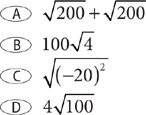
200
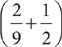
2. Which fraction, when added to the previous sum, yields a sum of 0?
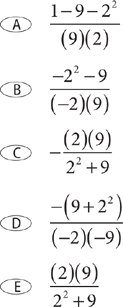
3. What is the tens digit in the dividend of the problem shown?
3
4
5
6
7
4. Given that x is a positive integer such that 19 divided by x has a remainder of 3, what is the sum of all the possible values of x?
12
20
24
28
32
5. Suppose n is an integer such that 2 < n2 < 100. If the units digit of n2 is 6 and the units digit of (n–1)2 is 5, what is the units digit of (n+1)2?
2
4
6
8
9
6. If the square root of the product of two positive integers is 15, which number CANNOT be the sum of the two integers?
34
42
50
78
226
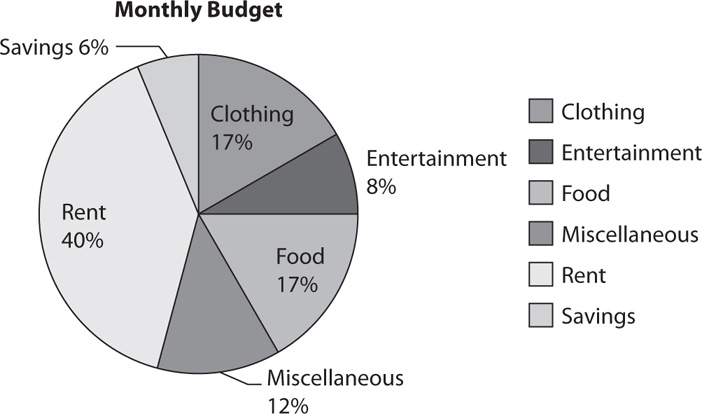
7. The preceding circle graph displays a budget for a monthly income of $3,500 (after taxes). According to the graph, how much more money is budgeted for rent than for food and clothing combined?
$60
$210
$595
$1,190
$1,400
8. The preceding line graph depicts the monthly sales from January to June for a small business. What is the greatest amount that the monthly sales in January could increase without changing the median?
$20,000 increase
$40,000 increase
$100,000 increase
Any amount increase
January sales cannot increase without changing the median.
9. How many different meal combinations consisting of one sandwich, one drink, and one type of chips are possible from a selection of eight types of sandwiches, five types of drinks, and seven types of chips?
280
140
40
35
20
10. In a video game, a player is faced with the task of moving from point A to point B to point C, and then returning from point C to point A through point B without retracing any path. There are 5 paths from point A to point B, and 8 paths from point B to point C. In how many different ways can the player accomplish the task?
2,240
1,600
1,120
68
24
11. Five people are to be seated in five identical chairs placed in a circle. How many different arrangements of the five people (relative to one another) in the five chairs are possible?
256
128
48
24
6
12. A box contains 7 black marbles, 6 green marbles, and 10 red marbles, all identical except for color. What is the probability of drawing a black or red marble when a single marble is drawn at random from the box?
13. A quiz consists of 5 multiple-choice questions, each of which has 4 possible answer choices (A, B, C, and D), one of which is correct. Suppose that an unprepared student does not read the questions but simply makes a random guess for each question. What is the probability that the student will guess correctly on at least one question?
14. Suppose you randomly draw two marbles, successively without replacement, from a box containing 8 red marbles and 6 blue marbles. What is the probability of drawing a blue marble on the second draw, given that you drew a red marble on the first draw? (Assume the marbles are identical except for color.)
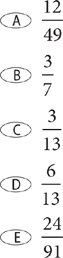
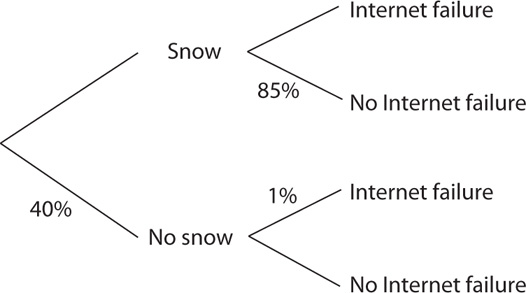
15. The preceding probability diagram represents the incidence of Internet failure during weather in which snow might occur. What is the probability that it snows and an Internet failure occurs?
0.4%
9%
39.6%
51%
60%
16. The residence status, by sex, of 250 senior students at a community college is shown in the preceding table. If one of the 250 students is randomly selected, what is the probability that the student resides on campus, given that the student selected is a male student? Express your answer as a decimal rounded to two places.
0.15
0.34
0.42
0.51
0.66
17. A real estate agent has determined probabilities for two neighboring houses, one of which is a model home. The probability that the model home will be sold is 0.60; the probability that the house next door will be sold is 0.50; and the probability that both houses will be sold is 0.40. Find the probability that at least one of the two houses will be sold.
30%
40%
50%
60%
70%
Questions 18 to 25 each presents a question and two statements, labeled (1) and (2), in which certain data are given. Using your knowledge of mathematics and everyday facts (such as the number of minutes in an hour or the meaning of the word perpendicular), decide whether the given data are sufficient to answer the question. Then select one of the answer choices that follow.
2, a2, …, 247
18. Suppose m is an integer such that 2 < m < 10. What is the units digit of m2?
(1) The units digit of (m + 1)2 is 4.
(2) The units digit of (m – 1)2 is 6.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. On the shelf of a flower shop are n vases, some of which contain 8 flowers and some of which contain 10 flowers. How many vases contain 10 flowers?
(1) The total number of flowers is 136.
(2) n = 15
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. Is xp a negative number?
(1) x < 0
(2) p < 0
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
21. Seth is studying for his fourth 100-point test in an economics class. What score must he earn on this test to have an average (mean) of 90 for the four tests?
(1) Seth has the following scores on the first three tests: 77, 91, and 94.
(2) The average of Seth’s scores on the first and third tests is 85.5.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
22. Set A consists of 20 numbers ranging from 1 to 10. Set B consists of 20 numbers ranging from 11 to 20. What is the average (arithmetic mean) of the 40 numbers in sets A and B combined?
(1) The average of the numbers in Set A is 6.7.
(2) the average of the numbers in Set B is 17.3.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
23. Is a > 58?
(1) 57 < a < 59
(2) 
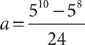
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
24. If a is an element of the set {12, 13, 15, 16, 18, 19, 21, 22}, what is the value of a?
(1) a is a multiple of 3.
(2) a is even.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
25. What is the average of a, b, and c?
(1) 2a + 3b + 5c = 42
(2) 4a + 3b + c = 30
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. C Choice C is the correct response because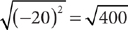 
.
2. D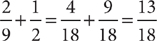 
, so look for an answer choice that equals 
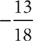. You can eliminate B and E because the quantities in these choices are positive. Check the remaining choices. For choice A, 
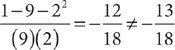, so eliminate A. For C, 
, so eliminate C. Choice D is correct because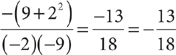 
.
3. D 35×7 = 245, and 245 + 20 = 265, so the tens digit of the dividend is 6.
4. D You must find all the positive integers that leave a remainder of 3 when you divide 19 by the integer. These integers are 4, 8, and 16, the sum of which is 28.
5. E The squares between 2 and 100 that have units digit 6 are 16 and 36, so n is either 4 or 6. Suppose n is 4; then 9 is the units digit of (n – 1)2 = 32 = 9. Thus, n is not 4. If n is 6, 5 is the units digit of (n – 1)2 = 52 = 25. The units digit of (n – 1)2 = 72 = 49 is 9.
6. B Let m and n be the two positive integers. Then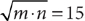 
, so m · n = 225. The positive factors of 225 are 1, 3, 5, 9, 15, 25, 45, 75, and 225. The possible two-factor combinations for m and n are 1 and 225, 3 and 75, 5 and 45, 9 and 25, and 15 and 15. The possible sums for the two-factor combinations are 226, 78, 50, 34, and 30, which makes choice B the correct response.
7. B The percent budgeted for rent is 40%. The percent budgeted for food and clothing combined is 17% + 17% = 34%. The percentage difference is 40% – 34% = 6%. Apply this percentage to find the difference in dollars: 6% of $3,500 = 0.06($3,500) = $210 more budgeted for rent than for food and clothing combined. Tip: Rather than working with the percentages first, you can obtain the same answer by computing the money amounts for each category first and then subtracting the amounts budgeted for food and clothing from the amount budgeted for rent.
8. D According to the line graph, monthly sales were $140,000 in January, $100,000 in February, $120,000 in March, $60,000 in April, $140,000 in May, and $120,000 in June. No computations are necessary for answering this question. The monthly revenues in January and May are the highest values shown on the graph. The median is the middle value, so it is not affected when one of these data values increases. In other words, the monthly revenue in January could increase by any amount without changing the median.
9. A The number of possible different meals is 8·5·7 = 280.
10. C There are 5 ways to go from A to B, 8 ways to go from B to C, 7 ways to go from C to B without retracing a path, and 4 ways to go from B to A without retracing a path. Therefore, the task can be accomplished in a total of 5·8·7·4 = 1,120 ways.
11. D For convenience, label the five people as P1, P2, P3, P4, and P5. The people are not assigned to particular seats but are only arranged relative to one another. Hence, the position of P1 is immaterial. What counts are the positions of the other four people relative to P1. Therefore, keeping P1 fixed, there are 4 × 3 × 2 × 1 = 24 different ways to arrange the other four people, so there are 24 different arrangements of the five people in a circle.
12. E There are 17 favorable outcomes (7 black marbles plus 10 red marbles) out of 23 total outcomes. Thus, P(black or red) =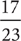 
.
13. D For any one question, there are 3 wrong answer choices out of 4 total answer choices, so the probability of guessing wrong on a particular question is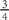 
. Because the student is randomly guessing, each guess on a question is independent of the guesses on the other questions, so the probability of getting all five questions wrong is the product of the probabilities for each question: P(none correct) 
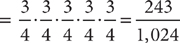. Therefore, the probability of at least one correct is 1 – P(none correct) 
.
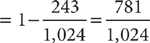14. D After a red marble is drawn and not replaced, 7 red marbles and 6 blue marbles are left in the box. Thus, the probability of drawing blue on the second draw is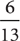 
.
15. B Fill in the missing probabilities.
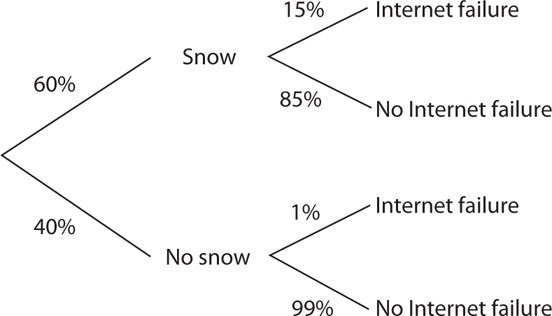
The probability that it snows and an Internet failure occurs is (60%)(15%) = 9%.
16. B Complete the table by filling in the row and column totals.
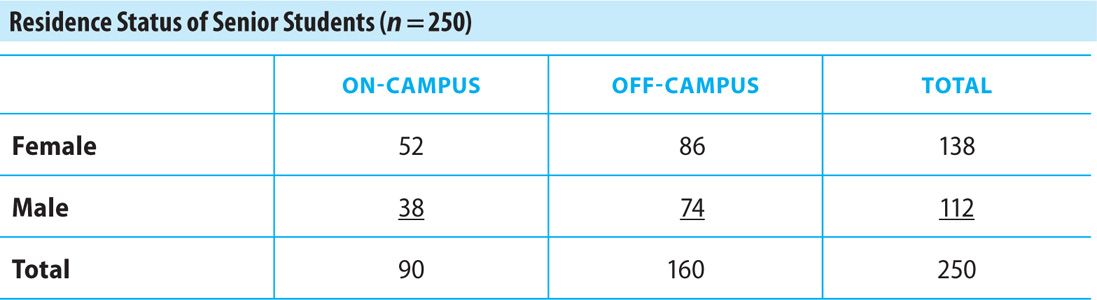
It’s given the student is male. The table shows that 38 of the 112 male students reside on campus. Thus, the probability that a randomly selected student resides on campus, given the student is male, is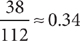 
.
17. E Let A = the event that the model home will be sold, and let B = the event that the house next door will be sold. Then P(A) = 0.60, P(B) = 0.50, and P(A ∩ B) = 0.40. The probability that at least one of the two houses will be sold is P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.60 + 0.50 – 0.40 = 0.70.
18. A From the question, you know that m is 3, 4, 5, 6, 7, 8, or 9. From the information in (1), m is 7 because the units digit of (7 + 1)2 is 4 because (82 = 64). None of the other possible values for m have this property, so (1) is sufficient. From the information in (2), m is either 5 or 7, not a single value, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
19. C Let x = the number of vases with 10 flowers and n – x = the number of vases with 8 flowers. Thus, the total number of flowers is 10x + 8(n – x) = 10x + 8n – 8x = 2x + 8n. With this equation, if you know the total number of flowers and the value of n, you can find the value of x. From the information in (1), 2x + 8n = 136, but the value of n is needed to determine x, so (1) is NOT sufficient. From the information in (2), n = 15, but the total number of flowers is needed to determine x, so (2) is NOT sufficient. Taking (1) and (2) together, 2x + 8(15) = 136, which you can solve for a single value of x. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
20. E If, as given in statement (1), x < 0, then xp is positive if p is even and negative if p is odd. For instance, if x = –1 and p = 2, xp = (–1)2 = 1 > 0, and if x = –1 and p = 1, xp = (–1)1 = –1 > 0. Thus, further information is needed, and (1) is NOT sufficient. If, as given in (2), p < 0, then the sign of xp cannot be determined without knowing whether x is positive or negative and whether p is odd or even. For instance, if x = –1 and p = –2, then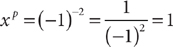 
, but if x =–1 and p =–3, then 
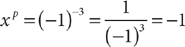. Therefore, (2) is NOT sufficient. Taking (1) and (2) together with x < 0 and p < 0, the sign of xp cannot be determined without knowing whether p is odd or even. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
21. A Let x = the required score for the fourth test. From the information in (1), you can write the equation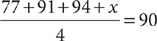 
and solve for a single value of x. Therefore, (1) is sufficient. From the information in (2), you can determine that the sum of the first and third tests is 2(85.5)= 171, but without knowing the score on the second test, you cannot determine x, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
22. C From the information in (1), you know the average of the 20 numbers in set A, but without further information about set B, the combined average cannot be determined, so (1) is NOT sufficient. From the information in (2), you know the average of the 20 numbers in set B, but without further information about set A, the combined average cannot be determined, so (2) is NOT sufficient. Taking (1) and (2) together, because there are equal numbers in each set, the average of the 40 numbers combined is the sum of the two averages divided by 2, which you can compute. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
23. B From the information in (1), a is any number between 57 and 59, but without further information, you cannot determine whether a > 58. So, statement (1) is NOT sufficient. From (2)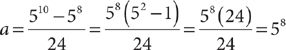 
. So (2) is sufficient to give a definite “No” to the question posed. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
24. E From the information in (1), a is 12, 15, 18, or 21. From the information in (2), a is 12, 16, 18, or 22. Neither provides a single value, so neither is sufficient. Taking (1) and (2) together, a is 12 or 18, again not a single value. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
25. C The average is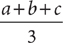 
. Tip: Notice that to answer the question, you do not need the specific values of a, b, and c. You need only the value of their sum, a + b + c. You cannot determine 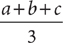from the equation in (1), because you cannot solve for the three variables or their sum, so (1) is NOT sufficient. You also cannot determine 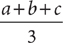from the equation in (2). Therefore, (2) also is NOT sufficient. Taking (1) and (2) together and adding the two equations yields the equation 6a + 6b + 6c = 72, which simplifies to a + b + c = 12. Then 
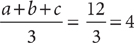. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
