Congruence and similarity
Angles
Lines
Polygons
Triangles
Quadrilaterals
Circles
Geometric solids
Perimeter, area, surface area, and volume
Pythagorean theorem
Coordinate geometry
This geometry review includes the following topics:
Congruence and similarity
Angles
Lines
Polygons
Triangles
Quadrilaterals
Circles
Geometric solids
Perimeter, area, surface area, and volume
Pythagorean theorem
Coordinate geometry
Congruent geometric figures have the same size and same shape. They will fit exactly on top of each other. The symbol @ denotes congruence.
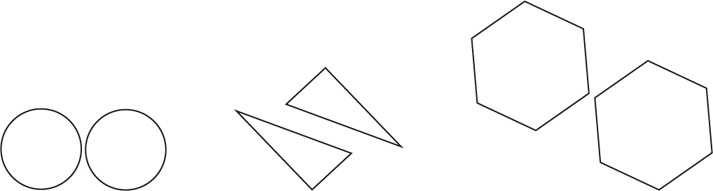
Corresponding parts of congruent figures are congruent.
Congruent triangles are triangles for which corresponding sides and corresponding angles are congruent. In the figure shown, triangles ABC and DEF are congruent. Hash marks identify the congruent parts.
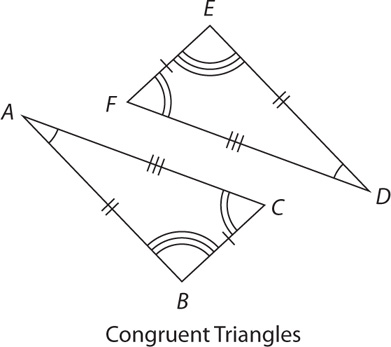
Two triangles are congruent in the following situations.
Side-Side-Side (SSS): If three sides of one triangle are congruent, correspondingly, to three sides of the other triangle.
Side-Angle-Side (SAS): If two sides and the included angle of one triangle are congruent, correspondingly, to two sides and the included angle of the other triangle.
Angle-Side-Angle (ASA): If two angles and the included side of one triangle are congruent, correspondingly, to two angles and the included side of the other triangle.
Angle-Angle-Side (AAS): If two angles and the nonincluded side of one triangle are congruent, correspondingly, to two angles and the nonincluded side of the other triangle.
Similar geometric figures have the same shape, but not necessarily the same size. The symbol ~ denotes similarity.
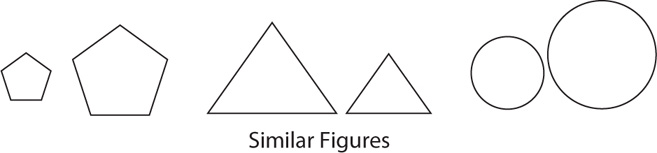
Corresponding angles of similar shapes are congruent. Corresponding lengths of similar shapes are proportional. That is, the ratios of the lengths are equal.
The ratio of the areas of two similar figures is the square of the ratio of the lengths of any two corresponding sides. For instance, if corresponding sides of two squares are in the ratio 4 to 1, then the ratio of the area of the larger square to the area of the smaller square is 42 to 12, or 16 to 1.
Angles are measured in degrees. One degree (°) is 
of a complete rotation around a circle.
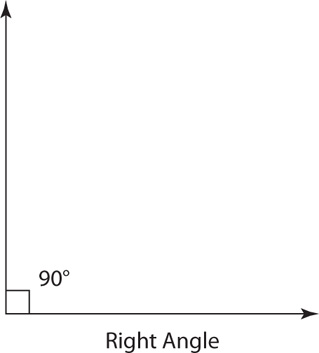
A right angle measures exactly 90°.
An acute angle measures greater than 0°, but less than 90°.
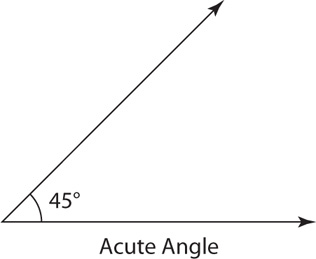
An obtuse angle measures greater than 90°, but less than 180°.
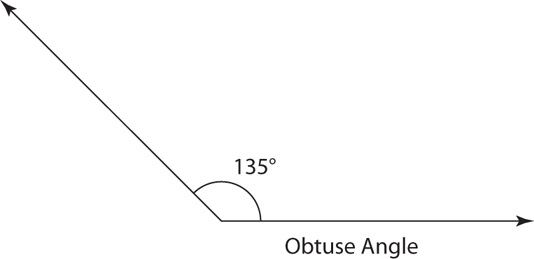
A straight angle measures exactly 180°.
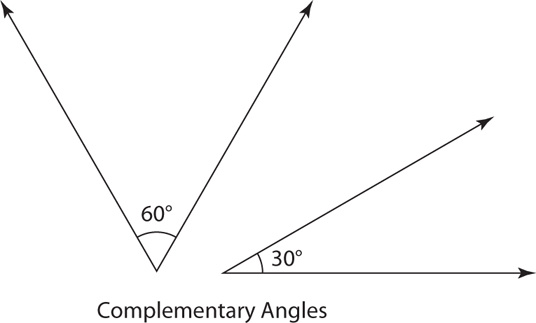
Two angles whose sum is 90° are complementary angles. Each is the other’s complement.
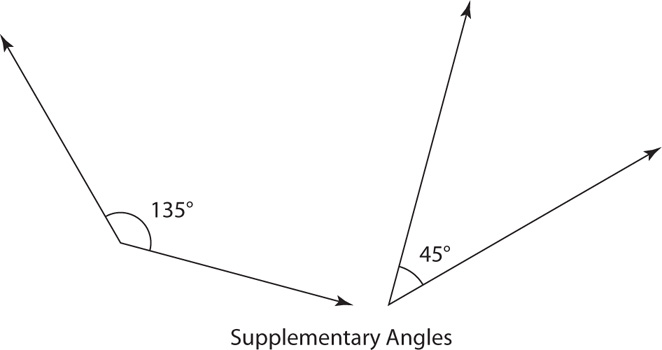
Two angles whose sum is 180° are supplementary angles. Each is the other’s supplement.
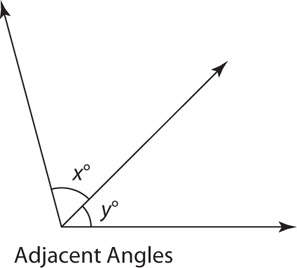
Adjacent angles are two angles that have a common vertex and a common side, with no overlap.
Vertical angles are two nonadjacent angles formed by two intersecting lines. Tip: Two intersecting lines form four angles.
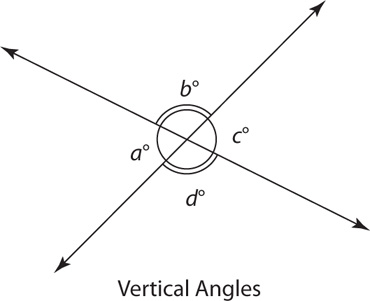
Vertical angles formed by two intersecting lines are congruent and thus have the same measure. In the figure shown, a° = c° and b° = d°.
Lines in the same plane can be parallel or intersecting. In geometry, plane is an undefined term. Intuitively, a plane is a two-dimensional, infinite surface. Intersecting lines cross at a point in the plane. Parallel lines never intersect. The distance between them is always the same. Perpendicular lines intersect at right angles. Here are examples.
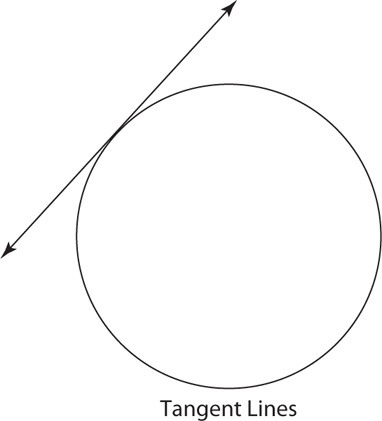
A tangent line to a circle intersects the circle in exactly one point.
The notation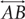 
stands for the line containing the points A and B and extending infinitely in both directions. To indicate 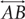is parallel to 
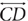, write 
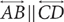. To indicate 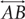is perpendicular to 
, write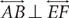 
.
The line segment is a part of a line connecting the points A and B and includes A and B. The points A and B are its endpoints. Its length is AB. Congruent segments have equal lengths.
The shortest distance from a point to a line is the perpendicular distance from the point to the line.
Two (distinct) lines that are perpendicular to the same line are parallel.
A line that is perpendicular to one of two parallel lines is perpendicular to the other one too.
A radius drawn to the point where a tangent line meets a circle is perpendicular to the tangent at that exact point.
A polygon is a simple, closed plane figure composed of sides that are straight line segments that meet only at their endpoints. The point at which the two sides of a polygon intersect is a vertex. A diagonal is a line segment that connects two nonconsecutive vertices.
Polygons are named by the number of sides they have. A triangle is a three-sided polygon. A quadrilateral is a four-sided polygon. A pentagon is a five-sided polygon. A hexagon is a six-sided polygon. A heptagon is a seven-sided polygon. An octagon is an eight-sided polygon. Other polygons with additional sides have special names as well. However, eventually, at a high number of sides, you simply speak of the polygon as an n-gon. A regular polygon has all sides and angles congruent.
An n-sided polygon has n interior angles and n exterior angles. The sum of the measures of its interior angles is (n – 2)180°. The sum of the measures of its exterior angles is 360°, no matter how many sides the polygon has.
An equilateral triangle has three congruent sides. An isosceles triangle has at least two congruent sides. A scalene triangle has no congruent sides.
An acute triangle has three acute angles. A right triangle has exactly one right angle.
An obtuse triangle has exactly one obtuse angle.
The triangle inequality holds that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Basically, for a triangle to exist, the longest side must be shorter than the sum of the other two sides. For example, 3, 8, and 10 can be the lengths of the sides of a triangle because 3 + 8 = 11, which is greater than 10, the longest side. But 2, 5, and 8 cannot be the lengths of the sides of a triangle, because 2 + 5 = 7, which is less than 8, the longest side.
If two sides of a triangle are congruent, then the angles opposite those sides are congruent (that is, base angles of an isosceles triangle are congruent); and, conversely, if two angles of a triangle are congruent, then the sides opposite those angles are congruent. In the figure shown, 
implies 
; and 
implies 
.
If two sides of a triangle are unequal in length, the measures of the angles opposite the two sides are unequal and the angle opposite the greater side is the greater angle.
If two angles of a triangle are unequal in measure, the lengths of the sides opposite the two angles are unequal and the side opposite the greater angle is the greater side.
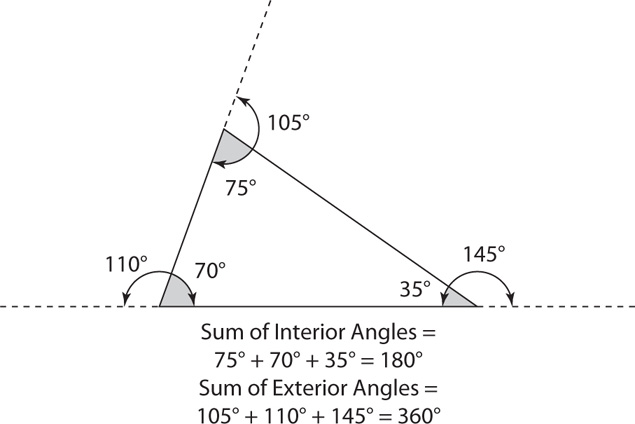
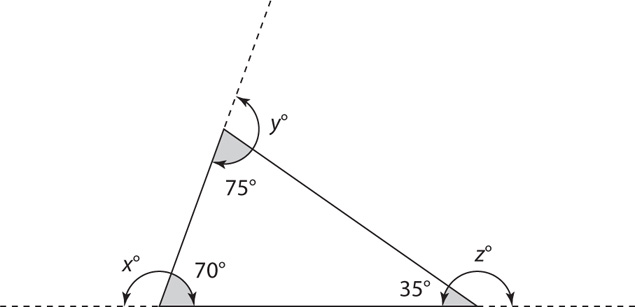
The measure of an exterior angle of a triangle equals the sum of the measures of the remote (nonadjacent) interior angles. For example, in the triangle shown below, x° = 75° + 35° = 110°, y° = 70° + 35° = 105°, and z° = 70° + 75° = 145°.
A median of a triangle is a line segment from a vertex of the triangle to the midpoint of the opposite side.
The medians of a triangle meet in a point that is 
of the way along each median, from the vertex to the opposite side.
In a right triangle, the median to the hypotenuse is one-half the length of the hypotenuse.
The line segment between the midpoints of two sides of a triangle is parallel to the third side and half as long.
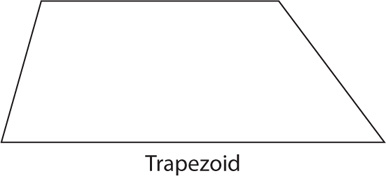
A trapezoid is a quadrilateral that has at least one pair of parallel sides.
A parallelogram is a quadrilateral whose opposite sides are parallel and congruent.
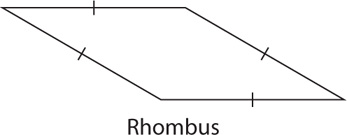
A rhombus is a parallelogram that has four congruent sides.
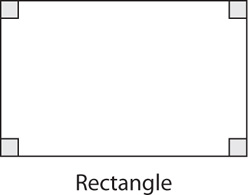
A rectangle is a parallelogram that has four interior right angles.
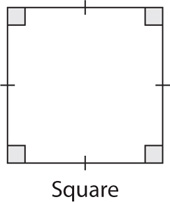
A square is a parallelogram that has four interior right angles and four congruent sides. It is a rectangle that has four congruent sides. You also might say that it is a rhombus that has four interior right angles.
If a quadrilateral’s diagonals bisect each other, the quadrilateral is a parallelogram.
If a quadrilateral has two sides that are parallel and congruent, the quadrilateral is a parallelogram.
The diagonals of a rectangle or square are congruent.
The diagonals of a rhombus or square are perpendicular to each other.
If a quadrilateral’s diagonals are perpendicular bisectors of each other, the quadrilateral is a rhombus.
A parallelogram that has one interior right angle has four interior right angles and is a rectangle.
Consecutive angles of a parallelogram are supplementary.
A circle is a closed plane figure for which all points are the same distance from the center within the circle.
A circle’s radius is a line segment joining the center of the circle to any point on the circle.
A circle’s diameter is a line segment through the center of the circle with endpoints on the circle. The diameter of a circle is twice the radius. Equivalently, the radius of a circle is half the diameter.
A chord of a circle is a line segment whose endpoints lie on the circle.
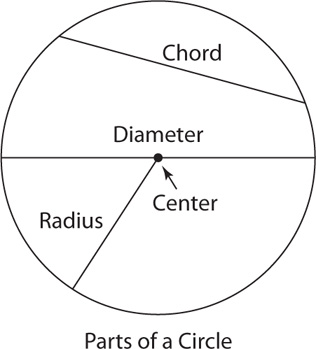
If a radius is drawn so that it is perpendicular to a chord, it bisects the chord.
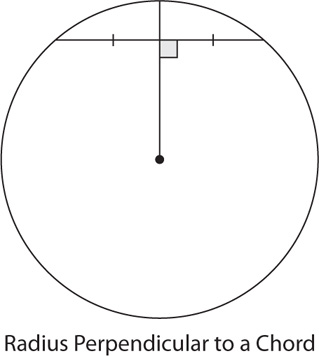
An angle inscribed in a semicircle is a right angle.
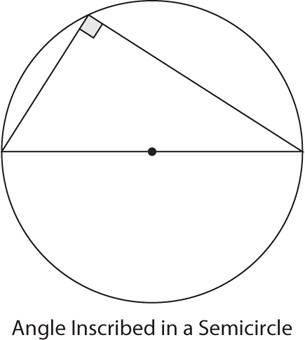
If two chords intersect within a circle, the product of the lengths of the segments formed for one chord equals the product of the lengths of the segments formed for the other chord.
A prism is a solid with two congruent, parallel bases. A prism’s lateral faces are parallelograms. (A lateral face is a side face.) In a right prism, the two bases are directly above each other and the lateral faces are rectangles. The bases of a prism can have the shape of any polygon. Prisms are named according to the shape of their bases. A cube is a right rectangular prism that has six congruent faces, all of which are squares. Here is an example.
A pyramid is a solid with exactly one polygon-shaped base. A pyramid’s lateral faces are triangles that meet at a point, called the apex. In a right pyramid, the apex is directly above the center of the base. The base can have the shape of any polygon. Pyramids are named according to the shape of their bases. Here is an example.
A cylinder has two parallel congruent bases, which are circles. In a right cylinder, the two bases are directly above each other. A rectangular side wraps around and connects the two bases.
A cone is a three-dimensional solid that has one circular base and a single apex. In a right cone, the apex is directly above the center of the base. A curved side wraps around to form the cone.
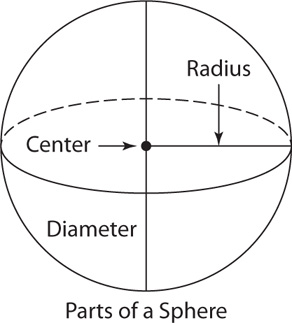
A sphere is a three-dimensional solid that is shaped like a ball. Every point on its surface is the same distance from the center within the sphere. The sphere’s radius is a line segment from the center of the sphere to any point on the sphere. The sphere’s diameter is a line segment joining two points of the sphere and passing through its center. The radius of the sphere is half the diameter. Equivalently, the diameter is twice the radius.
The perimeter of a simple, closed plane figure is the distance around it. Perimeter is measured in units of length such as inches (in), feet (ft), miles (mi), centimeters (cm), or meters (m).
The perimeter of a triangle is the sum of its three sides.
The perimeter, P, of a triangle that has sides of lengths 6 inches, 8 inches, and 10 inches is P = 6 in + 8 in + 10 in = 24 inches.
The perimeter of a quadrilateral is the sum of its four sides.
The perimeter, P, of a trapezoid that has sides of lengths 4 meters, 8 meters, 5 meters, and 10 meters is P = 4 m + 8 m + 5 m + 10 m = 27 meters.
The perimeter of a parallelogram is P = 2a + 2b = 2(a + b), where a is the length of one of the congruent sides and b is the length of one of the congruent bases.
The perimeter of a parallelogram that has congruent sides of length 14 feet and congruent bases of length 23 feet is P = 2(14 ft + 23 ft) = 74 feet.
The perimeter of a rectangle is P = 2l + 2w = 2(l + w), where l is its length and w is its width.
The perimeter of a rectangle that has length of 8 meters and width of 5 meters is P = 2(8 m + 5 m) = 26 meters.
The perimeter of a square is P = 4s, where s is the length of one of its sides.
The perimeter of a square whose sides are 12 centimeters is P = 4(12 cm) = 48 centimeters.
The perimeter of a circle is its circumference. The circumference of a circle is C = πd = 2πr, where d and r are the circle’s diameter and radius, respectively.
To the nearest inch, the circumference of a circle that has diameter 16 inches is C = π(16 in) ≈ (3.14)(16 in) ≈ 50 inches.
The area of a closed plane figure is the amount of surface enclosed by the boundary of the figure. Area is measured in square units such as square inches (in2), square feet (ft2), square miles (mi2), square centimeters (cm2), and square meters (m2).
The area of a triangle is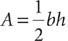 
, where b is the length of a base of the triangle, and h is the height for that base.
The area of a triangle that has a base of 8 inches and a height of 6 inches is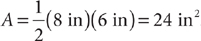 
.
The area of an equilateral triangle is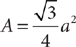 
, where a is the length of a side.
The area of an equilateral triangle that has sides of length 20 centimeters 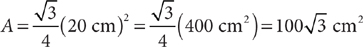is 
.
The area of a trapezoid is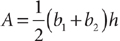 
, where b1 and b2 are the lengths of its bases and h is the perpendicular distance between the two bases.
The area of a trapezoid that has bases of 7 meters and 12 meters and a height of 4 meters i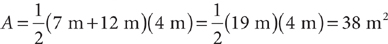s 
.
The area of a parallelogram is A = bh, where b is a base of the parallelogram and h is the perpendicular distance between the two bases.
The area of a parallelogram that has a base of 15 feet and a height of 8 feet is A = (15 ft) × (8 ft) = 120 ft2.
The area of a rectangle is A = lw, where l is its length and w is its width.
The area of a rectangle that has length of 25 meters and width of 7 meters is A = (25 m) × (7 m) = 175 m2.
The area of a square is A = s2, where s is the length of one of its sides.
The area of a square whose sides are 12 centimeters is A = (12 cm)2 = 144 cm2.
The area of a circle is A = πr2, where r is the circle’s radius.
To the nearest square inch, the area of a circle that has a radius of 8 inches is A = π(8 in)2 = π(64 in2) π (3.14)(64 in2) π 201 in2.
The surface area (SA) of a three-dimensional closed figure is the total area of its surface.
The surface area of a prism or pyramid is the sum of the areas of all faces of the figure.
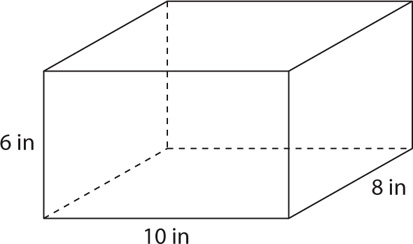
The surface area of the right rectangular prism (box) shown below is SA = 2(10 in)(8 in) + 2(10 in)(6 in) + 2(8 in)(6 in) = 160 in2 + 120 in2 + 96 in2 = 376 in2.
The surface area of a right cylinder is SA = 2(πr2) + (2πr)h, where r is the radius of one of the cylinder’s congruent bases and h is the perpendicular distance between the two bases.
The approximate surface area of a right cylinder in which the radius is 5 feet and the height is 14 feet is SA = 2[π(5 ft)2] + [2π(5 ft)](14 ft) = 2[π(25 ft2)] + [2π(5 ft)](14 ft) ≈ 2[(3.14)(25 ft2)] + [2(3.14)(5 ft)](14 ft) ≈ 597 ft2.
The surface area of a sphere is SA = 4πr2, where r is the radius of the sphere.
The approximate surface area of a sphere with radius of 7 feet is SA = 4πr2 = 4π(7 ft)2 = 4π(49 ft2) = 4(3.14)(49 ft2) ≈ 615 ft2.
Volume is a measure of the space or capacity inside a three-dimensional closed figure. Volume of geometric solids is measured in cubic units such as cubic inches (in3), cubic feet (ft3), cubic miles (mi3), cubic centimeters (cm3), and cubic meters (m3).
The volume of a prism or cylinder is V = Bh, where B is the area of one of the prism’s or cylinder’s congruent bases and h is the perpendicular distance between the two bases.
The volume of the right rectangular prism (box) shown below is V = Bh = [(l)(w)](h) = [(10 in)(8 in)](6 in) = 480 in3.
The approximate volume of a cylinder in which the radius, r, is 5 feet and the height, h, is 14 feet is V = Bh = [(πr2)](h) = [π(5 ft)2](14 ft) π [(3.14)(25 ft2)](14 ft) = 1,099 ft3.
The volume of a pyramid or cone is 
, where B is the area of the pyramid’s or cone’s base and h is the perpendicular distance from the apex to the base.
The volume of a square pyramid that has a 6-centimeter by 6-centimeter base and a height of 4 centimeters is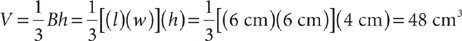 
.
The volume of a cone that has a radius, r, of 10 inches and a height, h, of 9 inches is 
.
The volume of a sphere: 
, where r is the radius of the sphere.
The approximate volume of sphere with radius of 7 feet is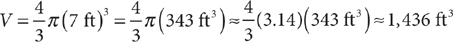 
.
In a right triangle, the hypotenuse is the side opposite the 90° angle. Tip: The hypotenuse is always the longest side of the right triangle. The other two sides are the legs.
The Pythagorean theorem tells us that, in a right triangle, c2 = a2 + b2, where c is the length of the hypotenuse and a and b are the lengths of the legs of the right triangle. For example, use the Pythagorean theorem to find the length, c, of the hypotenuse of the right triangle shown below.
The coordinate plane is defined by two real number lines, one horizontal and one vertical, intersecting at right angles at their zero points. The two real number lines are the coordinate axes. Commonly, the horizontal axis with positive direction to the right is the x-axis, and the vertical axis with positive direction upward is the y-axis. The two axes determine a plane. Their point of intersection is the origin.
The axes divide the coordinate plane into four quadrants. The quadrants are numbered with Roman numerals—I, II, III, and IV—beginning in the upper right and going around counterclockwise.
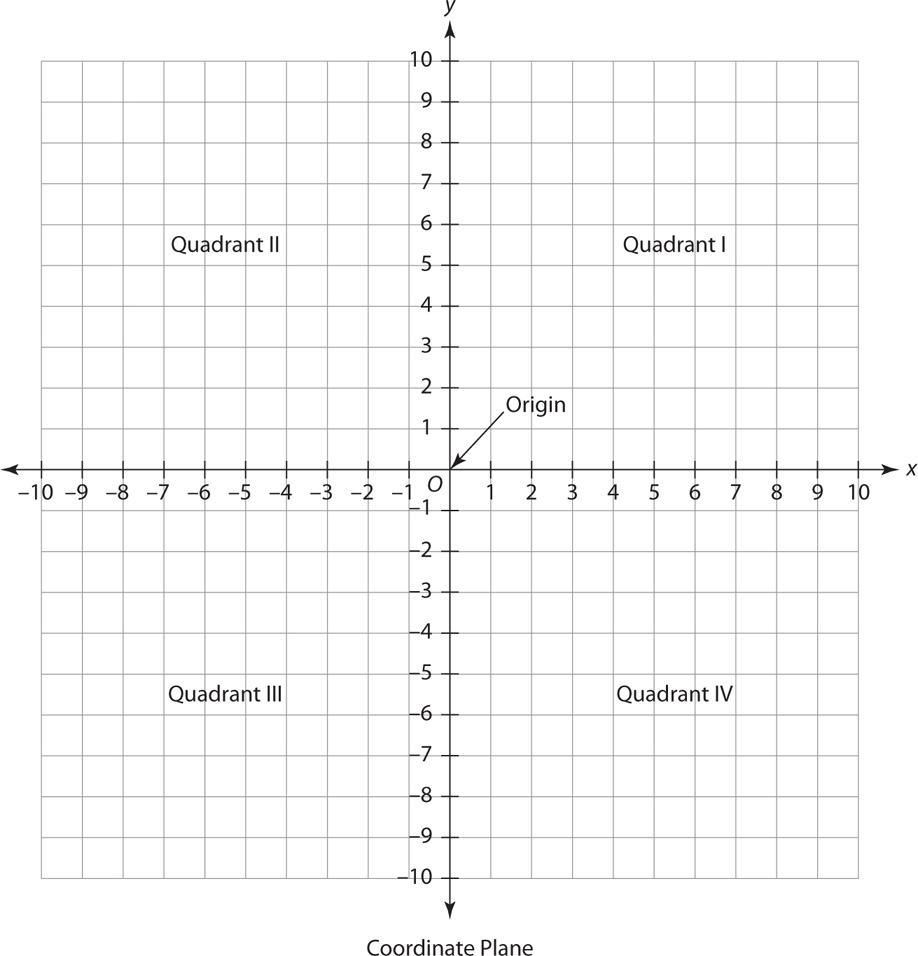
In the coordinate plane, each point P is identified by its coordinates, an ordered pair (x, y) of real numbers x and y. The ordered pair (0, 0) is the origin. The order in the ordered pair (x, y) that corresponds to a point P is important. The absolute value of the first coordinate, x, is the perpendicular horizontal distance (right or left) of the point P from the y-axis. If x is positive, P is to the right of the y-axis; if x is negative, it is to the left of the y-axis. The absolute value of the second coordinate, y, is the perpendicular vertical distance (up or down) of the point P from the x-axis. If y is positive, P is above the x-axis; if y is negative, it is below the x-axis. For instance, in the coordinate plane shown below, the point P has coordinates (–6, 9), the point Q has coordinates (2, 4), the point R has coordinates (0, –3), the point S has coordinates (–4, –7), and the point T has coordinates (5, –8).
Distance Between Two Points The distance between two points (x1, y1) and (x2, y2) in a coordinate plane is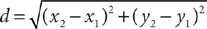 
. Here is an example.
The distance between (–6, 9) and (–4, –7) is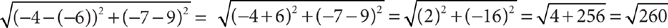 
Midpoint Between Two Points: The midpoint between two points (x1, y1) and (x2, y2) in a coordinate plane is the point with coordinates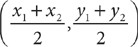 
. Here is an example.
The midpoint between (2, 4), and (0, –3) is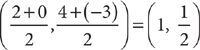 
.
Slope of a Line Through Two Points The slope m of a line through two distinct points, (x1, y1) and (x2, y2), is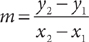 
, provided x1 ≠ x2. Here is an example.
The slope of the line through (–4, –7) and (2, 4) is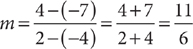 
.
The slope describes the steepness or slant of the line between the two points. Lines that slant upward from left to right have positive slopes, and lines that slant downward from left to right have negative slopes. Horizontal lines have zero slope. The slope of a vertical line is undefined.
If two lines are parallel, their slopes are equal; if two lines are perpendicular, their slopes are negative reciprocals of each other.
The graph of a function is a set of ordered pairs in the coordinate plane. The equation that defines the function generates the ordered pairs. The graphs of examples of four common functions are shown below.
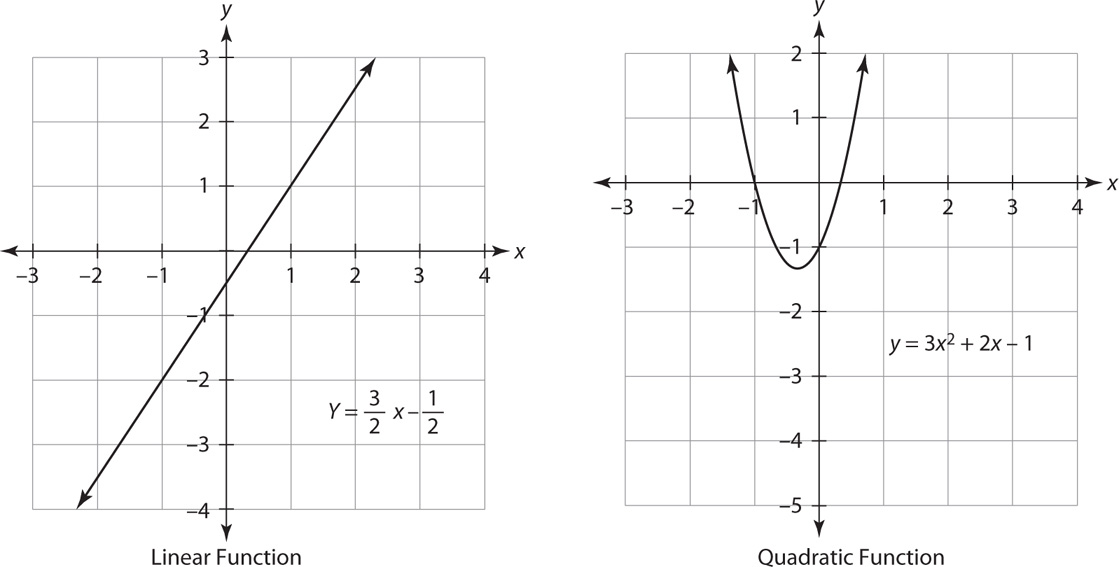
You can visually determine whether a graph is the graph of a function by using the vertical line test: A graph is the graph of a function if and only if no vertical line crosses the graph in more than one point. This test is the graphical equivalent of saying that no two different ordered pairs have the same first coordinate.
The distance from point (x1, y1) to the line whose equation is Ax + By + C = 0 is
For example, the distance from the point (–1, 2) to the line whose equation is 4x – 3y – 1 = 0 is
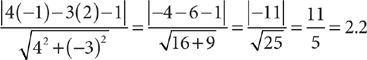
Directions: Select the best answer choice.
1. In triangle ABC, sides 
and 
are congruent. If the measure of angle C is 40°, what is the measure of angle A?
38°
40°
80°
100°
120°
2. Which set of numbers could be the lengths of the sides of a triangle?
7, 13, 17
5, 15, 20
5, 14, 6
1, 3, 5
13, 8, 5
3. In the preceding figure with the measures of the angles as shown, what is the measure of 
?
85°
75°
70°
65°
60°
4. In the preceding right triangle ABC,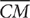 
is the median to the hypotenuse. If AC is 48 inches, BC is 20 inches, and AB is 52 inches, what is the measure in inches of ?
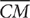24
26
28
30
32
5. In the preceding trapezoid PQRS, 
is the line segment connecting the midpoints of the two nonparallel sides 
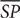and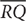 
. If PQ = 11 and TU = 7, what is the measure of 
?
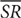3
4
5
6
7
6. In a circle whose radius is 17 centimeters, a chord is 8 centimeters from the center of the circle. What is the chord’s length in centimeters?
15
16
23
30
34
7. In the preceding diagram of circle C, chord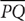 
intersects chord 
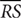at T. If PQ = 4x + 6, TQ = 5, RS = 6x + 8, and TS = 3, what is the value of x?
3
5
10
21
35
8. In the preceding right triangle ABC, 
is the altitude drawn to the hypotenuse 
. If AB = 18 and AC = 6, what is the length of 
?
1.5
2
3
12
16
9. A solid cube of metal has sides 18 centimeters long. A jeweler melts down the cube and uses all the molten metal to make three smaller cubes of exactly the same size. What is the length in centimeters of an edge of one of these smaller cubes?
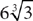
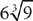
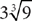
6
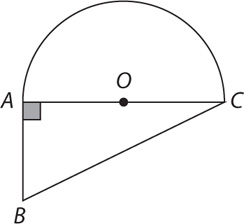
10. The preceding diagram shows a figure composed of right triangle ABC adjacent to semicircle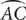 
. If AB = OC = x, what is the perimeter of the figure?
11. The preceding diagram shows the rectangle with vertices (–2, 0), (–2, 2), (4, 0), and (4, 2). What is the probability the x-coordinate of a randomly selected point in the rectangle is negative?
1
0
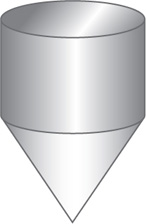
12. The grain storage bin shown in the preceding diagram has a right cylindrical top and a right conical base. The bin’s overall height is 25 feet. If the bin’s cylindrical top has radius 7 feet and its conical base has height 12 feet, what is the storage bin’s approximate capacity in cubic feet?
748
1,100
1,188
2,616
10,468
13. Disregarding units, if a sphere’s surface area equals its volume, what is the sphere’s diameter?
3π
6π
6
3
14. For a craft project, students will form a rectangular piece of cardboard with dimensions 20 centimeters by 18 centimeters into a gift box by cutting congruent squares out of each corner and then folding up and taping together the remaining flaps. If each congruent square that is cut from the corners has sides of length s, which expression represents the volume of the box?
4s3 – 76s2 + 360s
4s3 + 76s2 + 360s
s3 – 38s2 + 360s
s2 – 38s2 + 360s
4s3 – 76s + 360s
15. The preceding diagram shows the method that a park ranger is using to estimate the width of a river. If XC = 30 yards, BC = 80 yards, and XY = 60 yards, what is the river’s width in yards?
22
45
90
120
160
16. If the line through the points (–8, k) and (2, 1) is parallel to the line through the points (11, –1) and (7, k + 1), what is the value of k?
–4
2
4
17. A triangle in the (x, y) coordinate plane has vertices A(2, 3), B(–1, –1), and C(3, –4). What is the perimeter of the triangle?
Questions 18 to 25 each presents a question and two statements, labeled (1) and (2), in which certain data are given. Using your knowledge of mathematics and everyday facts (such as the number of minutes in an hour or the meaning of the word perpendicular), decide whether the given data are sufficient to answer the question. Then select one of the answer choices that follow.
18. Is the measure of ∠C greater than the measure of ∠A?
(1) 
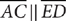
(2) m∠DEB = 58°
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. In the preceding figure, what is the ratio of x to y?
(1) ABCD is a parallelogram.
(2) 
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. In the (x, y) coordinate plane, (u, v) and (u + h, v + k) are two points on the line y = 2x + 5. What is the value of k?
(1) h = 3
(2) k = 2h
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
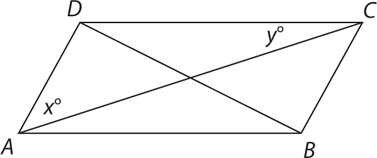
21. Is x > y?
(1) ABCD is a parallelogram.
(2) m∠DAB=50°
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
22. In the preceding figure, T is the midpoint of 
. What is the length of 
?
(1) ∠R ≅ ∠S
(2) PR = 10
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
23. For the preceding quadrilateral, what is m∠J + m∠K + m∠M in degrees?
(1) m∠L = 31°
(2) 
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
24. The preceding quadrilateral ABCD is a parallelogram. What is the length of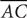 
?
(1) EC = 4
(2) AB = 6
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
25. In the preceding parallelogram LMNO, P is the point of intersection of the diagonals. What is the value of x0?
(1) Point M has coordinates (9, 10).
(2) Point N has coordinates (4, 10).
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is NOT sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. D Make a sketch, filling in the question information.
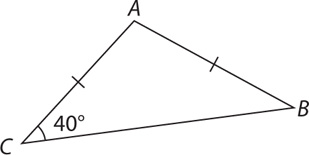
Angles C and B are base angles of an isosceles triangle, so their measures are equal, that is, m∠B = m∠C = 40°. The sum of the angles of a triangle is 180°. Thus, ∠A = 180°–2(40°) = 180° – 180° = 100°. Note: m∠X denotes “the measure of angle X.”
2. A In a triangle, the sum of the lengths of any two sides must be greater than the length of the third side (triangle inequality). The lengths given in choice A satisfy this criterion. The lengths given in the other answer choices do not.
3. C Start with the angles for which you can find the measure by using the given information. As you determine the measure of each angle, you will gain enough information to find the solution.
The measure of an exterior angle of a triangle equals the sum of the measures of the remote (nonadjacent) interior angles. Thus, m∠DCA = 100° = 30° + m∠E. Hence, m∠E = 100°–30° = 70°
4. B In a right triangle, the median to the hypotenuse is one-half the length of the hypotenuse, so the length in inches of 
is 26.
5. A The length of the segment connecting the midpoints of two nonparallel sides of a trapezoid is one-half the sum of the lengths of its bases. Thus,
6. D In a circle, a radius that is perpendicular to a chord bisects the chord. Let x = one-half the length of the chord. Then 2x = the length of the chord. Make a sketch, filling in the question information.
Using the Pythagorean theorem (omitting the units for convenience), x2 = 172 – 82 = 289 – 64 = 225, so x = 15, and 2x = 30.
7. B When two chords intersect within a circle, the products of their segments are equal. and 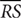are two chords in C intersecting at T, so (PT)(TQ) = (RT)(TS). PQ = PT + TQ, so 4x + 6 = PT + 5, and PT = 4x + 1. RS = RT + TS, so 6x + 8 = RT + 3, and RT = 6x + 5. Substitute into (PT)(TQ)=(RT)(TS), and solve for x.
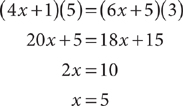
8. B In a right triangle, the altitude to the hypotenuse separates the triangle into two triangles that are similar to each other and to the original triangle. Therefore, ΔACD ~ ΔABC. Set up a proportion based on corresponding sides of similar triangles, and solve for AD.
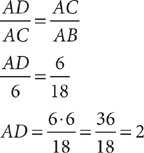
9. B The volume of the molten metal in one of the three smaller cubes is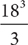 
. To find the length of an edge of one of the cubes, take the cube root of the volume.
10. A The perimeter of the figure = AB + BC + length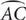 
. 
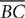is the hypotenuse of a right triangle with legs of lengths x and 2x. Use the Pythagorean theorem to find the length of BC in terms of x. 
The length of 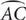is half the circumference of a circle with radius x. In terms of x, length 
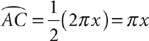. Thus, the perimeter AB + BC + length 
.
11. B The probability will be the area of the rectangular portion that lies in the second quadrant divided by the area of the entire rectangle. By inspection, you can see that the rectangular portion that lies in the second quadrant is the size of the rectangle. So the probability is that the x-coordinate of a randomly selected point in the rectangle is negative.
12. D The capacity of the storage bin is the volume of the cylindrical top, with radius 7 feet and height 13 feet (25 feet –12 feet ), plus the volume of the conical base, with radius 7 feet and height 12 feet. Therefore, the capacity in cubic feet of the storage bin equals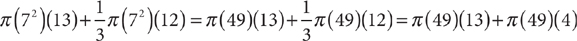 
. Rather than performing the calculations, to save time, get an approximate answer by rounding first: π(49)(13)+π(49)(4)≈3(50)(4) = 2,100. Compare this result to the answer choices; only choice D is close, so pick choice D.
13. C Let d = the sphere’s diameter; then d = 2r, where r is its radius. Set up the following equality and solve for r.
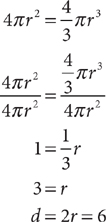
14. A Make a sketch, filling in the question information.
The volume of the box in cubic centimeters = l·w·h=(20–2s)(18–2s)s=(360–76s+4s2)s=4s3–76s2+360s.
15. C Let AX = x = the width of the river. Right triangles AXY and ACB are similar because they have common angle A. Set up a proportion based on corresponding sides, and solve for x (omitting the units for convenience):
Simplifying 
to lowest terms 
makes the calculations easier to do in this problem.
16. A Parallel lines have equal slopes. The slope of the line through points (x1, y1) and (x2, y2), is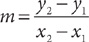 
. Set up an equation and solve for k.
slope through (–8, k) and (2,1) = slope through (11,–1) and (7, k+1)
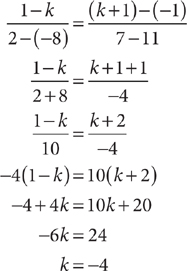
17. A The perimeter of the triangle is AB + BC + CA. The distance between points (x1,y1) and (x2, y2) is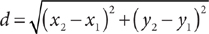 
. Therefore:
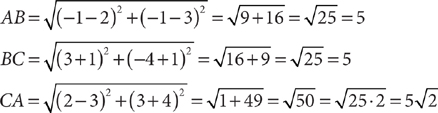
Thus, the perimeter is AB + BC + CA = 5+5+5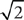
= 10+5.
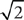18. D From the figure, because ED = DB, triangle EDB is isosceles. From the information in (1), m∠A = m∠DEB = 58° (corresponding angles of parallel lines are congruent). Also, m∠B = m∠DEB = 58° (base angles of an isosceles triangle are congruent). Thus, m∠C = 180°–2(58°), so (1) is SUFFICIENT. From the information in (2), m∠C = m∠DEB = 58° (base angles of an isosceles triangle are congruent). Thus, m∠C = 180°–2(58°), so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
19. C From the information in (1), 5x + 3y = 180° (any two consecutive angles of a parallelogram are supplementary), but further information is needed to determine 
, so (1) is NOT sufficient. From the information in (2), m∠1 = 120° but without further information, you cannot determine a relationship between m∠1 and 5x or 3y, so (2) is NOT sufficient. Taking (1) and (2) together, 3y = m∠1 = 120° (corresponding angles of parallel lines are congruent), which you can solve to obtain y = 40°. Then substituting into 5x + 3y = 180° gives 5x + 120° = 180°, which you can solve for x. Then using the value of x obtained and y = 40°, compute . Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
20. A From the question information, you can substitute the given coordinates into y = 2x + 5 to obtain the following system.
With the information in (1), the system is as follows:
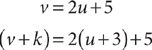
Substitute v = 2u +5 into the second equation, and solve for k.
Therefore, (1) is SUFFICIENT. With the information in (2), the system is as follows:
When simplified, the second equation is v = 2u +5, which is the same as the first equation. Thus, you need further information to determine k, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
21. E From the information in (1), m∠CAB = y° (alternate interior angles of parallel lines are congruent). If ABCD is a rhombus, then x° = y° (the diagonals of a rhombus bisect the vertex angles). Otherwise, x° ≠ y°. Thus, (1) does not provide sufficient information to answer definitely whether x > y. From the information in (2) you know only m∠DAB, which is not sufficient information to determine the relationship between x and y. Taking (1) and (2) together, you can establish that x° + y° = 50°, but there is not sufficient information to determine whether x > y. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
22. C From the question information,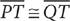 
. From the information in (1), ∠R≅∠S, ∠PTR≅∠QTS (vertical angles are congruent), and 
, so ΔPTR∝QTS, by Angle-Angle-Side (AAS). Thus, 
(corresponding parts of congruent triangles are congruent), but without further information, the length of cannot be determined, so (1) is NOT sufficient. From the information in (2) PR = 10, but further information is needed to establish a relationship between this information and QS. Thus, (2) also is NOT sufficient. Taking (1) and (2) together, from (1) you know that 
, and from (2) you know that PR = 10, so QS = 10. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
23. A JKLM is a convex quadrilateral, so the sum of its interior angles is (n –2)180° = (4–2)180° = 360°. From the information in (1), m∠J + m∠K+m∠M = 360°–31° = 329°, so (1) is SUFFICIENT. The information in (2), 
, cannot help you determine angle measures in the figure. Further information is needed, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
24. A Using the information in (1), the diagonals of a parallelogram bisect each other, so if EC = 4, then AC = 8; thus, (1) is SUFFICIENT. Using the information in (2),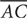 
and 
are sides in triangle ABC, but further information is needed to establish a relationship between their lengths, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
25. D From the question information, the diagonals of a parallelogram bisect each other, so (x0, y0) is the midpoint of 
as well as the midpoint of 
. From the information in (1), (x0, y0) is the midpoint between (0, 0) and (9, 10), so 
, and (1) is SUFFICIENT. From the information in (2), (x0, y0) is the midpoint between (4, 10) and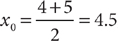 
, and (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
