2 Le Chiffre Indéchiffrable

For centuries, the simple monoalphabetic substitution cipher had been sufficient to ensure secrecy. The subsequent development of frequency analysis, first in the Arab world and then in Europe, destroyed its security. The tragic execution of Mary Queen of Scots was a dramatic illustration of the weaknesses of monoalphabetic substitution, and in the battle between cryptographers and cryptanalysts it was clear that the cryptanalysts had gained the upper hand. Anybody sending an encrypted message had to accept that an expert enemy codebreaker might intercept and decipher their most precious secrets.

The onus was clearly on the cryptographers to concoct a new, stronger cipher, something that could outwit the cryptanalysts. Although this cipher would not emerge until the end of the sixteenth century, its origins can be traced back to the fifteenth-century Florentine polymath Leon Battista Alberti. Born in 1404, Alberti was one of the leading figures of the Renaissance-a painter, composer, poet and philosopher, as well as the author of the first scientific analysis of perspective, a treatise on the housefly and a funeral oration for his dog. He is probably best known as an architect, having designed Rome’s first Trevi Fountain and having written De re aedificatoria, the first printed book on architecture, which acted as a catalyst for the transition from Gothic to Renaissance design.

Sometime in the 1460s, Alberti was wandering through the gardens of the Vatican when he bumped into his friend Leonardo Dato, the pontifical secretary, who began chatting to him about some of the finer points of cryptography. This casual conversation prompted Alberti to write an essay on the subject, outlining what he believed to be a new form of cipher. At the time, all substitution ciphers required a single cipher alphabet for encrypting each message. However, Alberti proposed using two or more cipher alphabets, switching between them during encipherment, thereby confusing potential cryptanalysts.

For example, here we have two possible cipher alphabets, and we could encrypt a message by alternating between them. To encrypt the message hello, we would encrypt the first letter according to the first cipher alphabet, so that h becomes A, but we would encrypt the second letter according to the second cipher alphabet, so that e becomes F. To encrypt the third letter we return to the first cipher alphabet, and to encrypt the fourth letter we return to the second alphabet. This means that the first l is enciphered as P, but the second l is enciphered as A. The final letter, o, is enciphered according to the first cipher alphabet and becomes D. The complete ciphertext reads AFPAD. The crucial advantage of Alberti’s system is that the same letter in the plaintext does not necessarily appear as the same letter in the ciphertext, so the repeated l in hello is enciphered differently in each case. Similarly, the repeated A in the ciphertext represents a different plaintext letter in each case, first h and then l.

Although he had hit upon the most significant breakthrough in encryption for over a thousand years, Alberti failed to develop his concept into a fully formed system of encryption. That task fell to a diverse group of intellectuals, who built on his initial idea. First came Johannes Trithemius, a German abbot born in 1462, then Giovanni Porta, an Italian scientist born in 1535, and finally Blaise de Vigenère, a French diplomat born in 1523. Vigenère became acquainted with the writings of Alberti, Trithemius and Porta when, at the age of twenty-six, he was sent to Rome on a two-year diplomatic mission. To start with, his interest in cryptography was purely practical and was linked to his diplomatic work. Then, at the age of thirty-nine, Vigenère decided that he had accumulated enough money for him to be able to abandon his career and concentrate on a life of study. It was only then that he examined in detail the ideas of Alberti, Trithemius and Porta, weaving them into a coherent and powerful new cipher.

Figure 11 Blaise de Vigenère. (photo credit 2.1)

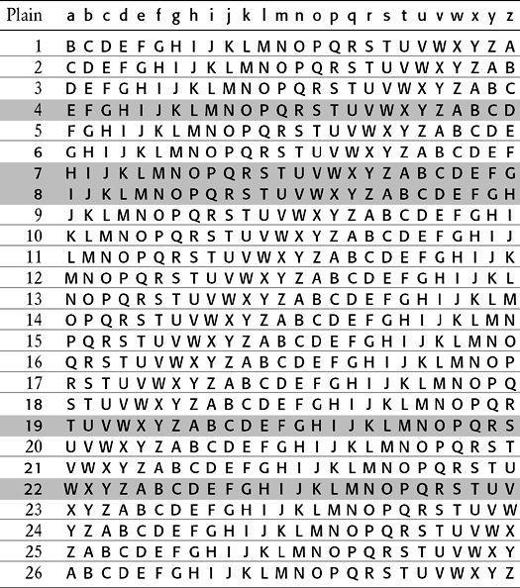
Although Alberti, Trithemius and Porta all made vital contributions, the cipher is known as the Vigenère cipher in honor of the man who developed it into its final form. The strength of the Vigenère cipher lies in its using not one, but 26 distinct cipher alphabets to encrypt a message. The first step in encipherment is to draw up a so-called Vigenère square, as shown in Table 3, a plaintext alphabet followed by 26 cipher alphabets, each shifted by one letter with respect to the previous alphabet. Hence, row 1 represents a cipher alphabet with a Caesar shift of 1, which means that it could be used to implement a Caesar shift cipher in which every letter of the plaintext is replaced by the letter one place further on in the alphabet. Similarly, row 2 represents a cipher alphabet with a Caesar shift of 2, and so on. The top row of the square, in lower case, represents the plaintext letters. You could encipher each plaintext letter according to any one of the 26 cipher alphabets. For example, if cipher alphabet number 2 is used, then the letter a is enciphered as C, but if cipher alphabet number 12 is used, then a is enciphered as M.

Table 3 A Vigenère square.

If the sender were to use just one of the cipher alphabets to encipher an entire message, this would effectively be a simple Caesar cipher, which would be a very weak form of encryption, easily deciphered by an enemy interceptor. However, in the Vigenère cipher a different row of the Vigenère square (a different cipher alphabet) is used to encrypt different letters of the message. In other words, the sender might encrypt the first letter according to row 5, the second according to row 14, the third according to row 21, and so on.

To unscramble the message, the intended receiver needs to know which row of the Vigenère square has been used to encipher each letter, so there must be an agreed system of switching between rows. This is achieved by using a keyword. To illustrate how a keyword is used with the Vigenère square to encrypt a short message, let us encipher divert troops to east ridge, using the keyword WHITE. First of all, the keyword is spelled out above the message, and repeated over and over again so that each letter in the message is associated with a letter from the keyword. The ciphertext is then generated as follows. To encrypt the first letter, d, begin by identifying the key letter above it, W, which in turn defines a particular row in the Vigenère square. The row beginning with W, row 22, is the cipher alphabet that will be used to find the substitute letter for the plaintext d. We look to see where the column headed by d intersects the row beginning with W, which turns out to be at the letter Z. Consequently, the letter d in the plaintext is represented by Z in the ciphertext.

To encipher the second letter of the message, i, the process is repeated. The key letter above i is H, so it is encrypted via a different row in the Vigenère square: the H row (row 7) which is a new cipher alphabet. To encrypt i, we look to see where the column headed by i intersects the row beginning with H, which turns out to be at the letter P. Consequently, the letter i in the plaintext is represented by P in the ciphertext. Each letter of the keyword indicates a particular cipher alphabet within the Vigenère square, and because the keyword contains five letters, the sender encrypts the message by cycling through five rows of the Vigenère square. The fifth letter of the message is enciphered according to the fifth letter of the keyword, E, but to encipher the sixth letter of the message we have to return to the first letter of the keyword. A longer keyword, or perhaps a keyphrase, would bring more rows into the encryption process and increase the complexity of the cipher. Table 4 shows a Vigenère square, highlighting the five rows (i.e., the five cipher alphabets) defined by the keyword WHITE.

Table 4 A Vigenère square with the rows defined by the keyword WHITE highlighted. Encryption is achieved by switching between the five highlighted cipher alphabets, defined by W, H, I, T and E.

The great advantage of the Vigenère cipher is that it is impregnable to the frequency analysis described in Chapter 1. For example, a cryptanalyst applying frequency analysis to a piece of ciphertext would usually begin by identifying the most common letter in the ciphertext, which in this case is Z, and then assume that this represents the most common letter in English, e. In fact, the letter Z represents three different letters, d, r and s, but not e. This is clearly a problem for the cryptanalyst. The fact that a letter which appears several times in the ciphertext can represent a different plaintext letter on each occasion generates tremendous ambiguity for the cryptanalyst. Equally confusing is the fact that a letter which appears several times in the plaintext can be represented by different letters in the ciphertext. For example, the letter o is repeated in troops, but it is substituted by two different letters—the oo is enciphered as HS.

As well as being invulnerable to frequency analysis, the Vigenère cipher has an enormous number of keys. The sender and receiver can agree on any word in the dictionary, any combination of words, or even fabricate words. A cryptanalyst would be unable to crack the message by searching all possible keys because the number of options is simply too great.

Vigenère’s work culminated in his Traicté des Chiffres (“A Treatise on Secret Writing”), published in 1586. Ironically, this was the same year that Thomas Phelippes was breaking the cipher of Mary Queen of Scots. If only Mary’s secretary had read this treatise, he would have known about the Vigenère cipher, Mary’s messages to Babington would have baffled Phelippes, and her life might have been spared.

Because of its strength and its guarantee of security, it would seem natural that the Vigenère cipher would be rapidly adopted by cipher secretaries around Europe. Surely they would be relieved to have access, once again, to a secure form of encryption? On the contrary, cipher secretaries seem to have spurned the Vigenère cipher. This apparently flawless system would remain largely neglected for the next two centuries.