CHAPTER 3
STATISTICAL CONCEPTS AND MARKET RETURNS
1. INTRODUCTION
Statistical methods provide a powerful set of tools for analyzing data and drawing conclusions from them. Whether we are analyzing asset returns, earnings growth rates, commodity prices, or any other financial data, statistical tools help us quantify and communicate the data’s important features. This chapter presents the basics of describing and analyzing data, the branch of statistics known as descriptive statistics. The chapter supplies a set of useful concepts and tools, illustrated in a variety of investment contexts. One theme of our presentation, reflected in the chapter’s title, is the demonstration of the statistical methods that allow us to summarize return distributions.
25 We explore four properties of return distributions:
• where the returns are centered (central tendency),
• how far returns are dispersed from their center (dispersion),
• whether the distribution of returns is symmetrically shaped or lopsided (skewness), and
• whether extreme outcomes are likely (kurtosis).
These same concepts are generally applicable to the distributions of other types of data, too.
The chapter is organized as follows. After defining some basic concepts in Section 2, in Sections 3 and 4 we discuss the presentation of data: Section 3 describes the organization of data in a table format, and Section 4 describes the graphic presentation of data. We then turn to the quantitative description of how data are distributed: Section 5 focuses on measures that quantify where data are centered, or measures of central tendency. Section 6 presents other measures that describe the location of data. Section 7 presents measures that quantify the degree to which data are dispersed. Sections 8 and 9 describe additional measures that provide a more accurate picture of data. Section 10 discusses investment applications of concepts introduced in Section 5.
2. SOME FUNDAMENTAL CONCEPTS
Before starting the study of statistics with this chapter, it may be helpful to examine a picture of the overall field. In the following, we briefly describe the scope of statistics and its branches of study. We explain the concepts of population and sample. Data come in a variety of types, affecting the ways they can be measured and the appropriate statistical methods for analyzing them. We conclude by discussing the basic types of data measurement.
2.1. The Nature of Statistics
The term statistics can have two broad meanings, one referring to data and the other to method. A company’s average earnings per share (EPS) for the last 20 quarters or its average returns for the past 10 years are statistics. We may also analyze historical EPS to forecast future EPS or use the company’s past returns to infer its risk. The totality of methods we employ to collect and analyze data is also called statistics.
Statistical methods include descriptive statistics and statistical inference (inferential statistics). Descriptive statistics is the study of how data can be summarized effectively to describe the important aspects of large data sets. By consolidating a mass of numerical details, descriptive statistics turns data into information. Statistical inference involves making forecasts, estimates, or judgments about a larger group from the smaller group actually observed. The foundation for statistical inference is probability theory, and both statistical inference and probability theory will be discussed in later chapters. Our focus in this chapter is solely on descriptive statistics.
2.2. Populations and Samples
Throughout the study of statistics we make a critical distinction between a population and a sample. In this section, we explain these two terms as well as the related terms “parameter” and “sample statistic.”
26• Definition of Population. A population is defined as all members of a specified group.
Any descriptive measure of a population characteristic is called a parameter. Although a population can have many parameters, investment analysts are usually concerned with only a few, such as the mean value, the range of investment returns, and the variance.
Even if it is possible to observe all the members of a population, it is often too expensive in terms of time or money to attempt to do so. For example, if the population is all telecommunications customers worldwide and an analyst is interested in their purchasing plans, she will find it too costly to observe the entire population. The analyst can address this situation by taking a sample of the population.
• Definition of Sample. A sample is a subset of a population.
In taking a sample, the analyst hopes it is characteristic of the population. The field of statistics known as sampling deals with taking samples in appropriate ways to achieve the objective of representing the population well. A later chapter addresses the details of sampling.
Earlier, we mentioned statistics in the sense of referring to data. Just as a parameter is a descriptive measure of a population characteristic, a sample statistic (statistic, for short) is a descriptive measure of a sample characteristic.
• Definition of Sample Statistic. A sample statistic (or statistic) is a quantity computed from or used to describe a sample.
We devote much of this chapter to explaining and illustrating the use of statistics in this sense. The concept is critical also in statistical inference, which addresses such problems as estimating an unknown population parameter using a sample statistic.
2.3. Measurement Scales
To choose the appropriate statistical methods for summarizing and analyzing data, we need to distinguish among different measurement scales or levels of measurement. All data measurements are taken on one of four major scales: nominal, ordinal, interval, or ratio.
Nominal scales represent the weakest level of measurement: They categorize data but do not rank them. If we assigned integers to mutual funds that follow different investment strategies, the number 1 might refer to a small-cap value fund, the number 2 to a large-cap value fund, and so on for each possible style. This nominal scale categorizes the funds according to their style but does not rank them.
Ordinal scales reflect a stronger level of measurement. Ordinal scales sort data into categories that are ordered with respect to some characteristic. For example, the Morningstar and Standard & Poor’s star ratings for mutual funds represent an ordinal scale in which one star represents a group of funds judged to have had relatively the worst performance, with two, three, four, and five stars representing groups with increasingly better performance, as evaluated by those services.
An ordinal scale may also involve numbers to identify categories. For example, in ranking balanced mutual funds based on their five-year cumulative return, we might assign the number 1 to the top 10 percent of funds, and so on, so that the number 10 represents the bottom 10 percent of funds. The ordinal scale is stronger than the nominal scale because it reveals that a fund ranked 1 performed better than a fund ranked 2. The scale tells us nothing, however, about the difference in performance between funds ranked 1 and 2 compared with the difference in performance between funds ranked 3 and 4, or 9 and 10.
Interval scales provide not only ranking but also assurance that the differences between scale values are equal. As a result, scale values can be added and subtracted meaningfully. The Celsius and Fahrenheit scales are interval measurement scales. The difference in temperature between 10°C and 11°C is the same amount as the difference between 40°C and 41°C. We can state accurately that 12°C = 9°C + 3°C, for example. Nevertheless, the zero point of an interval scale does not reflect complete absence of what is being measured; it is not a true zero point or natural zero. Zero degrees Celsius corresponds to the freezing point of water, not the absence of temperature. As a consequence of the absence of a true zero point, we cannot meaningfully form ratios on interval scales.
As an example, 50°C, although five times as large a number as 10°C, does not represent five times as much temperature. Also, questionnaire scales are often treated as interval scales. If an investor is asked to rank his risk aversion on a scale from 1 (extremely risk-averse) to 7 (extremely risk-loving), the difference between a response of 1 and a response of 2 is sometimes assumed to represent the same difference in risk aversion as the difference between a response of 6 and a response of 7. When that assumption can be justified, the data are measured on interval scales.
Ratio scales represent the strongest level of measurement. They have all the characteristics of interval measurement scales as well as a true zero point as the origin. With ratio scales, we can meaningfully compute ratios as well as meaningfully add and subtract amounts within the scale. As a result, we can apply the widest range of statistical tools to data measured on a ratio scale. Rates of return are measured on a ratio scale, as is money. If we have twice as much money, then we have twice the purchasing power. Note that the scale has a natural zero—zero means no money.
EXAMPLE 3-1 Identifying Scales of Measurement
State the scale of measurement for each of the following:
1. Credit ratings for bond issues.
27 2. Cash dividends per share.
3. Hedge fund classification types.
28 4. Bond maturity in years.
Solution to 1: Credit ratings are measured on an ordinal scale. A rating places a bond issue in a category, and the categories are ordered with respect to the expected probability of default. But the difference in the expected probability of default between AA− and A+, for example, is not necessarily equal to that between BB− and B+. In other words, letter credit ratings are not measured on an interval scale.
Solution to 2: Cash dividends per share are measured on a ratio scale. For this variable, 0 represents the complete absence of dividends; it is a true zero point.
Solution to 3: Hedge fund classification types are measured on a nominal scale. Each type groups together hedge funds with similar investment strategies. In contrast to credit ratings for bonds, however, hedge fund classification schemes do not involve a ranking. Thus such classification schemes are not measured on an ordinal scale.
Solution to 4: Bond maturity is measured on a ratio scale.
Now that we have addressed the important preliminaries, we can discuss summarizing and describing data.
3. SUMMARIZING DATA USING FREQUENCY DISTRIBUTIONS
In this section, we discuss one of the simplest ways to summarize data—the frequency distribution.
• Definition of Frequency Distribution. A frequency distribution is a tabular display of data summarized into a relatively small number of intervals.
Frequency distributions help in the analysis of large amounts of statistical data, and they work with all types of measurement scales.
Rates of return are the fundamental units that analysts and portfolio managers use for making investment decisions, and we can use frequency distributions to summarize rates of return. When we analyze rates of return, our starting point is the holding period return (also called the total return).
•
Holding Period Return Formula. The holding period return for time period
t,
Rt, is
where
Pt = price per share at the end of time period t
Pt−1 = price per share at the end of time period t − 1, the time period immediately preceding time period t
Dt = cash distributions received during time period t
Thus the holding period return for time period
t is the capital gain (or loss) plus distributions divided by the beginning-period price. (For common stocks, the distribution is a dividend; for bonds, the distribution is a coupon payment.)
Equation 3-1 can be used to define the holding period return on any asset for a day, week, month, or year simply by changing the interpretation of the time interval between successive values of the time index,
t.
The holding period return, as defined in
Equation 3-1, has two important characteristics. First, it has an element of time attached to it. For example, if a monthly time interval is used between successive observations for price, then the rate of return is a monthly figure. Second, rate of return has no currency unit attached to it. For instance, suppose that prices are denominated in euros. The numerator and denominator of
Equation 3-1 would be expressed in euros, and the resulting ratio would not have any units because the units in the numerator and denominator would cancel one another. This result holds regardless of the currency in which prices are denominated.
29With these concerns noted, we now turn to the frequency distribution of the holding period returns on the S&P 500 Index.
30 First, we examine annual rates of return; then we look at monthly rates of return. The annual rates of return on the S&P 500 calculated with
Equation 3-1 span the period January 1926 to December 2002, for a total of 77 annual observations. Monthly return data cover the period January 1926 to December 2002, for a total of 924 monthly observations.
We can state a basic procedure for constructing a frequency distribution as follows:
• Construction of a Frequency Distribution.
1. Sort the data in ascending order.
2. Calculate the range of the data, defined as Range = Maximum value − Minimum value.
3. Decide on the number of intervals in the frequency distribution, k.
4. Determine interval width as Range/k.
5. Determine the intervals by successively adding the interval width to the minimum value, to determine the ending points of intervals, stopping after reaching an interval that includes the maximum value.
6. Count the number of observations falling in each interval.
7. Construct a table of the intervals listed from smallest to largest that shows the number of observations falling in each interval.
In Step 4, when rounding the interval width, round up rather than down, to ensure that the final interval includes the maximum value of the data.
As the above procedure makes clear, a frequency distribution groups data into a set of intervals.
31 An
interval is a set of values within which an observation falls. Each observation falls into only one interval, and the total number of intervals covers all the values represented in the data. The actual number of observations in a given interval is called the
absolute frequency, or simply the frequency. The frequency distribution is the list of intervals together with the corresponding measures of frequency.
To illustrate the basic procedure, suppose we have 12 observations sorted in ascending order: −4.57, −4.04, −1.64, 0.28, 1.34, 2.35, 2.38, 4.28, 4.42, 4.68, 7.16, and 11.43. The minimum observation is −4.57 and the maximum observation is +11.43, so the range is +11.43 − (−4.57) = 16. If we set
k = 4, the interval width is 16/4 = 4.
Table 3-1 shows the repeated addition of the interval width of 4 to determine the endpoints for the intervals (Step 5).
Thus the intervals are [−4.57 to −0.57), [−0.57 to 3.43), [3.43 to 7.43), and [7.43 to 11.43].
32 Table 3-2 summarizes Steps 5 through 7.
Endpoints of Intervals
| −4.57 | + 4.00 = | −0.57 |
| −0.57 | + 4.00 = | 3.43 |
| 3.43 | + 4.00 = | 7.43 |
| 7.43 | + 4.00 = | 11.43 |
| Interval | | Absolute Frequency |
|---|
| A | −4.57 ≤ observation < −0.57 | 3 |
| B | −0.57 ≤ observation < 3.43 | 4 |
| C | 3.43 ≤ observation < 7.43 | 4 |
| D | 7.43 ≤ observation ≤ 11.43 | 1 |
Note that the intervals do not overlap, so each observation can be placed uniquely into one interval.
In practice, we may want to refine the above basic procedure. For example, we may want the intervals to begin and end with whole numbers for ease of interpretation. We also need to explain the choice of the number of intervals, k. We turn to these issues in discussing the construction of frequency distributions for the S&P 500.
We first consider the case of constructing a frequency distribution for the annual returns on the S&P 500 over the period 1926 to 2002. During that period, the return on the S&P 500 had a minimum value of −43.34 percent (in 1931) and a maximum value of +53.99 percent (in 1933). Thus the range of the data was +54% − (−43%) = 97%, approximately. The question now is the number k of intervals into which we should group observations. Although some guidelines for setting k have been suggested in statistical literature, the setting of a useful value for k often involves inspecting the data and exercising judgment. How much detail should we include? If we use too few intervals, we will summarize too much and lose pertinent characteristics. If we use too many intervals, we may not summarize enough.
We can establish an appropriate value for
k by evaluating the usefulness of the resulting interval width. A large number of empty intervals may indicate that we are trying to organize the data to present too much detail. Starting with a relatively small interval width, we can see whether or not the intervals are mostly empty and whether or not the value of
k associated with that interval width is too large. If intervals are mostly empty or
k is very large, we can consider increasingly larger intervals (smaller values of
k) until we have a frequency distribution that effectively summarizes the distribution. For the annual S&P 500 series, return intervals of 1 percent width would result in 97 intervals and many of them would be empty because we have only 77 annual observations. We need to keep in mind that the purpose of a frequency distribution is to
summarize the data. Suppose that for ease of interpretation we want to use an interval width stated in whole rather than fractional percents. A 2 percent interval width would have many fewer empty intervals than a 1 percent interval width and effectively summarize the data. A 2 percent interval width would be associated with 97/2 = 48.5 intervals, which we can round up to 49 intervals. That number of intervals will cover 2% × 49 = 98%. We can confirm that if we start the smallest 2 percent interval at the whole number −44.0 percent, the final interval ends at −44.0% + 98% = 54% and includes the maximum return in the sample, 53.99 percent. In so constructing the frequency distribution, we will also have intervals that end and begin at a value of 0 percent, allowing us to count the negative and positive returns in the data. Without too much work, we have found an effective way to summarize the data. We will use return intervals of 2 percent, beginning with −44% ≤
Rt < −42% (given as “−44% to −42%” in the table) and ending with 52% ≤
Rt ≤ 54%.
Table 3-3 shows the frequency distribution for the annual total returns on the S&P 500.
TABLE 3-3 Frequency Distribution for the Annual Total Return on the S&P 500, 1926-2002
Source: Frequency distribution generated with Ibbotson Associates EnCorr Analyzer.
Table 3-3 includes three other useful ways to present data, which we can compute once we have established the frequency distribution: the relative frequency, the cumulative frequency (also called the cumulative absolute frequency), and the cumulative relative frequency.
• Definition of Relative Frequency. The relative frequency is the absolute frequency of each interval divided by the total number of observations.
The
cumulative relative frequency cumulates (adds up) the relative frequencies as we move from the first to the last interval. It tells us the fraction of observations that are less than the upper limit of each interval. Examining the frequency distribution given in
Table 3-3, we see that the first return interval, −44 percent to −42 percent, has one observation; its relative frequency is 1/77 or 1.30 percent. The cumulative frequency for this interval is 1 because only one observation is less than −42 percent. The cumulative relative frequency is thus 1/77 or 1.30 percent. The next return interval has zero observations; therefore, its cumulative frequency is 0 plus 1 and its cumulative relative frequency is 1.30 percent (the cumulative relative frequency from the previous interval). We can find the other cumulative frequencies by adding the (absolute) frequency to the previous cumulative frequency. The cumulative frequency, then, tells us the number of observations that are less than the upper limit of each return interval.
As
Table 3-3 shows, return intervals have frequencies from 0 to 7 in this sample. The interval encompassing returns between −10 percent and −8 percent (−10% ≤
Rt < −8%) has the most observations, seven. Next most frequent are returns between 18 percent and 20 percent (18% ≤
Rt < 20%), with six observations. From the cumulative frequency column, we see that the number of negative returns is 23. The number of positive returns must then be equal to 77 − 23, or 54. We can express the number of positive and negative outcomes as a percentage of the total to get a sense of the risk inherent in investing in the stock market. During the 77-year period, the S&P 500 had negative annual returns 29.9 percent of the time (that is, 23/77). This result appears in the fifth column of
Table 3-3, which reports the cumulative relative frequency.
The frequency distribution gives us a sense of not only where most of the observations lie but also whether the distribution is evenly distributed, lopsided, or peaked. In the case of the S&P 500, we can see that more than half of the outcomes are positive and most of those annual returns are larger than 10 percent. (Only 11 of the 54 positive annual returns—about 20 percent—were between 0 and 10 percent.)
Table 3-3 permits us to make an important further point about the choice of the number of intervals related to equity returns in particular. From the frequency distribution in
Table 3-3, we can see that only five outcomes fall between −44 percent and −16 percent and between 38 percent and 54 percent. Stock return data are frequently characterized by a few very large or small outcomes. We could have collapsed the return intervals in the tails of the frequency distribution by choosing a smaller value of
k, but then we would have lost the information about how extremely poorly or well the stock market had performed. A risk manager may need to know the worst possible outcomes and thus may want to have detailed information on the tails (the extreme values). A frequency distribution with a relatively large value of
k is useful for that. A portfolio manager or analyst may be equally interested in detailed information on the tails; however, if the manager or analyst wants a picture only of where most of the observations lie, he might prefer to use an interval width of 4 percent (25 intervals beginning at −44 percent), for example.
The frequency distribution for monthly returns on the S&P 500 looks quite different from that for annual returns. The monthly return series from January 1926 to December 2002 has 924 observations. Returns range from a minimum of approximately −30 percent to a maximum of approximately +43 percent. With such a large quantity of monthly data we must summarize to get a sense of the distribution, and so we group the data into 37 equally spaced return intervals of 2 percent. The gains from summarizing in this way are substantial.
Table 3-4 presents the resulting frequency distribution. The absolute frequencies appear in the second column, followed by the relative frequencies. The relative frequencies are rounded to two decimal places. The cumulative absolute and cumulative relative frequencies appear in the fourth and fifth columns, respectively.
TABLE 3-4 Frequency Distribution for the Monthly Total Return on the S&P 500, January 1926 to December 2002
Source: Frequency distribution generated with Ibbotson Associates EnCorr Analyzer.
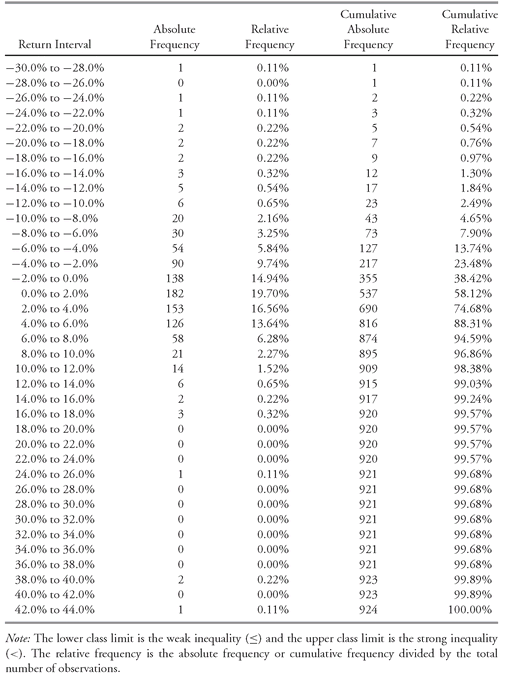
The advantage of a frequency distribution is evident in
Table 3-4, which tells us that the vast majority of observations (599/924 = 65 percent) lie in the four intervals spanning −2 percent to +6 percent. Altogether, we have 355 negative returns and 569 positive returns. Almost 62 percent of the monthly outcomes are positive. Looking at the cumulative relative frequency in the last column, we see that the interval −2 percent to 0 percent shows a cumulative frequency of 38.42 percent, for an upper return limit of 0 percent. This means that 38.42 percent of the observations lie below the level of 0 percent. We can also see that not many observations are greater than +12 percent or less than −12 percent. Note that the frequency distributions of annual and monthly returns are not directly comparable. On average, we should expect the returns measured at shorter intervals (for example, months) to be smaller than returns measured over longer periods (for example, years).
Next, we construct a frequency distribution of average inflation-adjusted returns over 1900-2000 for 16 major equity markets.
EXAMPLE 3-2 Constructing a Frequency Distribution
How have equities rewarded investors in different countries in the long run? To answer this question, we could examine the average annual returns directly.
33 The worth of a nominal level of return depends on changes in the purchasing power of money, however, and internationally there have been a variety of experiences with price inflation. It is preferable, therefore, to compare the average real or inflation-adjusted returns earned by investors in different countries. Dimson, Marsh, and Staunton (2002) presented authoritative evidence on asset returns in 16 countries for the 101 years 1900-2000.
Table 3-5 excerpts their findings for average inflation-adjusted returns.
Table 3-6 summarizes the data in
Table 3-5 into six intervals spanning 4 percent to 10 percent.
As
Table 3-6 shows, there is substantial variation internationally of average real equity returns. Three-fourths of the observations fall in one of three intervals: 6.0 to 7.0 percent, 7.0 to 8.0 percent, or 9.0 to 10.0 percent. Most average real equity returns are between 6.0 percent and 10 percent; the cumulative relative frequency of returns less than 6.0 percent was only 12.50 percent.
TABLE 3-5 Real (Inflation-Adjusted) Equity Returns: Sixteen Major Equity Markets, 1900-2000
Source: Dimson, Marsh, and Staunton (2002),
Table 4-3. Swiss equities date from 1911.
| Country | Arithmetic Mean |
|---|
| Australia | 9.0% |
| Belgium | 4.8% |
| Canada | 7.7% |
| Denmark | 6.2% |
| France | 6.3% |
| Germany | 8.8% |
| Ireland | 7.0% |
| Italy | 6.8% |
| Japan | 9.3% |
| Netherlands | 7.7% |
| South Africa | 9.1% |
| Spain | 5.8% |
| Sweden | 9.9% |
| Switzerland | 6.9% |
| United Kingdom | 7.6% |
| United States | 8.7% |
TABLE 3-6 Frequency Distribution of Average Real Equity Returns
4. THE GRAPHIC PRESENTATION OF DATA
A graphical display of data allows us to visualize important characteristics quickly. For example, we may see that the distribution is symmetrically shaped, and this finding may influence which probability distribution we use to describe the data. In this section, we discuss the histogram, the frequency polygon, and the cumulative frequency distribution as methods for displaying data graphically. We construct all of these graphic presentations with the information contained in the frequency distribution of the S&P 500 shown in either
Table 3-3 or
Table 3-4.
4.1. The Histogram
A histogram is the graphical equivalent of a frequency distribution.
• Definition of Histogram. A histogram is a bar chart of data that have been grouped into a frequency distribution.
The advantage of the visual display is that we can see quickly where most of the observations lie. To see how a histogram is constructed, look at the return interval 18% ≤
Rt < 20% in
Table 3-3. This interval has an absolute frequency of 6. Therefore, we erect a bar or rectangle with a height of 6 over that return interval on the horizontal axis. Continuing with this process for all other return intervals yields a histogram.
Figure 3-1 presents the histogram of the annual total return series on the S&P 500 from 1926 to 2002.
In the histogram in
Figure 3-1, the height of each bar represents the absolute frequency for each return interval. The return interval −10% ≤
Rt < −8% has a frequency of 7 and is represented by the tallest bar in the histogram. Because there are no gaps between the interval limits, there are no gaps between the bars of the histogram. Many of the return intervals have zero frequency; therefore, they have no height in the histogram.
FIGURE 3-1 Histogram of S&P 500 Annual Total Returns: 1926 to 2002
Source: Ibbotson EnCorr Analyzer.
FIGURE 3-2 Histogram of S&P 500 Monthly Total Returns: January 1926 to December 2002
Figure 3-2 presents the histogram for the distribution of monthly returns on the S&P 500. Somewhat more symmetrically shaped than the histogram of annual returns shown in
Figure 3-1, this histogram also appears more bell-shaped than the distribution of annual returns.
4.2. The Frequency Polygon and the Cumulative Frequency Distribution
Two other graphical tools for displaying data are the frequency polygon and the cumulative frequency distribution. To construct a
frequency polygon, we plot the midpoint of each interval on the
x-axis and the absolute frequency for that interval on the
y-axis; we then connect neighboring points with a straight line.
Figure 3-3 shows the frequency polygon for the 924 monthly returns for the S&P 500 from January 1926 to December 2002.
In
Figure 3-3, we have replaced the bars in the histogram with points connected with straight lines. For example, the return interval 0 percent to 2 percent has an absolute frequency of 182. In the frequency polygon, we plot the return-interval midpoint of 1 percent and a frequency of 182. We plot all other points in a similar way.
34 This form of visual display adds a degree of continuity to the representation of the distribution.
FIGURE 3-3 Frequency Polygon of S&P 500 Monthly Total Returns: January 1926 to December 2002
Source: Ibbotson Associates.
Another form of line graph is the cumulative frequency distribution. Such a graph can plot either the cumulative absolute or cumulative relative frequency against the upper interval limit. The cumulative frequency distribution allows us to see how many or what percent of the observations lie below a certain value. To construct the cumulative frequency distribution, we graph the returns in the fourth or fifth column of
Table 3-4 against the upper limit of each return interval.
Figure 3-4 presents a graph of the cumulative absolute distribution for the monthly returns on the S&P 500. Notice that the cumulative distribution tends to flatten out when returns are extremely negative or extremely positive. The steep slope in the middle of
Figure 3-4 reflects the fact that most of the observations lie in the neighborhood of −2 percent to 6 percent.
We can further examine the relationship between the relative frequency and the cumulative relative frequency by looking at the two return intervals reproduced in
Table 3-7. The first return interval (0 percent to 2 percent) has a cumulative relative frequency of 58.12 percent. The next return interval (2 percent to 4 percent) has a cumulative relative frequency of 74.68 percent. The change in the cumulative relative frequency as we move from one interval to the next is the next interval’s relative frequency. For instance, as we go from the first return interval (0 percent to 2 percent) to the next return interval (2 percent to 4 percent), the change in the cumulative relative frequency is 74.68% − 58.12% = 16.56%. (Values in the table have been rounded to two decimal places.) The fact that the slope is steep indicates that these frequencies are large. As you can see in the graph of the cumulative distribution, the slope of the curve changes as we move from the first return interval to the last. A fairly small slope for the cumulative distribution for the first few return intervals tells us that these return intervals do not contain many observations. You can go back to the frequency distribution in
Table 3-4 and verify that the cumulative absolute frequency is only 23 observations (the cumulative relative frequency is 2.49 percent) up to the 10th return interval (−12 percent to −10 percent). In essence, the slope of the cumulative absolute distribution at any particular interval is proportional to the number of observations in that interval.
FIGURE 3-4 Cumulative Absolute Frequency Distribution of S&P 500 Monthly Total Returns: January 1926 to December 2002
Source: Ibbotson Associates.
TABLE 3-7 Selected Class Frequencies for the S&P 500 Monthly Returns
5. MEASURES OF CENTRAL TENDENCY
So far, we have discussed methods we can use to organize and present data so that they are more understandable. The frequency distribution of an asset class’s return series, for example, reveals the nature of the risks that investors may encounter in a particular asset class. As an illustration, the histogram for the annual returns on the S&P 500 clearly shows that large positive and negative annual returns are common. Although frequency distributions and histograms provide a convenient way to summarize a series of observations, these methods are just a first step toward describing the data. In this section we discuss the use of quantitative measures that explain characteristics of data. Our focus is on measures of central tendency and other measures of location or location parameters. A measure of central tendency specifies where the data are centered. Measures of central tendency are probably more widely used than any other statistical measure because they can be computed and applied easily. Measures of location include not only measures of central tendency but other measures that illustrate the location or distribution of data.
In the following subsections we explain the common measures of central tendency—the arithmetic mean, the median, the mode, the weighted mean, and the geometric mean. We also explain other useful measures of location, including quartiles, quintiles, deciles, and percentiles.
5.1. The Arithmetic Mean
Analysts and portfolio managers often want one number that describes a representative possible outcome of an investment decision. The arithmetic mean is by far the most frequently used measure of the middle or center of data.
• Definition of Arithmetic Mean. The arithmetic mean is the sum of the observations divided by the number of observations.
We can compute the arithmetic mean for both populations and samples, known as the population mean and the sample mean, respectively.
5.1.1. The Population Mean The population mean is the arithmetic mean computed for a population. If we can define a population adequately, then we can calculate the population mean as the arithmetic mean of all the observations or values in the population. For example, analysts examining the fiscal 2002 year-over-year growth in same-store sales of major U.S. wholesale clubs might define the population of interest to include only three companies: BJ’s Wholesale Club (NYSE: BJ), Costco Wholesale Corporation (Nasdaq: COST), and Sam’s Club, part of Wal-Mart Stores (NYSE: WMT).
35 As another example, if a portfolio manager’s investment universe (the set of securities she must choose from) is the Nikkei-Dow Jones Average, the relevant population is the 225 shares on the First Section of the Tokyo Stock Exchange that compose the Nikkei.
•
Population Mean Formula. The
population mean, µ, is the arithmetic mean value of a population. For a finite population, the population mean is
(3-2)
where
N is the number of observations in the entire population and
Xi is the
ith observation.
The population mean is an example of a parameter. The population mean is unique; that is, a given population has only one mean. To illustrate the calculation, we can take the case of the population mean of current price-to-earnings ratio (P/E) of stocks of U.S. companies running major wholesale clubs as of the beginning of September 2003. As of that date, the current P/Es for BJ, COST, and WMT were 16.73, 22.02, and 29.30, respectively, according to First Call/Thomson Financial. Thus the population mean current P/E on that date was µ = (16.73 + 22.02 + 29.30)/3 = 68.05/3 = 22.68.
5.1.2. The Sample Mean The sample mean is the arithmetic mean computed for a sample. Many times we cannot observe every member of a set; instead, we observe a subset or sample of the population. The concept of the mean can be applied to the observations in a sample with a slight change in notation.
•
Sample Mean Formula. The
sample mean or average,
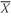
(read “X-bar”), is the arithmetic mean value of a sample:
where
n is the number of observations in the sample.
Equation 3-3 tells us to sum the values of the observations (
Xi ) and divide the sum by the number of observations. For example, if the sample of P/E multiples contains the values 35, 30, 22, 18, 15, and 12, the sample mean P/E is 132/6 = 22. The sample mean is also called the arithmetic average.
36 As we discussed earlier, the sample mean is a statistic (that is, a descriptive measure of a sample).
Means can be computed for individual units or over time. For instance, the sample might be the 2003 return on equity (ROE) for the 300 companies in the Financial Times Stock Exchange (FTSE) Eurotop 300, an index of Europe’s 300 largest companies. In this case, we calculate mean ROE in 2003 as an average across 300 individual units. When we examine the characteristics of some units at a specific point in time (such as ROE for the FTSE Eurotop 300), we are examining cross-sectional data. The mean of these observations is called a cross-sectional mean. On the other hand, if our sample consists of the historical monthly returns on the FTSE Eurotop 300 for the past five years, then we have time-series data. The mean of these observations is called a time-series mean. We will examine specialized statistical methods related to the behavior of time series in the chapter on times-series analysis.
Next, we show an example of finding the sample mean return for equities in 16 European countries for 2002. In this case, the mean is cross-sectional because we are averaging individual country returns.
EXAMPLE 3-3 Calculating a Cross-Sectional Mean
The MSCI EAFE (Europe, Australasia, and Far East) Index is a free float-adjusted market capitalization index designed to measure developed-market equity performance excluding the United States and Canada.
37 As of the end of 2002, the EAFE consisted of 21 developed market country indexes, including indexes for 16 European markets, 2 Australasian markets (Australia and New Zealand), and 3 Far Eastern markets (Hong Kong, Japan, and Singapore).
Suppose we are interested in the local currency performance of the 16 European markets in the EAFE in 2002, a severe bear market year. We want to find the sample mean total return for 2002 across these 16 markets. The return series reported in
Table 3-8 are in local currency (that is, returns are for investors living in the country). Because this return is not stated in any single investor’s home currency, it is not a return any single investor would earn. Rather, it is an average of returns in 16 local currencies.
TABLE 3-8 Total Returns for European Equity Markets, 2002
| Market | Total Return in Local Currency |
|---|
| Austria | −2.97% |
| Belgium | −29.71% |
| Denmark | −29.67% |
| Finland | −41.65% |
| France | −33.99% |
| Germany | −44.05% |
| Greece | −39.06% |
| Ireland | −38.97% |
| Italy | −23.64% |
| Netherlands | −34.27% |
| Norway | −29.73% |
| Portugal | −28.29% |
| Spain | −29.47% |
| Sweden | −43.07% |
| Switzerland | −25.84% |
| United Kingdom | −25.66% |
Using the data in
Table 3-8, calculate the sample mean return for the 16 equity markets in 2002.
Solution: The calculation applies
Equation 3-3 to the returns in
Table 3-8: (−2.97 − 29.71 − 29.67 − 41.65 − 33.99 − 44.05 − 39.06 − 38.97 − 23.64 − 34.27 − 29.73 − 28.29 − 29.47 − 43.07 − 25.84 − 25.66)/16 = −500.04/16 = −31.25 percent.
In Example 3-3, we can verify that seven markets had returns less than the mean and nine had returns that were greater. We should not expect any of the actual observations to equal the mean, because sample means provide only a summary of the data being analyzed. As an analyst, you will often need to find a few numbers that describe the characteristics of the distribution. The mean is generally the statistic that you will use as a measure of the typical outcome for a distribution. You can then use the mean to compare the performance of two different markets. For example, you might be interested in comparing the stock market performance of investments in Pacific Rim countries with investments in European countries. You can use the mean returns in these markets to compare investment results.
FIGURE 3-5 Center of Gravity Analogy for the Arithmetic Mean
5.1.3. Properties of the Arithmetic Mean The arithmetic mean can be likened to the center of gravity of an object.
Figure 3-5 expresses this analogy graphically by plotting nine hypothetical observations on a bar. The nine observations are 2, 4, 4, 6, 10, 10, 12, 12, and 12; the arithmetic mean is 72/9 = 8. The observations are plotted on the bar with various heights based on their frequency (that is, 2 is one unit high, 4 is two units high, and so on). When the bar is placed on a fulcrum, it balances only when the fulcrum is located at the point on the scale that corresponds to the arithmetic mean.
As analysts, we often use the mean return as a measure of the typical outcome for an asset. As in the example above, however, some outcomes are above the mean and some are below it. We can calculate the distance between the mean and each outcome and call it a deviation. Mathematically, it is always true that the sum of the deviations around the mean equals 0. We can see this by using the definition of the arithmetic mean shown in
Equation 3-3, multiplying thus be calculated as follows: both sides of the equation by
n:
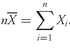
. The sum of the deviations from the mean can thus be calculated as follows:
Deviations from the arithmetic mean are important information because they indicate risk. The concept of deviations around the mean forms the foundation for the more complex concepts of variance, skewness, and kurtosis, which we will discuss later in this chapter.
An advantage of the arithmetic mean over two other measures of central tendency, the median and mode, is that the mean uses all the information about the size and magnitude of the observations. The mean is also easy to work with mathematically.
A property and potential drawback of the arithmetic mean is its sensitivity to extreme values. Because all observations are used to compute the mean, the arithmetic mean can be pulled sharply upward or downward by extremely large or small observations, respectively. For example, suppose we compute the arithmetic mean of the following seven numbers: 1, 2, 3, 4, 5, 6, and 1,000. The mean is 1,021/7 = 145.86 or approximately 146. Because the magnitude of the mean, 146, is so much larger than that of the bulk of the observations (the first six), we might question how well it represents the location of the data. In practice, although an extreme value or outlier in a financial dataset may only represent a rare value in the population, it may also reflect an error in recording the value of an observation, or an observation generated from a different population from that producing the other observations in the sample. In the latter two cases in particular, the arithmetic mean could be misleading. Perhaps the most common approach in such cases is to report the median in place of or in addition to the mean.
38 We discuss the median next.
5.2. The Median
A second important measure of central tendency is the median.
•
Definition of Median. The
median is the value of the middle item of a set of items that has been sorted into ascending or descending order. In an odd-numbered sample of
n items, the median occupies the (
n + 1)/2 position. In an even-numbered sample, we define the median as the mean of the values of items occupying the
n/2 and (
n + 2)/2 positions (the two middle items).
39 Earlier we gave the current P/Es of three wholesale clubs as 16.73, 22.02, and 29.30. With an odd number of observations (n = 3), the median occupies the (n + 1)/2 = 4/2 = 2nd position. The median P/E was 22.02. The P/E value of 22.02 is the “middlemost” observation: One lies above it, and one lies below it. Whether we use the calculation for an even- or odd-numbered sample, an equal number of observations lie above and below the median. A distribution has only one median.
A potential advantage of the median is that, unlike the mean, extreme values do not affect it. The median, however, does not use all the information about the size and magnitude of the observations; it focuses only on the relative position of the ranked observations. Calculating the median is also more complex; to do so, we need to order the observations from smallest to largest, determine whether the sample size is even or odd, and, on that basis, apply one of two calculations. Mathematicians express this disadvantage by saying that the median is less mathematically tractable than the mean.
To demonstrate finding the median, we use the data from Example 3-3, reproduced in
Table 3-9 in ascending order, of the 2002 total return for European equities. Because this sample has 16 observations, the median is the mean of the values in the sorted array that occupy the 16/2 = 8th and 18/2 = 9th positions. Norway’s return occupies the eighth position with a return of −29.73 percent, and Belgium’s return occupies the ninth position with a return of −29.71 percent. The median, as the mean of these two returns, is (−29.73 − 29.71)/2 = −29.72 percent. Note that the median is not influenced by extremely large or small outcomes. Had Germany’s total return been a much lower value or Austria’s total return a much larger value, the median would not have changed.
TABLE 3-9 Total Returns for European Equity Markets, 2002 (in ascending order)
| No. | Market | Total Return in Local Currency |
|---|
| 1 | Germany | −44.05% |
| 2 | Sweden | −43.07% |
| 3 | Finland | −41.65% |
| 4 | Greece | −39.06% |
| 5 | Ireland | −38.97% |
| 6 | Netherlands | −34.27% |
| 7 | France | −33.99% |
| 8 | Norway | −29.73% |
| 9 | Belgium | −29.71% |
| 10 | Denmark | −29.67% |
| 11 | Spain | −29.47% |
| 12 | Portugal | −28.29% |
| 13 | Switzerland | −25.84% |
| 14 | United Kingdom | −25.66% |
| 15 | Italy | −23.64% |
| 16 | Austria | −2.97% |
Using a context that arises often in practice, Example 3-4 shows how to use the mean and median in a sample with extreme values.
EXAMPLE 3-4 Median and Arithmetic Mean: The Case of the Price – Earnings Ratio
Suppose a client asks you for a valuation analysis on the seven-stock U.S. common stock portfolio given in
Table 3-10. The stocks are equally weighted in the portfolio. One valuation measure that you use is P/E, the ratio of share price to earnings per share (EPS). Many variations exist for the denominator in the P/E, but you are examining P/E defined as current price divided by the current mean of all analysts’ EPS estimates for the company for the current fiscal year (“Consensus Current EPS” in the table).
40 The values in
Table 3-10 are as of 11 September 2003. For comparison purposes, the consensus current P/E on the S&P 500 was 23.63 at that time.
Using the data in
Table 3-10, address the following:
1. Calculate the arithmetic mean P/E.
2. Calculate the median P/E.
3. Evaluate the mean and median P/Es as measures of central tendency for the above portfolio.
Source: First Call/Thomson Financial.
| Stock | Consensus Current EPS | Consensus Current P/E |
|---|
| Exponent Inc. (Nasdaq: EXPO) | 1.23 | 13.68 |
| Express Scripts (Nasdaq: ESRX) | 3.19 | 19.07 |
| General Dynamics (NYSE: GD) | 4.95 | 17.56 |
| Limited Brands (NYSE: LTD) | 1.06 | 15.60 |
| Merant plc (Nasdaq: MRNT) | 0.03 | 443.33 |
| Microsoft Corporation (Nasdaq: MSFT) | 1.11 | 25.61 |
| O’Reilly Automotive, Inc. (Nasdaq: ORLY) | 1.84 | 21.01 |
Solution to 1: The mean P/E is (13.68 + 19.07 + 17.56 + 15.60 + 443.33 + 25.61 + 21.01)/7 = 555.86/7 = 79.41.
Solution to 2: The P/Es listed in ascending order are:
The sample has an odd number of observations with n = 7, so the median occupies the (n + 1)/2 = 8/2 = 4th position in the sorted list. Therefore, the median P/E is 19.07.
Solution to 3: Merant’s P/E of approximately 443 tremendously influences the value of the portfolio’s arithmetic mean P/E. The mean P/E of 79 is much larger than the P/E of six of the seven stocks in the portfolio. The mean P/E also misleadingly suggests an orientation to stocks with high P/Es. The mean P/E of the stocks excluding Merant, or excluding the largest- and smallest-P/E stocks (Merant and Exponent), is below the S&P 500’s P/E of 23.63. The median P/E of 19.07 appears to better represent the central tendency of the P/Es.
It frequently happens that when a company’s EPS is close to zero—at a low point in the business cycle, for example—its P/E is extremely high. The high P/E in those circumstances reflects an anticipated future recovery of earnings. Extreme P/E values need to be investigated and handled with care. For reasons related to this example, analysts often use the median of price multiples to characterize the valuation of industry groups.
5.3. The Mode
The third important measure of central tendency is the mode.
•
Definition of Mode. The
mode is the most frequently occurring value in a distribution.
41 A distribution can have more than one mode or even no mode. When a distribution has one most frequently occurring value, the distribution is said to be unimodal. If a distribution has two most frequently occurring values, then it has two modes, and we say it is bimodal. If the distribution has three most frequently occurring values, then it is trimodal. When all the values in a data set are different, the distribution has no mode because no value occurs more frequently than any other value.
Stock return data and other data from continuous distributions may not have a modal outcome. When such data are grouped into intervals, however, we often find an interval (possibly more than one) with the highest frequency: the
modal interval (or intervals). For example, the frequency distribution for the monthly returns on the S&P 500 has a modal interval of 0 percent to 2 percent, as shown in
Figure 3-2; this return interval has 182 observations out of a total of 924. The modal interval always has the highest bar in the histogram.
The mode is the only measure of central tendency that can be used with nominal data. When we categorize mutual funds into different styles and assign a number to each style, the mode of these categorized data is the most frequent mutual fund style.
EXAMPLE 3-5 Calculating a Mode
Table 3-11 gives the credit ratings on senior unsecured debt as of September 2002 of nine U.S. department stores rated by Moody’s Investors Service. In descending order of credit quality (increasing expected probability of default), Moody’s ratings are Aaa, Aa1, Aa2, Aa3, A1, A2, A3, Baa1, Baa2, Baa3, Ba1, Ba2, Ba3, B1, B2, B3, Caa, Ca, and C.
42
Using the data in
Table 3-11, address the following concerning the senior unsecured debt of U.S. department stores:
1. State the modal credit rating.
2. State the median credit rating.
Solution to 1: The group of companies represents seven distinct credit ratings, ranging from A2 to B1. To make our task easy, we first organize the ratings into a frequency distribution.
All credit ratings have a frequency of 1 except for Baa1, which has a frequency of 3. Therefore, the modal credit rating of U.S. department stores as of the date of the Moody’s report was Baa1. Moody’s considers bonds rated Baa1 to be medium-grade obligations—they are neither highly protected nor poorly secured.
TABLE 3-11 Senior Unsecured Debt Ratings: U.S. Department Stores, September 2002
Source: Moody’s Investors Service.
| Company | Credit Rating |
|---|
| Dillards, Inc. | Ba3 |
| Federated Department Stores, Inc. | Baa1 |
| Kohl’s Corporation | A3 |
| May’s Department Stores Company | A2 |
| Neiman Marcus Group, Inc. | Baa2 |
| Nordstom, Inc. | Baa1 |
| Penney, JC, Company, Inc. | Ba2 |
| Saks Incorporated | B1 |
| Sears, Roebuck and Co. | Baa1 |
Solution to 2: For the group,
n = 9, an odd number. The group’s median occupies the (
n + 1)/2 = 10/2 = 5th position. We see from
Table 3-12 that Baa1 occupies the fifth position. Therefore, the median credit rating as of September 2002 was Baa1.
TABLE 3-12 Senior Unsecured Debt Ratings: U.S. Department Stores, Distribution of Credit Ratings
| Credit Rating | Frequency |
|---|
| A2 | 1 |
| A3 | 1 |
| Baa1 | 3 |
| Baa2 | 1 |
| Ba2 | 1 |
| Ba3 | 1 |
| B1 | 1 |
5.4. Other Concepts of Mean
Earlier we explained the arithmetic mean, which is a fundamental concept for describing the central tendency of data. Other concepts of mean are very important in investments, however. In the following, we discuss such concepts.
5.4.1. The Weighted Mean The concept of weighted mean arises repeatedly in portfolio analysis. In the arithmetic mean, all observations are equally weighted by the factor 1/n (or 1/N). In working with portfolios, we need the more general concept of weighted mean to allow different weights on different observations.
To illustrate the weighted mean concept, an investment manager with $100 million to invest might allocate $70 million to equities and $30 million to bonds. The portfolio has a weight of 0.70 on stocks and 0.30 on bonds. How do we calculate the return on this portfolio?
TABLE 3-13 Total Returns for Canadian Equities and Bonds, 1998—2002
| Year | Equities | Bonds |
|---|
| 1998 | −1.6% | 9.1% |
| 1999 | 31.7% | −1.1% |
| 2000 | 7.4% | 10.3% |
| 2001 | −12.6% | 8.0% |
| 2002 | −12.4% | 8.7% |
The portfolio’s return clearly involves an averaging of the returns on the stock and bond investments. The mean that we compute, however, must reflect the fact that stocks have a 70 percent weight in the portfolio and bonds have a 30 percent weight. The way to reflect this weighting is to multiply the return on the stock investment by 0.70 and the return on the bond investment by 0.30, then sum the two results. This sum is an example of a weighted mean. It would be incorrect to take an arithmetic mean of the return on the stock and bond investments, equally weighting the returns on the two asset classes.
Consider a portfolio invested in Canadian stocks and bonds in which the stock component is indexed on the S&P/TSX Composite Index and the bond component is indexed on the RBC Capital Markets Canadian Bond Market Index. These indexes represent the broad Canadian equity and bond markets, respectively. The portfolio manager allocates 60 percent of the portfolio to Canadian stocks and 40 percent to Canadian bonds.
Table 3-13 presents total returns for these indexes for 1998 to 2002.
•
Weighted Mean Formula. The
weighted mean 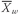
(read
“X -bar sub-
w”) for a set of observations
X1,
X2, . . . ,
Xn with corresponding weights of
w1,
w2, . . . ,
wn is computed as
where the sum of the weights equals 1; that is,
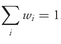
.
In the context of portfolios, a positive weight represents an asset held long and a negative weight represents an asset held short.
43The return on the portfolio under consideration is the weighted average of the return on Canadian stocks and Canadian bonds (the weight on stocks is 0.60; that on bonds is 0.40). Apart from expenses, if the portfolio tracks the indexes perfectly, we find, using
Equation 3-4, that
It should be clear that the correct mean to compute in this example is the weighted mean and not the arithmetic mean. If we had computed the arithmetic mean for 1998, we would have calculated a return equal to ½(−1.6%) + ½(9.1%) = (−1.6% + 9.1%)/2 = 3.8%. Given that the portfolio manager invested 60 percent in stocks and 40 percent in bonds, the arithmetic mean would underweight the investment in stocks and overweight the investment in bonds, resulting in a number for portfolio return that is too high by 1.1 percentage points (3.8% − 2.7%).
Now suppose that the portfolio manager maintains constant weights of 60 percent in stocks and 40 percent in bonds for all five years. This method is called a constant-proportions strategy. Because value is price multiplied by quantity, price fluctuation causes portfolio weights to change. As a result, the constant-proportions strategy requires rebalancing to restore the weights in stocks and bonds to their target levels. Assuming that the portfolio manager is able to accomplish the necessary rebalancing, we can compute the portfolio returns in 1999, 2000, 2001, and 2002 with
Equation 3-4 as follows:
Portfolio return for 1999 = 0.60(31.7) + 0.40(−1.1) = 18.6%
Portfolio return for 2000 = 0.60(7.4) + 0.40(10.3) = 8.6%
Portfolio return for 2001 = 0.60(−12.6) + 0.40(8.0) = −4.4%
Portfolio return for 2002 = 0.60(−12.4) + 0.40(8.7) = −4.0%
We can now find the time-series mean of the returns for 1998 through 2002 using
Equation 3-3 for the arithmetic mean. The time-series mean total return for the portfolio is (2.7 + 18.6 + 8.6 − 4.4 − 4.0)/5 = 21.5/5 = 4.3 percent.
Instead of calculating the portfolio time-series mean return from portfolio annual returns, we can calculate the arithmetic mean bond and stock returns for the five years and then apply the portfolio weights of 0.60 and 0.40, respectively, to those values. The mean stock return is (−1.6 + 31.7 + 7.4 − 12.6 − 12.4)/5 = 12.5/5 = 2.5 percent. The mean bond return is (9.1 − 1.1 + 10.3 + 8.0 + 8.7)/5 = 35.0/5 = 7.0 percent. Therefore, the mean total return for the portfolio is 0.60(2.5) + 0.40(7.0) = 4.3 percent, which agrees with our previous calculation.
EXAMPLE 3-6 Portfolio Return as a Weighted Mean
Table 3-14 gives information on the estimated average asset allocation of Canadian pension funds as well as four-year asset class returns.
44
TABLE 3-14 Asset Allocation for Average Canadian Pension Fund as of 31 March 2003
Source: Standard Life Investments, Inc.
| Asset Class | Asset Allocation (Weight) | Asset Class Return (%) |
|---|
| Equities | 34.6 | 0.6 |
| U.S. equities | 10.8 | −9.3 |
| International equities | 6.4 | —10.5 |
| Bonds | 34.0 | 6.0 |
| Mortgages | 1.3 | 9.0 |
| Real estate | 4.5 | 10.2 |
| Cash and equivalents | 8.4 | 4.2 |
Using the information in
Table 3-14, calculate the mean return earned by the average Canadian pension fund over the four years ending 31 March 2003.
Solution: Converting the percent asset allocation to decimal form, we find the mean return as a weighted average of the asset class returns. We have
The previous examples illustrate the general principle that a portfolio return is a weighted sum. Specifically, a portfolio’s return is the weighted average of the returns on the assets in the portfolio; the weight applied to each asset’s return is the fraction of the portfolio invested in that asset.
Market indexes are computed as weighted averages. For market-capitalization indexes such as the CAC-40 in France or the S&P 500 in the United States, each included stock receives a weight corresponding to its outstanding market value divided by the total market value of all stocks in the index.
Our illustrations of weighted mean use past data, but they might just as well use forward-looking data. When we take a weighted average of forward-looking data, the weighted mean is called
expected value. Suppose we make one forecast for the year-end level of the S&P 500 assuming economic expansion and another forecast for the year-end level of the S&P 500 assuming economic contraction. If we multiply the first forecast by the probability of expansion and the second forecast by the probability of contraction and then add these weighted forecasts, we are calculating the expected value of the S&P 500 at year-end. If we take a weighted average of possible future returns on the S&P 500, we are computing the S&P 500’s expected return. The probabilities must sum to 1, satisfying the condition on the weights in the expression for weighted mean,
Equation 3-4.
5.4.2. The Geometric Mean The geometric mean is most frequently used to average rates of change over time or to compute the growth rate of a variable. In investments, we frequently use the geometric mean to average a time series of rates of return on an asset or a portfolio or to compute the growth rate of a financial variable such as earnings or sales. In the chapter on the time value of money, for instance, we computed a sales growth rate (Example 1-17). That growth rate was a geometric mean. Because of the subject’s importance, in a later section we will return to the use of the geometric mean and offer practical perspectives on its use. The geometric mean is defined by the following formula.
•
Geometric Mean Formula. The
geometric mean,
G, of a set of observations
X1, X2, . . . ,
Xn is
with
Xi ≥ 0 for
i = 1, 2, . . . ,
n.
Equation 3-5 has a solution, and the geometric mean exists, only if the product under the radical sign is non-negative. We impose the restriction that all the observations
Xi in
Equation 3-5 are greater than or equal to zero. We can solve for the geometric mean using
Equation 3-5 directly with any calculator that has an exponentiation key (on most calculators,
yx). We can also solve for the geometric mean using natural logarithms.
Equation 3-5 can also be stated as
or as
When we have computed ln G, then G = elnG (on most calculators, the key for this step is ex).
Risky assets can have negative returns up to −100 percent (if their price falls to zero), so we must take some care in defining the relevant variables to average in computing a geometric mean. We cannot just use the product of the returns for the sample and then take the
nth root because the returns for any period could be negative. We must redefine the returns to make them positive. We do this by adding 1.0 to the returns expressed as decimals. The term (1 +
Rt) represents the year-ending value relative to an initial unit of investment at the beginning of the year. As long as we use (1 +
Rt ), the observations will never be negative because the biggest negative return is −100 percent. The result is the geometric mean of 1 +
Rt ; by then subtracting 1.0 from this result, we obtain the geometric mean of the individual returns
Rt. For example, the returns on Canadian stocks as represented by the S&P/TSX Composite Index during the 1998—2002 period were given in
Table 3-13 as −0.016, 0.317, 0.074, −0.126, and −0.124, putting the returns into decimal form. Adding 1.0 to those returns produces 0.9840, 1.317, 1.074, 0.874, and 0.876. Using
Equation 3-5 we have

. This number is 1 plus the geometric mean rate of return. Subtracting 1.0 from this result, we have 1.012792 − 1.0 = 0.012792 or approximately 1.3 percent. The geometric mean return for Canadian stocks during the 1998 – 2002 period was 1.3 percent.
An equation that summarizes the calculation of the geometric mean return,
RG, is a slightly modified version of
Equation 3-5 in which the
Xi represent “1 + return in decimal form.” Because geometric mean returns use time series, we use a subscript
t indexing time as well.
which leads to the following formula:
•
Geometric Mean Return Formula. Given a time series of holding period returns
Rt, t = 1, 2, . . . ,
T, the geometric mean return over the time period spanned by the returns
R1 through
RT is
We can use
Equation 3-6 to solve for the geometric mean return for any return data series. Geometric mean returns are also referred to as compound returns. If the returns being averaged in
Equation 3-6 have a monthly frequency, for example, we may call the geometric mean monthly return the compound monthly return. The next example illustrates the computation of the geometric mean while contrasting the geometric and arithmetic means.
EXAMPLE 3-7 Geometric and Arithmetic Mean Returns (1)
As a mutual fund analyst, you are examining, as of early 2003, the most recent five years of total returns for two U.S. large-cap value equity mutual funds.
Based on the data in
Table 3-15, address the following:
1. Calculate the geometric mean return of SLASX.
2. Calculate the arithmetic mean return of SLASX and contrast it to the fund’s geometric mean return.
3. Calculate the geometric mean return of PRFDX.
4. Calculate the arithmetic mean return of PRFDX and contrast it to the fund’s geometric mean return.
Solution to 1: Converting the returns on SLASX to decimal form and adding 1.0 to each return produces 1.162, 1.203, 1.093, 0.889, and 0.830. We use
Equation 3-6 to find SLASX’s geometric mean return:
TABLE 3-15 Total Returns for Two Mutual Funds, 1998—2002
Source: American Association of Individual Investors (AAII).
| Year | Selected American Shares (SLASX) | T. Rowe Price Equity Income (PRFDX) |
|---|
| 1998 | 16.2% | 9.2% |
| 1999 | 20.3% | 3.8% |
| 2000 | 9.3% | 13.1% |
| 2001 | −11.1% | 1.6% |
| 2002 | —17.0% | —13.0% |
Solution to 2: For SLASX,
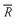
= (16.2 + 20.3 + 9.3 − 11.1 − 17.0)/5 = 17.7/5 = 3.54%. The arithmetic mean return for SLASX exceeds the geometric mean return by 3.54 − 2.43 = 1.11% or 111 basis points.
Solution to 3: Converting the returns on PRFDX to decimal form and adding 1.0 to each return produces 1.092, 1.038, 1.131, 1.016, and 0.870. We use
Equation 3-6 to find PRFDX’s geometric mean return:
Solution to 4: For PRFDX,
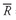
= (9.2 + 3.8 + 13.1 + 1.6 − 13.0)/5 = 14.7/5 = 2.94%. The arithmetic mean for PRFDX exceeds the geometric mean return by 2.94 − 2.53 = 0.41% or 41 basis points. The table below summarizes the findings.
TABLE 3-16 Mutual Fund Arithmetic and Geometric Mean Returns: Summary of Findings
| Fund | Arithmetic Mean | Geometric Mean |
|---|
| SLASX | 3.54% | 2.43% |
| PRFDX | 2.94% | 2.53% |
In Example 3-7, for both mutual funds, the geometric mean return was less than the arithmetic mean return. In fact, the geometric mean is always less than or equal to the arithmetic mean.
45 The only time that the two means will be equal is when there is no variability in the observations—that is, when all the observations in the series are the same.
46 In Example 3-7, there was variability in the funds’ returns; thus for both funds, the geometric mean was strictly less than the arithmetic mean. In general, the difference between the arithmetic and geometric means increases with the variability in the period-by-period observations.
47 This relationship is also illustrated by Example 3-7. Even casual inspection reveals that the returns of SLASX are more variable than those of PRFDX, and consequently, the spread between the arithmetic and geometric mean returns is larger for SLASX (111 basis points) than for PRFDX (41 basis points).
48 The arithmetic and geometric mean also rank the two funds differently. Although SLASX has the higher arithmetic mean return, PRFDX has the higher geometric mean return. How should the analyst interpret this result?
The geometric mean return represents the growth rate or compound rate of return on an investment. One dollar invested in SLASX at the beginning of 1998 would have grown to (1.162)(1.203)(1.093)(0.889)(0.830) = $1.127, which is equal to 1 plus the geometric mean return compounded over five periods: (1.0243)5 = $1.127, confirming that the geometric mean is the compound rate of return. For PRFDX, one dollar would have grown to a larger amount, (1.092)(1.038)(1.131)(1.016)(0.870) = $1.133, equal to (1.0253)5. With its focus on the profitability of an investment over a multiperiod horizon, the geometric mean is of key interest to investors. The arithmetic mean return, focusing on average single-period performance, is also of interest. Both arithmetic and geometric means have a role to play in investment management, and both are often reported for return series. Example 3-8 highlights these points in a simple context.
EXAMPLE 3-8 Geometric and Arithmetic Mean Returns (2)
A hypothetical investment in a single stock initially costs €100. One year later, the stock is trading at €200. At the end of the second year, the stock price falls back to the original purchase price of €100. No dividends are paid during the two-year period. Calculate the arithmetic and geometric mean annual returns.
Solution: First, we need to find the Year 1 and Year 2 annual returns with
Equation 3-1.
Return in Year 1 = 200/100 − 1 = 100%
Return in Year 2 = 100/200 − 1 = −50%
The arithmetic mean of the annual returns is (100% − 50%)/2 = 25%.
Before we find the geometric mean, we must convert the percentage rates of return to (1 +
Rt ). After this adjustment, the geometric mean from
Equation 3-6 is
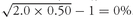
.
The geometric mean return of 0 percent accurately reflects that the ending value of the investment in Year 2 equals the starting value in Year 1. The compound rate of return on the investment is 0 percent. The arithmetic mean return reflects the average of the one-year returns.
5.4.3. The Harmonic Mean The arithmetic mean, the weighted mean, and the geometric mean are the most frequently used concepts of mean in investments. A fourth concept, the harmonic mean,
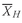
, is appropriate in a limited number of applications.
49•
Harmonic Mean Formula. The
harmonic mean of a set of observations
X1,
X2, . . . ,
Xn is
with
Xi > 0 for
i = 1, 2, . . . ,
n.
The harmonic mean is the value obtained by summing the reciprocals of the observations—terms of the form 1/Xi—then averaging that sum by dividing it by the number of observations n, and, finally, taking the reciprocal of the average.
The harmonic mean may be viewed as a special type of weighted mean in which an observation’s weight is inversely proportional to its magnitude. The harmonic mean is a relatively specialized concept of the mean that is appropriate when averaging ratios (“amount per unit”) when the ratios are repeatedly applied to a fixed quantity to yield a variable number of units. The concept is best explained through an illustration. A well-known application arises in the investment strategy known as cost averaging, which involves the periodic investment of a fixed amount of money. In this application, the ratios we are averaging are prices per share at purchases dates, and we are applying those prices to a constant amount of money to yield a variable number of shares.
Suppose an investor purchases €1,000 of a security each month for n = 2 months. The share prices are €10 and €15 at the two purchase dates. What is the average price paid for the security?
In this example, in the first month we purchase €1,000/€10 = 100 shares, and in the second month we purchase €1,000/€15 = 66.67, or 166.67 shares in total. Dividing the total euro amount invested, €2,000, by the total number of shares purchased, 166.67, gives an average price paid of €2,000/166.67 = €12. The average price paid is in fact the harmonic mean of the asset’s prices at the purchase dates. Using
Equation 3-7, the harmonic mean price is 2/[(1/10) + (1/15)] = €12. The value €12 is less than the arithmetic mean purchase price (€10 + €15)/2 = €12.5. However, we could find the correct value of €12 using the weighted mean formula, where the weights on the purchase prices equal the shares purchased at a given price as a proportion of the total shares purchased. In our example, the calculation would be (100/166.67)€10.00 + (66.67/166.67)€15.00 = €12. If we had invested varying amounts of money at each date, we could not use the harmonic mean formula. We could, however, still use the weighted mean formula in a manner similar to that just described.
A mathematical fact concerning the harmonic, geometric, and arithmetic means is that unless all the observations in a dataset have the same value, the harmonic mean is less than the geometric mean, which in turn is less than the arithmetic mean. In the illustration given, the harmonic mean price was indeed less than the arithmetic mean price.
6. OTHER MEASURES OF LOCATION: QUANTILES
Having discussed measures of central tendency, we now examine an approach to describing the location of data that involves identifying values at or below which specified proportions of the data lie. For example, establishing that 25, 50, and 75 percent of the annual returns on a portfolio are at or below the values −0.05, 0.16, and 0.25, respectively, provides concise information about the distribution of portfolio returns. Statisticians use the word quantile (or fractile) as the most general term for a value at or below which a stated fraction of the data lies. In the following, we describe the most commonly used quantiles—quartiles, quintiles, deciles, and percentiles—and their application in investments.
6.1. Quartiles, Quintiles, Deciles, and Percentiles
We know that the median divides a distribution in half. We can define other dividing lines that split the distribution into smaller sizes. Quartiles divide the distribution into quarters, quintiles into fifths, deciles into tenths, and percentiles into hundredths. Given a set of observations, the yth percentile is the value at or below which y percent of observations lie. Percentiles are used frequently, and the other measures can be defined with respect to them. For example, the first quartile (Q1) divides a distribution such that 25 percent of the observations lie at or below it; therefore, the first quartile is also the 25th percentile. The second quartile (Q2) represents the 50th percentile, and the third quartile (Q3) represents the 75th percentile because 75 percent of the observations lie at or below it.
When dealing with actual data, we often find that we need to approximate the value of a percentile. For example, if we are interested in the value of the 75th percentile, we may find that no observation divides the sample such that exactly 75 percent of the observations lie at or below that value. The following procedure, however, can help us determine or estimate a percentile. The procedure involves first locating the position of the percentile within the set of observations and then determining (or estimating) the value associated with that position.
Let
Py be the value at or below which
y percent of the distribution lies, or the
yth percentile. (For example,
P18 is the point at or below which 18 percent of the observations lie; 100 − 18 = 82 percent are greater than
P18.) The formula for the position of a percentile in an array with
n entries sorted in ascending order is
where
y is the percentage point at which we are dividing the distribution and
Ly is the location (
L) of the percentile (
Py) in the array sorted in ascending order. The value of
Ly may or may not be a whole number. In general, as the sample size increases, the percentile location calculation becomes more accurate; in small samples it may be quite approximate.
As an example of the case in which
Ly is not a whole number, suppose that we want to determine the third quartile of returns for 2002 (
Q3 or
P75) for the 16 European equity markets given in
Table 3-8. According to
Equation 3-8, the position of the third quartile is
L75 = (16 + 1)75/100 = 12.75, or between the 12th and 13th items in
Table 3-9, which ordered the returns into ascending order. The 12th item in
Table 3-9 is the return to equities in Portugal in 2002, −28.29 percent. The 13th item is the return to equities in Switzerland in 2002, −25.84 percent. Reflecting the “0.75” in “12.75,” we would conclude that
P75 lies 75 percent of the distance between −28.29 percent and −25.84 percent.
To summarize:
• When the location, Ly, is a whole number, the location corresponds to an actual observation. For example, if Italy had not been included in the sample, then n + 1 would have been 16 and, with L75 = 12, the third quartile would be P75 = X12, where Xi is defined as the value of the observation in the ith (i = L75) position of the data sorted in ascending order (i.e., P75 = −28.29).
• When Ly is not a whole number or integer, Ly lies between the two closest integer numbers (one above and one below), and we use linear interpolation between those two places to determine Py. Interpolation means estimating an unknown value on the basis of two known values that surround it (lie above and below it); the term “linear” refers to a straight-line estimate. Returning to the calculation of P75 for the equity returns, we found that Ly = 12.75; the next lower whole number is 12 and the next higher whole number is 13. Using linear interpolation, P75 ≈ X12 + (12.75 − 12)(X13 − X12). As above, in the 12th position is the return to equities in Portugal, so X12 = −28.29 percent; X13 = −25.84 percent, the return to equities in Switzerland. Thus our estimate is P75 ≈ X12 + (12.75 − 12)(X13 − X12 ) = −28.29 + 0.75[−25.84 − (−28.29)] = −28.29 + 0.75(2.45) = −28.29 + 1.84 = −26.45 percent. In words, −28.29 and −25.84 bracket P75 from below and above, respectively. Because 12.75 − 12 = 0.75, using linear interpolation we move 75 percent of the distance from −28.29 to −25.84 as our estimate of P75. We follow this pattern whenever Ly is non-integer: The nearest whole numbers below and above Ly establish the positions of observations that bracket Py and then interpolate between the values of those two observations.
Example 3-9 illustrates the calculation of various quantiles for the dividend yield on the components of a major European equity index.
EXAMPLE 3-9 Calculating Percentiles, Quartiles, and Quintiles
The DJ EuroSTOXX 50 is an index of Europe’s 50 largest publicly traded companies as measured by market capitalization.
Table 3-17 shows the dividend yields on the 50 component stocks in the index as of mid-2003, ranked in ascending order.
TABLE 3-17 Dividend Yields on the Components of the DJ EuroSTOXX 50
Using the data in
Table 3-17, address the following:
1. Calculate the 10th and 90th percentiles.
2. Calculate the first, second, and third quartiles.
3. State the value of the median.
4. How many quintiles are there, and to what percentiles do the quintiles correspond?
5. Calculate the value of the first quintile.
Solution to 1: In this example,
n = 50. Using
Equation 3-8,
Ly = (
n + 1)
y/100 for position of the
yth percentile, so for the 10th percentile we have
L10 = (50 + 1)(10/100) = 5.1
L10 is between the fifth and sixth observations with values
X5 = 0.26 and
X6 = 1.09. The estimate of the 10th percentile (first decile) for dividend yield is
For the 90th percentile,
L90 = (50 + 1)(90/100) = 45.9
L90 is between the 45th and 46th observations with values
X45 = 5.15 and
X46 = 5.66, respectively. The estimate of the 90th percentile (ninth decile) is
Solution to 2: The first, second, and third quartiles correspond to P25, P50, and P75, respectively.
Solution to 3: The median is the 50th percentile, 2.65 percent. This is the same value that we would obtain by taking the mean of the n/2 = 50/2 = 25th item and (n + 2)/2 = 52/2 = 26th item, consistent with the procedure given earlier for the median of an even-numbered sample.
Solution to 4: There are four quintiles, and they correspond to P20, P40, P60, and P80.
Solution to 5: The first quintile is P20.
The estimate of the first quintile is
6.2. Quantiles in Investment Practice
In this section, we discuss the use of quantiles in investments. Quantiles are used in portfolio performance evaluation as well as in investment strategy development and research.
Investment analysts use quantiles every day to rank performance—for example, the performance of portfolios. The performance of investment managers is often characterized in terms of the quartile in which they fall relative to the performance of their peer group of managers. The Morningstar mutual fund star rankings, for example, associates the number of stars with percentiles of performance relative to similar-style mutual funds.
Another key use of quantiles is in investment research. Analysts refer to a group defined by a particular quantile as that quantile. For example, analysts often refer to the set of companies with returns falling below the 10th percentile cutoff point as the bottom return decile. Dividing data into quantiles based on some characteristic allows analysts to evaluate the impact of that characteristic on a quantity of interest. For instance, empirical finance studies commonly rank companies based on the market value of their equity and then sort them into deciles. The 1st decile contains the portfolio of those companies with the smallest market values, and the 10th decile contains those companies with the largest market value. Ranking companies by decile allows analysts to compare the performance of small companies with large ones.
We can illustrate the use of quantiles, in particular quartiles, in investment research using the example of Bauman, Conover, and Miller (1998). That study compared the performance of international growth stocks to value stocks. Typically, value stocks are defined as those for which the market price is relatively low in relation to earnings per share, book value per share, or dividends per share. Growth stocks, on the other hand, have comparatively high prices in relation to those same measures. The Bauman et al. classification criteria were the following valuation measures: price-to-earnings (P/E), price-to-cash flow (P/CF), price-to-book value (P/B), and dividend yield (D/P). They assigned one-fourth of the total sample with the lowest P/E on 30 June of each year from 1986 to 1996 (the value group) to Quartile 1, and the one-fourth with the highest P/E of each year (the growth group) to Quartile 4. The stocks with the second-highest P/E formed Quartile 3, and the stocks with the second-lowest P/E, Quartile 2. The authors repeated this process for each of the four fundamental factors. Treating each quartile group as a portfolio composed of equally weighted stocks, they were able to compare the performance of the various value/growth quartiles. Table 1 from their study is reproduced as
Table 3-18.
TABLE 3-18 Mean Annual Returns of Value and Growth Stocks Based on Selected Characteristics, 1986—1996
Source: Bauman et al.
Table 3-18 reports each valuation factor’s median, mean return, and standard deviation for each quartile grouping. Moving from Quartile 1 to Quartile 4, P/E, P/CF, and P/B increase, but D/P decreases. Regardless of the selection criteria, international value stocks outperformed international growth stocks during the sample period.
Bauman, Conover, and Miller also divided companies into one of four quartiles based on market value of equity. Then they examined the returns to the stocks in the quartiles. Table 7 from their article is reproduced here as
Table 3-19. As the table shows, the small-company portfolio had a median market value of $46.6 million and the large-company portfolio had a median value of $2,472.3 million. Large companies were more than 50 times larger than small companies, yet their mean stock returns were less than half those of the small companies (small, 22.0 percent; large, 10.8 percent). Overall, Bauman et al. found two effects. First, international value stocks (as the authors defined them) outperformed international growth stocks. Second, international small stocks outperformed international large stocks.
The authors’ next step was to examine how value and growth stocks performed while controlling for size. This step involved constructing 16 different value/growth and size portfolios (4 × 4 = 16) and investigating the interaction between these two fundamental factors. They found that international value stocks outperformed international growth stocks except when market capitalization was very small. For portfolio managers, these findings suggest that value stocks offered investors relatively more favorable returns than did growth stocks in international markets during the specific time period studied.
TABLE 3-19 Mean Annual Returns of International Stocks Grouped by Market Capitalization, 1986—1996
Source: Bauman et al.
7. MEASURES OF DISPERSION
As the well-known researcher Fischer Black has written, “[t]he key issue in investments is estimating expected return.”
50 Few would disagree with the importance of expected return or mean return in investments: The mean return tells us where returns, and investment results, are centered. To completely understand an investment, however, we also need to know how returns are dispersed around the mean.
Dispersion is the variability around the central tendency. If mean return addresses reward, dispersion addresses risk.
In this section, we examine the most common measures of dispersion: range, mean absolute deviation, variance, and standard deviation. These are all measures of absolute dispersion. Absolute dispersion is the amount of variability present without comparison to any reference point or benchmark.
These measures are used throughout investment practice. The variance or standard deviation of return is often used as a measure of risk pioneered by Nobel laureate Harry Markowitz. William Sharpe, another winner of the Nobel Prize in economics, developed the Sharpe ratio, a measure of risk-adjusted performance. That measure makes use of standard deviation of return. Other measures of dispersion, mean absolute deviation and range, are also useful in analyzing data.
7.1. The Range
We encountered range earlier when we discussed the construction of frequency distribution. The simplest of all the measures of dispersion, range can be computed with interval or ratio data.
•
Definition of Range. The
range is the difference between the maximum and minimum values in a dataset:
As an illustration of range, the largest monthly return for the S&P 500 in the period from January 1926 to December 2002 is 42.56 percent (in April 1933) and the smallest is −29.73 percent (in September 1931). The range of returns is thus 72.29 percent [42.56 percent − (−29.73 percent)]. An alternative definition of range reports the maximum and minimum values. This alternative definition provides more information than does the range as defined in
Equation 3-9.
One advantage of the range is ease of computation. A disadvantage is that the range uses only two pieces of information from the distribution. It cannot tell us how the data are distributed (that is, the shape of the distribution). Because the range is the difference between the maximum and minimum returns, it can reflect extremely large or small outcomes that may not be representative of the distribution.
51
7.2. The Mean Absolute Deviation
Measures of dispersion can be computed using all the observations in the distribution rather than just the highest and lowest. The question is, how should we measure dispersion? Our previous discussion on properties of the arithmetic mean introduced the notion of distance or deviation from the mean
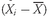
as a fundamental piece of information used in statistics. We could compute measures of dispersion as the arithmetic average of the deviations around the mean, but we would encounter a problem: The deviations around the mean always sum to 0. If we computed the mean of the deviations, the result would also equal 0. Therefore, we need to find a way to address the problem of negative deviations canceling out positive deviation.
One solution is to examine the absolute deviations around the mean as in the mean absolute deviation.
•
Mean Absolute Deviation Formula. The
mean absolute deviation (MAD) for a sample is
(3-10)
where
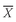
is the sample mean and
n is the number of observations in the sample.
In calculating MAD, we ignore the signs of the deviations around the mean. For example, if
Xi = −11.0 and
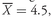
, the absolute value of the difference is | − 11.0 − 4.5| = | − 15.5| = 15.5. The mean absolute deviation uses all of the observations in the sample and is thus superior to the range as a measure of dispersion. One technical drawback of MAD is that it is difficult to manipulate mathematically compared with the next measure we will introduce, variance.
52 Example 3-10 illustrates the use of the range and the mean absolute deviation in evaluating risk.
EXAMPLE 3-10 The Range and the Mean Absolute Deviation
Having calculated mean returns for the two mutual funds in Example 3-7, the analyst is now concerned with evaluating risk.
TABLE 3-15 (repeated) Total Returns for Two Mutual Funds, 1998—2002
Source: AAII.
| Year | Selected American Shares (SLASX) | T. Rowe Price Equity Income (PRFDX) |
|---|
| 1998 | 16.2% | 9.2% |
| 1999 | 20.3% | 3.8% |
| 2000 | 9.3% | 13.1% |
| 2001 | —11.1% | 1.6% |
| 2002 | —17.0% | —13.0% |
Based on the data in
Table 3-15 repeated above, answer the following:
1. Calculate the range of annual returns for (A) SLASX and (B) PRFDX, and state which mutual fund appears to be riskier based on these ranges.
2. Calculate the mean absolute deviation of returns on (A) SLASX and (B) PRFDX, and state which mutual fund appears to be riskier based on MAD.
Solutions to 1:
a. For SLASX, the largest return was 20.3 percent and the smallest was −17.0 percent. The range is thus 20.3 − (−17.0) = 37.3%.
b. For PFRDX, the range is 13.1 − (−13.0) = 26.1%. With a larger range of returns than PRFDX, SLASX appeared to be the riskier fund during the 1998 – 2002 period.
Solutions to 2:
a. The arithmetic mean return for SLASX as calculated in Example 3-7 is 3.54 percent. The MAD of SLASX returns is
b. The arithmetic mean return for PRFDX as calculated in Example 3-7 is 2.94 percent. The MAD of PRFDX returns is
SLASX, with a MAD of 14.1 percent, appears to be much riskier than PRFDX, with a MAD of 6.9 percent.
7.3. Population Variance and Population Standard Deviation
The mean absolute deviation addressed the issue that the sum of deviations from the mean equals zero by taking the absolute value of the deviations. A second approach to the treatment of deviations is to square them. The variance and standard deviation, which are based on squared deviations, are the two most widely used measures of dispersion. Variance is defined as the average of the squared deviations around the mean. Standard deviation is the positive square root of the variance. The following discussion addresses the calculation and use of variance and standard deviation.
7.3.1. Population Variance If we know every member of a population, we can compute the population variance. Denoted by the symbol σ2, the population variance is the arithmetic average of the squared deviations around the mean.
•
Population Variance Formula. The
population variance is
where µ is the population mean and
N is the size of the population.
Given knowledge of the population mean, µ, we can use
Equation 3-11 to calculate the sum of the squared differences from the mean, taking account of all
N items in the population, and then to find the mean squared difference by dividing the sum by
N. Whether a difference from the mean is positive or negative, squaring that difference results in a positive number. Thus variance takes care of the problem of negative deviations from the mean canceling out positive deviations by the operation of squaring those deviations. The P/Es for BJ, COST, and WMT were given earlier as 16.73, 22.02, and 29.30, respectively. We calculated the mean P/E as 22.68. Therefore, the population variance of the P/Es is (1/3)[(16.73 − 22.68)
2 + (22.02 − 22.68)
2 + (29.30 − 22.68)
2] = (1/3)(−5.95
2 + −0.66
2 + 6.62
2) = (1/3)(35.4025 + 0.4356 + 43.8244) = (1/3)(79.6625) = 26.5542.
7.3.2. Population Standard Deviation Because the variance is measured in squared units, we need a way to return to the original units. We can solve this problem by using standard deviation, the square root of the variance. Standard deviation is more easily interpreted than the variance because standard deviation is expressed in the same unit of measurement as the observations.
•
Population Standard Deviation Formula. The
population standard deviation, defined as the positive square root of the population variance, is
where µ is the population mean and
N is the size of the population.
Using the example of the P/Es for BJ, COST, and WMT, according to
Equation 3-12 we would calculate the variance, 26.5542, then take the square root:
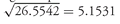
or approximately 5.2.
Both the population variance and standard deviation are examples of parameters of a distribution. In later chapters, we will introduce the notion of variance and standard deviation as risk measures.
In investments, we often do not know the mean of a population of interest, usually because we cannot practically identify or take measurements from each member of the population. We then estimate the population mean with the mean from a sample drawn from the population, and we calculate a sample variance or standard deviation using formulas different from
Equations 3-11 and
3-12. We shall discuss these calculations in subsequent sections. However, in investments we sometimes have a defined group that we can consider to be a population. With well-defined populations, we use
Equations 3-11 and
3-12, as in the following example.
EXAMPLE 3-11 Calculating the Population Standard Deviation
Table 3-20 gives the yearly portfolio turnover for the 10 U.S. equity funds that composed the 2002 Forbes Magazine Honor Roll.
53 Portfolio turnover, a measure of trading activity, is the lesser of the value of sales or purchases over a year divided by average net assets during the year. The number and identity of the funds on the Forbes Honor Roll changes from year to year.
TABLE 3-20 Portfolio Turnover: 2002 Forbes Honor Roll Mutual Funds
Source: Forbes (2003).
| Fund | Yearly Portfolio Turnover |
|---|
| FPA Capital Fund (FPPTX) | 23% |
| Mairs & Power Growth Fund (MPGFX) | 8% |
| Muhlenkamp Fund (MUHLX) | 11% |
| Longleaf Partners Fund (LLPFX) | 18% |
| Heartland Value Fund (HRTVX) | 56% |
| Scudder—Dreman High Return Equity-A (KDHAX) | 29% |
| Clipper Fund (CFIMX) | 23% |
| Weitz Value Fund (WVALX) | 13% |
| Third Avenue Value Fund (TAVFX) | 16% |
| Dodge & Cox Stock Fund (DODGX) | 10% |
Based on the data in
Table 3-20, address the following:
1. Calculate the population mean portfolio turnover for the period used by Forbes for the ten 2002 Honor Roll funds.
2. Calculate the population variance and population standard deviation of portfolio turnover.
3. Explain the use of the population formulas in this example.
Solution to 1: µ = (23 + 8 + 11 + 18 + 56 + 29 + 23 + 13 + 16 + 10)/10 = 207/ 10 = 20.7 percent
Solution to 2: Having established that µ = 20.7, we can calculate
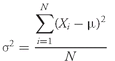
by first calculating the numerator in the expression and then dividing by
N = 10. The numerator (the sum of the squared differences from the mean) is
Thus σ2 = 1,784.1/10 = 178.41.
To calculate standard deviation,
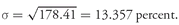
. (The unit of variance is percent squared, so the unit of standard deviation is percent.)
Solution to 3: If the population is clearly defined to be the Forbes Honor Roll funds in one specific year (2002), and if portfolio turnover is understood to refer to the specific one-year period reported upon by
Forbes, the application of the population formulas to variance and standard deviation is appropriate. The results of 178.41 and 13.357 are, respectively, the cross-sectional variance and standard deviation in yearly portfolio turnover for the 2002 Forbes Honor Roll Funds.
54
7.4. Sample Variance and Sample Standard Deviation
7.4.1. Sample Variance In many instances in investment management, a subset or sample of the population is all that we can observe. When we deal with samples, the summary measures are called statistics. The statistic that measures the dispersion in a sample is called the sample variance.
•
Sample Variance Formula. The
sample variance is
where
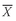
is the sample mean and
n is the number of observations in the sample.
Equation 3-13 tells us to take the following steps to compute the sample variance:
i. Calculate the sample mean,
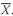
.
ii. Calculate each observation’s squared deviation from the sample mean,
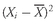
.
iii. Sum the squared deviations from the mean:
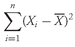
iv. Divide the sum of squared deviations from the mean by
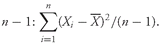
.
We will illustrate the calculation of the sample variance and the sample standard deviation in Example 3-12.
We use the notation
s2 for the sample variance to distinguish it from population variance, σ
2. The formula for sample variance is nearly the same as that for population variance except for the use of the sample mean,
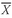
, in place of the population mean, µ, and a different divisor. In the case of the population variance, we divide by the size of the population,
N. For the sample variance, however, we divide by the sample size minus 1, or
n − 1. By using
n − 1 (rather than
n) as the divisor, we improve the statistical properties of the sample variance. In statistical terms, the sample variance defined in
Equation 3-13 is an unbiased estimator of the population variance.
55 The quantity
n − 1 is also known as the number of degrees of freedom in estimating the population variance. To estimate the population variance with
s2, we must first calculate the mean. Once we have computed the sample mean, there are only
n − 1 independent deviations from it.
7.4.2. Sample Standard Deviation Just as we computed a population standard deviation, we can compute a sample standard deviation by taking the positive square root of the sample variance.
•
Sample Standard Deviation Formula. The
sample standard deviation,
s, is
where
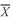
is the sample mean and
n is the number of observations in the sample.
To calculate the sample standard deviation, we first compute the sample variance using the steps given. We then take the square root of the sample variance. Example 3-12 illustrates the calculation of the sample variance and standard deviation for the two mutual funds introduced earlier.
EXAMPLE 3-12 Calculating Sample Variance and Sample Standard Deviation
After calculating the geometric and arithmetic mean returns of two mutual funds in Example 3-7, we calculated two measures of dispersions for those funds, the range and mean absolute deviation of returns, in Example 3-10. We now calculate the sample variance and sample standard deviation of returns for those same two funds.
TABLE 3-15 (repeated) Total Returns for Two Mutual Funds, 1998—2002
Source: AAII.
| Year | Selected American Shares (SLASX) | T. Rowe Price Equity Income (PRFDX) |
|---|
| 1998 | 16.2% | 9.2% |
| 1999 | 20.3% | 3.8% |
| 2000 | 9.3% | 13.1% |
| 2001 | —11.1% | 1.6% |
| 2002 | —17.0% | —13.0% |
Based on the data in
Table 3-15 repeated above, answer the following:
1. Calculate the sample variance of return for (A) SLASX and (B) PRFDX.
2. Calculate sample standard deviation of return for (A) SLASX and (B) PRFDX.
3. Contrast the dispersion of returns as measured by standard deviation of return and mean absolute deviation of return for each of the two funds.
Solution to 1: To calculate the sample variance, we use
Equation 3-13. (Deviation answers are all given in percent squared.)
a.
SLASX i. The sample mean is
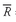
= (16.2 + 20.3 + 9.3 − 11.1 − 17.0)/5 = 17.7/5 = 3.54%.
ii. The squared deviations from the mean are
(16.2 − 3.54)2 = (12.66)2 = 160.2756
(20.3 − 3.54)2 = (16.76)2 = 280.8976
(9.3 − 3.54)2 = (5.76)2 = 33.1776
(−11.1 − 3.54)2 = (−14.64)2 = 214.3296
(−17.0 − 3.54)2 = (−20.54)2 = 421.8916
iii. The sum of the squared deviations from the mean is 160.2756 + 280.8976 + 33.1776 + 214.3296 + 421.8916 = 1,110.5720.
iv. Divide the sum of the squared deviations from the mean by n − 1: 1,110.5720/(5 − 1) = 1,110.5720/4 = 277.6430.
b.
PRFDX i. The sample mean is
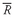
= (9.2 + 3.8 + 13.1 + 1.6 − 13.0)/5 = 14.7/5 = 2.94%.
ii. The squared deviations from the mean are
(9.2 − 2.94)2 = (6.26)2 = 39.1876
(3.8 − 2.94)2 = (0.86)2 = 0.7396
(13.1 − 2.94)2 = (10.16)2 = 103.2256
(1.6 − 2.94)2 = (−1.34)2 = 1.7956
(−13.0 − 2.94)2 = (−15.94)2 = 254.0836
iii. The sum of the squared deviations from the mean is 39.1876 + 0.7396 + 103.2256 + 1.7956 + 254.0836 = 399.032.
iv. Divide the sum of the squared deviations from the mean by n − 1: 399.032/4 = 99.758.
Solution to 2: To find the standard deviation, we take the positive square root of variance.
a. For SLASX,

or 16.7 percent.
b. For PRFDX,
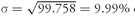
or 10.0 percent.
Solution to 3:
Table 3-21 summarizes the results from Part 2 for standard deviation and incorporates the results for MAD from Example 3-10.
Note that the mean absolute deviation is less than the standard deviation. The mean absolute deviation will always be less than or equal to the standard deviation because the standard deviation gives more weight to large deviations than to small ones (remember, the deviations are squared).
TABLE 3-21 Two Mutual Funds: Comparison of Standard Deviation and Mean Absolute Deviation
| Fund | Standard Deviation | Mean Absolute Deviation |
|---|
| SLASX | 16.7% | 14.1% |
| PRFDX | 10.0% | 6.9% |
Because the standard deviation is a measure of dispersion about the arithmetic mean, we usually present the arithmetic mean and standard deviation together when summarizing data. When we are dealing with data that represent a time series of percent changes, presenting the geometric mean—representing the compound rate of growth—is also very helpful.
Table 3-22 presents the historical geometric and arithmetic mean returns, along with the historical standard deviation of returns, for various equity return series. We present these statistics for nominal (rather than inflation-adjusted) returns so we can observe the original magnitudes of the returns.
TABLE 3-22 Equity Market Returns: Means and Standard Deviations
Source: Ibbotson EnCorr Analyzer; Dimson et al.
7.5. Semivariance, Semideviation, and Related Concepts
An asset’s variance or standard deviation of returns is often interpreted as a measure of the asset’s risk. Variance and standard deviation of returns take account of returns above and below the mean, but investors are concerned only with downside risk, for example, returns below the mean. As a result, analysts have developed semivariance, semideviation, and related dispersion measures that focus on downside risk.
Semivariance is defined as the average squared deviation below the mean.
Semideviation (sometimes called semistandard deviation) is the positive square root of semivariance. To compute the sample semivariance, for example, we take the following steps:
i. Calculate the sample mean.
ii. Identify the observations that are smaller than the mean (discarding observations equal to and greater than the mean); suppose there are n∗ observations smaller than the mean.
iii. Compute the sum of the squared negative deviations from the mean (using the n∗ observations that are smaller than the mean).
iv. Divide the sum of the squared negative deviations from Step iii by
n∗ − 1. A formula for semivariance is
To take the case of Selected American Shares with returns (in percent) of 16.2, 20.3, 9.3, −11.1, and −17.0, we earlier calculated a mean return of 3.54 percent. Two returns, −11.1 and −17.0, are smaller than 3.54 (
n∗ = 2). We compute the sum of the squared negative deviations from the mean as (−11.1 − 3.54)
2 + (−17.0 − 3.54)
2 = −14.64
2 + (−20.54)
2 = 214.3296 + 421.8916 = 636.2212. With
n* − 1 = 1, we conclude that semivariance is 636.2212/1 = 636.2212 and that semideviation is
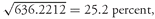
, approximately. The semideviation of 25.2 percent is greater than the standard deviation of 16.7 percent. From this downside risk perspective, therefore, standard deviation understates risk.
In practice, we may be concerned with values of return (or another variable) below some level other than the mean. For example, if our return objective is 10 percent annually, we may be concerned particularly with returns below 10 percent a year. We can call 10 percent the target. The name
target semivariance has been given to average squared deviation below a stated target, and
target semideviation is its positive square root. To calculate a sample target semivariance, we specify the target as a first step. After identifying observations below the target, we find the sum of the squared negative deviations from the target and divide that sum by the number of observations below the target minus 1. A formula for target semivariance is
where
B is the target and
n∗ is the number of observations below the target. With a target return of 10 percent, we find in the case of Selected American Shares that three returns (9.3, −11.1, and −17.0) were below the target. The target semivariance is [(9.3 − 10.0)
2 + (—1.1 − 10.0)
2 + (−17.0 − 10.0)
2]/(3 − 1) = 587.35, and the target semideviation is

= 24.24 percent, approximately.
When return distributions are symmetric, semivariance is a constant proportion (one-half) of variance and the two measures are effectively equivalent. For asymmetric distributions, variance and semivariance rank prospects’ risk differently.
56 Semivariance (or semideviation) and target semivariance (or target semideviation) have intuitive appeal, but they are harder to work with mathematically than variance.
57 Variance or standard deviation enters into the definition of many of the most commonly used finance risk concepts, such as the Sharpe ratio and beta. Perhaps because of these reasons, variance (or standard deviation) is much more frequently used in investment practice.
7.6. Chebyshev’s Inequality
The Russian mathematician Pafnuty Chebyshev developed an inequality using standard deviation as a measure of dispersion. The inequality gives the proportion of values within k standard deviations of the mean.
• Definition of Chebyshev’s Inequality. According to Chebyshev’s inequality, the proportion of the observations within k standard deviations of the arithmetic mean is at least 1 − 1/k2 for all k > 1.
Table 3-23 illustrates the proportion of the observations that must lie within a certain number of standard deviations around the sample mean.
When k = 1.25, for example, the inequality states that the minimum proportion of the observations that lie within ±1.25s is 1 − 1/(1.25)2 = 1 − 0.64 = 0.36 or 36 percent.
The most frequently cited facts that result from Chebyshev’s inequality are that a two-standard-deviation interval around the mean must contain at least 75 percent of the observations and a three-standard-deviation interval around the mean must contain at least 89 percent of the observations, no matter how the data are distributed.
The importance of Chebyshev’s inequality stems from its generality. The inequality holds for samples and populations and for discrete and continuous data regardless of the shape of the distribution. As we shall see in the chapter on sampling, we can make much more precise interval statements if we can assume that the sample is drawn from a population that follows a specific distribution called the normal distribution. Frequently, however, we cannot confidently assume that distribution.
TABLE 3-23 Proportions from Chebyshev’s Inequality
| k | Interval Around the Sample Mean | Proportion |
|---|
| 1.25 | 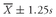 | 36% |
| 1.50 | 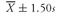 | 56% |
| 2.00 | 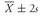 | 75% |
| 2.50 | 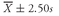 | 84% |
| 3.00 | 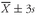 | 89% |
| 4.00 | 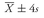 | 94% |
| Note: Standard deviation is denoted as s. |
The next example illustrates the use of Chebyshev’s inequality.
EXAMPLE 3-13 Applying Chebyshev’s Inequality
According to
Table 3-22, the arithmetic mean monthly return and standard deviation of monthly returns on the S&P 500 were 0.97 percent and 5.65 percent, respectively, during the 1926—2002 period, totaling 924 monthly observations. Using this information, address the following:
1. Calculate the endpoints of the interval that must contain at least 75 percent of monthly returns according to Chebyshev’s inequality.
2. What are the minimum and maximum number of observations that must lie in the interval computed in Part 1, according to Chebyshev’s inequality?
Solution to 1: According to Chebyshev’s inequality, at least 75 percent of the observations must lie within two standard deviations of the mean,
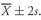
. For the monthly S&P 500 return series, we have 0.97% ± 2(5.65%) = 0.97% ± 11.30%. Thus the lower endpoint of the interval that must contain at least 75 percent of the observations is 0.97% − 11.30% = −10.33%, and the upper endpoint is 0.97% + 11.30% = 12.27%.
Solution to 2: For a sample size of 924, at least 0.75(924) = 693 observations must lie in the interval from −10.33% to 12.27% that we computed in Part 1. Chebyshev’s inequality gives the minimum percentage of observations that must fall within a given interval around the mean, but it does not give the maximum percentage.
Table 3-4, which gave the frequency distribution of monthly returns on the S&P 500, is excerpted below. The data in the excerpted table are consistent with the prediction of Chebyshev’s inequality. The set of intervals running from −10.0% to 12.0% is just slightly narrower than the two-standard-deviation interval −10.33% to 12.27%. A total of 886 observations (approximately 96 percent of observations) fall in the range from −10.0% to 12.0%.
TABLE 3-4 (Excerpt) Frequency Distribution for the Monthly Total Return on the S&P 500, January 1926 to December 2002
| Return Interval | Absolute Frequency |
|---|
| −10.0% to −8.0% | 20 |
| −8.0% to −6.0% | 30 |
| −6.0% to −4.0% | 54 |
| −4.0% to −2.0% | 90 |
| −2.0% to 0.0% | 138 |
| 0.0% to 2.0% | 182 |
| 2.0% to 4.0% | 153 |
| 4.0% to 6.0% | 126 |
| 6.0% to 8.0% | 58 |
| 8.0% to 10.0% | 21 |
| 10.0% to 12.0% | 14 |
| 886 |
7.7. Coefficient of Variation
We noted earlier that standard deviation is more easily interpreted than variance because standard deviation uses the same units of measurement as the observations. We may sometimes find it difficult to interpret what standard deviation means in terms of the relative degree of variability of different sets of data, however, either because the datasets have markedly different means or because the datasets have different units of measurement. In this section we explain a measure of relative dispersion, the coefficient of variation that can be useful in such situations. Relative dispersion is the amount of dispersion relative to a reference value or benchmark.
We can illustrate the problem of interpreting the standard deviation of datasets with markedly different means using two hypothetical samples of companies. The first sample, composed of small companies, includes companies with 2003 sales of €50 million, €75 million, €65 million, and €90 million. The second sample, composed of large companies, includes companies with 2003 sales of €800 million, €825 million, €815 million, and €840 million. We can verify using
Equation 3-14 that the standard deviation of sales in both samples is €16.8 million.
58 In the first sample, the largest observation, €90 million, is 80 percent larger than the smallest observation, €50 million. In the second sample, the largest observation is only 5 percent larger than the smallest observation. Informally, a standard deviation of €16.8 million represents a high degree of variability relative to the first sample, which reflects mean 2003 sales of €70 million, but a small degree of variability relative to the second sample, which reflects mean 2003 sales of €820 million.
The coefficient of variation is helpful in situations such as that just described.
•
Coefficient of Variation Formula. The
coefficient of variation, CV, is the ratio of the standard deviation of a set of observations to their mean value:
59 (3-15)
where
s is the sample standard deviation and
X is the sample mean.
When the observations are returns, for example, the coefficient of variation measures the amount of risk (standard deviation) per unit of mean return. Expressing the magnitude of variation among observations relative to their average size, the coefficient of variation permits direct comparisons of dispersion across different datasets. Reflecting the correction for scale, the coefficient of variation is a scale-free measure (that is, it has no units of measurement).
We can illustrate the application of the coefficient of variation using our earlier example of two samples of companies. The coefficient of variation for the first sample is (€16.8 million)/(€70 million) = 0.24; the coefficient of variation for the second sample is (€16.8 million)/(€820 million) = 0.02. This confirms our intuition that the first sample had much greater variability in sales than the second sample. Note that 0.24 and 0.02 are pure numbers in the sense that they are free of units of measurement (because we divided the standard deviation by the mean, which is measured in the same units as the standard deviation). If we need to compare the dispersion among data sets stated in different units of measurement, the coefficient of variation can be useful because it is free from units of measurement. Example 3-14 illustrates the calculation of the coefficient of variation.
EXAMPLE 3-14 Calculating the Coefficient of Variation
Table 3-24 summarizes annual mean returns and standard deviations for several major U.S. asset classes, using an option in Ibbotson EnCorr Analyzer to convert monthly return statistics to annual ones.
TABLE 3-24 Arithmetic Mean Annual Return and Standard Deviation of Returns, U.S. Asset Classes, 1926—2002
Source: Ibbotson EnCorr Analyzer.
| Asset Class | Arithmetic Mean Return | Standard Deviation of Return |
|---|
| S&P 500 | 12.3% | 21.9% |
| U.S. small stock | 16.9% | 35.1% |
| U.S. long-term corporate | 6.1 % | 7.2% |
| U.S. long-term government | 5.8% | 8.2% |
| U.S. 30-day T-bill | 3.8% | 0.9% |
Using the information in
Table 3-24, address the following:
1. Calculate the coefficient of variation for each asset class given.
2. Rank the asset classes from most risky to least risky using CV as a measure of relative dispersion.
3. Determine whether there is more difference between the absolute or the relative riskiness of the S&P 500 and U.S. small stocks. Use the standard deviation as a measure of absolute risk and CV as a measure of relative risk.
Solution to 1:
S&P 500: CV = 21.9%/12.3% = 1.780
U.S. small stock: CV = 35.1%/16.9% = 2.077
U.S. long-term corporate: CV = 7.2%/6.1% = 1.180
U.S. long-term government: CV = 8.2%/5.8% = 1.414
U.S. 30-day T-bill: CV = 0.9%/3.8% = 0.237
Solution to 2: Based on CV, the ranking is U.S. small stocks (most risky), S&P 500, U.S. long-term governments, U.S. long-term corporates, and U.S. 30-day T-bills (least risky).
Solution to 3: As measured both by standard deviation and CV, U.S. small stocks were riskier than the S&P 500. However, the CVs reveal less difference between small stock and S&P 500 return variability than that suggested by the standard deviations alone. The standard deviation of small stock returns was (35.1 − 21.9)/21.9 = 0.603 or about 60 percent larger than S&P 500 returns, compared with a difference in the CV of (2.077 − 1.780)/1.780 = 0.167 or 17 percent.
7.8. The Sharpe Ratio
Although CV was designed as a measure of relative dispersion, its inverse reveals something about return per unit of risk because the standard deviation of returns is commonly used as a measure of investment risk. For example, a portfolio with a mean monthly return of 1.19 percent and a standard deviation of 4.42 percent has an inverse CV of 1.19%/4.42% = 0.27. This result indicates that each unit of standard deviation represents a 0.27 percent return.
A more precise return—risk measure recognizes the existence of a risk-free return, a return for virtually zero standard deviation. With a risk-free asset, an investor can choose a risky portfolio, p, and then combine that portfolio with the risk-free asset to achieve any desired level of absolute risk as measured by standard deviation of return, sp. Consider a graph with mean return on the vertical axis and standard deviation of return on the horizontal axis. Any combination of portfolio p and the risk-free asset lies on a ray (line) with slope equal to the quantity (Mean return − Risk-free return) divided by sp. The ray giving investors choices offering the most reward (return in excess of the risk-free rate) per unit of risk is the one with the highest slope. The ratio of excess return to standard deviation of return for a portfolio p—the slope of the ray passing through p—is a single-number measure of a portfolio’s performance known as the Sharpe ratio, after its developer, William F. Sharpe.
•
Sharpe Ratio Formula. The
Sharpe ratio for a portfolio
p, based on historical returns, is defined as
(3-16)
where
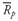
is the mean return to the portfolio,
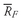
is the mean return to a risk-free asset, and
sp is the standard deviation of return on the portfolio.
60 The numerator of the Sharpe measure is the portfolio’s mean return minus the mean return on the risk-free asset over the sample period. The
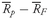
term measures the extra reward that investors receive for the added risk taken. We call this difference the
mean excess return on portfolio
p. Thus the Sharpe ratio measures the reward, in terms of mean excess return, per unit of risk, as measured by standard deviation of return. Those risk-averse investors who make decisions only in terms of mean return and standard deviation of return prefer portfolios with larger Sharpe ratios to those with smaller Sharpe ratios.
To illustrate the calculation of the Sharpe ratio, consider the performance of the S&P 500 and U.S. small stocks during the 1926—2002 period, as given previously in
Table 3-24. Using the mean U.S. T-bill return to represent the risk-free rate, we find
Although U.S. small stocks earned higher mean returns, they performed slightly less well than the S&P 500, as measured by the Sharpe ratio.
The Sharpe ratio is a mainstay of performance evaluation. We must issue two cautions concerning its use, one related to interpreting negative Sharpe ratios and the other to conceptual limitations.
Finance theory tells us that in the long run, investors should be compensated with additional mean return above the risk-free rate for bearing additional risk, at least if the risky portfolio is well diversified. If investors are so compensated, the numerator of the Sharpe ratio will be positive. Nevertheless, we often find that portfolios exhibit negative Sharpe ratios when the ratio is calculated over periods in which bear markets for equities dominate. This raises a caution when dealing with negative Sharpe ratios. With positive Sharpe ratios, a portfolio’s Sharpe ratio decreases if we increase risk, all else equal. That result is intuitive for a risk-adjusted performance measure. With negative Sharpe ratios, however, increasing risk results in a numerically larger Sharpe ratio (for example, doubling risk may increase the Sharpe ratio from −1 to −0.5). Therefore, in a comparison of portfolios with negative Sharpe ratios, we cannot generally interpret the larger Sharpe ratio (the one closer to zero) to mean better risk-adjusted performance.
61 Practically, to make an interpretable comparison in such cases using the Sharpe ratio, we may need to increase the evaluation period such that one or more of the Sharpe ratios becomes positive; we might also consider using a different performance evaluation metric.
The conceptual limitation of the Sharpe ratio is that it considers only one aspect of risk, standard deviation of return. Standard deviation is most appropriate as a risk measure for portfolio strategies with approximately symmetric return distributions. Strategies with option elements have asymmetric returns. Relatedly, an investment strategy may produce frequent small gains but have the potential for infrequent but extremely large losses.
62 Such a strategy is sometimes described as picking up coins in front of a bulldozer; for example, some hedge fund strategies tend to produce that return pattern. Calculated over a period in which the strategy is working (a large loss has not occurred), this type of strategy would have a high Sharpe ratio. In this case, the Sharpe ratio would give an overly optimistic picture of risk-adjusted performance because standard deviation would incompletely measure the risk assumed.
63 Therefore, before applying the Sharpe ratio to evaluate a manager, we should judge whether standard deviation adequately describes the risk of the manager’s investment strategy.
Example 3-15 illustrates the calculation of the Sharpe ratio in a portfolio performance evaluation context.
EXAMPLE 3-15 Calculating the Sharpe Ratio
In earlier examples, we computed the various statistics for two mutual funds, Selected American Shares (SLASX) and T. Rowe Price Equity Income (PRFDX), for a five-year period ending in December 2002.
Table 3-25 summarizes selected statistics for these two mutual funds for a longer period, the 10-year period ending in 2002.
TABLE 3-25 Mutual Fund Mean Return and Standard Deviation of Return, 1993—2002
Source: AAII.
| Fund | Arithmetic Mean | Standard Deviation of Return |
|---|
| SLASX | 12.58% | 19.44% |
| PRFDX | 11.64% | 13.65% |
The U.S. 30-day T-bill rate is frequently used as a proxy for the risk-free rate.
Table 3-26 gives the annual return on T-bills for the 1993—2002 period.
TABLE 3-26 Annualized U.S. 30-Day T-Bill Rates of Return, 1993—2002
Source: Ibbotson Associates.
| Year | Return |
|---|
| 1993 | 2.90% |
| 1994 | 3.90% |
| 1995 | 5.60% |
| 1996 | 5.21% |
| 1997 | 5.26% |
| 1998 | 4.86% |
| 1999 | 4.68% |
| 2000 | 5.89% |
| 2001 | 3.83% |
| 2002 | 1.65% |
Using the information in
Tables 3-25 and
3-26, address the following:
1. Calculate the Sharpe ratios for SLASX and PRFDX during the 1993—2002 period.
2. State which fund had superior risk-adjusted performance during this period, as measured by the Sharpe ratio.
Solution to 1: We already have in hand the means of the portfolio return and standard deviations of returns. The mean annual risk-free rate of return from 1993 to 2002, using U.S. T-bills as a proxy, is (2.90 + 3.90 + 5.60 + 5.21 + 5.26 + 4.86 + 4.68 + 5.89 + 3.83 + 1.65)/10 = 43.78/10 = 4.38 percent.
Solution to 2: PRFDX had a higher positive Sharpe ratio than SLASX during the period. As measured by the Sharpe ratio, PRFDX’s performance was superior.
8. SYMMETRY AND SKEWNESS IN RETURN DISTRIBUTIONS
Mean and variance may not adequately describe an investment’s distribution of returns. In calculations of variance, for example, the deviations around the mean are squared, so we do not know whether large deviations are likely to be positive or negative. We need to go beyond measures of central tendency and dispersion to reveal other important characteristics of the distribution. One important characteristic of interest to analysts is the degree of symmetry in return distributions.
If a return distribution is symmetrical about its mean, then each side of the distribution is a mirror image of the other. Thus equal loss and gain intervals exhibit the same frequencies. Losses from −5 percent to −3 percent, for example, occur with about the same frequency as gains from 3 percent to 5 percent.
One of the most important distributions is the normal distribution, depicted in
Figure 3-6. This symmetrical, bell-shaped distribution plays a central role in the mean—variance model of portfolio selection; it is also used extensively in financial risk management. The normal distribution has the following characteristics:
• Its mean and median are equal.
• It is completely described by two parameters—its mean and variance.
• Roughly 68 percent of its observations lie between plus and minus one standard deviation from the mean; 95 percent lie between plus and minus two standard deviations; and 99 percent lie between plus and minus three standard deviations.
A distribution that is not symmetrical is called
skewed. A return distribution with positive skew has frequent small losses and a few extreme gains. A return distribution with negative skew has frequent small gains and a few extreme losses.
Figure 3-7 shows positively and negatively skewed distributions. The positively skewed distribution shown has a long tail on its right side; the negatively skewed distribution has a long tail on its left side. For the positively skewed unimodal distribution, the mode is less than the median, which is less than the mean. For the negatively skewed unimodal distribution, the mean is less than the median, which is less than the mode.
64 Investors should be attracted by a positive skew because the mean return falls above the median. Relative to the mean return, positive skew amounts to a limited, though frequent, downside compared with a somewhat unlimited, but less frequent, upside.
FIGURE 3-6 Properties of a Normal Distribution (EV = Expected Value)
Source: Reprinted with permission from Fixed Income Readings for the Chartered Financial Analyst® Program. Copyright 2000, Frank J. Fabozzi Associates, New Hope, PA.
Source: Reprinted with permission from Fixed Income Readings for the Chartered Financial Analyst®Program. Copyright 2000, Frank J. Fabozzi Associates, New Hope, PA.
Skewness is the name given to a statistical measure of skew. (The word “skewness” is also sometimes used interchangeably for “skew.”) Like variance, skewness is computed using each observation’s deviation from its mean.
Skewness (sometimes referred to as relative skewness) is computed as the average cubed deviation from the mean standardized by dividing by the standard deviation cubed to make the measure free of scale.
65 A symmetric distribution has skewness of 0, a positively skewed distribution has positive skewness, and a negatively skewed distribution has negative skewness, as given by this measure.
We can illustrate the principle behind the measure by focusing on the numerator. Cubing, unlike squaring, preserves the sign of the deviations from the mean. If a distribution is positively skewed with a mean greater than its median, then more than half of the deviations from the mean are negative and less than half are positive. In order for the sum to be positive, the losses must be small and likely, and the gains less likely but more extreme. Therefore, if skewness is positive, the average magnitude of positive deviations is larger than the average magnitude of negative deviations.
A simple example illustrates that a symmetrical distribution has a skewness measure equal to 0. Suppose we have the following data: 1, 2, 3, 4, 5, 6, 7, 8, and 9. The mean outcome is 5, and the deviations are −4, −3, −2, −1, 0, 1, 2, 3, and 4. Cubing the deviations yields −64, −27, −8, −1, 0, 1, 8, 27, and 64, with a sum of 0. The numerator of skewness (and so skewness itself) is thus equal to 0, supporting our claim. Below we give the formula for computing skewness from a sample.
TABLE 3-27 S&P 500 Annual and Monthly Total Returns, 1926-2002: Summary Statistics
Source: Ibbotson EnCorr Analyzer.
•
Sample Skewness Formula.
Sample skewness (also called
sample relative skewness),
SK, is
where
n is the number of observations in the sample and
s is the sample standard deviation.
66 The algebraic sign of
Equation 3-17 indicates the direction of skew, with a negative
SK indicating a negatively skewed distribution and a positive
SK indicating a positively skewed distribution. Note that as
n becomes large, the expression reduces to the mean cubed deviation,
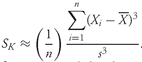
. As a frame of reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of ±0.5 would be considered unusually large.
Table 3-27 shows several summary statistics for the annual and monthly returns on the S&P 500. Earlier we discussed the arithmetic mean return and standard deviation of return, and we shall shortly discuss kurtosis.
Table 3-27 reveals that S&P 500 annual returns during this period were negatively skewed while monthly returns were positively skewed, and the magnitude of skewness was greater for the monthly series. We would find for other market series that the shape of the distribution of returns often depends on the holding period examined.
Some researchers believe that investors should prefer positive skewness, all else equal—that is, they should prefer portfolios with distributions offering a relatively large frequency of unusually large payoffs.
67 Different investment strategies may tend to introduce different types and amounts of skewness into returns. Example 3-16 illustrates the calculation of skewness for a managed portfolio.
EXAMPLE 3-16 Calculating Skewness for a Mutual Fund
Table 3-28 presents 10 years of annual returns on the T. Rowe Price Equity Income Fund (PRFDX).
TABLE 3-28 Annual Rates of Return: T. Rowe Price Equity Income, 1993-2002
Source: AAII.
| Year | Return |
|---|
| 1993 | 14.8% |
| 1994 | 4.5% |
| 1995 | 33.3% |
| 1996 | 20.3% |
| 1997 | 28.8% |
| 1998 | 9.2% |
| 1999 | 3.8% |
| 2000 | 13.1% |
| 2001 | 1.6% |
| 2002 | −13.0% |
Using the information in
Table 3-28, address the following:
1. Calculate the skewness of PRFDX showing two decimal places.
2. Characterize the shape of the distribution of PRFDX returns based on your answer to Part 1.
Solution to 1: To calculate skewness, we find the sum of the cubed deviations from the mean, divide by the standard deviation cubed, and then multiply that result by
n/[(
n − 1)(
n − 2)].
Table 3-29 gives the calculations.
Source: AAII.
In this example, five deviations are negative and five are positive. Two large positive deviations, in 1995 and 1997, are more than offset by a very large negative deviation in 2002 and a moderately large negative deviation in 2001, both bear market years. The result is that skewness is a very small negative number.
Solution to 2: Based on this small sample, the distribution of annual returns for the fund appears to be approximately symmetric (or very slightly negatively skewed). The negative and positive deviations from the mean are equally frequent, and large positive deviations approximately offset large negative deviations.
9. KURTOSIS IN RETURN DISTRIBUTIONS
In the previous section, we discussed how to determine whether a return distribution deviates from a normal distribution because of skewness. One other way in which a return distribution might differ from a normal distribution is by having more returns clustered closely around the mean (being more peaked) and more returns with large deviations from the mean (having fatter tails). Relative to a normal distribution, such a distribution has a greater percentage of small deviations from the mean return (more small surprises) and a greater percentage of extremely large deviations from the mean return (more big surprises). Most investors would perceive a greater chance of extremely large deviations from the mean as increasing risk.
Kurtosis is the statistical measure that tells us when a distribution is more or less peaked than a normal distribution. A distribution that is more peaked than normal is called
leptokurtic (
lepto from the Greek word for slender); a distribution that is less peaked than normal is called
platykurtic (
platy from the Greek word for broad); and a distribution identical to the normal distribution in this respect is called
mesokurtic (
meso from the Greek word for middle). The situation of more-frequent extremely large surprises that we described is one of leptokurtosis.
68
Figure 3-8 illustrates a leptokurtic distribution. It is more peaked and has fatter tails than the normal distribution.
The calculation for kurtosis involves finding the average of deviations from the mean raised to the fourth power and then standardizing that average by dividing by the standard deviation raised to the fourth power.
69 For all normal distributions, kurtosis is equal to 3. Many statistical packages report estimates of
excess kurtosis, which is kurtosis minus 3.
70 Excess kurtosis thus characterizes kurtosis relative to the normal distribution. A normal or other mesokurtic distribution has excess kurtosis equal to 0. A leptokurtic distribution has excess kurtosis greater than 0, and a platykurtic distribution has excess kurtosis less than 0. A return distribution with positive excess kurtosis—a leptokurtic return distribution—has more frequent extremely large deviations from the mean than a normal distribution. Below is the expression for computing kurtosis from a sample.
Source: Reprinted with permission from Fixed Income Readings for the Chartered Financial Analyst®Program. Copyright 2000, Frank J. Fabozzi Associates, New Hope, PA.
•
Sample Excess Kurtosis Formula. The
sample excess kurtosis is
where
n is the sample size and
s is the sample standard deviation.
In
Equation 3-18,
sample kurtosis is the first term. Note that as
n becomes large,
Equation 3-18 approximately equals
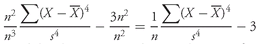
. For a sample of 100 or larger taken from a normal distribution, a sample excess kurtosis of 1.0 or larger would be considered unusually large.
Most equity return series have been found to be leptokurtic. If a return distribution has positive excess kurtosis (leptokurtosis) and we use statistical models that do not account for the fatter tails, we will underestimate the likelihood of very bad or very good outcomes. For example, the return on the S&P 500 for 19 October 1987 was 20 standard deviations away from the mean daily return. Such an outcome is possible with a normal distribution, but its likelihood is almost equal to 0. If daily returns are drawn from a normal distribution, a return four standard deviations or more away from the mean is expected once every 50 years; a return greater than five standard deviations away is expected once every 7,000 years. The return for October 1987 is more likely to have come from a distribution that had fatter tails than from a normal distribution. Looking at
Table 3-27 given earlier, the monthly return series for the S&P 500 has very large excess kurtosis, approximately 9.5. It is extremely fat-tailed relative to the normal distribution. By contrast, the annual return series has very slightly negative excess kurtosis (roughly −0.2). The results for excess kurtosis in the table are consistent with research findings that the normal distribution is a better approximation for U.S. equity returns for annual holding periods than for shorter ones (such as monthly).
71The following example illustrates the calculations for sample excess kurtosis for one of the two mutual funds we have been examining.
EXAMPLE 3-17 Calculating Sample Excess Kurtosis
Having concluded in Example 3-16 that the annual returns on T. Rowe Price Equity Income Fund were approximately symmetrically distributed during the 1993-2002 period, what can we say about the kurtosis of the fund’s return distribution?
Table 3-28 (repeated below) recaps the annual returns for the fund.
TABLE 3-28 (repeated) Annual Rates of Return: T. Rowe Price Equity Income, 1993-2002
Source: AAII.
| Year | Return |
|---|
| 1993 | 14.8% |
| 1994 | 4.5% |
| 1995 | 33.3% |
| 1996 | 20.3% |
| 1997 | 28.8% |
| 1998 | 9.2% |
| 1999 | 3.8% |
| 2000 | 13.1% |
| 2001 | 1.6% |
| 2002 | −13.0% |
Using the information from
Table 3-28 repeated above, address the following:
1. Calculate the sample excess kurtosis of PRFDX showing two decimal places.
2. Characterize the shape of the distribution of PRFDX returns based on your answer to Part 1 as leptokurtic, mesokurtic, or platykurtic.
Solution to 1: To calculate excess kurtosis, we find the sum of the deviations from the mean raised to the fourth power, divide by the standard deviation raised to the fourth power, and then multiply that result by
n(
n + 1)/[(
n − 1)(
n − 2)(
n − 3)]. This calculation determines kurtosis. Excess kurtosis is kurtosis minus 3(
n − 1)
2/[(
n − 2)(
n − 3)].
Table 3-30 gives the calculations.
Source: AAII.
Solution to 2: The distribution of PRFDX’s annual returns appears to be mesokurtic, based on a sample excess kurtosis close to zero. With skewness and excess kurtosis both close to zero, PRFDX’s annual returns appear to have been approximately normally distributed during the period.
72
10. USING GEOMETRIC AND ARITHMETIC MEANS
With the concepts of descriptive statistics in hand, we will see why the geometric mean is appropriate for making investment statements about past performance. We will also explore why the arithmetic mean is appropriate for making investment statements in a forward-looking context.
For reporting historical returns, the geometric mean has considerable appeal because it is the rate of growth or return we would have had to earn each year to match the actual, cumulative investment performance. In our simplified Example 3-8, for instance, we purchased a stock for €100 and two years later it was worth €100, with an intervening year at €200. The geometric mean of 0 percent is clearly the compound rate of growth during the two years. Specifically, the ending amount is the beginning amount times (1 + RG)2. The geometric mean is an excellent measure of past performance.
Example 3-8 illustrated how the arithmetic mean can distort our assessment of historical performance. In that example, the total performance for the two-year period was unambiguously 0 percent. With a 100 percent return for the first year and −50 percent for the second, however, the arithmetic mean was 25 percent. As we noted previously, the arithmetic mean is always greater than or equal to the geometric mean. If we want to estimate the average return over a one-period horizon, we should use the arithmetic mean because the arithmetic mean is the average of one-period returns. If we want to estimate the average returns over more than one period, however, we should use the geometric mean of returns because the geometric mean captures how the total returns are linked over time.
As a corollary to using the geometric mean for performance reporting, the use of
semilogarithmic rather than arithmetic scales is more appropriate when graphing past performance.
73 In the context of reporting performance, a semilogarithmic graph has an arithmetic scale on the horizontal axis for time and a logarithmic scale on the vertical axis for the value of the investment. The vertical axis values are spaced according to the differences between their logarithms. Suppose we want to represent £1, £10, £100, and £1,000 as values of an investment on the vertical axis. Note that each successive value represents a 10-fold increase over the previous value, and each will be equally spaced on the vertical axis because the difference in their logarithms is roughly 2.30; that is, ln 10 − ln 1 = ln 100 − ln 10 = ln 1,000 − ln 100 = 2.30. On a semilogarithmic scale, equal movements on the vertical axis reflect equal percentage changes, and growth at a constant compound rate plots as a straight line. A plot curving upward reflects increasing growth rates over time. The slopes of a plot at different points may be compared in order to judge relative growth rates.
In addition to reporting historical performance, financial analysts need to calculate expected equity risk premiums in a forward-looking context. For this purpose, the arithmetic mean is appropriate.
We can illustrate the use of the arithmetic mean in a forward-looking context with an example based on an investment’s future cash flows. In contrasting the geometric and arithmetic means for discounting future cash flows, the essential issue concerns uncertainty. Suppose an investor with $100,000 faces an equal chance of a 100 percent return or a −50 percent return, represented on the tree diagram as a 50/50 chance of a 100 percent return or a −50 percent return per period. With 100 percent return in one period and −50 percent return in the other, the geometric mean return is
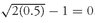
.
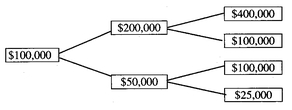
The geometric mean return of 0 percent gives the mode or median of ending wealth after two periods and thus accurately predicts the modal or median ending wealth of $100,000 in this example. Nevertheless, the arithmetic mean return better predicts the arithmetic mean ending wealth. With equal chances of 100 percent or −50 percent returns, consider the four equally likely outcomes of $400,000, $100,000, $100,000, and $25,000 as if they actually occurred. The arithmetic mean ending wealth would be $156,250 = ($400,000 + $100,000 + $100,000 + $25,000)/4. The actual returns would be 300 percent, 0 percent, 0 percent, and −75 percent for a two-period arithmetic mean return of (300 + 0 + 0 − 75)/4 = 56.25 percent. This arithmetic mean return predicts the arithmetic mean ending wealth of $100,000 × 1.5625 = $156,250. Noting that 56.25 percent for two periods is 25 percent per period, we then must discount the expected terminal wealth of $156,250 at the 25 percent arithmetic mean rate to reflect the uncertainty in the cash flows.
Uncertainty in cash flows or returns causes the arithmetic mean to be larger than the geometric mean. The more uncertain the returns, the more divergence exists between the arithmetic and geometric means. The geometric mean return approximately equals the arithmetic return minus half the variance of return.
74 Zero variance or zero uncertainty in returns would leave the geometric and arithmetic returns approximately equal, but real-world uncertainty presents an arithmetic mean return larger than the geometric. For example, Dimson et al. (2002) reported that from 1900 to 2000, U.S. equities had nominal annual returns with an arithmetic mean of 12 percent and standard deviation of 19.9 percent. They reported the geometric mean as 10.1 percent. We can see the geometric mean is approximately the arithmetic mean minus half of the variance of returns:
RG ≈ 0.12 − (1/2)(0.199
2) = 0.10.
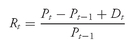 where
where
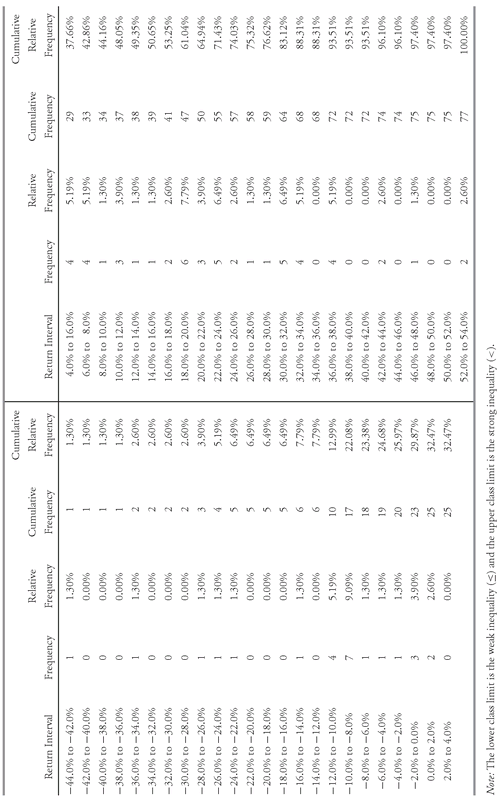

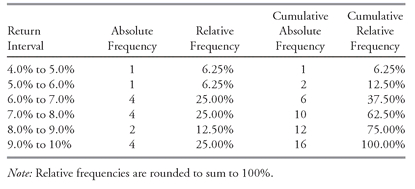
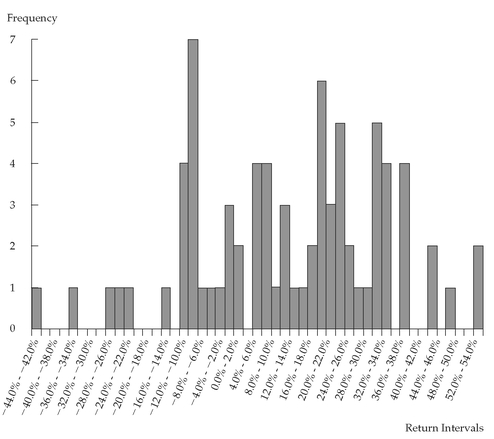
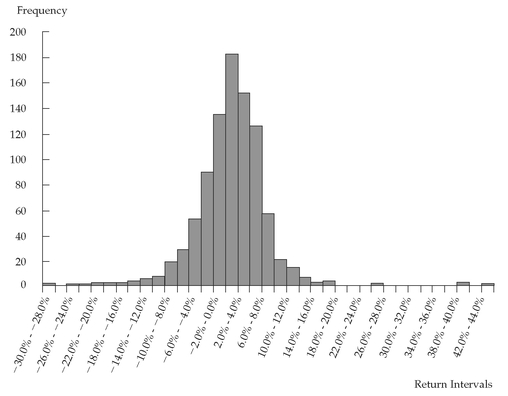
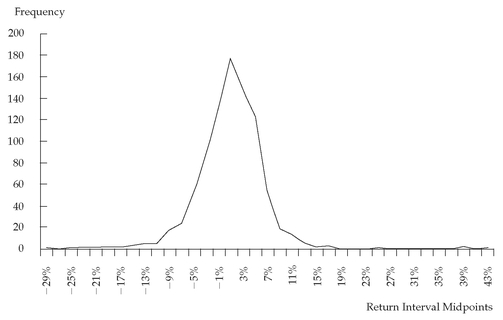
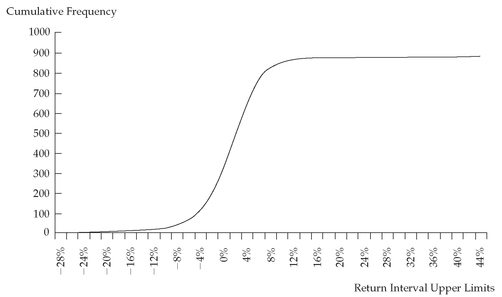

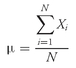
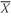 (read “X-bar”), is the arithmetic mean value of a sample:
(read “X-bar”), is the arithmetic mean value of a sample: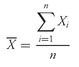
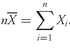 . The sum of the deviations from the mean can thus be calculated as follows:
. The sum of the deviations from the mean can thus be calculated as follows: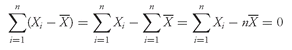

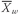 (read “X -bar sub-w”) for a set of observations X1, X2, . . . , Xn with corresponding weights of w1, w2, . . . , wn is computed as
(read “X -bar sub-w”) for a set of observations X1, X2, . . . , Xn with corresponding weights of w1, w2, . . . , wn is computed as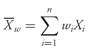
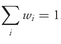 .
.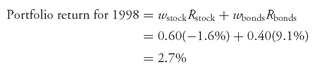

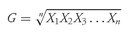
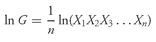
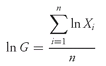
 . This number is 1 plus the geometric mean rate of return. Subtracting 1.0 from this result, we have 1.012792 − 1.0 = 0.012792 or approximately 1.3 percent. The geometric mean return for Canadian stocks during the 1998 – 2002 period was 1.3 percent.
. This number is 1 plus the geometric mean rate of return. Subtracting 1.0 from this result, we have 1.012792 − 1.0 = 0.012792 or approximately 1.3 percent. The geometric mean return for Canadian stocks during the 1998 – 2002 period was 1.3 percent.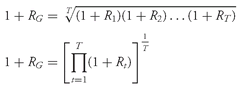
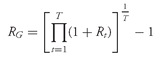
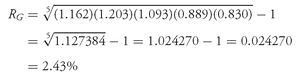
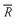 = (16.2 + 20.3 + 9.3 − 11.1 − 17.0)/5 = 17.7/5 = 3.54%. The arithmetic mean return for SLASX exceeds the geometric mean return by 3.54 − 2.43 = 1.11% or 111 basis points.
= (16.2 + 20.3 + 9.3 − 11.1 − 17.0)/5 = 17.7/5 = 3.54%. The arithmetic mean return for SLASX exceeds the geometric mean return by 3.54 − 2.43 = 1.11% or 111 basis points.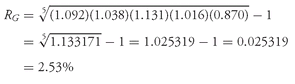
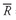 = (9.2 + 3.8 + 13.1 + 1.6 − 13.0)/5 = 14.7/5 = 2.94%. The arithmetic mean for PRFDX exceeds the geometric mean return by 2.94 − 2.53 = 0.41% or 41 basis points. The table below summarizes the findings.
= (9.2 + 3.8 + 13.1 + 1.6 − 13.0)/5 = 14.7/5 = 2.94%. The arithmetic mean for PRFDX exceeds the geometric mean return by 2.94 − 2.53 = 0.41% or 41 basis points. The table below summarizes the findings.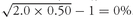 .
.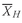 , is appropriate in a limited number of applications.
, is appropriate in a limited number of applications.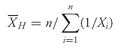
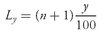
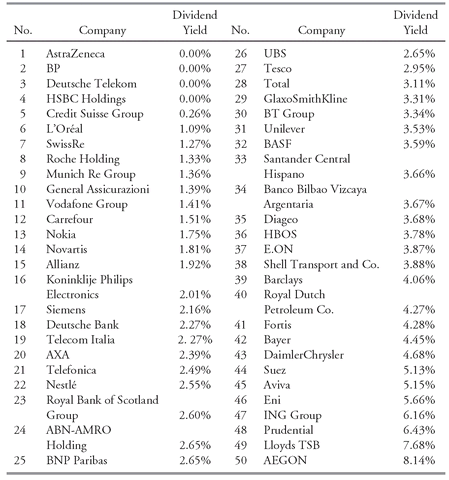
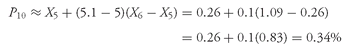
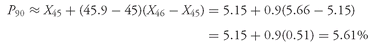

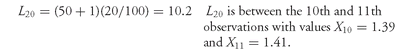
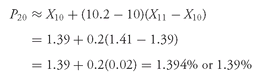
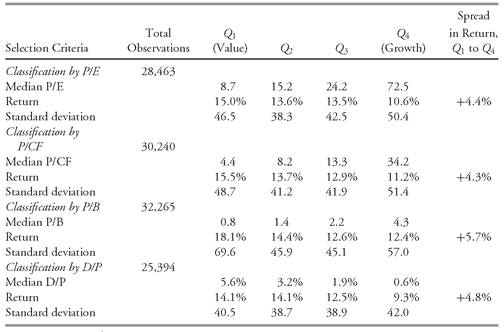
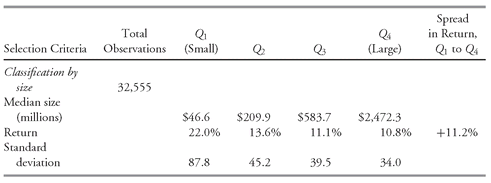
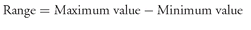
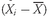 as a fundamental piece of information used in statistics. We could compute measures of dispersion as the arithmetic average of the deviations around the mean, but we would encounter a problem: The deviations around the mean always sum to 0. If we computed the mean of the deviations, the result would also equal 0. Therefore, we need to find a way to address the problem of negative deviations canceling out positive deviation.
as a fundamental piece of information used in statistics. We could compute measures of dispersion as the arithmetic average of the deviations around the mean, but we would encounter a problem: The deviations around the mean always sum to 0. If we computed the mean of the deviations, the result would also equal 0. Therefore, we need to find a way to address the problem of negative deviations canceling out positive deviation.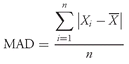
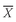 is the sample mean and n is the number of observations in the sample.
is the sample mean and n is the number of observations in the sample.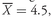 , the absolute value of the difference is | − 11.0 − 4.5| = | − 15.5| = 15.5. The mean absolute deviation uses all of the observations in the sample and is thus superior to the range as a measure of dispersion. One technical drawback of MAD is that it is difficult to manipulate mathematically compared with the next measure we will introduce, variance.
, the absolute value of the difference is | − 11.0 − 4.5| = | − 15.5| = 15.5. The mean absolute deviation uses all of the observations in the sample and is thus superior to the range as a measure of dispersion. One technical drawback of MAD is that it is difficult to manipulate mathematically compared with the next measure we will introduce, variance.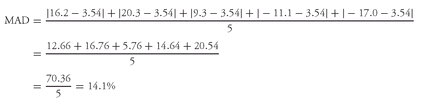
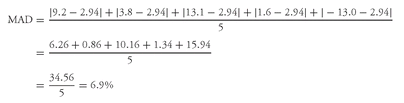
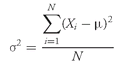
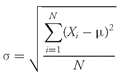
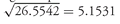 or approximately 5.2.
or approximately 5.2.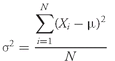 by first calculating the numerator in the expression and then dividing by N = 10. The numerator (the sum of the squared differences from the mean) is
by first calculating the numerator in the expression and then dividing by N = 10. The numerator (the sum of the squared differences from the mean) is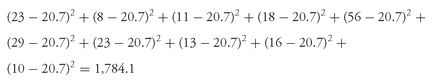
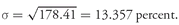 . (The unit of variance is percent squared, so the unit of standard deviation is percent.)
. (The unit of variance is percent squared, so the unit of standard deviation is percent.)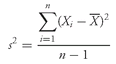
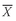 is the sample mean and n is the number of observations in the sample.
is the sample mean and n is the number of observations in the sample.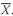 .
.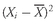 .
.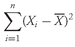
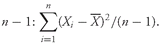 .
.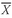 , in place of the population mean, µ, and a different divisor. In the case of the population variance, we divide by the size of the population, N. For the sample variance, however, we divide by the sample size minus 1, or n − 1. By using n − 1 (rather than n) as the divisor, we improve the statistical properties of the sample variance. In statistical terms, the sample variance defined in
, in place of the population mean, µ, and a different divisor. In the case of the population variance, we divide by the size of the population, N. For the sample variance, however, we divide by the sample size minus 1, or n − 1. By using n − 1 (rather than n) as the divisor, we improve the statistical properties of the sample variance. In statistical terms, the sample variance defined in 
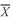 is the sample mean and n is the number of observations in the sample.
is the sample mean and n is the number of observations in the sample.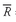 = (16.2 + 20.3 + 9.3 − 11.1 − 17.0)/5 = 17.7/5 = 3.54%.
= (16.2 + 20.3 + 9.3 − 11.1 − 17.0)/5 = 17.7/5 = 3.54%. = (9.2 + 3.8 + 13.1 + 1.6 − 13.0)/5 = 14.7/5 = 2.94%.
= (9.2 + 3.8 + 13.1 + 1.6 − 13.0)/5 = 14.7/5 = 2.94%. or 16.7 percent.
or 16.7 percent. or 10.0 percent.
or 10.0 percent.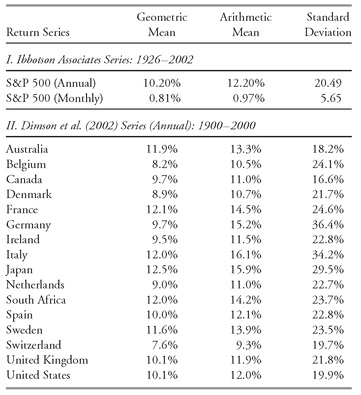
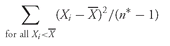
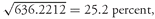 , approximately. The semideviation of 25.2 percent is greater than the standard deviation of 16.7 percent. From this downside risk perspective, therefore, standard deviation understates risk.
, approximately. The semideviation of 25.2 percent is greater than the standard deviation of 16.7 percent. From this downside risk perspective, therefore, standard deviation understates risk.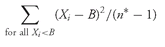
 = 24.24 percent, approximately.
= 24.24 percent, approximately.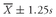
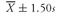
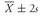
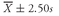
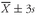
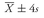
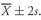 . For the monthly S&P 500 return series, we have 0.97% ± 2(5.65%) = 0.97% ± 11.30%. Thus the lower endpoint of the interval that must contain at least 75 percent of the observations is 0.97% − 11.30% = −10.33%, and the upper endpoint is 0.97% + 11.30% = 12.27%.
. For the monthly S&P 500 return series, we have 0.97% ± 2(5.65%) = 0.97% ± 11.30%. Thus the lower endpoint of the interval that must contain at least 75 percent of the observations is 0.97% − 11.30% = −10.33%, and the upper endpoint is 0.97% + 11.30% = 12.27%.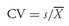
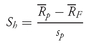
 is the mean return to the portfolio,
is the mean return to the portfolio,  is the mean return to a risk-free asset, and sp is the standard deviation of return on the portfolio.
is the mean return to a risk-free asset, and sp is the standard deviation of return on the portfolio. term measures the extra reward that investors receive for the added risk taken. We call this difference the mean excess return on portfolio p. Thus the Sharpe ratio measures the reward, in terms of mean excess return, per unit of risk, as measured by standard deviation of return. Those risk-averse investors who make decisions only in terms of mean return and standard deviation of return prefer portfolios with larger Sharpe ratios to those with smaller Sharpe ratios.
term measures the extra reward that investors receive for the added risk taken. We call this difference the mean excess return on portfolio p. Thus the Sharpe ratio measures the reward, in terms of mean excess return, per unit of risk, as measured by standard deviation of return. Those risk-averse investors who make decisions only in terms of mean return and standard deviation of return prefer portfolios with larger Sharpe ratios to those with smaller Sharpe ratios.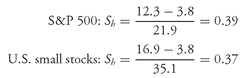
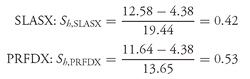
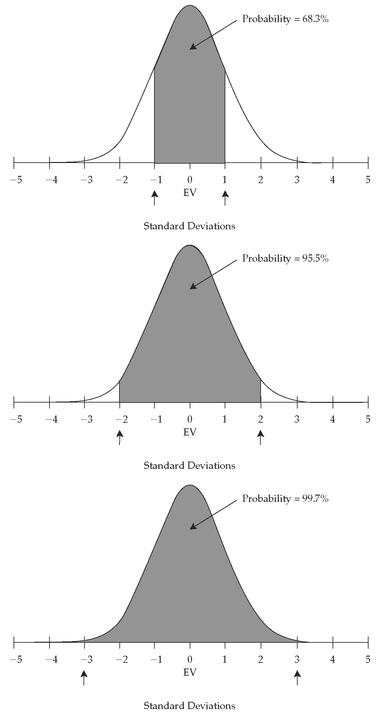

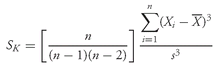
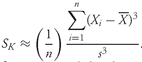 . As a frame of reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of ±0.5 would be considered unusually large.
. As a frame of reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of ±0.5 would be considered unusually large.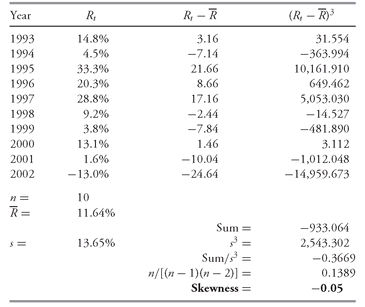
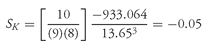
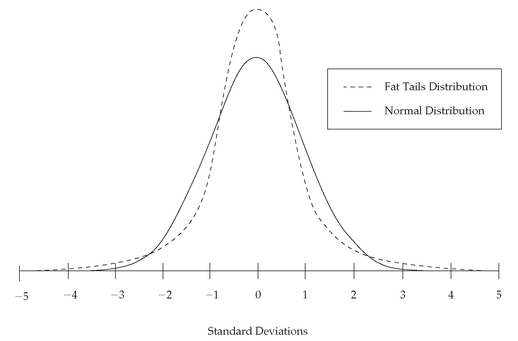
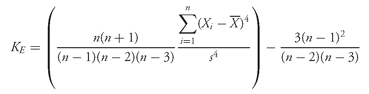
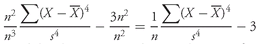 . For a sample of 100 or larger taken from a normal distribution, a sample excess kurtosis of 1.0 or larger would be considered unusually large.
. For a sample of 100 or larger taken from a normal distribution, a sample excess kurtosis of 1.0 or larger would be considered unusually large.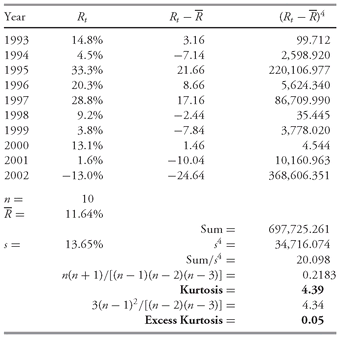

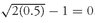 .
.