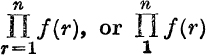 , or Π f(r) for r = 1 to n.
, or Π f(r) for r = 1 to n.CHAPTER XII
It is known that, if a polynomial p0xn + p1xn–1 + … + pn of degree n is zero for x = c, then x – c is a factor of it; also that, if the polynomial is zero for n different values x = c1, x = c2, … , x = cn, it must be identical with p0(x – c1)(x – c2) … (x – cn).
This is also true when c1, c2, … , p0, p1, p2, … are complex numbers, see p. 142, Note 2 (iii).
We proceed to apply this result to factorize various trigonometrical expressions.
Notation for Products. Corresponding to the use of the symbol ∑ to represent sums, it is convenient to use Π to represent products.
Thus we denote f(1) .f(2) .f(3). 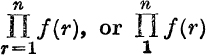 , or Π f(r) for r = 1 to n.
, or Π f(r) for r = 1 to n.
FACTORS OF ALGEBRAIC FUNCTIONS
Factors of xn – 1. xn – 1 = 0 if x is a value of ![]() , and the n different values are given by
, and the n different values are given by ![]() , for r = 1, 2, …, n.
, for r = 1, 2, …, n.
Corresponding to each of these values we have a factor
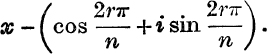
Since r = – k and r = n – k give the same value to ![]() we may use 0, – 1, – 2, … as values of r instead of n, n – 1, n – 2, ….
we may use 0, – 1, – 2, … as values of r instead of n, n – 1, n – 2, ….
(i) n even. We take r = 0, ±1, ±2, … ±(![]() n – 1), and
n – 1), and ![]() n, thus getting (
n, thus getting (![]() n – 1) pairs of factors, and the two single factors given by 0 and
n – 1) pairs of factors, and the two single factors given by 0 and ![]() n, i.e. 2(
n, i.e. 2(![]() n – 1) + 2, = n, in all.
n – 1) + 2, = n, in all.
The factors corresponding to r = ±k are

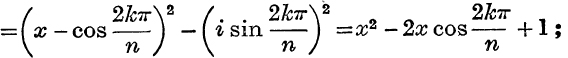
the factors corresponding to r = 0, r = ![]() are x – 1, x + 1. Thus,
are x – 1, x + 1. Thus,
![]()
(ii) n odd. Here we take r = 0, ± 1, ± 2, …, ± ![]() , which gives
, which gives 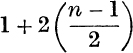 , factors. Thus,
, factors. Thus,
![]()
Factors of xn + 1. xn + 1 = 0 if
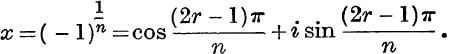
If n is even, we take 2r – 1 = ± 1, ± 3, …, ± (n – 1); and if n is odd, we take 2r – 1 = ± 1, ± 3, …, ± (n ± 2), and n; this last value gives the factor x – cos π – i sin π = x + 1. Thus,
If n is even, we take 2r – 1 = ± 1, ± 3, … , ± (n – 1); and if n is odd, we take 2r – 1 = ± 1, ± 3, …, ± (n – 2), and n ; this last value gives the factor x – cos π – i sin π = x + 1. Thus,
![]()
![]()
It should be remarked that, although the work of this chapter is in complex algebra, the formulae (1) (2) (3) (4) are true results of real algebra. If the products on the right were multiplied out we know that they would come to xn ± 1 because we have proved the equality in complex algebra. The results could be obtained, although not so shortly, by using only the methods of real algebra, see Ex. XII. a, Nos. 13, 14.
EXERCISE XII. a
1. In complex algebra what are the factors of x3 – 1 ?
2. In real algebra what are the factors of x3 – 1 ?
3. Obtain from first principles the factors of x4 + 1, and deduce quadratic factors not involving i. Show that these can also be found by writing x4 + 1 as the difference between two squares.
4. Find the complex factors of x5 – 1 ; deduce the real quadratic factors of x4 + x3 + x2 + x + 1. Verify the result by writing x4 + x3 + x2 + x + 1 = x2(x2 + x + 1 + ![]() +
+ ![]() )" and putting x +
)" and putting x + ![]() + y.
+ y.
5. Obtain from first principles the quadratic factors of

6. Express x10 – x5 + 1 in quadratic factors.
7. Find the values of cos θ for which
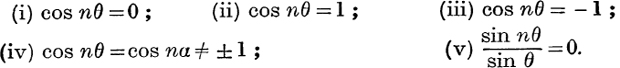
8. If n is even, find the values of sin θ for which
![]()
9. If n is odd, find the values of sin θ for which
![]()
10. Solve x2n – 2xn cos nα + 1 = 0.
11. Write down the factors of x2n + l, and deduce those of (1 + x)2n + (l – x)2n.
12. Show that the solutions of (1 + x)2n + (1 – x)2n = 0 are
![]()
Deduce that 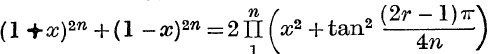 .
.
Hence prove that 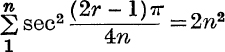 .
.
13. If un ≡ x2n – 2xnan cos nθ + a2n, prove that
![]()
Hence prove by induction that x2 – 2ax cos θ + a2 is a factor of x2n – 2xnan cos nθ + a2n, and deduce that ![]() is also a factor, where r is any integer.
is also a factor, where r is any integer.
14. Use No. 13 to factorize, by the methods of real algebra, xn – 1, when n is even. [Put a = 1, θ = 0.]
FACTORS OF TRIGONOMETRIC FUNCTIONS
We have shown, in Chapter IX., that certain functions, like cos nθ, sin nθ, are polynomials in cos θ or sin θ. The results are given in Ex. IX. e, Nos. 12-25. Corresponding to each of these results it is possible, by the method stated at the beginning of the present chapter, to obtain an expression in factors for each of these functions. An essential step in the process is to find the values of cos θ or sin θ for which the function vanishes, and the reader who has worked Ex. XII. a, Nos. 7, 8, 9 will already have found the values.
We will give the reasoning in full for one example, and the reader will then be able to supply it for the others. The results are given in Ex. XII. b, Nos. 3-13.
Factors of sin nθ when n is odd. It is known from Chapter IX., that, when n is odd, sin nθ is a polynomial,
![]()
of degree n in sin θ. To find the values of sin θ for which the polynomial is zero we put sin nθ = 0; this gives θ = ![]() , and the n different values of sin θ are sin
, and the n different values of sin θ are sin ![]() for r = 0, ±1, ±2, … ±
for r = 0, ±1, ±2, … ± ![]() .
.
The factors corresponding to r = 0, r = ± k are sin θ, sin θ – sin ![]() , and sin θ + sin
, and sin θ + sin ![]() , and the product of the last two is sin2θ – sin2
, and the product of the last two is sin2θ – sin2 ![]() ; thus,
; thus,
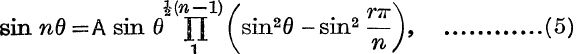
where A =the coefficient of sinnθ in the polynomial = ![]() .
.
It is convenient, however, to divide each factor by a term ![]() ; thus
; thus
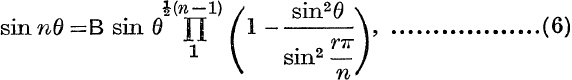
where 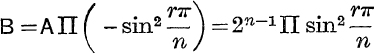 . It is not, however, necessary to use the value of A ; dividing each side of (6) by sin θ and making θ → 0, we get
. It is not, however, necessary to use the value of A ; dividing each side of (6) by sin θ and making θ → 0, we get 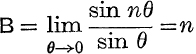 thus,
thus,
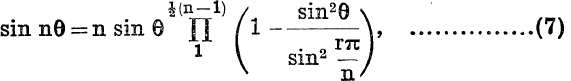
and it has been proved incidentally that
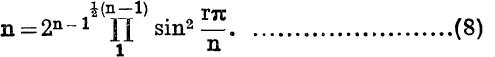
From formula (8), 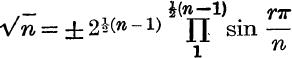 , but all the angles have positive sines;
, but all the angles have positive sines;
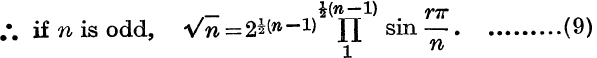
Other results of this kind can be deduced from the factors of ![]() , when n is even, and from the factors of cos nθ. See Ex. XII. b, Nos. 18-25.
, when n is even, and from the factors of cos nθ. See Ex. XII. b, Nos. 18-25.
Another deduction is often made from equation (7) by putting nθ = ϕ and making n → ∞, but, as explained in the Preface, the consideration of Infinite Products is held over for the companion volume. It is found that (see Ex. XII. f, Nos. 23, 24)
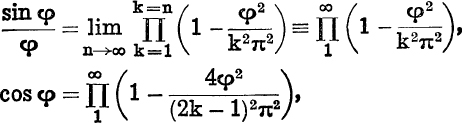
and, by putting ϕ = ![]() in the first,
in the first,
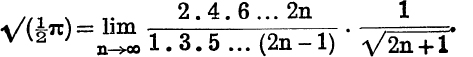
EXERCISE XII. b.
[For convenience of reference some results proved in the text are included.]
1. Obtain from first principles the factors of
![]()
regarded as functions of sin π.
2. Obtain from first principles the factors of
![]()
regarded as functions of cos π.
Verify some of the following results (Nos. 3-13) :
3. 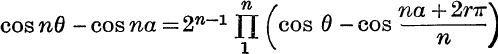 .
.
4. 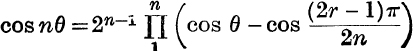 .
.
6. 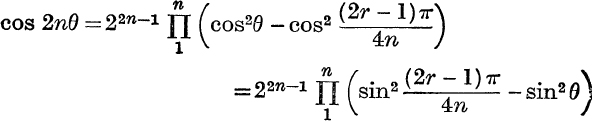 .
.
7. 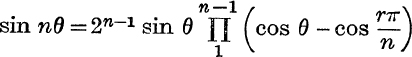 .
.
8. 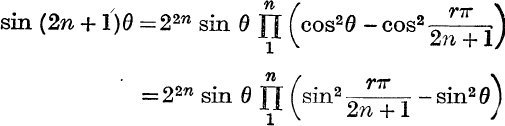 .
.
9. 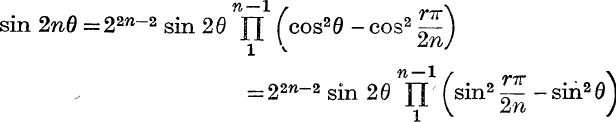 .
.
10. If n is odd, 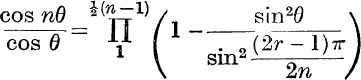 .
.
11. If n is even, 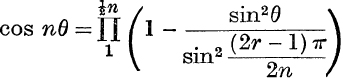 .
.
12. If n is odd, 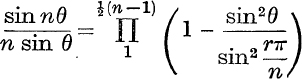 .
.
13. If n is even, 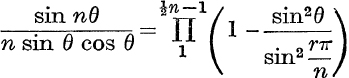 .
.
14. Express ![]() as a product of three factors.
as a product of three factors.
15. Find the factors, if any, of sin nπ – sin nα, regarded as a function of sin π.
16. Show how to deduce No. 4 from No. 3.
17. By writing ![]() – π for π in Nos. 10, 11, 12, 13, find the values of
– π for π in Nos. 10, 11, 12, 13, find the values of
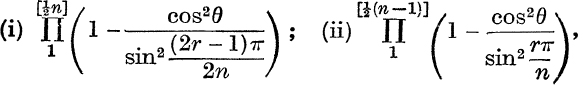
where n may be odd or even. See footnote on p. 46.
18. Prove that 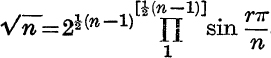 .
.
19. Prove that 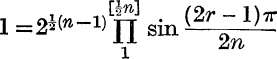 .
.
20. Prove that  .
.
21. Prove that 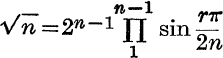 .
.
22. If n is even, prove that 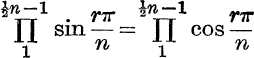 , and that
, and that
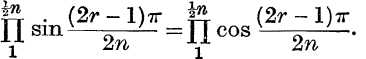
23. If n is odd, prove that 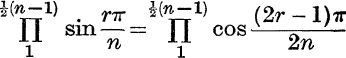 , and that
, and that 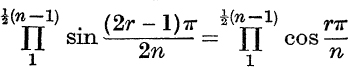 .
.
24. Evaluate 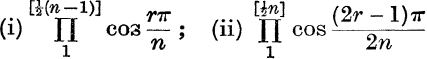 ; each for n odd, and for n even.
; each for n odd, and for n even.
25. Prove that the results of Nos. 20 and 21 hold when the sines are replaced by cosines.
26. Prove that ![]() .
.
27. Prove that ![]() .
.
28. Prove that ![]() .
.
29. Prove that 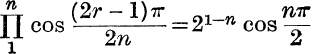 .
.
30. Evaluate 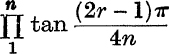 .
.
32. Prove that 1 + cos θ is a factor of 1 + cos 5θ and find the other factors.
33. Prove that 2 cos θ + 1 is a factor of 2 cos 5θ + 1, and find the other factors. Deduce that
![]()
34. Factorize x2n – 2xn cos nθ + 1, using Ex. XII. a, No. 10.
35. Prove that ch nx – cos na = 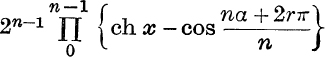 .
.
36. Prove that 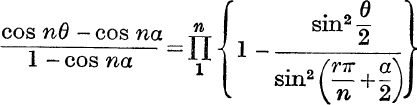
Factors of x2n – 2xn cos nα + 1. The equation
![]()
is a quadratic in xn, with roots cos nα ± i sin nα; thus the 2n values of x are 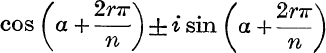 , for r = 0, 1, 2,…, (n – 1).
, for r = 0, 1, 2,…, (n – 1).
The product of the factors corresponding to r = k is
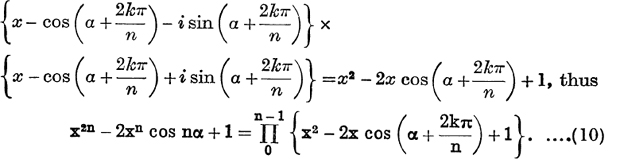
Many results can be deduced from formula (10).
(i) Putting α = 0, α = ![]() and taking the square root, we get equations (1), (2), (3), (4). The reader should verify this.
and taking the square root, we get equations (1), (2), (3), (4). The reader should verify this.
(ii) Dividing by xn,
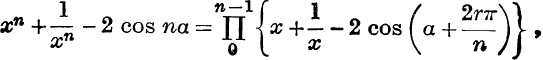
and, putting x = cos θ + i sin θ, we have
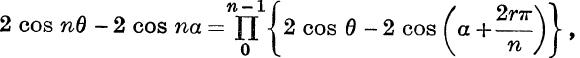
i. e.
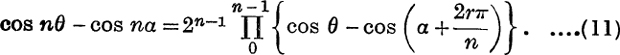
This is the same as Ex. XII. b, No. 3, and can, of course, be proved directly in the usual manner.
(iii) Putting x = 1, α = 2β in (10),
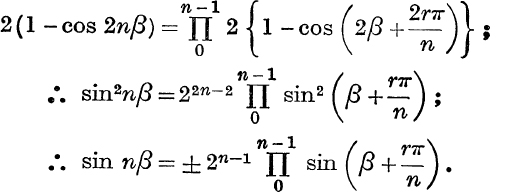
Now, if 0 < β < ![]() , each factor on the right is positive, and so is sin nβ. Also, as β increases, sin nβ changes sign whenever β passes through a value
, each factor on the right is positive, and so is sin nβ. Also, as β increases, sin nβ changes sign whenever β passes through a value ![]() , and at the same time one factor on the right changes sign. Thus the ambiguous sign is always a +, and
, and at the same time one factor on the right changes sign. Thus the ambiguous sign is always a +, and
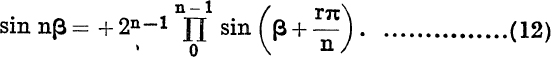
Similar results to (12) can be found by the substitutions indicated in Ex. XII. c, Nos. 1-5.
(iv) From (12), by taking logarithms
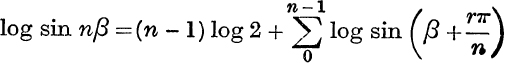
and, differentiating with respect to β,
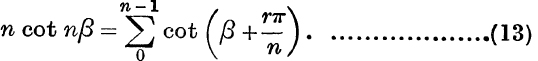
This may also be proved by the methods of Chapter XI.
(v) De Moivre's and Cotes' Properties of a Circle. If A0A1A2 … An–1 is a regular polygon inscribed in a circle centre O, radius a, and P is a point such that OP = x, ![]() (OA0, OP) = θ, then
(OA0, OP) = θ, then
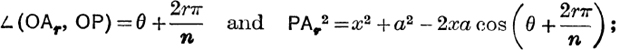
![]() by formula (10),
by formula (10),
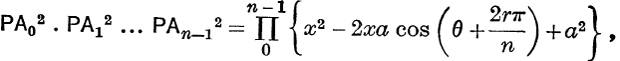
or
![]()
This is called. de Moivre’s property.
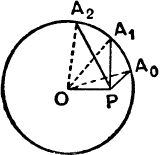
FIG. 78.
If P lies on OA0 so that θ = 0, PA0 … PAn–1 = xn ~ an.
If OP bisects ![]() An–1OA0, so that θ =
An–1OA0, so that θ = ![]() , PA0.PA1 … PAn–1, = xn + an.
, PA0.PA1 … PAn–1, = xn + an.
These special results are called Cotes’ properties.
Comparison of Series and Products. A number of identities can be obtained by comparing values obtained for the same function as a sum and as a product.
For example, if n is odd, 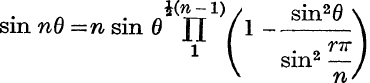 and also, from Ex. IX. e, No. 25,
and also, from Ex. IX. e, No. 25,
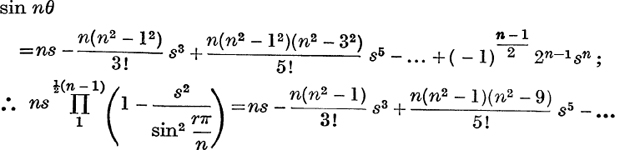
is an identity.
Equating coefficients of s3 on the two sides,
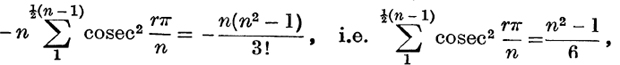
a result which has been proved (p. 209) in another way.
Other results can be obtained by equating other powers of s, and by using the formulae for sin nθ (n even) and cos nθ.
The formula for ∑ cosec2(rπ/n) was used on p. 210 to prove that ∑I/n2 = π2/6. In some of the older text-books this result is obtained by equating coefficients of θ3 in the series and product expressions for sin θ, (see pp. 80 and 223). Such a process requires careful justification, and the product expression is itself obtained, not without difficulty, from equation (7). It seemed more satisfactory to deduce the sum ∑1/n2 directly from ∑cosec2(rπ/n), the infinite product being left for the companion volume.
EXERCISE XII. c.
By substituting ±1 for x, and 2β or 2β + ![]() for α, in formula (10), prove the following results (Nos. 1-5).
for α, in formula (10), prove the following results (Nos. 1-5).
1. 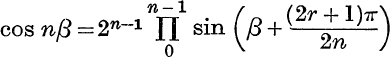 .
.
2. 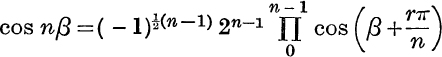 , if n is odd.
, if n is odd.
3. 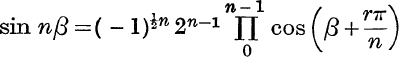 , if n is even.
, if n is even.
4. 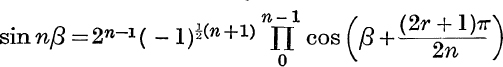 , if n is odd.
, if n is odd.
5. 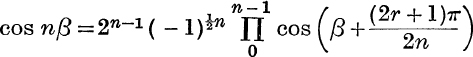 , if n is even.
, if n is even.
6. Show how to deduce Nos. 4 and 5 from No. 1, and Nos. 2 and 3 from formula (12).
7. What result can be deduced from No. 1, by taking logarithms of each side and then differentiating w.r.t. β ?
8. Simplify
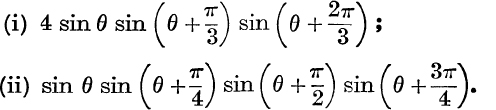
9. Simplify 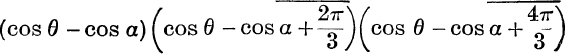
10. Prove that 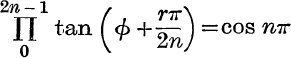 .
.
11. Prove that 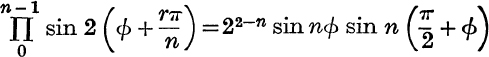 .
.
12. Prove that 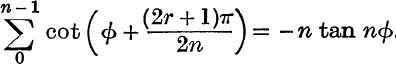 .
.
13. Prove that 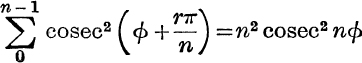 .
.
14. A1A2 … An is a regular polygon inscribed in a circle, centre O, and radius a. P is a point on the circumference such that ![]() POA1 = θ; prove that PA1 . PA2 … PAn = 2an sin
POA1 = θ; prove that PA1 . PA2 … PAn = 2an sin ![]() .
.
15. A square A1A2A3A4 and a regular pentagon B1B2B3B4B5 are inscribed in a circle of radius a; prove that the continued product of the chords ArBs is numerically equal to 2a20 sin 20θ, where 2θ is the angle subtended at the centre by any one of the chords.
16. A1A2 … A2n is a regular polygon inscribed in a circle centre O, radius a, and P is a point on the circumference such that ![]() POA1 = θ; prove that the continued product of the perpendiculars from P to OA1, OA2, … OAn is 21–nan sin nθ.
POA1 = θ; prove that the continued product of the perpendiculars from P to OA1, OA2, … OAn is 21–nan sin nθ.
17. A0A1A2 … A2n is a regular polygon inscribed in a circle of radius a of which A0C is a diameter; prove that CA1 . CA2 … CAn = an.
18. With the data of No. 14, show that the continued product of the chords ArAs is ![]() .
.
19. With the data of No. 16, if OB bisects A1A2, prove that the product of the perpendiculars from A1, A2, …, A2n to OB is a2n22–2n.
20. If n is even, prove that 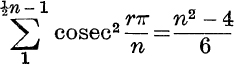 .
.
21. If n is even, prove that 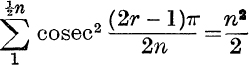
22. If n is odd, prove that 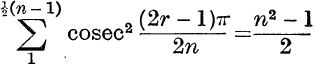 .
.
23. If n is odd, prove that the sum of the squares of the products two at a time of the cosecants of
![]()
and deduce that 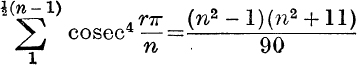
24. Evaluate  , when n is even.
, when n is even.
25. Evaluate ![]() , for r = 1 to
, for r = 1 to ![]() n, when n is even, and for r = 1 to
n, when n is even, and for r = 1 to ![]() (n – 1), when n is odd.
(n – 1), when n is odd.
PARTIAL FRACTIONS
If f(x) and F(x) are polynomials in x of which f(x) has the smaller degree, and if F(x) ≡ (x – a)g(x), where g(a) ≠ 0, then it is known from Algebra that
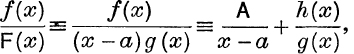
where A is independent of x, and h(x) is a polynomial of smaller degree than g(x).
The value of A may be proved to be ![]() .
.
Alternatively, 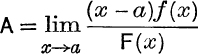 . This limit can then be evaluated by algebraic methods; or, by using a theorem in the Calculus, we have
. This limit can then be evaluated by algebraic methods; or, by using a theorem in the Calculus, we have
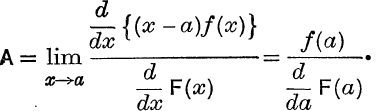
If F(x) ≡ c(x – a1)(x – a2) … (x – an), where no two factors are equal, repeated applications of the above give
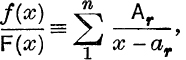
where Ar can be found by either of the methods described above.
These results are also true when a1, a2, … are complex.
Example 1. Express ![]() as the sum of three partial fractions.
as the sum of three partial fractions.
Since x3 – 1 ≡ (x – 1)(x – w)(x – w2), where ![]() , we may write
, we may write
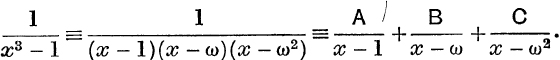
A, B, C may be evaluated in any of the following ways :
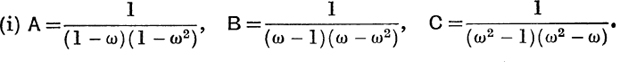
It may be shown that these give 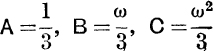 .
.
(iii) 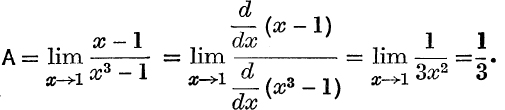
Similarly, 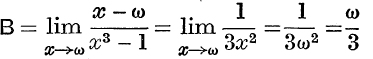
and 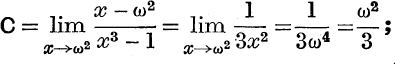
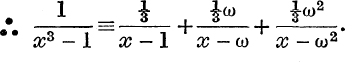
Note. The last two fractions can of course be combined, so as to give the ordinary result in real algebra,
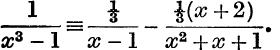
Example 2. Express 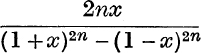 as the sum of fractions with quadratic denominators.
as the sum of fractions with quadratic denominators.
The denominator is a polynomial of degree 2n – 1 in x, which is zero if 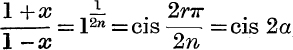 , where
, where ![]() .
.
This gives
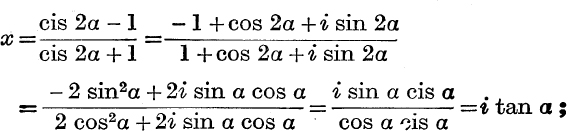
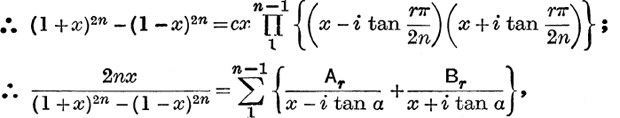
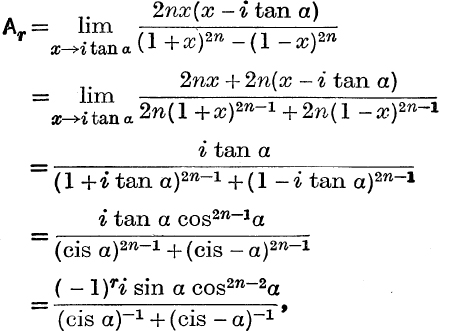
because (cis α)2n = cis (rπ) = (– 1)r;
hence Ar = (– l)r .![]() i sin α cos2n–3α,
i sin α cos2n–3α,
Writing – i for i, we have Br = – (– 1)r . ![]() i sin α cos 2n–3α;
i sin α cos 2n–3α;
![]() the expression
the expression
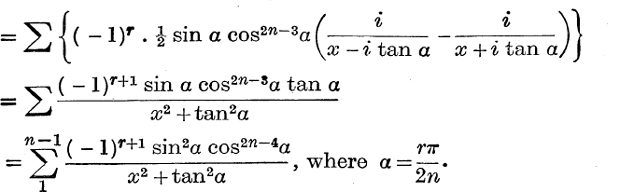
Example 3. Express ![]() as the sum of fractions.
as the sum of fractions.
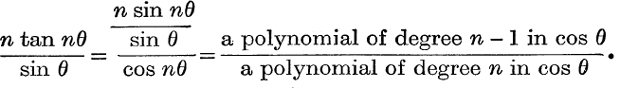
The denominator is zero when
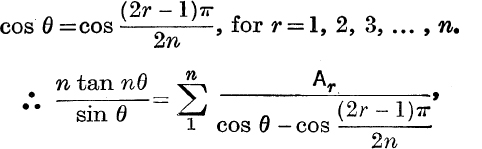
where 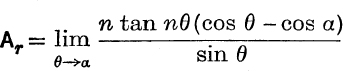 and
and ![]() .
.
The value of Ar may be found in either of the following ways :
(ii) 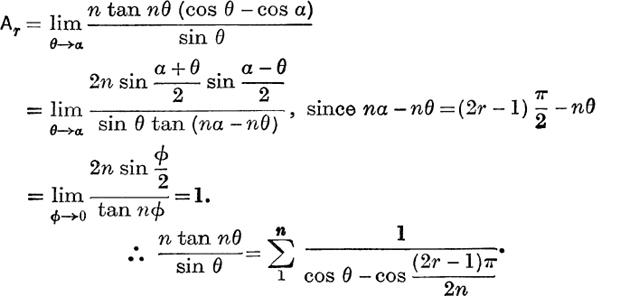
Note. This result may also be obtained as follows :
From Ex. XII. b, No. 4, 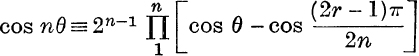 ;
;
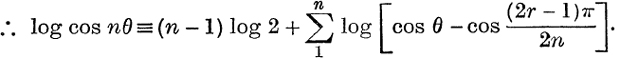
Now differentiate each side w.r.t. θ.
EXERCISE XII. d.
1. Find the real partial fractions of ![]() .
.
2. Express ![]() in partial fractions with quadratic denominators.
in partial fractions with quadratic denominators.
3. Prove that 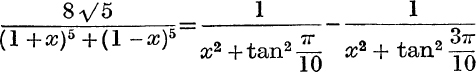 .
.
4. Express ![]() in partial fractions with quadratic denominators.
in partial fractions with quadratic denominators.
5. Express ![]() in partial fractions when n > 3.
in partial fractions when n > 3.
6. If n is odd, prove that
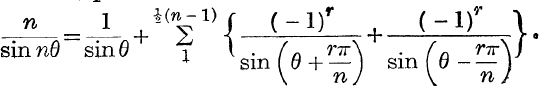
8. Prove that 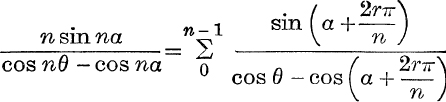 .
.
9. Prove that 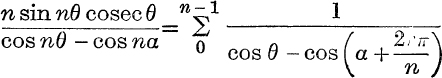 .
.
10. Prove that 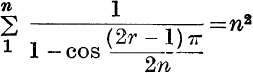 .
.
11. Prove that 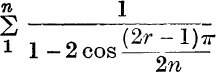 equal0 or
equal0 or ![]() according as n is or is not a multiple of 3.
according as n is or is not a multiple of 3.
12. Express ![]() sas a sum of n partial fractions.
sas a sum of n partial fractions.
13. Prove that 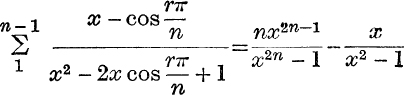 , and deduce an expression for
, and deduce an expression for 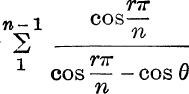 .
.
14. Prove that 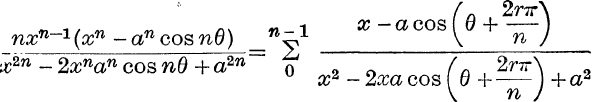 .
.
15. If n is even and ![]() , prove that
, prove that ![]() is the sum, for r = 1, 2, …,
is the sum, for r = 1, 2, …, ![]() n – 1, of
n – 1, of
![]()
16. Prove that 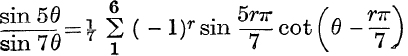 .
.
18. Prove that 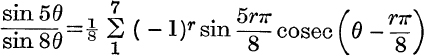 .
.
19. Prove that
![]()
and express 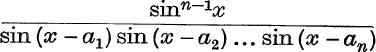 in a similar form.
in a similar form.
20. Prove that
![]()
21. Prove that
![]()
22. A1A2 … An is a regular polygon inscribed in a circle, centre O, radius α; P is a point of its plane such that OP = x, and ![]() POA1 = θ prove that
POA1 = θ prove that
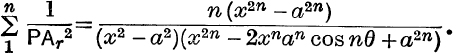
EASY MISCELLANEOUS EXAMPLES
EXERCISE XII. e.
1. Express x2n – a2n as the product of n quadratic factors.
2. Express x6 – x3 + 1 in the form П(x – a) and prove that
![]()
3. Prove that
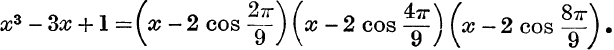
4. Prove that
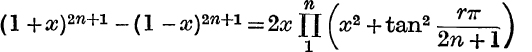
and deduce that 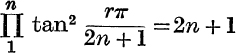 .
.
5. Express (x + 1)2n – (x – 1)2n in the form
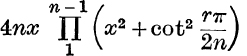
and deduce the value 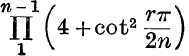 .
.
6. Express ![]() as a product of factors linear in sin θ.
as a product of factors linear in sin θ.
7. Prove that
![]()
Prove the following (Nos. 8-16) :
8. cos θ – cos ϕ is a factor of 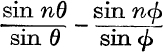 .
.
9. 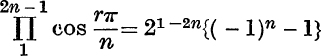 .
.
10. 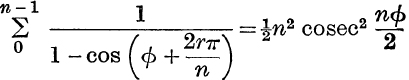 .
.
11. 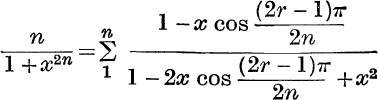 .
.
12. 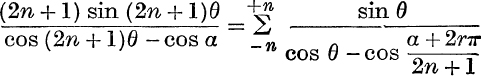 .
.
13. 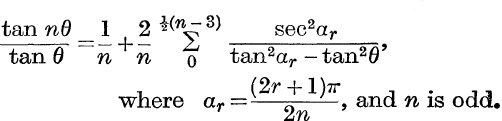 .
.
14. 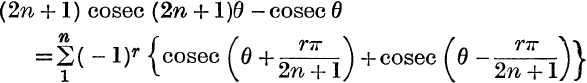 .
.
15. 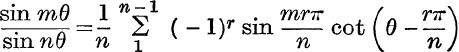 ,
,
where m and n are odd, and 0 < m < n.
16. 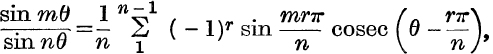
where m + n are odd, and 0 < m < n.
17. Express cosec (x – a) cosec (x – b) cosec (x – c) in the form A cosec (x – a) + B cosec (x – b) + C cosec (x – c), where A, B, C are independent of x; also extend to the case of 2n + 1 factors.
18. Express cosec (x – a) cosec (x – b) in the form
![]()
where A, B are independent of x; also extend to the case of 2n factors.
19. Express 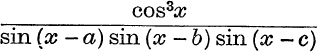 in the form
in the form
![]()
where A, B, C, D are independent of x.
20. A1A2 … An is a regular polygon inscribed in a circle, centre O, radius a. PQ, QR are equal chords, such that ![]() POQ = α and
POQ = α and ![]() A1OQ = β. Prove that the product of the perpendiculars from A1, A2, … , An to the chord PR is 21–nan(cos nα – cos nβ).
A1OQ = β. Prove that the product of the perpendiculars from A1, A2, … , An to the chord PR is 21–nan(cos nα – cos nβ).
HARDER MISCELLANEOUS EXAMPLES
EXERCISE XII. f.
1. Prove that cos 7θ – cos 8θ is divisible by 2 cos 5θ +1 and find the other factor.
2. Prove that
![]()
and factorize the expression on the right-hand side.
3. If m and n are odd co-prime integers, prove that ![]() is a polynomial in cos θ of degree mn – m – n + 1, with factors of the form
is a polynomial in cos θ of degree mn – m – n + 1, with factors of the form ![]() , for values of r from 1 to mn – 1 which are not multiples of m or n.
, for values of r from 1 to mn – 1 which are not multiples of m or n.
4. Prove that 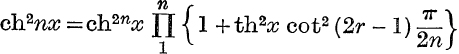 .
.
5. Write down the results obtained by taking the square root of each side in No. 4, (i) if n is even, (ii) if n is odd.
6. If n is even, prove that
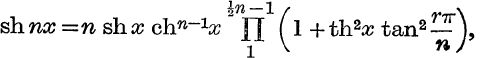
and find a corresponding result when n is odd.
Prove the following (Nos. 7-14):
7. 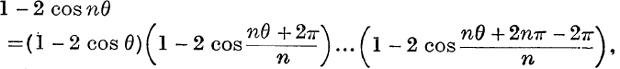
if n2 = 1 (mod 6).
8. 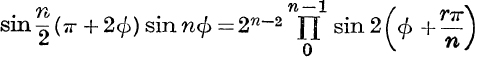 .
.
10. 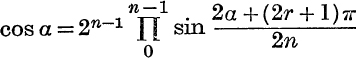 .
.
11. 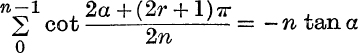 .
.
12. 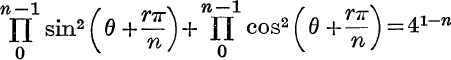 , if n is odd.
, if n is odd.
13. ![]() .
.
14. 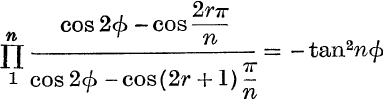 .
.
15. Prove that the product of the perpendiculars drawn from the vertices of a regular n-gon inscribed in the circle x2 + y2 = 9a2 to a tangent to the circle x2 + y2 = 25a2 is
![]()
where α is one of the angles between the tangent and a side of the polygon.
16. A regular polygon A1A2 … An is inscribed in a circle, centre O; P is a point in space such that the projection of OP on the plane of the circle makes an angle α with OA1; r1 and r2 are the greatest and least distances of P from the circumference, and 2s = r1 + r2, 2d = r1 – r2. Prove that PA1 . PA2 … PAn = ![]() .
.
17. Prove that 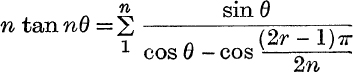 .
.
18. Prove that 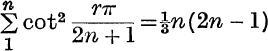 .
.
19. Prove that ![]() ,and deduce that
,and deduce that
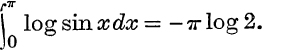
20. If N1, N2, …, Nm are the integers less than N and prime to it and ![]() , prove that 2m sin N1αsinN2α … sinNmα = 1, unless N is itseli prime, in which case the product equals N.
, prove that 2m sin N1αsinN2α … sinNmα = 1, unless N is itseli prime, in which case the product equals N.
21. If n1, n2, … nt are the integers less than 2n which are not powers of 2 (2° being reckoned as a power of 2), and if ![]() prove that
prove that 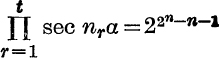 .
.
22. Prove tbat
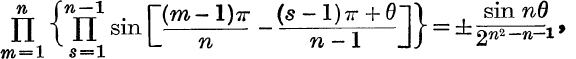
and determine the ambiguous sign.
23. Express sin x as an infinite product as follows:
(i) Differentiate θ cosec θ and θ cot θ; hence prove, for 0 < θ < ϕ < ![]() π, that θ cosec ϕ < ϕ cosec ϕ, and θ cot θ > ϕ cot ϕ.
π, that θ cosec ϕ < ϕ cosec ϕ, and θ cot θ > ϕ cot ϕ.
Deduce that
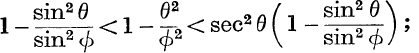
(ii) If n is an odd integer, and r takes the values 1, 2, …, ![]() (n – 1), prove that, for 0 < x < π,
(n – 1), prove that, for 0 < x < π,
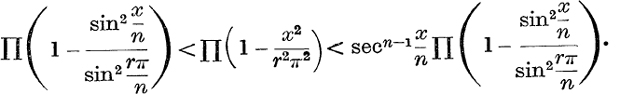
(iii) Use equation (7), p. 222, and Example 7, p. 70, to deduce that 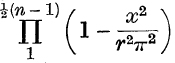 lies between two expressions which tend to sin x/x when n → ∞ .
lies between two expressions which tend to sin x/x when n → ∞ .
This proves that, for 0 < x < π,
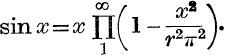
(iv) If 0 < (θ, ϕ) < ![]() π, prove that
π, prove that
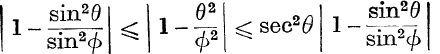
and hence establish the result of (iii) for all values of x.
24. Use Ex. XII. b, No. 10, and the method of No. 23 above to express cos x as an infinite product.