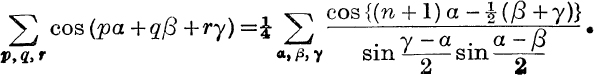CHAPTER IX

DE MOIVRE’S THEOREM AND APPLICATIONS

Definition of aⁿ, where a is complex and n is a rational number. For integral values of n, the definition has been given on pp. 140, 141. If n is fractional, it is equal to , where p and q are integers, and there is no loss of generality in supposing that q is positive ; and then any value of z which satisfies the equation, z^q = a^p, is called a value of aⁿ. We reserve the notation, for the principal value of aⁿ, as defined on p. 165.

De Moivre’s Theorem. If n is any rational number,

 

(i) First, suppose that n is a positive integer.

We have proved on p. 151, by actual multiplication, that

 

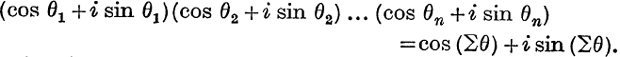
Putting θ₁ = θ₂ = … = θ_n = θ, we have

 

(ii) Next, suppose that n is a negative integer. Put n = – m. Then (cos θ + i sin θ)ⁿ = (cos θ + i sin θ)^–m, and this, by definition, 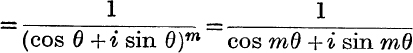, by (i).

But (cos mθ + i sin mθ)(cosmθ – i sin mθ) = cos²mθ – i² sin²mθ = 1;

 

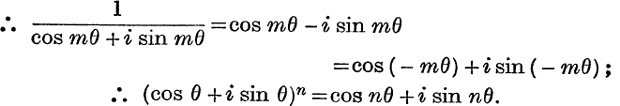
Therefore, if n is a positive or negative integer, there is only one value of (cos θ + i sin θ)ⁿ, and this value is cos nθ + i sin nθ.

(iii) Next, suppose that n is a fraction. Put n = , where p, q are integers and q is positive.

In this case (cos θ + i sin θ)ⁿ is many-valued, and we shall prove presently that it has q values. At the moment, we merely wish to show that cos nθ + i sin nθ is one value of (cos θ + i sin θ)n.

By (i), .

Also by (i) or (ii), cos pθ + i sinpθ = (cos θ + i sin θ)^p;

 

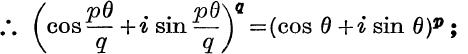
by the definition of aⁿ, given above, it follows that

 

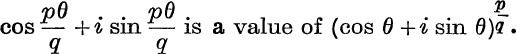
The theorem is therefore proved for all rational values of n.

Writing – θ for θ, we see that cos nθ – i sin nθ is a value of (cos θ – i sin θ)ⁿ, for all rational values of n.

The values of (cos θ + i sin θ), where p, q are integers and q is positive.  De Moivre’s Theorem states that 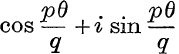is one value of (cos θ + i sin θ). Suppose that s(cos ϕ + i sin ϕ) represents any value of (cos θ + i sin θ).

Then, by definition,.

 

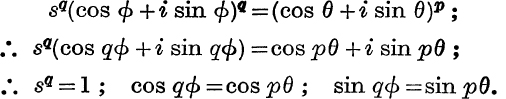
But s is positive, since it is the modulus of a complex number;

s^q – 1 requires that s = 1; since, if s > 1, s^q > 1 and if 0 ≤ s < 1, s^q < 1.

Also the other equations require that qϕ = pθ + 2rπ, where r is an integer or zero.

Taking, in succession, r = 0, 1, 2, …, (q – 1), we obtain the q values,

 

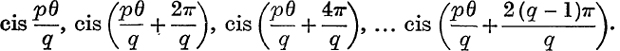
These q values are all distinct, because the angles given by r = r₁, r = r₂ differ by 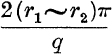, which is less than 2π, since |r₁ – r₂| < q.

Also, no further values are given by other values of r, because a,ny other value of r must differ from one of the numbers 0, 1,2, …, (q – 1) by a multiple of q.

If p, q are prime to one anothe:, the same results may be written, but in a different order, as

 

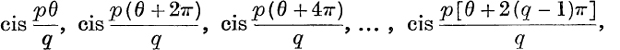
because the numbers 0, p, 2p, 3p, …, (q – 1)p are congruent (mod. q) to 0, 1, 2, …, (q – 1), in some order.

If p is not prime to q, the function (cos θ + i sin θ) is taken to mean {(cos θ + i sin θ)^p} and has therefore q distinct values, viz., the q values of (cospθ + i sin pθ); these may be written,

 

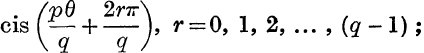
but in this case, the expression 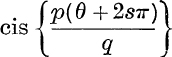, where s is any integer, does not assume q distinct values and therefore does not represent all the values of (cos θ + i sin θ). Thus, the function has the 8 values given by , and is distinct from the two-valued function ; its 8 values are represented by

 

where s is any integer, has only 2 distinct values. Cf. Ex. IX. a, No. 8.

Principal Value of (cos θ + i sin θ).  The principal value of (cos θ + i sinθ) is taken to be cis , only if – π < θ ≤ π.

Otherwise, if k is the (positive or negative) integer such that – π < θ + 2kπ ≤ π, the principal value of (cos θ + i sin θ) is taken to be

 

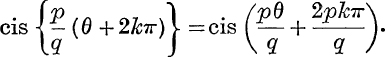
For any given value of k, this can of course be reduced to the form, 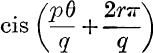where r is some integer less than q.

This definition of principal value holds whether p is prime to q

The reader should notice that the principal value of (cos θ + i sin θ), where – π < θ ≤ π, is not the same as the principal value of (cos pθ + i sin pθ), unless also – π < pθ ≤ π.

Further, the principal value of the qth root of (cos θ + i sin θ)^p or the principal qth root of (cos θ + i sin θ)^p is taken to mean the principal value of (cos θ + i sin θ), as defined above. Thus the principal value of the 8th root of (cos θ + i sin θ)⁴ means the principal value of (cos θ + i sin θ), and this is defined above as

 

where k is the integer given by – π < θ + 2kπ ≤ π. The principal value of (cos θ + i sin θ) is therefore the same as the principal value of (cos θ + i sin θ), but it is not the same as the principal value of (cos 4θ + i sin 4θ), unless, with the same notation as before, –π < 4(θ + 2kπ) ≤ π. Cf. Ex. IX. a, No. 10.

Values of z.  Definition.  If r is any real positive number, and if p and q are integers, q being positive, the symbol denotes the (unique) positive qth root of r^p.

Every complex number, z, can be written in the form,

 

where

 

the values of z may be written

 

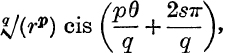
where s = 0, 1, 2, … , (q – 1).

Thus there are q values, whether p is prime to q or not; and of these, since – π < θ ≤ π, the principal value is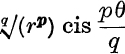

Geometrical Representation of Powers and Roots.  Fig. 76 represents the circle |z| = l in the Argand Diagram. The point P₁ which represents the complex number (cos θ + i sin θ) lies on the circle, and the arc AP₁, measured from the point A, (1, 0), is of length θ.

 

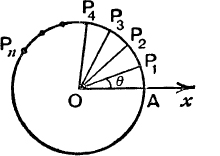
FIG. 76.

To apply the geometrical method of construction, given on p. 151, for the points representing the numbers

 

we construct in succession the triangles P₁OP₂, P₂OP₃, … , P_n–1OP_n, each similar to ΔAOP₁. The points P₂, P₃, … , P_n, being on the circle at arcual distances 2θ, 3θ, …, nθ from A, represent the numbers

 

This illustrates part (i) of de Moivre’s Theorem.

Suppose now, see Fig. 77, that Q, is the point on the circle which represents cos α + i sin α, and that we want to represent geometrically an nth root of that number. We shall have to find a point P on the circle such that the arc AQ = n. arc AP ; but as the arcual distance of Q from A can be regarded as α or α + 2π or α + 4π or … or α + 2rπ, where r is any integer, the arc AP may be taken as , where r is any integer. This gives n points P, say P₁, P₂, … P_n, representing the n nth roots of cos α + i sin α. P₁P₂ … P_n is a regular polygon inscribed in the circle.

 

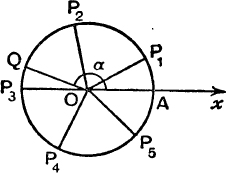
FIG. 77.

Note. The q values of (cos α + i sin α) can also be represented in a similar way ; similarly the nth roots of c (cos α + i sin α) can be represented by the corners of a regular n-sided polygon inscribed in the circle, centre the origin, radius .

Example 1. What is the principal value of and what are its other values ?

 

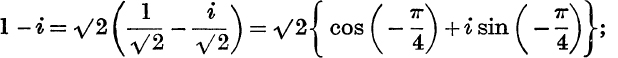
the principal value of is

 

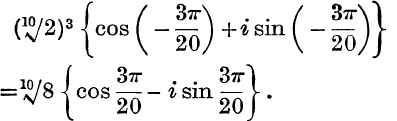
Also any value of can be expressed in the form

 

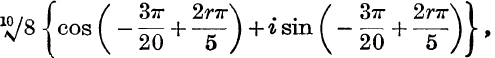
where r = 0, 1, 2, 3, 4.

Example 2. Solve (x - l)n = xn.

Take the nth root of each side;

 

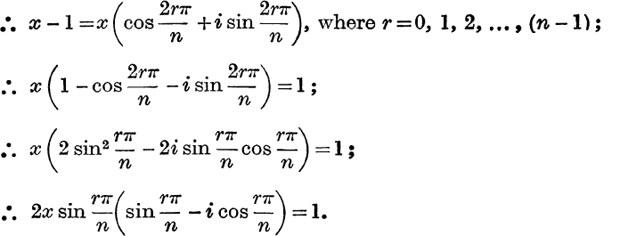
Multiplying each side by ,

 

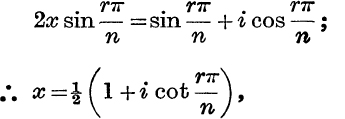
where r = 1, 2, …, (n – 1).

Example 3. Points P and Q, in the Argand Diagram represent the complex numbers z and w. If |z| = 1 and if am z steadily increases from – π to + π, describe the corresponding motion of Q if

(i) w = z   (ii) w = .

If .

(i) For each position of P, there are 3 positions of Q, say Q₁, Q₂, Q₃, which move continuously along the circle |z| = 1, anti-clockwise. Q₁ moves from θ = – to θ = + ; and at the same time, Q₂ moves from θ = + to θ = π, and Q₃ moves from θ = –π to θ = + .

(ii) for – π < θ < π; there is only one position of Q for each position of P, and Q moves from θ = – to θ = + .

EXERCISE IX. a.

1. Write down the square roots of

(i) cos 2θ + isin 2θ;

(ii) cos 3ϕ – isin 3θ;

(iii) sin θ + i cos θ;

(iv) i;

(v) –i.

2. Write down the cube roots of (i) cos 3θ + isin 3θ; (ii) 1; (iii) i; (iv) – i; (v) cos θ – i sin θ; (vi) sin θ – i cos θ.

3. Write down the values of (i) (– l); (ii) (– i); (iii) (1 + i); (iv) (1 – i); (v) 128.

4. Write down all the roots of (i) x⁵ = 1; (ii) x⁴ + 1 =0.

5. Represent in the Argand Diagram (i) the cube roots of – 1; (ii) the fourth roots of i; (iii) the fifth roots of 32; (iv) (– 5 – 12i)³.

6. Simplify .

7. Simplify .

8. Give (i) the two values of 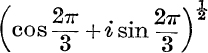; (ii) the eight values of 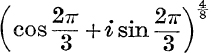; state which are the principal values.

9. Give the principal values of

 

10. Give (i) the principal 8th root of ;

(ii) the principal square root of .

11. Find (i) the product, (ii) the sum, of the five values of (cos π + isin π). Of what equation are these five values the roots ?

12. Use the result of No. 4 (i) to write down factors of x⁵ – 1, and deduce that .

13. Solve xⁿ = 1. What is the sum of the roots ? If a is a root other than unity, prove that 1 + α + α² + … + α^n–1 = 0.

14. Find the roots of x⁶ = 1 which do not satisfy x² + x + 1 =0.

15. Solve (x + i)⁶ + (x – i)₆ = 0.

16. Solve (1 + x)ⁿ = (1 – x)ⁿ.

17. Solve x²ⁿ – 2xⁿ cos nα + 1 = 0.

18. Solve x⁹ + x⁵ – x⁴ = l.

19. If z = cis θ, express in the form A + Bi, (i) for 0 < θ < π, (ii) for π < θ < 2π.

20. How many values are there of (i) i + (–i); (ii) i × (–i) ?

21. Find the principal value of (1 + cos θ + i sin θ)

 

22. A regular hexagon is inscribed in the circle |z| = 1 in the Argand Diagram, and one vertex represents cos a + i sin α. What do the others represent ?

23. Two points P and Q, in the Argand Diagram represent complex numbers z and w, the modulus of z being unity. P moves so that am z steadily increases from – π to + π.

Describe the corresponding motion of Q when

 

24. Answer the same question as in No. 23 for

 

25. Answer the same question as in No. 23 for

 

26. Answer the same question as in No. 23 for

 

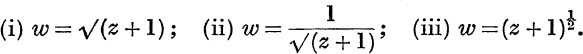
27. By using substitutions of the form a = cis 2α in the identity,

 

prove that sin(θ₁ – θ₂)sin(θ₃ – θ₄) + … + … = 0.

Expression of Powers of cos θ and sin θ in terms of Multiple Angles. The student no doubt realises already the great importance of formulae, such as sin²θ = (1 – cos 2θ), cos³θ = (3 cos θ + cos 3θ), etc. Besides being essential for dealing with all kinds of identities, they are wanted, for example, for the integration of powers of sin θ and cos θ, and for the summation of series like ∑(sin²nθ), ∑cos²(θ + nϕ), etc. We shall now investigate expressions for

 

If cos θ + i sin θ = z, then cos θ – i sin θ = ;

 

also cos nθ, i sin nθ = zⁿ and cos nθ – i sin nθ = ;

 

By means of (2) and the binomial theorem for a positive integral index, the functions cosⁿθ, sinⁿθ, cos^pθ sin^qθ, etc., can be expressed in terms of z and expanded in powers of z and 1/z.

By means of (3), the expression in powers of z and 1/z can be replaced by cosines or sines of multiple angles.

Example 4. Express cos⁵ θ in terms of multiple angles.

from (2),

 

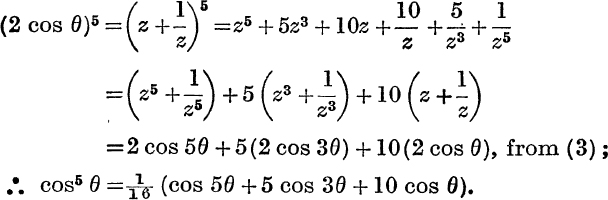
Check by putting θ = 0.

Example 5. Express sin⁵θ in terms of multiple angles.

from (2),

 

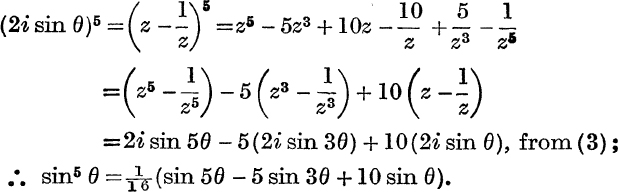
Check by putting θ = .

Example 6. Express cos³θ sin⁴θ in terms of multiple angles.

from (2),

 

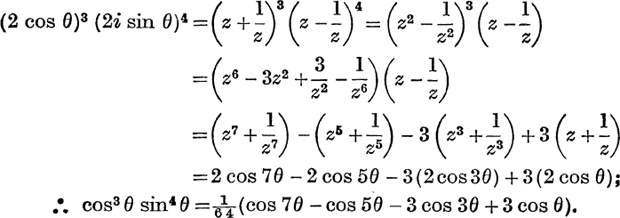
Check by putting θ = .

Note. It is instructive to consider the form of the expansion in the general case. It is evident that cosⁿθ can always be expressed as a sum of cosines of multiples of θ, since it depends on the binomial expansion of 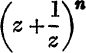. Rut sinⁿθ depends on the expansion of 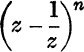, which involves terms like 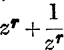if n is even, and terms like if n is odd. Therefore sinⁿθ can be expanded in terms of cosines or sines of multiples of θ according as n is even or odd. For the details, see Ex. IX. b, Nos. 15-18.

EXERCISE IX. b.

1. If z = cos θ + i sin θ, write down the values of and in terms of θ.

2. Express cos 7θ and sin 6θ in terms of cos θ + i sin θ.

Use the general method to express the following in terms of cosines or sines of multiples of θ.

3. cos³θ.

4. cos⁴θ.

5. cos⁷θ.

6. sin⁴θ.

7. sin⁷θ.

8. sin³θ cos θ.

9. cos⁴θ sin₃θ.

10. cos⁵θ sin⁴θ.

11. Prove that 16 cos⁵θ – cos 5θ = 5 cos θ(1 + 2 cos 2θ).

12. Evaluate by means of expansions in terms of multiples of θ.

13. Evaluate ∫sin⁴θ cos⁶θ dθ.

14. Explain how to find the value of

 

15. Prove that, if n is even, 2^n–1 cosnθ = cos nθ + n cos (n – 2)θ + … and that there are + 1 terms, of which the last is . Show that the others after the first are the values of

 

16. Prove that, if n is odd,

 

17. Prove that 2^2n–1(–1)ⁿ sin²ⁿθ

 

and give the general term.

18. Prove that 2²ⁿ(–1)ⁿ sin²ⁿ⁺¹θ

 

and give the general term.

19. If cos³θ sin⁴θ is expressed in the form

 

deduce by differentiation that A₁ + 9A₃ + 25A₅ + 49A₇ = 0, and find the value of A₁ + 3⁴A₃ + 5⁴A₅ + 7⁴A₇. Verify the result by means of Example 6, p. 170.

Expansions of cos nθ, sin nθ, and tan nθ, where n is any positive integer. We have

 

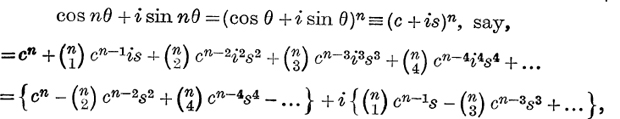
and so, by equating the first and second parts of the two complex numbers,

 

 

Also cosnθ + i sin nθ = cosⁿθ (1 + itan θ)ⁿ ≡ cosⁿθ (1 + it)ⁿ, say, which gives the same results as before in the form

 

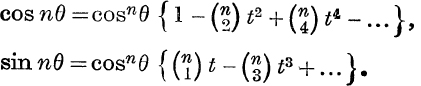
By division,

 

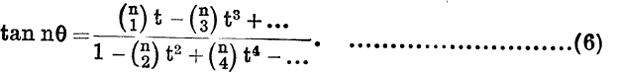
Expansion of tan (θ₁ + θ₂ + … + θ_n).

Similarly, cos (θ₁ + θ₂ + … + θ_n) + i sin (θ₁ + θ₂ + … + θ_n)

 

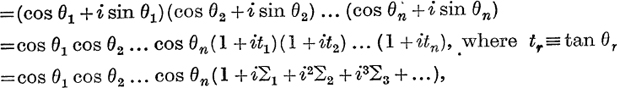
where ∑_r denotes the sum of the products of tan θ₁, tan θ₂, … taken r at a time.

Equating the first and second parts of the complex numbers,

 

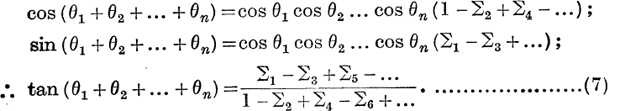
Formula (7) is easily remembered; it includes (6) as the special case when θ₁, θ₂, … θ_n are equal.

Formula (6) expresses tan nθ in terms of tan θ. Formulae (4), (5) can be transformed by means of the identity sin²θ + cos²θ = 1, so that, for example, cos nθ can be expressed entirely in terms of cos θ as in the example below. The general results will be discussed on p. 178.

Example 7. Express cos 6θ in terms of cos θ.

We have

 

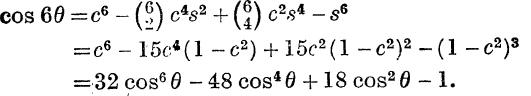
EXERCISE IX. c.

From formulae (4) and (5) find expressions for

1. sin 5θ in terms of sin θ.

2. cos 5θ in terms of cos θ.

3. in terms of cos θ.

4. cos 6θ in terms of sin θ.

5. Give the formulae for tan 4θ and tan 5θ in terms of tan θ.

6. What equation is satisfied by tan θ if tan 6θ = 0 ?

7. What equation is satisfied by tan θ if 7θ = ?

8. Give the expansion of tan (θ₁ + θ₂ – θ₃).

9. Give the relations holding between the tangents if (i) θ₁ + θ₂ + θ₃ = π; (ii) θ₁ + θ₂ + θ₃ + θ₄ = 2π ; (iii) θ₁ + θ₂ + θ₃ = .

10. What results can be deduced from

 

where n is a positive integer ?

11. Give the last terms in the formulae (4) and (5), (i) if n is even, (ii) if n is odd.

12. Give the last terms of the numerator and denominator of the formula for tan nθ, (i) if n is even, (ii) if n is odd.

13. Show that the coefficient of cⁿ in

 

14. Prove that , and give the last term.

15. Prove that sec θ cos 5θ = 1 – 12 sin² θ + 16 sin⁴θ.

16. In any triangle ABC, prove that

 

17. Find the equation whose roots are .

18. If tan θ₁, tan θ₂, tan θ₃, tan θ₄ are the roots of the equation t⁴ + bt³ + ct² + et + f = 0, find the value of tan (θ₁ + θ₂ + θ₃ + θ₄).

Summation of Series. Sum the series

 

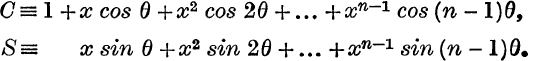
Put cos θ + i sin θ = z.

Then

 

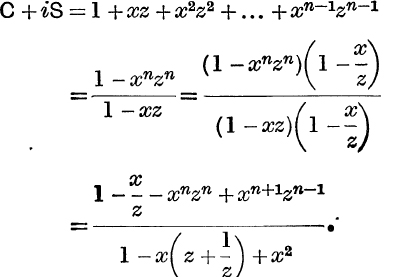
But = cos θ – i sin θ and z + = 2 cos θ;

 

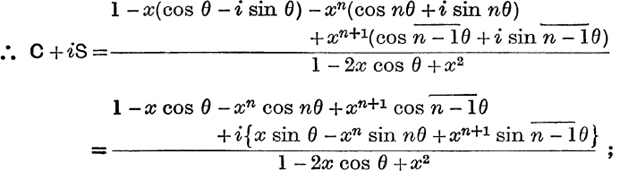
by equating the first and second parts, we have

 

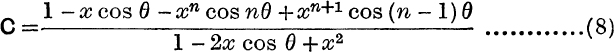
and

 

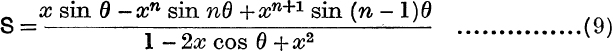
These results may also be obtained by multiplying the given series by 1 – 2x cos ϕ + x² and showing that in the product all the terms disappear except a few at the beginning and end.

Note. If |x| < 1, since , we see that

 

and

 

Example 8. Sum the series

 

Put cos α + i sin α = α, cos β + i sin β = b.

Then the given series is the first part of the complex number

 

but

 

 

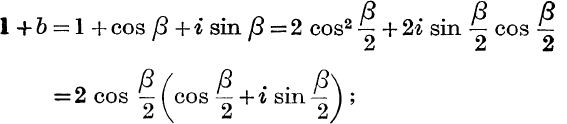
EXERCISE IX. d.

1. Sum to n terms,

 

Deduce the sum to infinity.

2. (i) Sum to n terms,

 

(ii) Deduce the sum to infinity if θ is not a multiple of π.

3. (i) Sum to n terms,

 

(ii) Deduce the sum to infinity if θ is not an odd multiple of

4. If n is a positive integer, express in the form A + Bi. when a = cis α, b = cis β.

What results can be deduced from the identity,

 

5. If n is odd, prove that

 

6. If n is even, sum the series

 

7. Sum to n + 1 terms,

 

8. Sum to n + 1 terms,

 

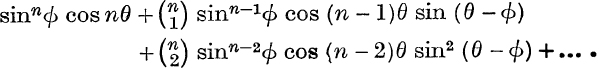
9. Prove that, in any triangle ABC, if b < c, the sum to infinity of .

10. Use the identity,

 

to obtain an expansion for .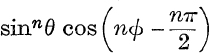

11. Prove that, in any triangle ABC, cⁿ = aⁿ cos nB +

 

to n + 1 terms.

12. If |x| < 1, find the coefficients of xⁿ in the expansions in powers Of x Of

 

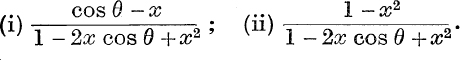
13. If θ is not a multiple of π, find the sum to infinity of

 

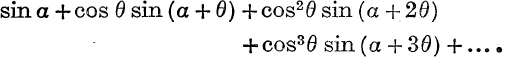
14. Sum to n + 1 terms,

 

15. Sum to n + 1 terms,

 

16. What results can be deduced by writing cis θ for z in

 

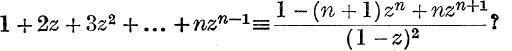
17. Sum to n terms,

 

18. Prove that, if |x| < 1,

 

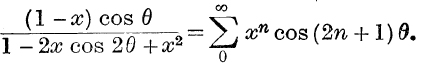
Deduce that 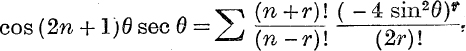for r = 0 to n, where 0! is taken to mean unity.

19. If ac > b² and , prove that Can be expanded in powers of x and that the coefficient of xⁿ is

 

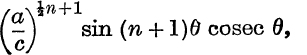
where .

20. Provethat

 

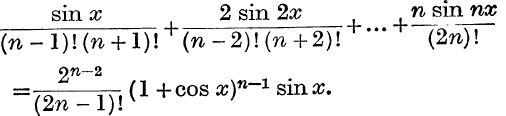
Expansions of cos nθ, sin nθ in terms of cos θ, sin θ separately.

We suppose that n is a positive integer, and we write cos θ = c, sin θ = s.

Forms of the Expansions.

(i) From ,

putting

 

we see that cos nθ is a polynomial in cos θ of degree n,

 

the last term being a₁c if n is odd, and a₀ if n is even.

(ii) Differentiation w.r.t. θ gives (cf. foot of p. 128) n sin nθ

 

 

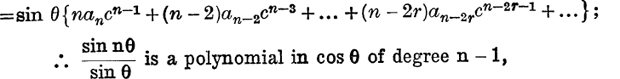
the last term being b₀ if n is odd, and b₁c if n is even.

(iii) Changing θ to – θ, we get

if n is even,

 

and

 

and, if n is odd,

 

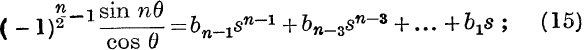
and

 

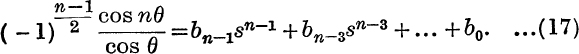
The forms of the results are easily recalled by means of the special cases when n = 2, 3, …; thus

 

can be expressed as polynomials in cos θ; and

 

can be expressed as polynomials in sin θ.

Relation between Consecutive Coefficients.

From    cos nθ = a_ncⁿ + a_n–2c^n–2 + … ≡ ∑a_rc^r, by differentiating twice with respect to θ, (cf. foot of p. 128), we get

 

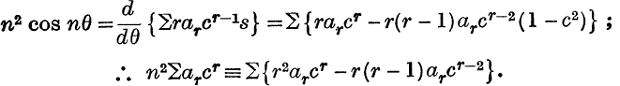
Equate coefficients of c^r;

 

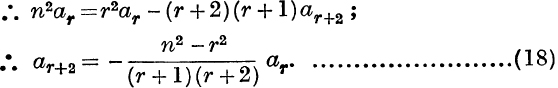
A similar result to (18) can be found, by the same process, for each of the expansions. Such results enable us to calculate all the coefficients, if one coefficient is known. In applying this method we begin by finding the first or the last coefficient of the expansion (12-17), according as we wish to have the result arranged in descending or ascending powers.

When one expansion has been obtained, any other expansion can be deduced rapidly from it by one of the methods given on p. 178.

The First and Last Coefficients.

(i) From , it follows that

 

Also, if n is even, putting θ = in (12), we have

 

And, if n is odd,

 

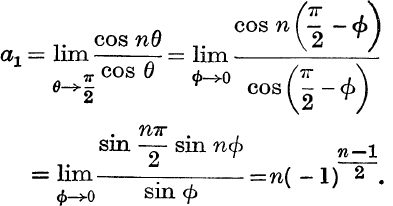
(ii) For the expansion of , by differentiating as on p. 178, we see that, in (13), b_n–1 = a_n = 2^n–1.

Also, if n is even,

 

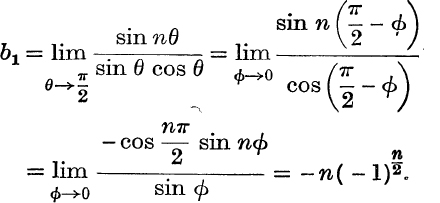
And, if n is odd,

 

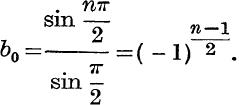
(iii) The first and last coefficients in the expansions (14) to (17) can be obtained in the same way or may be deduced from the results of (i) and (ii) by writing – θ for 0.

Note. The numerical value of the coefficient of the term of highest degree is in every case 2^n–1. As regards the sign to be attached, this can be conjectured from special cases. Thus, and 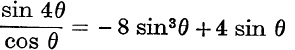suggest that the leading coefficient of 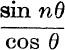, when n is even, is .

For convenience of reference., the various expansions are given in Ex. IX. e, Nos. 12-25. An example is added below to illustrate the method which should be followed in any required special case.

We have assumed that n is a positive integer. It is natural to enquire whether the expansions in Ex. IX. e, Nos. 14-17, 22-25 can be interpreted if n is fractional, when the series involved are evidently no longer finite. This involves a discussion which is beyond the range of this book; see Bromwich, Infinite Series, 1st ed., Ch. IX. § 68.

Example 9. Discuss, ab initio, the expansion of 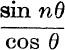, where n is even, in ascending powers of sin θ.

From

 

it follows that

 

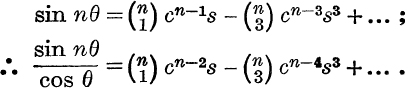
Since n is even, by using c² = 1 – s², we can express c^n–2, c^n–4, etc., as polynomials in s.

Therefore 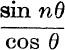can be expressed as a polynomial of degree n – 1 in sin θ. [It cannot be expressed as a polynomial in cos θ.]

We may therefore write, for n even,

 

Differentiating,

 

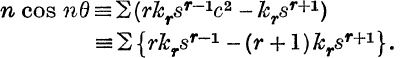
Differentiating again,

 

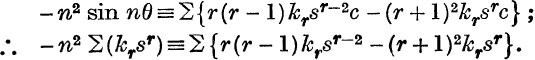
Equating coefficients of s^r,

 

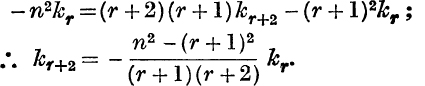
But

 

if n is even,

 

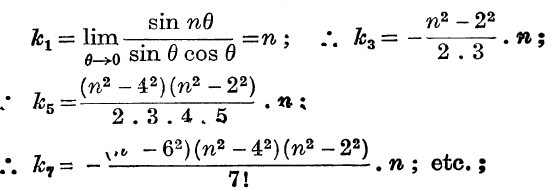
EXERCISE IX. e.

Which of the functions in Nos. 1-6 can be expressed as polynomials in sin θ, and which of them as polynomials in cos θ ?

In each case, use the methods of pp. 179, 180 to obtain (a) the term of lowest degree, (b) the term of highest degree.

1. sin nθ, if n is odd.

2. cos nθ, if n is even.

3. , if n is even.

4. , if n is odd.

5. , if n is odd.

6. , if n is even.

7. Assuming that cosnϕ = a₀ + a₂sin²θ + … + a_nsinⁿθ, where n is even, find the value of a₀. Then find by differentiation the other coefficients.

8. Assuming that sin nθ = a₁ sin θ + a₃ sin³θ + … + a_n sinⁿθ, where n is odd, find the value of a₁. Then find by differentiation the other coefficients.

9. Prove by differentiation that the constants in equation (13), p. 178, are connected by the relation,

 

10. Prove that , where y = 2 cos 2θ.

11. Prove that , where x = 2 cos θ.

12.

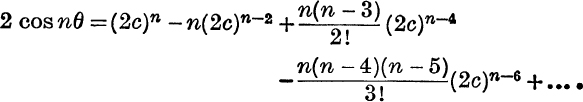
13.

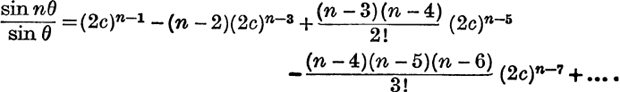
14. n even,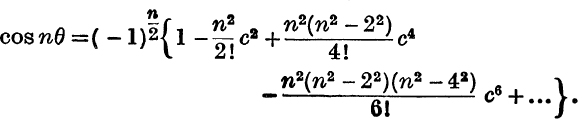

15. n odd,

16. n even,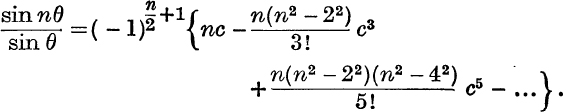

17. n odd,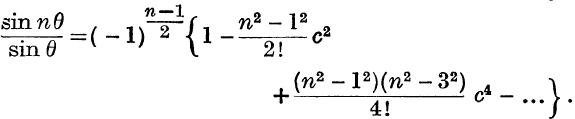

18. n even,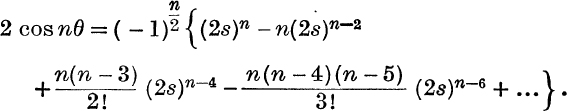

19. n odd,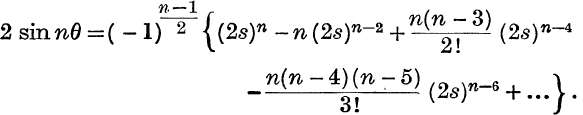

20. n even,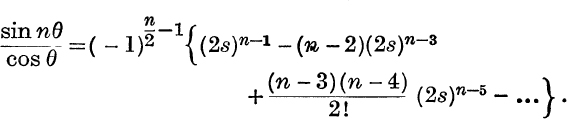

21. n odd,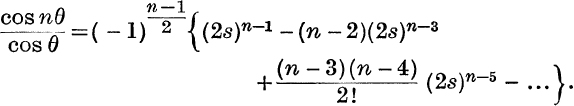

22. n even,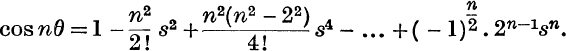

23. n odd,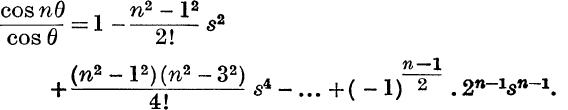

24. n even,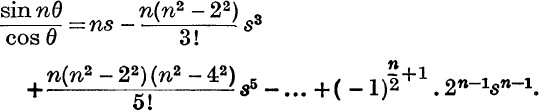

25. n odd,

26. What are the coefficients of c^n–8 and c^n–10 in the expansion of cos nθ in powers of cos θ ?

27. What result can be deduced from No. 24 by writing 2p for n and for θ ?

28. Prove that

 

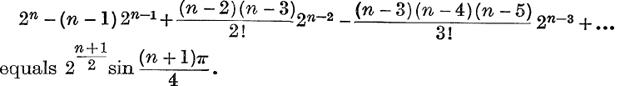
29. Prove that .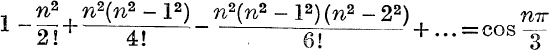

30. Prove that .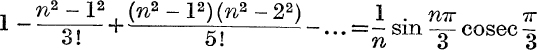

31. By writing x =cos θ + i sin θ, show how to express as a polynomial of degree n in .

32. Express in terms of .

33. Express as a cubic in .

34. Verify that the coefficient of c^2r+1 in the expansion in No. 15 is the same as the coefficient of c^2r+1 in the expansion of cosnfl in No. 12, if n is odd.

35. Verify that the coefficient of c^2r in the expansion in No. 14 is the same as the coefficient of c^2r in the expansion of cosnθ in No. 12, if n is even.

36. If y = sin nθ and θ = sin^–1 x, show that

 

Differentiate this k times by Leibnitz’ Theorem and deduce that y_k+2 = (k² – n²)y_k, where y_r is the value for x = 0 of . What are the values of y₀, y₁, y₂, y_k ? Obtain the result of No. 25 by assuming Maclaurin’s Theorem.

37. If y = cos nθ and ϕ = sin^–1x, show that

 

Hence obtain the result of No. 22 by the method of No. 36.

EASY MISCELLANEOUS EXAMPLES

EXERCISE IX. f.

1. Solve x⁶ + x⁵ + x⁴ + x³ + x² + x + l = 0.

2. Solve x¹² – x⁶ + 1 = 0.

3. Solve (ax – b)ⁿ = (a – bx)ⁿ.

4. Solve (1 – xi)ⁿ + i(l + xi)ⁿ = 0.

5. Find which roots of x¹⁰ = 1 make x⁴ + x³ + x² + x + 1 = 0.

6. If x⁵ = 1, prove that x⁴ + x – x³ – x² = 0 or ± .

7. Given that tan α = 2, find tan 3α. Use the result to find the cube roots of 88 + 16i.

8. Expand (1 – i){(1 – xi)ⁿ + i(1 + xi)ⁿ} in powers of x.

9. If , expand in powers of x:

 

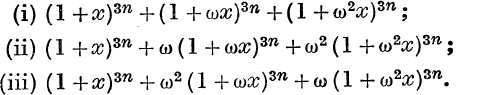
10. If x¹³ = l, x ≠ 1, and if y₁ = x + x³ + x⁹, y₂ = x² + x⁵ + x⁶, y₃ = x⁴ + x¹⁰ + x¹², y₄ = x⁷ + x⁸ + x¹¹, prove that

 

11. Solve cis rθ = cis sθ where r, s are unequal positive integers.

12. Show that the roots of (1 – z)ⁿ = zⁿ are of the form + Bi.

13. Prove that the points which represent the roots of zⁿ = (z + 1)ⁿ in the Argand Diagram are collinear.

14. Prove that |z| = 1, z ≠ 1, points representing lie on an ortnogonai line-pair.

15. Prove that the points representing 1, –1, a + bi, and are concyclic.

16. If the point which represents z moves on the circle |z| = 1, find the loci of the points which represent

 

17. If α, β are the roots of t² – 2t + 2 = 0, prove that 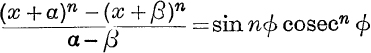, where cot ϕ = x + 1.

18. Sum to n + 1 terms, .

19. Prove that

 

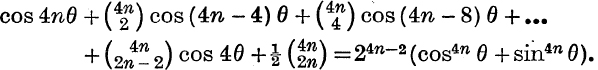
20. (i) Prove that can exPressed as a polynomial in of degree n. Find the coefficient of and the constant term.

(ii) Also show that sin³ϕ is a factor of (2n + 1) sin θ – sin (2n + 1)θ.

21. If u_n = (n + 1) sin nθ – n sin (n + 1) θ, find the value of u_n – u^n–1, and prove that 1 – cos θ is a factor of u_n.

22. Prove geometrically that, if z = cis θ, and – π < θ < π, then as n → ∞

23. If cos³ θ sin⁴ θ ≡ A₁ cos θ + A₃COS 3θ + A₅cos 5θ + A₇ cos 7θ, prove that

 

24. Use the identity,

 

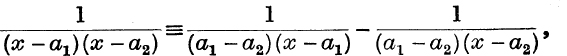
to show that

 

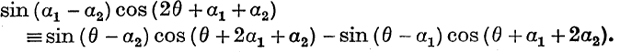
25. Use the identity,

 

to show that

 

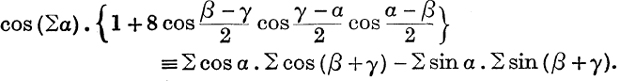
26. Prove that

 

where s ≡ sin θ and n is a positive integer.

HARDER MISCELLANEOUS EXAMPLES

EXERCISE IX. g.

1. Express x⁷ + 1 as the product of four factors.

2. Express x⁸ + x⁷ + x⁶ + … + x + 1 as the product of four factors,

3. If , and if r and p are prime to n, prove that

 

4. If p, q are real and (x + p)² + q² ≡ (x + a)(x + β), prove that 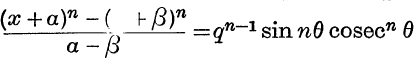, where .

5. If x = 2 cos θ, prove that .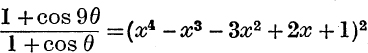

6. If u_n – 2u_n+1 cos θ + u_n+2 = 0, and also u₁ = p sin θ + q cos θ and u₂ sin 2θ + q cos 2θ, prove that u_n = p sin nθ + q cos nθ.

7. Deduce trigonometrical identities from the relation

 

8. If (1 + x)ⁿ = a₀ + ∑arxr, where n is a positive integer, prove that

 

9. If r² = a² + b² + c² and prove that

 

10. If ∑ cos θ_r = 0 = ∑ sin θ_r, prove that

 

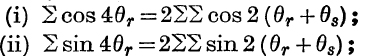
where r and s are 1, 2, 3, 4, 5 and are unequal.

11. Prove that, if 2 (ad + bc) = (a + d)(b + c), the four points representing the complex numbers a, b, c, d are concyclic and form a harmonic range on the circle.

12. If a, b, c, A, B, C are real and ac > b², AC > B², prove that the points representing the roots of az² + 2bz + c = 0, Az² + 2Bz + C = 0 are concyclic with the origin if bC = cB.

13. If w, z are complex numbers such that |z| = 1 and = 1 – z + z², and if they are represented by the points P, Q prove that PQ, passes through the point (1,0) and that the x-axis bisects an angle between OP and OQ.

14. If α₁, α₂, α₃, α₄, α₅ are the fifth roots of unity, prove that , for r = 1 to 5, equals tan^–1 + nπ where n is an integer or zero.

15. Use the relation 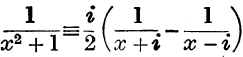to prove that

 

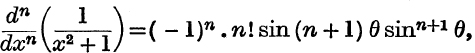
where x = cot θ.

16. Prove that , where x = cot θ.

17. Prove that

 

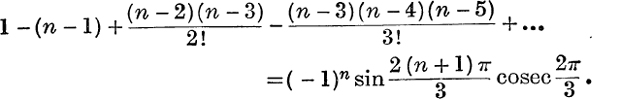
18. Prove that

 

19. Prove that

 

20. Prove that

 

21. Find the coefficient of xⁿ in (1 + 2xcos θ + x²)ⁿ and deduce that equals

 

22. If c_r is the coefficient of x^r in (x^–n + … + x^–1 + 1 + x + … + xⁿ)⁴, prove that

 

and deduce that

 

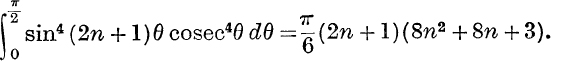
23. Prove that 2 cosec α ∑ {sin rα cos (n – r) β}, for r = 1 to n – 1, is equal to

 

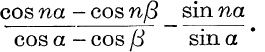
24. If p, q, r are any positive integers or zero, subject to p + q + r = n, prove that