CHAPTER V
EXPANSIONS IN SERIES
Power Series. An expression of the form
is called a power series in x.
Let ϕn(x) denote the sum of the first n terms,
then
If, for some or all values of x, 
exists and is, say, ϕ(x), the series is called convergent for those values of x, and ϕ(x) is called the sum to infinity. Also, the series is called the expansion of ϕ(x) in powers of x, and we write
The most useful expansions are those which are “rapidly convergent,” i.e. those in which ϕn(x) is a good approximation to ϕ(x) for reasonably small values of n.
It is most important to distinguish between the meanings of the following:
and
The first means the sum of n terms of the given series, and is obtained by successive addition.
The second means 
(a0 + a1x + a2x2 +… + an–1 xn–1), if this limit exists, and is undefined if this limit does not exist. Sometimes, however, the second is written down when it is merely proposed to discuss the existence of the limit.
The Geometric Progression; l – x + x2 – x3 + ….
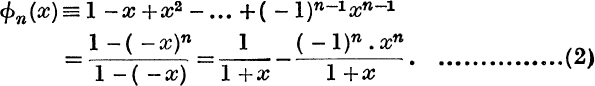
But, if –1 < x < 1, xn = 0, see limit (i) below;
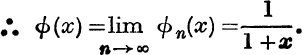
Therefore, if –1 < x < 1, the power series 1 – x + x2 – x3 + … is convergent and has 
for sum to infinity.
Two Important Limits.
(i) If
Consider first 0 < x < 1; put x = 1 – p, so that 0 < p < 1.
Then
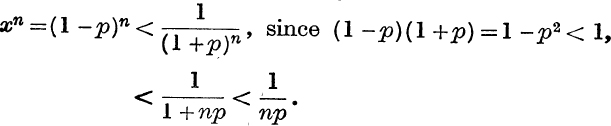
∴ xn can be made less than any given positive number, 
, by taking n large enough,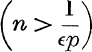 
; but xn is positive;
Also ( – x)n = ( – l)n . xn; therefore the result holds also for – 1 < x < 0.
(ii) For all values of x,
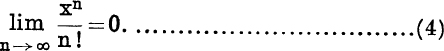
Consider first x > 0 ; take any fixed integer k greater than 2x.
Then, if 
,
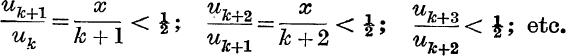
∴ by multiplication, 
; but un is positive;
Also, as in (i), the result can be extended to all negative values of x.
The Symbol |x|. It is often convenient to use the symbol |x | to denote the value of x if x is positive and the value of –x if x is negative.
Thus, the condition – 1 < x < 1 is written more shortly in the form |x| < 1; the statement that x lies in the range of values a – to a + is represented by | x – a | < ; the positive square root of a2 may be written | a | ; etc.
The statement in equation (3) above would therefore often be given in the form :
Expansions of sinx and cosx. We proceed to expand sin x and cos x in power series, and for the sake of completeness we include the fundamental results upon which the proof depends.
If 0 < x < 
π, and the angles are measured in radians, we assume that.
When x → 0, cos x → 1, thus 
→ l. Since the value of is unaltered when x is changed to – x, it follows that lim = 1 when x → 0 m any manner. This result is required for the differentiation of sin x and cos x.
By the definition of a differential coefficient,
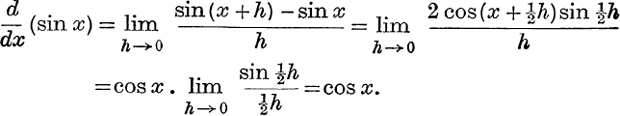
Similarly, 
(cos x) = – sin x, or this may be deduced from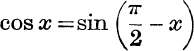 
. Also, results like
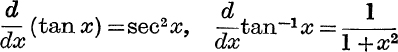
may be derived by the usual processes of the Calculus.
If f(x) is a one-valued integrable function of x which is positive for 0 < x < a, then the function f1(x), defined by
where 0 < x < a, is also necessarily positive. Similarly, if f2 (x) is defined by
this new function is also positive, and by continuing the process we get a series of functions all positive in the range 0 < x < a.
Now take f(x) = x – sin x, and suppose that x is positive; then f(x) is one-valued and positive, and therefore
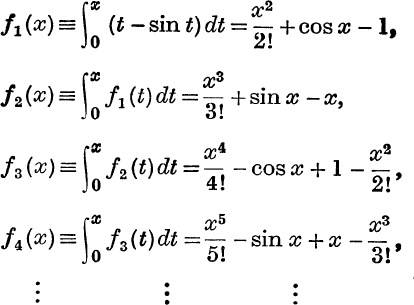
are all positive. Thus, if x is positive and p is any positive integer,
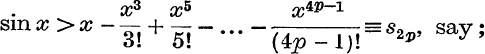
and
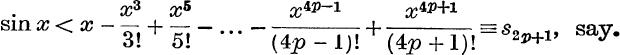
These inequalities may be written : s2p < sin x < s2p+1;
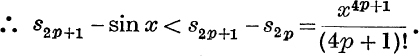
But by limit (ii), p. 78,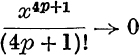 
, when p → ∞ .
Also s2p+1 – sin x is positive; ∴ s2p+1 → sin x when p → ∞.
Similarly, since
∴ sin x is the sum to infinity of the series, 
.
When x is changed into – x, every term of the series changes sign, and so does sin x. Therefore the result holds also when x is negative; it is obviously true also if x = 0. We have therefore
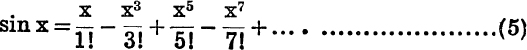
for all values of x.
Similarly, from the relations on p. 80,
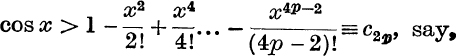
and
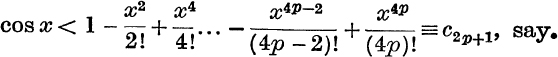
Hence, c2p < cos x < c2p+1, where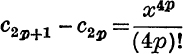 
.
Therefore, by the same argument as before, it follows that
We have therefore
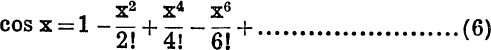
for all values of x.
Note. Attention should be called to a crucial point in the argument used in these proofs. The fact that 
shows that if either s2p+1 or s2P tends to a limit, the other must tend to the same limit; but it does not ensure that either of them actually tends to a limit. It is essential to prove that the limit exists. This is done by the inequality,
which shows that 0 < (s2p+1 – sin x) < (s2p+1 – s2p), and therefore
Hence s2p+1 → sin x, when p → ∞ . It then follows that s2p → sin x, or this can be proved in the same way. Both these results are needed to show that the sum to n terms tends to sin x when n → ∞.
Example 1. Calculate sin 36° to 4 significant figures.
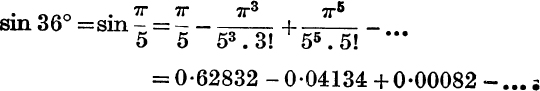
Also, with the notation of p. 80,
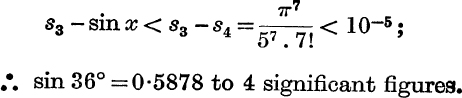
Example 2. Find the first three terms of the expansion of tan x in powers of x.
Since tan (–x) = – tan x, tan x is an odd function of x. If then we assume that tan x can be expanded in powers of x, the expansion must be of the form tan x = Ax + Bx3 + Cx5 + ….
Then
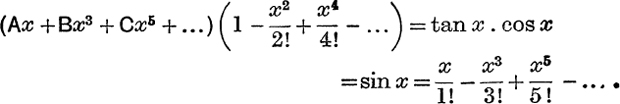
Equating coefficients : 
;
It should be noted that this process does not prove that tan x can be expanded as a convergent power series in x. This is, however, true, and, for small values of x, x, x + 
x3, 
, are successive approximations to tan x.
Example 3. Show how to expand cos2x and sin3 x in powers of x.
Use the formulae : 2 cos2 x = 1 + cos 2x, 4 sin3x = 3 sin x – sin 3x.
Example 4. Solve cos θ = θ, approximately.
Inspection of a rough graph shows that there is only one root and that its value is approximately 0·7. For a value of θ of this size, we have cos θ 
1 – θ2; ∴ 1 – θ2 θ;
Put θ = 0·7 + a, then cos(0·7 + a) = 0·7 + a;
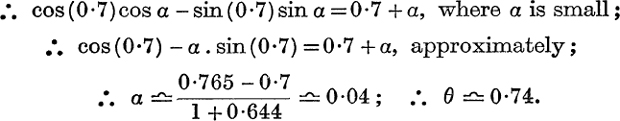
A closer approximation, θ 0·739, could be found by putting θ = 0·74 + β, and repeating the process just used.
EXERCISE V. a.
Find the sums to infinity of the series in Nos. 1-5.
1. 
2. 
3. 
4. 
5. 
6. Show that the positive square root of the sum of
7. Calculate from the series the cosine of 1 radian, correct to 3 significant figures.
8. Calculate from the series the sine of 3°, correct to 3 significant figures.
9. Prove that tan x – sin x x3, if x is small.
10. Prove that 
, if θ is small.
11. Express x cosec x in powers of x, neglecting x6 and higher powers.
12. Express 
as a power series in x and give the general term. Also express it as a power series in 
.
13. Find the general term in the expansion of cos3 x in powers of x.
14. Show that 
differs from θ by about 
when θ is small.
15. Find whether tan x – 24 tan 
or 4 sin x – 15x is the greater when x is small and positive.
16. Prove that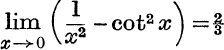 
.
17. If a is small, prove that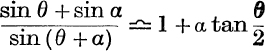 
.
18. Find an approximate solution of cos θ = 2θ.
19. Find an approximate solution near to 
of tan θ = θ.
20. If tan (θ – ϕ) = (1 + λ) tan ϕ and λ is small, prove that one value of tan ϕ is approximately (1 – λ) tan 
.
21. Prove that, for 0 < x < π,
22. Prove that 
, when 0 < x < 
.
23. From 
, obtain the successive approximations, θ sin θ, θ sin θ + 
sin3 θ, θ sin θ + sin3 θ + 
sin5 θ, θ being small.
24. If nt = ϕ – sin ϕ, and 3 is negligible, prove that
25. By the method of p. 80, show that, if a: is positive, ex – 1,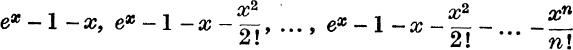 
, are all positive.
26. By the method of p. 80, show that, if x is positive,
The Logarithmic Series. In equation (1), p. 77, a0 is the value of ϕ(x) for x = 0, and a0 + a1x is its approximate value for a small, positive or negative, value of x. Thus the fact that log x is meaningless when x ≤ 0 suggests that it cannot be expanded as a power series in x. But the function log(l + x) is capable of expansion for a certain range of values of x.
Using the sum of a G.P. given in equation (2) we have
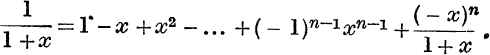
We shall suppose that y is a positive number; then
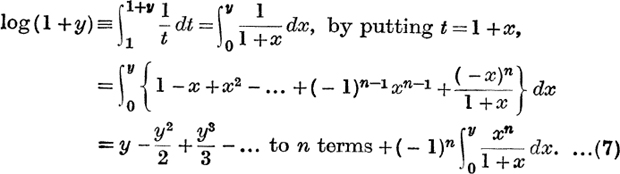
Also
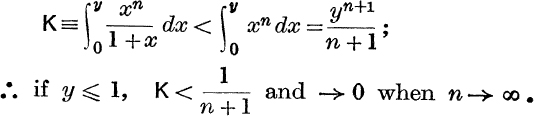
∴ from (7),
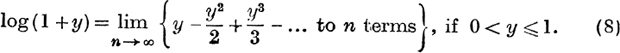
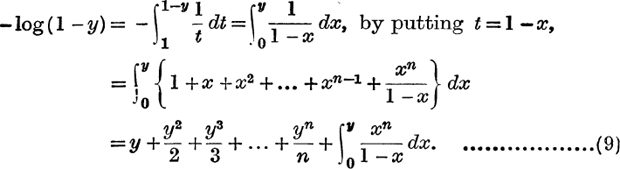
Also
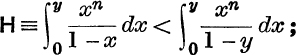
∴ since
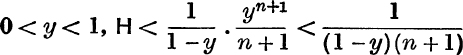
and H → 0 when n → ∞;
∴ from (9),
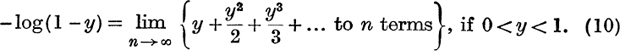
The results of (8) and (10) may be combined into the single statement that log(l + x) is the sum to infinity of the series 
provided that 0 < x ≤ 1 or – 1 < x < 0. Also the result is true for x = 0. We therefore write
Note. Care must be taken about the insertion in (11) of such a value as 
for x. This gives a true result if n is positive. If, however, it were now proposed to make n → ∞, it could not be assumed that either side had a limit, or that if the limits existed they must be equal. Actually in this case the limits do not exist.
The proof above that H → 0 definitely requires y < 1, not merely y ≤ 1.
From
and
by subtracting and dividing by 2, we have
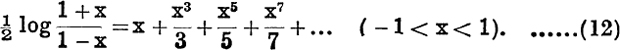
An alternative form of this result is obtained by putting
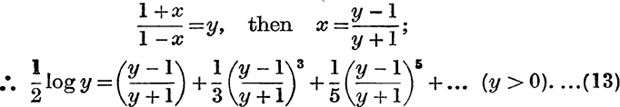
Equations (12) and (13) may be used for the numerical computation of logarithms ; convenient methods of proceeding are indicated in Ex. V. b, No. 4 and Ex. V. e, Nos. 17, 18.
Example 5. Find the sum to infinity of
The nth term is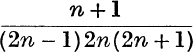 
, and may be expressed in Partial Fractions (see p. 231) in the form
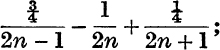
∴ the sum to n terms is
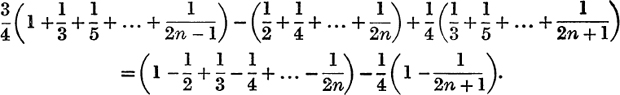
When n → ∞ the limits of the two brackets are log 2 and 1; ∴ the sum to infinity is log 2 – 
.
EXERCISE V. b.
1. Write down the sums to infinity of the series
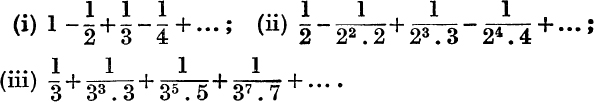
2. Prove the following results, finding the conditions under which they hold :
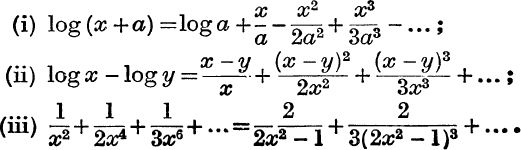
3. Expand the following functions as power series in x, giving the coefficients of xn and the conditions of validity :
(i) 
;
(ii) log {( 1 – x)( 1 + 3x)};
(iii) log ( 1 + 5x + 6x2);
(iv) log (x2 + 2x + 1);
(v) log (x + 2);
(vi) log (x2 + 3x + 2);
(vii) 
;
(viii) log ( 1 + x + x2).
4. (i) Use series (13) to calculate log 2 to 4 places of decimals ;
(ii) Use series (13) to calculate log 
, log 
, and log 
, each to 4 places of decimals;
(iii) Use the results of (i) and (ii) to obtain the logarithms of 3, 4, 5, 6, 7, 8, 9 and 10;
(iv) Prove that log10N = logeN ÷ loge 10 and use the results of (iii) to deduce the corresponding logarithms to base 10.
5. What is the coefficient of xn in the expansions of the following functions as power series in x and for what values of x are the expansions valid ?
(i) (1 – 2x)log(l – 2x);
(ii) (1 + 3x)2 log(l + 3x);
(iii) 
.
6. Given that |x| < 1, find the sums to infinity of the series whose nth terms are
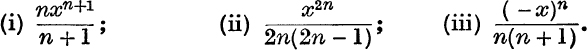
7. Express 
in powers of 
when |x| > 1.
8. Express 2 1og n – log(n + 1) – log(n – 1) as a power series in 
when n > 1.
9. Express log(x + 2) – 2 1og(x + 1) + 2 log (x – 1) – log(x – 2) as a series of powers of 
, and find for what values of x the expansion is valid.
Sum to infinity the following series :
10. 
11. 
12. 
13. 
14. 
15. 
16. Prove that 
unless A = nπ; deduce that the sum to infinity of 
is log 3.
17. Evaluate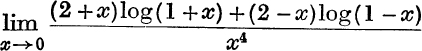 
.
18. Evaluate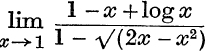 
.
19. If x log x + x – l = , which is small, prove that 
.
20. Find approximate solutions of the equation 
.
Gregory's Expansion of tan–1x. From the sum of a G.P., equation (2), p. 77, we have
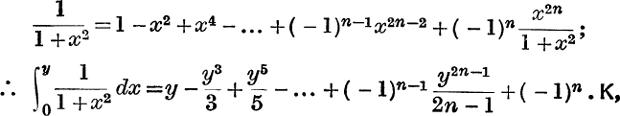
where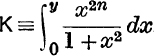 
If –1 ≤ y ≤ + 1, the numerical value of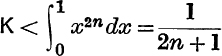 
;
∴ the sum to infinity of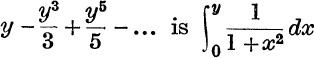 
.
But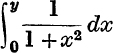 
is the value of tan–1y between 
and 
;
provided that – 1 ≤ y ≤ 1, and that the value taken for tan–1 y lies in the range from 
to 
, inclusive.
Evaluation of π. By using (14), we can obtain π as the sum to infinity of a series. Putting y = 1, we have
This series converges so slowly that for practical calculation it is necessary to employ alternative series (Ex. V. c, Nos. 3, 4).
The reader should verify the following results:
(i) Machine’s formula, 
.
(ii) Rutherford’s formula, 
.
These give π as the sum to infinity of rapidly convergent series.
EXERCISE V. c.
1. Find the sums to infinity of
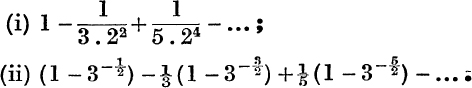
2. Give the sum to infinity of tan x – tan3 x + 
tan5 x – … when
3. Calculate π to five places of decimals by Machin’s or Rutherford’s formula.
4. Calculate π to four places of decimals by the formula,
5. Simplify tan–1 + tan–1 and use the result to express π as the sum to infinity of a series.
6. Find the sum to infinity of
7. Find, when possible, the sum to infinity of
8. Expand, when possible, 
as a power series in tan θ.
9. If 
, and x is so small that x7 is negligible, obtain the successive approximations 
.
Interpret this with x = tan θ.
10. If is small, prove that one root of tan–1 x = – x is given by 
, and find the next approximation.
The Exponential Series.
If we assume that the function exp (x) or ex can be expanded in the form
and if we also assume that
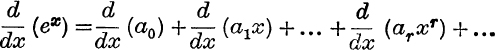
and that we may continue to differentiate in this way, it is easy to find the values of a0, a1, a2, … .
Putting x =0 in the first equation, we have 1 = a0.
The second equation is
The equations obtained by continuing the process are
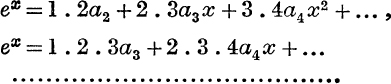
Putting x = 0 in these, we have
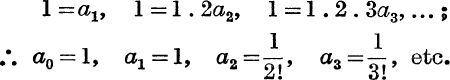
Therefore the expansion is
But the assumptions stated above are not easy to justify. A valid process which sometimes replaces this method is based on Maclaurin’s Theorem. We shall now, however, proceed to obtain the result by a different method, based on integration by parts.
To prove that the series 
is convergent for all values of x and that its sum to infinity is ex.
Put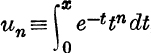 
, n being a positive integer.
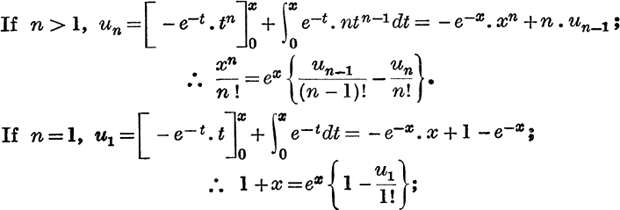
∴ by adding the results for n = 1, 2, 3, , m,
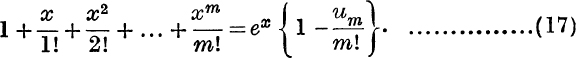
We shall now prove that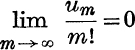 
.
Consider first x > 0; then for 0 < t < x, 
;
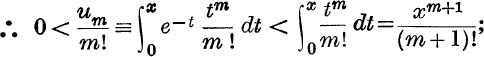
∴ by limit (ii) on p. 78, 
when m → ∞.
Next suppose x < 0 and put x = – y so that y > 0.
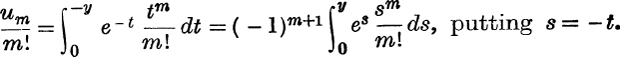
But for 0 < s < y, es < ey;
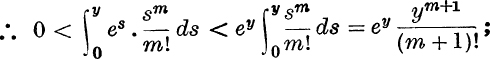
∴ by limit (ii) on p. 78,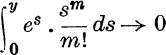 
when m → ∞;
The required result therefore follows from equation (17).
Calculation of e. Putting x = 1 in (16) we have
∴ e is greater than the sum, sn, to n terms of this series; but
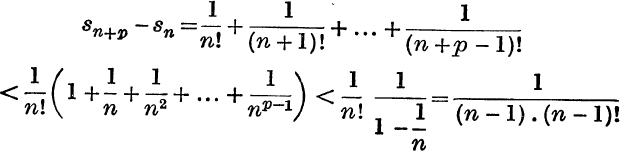
and as this is true for all positive values of p, it follows that
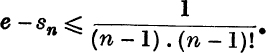
For example, taking n = 10, we get
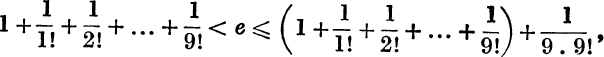
and this is found to give the value of e to 6 places of decimals.
Note. If a function f(p), which → a limit l when p → ∞, satisfies the inequality f(p)< K for all values of p, K being independent of p, the correct conclusion is not l < K but l ≤ K. Thus in the above work the conclusion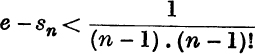 
would not be justified; it can however be proved thus:
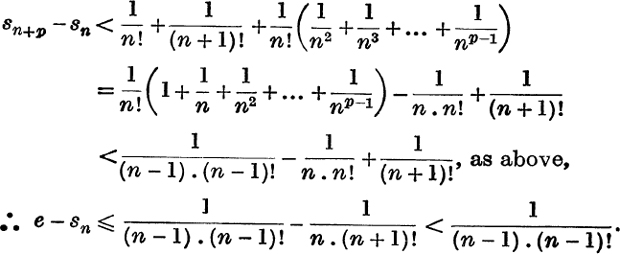
Nature of e. It is easy to see that e is not rational. For if 
where p, q are integers,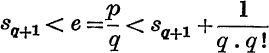 
and multiplication by q! gives 
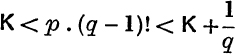, where K is an integer, but p.(q – 1)! is also an integer, so the inequalites cannot be true.
The Compound Interest Law. It was proved on p. 64 that 
. We shall now show that every function y which has the property 
is of the form Aex where A is constant.
If
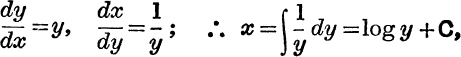
and, if we put C = – log A, we have
The equation means that y is a function whose rate of increase with respect to x is y. This is the rate that occurs if money is lent at Compound Interest at 100 per cent, per unit time, the interest being added continuously. Thus if £A is lent under these conditions, and the unit of time is a year, the amount after x years is £(Aex).
If the interest is compounded at intervals of 
th of a year, the amount after kx periods for each of which the interest is 
per cent. would be 
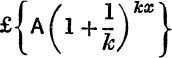. For continuous addition of interest we make k → ∞; we may therefore expect that
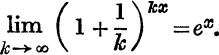
Writing 
for k, and successively x, – x, for y, we have
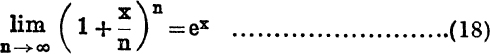
and
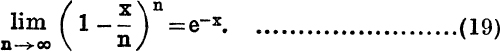
Formal proofs of these limits will be given in the companion volume on Analysis; another method of proof is indicated in Ex. IV, g, Nos. 15, 16, 19.
Example 6. Find (in terms of e) the sum to infinity of the series
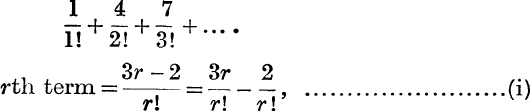
which if r > 1,
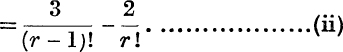
Thus, by (i),
and (ii) gives
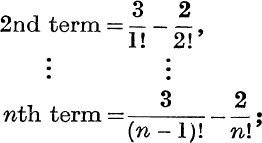
∴ the sum to n terms is
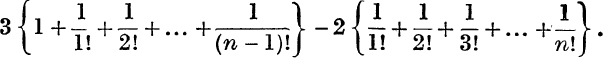
When n → ∞ the sums within the brackets tend to e and to (e – 1) respectively, thus the sum to infinity = 3e – 2(e – 1) = e + 2.
Example 7. Find the sum to infinity of
If r > 1, the rth term is
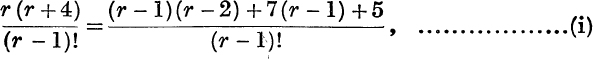
and this, if r > 2,
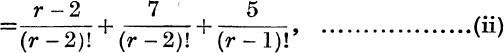
and this, if r > 3,
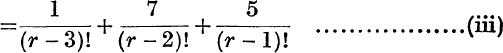
and (iii) gives all the later terms.
Thus the sum to infinity is found, by the method of Example 6, to be e + 7e + 5e = 13e.
Note. In the above example, the exceptional terms at the beginning of the series could be found by (iii) if conventions were made to the effect that 0! = 1 and 
when a is a negative integer. The reason that they can be found in this way is shown by (i) and (ii).
Example 8. Find, by successive approximations, x in terms of a, when x + ex = 1 + a, and a is small.
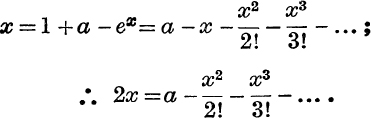
For first approximation, neglect a2; then
For second approximation, neglect a3; then
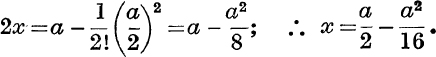
For third approximation, neglect a4; then
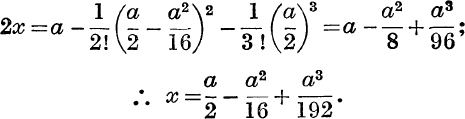
For fourth approximation, neglect a5; then
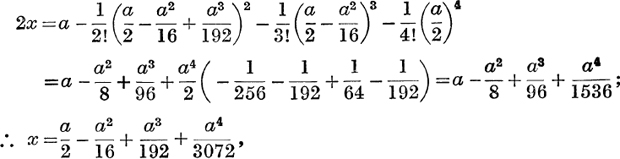
and so on.
EXERCISE V. d.
Find (in terms of e) the sums to infinity of the series in Nos. 1-16.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
Find the values of the following :
17. 
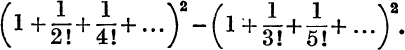
18. 
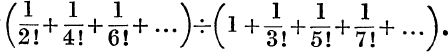
Find the sums to infinity of the series whose rth terms are
19. 
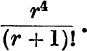
20. 
21. 
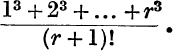
22. 
23. 
24. 
25. 
Expand the following in power series, giving the coefficient of xn in each :
26. ex(2 + 3x).
27. 
28. 
29. 
30. 
31. Sum the series 
.
32. Sum the series 
.
33. Find the coefficient of x4 in (ex + e–x)n.
34. Evaluate 
.
35. Evaluate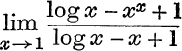 
.
36. If x is small, prove that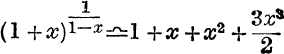 
.
37. Show that
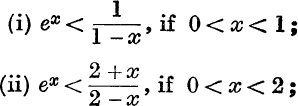
and examine the results when x is negative.
EASY MISCELLANEOUS EXAMPLES.
EXERCISE V. e.
1. Give the sums to infinity of :
(i) 
(ii) 
(iii) 
(iv) 
(v) 
(vi) 
2. Show that the sum to infinity of 
is the square of that of 
.
3. Prove that 
, if θ is small.
4. Show that the error involved in replacing θ by 
is about 
if θ is small. Hence solve sin θ = 
θ approximately.
5. Find an approximation to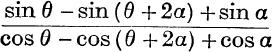 
when α is so small that α3 is negligible.
6. Prove that 
, if θ6 is negligible.
7. If cos (α + θ) = cos α cos ϕ – cos β sin α sin ϕ, where ϕ is small, prove that one value of θ is nearly ϕ cos β + ϕ2 cot α sin2 β.
8. If is small and positive, prove that 
has three roots.
9. Show that 
is an approximate solution of
and find a better approximation.
10. If x is small, and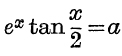 
, prove that
11. If θ is small, and θ cot θ = 1 – , prove that 
.
12. Prove that the sum to infinity of
13. If n is positive, prove that the sum to infinity of
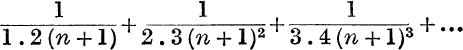
is 
.
14. Expand as power series in x, giving the general terms:
15. Express log (x + y) – log (x – y) as a series of powers of 
, stating when this is possible.
16. Express 2 log (x + h) – log x – log (x + 2h) as a series of powers of 
and state when this is possible.
17. Prove that 
and hence evaluate log 10, given that log 2 = ·693147. Deduce the value of log10 2.
18. If 
and 
, prove that
and hence calculate log 2 to 3 places of decimals.
19. If 0 < θ < 
, prove that 
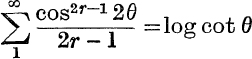. What happens if < θ < π ?
20. Find the sum to infinity of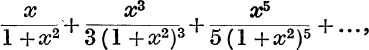 
and the values of x for which it converges. Expand the sum in another way and find the coefficient of x3n in the new expansion.
21. Find the sums to infinity of :
(i) 
(ii) 
(iii) 
(iv) 
and prove that in (iv) the sum to n terms differs from the sum to infinity by less than 
.
22. Prove that the sum to n terms of the series
is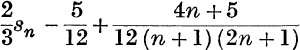 
, where sn is the Sum to 2n terms of 
Hence find the sum to infinity.
23. If x is small, prove that
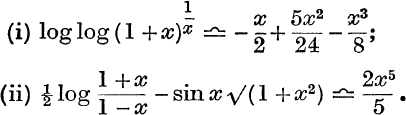
24. Prove that 
if 0 < θ < π.
25. Prove that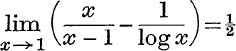 
.
26. Find the sums to infinity of
where |x| < 1.
27. Evaluate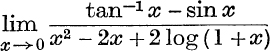 
.
28. Neglecting x8, choose numerical values for a and b, so that
29. Expand when possible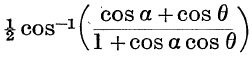 
as a Power senes in 
, and state the conditions of validity.
Find the sums to infinity of the series whose rth terms are
30. 
31. 
32. 
33. 
34. 
35. 
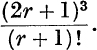
36. Express 
as a power series in x, proving that the coefficient of xn is 
.
37. Prove that e3x – 4ex + 6e–x – 4e–3x + e–5x 16(x4 – x5) if x is small.
38. Prove that (1 + x)1+x 1 + x + x2 + x3 if x is small.
39. If x is large, prove that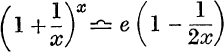 
.
40. If x is large, prove that 
.
41. If xn+p = an, p is small compared to n, and a > 0, prove that 
.
42. Expand 1 – a cos u in ascending powers of a as far as a3, if a is small and u = k + a sin u.
HARDER MISCELLANEOUS EXAMPLES.
EXERCISE V. f.
1. Find an approximation for 
, when θ is small.
2. If a > 2b > 0 and 0 < x < π, prove that 
.
3. Prove the inequalities (due in effect to Archimedes)
4. If x and y are the lengths of the sides of regular polygons of n sides inscribed in a circle and circumscribed about it, prove that the circumference of the circle is approximately 
.
5. If A and B are the areas of the polygons in No. 4, prove that the area of the circle is approximately (2B + A).
6. Two regular polygons of m and n sides have equal perimeters l. Prove that if m and n are large the areas of the polygons differ by about 
.
7. Show that log 7 differs from 2 log 3 + 2 log 5 – 5 log 2 – 
by less than 
.
8. If x is small, prove that log (sec x) = 2 tan2 , neglecting x6.
9. If 
where x2 < 1, prove that if n is even an = 0, and that if n is odd and a multiple of 3, 
, and that if n is prime to 6, 
.
10. Find the coefficient of xn in the expansion of
Consider separately the cases when n = 0, 1, 2, 3, 4, 5, (mod 6).
11. If a, b, c are consecutive positive integers, prove that
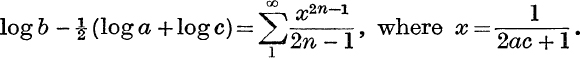
12. Assuming that the coefficients of x3n may be equated when the two sides of the identity log (1 + x3) ≡ log (1 + x) + log (1 – x + x2) are expanded in powers of x, find the sum of the series
13. From the identity log (1 – ax)(1 – βx) ≡ log (1 – sx + px2), where s = α + β, p = αβ, by expanding and equating coefficients of various powers of x, show that
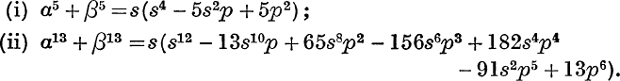
14. If α + β + γ = 0, βγ + γα + αβ = – s, αβγ = p, prove by a method similar to that of No. 13, that
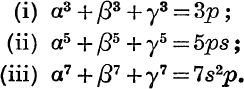
15. Deduce by expansion of log (1 – ax)(1 – βx)(1 – γx)(l – δx) that
16. Express αn + βn in. terms of p and q, where α, β are the roots of x2 – px + q = 0.
17. Use the identity 
and the expansion of log (1 + x) to prove that
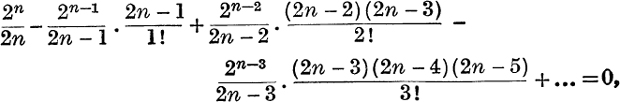
where n is an odd positive integer.
18. If |x| < 1, prove that (1 + x)1+x(l – x)1–x ≥ 1.
Deduce that 
if a, b are positive and unequal.
19. If x > y > z > 0, prove that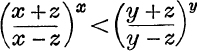 
.
20. If x is small, show that the following functions can be arranged in ascending order of magnitude by expanding in powers of x, as far as x3 only, and arrange them :
(i) sin (tan–1 x);
(ii) tan (sin–1 x);
(iii) tan–1 (tan–1x);
(iv) tan (tan x);
(v) sin (sin x);
(vi) sin–1 (sin–1 x).
21. Evaluate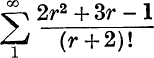 
.
22. If x > 0, prove that (x – 3) ex + x2 + 2x + 3 > 0.
23. If x is large prove that 
.
24. If p is small, prove that successive approximations to a root of x2+p = a2 are a, a – ap log a, and a{1 – p log a + 
p2 (2 + log a) log a}, where a > 0.
25. Show that the coefficient of xn in e(ex) is
and hence find the sum of the series in the bracket for n = 4.
26. Prove that 
differs from 
by less than 
.
27. Apply the inequalities 
, where n is positive, to show that 
is less than 
but greater than 
.
28. If n is a positive integer, by expanding (ex – l)n in two ways and comparing the coefficients of various powers of x, prove that
and find the values of
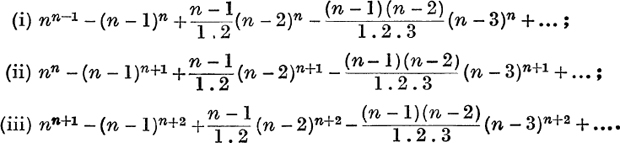
29. If n is a positive integer, prove that
30. If n is a positive integer, prove that
31. By expanding (ex + l)n – (ex – l)n in two ways, prove that c1(n – l)3 + c3(n – 3)3 +…. = n2(n + 3). 2n–4,
32. If n is a fixed positive integer and x is positive, prove by differentiation that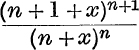 
increases with x. Deduce that
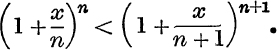
33. If n is a positive integer and 0 < x < n, use the method of No. 32 to find whether 
or 
is the greater.