CHAPTER VIII
The Idea of Number. In elementary algebra it is found that certain equations have solutions, whereas others, almost of the same form, have none. The idea of number is gradually generalised, and the possibility of the solution of a particular equation may depend on the point to which the process of generalisation has been pushed. Consider the equations:
In the algebra of natural numbers (i) and (iv) are satisfied by x = 2 and the others have no solutions. In the algebra of fractions (i) and (iv) are satisfied by 
and (ii) by 
. In the algebra of directed (positive and negative) numbers of the type 
, each of the first three has a solution and (iv) has the two solutions + and –, but (v) and (vi) cannot be satisfied.
The most difficult step in the process of generalisation is the introduction of the real (rational and irrational) numbers ; this will be discussed in the companion volume on Analysis. In real algebra 
is available for the solution of equation (v). For many purposes it is enough to have a number which approximately satisfies an equation, and this is the reason why the introduction of irrationals is not urgent.
The rational real numbers have properties exactly analogous to those of the directed numbers , in much the same way as the positive directed numbers have properties like the signless fractions. No real number satisfies the equation x2 = –1, even approximately.
In the present Chapter, by introducing the complex numbers, we shall carry out a further generalisation of the notion of number, and by suitable new definitions of the meanings of addition, multiplication, etc., shall show that equations like x2 = –1 (in which –1, as well as x, is a complex number) are satisfied by numbers of the new type.
Definition of a Complex Number. Consider a plane and in it two rectangular axes Ox, Oy. The position of a point P in this plane, or the displacement made in moving from the origin O to the point P, requires for its determination two real numbers, e.g. the coordinates of P referred to Ox, Oy.
An ordered pair of real numbers is called a complex number ; and if a and b, in that order, are the real numbers, the complex number is denoted by the symbol [a, b].
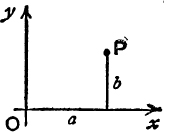
FIG. 64.
Thus there is a unique complex number corresponding to every point P of the plane, viz. the number [a, b] corresponds to the point P whose coordinates are (a, b). Conversely, given a complex number [a, b], there is a unique corresponding point P, with coordinates (a, b), or a unique corresponding displacement, whose components along the axes are a and b.
The statement that the pair of numbers which constitute a complex number is “ordered” means that [a, b] and [b, a] are distinct complex numbers (unless a = b). But for this, the one-to-one correspondence between complex numbers and points in a plane would not hold ; just as the points (2, 5) and (5, 2) are distinct, so too are the complex numbers [2, 5] and [5, 2].
Definitions of Fundamental Operations. In a logical introduction to the theory of fractions or negative numbers, it is necessary to begin by defining the meanings of the elementary operations as applied to these numbers. In the same way, we must start here by making definitions of equality, addition, etc., for complex numbers.
These definitions simply state what meanings are to be given to the signs =, +, –, ×, and ÷, in this new kind of algebra, which might be called the ‘algebra of ordered number-pairs’, but is actually called the ‘algebra of complex numbers’.
(i) Equality. The two complex numbers [a, b] and [c, d] are called equal if and ojily if a = c and b = d. In this case, we write [a, b] = [c, d].
This definition secures that the points (and displacements), which correspond to two complex numbers, are the same points (and the same displacements) if and only if the complex numbers are “equal.”
(ii) Addition. The complex number [a + c, b + d] is called the sum of the two complex numbers [a, b] and [c, d]; and we write
If P and Q, are the points corresponding to [a, b] and [c, d], see Fig. 65, and if QOPR is a parallelogram, the point R corresponds to [a + c, b + d], for the projection of OR on Ox is equal to the sum of the projections of OP, PR or OP, OQ on Ox; and similarly for projections on Oy.
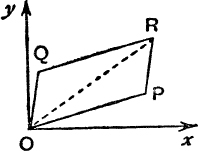
FIG. 65.
In vector notation, 
, so the displacement corresponding to the sum of two complex numbers is the vector sum of the displacements corresponding to the numbers.
(iii) Subtraction is defined by the relation,
This is chosen because, by equation (1),
(iv) Multiplication is defined by the relation,
The reason for this (at first sight peculiar) definition will become apparent in the next few pages, see especially Note 2, p. 142 A complete discussion will be given in the companion volume on Analysis. Any definition is legitimate, if not self-contradictory, and this one happens to be the most convenient and useful one to make.
(v) Division, [a, b] ÷ [c, d] is defined as the complex number [x, y] given by [x, y] × [c, d] = [a, b], provided that such a number exists.
By (3), this gives
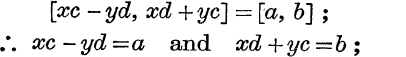
solving,
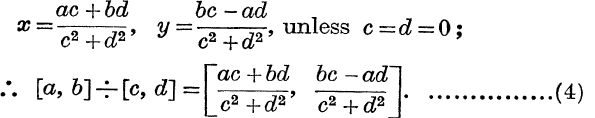
This definition of division excludes the divisor [0, 0]. The number [0, 0] plays a part in the theory of complex numbers, analogous to that played by 0 in the theory of real numbers. Division by [0, 0] is not defined.
EXERCISE VIII. a.
[The beginner should work through all the examples in this Exercise.]
1. What are the values of [1,5] + [2, 3] and [2, 3] + [1, 5] ?
What general law does this illustrate ?
2. What are the values of [2, 5] × [3, 4] and [3, 4] × [2, 5] ?
What general law does this illustrate ?
3. Verify by a numerical example, or show algebraically, that
4. What are the values of :
(i) [2, 0] + [3, 0];
(ii) [a, 0] + [c, 0] ;
(iii) [2, 0] × [3, 0];
(iv) [a, 0] × [c, 0];
(v) [a, b] + [a, b] + [a, b] + [a,+ b] + [a, b] and [a, b] × [5, 0]?
5. What are a, b if [3, 5] + [a, b] = [7, 8]?
6. What are the values of :
(i) [3, 5] + [–2, 8];
(ii) [–9, 2] + [–7, –1];
(iii) [–6, –4] – [2, –9];
(iv) [–6, –4] + [–2, 9];
(v) [6, 1] × [3, 0];
(vi) [6, 1] × [0, 3];
(vii) [4, 5] × [–8, 2];
(viii) [3, 11] ÷ [2, 3].
7. Simplify
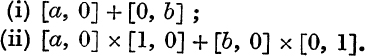
8. Write down the square of [a, b], i.e. [a, b] × [a, b]. What are the squares of [1, 0], [– 1, 0], [0, 1], [0, –1]?
9. Simplify [cos θ, sin θ] × [cos ϕ, sin ϕ].
10. If [a, b] × [c, d] = [0, 0], prove that (a2 + b2)(c2 + d2) = 0, and hence that either [a, b] or else [c, d] must be [0, 0].
Notation. It appears from results such as those of Ex. VIII. a, No. 4, that complex numbers of the special type [a, 0] behave rather like real numbers. It is therefore convenient to denote [a, 0] by the symbol a, and in particular [0, 0] by 0. There is a precedent for this in elementary algebra, where, for example, the symbol 2 is used with several different meanings : sometimes it means the natural number 2, sometimes the fraction , sometimes the directed number + and later ‘the real number 2’ now it is given a further possible meaning, the complex number [2, 0]. Complex numbers of the form [a, 0] correspond to points on the x-axis.
It is also convenient to use an abbreviated notation for complex numbers which correspond to points on the y-axis. The number [0, a] is denoted by ia or ai, and in particular [0, 1] by i.
Further, since [a, b] = [a, 0] + [0, b] and since [a, 0] and [0, b] are denoted by a and bi or ib, the general complex number [a, b] is denoted by a + bi or a + ib.
Just as in real algebra x × x × x × … to n factors is denoted by xn, so, if z is any complex number a + ib and n is a positive integer, the product z × z × z × … to n factors is denoted by zn. Also 
is written z–n and, in particular, 
is written z–1.
Mechanical Application of Algebraic Processes. If a, b, c, d, i stand for ordinary real numbers, we have :
(i) (a + bi) + (c + di) = (a + c) + (b + d)i;
(ii) (a + bi) × (c + di) = (ac + bdi2) + (ad + bc)i.
If, on the other hand, a + bi and c + di stand for the complex numbers [a, b] and [c, d), we have
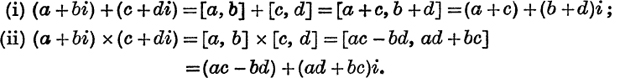
The two relations (i) are identical in form, as they stand; the two relations (ii) become identical in form, if – 1 is written for i2.
Thus, the correct results of both addition and multiplication are given by a mechanical application of the ordinary processes of algebra to the symbols in their abbreviated form, provided that –1 is written for i2, wherever it occurs.
The reader may have anticipated this fact from the result obtained in Ex. VIII. a, No. 8, where he found that
or, using the abbreviated notation, i2 = –1.
Other operations, subtraction, division, etc., can always be reduced so as ultimately to depend upon addition and multiplication [see the definitions on pp. 138, 139]. The statement in italics therefore holds for all the fundamental processes of algebra.
Note 1. The equation, i2 = –1, does not mean that there exists a number i whose square is the negative number –1. In this equation, i is simply an abbreviation for [0, 1], and –1 is not the negative number –1, but an abbreviation for [– 1, 0].
Nor does the equation imply that [0, 1] is the only complex number whose square is [–1, 0], and in fact, as was found in Ex. VIII. a, No. 8, [0, –1] is another complex number whose square is [–1, 0]. The equation, x2 = –1, has two roots if it is an equation in complex algebra, i.e. if x and –1 denote ordered number–pairs. In real algebra, it has no roots. More generally, it will appear later that the equation of the nth degree in complex algebra always has n roots (subject only to the usual conventions of language with respect to “equal “ roots). In real algebra it may have n roots or fewer.
Note 2. The advantages of the definitions on p. 139 can now be partly appreciated :
(i) It appears that complex numbers of the form [n, 0] have properties much like those of the real number n. From the law of addition, [a, b] + [a, b] + … to n terms, equals [na, nb], and from the law of multiplication [a, b] × [n, 0] also equals [na, nb].
Therefore, [a, b] + [a, b] + … to n terms = [a, b] × [n, 0].
This would not be true if multiplication was, for example, defined by the relation [a, b] × [c, d] = [ac, bd].
(ii) It is desirable that fundamental laws should be the same for complex as for real algebra. The reader who has worked Ex. VIII. a, Nos. 1-3, has verified this in some cases and should be able to do so in general.
(iii) The result of Ex. VIII. a, No. 10, shows that the fundamental factor theorem, that if the product of two numbers is zero then one of the numbers is zero, also holds in complex algebra.
We give now some examples of the manipulation of complex numbers. .
Example 1. Calculate [x, y]3.
By the principle established on p. 141, we have
writing – 1 for i2 and –i for i3(= i2. i), we have
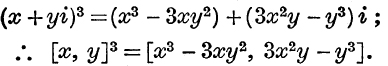
The reader should show that the same result is obtained by two applications of the law of multiplication for complex numbers.
Example 2. Divide [a, b] by [c, d] when [c, d] ≠ [0, 0].
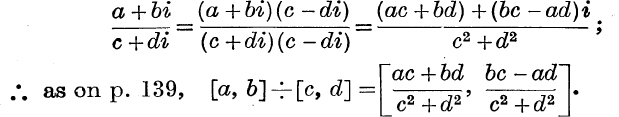
Example 3. Expand [x, y]n, where n is a positive integer.
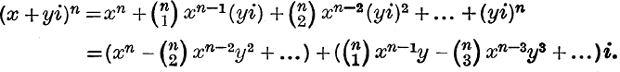
Nomenclature. Complex numbers of the form [x, 0] are sometimes called “real,” and those of the form [0, y] are called, in contrast, “pure imaginary.” This language, which is a legacy from the time when the theory of complex numbers was imperfectly understood, is most unfortunate and should be avoided. In the same way, when a function of [x, y] has been expressed in the form [a, b], e.g. [x, y]3 = [x3 – 3xy2, 3x2y – y3], in Example 1 above, the expressions a and b are often called the real and imaginary parts of the function; this is an equally misleading form of words. They may be called the “first and second parts” of the function.
Complex numbers of the form [a, b], [a, –b] or a + bi, a – bi are called conjugate. This name is due to Cauchy.
If, as in Examples 1-3 above, a function of a complex number has been reduced to the standard form [a, b] of a complex number, we have an equation of the form
In this case, it also follows that
for the only property of i that is used in the work is i2 = – 1, that is [0, l]2 = [–1, 0], and this remains true if i is replaced everywhere by –i, since [0, –1]2 = [–1, 0].
HISTORICAL NOTE. The idea of the possibility of dealing with the square root of a negative number is certainly as old as the time of Diophantus (c. 245-330) and arose from attempts to solve special equations. Probably Cardan (1501-1576) was the first to assume the application of algebraic processes to symbols of the form, 
. He discussed the problem : divide 10 into two parts whose product is 40, and gave as the answer 5 + 
and 5 – , (not however in this form) ; he then showed that his answers satisfied the given conditions, if the ordinary rules of algebra were applied.
Complex numbers were used freely by Euler (1707-1788), to whom the symbol i for 
is due, and by many of his contemporaries (John Bernouilli, Cotes, De Moivre, etc.). Their real nature was first made clear by Wessel (1797) and Argand (1806), who introduced the geometrical interpretation. The name “complex number” is due to Gauss (1777-1855), who developed in far greater detail than Wessel or Argand, but on similar lines, the fundamental principles of the theory and also used them in his investigations of the properties of natural numbers. The work of Gauss prepared the way for the discoveries of Cauchy, Riemann and many others which form the foundation of modern Analysis and play a large part in modern mathematical Physics.
EXERCISE VIII. b.
1. Express the following complex numbers in an alternative form:
2. Express the following complex numbers in the bracket form :
3. Simplify the following :
(i) [3, 2] + [I, – 5]
(ii) [4, 6] – [6, 6]
(iii) [1, 2] × [3, 4]
(iv) [2,0] ÷ [3,0]
(v) (2 + 3 i) – (3 – 4i)
(vi) (1 + i) + (1 – i)
(vii) 3i × 4i
(viii) 3i ÷ r
(ix) [α, β] + [0, 0]
(x) [α, β] × [0, 0]
(xi) [α, β] × [1, 0]
(xii) (7 – 9i) ÷ (1 + i).
Express the following, Nos. 4-30, in the form X + Yi :
4. (1 + 2i) × 3.
5. 5i × (1 – i).
6. (1 + i) × (1 – i).
7. (2 + i)(3 – 2i).
8. (4 + 3i)2.
9. (a + bi)2.
10. i(a + bi).
11. ai × bi.
12. a ÷ i.
13. (cos θ + i sin θ)(cos ϕ + i sin ϕ).
14. (cos θ + i sin θ)(cos θ – i sin θ).
15. (cos θ + i sin θ)(cos ϕ – i sin ϕ).
16. (cos θ + i sin θ)2.
17. [r cos θ, r sin θ] × [s cos ϕ, s sin ϕ].
18. [cos θ, sin θ] ÷ [cos ϕ, sin ϕ].
19. (x – cos θ – i sin θ)(x – cos θ + i sin θ).
20. (x + sin ϕ + i cos ϕ)(x + sin ϕ – i cos ϕ).
21. (1 + i)2.
22. (1 – i)3.
23. 
.
24. 
.
25. 
.
26. 
.
27. (x – iy)2
28. 
.
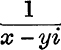29. 
.
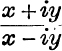30. 
, where z = [x, y].
31. Simplify (i) (1 + i)–2 + (1 – i)–2; (ii) (1 + i)–4 + (1 – i)–4
32. If (2 + 3i)(3 – 4i) = a + bi, find the value of a2 + b2.
33. Show that the cubes of 
are each 1.
34. Simplify (x + yi)(x – yi) and factorise (x – 1)2 + (y – 2)2.
35. If (x + yi)n = a + bi, express a2 + b2 in terms of x, y.
36. What is the series whose nth term is (1 + i2n)(1 + in)?
37. Find real numbers x and y such that
38. Prove that [3, 4] is one root of the equation z2 – 6z + 25 = 0, and find the other root?
39. If 
, where A > 0, prove that A2 – B2 = x and 2AB = y. Hence express 
in the form A + Bi.
Similarly express 
in the form A + Bi.
40. What is the condition that one root of the equation 
is of the from [k, 0] ?
The Argand Diagram. The figure, referred to on pp. 137, 138, in which the point P, or the displacement 
, corresponding to a complex number [x, y], = x + yi, is considered, is called the Argand Diagram.
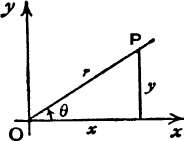
FIG. 66.
Modulus and Amplitude. If the length of OP is r units, and if 
(OP, Ox) = θ, then we have
also
and
r is called the modulus, or sometimes the absolute value, of the complex number x + yi, and is denoted by |x + yi| or by mod (x + yi).
θ is called the amplitude of the. complex number x + yi, and is denoted by am (x + yi).
A complex number is expressed in terms of its modulus and amplitude by the relation
or sometimes, if there is no danger of ambiguity, by x + yi – (r, θ).
It is customary to denote the complex number x + yi by z and to write r = |z|, θ = am (z). If this is done, z is called the argument of the point P in the Argand Diagram. The symbol |z| for modz is due to Weierstrass ; its use in connection with real numbers has been explained on p. 78.
The Modulus-Amplitude Form. It is frequently necessary to express a complex number, given in the form x + yi, in terms of its modulus and amplitude.
By definition, r is essentially positive and its value is obtained uniquely from 
.
Equation (8) shows that there is also a unique value of θ in the range – π < θ ≤ + π; but any value of θ which differs from this value by a multiple of 2π would lead to the same representative point P and is therefore a possible value for am (x + yi). The unique value of θ in the range –π < θ ≤ + π is called the principal value of the amplitude.
Since x = r cos θ, y = r sin θ, it follows that 
; but this equation is not sufficient to determine the amplitude, since it gives two values of θ between – π and + π. Of these two values, it is necessary to select that one for which 
and therefore also 
Example 4. Find the modulus and amplitude of – 2 + 3i.
From Fig. 67,
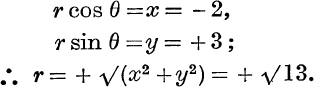
And θ is the angle 
given by
As is pointed out above, it is not sufficient to say that θ is the angle given by 
.
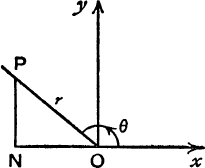
FIG. 67.
Example 5. Express 1 – cos θ – i sin θ in the modulus-amplitude form.
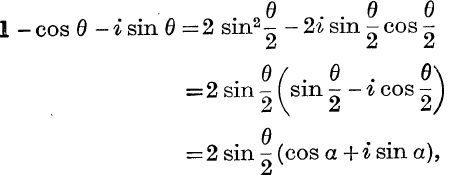
where α is chosen so that cos α = sin 
and sin α = – cos .
These conditions are satisfied by 
.
The result now obtained is of the required form only if sin is positive, i.e. if 4nπ < θ < (4n + 2)π.
If sin is negative, i.e. if (4n – 2)π < θ < 4nπ, we write
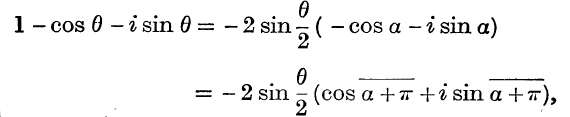
where 
, as before.
It is instructive to consider this example geometrically. We shall take the special case, 0 < θ < π. In Fig. 68, the points A and P represent the complex numbers 1 and cos θ + sin θ.
To find the point corresponding to 1 – (cos θ + i sin θ), we take the displacement 
, and this is 
. Now AOP = θ, and OA, OP are each of unit length; the length of PA is 2 sin , and the principal value of the amplitude of is measured by the angle from Ox to PA, which is 
.
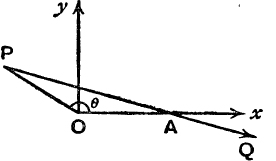
FIG. 68.
as before,
Note. In numerical examples, the modulus and amplitude can often be written down by reference to a figure.
EXERCISE VIII. c.
Draw figures and give the modulus and the principal value of the amplitude of the complex numbers in Nos. 1-16.
1. 1.
2. – 1.
3. i
4. – i.
5. 1 + i 
.
6. 1 – i.
7. – 1 + i
8. – 1 – i
9. i – .
10. 1 + i.
11. – 1 + i.
12. – 1 –i.
13. 1 – i.
14. i – 1.
15. – i.
16. – i – .
Express in the modulus-amplitude form :
17. 3 + 4 i.
18. + 1 –i.
19. – 3 + 4i.
20. – 3 – 4i.
21. – 2 –i.
22. cos α – isin α.
23. sin α – i cos α.
24. sin α + i cos α.
25. What are the modulus and the principal value of the amplitude of cos2α + i sin α cos α if
Express in the modulus–amplitude form :
26. 1 + i tan α.
27. 1 – i cot α.
28. tan β – i.
29. – sin β – i cos β.
30. 1 + cos θ + i sin θ.
31. 1 + cos α – i sin α.
32. 1 + sin θ + i cos θ.
33. cos α + i sin α + cos β + i sin β.
34. cos α – i sin β + i(sin α + i cos β).
35. 1 + r cos ϕ + ir sin ϕ.
36. Interpret geometrically the relation
, and generalise the result.
37. Interpret geometrically the relation
.
38. By using geometrical considerations, find r1 and r2, if
, where 
.
Applications of the Argancl Diagram. It was shown on p. 139 that if P and Q are the points of the Argand Diagram corresponding to the complex numbers, a + bi = z1 and c + di = z2, then the point R which corresponds to their sum, z1 + z2, is found by completing the parallelogram QOPR.
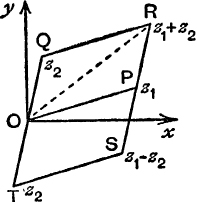
FIG. 69.
Since the length of OR is not greater than the sum of the lengths of OP and OQ, we have, see Fig. 69,
The reader should show in a similar way, or deduce from (9) (see Ex. VIII. d, No. 5) that
and
Suppose A and P are the points of the Argand Diagram corresponding to the fixed complex number z1 and the variable complex number z, see Fig. 70.
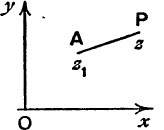
FIG. 70.
Then z – z1 corresponds to the displacement 
, and |z – z1| is the length of AP.
If |z – z1| = constant = c, say, then P moves on a circle, centre A, radius c.
If am (z – z1) = constant = α, say, then P moves on the half–line AP, such that (AP, Ox) = α.
If z = kz1, where k is a positive or negative number, P is a point on the line OA such that 
.
Example 6. Two points P and Q in the Argand Diagram represent complex numbers z and 2z + 3 + i. If P moves round the circle, centre the origin and radius k, how does Q move ?
If z′ ≡ 2z + 3 + i, |z′ – 3 – i| = |2z| = 2|z| = 2k;
Q, moves on the circle of radius 2k whose centre represents the complex number 3 + i, i.e. the point whose coordinates are (3, 1).
Otherwise : the point representing 2z is at R in OP produced so that OR = 2OP, see Fig. 71, and the displacement from R to Q consists of 3 units parallel to Ox and 1 unit parallel to Oy. As P describes the given circle, R describes concenbric circle of radius 2k, and thus Q describes the circle found by displacing this circle a distance 3 units parallel to Ox and 1 unit parallel to Oy.
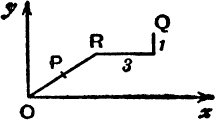
FIG. 71.
EXERCISE VIII. d.
1. Given two points A, B in the Argand Diagram, representing the complex numbers α and β, construct the points which represent (i) α – β; (ii) 
(α + β); (iii) α + 2β; (iv) α – 3β.
2. A, B, C are collinear points, such that AB = BC. If A and B represent complex numbers α and β, what does C represent ?
3. A, B, C are collinear points, such that AB = 2BC. If A, B, C represent complex numbers α, β, γ, what is the relation between α, β, γ ?
4. A given point P represents the complex number z. Construct the points which represent (i) 2z; (ii) – 3z; (iii) z + 3; (iv) z – 7, (v) 4z + 9 ; (vi) 8 – 3z.
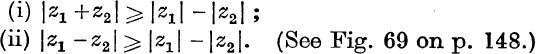
6. If P and Q represent the complex numbers z1 and z2, state the geometrical condition for the equality signs in No. 5.
7. If |z| = 1, what is the locus of P, when it represents the complex numbers (i) 3z; (ii) z + 3; (iii) 4z + 9 ?
8. If P represents the complex number z, what facts about the position of P are expressed by
(i) |z| = 5;
(ii) |z – 1| = 2;
(iii) |z + 2| = 3;
(iv) |2z – 1| = 3;
(v) |z – 2 – 3i| =4;
(vi) am (z) = 0.
9. Use the modulus notation to express that tfye point P which represents the complex number z lies
(i) inside the circle, centre (8, 9), radius 7;
(ii) on the circle, centre (a, b), radius c;
(iii) outside the circle, centre (– 1, 0), radius 1.
10. What are the greatest and least values of |z – 3| if |z| ≤ 1 ?
11. What are the greatest and least values of |z + 2| if |z| ≤ 1. ?
12. What are the greatest and least values of |z| if |z – 5| ≤ 2 ?
13. What are the greatest and least values of |z + l| if |z – 4| ≤ 3 ?
14. What are the greatest and least values of |z – 4| if |z + 3i| ≤ 1 ?
15. A variable point P represents z; what can be said about the position of P if 1 < |z + 2 – 3i| < 2 ?
16. If |z| < 1, what can be said about the possible positions of the point which represents 1 + z ?
17. If |z| < l, prove that the principal value of am(l + z) lies between – 
and + .
18. If |z| = find the range of principal values of am(l + z).
19. If P1 and P2 represent the complex numbers z1 and z2 and if m1 and m2 are any positive or negative numbers, (m1 + m2 ≠ 0), explain the significance of the point 
.
20. Generalise No. 19.
Products. Let the numbers corresponding to P and Q, expressed in the modulus-amplitude form, be r(cos θ + i sin θ) and s(cos ϕ + i sin ϕ); then the polar coordinates of P, Q are (r, θ) and (s, ϕ).
The product of the numbers is [r cos θ, r sin θ] × [s cosϕ, s sin ϕ].
By definition, this equals
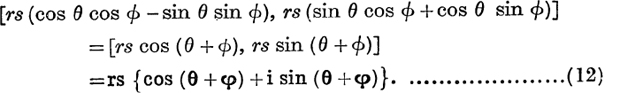
This result may be expressed in the form
But the second result in (13) is not necessarily true of the principal values.
From (12) we see that the product is represented by the point K whose polar coordinates are (rs, θ + ϕ), which is found by taking the point A (1, 0) and making the triangle QOK directly similar to the triangle AOP. For, OK : OQ = OP : OA, OK = rs; also
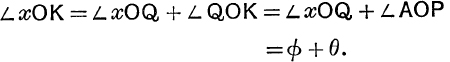
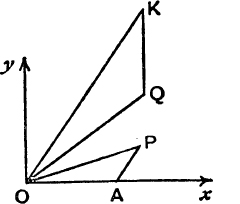
FIG. 72.
Repeated applications of formula (12) give
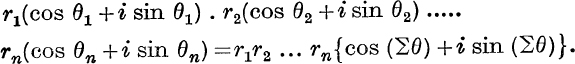
In particular, if r1 = r2 = … = rn = 1 and θ1 = θ2 = … = θn = θ, we have
where n is any positive integer.
This is a special case of an important theorem which will be discussed in Chapter IX.
Quotients. An expression for the result obtained when one complex number is divided by another may be deduced from formula (12) as follows:
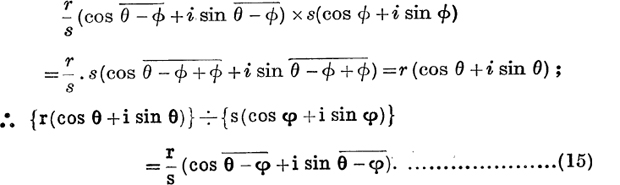
This result may be expressed in the form
But the second result in (16) is not necessarily true of principal values.
In particular, putting θ = 0, r = s = 1, we have
If P, Q represent the complex numbers
the point H which represents {r(cos θ + i sin θ)} ÷ {s(cos ϕ + i sin ϕ)} is obtained by making P in Fig. 73 play the part of K in Fig. 72. Thus, if A is the point (1, 0), construct the triangle AOH directly similar to the triangle QOP; then H represents
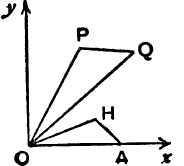
FIG. 73.
Notation. The expression cos θ + i sin θ is often denoted by cis θ, and (cos θ + i sin θ)n is denoted by cisnθ. Equation (14) may then be written, cisnθ = cisnθ. And since, from (17),
we may denote cos θ – i sin θ either by cis (– θ) or by (cis θ)–1.
Example 7. The points B, P, Q in the Argand Diagram represent the complex numbers 2, z, z2. If P describes the circle on OB as diameter, find the locus of Q.
In Fig. 74, A is the centre of the given circle; the triangles AOP, POQ are similar; therefore, if (r, θ) are the polar coordinates of Q,
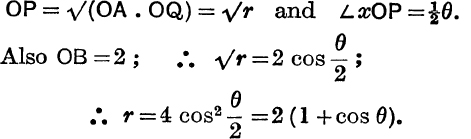
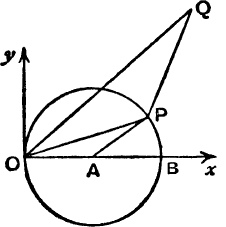
FIG. 74.
This is the polar equation of a cardioid. The reader should sketch the locus.
Example 8. The points B, P, R in the Argand Diagram represent the complex numbers 2, z, 
, If P describes the circle on OB as diameter, find the locus of R.
In Fig. 75, A is the centre of the given circle ; the triangles ROA, AOP are similar, by the construction given above (see Fig. 73). But OA = AP; OR = RA; the locus of R is the perpendicular bisector of OA, namely the line x =
Otherwise: if K is the image of R in the x-axis, OP . OK = OP .OR =OA2 = 1; P, K are inverse points w.r.t. the circle, |z| = 1. the locus of K is the straight line, x = . But R is the image of K in Ox; the locus of R is also the straight line, x = . This application of inversion is important.
FIG. 75.
It should be noticed that as P moves in an anti–clockwise direction round the circle from B towards O along the upper semicircle, K moves from the x–axis upwards towards + ∞, and therefore R moves from the x-axis downwards towards – ∞. Also when P continues from O to B along the lower semi-circle, K moves upwards from – ∞ to the x-axis, and so R moves downwards from + ∞ to the x-axis.
EXERCISE VIII. e.
Simplify the following: (Nos. 1-24).
1. 
.
2. 
.
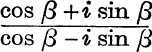3. 
.
4. 
.
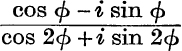5. 
.
6. 
.
7. 
.
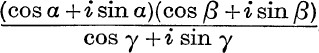8. 
.
9. (cos θ – i sin θ)3
10. (cos 2θ + i sin 2θ)3
11. 
.
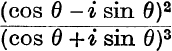12. 
.
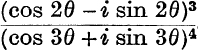13. 
.
14. 
.
15. (sin θ + i cos θ)3
16. (sin θ – i cos θ)5
17. (1 + cos θ + i sin θ)3.
18. (1 + i sin θ – cos θ)4.
19. 
.
20. 
.
21. 
.
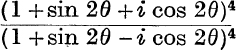22. 
.
23. 
.
24. 
.
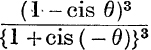25. Write down the cubes of 
. What inference can be drawn from the results ?
26. Write down the values of
What inference can be drawn ?
27. Simplify cis A cis B cis C, if A +B +C = π.
28. Simplify (cis θ)n + (cis θ)–n.
29. If z =cos θ + i sin θ, express in terms of θ
30. If u =cis θ, v = cis ϕ, express 
in terms of θ, ϕ.
31. If n is a positive integer, prove that
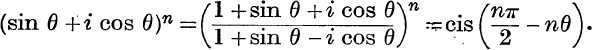
32. If the complex number z is represented by the given point P, and if |z| = 1, show how to construct the points which represent
33. Given the point P which represents any complex number z, construct the points which represent
34. If the point P which represents the complex number z moves along the x-axis from x = – 1 to x = + 1, describe the corresponding motions of the points which represent z + a + bi, az, iz, and (a + bi)z.
35. If the point P in No. 34 moves with uniform speed, describe the corresponding motions of the points representing z2 and 1/z.
36. 3If z1 = l/z, z2 = l/(l – z1), z3 = l/(l – z2), and the point which represents z moves along the x-axis from x = – 1 to x = + 1, find the corresponding motions of the points representing, z1, z2, z3.
37. If the point which represents the complex number z moves round the circle |z| = 1 in the anti–clockwise direction starting from the point (1, 0), describe the motions of the points which represent the complex numbers
38. Answer the same question as in No. 37 for
39. Answer the same question as in No. 37 for
where a, b, c, d are real numbers.
40. Answer the same question as in No. 37 for
41. If z1 = (1 – iz)/(z – i) and the point representing z moves from – 1 to + 1 along the x-axis, how does the point which represents z1 move ?
42. With the notation of No. 41, if
describe the motions of the points which represent z2, z3, z4, ….
43. If P is a given point on the circle |z – 1| = 1, state a construction for the point Q, such that the complex number represented by P is the square of that represented by Q. Find the locus of Q when P moves round the circle.
Principal Values. When a function, f(x), such as sin–1x, tan–1x, or am(x + 3i) has more than one real value for a given value, x1 of x, the numerically least of these values is called the principal value of f(x) corresponding to x = x1; and if there are two numerically equal least values, the positive one is called the principal value.
.Thus tan–1(– 1) has values 
and of these we call – 
the principal value. Again cos–1 has values 2nπ ± 
, which include both + and – ; of these, we call + the principal value.
The aggregate of these selected principal values of f(x) is called the range of principal values of f(x).
There is no recognised standard notation for distinguishing principal values from general values. We shall henceforward usually mean by sin–1x the principal value of the function, and, if we wish to call special attention to the fact that the general value is intended we shall write Sin–1x; similarly we shall use Tan–1x, Am z, etc., to denote general values. But, if the context is such as to remove any possibility of ambiguity, sin–1x, cos–1x, etc., may be used to represent general values.
The beginner is advised not to omit any of the examples which are marked with an asterisk in Ex.VIII. f. No. 8 is particularly important.
EXERCISE VIII. f.
Verify the results of Nos. 1-4.
1.* – ≤ sin–1x ≤
2.* 0 ≤ cos–1x ≤ π.
3.* – < tan–1 <
4.* – π < am(x + iy) ≤ π.
5.* Draw rough graphs of sin–1x, cos–1x, and tan–1x.
6. Find the values of (i) sin–1x + cos–1x; (ii) tan–1x + cot–1x.
7. For what values of x is sin–1x equal to
8.* From the definition – π < am(x + iy) ≤ π, prove that
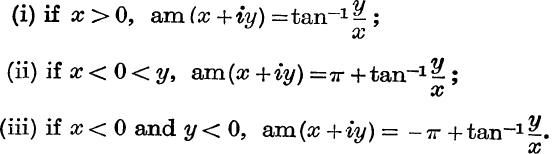
9. What are the values of am (x + yi), (i) when y = 0, (ii) when x = 0 ? Draw the graphs of am x and am ix.
10. Draw the graphs of (i) am(x + ix); (ii) am(x – ix).
11. If m is positive, for what values of n is 
?
Answer the same question when m is negative.
Can tan–1m + tan–1n be < – ?
12.* Prove that the value of k in the formula
is zero unless mn > 1, and that if mn < 1, is + 1 or – 1, according as m and n are positive or negative.
13.* If r1, θ1 and r2, θ2 are the moduli, and principal values of the amplitudes, of two complex numbers, and r, θ of their product, prove that
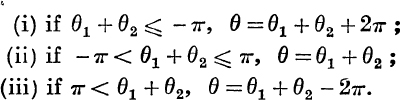
14. Draw the graph of 
.
15. Draw the graph of 2 cos–1x – cos–1 (2x2 – 1).
16.* What meanings must be assigned to the many valued functions Sin–1x, Cos–1x, Tan–1x in order that the following relations may be true ?
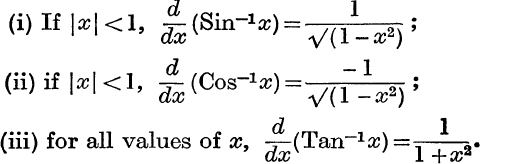
EASY MISCELLANEOUS EXAMPLES
EXERCISE VIII. g.
1. Express in the modulus-amplitude form (i) 
; (ii) (1 + i)n
2. Evaluate 
.
3. If z = cis θ, prove that 
, and that
4. If n is a positive integer, prove that
5. If A, B, C are the vertices of a triangle in the Argand Diagram representing the complex numbers α, β, γ, what are the points which represent (i) (β + γ); (ii)
(α + β + γ); (iii) kα + (1 – k)β, where k is a real number ?
6. ABCD is a quadrilateral in the Argand Diagram ; E, F, G, H, P, Q are the middle points of AB, BC, CD, DA, AC, BD. If A, B, C, D represent the complex numbers α, β, γ, δ, what numbers are represented by E, G and the middle points of EG, FH, PQ ? What conclusion can be drawn from these results ?
7. Four points represent the complex numbers α, β, γ, δ. Interpret geometrically the condition α + γ = β + δ.
8. Two fixed points A, B and a variable point P represent the complex numbers α, β, z. Find the locus of P if
9. Verify that 
are four fourth roots of – 1, and deduce two quadratic factors of x4, + 1.
10. If a = cis 2α, b = cis 2β, c = cis2γ, and d = cis2δ, express in the modulus-amplitude form
11. If a = cis θ and b = cis ϕ, prove that 
.
12. Interpret geometrically the relation z = α + t(β – α), where α and β are fixed complex numbers and t is a real variable.
13. If |z| = 1 and am z = θ, find the values of
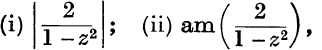
where am w denotes the principal value of the amplitude of w.
14. If |z1 – z2| = |z1 + z2|, prove that amz1 and amz2 differ by or 
15. Two fixed points, A and B, and a variable point P, represent the complex numbers α, β, and z. Find the locus of P if
16. In No. 15, if β becomes variable and P describes a given curve ∑, what is the locus of the point that represents β, if (i) β = α + z, (ii) β = az, and (iii) β = |α| ÷ z.
17. The transformations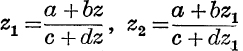 
give z2 in terms of z. Find a, b, c, d so that the resulting single transformation may be z2 = 1 – .
18. The transformation 
when repeated a second time leads to . Do any other transformations of the form 
have this property ?
19. What is the condition that the equations 3x + 4y = p, x2 + y2 = c2 can only be solved in the algebra of complex numbers ?
20. If ω3 = 1, bat ω is not 1, prove that
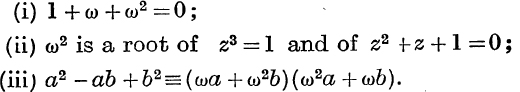
21. With the notation of No. 20, find the values of
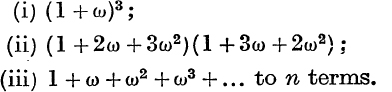
22. With the notation of No. 20, expand
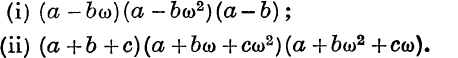
HARDER MISCELLANEOUS EXAMPLES.
EXERCISE VIII. h.
1. Simplify
2. Prove that 
.
3. Express 
in the form x + yi, and prove that x2 + y2 = 4x – 3
4. If p + iq = x cis α cis θ + y cis β cis θ, obtain a relation independent of θ.
5. If cis α = α and cis β = b, prove that 
.
6. If a = cis2α, b = cis2β, c = cis2γ, and d = cis2δ, express in the modulus-amplitude form
7. If (1 + cisθ)(l + cis2θ) = u + iv, prove that
8. If (1 + ix1)(l + ix2)(1 + ix3) = A + Bi, prove that
9. The complex numbers a, z, z – α are represented by points A, P, Q,. If A is fixed and P describes a given curve, what is the locus of Q ?
10. If the point P, which represents the complex number z, describes the circle centre (1, 0) and radius 1, what Jocus is described by the point representing 
, where a, b, c are real ?
11. If |z2 – 1| = 2, prove that the point P, which represents z, moves so that PA. PB is constant, where A and B are certain fixed points.
12. If the point which represents z moves on the unit circle, centre O, what curve is described by the point representing 2z + z2 ?
13. If z = x + yi, where y is positive, prove that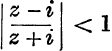 
.
14. If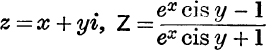 
and 
, prove that |Z| < 1.
15. The fixed points A, B and the variable point P represent the complex numbers α, β, γ. What is the locus of P, if
16. If z1(a2 – a3) + z2(a3 – a1) + z3(a1 – a2) = 0, and a1, a2, a3 are real, prove that the points which represent the complex numbers z1, z2, z3, are collinear.
17. If A, B, C are points which represent complex numbers α, β, γ, and a = |β – γ|, b = |γ – α|, c = |α – β| prove that the in-centre of ABC represents 
. What numbers do the e-centres represent?
18. Interpret the relation 
between the complex numbers α, β, γ, and prove that α2 + β2 + γ2 = βγ + γα + αβ follows from it.
19. Interpret the relation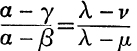 
between the six complex numbers α, β, γ, λ, μ, v, and show that it can be written
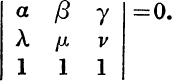
20. If a and b are real, prove geometrically that
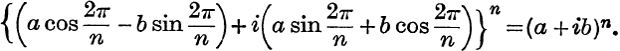
21. An ellipse in the Argand Diagram has foci (±d, 0) and z1, z2 are complex numbers which correspond to the ends of conjugate semi-diameters, prove that 
.
22. Draw the graphs of (i) cosec–1x; (ii) sec–1x; (iii) cot–1x; for principal values only.
23. Draw the graph of sec x + sec y + 2 = 0.
24. Prove that, unless x = (2n + 1)π,
25. Prove that the relation z = (1 + Zi)/(Z + i) transforms the part of the axis of x between the points z = – 1 and z = + 1 into a semicircle passing through the points Z = 1 and Z = – 1. Find all the figures that can be found from the originally selected part of the axis of x by successive applications of this transformation.
26. If ω3 = 1, but ω ≠ 1, prove that ωn + ω2n = 2 or – 1, where n is a positive integer.
27. Prove that x2 + xy + y2 is a factor of (x + y)n – xn – yn, where n is odd and not divisible by 3.
28. Prove that x2 + y2 + z2 – yz – zx – xy is a factor of
29. Prove that (x2 + y2 + z2 – yz – zx – xy)2 is a factor of
30. Write down the product of x + yω + zω2, x + yω2 + zω where 
; hence express x3 + y3 + z3 – 3xyz and
each as the product of three factors. Prove that the first expression is the square root of the second.
31. If fn(x) is the sum to n terms of the series whose rth term is arxr, what do the expressions,
represent when ω3 = 1 but ω ≠ 1 ?