Source Identification Under Sensor Observations: A Gaussian Source Estimator

In this chapter, we introduce a propagation source estimator under sensor observations: Gaussian source estimator. According to Chap. 5, sensors are firstly injected into networks, and then the propagation dynamics over these sensor nodes are collected, including their states, state transition time and infection directions. There have been many approaches proposed under sensor observations, including Bayesian based method, Gaussian based method, Moon-Walk based method, etc. Here, we particular present the details of the Bayesian based method. For the techniques involved in other methods, readers could refer to Chap. 9 for details.

8.1 Introduction

Localizing the source of a malicious attack, such as rumors or computer viruses, is an extremely desirable but challenging task. The ability to estimate the source is invaluable in helping authorities contain the malicious attacks or infection. In this context, the inference of the unknown source was analyzed in [160, 161]. These methods assume that we know the state of all nodes in the network. However, having the observation on an entire network is hardly possible. Pinto et al. [146] proposed to locate the source of propagation under the practical constraint that only a small fraction of nodes can be observed. This is the case, for example, when locating a spammer who is sending undesired emails over the internet, where it is clearly impossible to monitor all the nodes. Thus, the main difficulty is to develop tractable estimators that can be efficiently implemented (i.e., with subexponential complexity), and that perform well on multiple topologies.

8.2 Network Model

We first introduce the network model used in [146]. The underlying network where a malicious attack takes place is modeled by a finite, undirected graph G(V, E), where the vertex/node set V has N nodes, and the edge set E has L edges (see Fig. 8.1 for illustration). Assume that the graph G is a known priori. The propagation source, s ^∗∈ G, is the vertex that initiates the propagation. Suppose s ^∗ as a random variable with uniform distribution over the set V , i.e., so that any node in the network is equally likely to be the source.

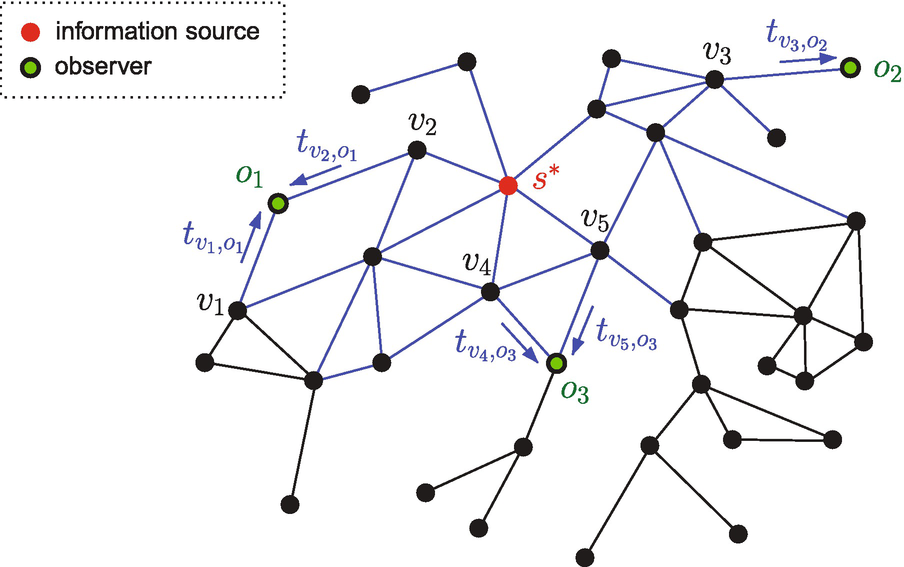
../images/466717_1_En_8_Chapter/466717_1_En_8_Fig1_HTML.png — Fig. 8.1
Source estimation on graph G. At time t = t ^∗, the propagation source s ^∗ initiates the propagation of a malicious attack. In this example, there are three observers/sensors, which measure from which neighbors and at what time they were attacked. The goal is to estimate, from these observations, which node in G is the propagation source

The propagation process is modeled as follows. At time t, each vertex u ∈ G presents one of two possible statuses: (a) infected, if it has already been attacked from any of its neighbors; or (b) susceptible, if it has not been infected/attacked so far. Let V (u) denote the set of vertices directly connected to u, i.e., the neighborhood or vicinity of u. Suppose u is in the susceptible state and, at time t _u, receives the attack for the first time from one neighbor, say s, thus becoming infected. Then, u will re-transmit the malicious attack to all its other neighbors, so that each neighbor v ∈ V (u)∖s receives the attack at time t _u + θ _uv, where θ _uv denotes the random propagation delay associated with edge (u, v). The random variables {θ _uv} for different edges (u, v) have a known, arbitrary joint distribution. The propagation process is initiated by the source x ^∗ at an unknown time t = t ^∗.

Let $O:=\{o_k\}^K_{k=1}\in G$ denote the set of K observers/sensors, whose location on the network G is already known. Each observer measures from which neighbor and at what time it received the attack. Specifically, if t _v,o denotes the absolute time at which observer o receives the attack from its neighbor v, then the observation set is composed of tuples of direction and time measurements, i.e., $\mathcal {O}:=\{(o,v, t_{v,o})\}$ , for all o ∈ O and v ∈ V (o).

8.3 Source Estimator

Pinto et al. [146] recovered the source location from measurements taken at the observers by adopting a maximum probability of localization criterion, which corresponds to designing an estimator $\hat {s}(\cdot )$ such that the localization probability $P_{loc}:=\mathbf {P}(\hat {s}(\mathcal {O}=s^*))$ is maximized. Since s ^∗ is assumed to be uniformly random over the network G, the optimal estimator is the maximum likelihood (ML) estimator,

$\displaystyle \begin{aligned} \begin{array}{ll} \hat{s}(\mathcal{O}) & = \mbox{arg}~\displaystyle \max_{s\in G} \mathbf{P}(\mathcal{O}|s^*=s)\\ & = \mbox{arg}~\displaystyle \max_{s\in G} \sum_{\Pi_s}\mathbf{P}(\Pi_s|s^*=s)\times \int\cdots\int g(\theta_1,\cdots,\theta_L,\mathcal{O}, \Pi_s, s)d \theta_1\cdots \theta_L. \end{array} \end{aligned}$

(8.1)

Wherein, Π_s is the set of all possible paths $\{\mathcal {P}_{s,o_k}\}^K_{k=1}$ between the source s and the observers in the graph G. The set $\{\theta _l\}^L_{l=1}$ represents the propagation delays for all edges of the graph G. The deterministic function g depends on the joint distribution of the propagation delays. Note that, the estimator in Eq. (8.1) is calculated through averaging over two different sources of randomness: (a) the uncertainty in the paths that the attack takes to reach the observers, and (b) the uncertainty in the time that the attack takes to cross the edges of the graph G. Due the combinatorial nature of Eq. (8.1), its complexity increases exponentially with the number of nodes in G, and is therefore intractable. In order to address this problem, Pinto et al. [146] proposed a method of complexity O(N) that is optimal for general trees, and a strategy of complexity O(N ³) that is suboptimal for general graphs.

8.4 Source Estimator on a Tree Graph

Consider the case of an underlying tree T. Because a tree does not contain cycles, only a subset O _a ∈ O of the observers will receive the attack emitted by the unknown source. Then, $O_a=\{o_k\}^{K_a}_{k=1}$ is called the set of K _a active observers. The observations made by the nodes in O _a provide two types of information. (a) The first information is the direction in which attack arrives to the active observers, which uniquely determines a subset T _a ∈ T of regular nodes. Hence, T _a is called active subtree, (see the left figure in Fig. 8.2). (b) The second information is the timing at which the attack arrives to the active observers, denoted by $\{t_k\}^{K_a}_{k=1}$ , which is used to localize the source within the set T _a. It is also convenient to label the edges of T _a as E(T _a) = {1, 2, ⋯ , E _a}, so that the propagation delay associated with edge i ∈ E is denoted by θ _i (see the left figure in Fig. 8.2). Assume that the propagation delays associated with the edges of T are independent identically distributed random variables with Gaussian distribution N(μ, σ ²), where the mean μ and variance σ ² are known. Based on these definitions, the following result can be concluded.

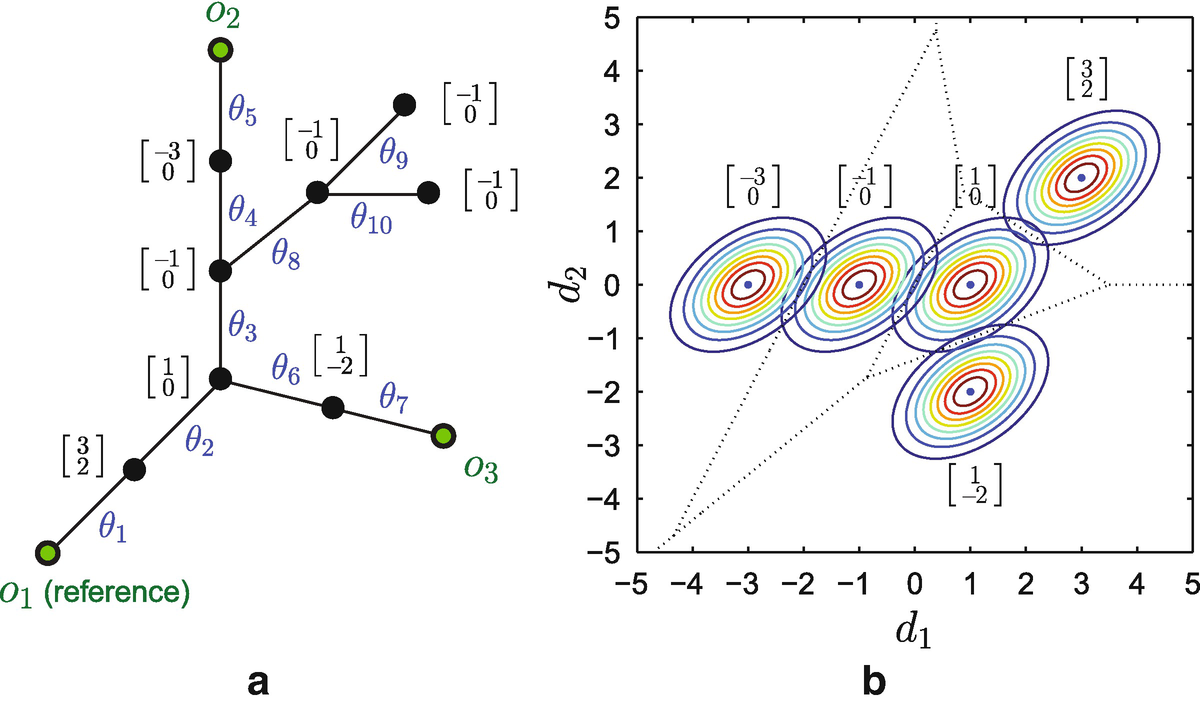
../images/466717_1_En_8_Chapter/466717_1_En_8_Fig2_HTML.png — Fig. 8.2
(a) Active tree T _a. The vector next to each candidate source s is the normalized deterministic delay $\tilde { \boldsymbol {\mu }}_s:= \boldsymbol {\mu }_s/\mu$ . The normalized delay covariance for this tree is $\tilde {\mathbf {A}}:=\mathbf {A}/\sigma ^2=[5,2;2,4]$ . (b) Equiprobability contours of the probability density function P(d|s ^∗ = s) for all s ∈ T _a, and the corresponding decision regions. For a given observation d, the optimal estimator chooses the source s that maximizes P(d|s ^∗ = s)

$$\tilde { \boldsymbol {\mu }}_s:= \boldsymbol {\mu }_s/\mu $$ — Fig. 8.2
(a) Active tree T _a. The vector next to each candidate source s is the normalized deterministic delay $\tilde { \boldsymbol {\mu }}_s:= \boldsymbol {\mu }_s/\mu$ . The normalized delay covariance for this tree is $\tilde {\mathbf {A}}:=\mathbf {A}/\sigma ^2=[5,2;2,4]$ . (b) Equiprobability contours of the probability density function P(d|s ^∗ = s) for all s ∈ T _a, and the corresponding decision regions. For a given observation d, the optimal estimator chooses the source s that maximizes P(d|s ^∗ = s)

Proposition 8.1 (Optimal Estimation in General Trees)

For a general propagation tree T, the optimal estimator is given by

$\displaystyle \begin{aligned} \hat{s} = \mathit{\mbox{arg}}~\displaystyle \max_{s\in T_a} \boldsymbol{\mu}^T_s{\mathbf{A}}^{-1}(\mathbf{d}-\frac{1}{2}\boldsymbol{\mu}_s), \end{aligned}$

(8.2)

where d is the observed delay, μ _s is the deterministic delay, and A is the delay covariance, given by

$\displaystyle \begin{aligned}{}[\mathbf{d}]_k = t_{k+1} - t_k, \end{aligned}$

(8.3)

$\displaystyle \begin{aligned}{}[\boldsymbol{\mu}_s]_k = \mu(|P(s,o_{k+1})| - |P(s,o_1)|), \end{aligned}$

(8.4)

$\displaystyle \begin{aligned}{}[\mathbf{A}]_{k,i} = \sigma^2\times \left\{ \begin{array}{ll} |P(o_1,o_{k+1})|, & k=i,\\ |P(o_1,o_{k+1}) \cap P(1,o_{i+1})|, & k\neq i,\\ \end{array} \right. \end{aligned}$

(8.5)

for k, i = 1, ⋯ , K _a − 1, with |P(u, v)| denoting the number of edges (i.e., the length) of the path connecting vertices u and v. Readers could refer to [ 146 ] for the detailed proof of this proposition.

Note that, when node s is chosen as the source, μ _s and A represent, respectively, the mean and covariance of the observed delay d (see Fig. 8.1 for illustration).

Proposition 8.1 reduces the estimator in (8.1) to a tractable expression, where the parameters can be simply obtained from path lengths in the tree T. Furthermore, the complexity of Eqs. (8.2)–(8.5) scales as O(N) with the number of nodes N in the tree. The full proof of the complexity is given in the Supplemental Material in [146]. The sparsity implies that the distance between observers is large, and so is the number of random variables of the sum

$\displaystyle \begin{aligned} d_k = t_{k+1} - t_1 = \displaystyle \sum_{i\in P(s^*, o_{k+1})} \theta_i - \displaystyle \sum_{i\in P(s^*, o_1)} \theta_i. \end{aligned}$

(8.6)

Based on the central limit theorem, the observer delay vector d can be closely approximated by a Gaussian random vector.

8.5 Source Estimator on a General Graph

Now consider the most general case of source estimation on a general graph G. When the malicious attack is propagated on the network, there is a tree corresponding to the first time each node gets informed, which spans all nodes in G. Note that, the number of spanning trees can be exponentially large. Pinto et al. [146] assume that the actual propagation tree is a breadth-first search (BFS) tree. This corresponds to assuming that the attack travels from the source to each observer along a minimum-length path, which is intuitively satisfying. Then, the resulting estimator can be written as

$\displaystyle \begin{aligned} \hat{s} = \mbox{arg}~\displaystyle \max_{s\in G} S(s, \mathbf{d}, T_{bfs,s}), \end{aligned}$

(8.7)

where $S=\boldsymbol {\mu }^T_s{\mathbf {A}}_s^{-1}(\mathbf {d}-\frac {1}{2}\boldsymbol {\mu }_s)$ , with parameters μ _s and A _s computed with respect to the BFS tree T _bfs,s rooted at s. It can easily shown that the complexity of Eq. (8.7) scales subexponentially with N, as O(N ³).

Therefore, Eqs. (8.2) and (8.7) gives the propagation source estimator for a tree graph and a general graph, respectively. The computational complexity of these two estimators are O(N) and O(N ³), respectively. We call these estimators as Gaussian source estimators.

To test the effectiveness of the proposed approach, Pinto et al. [146] used the well-documented case of cholera outbreak that occurred in the KwaZulu-Natal province, South Africa, in 2000. Propagation source identification was performed by monitoring the daily cholera cases reported in K communities (the observers). The experimental results show that by monitoring only 20% of the communities, the Gaussian estimator achieves an average error of less than four hops between the estimated source and the first infected community. This small distance error may enable a faster emergency response from the authorities in order to contain an outbreak.

8. Source Identification Under Sensor Observations: A Gaussian Source Estimator

8.1 Introduction

8.2 Network Model

8.3 Source Estimator

8.4 Source Estimator on a Tree Graph

Proposition 8.1 (Optimal Estimation in General Trees)

8.5 Source Estimator on a General Graph