Chapter 7 Meno’s Paradox
Before programmable electronic computers existed, the word “computer” referred to a human being hired to perform calculations. The ancestors of the objects we now call computers were, in their own time, called “mechanical computers,” to distinguish them from the humanoid kind. In the 1940s, when “computer” started to transition over to the meaning it has today, the people who worked with the machines pondered the difference: on the one hand, newfangled mechanical computers were nothing but a set of switches; on the other hand, that is also a way to describe a human brain. And it was easy to see that computers were bound to become vastly more complex, adding more and more switches, in the decades to come. Is there some threshold of complexity that, when crossed, qualifies a computer as a thinker? If yes, how would we know where that threshold is or when it had been crossed?
These are hard questions. They are hard in large part because we are not sure what we mean by “think.” Forget about machines. When do I myself count as thinking? Do nonhuman animals think? What is thinking? If we cannot answer these questions, we seem very far from being able to say what it would be for a machine to think. Faced with this predicament, one of the pioneers of computing, Alan Turing, proposed that we set aside thorny philosophical debates about the nature of thought in favor of a simple test.1 The test involves three participants: two human beings and a machine. Each is located in a separate room. The first human, call her A, communicates, via text, with both the other human and also with the machine. If A cannot tell which of her interlocutors is a machine, then the machine has passed the test—it now officially counts as thinking.
Turing transformed a vague question—Can machines think?—into a well-defined problem—Can you construct a machine that can pass a specific test? This type of transformation is often useful. If I want to know which surgeon is best at performing bypass surgery, or which foreign language class to enroll in, or which neighborhood I should move to, the first step will likely be to transform these vague goals into more specific desiderata. I might want to compare rates of complications, or the grades that students who took various courses achieved on standardized language exams, or the distances between candidate neighborhoods and my workplace. Someone faced with the question “Which surgeon has a low rate of complications for bypass surgery?” understands what to do next in order to make progress on the investigation; “Who is a good surgeon?” by contrast, invites the stymied response, “It depends what you mean by good.”
It is true that in many cases I may be interested in more than one data point—not only the rate of complications, but how booked the surgeon is, whether they accept my insurance, what medical school they went to, whether my friends have referred them, and so on. Complexity adds steps, but even a complex set of desiderata is actionable; the set of actions will simply take longer. Imagine someone who says: “I don’t want the surgeon with a low rate of complications, or one covered by my insurance, or one who went to a prestigious medical school, etc. . . . I just want a good surgeon.” We are likely to respond that “Find me a good surgeon!” is not a well-defined problem. Even if we want to help this person, we are not sure how to do so. For suppose that somehow we stumbled across “a good surgeon”; how would we know that we had?
Philosophers have faced this complaint for a long time. Philosophical inquiry is not an attempt to solve well-defined problems; it is, instead, an attempt to ask important questions. It has often been noted that much, if not all, of the territory now claimed by science once belonged to philosophy. When philosophical questions can be reformulated as problems, that is when they leave the orbit of philosophy. Consider questions such as What is motion, change, cause? Or: What allows something to be counted as alive? Or: How can different substances be mixed together? Each of these was, at one time, a purely philosophical question, before the disciplines of physics, biology, and chemistry turned them into a set of interrelated and more precisely formulated problems. (Though it is worth remarking that each of those disciplines retains ties to their ancestral philosophical questions.) The same holds for logic, economics, and computer science. Back when they were more poorly formulated, their questions were philosophical questions.
But not all philosophical questions have been converted into problems. When philosophers and nonphilosophers face off over one of the unconverted questions, the ensuing interactions tend to go awry. The nonphilosopher is liable to be frustrated by questions such as “Is there free will?” or “What is justice?” or “How should one live?”; to reply that “it depends what you mean by ‘free’ or ‘justice’ or ‘should’ ”; to dismiss the question as ill-defined; to doubt whether the philosopher would have a way of recognizing the answer if it were staring her in the face. The nonphilosopher may be too polite to give full verbal expression to her incredulity, but inside she wonders, “What makes these philosophers think that they are doing anything at all?”
Meetings between philosophers and nonphilosophers so reliably result in such a culture clash that the typical encounter deserves a name. I will call it “the primal scene.” The specter of the primal scene hovers over every introduction to philosophy class, and the students in the class will often find themselves reenacting the scene when they go home for break and explain to their parents that they are studying philosophy. When philosophers confront complaints about whether philosophy has or can or ever will make progress, and the complainers seem to have little interest in philosophy outside of raising this complaint, that interaction tends to be a version of the primal scene.
I. Meno’s Paradox
Plato dramatizes the primal scene in the Meno. Socrates asks Meno, “What is virtue?” Meno offers three answers, each of which is refuted by Socrates. When Socrates asks Meno to try again, Meno explodes in a shower of incredulous questions:
How will you look for it, Socrates, when you do not know at all what it is? How will you aim to search for something you do not know at all? If you should meet with it, how will you know that this is the thing that you did not know?2
Socrates immediately recognizes what is happening. He has clearly encountered the primal scene before:
I know what you want to say, Meno. Do you realize what a debater’s argument you are bringing up, that a person cannot search either for what he knows or for what he does not know? He cannot search for what he knows—since he knows it, there is no need to search—nor for what he does not know, for he does not know what to look for.3
Socrates’ reformulation, which precisifies Meno’s skeptical challenge into a dilemma, is called Meno’s paradox. It calls into question the very possibility of searching: either the search is unnecessary, because you already have what you’re looking for, or it is impossible, because you don’t know what you’re looking for, and so wouldn’t know it if you found it.
Meno is not complaining generally about any and every kind of search. He would not say that it is impossible to search for one’s keys or for the answer to an arithmetic problem, or that one can’t look a word up in a dictionary. Meno’s paradox targets the specific kind of search that he has only now, after extended conversation, come to understand himself as having been dragooned into. It is important to emphasize that Meno did not raise his challenge immediately, when Socrates first asked him, “What is virtue?”
In the opening of the dialogue, when first Socrates posed that question, Meno was not of the opinion that it would be impossible to answer. Quite the contrary. As I emphasized when we first examined this encounter, in chapter 2, after Socrates asks Meno what virtue is, Meno repeatedly insists that it is trivially easy to answer:
It is not hard to tell you, Socrates. First, if you want the virtue of a man, it is easy to say that a man’s virtue consists of being able to manage public affairs and in so doing to benefit his friends and harm his enemies and to be careful that no harm comes to himself; if you want the virtue of a woman, it is not difficult to describe: she must manage the home well, preserve its possessions, and be submissive to her husband; the virtue of a child, whether male or female, is different again, and so is that of an elderly man, if you want that, or if you want that of a free man or a slave. And there are very many other virtues, so that one is not at a loss to say what virtue is. There is virtue for every action and every age, for every task of ours and every one of us—and, Socrates, the same is true for wickedness.4
This is an impressive speech about virtue, one that Meno has evidently come prepared to rattle off. But Socrates is dissatisfied. He did not want to hear the different virtues of different kinds of people. He wanted to know what these different kinds of virtue all have in common: “Even if they are many and various, all of them have one and the same form which makes them virtues, and it is right to look to this when one is asked to make clear what virtue is.”5 Socrates wants to know what virtue itself is: “Tell me the nature of virtue as a whole and stop making many out of one . . . allow virtue to remain whole and sound, and tell me what it is.”6 Meno tries again, but all of his subsequent answers also end up in the same difficulty. Socrates complains, “I begged you just now not to break up or fragment virtue.”7
In response to this complaint, Meno, who has studied with the famous sophist Gorgias, offers a complaint of his own. Meno insists that he is usually quite good at talking about virtue: “Yet I have made many speeches about virtue before large audiences on a thousand occasions, very good speeches as I thought, but now I cannot even say what it is.”8 But of course he is usually permitted to do what Socrates won’t let him do—chop virtue up into pieces. Someone with expertise in the world of surgeons might say, “I can tell you which surgeon has the lowest rage of complications, which has the most availability, which accepts your insurance, and so on.” We are likely to sympathize with the frustrations of a person who is faced with the demand to simply find a good surgeon, and their doubts about what—if not low complications, availability, and so on—the demander can mean by “good.” Many a philosopher can think back to a time when, not yet having been converted to the philosophical enterprise, she played the part of the nonphilosopher, skeptically challenging some philosopher to prove that the sort of thing philosophers look for is even findable. Those of us who have played both parts in the primal scene appreciate where Meno is coming from—but we are, at the same time, cognizant of what he is missing.
There are certainly times and places where it is appropriate to convert a vague question into a more precise and delimited problem. But this conversion does not always work out in the way one anticipated. Recall the question of whether computers would ever be able to think. Seven decades after Turing’s death, the problem posed by his test stands as solved. Large language models (LLMs) produce essays that fool teachers into thinking that students wrote them, secure high grades on examinations for would-be economists and doctors, and serve as substitutes for texts composed by human beings, such as those on Wikipedia and in online encyclopedias. LLMs have passed the Turing test with flying colors.
What has the response been? Not widespread acknowledgment of the need to make room for a new set of thinkers in our midst, but a debate—between those eager for innovation and those fearing misuse—over the degree to which we should regulate LLMs. Few appear concerned with the ethics of regulating thought, because few even consider the possibility that LLMs are actually thinking. It appears that when we converted the question, “Can machines think?” into the problem, “Construct a machine that passes this test,” something got lost in translation. Insofar as some of us are still moved to wonder what it would mean for a machine to actually engage in thought, we may indeed find ourselves cast back on philosophical shores, wondering: What is thinking, after all?
This chapter is about how it is possible to make positive progress on this question, and the others like it. It addresses the worry—shared, we can now see, between Alcibiades and Meno—that philosophy, so long as it remains resolutely philosophical, orienting itself around questions and not problems, is consigned to be negative and destructive. We have seen how refutation works. But how does inquiry work?
II. Questions and Problems
The distinction between a question and a problem turns out to be the key to understanding both Meno’s paradox and the “primal scene.” Consider the etymologies of those two words. “Problem” comes from the Greek problēma, which means an obstacle or barrier. The prefix “pro” means before or in front of, and the verb is ballō, to throw. Problēma was the word used for something that is thrown before you and impedes your way—so a wall can count as a problēma; so can a shield, or one’s horse’s armor.9 If I am trying to kill you, your shield, the armor on your horse, and the wall behind which you hide constitute problēmata—problems—for me.
A problem is something you need to move out of the way so that you can go on with what you were doing before the problem arose. A question is a very different sort of beast. To ask a question is to be on a quest: the word “question” comes from the Latin quaerere, which means to seek or search or pursue or hunt. At the end of your hunt, you have caught what you wanted: the answer, or the quarry, or the Holy Grail. Your quest wasn’t a distraction from some underlying project; it was the underlying project. At the end of the problem-solving process, you have eliminated something—the solution to a problem dissolves the problem—whereas at the end of the question-answering process, you have something—whatever it was you are looking for. The question culminates in its answer.
One way to see the difference between questions and problems is to compare how they are transferred. When you present your problem to someone else, you are setting a task before them: this is what you need to solve. They don’t necessarily need to know why you need it solved, because one person can eliminate an obstacle to another’s progress toward a goal without sharing that goal. That is why the transfer of a problem characteristically takes the form of a command—though of course the expression of this command can be softened in the direction of a request (“Please?”), or propped up with added incentives (“I’ll pay you . . .”). When I pose a question, by contrast, I am not commanding, deferring, or delegating—I am sharing or inviting. I hope to captivate your interest, to whet your curiosity, to make my question your question, to entice you to join me in the hunt. Whereas the symbol for a question is the question mark, the symbol for a problem is the exclamation point. Motives are exogenous to problem-solving, but endogenous to question-answering.
Admittedly, we often express problems interrogatively. Instead of commanding you to find my keys, I might ask you where they are. But “Where are my keys?” is a problem hiding in question clothing. To see this, consider some possible answers. “Not on the surface of the sun” truthfully gives the location of my keys, as does, “Wherever your keys are.” Nonetheless, these are bad answers, and they are bad precisely because they do not help me achieve the goal—leaving the house, opening a locked door, rubbing my lucky rabbit’s foot—to which keylessness constituted an impediment. Consider the reply “They are in your room.” This is a good reply if you have a small, tidy room, but if your room is large and cluttered, you might need the location demarcated more specifically. Whether or not it is a good reply is a function of whether or not it solves the problem. Indeed, “Here, take mine” could be a good reply to “Where are my keys?” if what is needed is to leave the house quickly, and if we have copies of the same key. A good reply doesn’t need to offer an answer to the question, “Where are my keys?” as long as it resolves the problem of not being able to leave the house.
If we try to imagine a version of “Where are my keys?” that is resolutely inquisitive—the person is really after knowledge of the location of his keys—we will start to feel the force of Meno’s paradox. Suppose I tell you that your keys are in your room, but you turn down that answer. They are also in your house, and in the city where your house is located, and some large number of miles from the Eiffel Tower. You don’t like those answers, either. Do I need to add that they are on your desk? Sitting at the center of a patch of light cast by your desk lamp? Do you need to know their GPS coordinates? Down to how many decimal points? What about them being exactly where they are? Or not on the surface of the sun? Someone who just wants to know where his keys are and cannot give us any sense of the kind of problem he’s trying to solve by locating them leaves us with a baffling array of possible responses. We may feel either that there is no correct answer—that he would not know it if he saw it—or if he insists that there is an answer (“It’s the one about the patch of light”) that can only be because he had settled upon it in advance.
We can now say why the scope of Meno’s paradox is much narrower than it might first appear to be. Most searches aim to arrive neither at what I know, nor at what I don’t know, but at a way to keep doing what I was doing before I ran into a problem. Likewise, most questions are merely inquisitive repackagings of problems. Perhaps there is no definitive answer to the question, “Where are my keys?”—no reason to pick “in the patch of light” over “on planet Earth.” This needn’t pose any difficulty in a world where no one is ever asking that question, because all we were ever trying to do was find solutions to the problem of keylessness. That problem is typically well defined, to the point where it is easy for the answerer to tell that “on planet Earth” would be a bad answer whereas a variety of others—“on your desk,” “near your lamp,” and so on—would all be equally good. We don’t run into Meno’s paradox when we search for our keys, or look words up in the dictionary, or ask after the sum of a series of numbers, because in all of those cases we are looking for solutions to well-defined problems.
Any time I ask an expert for a piece of information, I am posing a problem rather than asking a question. True, I may put a question mark at the end of my request: When was Napoleon born? What is the atomic number of helium? Where is the ocean deepest? Nonetheless, my readiness to let them be in charge of what the correct answer looks like is the telltale sign that I am not on a quest. I do not expect, after hearing their answer, to say “Aha!” The Aha! of understanding is associated with questions, rather than problems. It expresses the feeling that, in getting what you were searching for, you got exactly what you wanted.
When I ask for information what I actually want is something distinct from the information itself—namely, to move on with whatever activity was impeded by the problem posed by the absence of that information. There is always an ulterior motive for seeking out information, some use to which I aim to put it, even if that use is merely to relieve the itch of curiosity or a period of boredom. This ulterior motive is precisely what allows me to produce a “well-defined” formulation of the circumstances under which the problem will count as solved. I can tell you, in advance, what stands in the way of my moving on: I want whatever will allow me to fill in the blank on the test, or advance to the next stage of my research project, or leave the house, or sate my curiosity, or ease my boredom.
A question, by contrast, counts as answered when I have the answer. There is nothing that comes next. So if you ask me to tell you what it will be like for me to have the answer, I am forced to reply that I will only be able to do that once I have it. The state of having the answer is simply the state of knowing something that I do not yet know, and so cannot identify for you.
But how can it be that when I have the answer, I recognize it as being just what I was looking for (“Aha!”), but I can’t tell you, in advance, what it is going to look like? This is Meno’s paradox.

Problems tend to come packaged with an accepted methodology for approaching them, which is to say, a system that has been developed for solving problems of that kind. This is a selection effect: we don’t even notice most of what obstructs our goals, because a problem only precipitates out of the giant mush of things I might try to do when its solution promises to come cheaply, relative to other problems that might so precipitate. If I want something that is available both in town A and in town B, and there are roads between me and town A, but an ocean between me and town B, I do not ask myself, “How do I cross the ocean?”; I only ask, “Which roads should I take?” The former problem does not even show up, to me, as a problem. That is why problems and standardized tools for solving them—know-how, skills, algorithms, machines, formulas, instruments, systems, procedures, and so on—tend to go hand in hand. Where there is a problem, there tends to also be (at least) the makings of a road that one ought to travel in order to arrive at the solution. Problems are characteristically tractable.
Noam Chomsky wrote, “Science is a bit like the joke about the drunk who is looking under a lamppost for a key that he has lost on the other side of the street, because that’s where the light is. It has no other choice.”10 But in fact it makes a lot of sense to look for one’s keys under the light; and, not finding them, to move on to alternative solutions to the problem of keylessness—having new keys made or staying at a friend’s place, for instance. Assuming that those alternative solutions are easier than searching for keys in the dark, there is no reason to do the latter. What Chomsky is observing is that in science, as in life, one’s tools determine one’s problems. It is only if we recast the role played by the keys in this metaphor, and imagine that “the drunk” is searching not for the solution to some (scientific, or other) problem but to the answer to a question, that the joke becomes a legitimate critique. If the keys themselves are what you want, you must search wherever you need to search, in the light and in the dark, even if you have no idea in advance how that search will proceed.
Most of the time, when a search runs into trouble—we don’t know how to proceed, we don’t know how to get help—we are willing to do one of two things. The first is give up. The second is find some way of turning our question into a problem. “Who is a good surgeon?” becomes “Compare the rates of complications,” and so on. A problem is tractable; it can be handed to someone else; it can be formulated in a manner that is “well defined” in the sense that the terms of the solution can be specified in advance; it comes packaged with a procedure, which is to say, a reason to believe that it can be solved. But it is possible to imagine a scenario where someone is not interested in who has the lowest rates of complications, or who went to the best medical school, and so on; where she really does want to know what makes a surgeon a good surgeon—“Who is the good surgeon?”—because she aspires to become one.
Recall that when Meno was asked to define virtue, he offered correlates of it, instead. Obedience is what Meno thinks virtue looks like in a slave; whereas power or wealth or connections indicate virtue in the kind of man Meno wants to be. This is akin to saying a good surgeon is the one with low rates of complications, or who went to a good medical school, or comes recommended by one’s friends. Socrates complains that this approach leaves virtue fragmented: when you look at the actual parts of virtue—namely, the various virtues—a question remains as to what holds them all together. The question is: What do virtues such as justice, courage, and generosity have in common? The answer to that is not going to be “money,” or “power,” or “obedience.”
If the reason you seek a good surgeon is because you have a medical problem, you might look at complication rates or what school they went to, but if you want to be a good surgeon you will think about it differently. You will consider the elements of the practice of surgery—the parts proper to it—such as diagnosis, managing a surgical team, actually wielding a scalpel or laser, providing postoperative care. The common core of these activities, if they are considered as parts of a single project, will be something like: cutting into people for the sake of their health. Doing that well is the key to being a good surgeon; complication rates and alma maters are, at best, mere correlates.
When Socrates insists that Meno keep virtue whole and not split it into parts, he is reminding Meno that “What is virtue?” is a question, not a problem. This is, more generally, what Socrates is doing when he asks his interlocutor after “the X itself,” or to look to “the Form of X” or to tell him “the definition of X.” Socrates is convinced that there is such a thing as virtue, that virtue is a suitable target for an inquiry: it could be the endpoint of what you wanted to know. The answer to the question, “What is virtue?” is something to “Aha!” over. Consider, by contrast with virtue, a shmiraffe. I am going to define “shmiraffe” as: a giraffe plus one foot of air around it in every direction. A shmiraffe is, unlike virtue, not a suitable target for Socratic inquiry; faced with “What is a shmiraffe?” the correct thing to do is to split it into parts—the giraffe and the air around it—and not try to find anything that holds those parts together. One is not inclined to hope that sustained inquiry will expose the form or essence of a shmiraffe. Whether a giraffe has a Form or essence is debatable: Aristotle thinks the answer is yes, giraffes are one of the basic building blocks of reality, whereas a contemporary scientist might disagree, and argue that a giraffe can be reduced to (“is really nothing over and above”) a collection of atoms. But everyone—Plato, Aristotle, and the contemporary scientist—will be on the same page when it comes to shmiraffes. No one thinks that concept is a suitable target for an inquiry into the nature of things. Nonetheless, the concept of a shmiraffe might yet be useful for solving problems. It has already proved useful for solving the problem of illustrating, to you, what it means for something to lack the unity requisite for Socratic inquiry.
Socrates is always telling his interlocutors to treat what he is saying as a question about what X is, not as a problem about how to find an X. He’ll instruct them not to break X into pieces, or not to simply give an example of X. In this context, the famously obscure notion of a Platonic Form can be understood in a relatively straightforward way. Socrates sometimes speaks of the Form of Justice, or the Form of Piety, or the Form of whatever X he and his interlocutor are examining. “The Form of X” simply refers to the version of X that you must have in mind so as to answer the question “What is X?” This is why “The Form of X” is synonymous with “X itself” or “the essence of X.” The Form of X is what you look to in order to produce a definition of X. The Form of X is X, considered as a question to be answered, rather than as a problem to be solved.
It is worth noting the difference between a Socratic definition, which stands as the goal of inquiry, and the kind of definition I gave of “shmiraffe.” The second kind of definition is one that allows us to sharpen our statement of a problem; such a definition can even, for maximum precision, be articulated in a formal language—using mathematical or logical notation—instead of a natural one. That kind of a definition is a tool. It serves as a prerequisite for the real work in service of which the definition is introduced; a Socratic definition, by contrast, is the endpoint, the quarry.
A misunderstanding characteristic of the primal scene is when the philosopher is asked to provide a definition of the very term she hoped the conversation would explicate. The nonphilosopher sees definition as the prerequisite for solving whatever problem the philosopher wanted us to solve, but there was no such problem. The philosopher wasn’t posing a problem. She was asking a question.
III. A Demonstration of the Socratic Method
Once it has become clear to Meno what Socrates wants to do—inquire—Meno doubts whether it is something that can be done. If I can’t tell you, in advance, what the answer is going to be, how will I recognize it when I get it?
There is one arena in which it is relatively easy to make sense of what it would mean to be on the hunt for some particular thing you do not yet have: hunting. Imagine you are on the trail of an animal that you are trying to capture or kill. It is only once you are in some kind of contact with it, by way of its scent, or some hairs from its body, or its footprints, or the sound of its movements, or a glimpse of it in your peripheral vision, that we would say you are tracking it in any substantive sense. Suppose you had none of these things and were wandering aimlessly in the animal’s habitat. If you suddenly saw such a clue—a footprint or a hair—you might think to yourself, “I’ve got him!” That is the moment when your quest begins in earnest. We can grasp the requirement that you must “have” the animal in order to seek the animal: there is such a thing as “having” from a distance, when the search is underway, and there is another kind of “having” from closer up, when the search is complete. Being on the hunt—actually searching—might require the first kind of contact with your quarry, even though it obviously cannot require the second kind.
But how far can this distinction between two kinds of contact take us? When it comes to hunting we can draw distinctions that rely on properties of three dimensional space—close versus distant contact—because our quarry is a physical object. Socrates holds that there is an analog to “picking up the scent” in the space of ideas: when two people both have answers to a question, even if neither of those answers constites knowledge, the answers of the one can be tested against those of the other. This is a kind of hunt that cannot be undertaken alone.
Witness this exchange:
Socrates: I want to examine and seek together with you what it [virtue] may be.
Meno: How will you look for it, Socrates, when you do not know at all what it is? How will you aim to search for something you do not know at all? If you should meet with it, how will you know that this is the thing that you did not know?11
And a bit later in the dialogue:
Socrates: Since we are of one mind that one should seek to find out what one does not know, shall we try to find out together what virtue is?12
I have italicized the pronouns here to expose the contrast between Meno asking how Socrates will inquire, and Socrates proposing a joint inquiry: Meno sees himself as presenting a difficulty to Socrates, whereas, as Socrates sees it, he and Meno are in a difficulty together. I have also italicized the word “how,” which occurs three times in Meno’s speech. As we saw when I first quoted Meno’s questions, earlier on, Socrates goes on to rephrase them into a dilemma (you can look neither for what you already know, nor for what you don’t know), but what Meno himself originally expresses is not any kind of paradox but instead a demand for a procedure: how, how, how. These two presuppositions on Meno’s part—that Socrates will be on his own, and that he will have to rely on some antecedently approved procedure—are connected. When it comes to, for instance, the problem of finding the sum of a series of numbers, we embark on solving it with advance knowledge of the procedure by which we will proceed: addition. Meno’s demands are appropriate for problems; by making these demands, he suggests that problems are the only thing we can think about.
Meno’s paradox poses a real threat to the Socratic project, because all of Socrates’ questions are genuine questions, and not problems. Targeting things of fundamental importance to us, they stubbornly and persistently resist being transformed into problems. Untimely questions ask after the things we actually want, rather than the things we must remove to pursue the things we want. Having an untimely question and having an answer to such a question: we have seen that, and why, these two states come together. But there is a difference—all the difference in the world—between having an answer to a question and having knowledge that the answer is correct.
The difference made Socrates who he was: he himself was defined by his awareness of his own ignorance, which is to say, understanding that his answers to untimely questions did not yet qualify as knowledge. He recognized the space between an answered question and a question whose answer has the finality of knowledge—but equally significantly, he recognized that this space only becomes inquisitively relevant in the company of another. Alone, we do fall prey to Meno’s paradox: our answer either satisfies us or we lose hold of the question. But if you and I both have the same question yet different answers, a path opens up: we can test our answers against each other. This process is Socratic inquiry. The Socratic method is a way you can make progress without knowing in advance how you are going to do so.
We can now see why Socrates calls Meno’s question unfair, a “debater’s trick.” Meno demands to be shown how Socrates can, by himself, do something that in fact he can only do with Meno: “How are you going to find virtue if I don’t help you?” The primal scene always involves such a request for advance guarantees. The nonphilosopher hesitates to dip his toe into the waters of philosophy unless he first finds out what exactly is he going to be doing, and what he will get out of it. He wants the practice and the payoff of philosophy translated for him into extra-philosophical terms. The reader of this book may feel herself tempted to make the same impatient demand: show me some philosophical progress! She wants to stand on the sidelines and watch—passive, uninvested, safe—and assess whether some other people are making advances toward knowledge of untimely questions. If she likes what she sees, then she may decide to jump in.
I can’t satisfy this request as it stands, nor could Socrates. Trying to assess an inquiry into untimely questions from the outside—that is, without recognizing them as your questions, and without asking yourself whether you are making progress—is like trying to assess what water feels like without touching it. So, what is Socrates to do, if he can’t convince Meno to continue with the inquiry without offering him a display that would serve as some kind of “proof,” and if he also doesn’t think it makes sense to put philosophical inquiry on display? Socrates decides to put nonphilosophical inquiry on display. Socrates cannot offer Meno a demonstration as to how inquiry into some (genuine) question makes progress, if the demonstration must meet both the requirement that Meno relates to it as a passive, detached spectator, as well as the requirement that the question being inquired into is an untimely one. But he can offer a demonstration that meets only the first requirement, which is what he does.
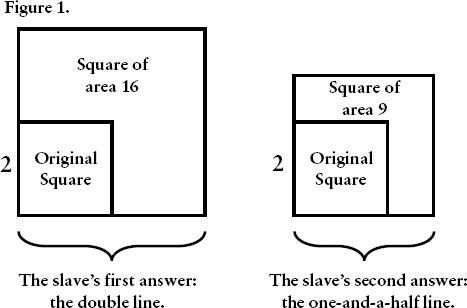
He invites Meno’s slave, who is unversed in geometry, to answer the following question: What is the line from which the double square comes? Suppose you have a square, let’s call it S, with a side of length 2 and an area of 4, and you want a square twice as big as S, with an area of 8. How do you draw, in the diagram containing S, the line that will serve as the side of the square with twice the area of S? Socrates initiates an inquiry into that line.
Socrates: Come now, try to tell me how long each side of this will be. The side of this [S] is two feet. What about each side of the one which is its double?
Slave: Obviously, Socrates, it will be twice the length.13
The slave finds it “obvious” (recall Meno’s opening response to Socrates) that the answer is the line of length 4. But he is wrong, since that line will produce a square quadruple the area of S, with an area of 16, not 8. After the slave himself comes to see this by way of some follow up questions, Socrates invites him to try again.
Socrates: The line on which the eight-foot square is based must then be longer than this one of two feet, and shorter than that one of four feet?
Slave: It must be.
Socrates: Try to tell me then how long a line you say it is.
Slave: Three feet.14
Next, the slave proposes a line one and a half times the length of the side of S, of length 3; but this is also incorrect, because it yields a square with an area of 9.
At this point Socrates interrupts the demonstration and turns to Meno, so that Meno can keep an eye on one feature of it in particular:
Look then how he will come out of his perplexity while searching along with me. I shall do nothing more than ask questions and not teach him. Watch whether you find me teaching and explaining things to him instead of asking for his opinion.15
Socrates goes back to the quadruple square, which is composed of four copies of S, and asks the slave what happens if they cut each S along the diagonal. The slave answers that the 8 resultant triangles will each have the area of half of the original square; since the area of the whole quadruple square is 16, he is then able to conclude, under more questioning, that four of those triangles, taken together, form a square double the size of the original, that is, 8. Thus the answer is: the diagonal. The double square comes from the diagonal. The slave is able to arrive at this conclusion, without being taught, by “searching along” with Socrates.
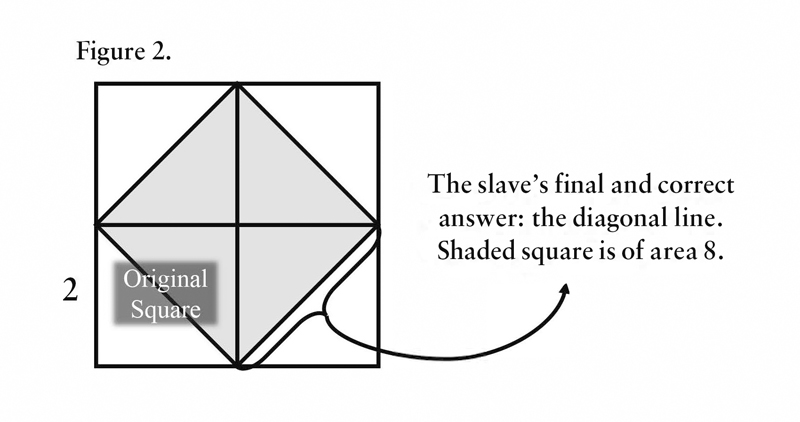
Notice that although we can readily name the desired line, there is no easy way to specify its length. If the slave had been asked, at the outset, to describe in generic terms what the answer would look like, he might well have insisted that one way or another it would have to be able to be produced out of the units based off of the side of S. If the double line is too long, and the 1.5 line is too short, perhaps one ought to try the 1.75 line, and so on. His assumptions about the procedure required for finding the answer would have been wrong. Had he been allowed to search for his keys under that particular streetlight, he would never have found them, due to the fact that the diagonal is incommensurable with the side of the square. The slave, as an answerer, makes progress without a procedure, which is to say, without knowing in advance exactly how he will take the next step. If he had been presented with the problem of finding the line from which the double square comes, he would have been unable to do so, since he had no procedure for approaching this problem. But he is able to make progress on the corresponding question, by inquiring into it, with Socrates.
The reason it is possible for the slave to learn merely by answering questions is that the Socratic method is not a one-and-done affair. If the slave were only allowed to answer once, his false initial response would doom the inquiry. Socrates subjects the slave’s answers to further examination in such a way that even a false answer is made useful, becoming part of the route to the truth. Socratic questioning makes it possible for the slave to answer inquisitively: not as if he already knows, but with a view to knowing. Of course, this only works because Socrates himself has an answer—a pretty good one—to the question of where the double square comes from.
Does Socrates consider his own answer about the diagonal to be a final answer—to count as knowledge? Or does he think true knowledge of the line from which the double square comes would require a more systematic grasp of geometry than he possesses? We never learn the answer to this question, since the mathematical demonstration is only a “toy example” meant to analogically illustrate the practice of inquiry. Socrates is emphatic that he is not teaching the slave—he only proceeds by questioning—so even if he had knowledge, he was not conveying it. Perhaps it does not matter to Socrates whether he himself has more to learn about geometry. But it does matter a great deal that he considers his answers about virtue to be unfinished, imperfect, and calling for further inquiry.
Equally important, however, is the fact that Socrates does have answers. In part three, we will examine some of his answers on the topics of love, death, and politics, but we have already encountered others: there is no such thing as weakness of will, revenge (in all its guises) is incoherent, it is better to have injustice done to you than to do it. Moreover, he is famous for his answers. In the Laches, one of his interlocutors describes the view that virtue is knowledge as a well-known Socratic position.16 That answer is itself tested, and modified, over the course of the Meno; the dialogue ends with the revised position that when someone has virtue, that is either because they have knowledge or because they have true opinion. It is only because Socrates has a sense of where he’s headed when he asks after virtue that he has a place from which to refute Meno’s initial three definitions.
More generally, the reason why his interlocutors can answer inquisitively is because Socrates asks the kinds of questions—pushy questions—that are inflected by answers that have themselves been honed by years of inquiry. Pushy questions inspire inquisitive answers, which, in turn, help push further toward knowledge.
IV. Past Lives?
Let’s reanimate Meno’s skeptical challenge one last time. If two people have different answers to a question, each of them will, naturally, think that they are right. Why think that they can make progress by comparing their answers?
Among readers of Socratic dialogues, Meno’s paradox often shows up as the worry that Socrates asks leading questions. A leading question is a question that “forces” an answer, comparable to how a magician forces a card when he offers you what appears to be a free choice but uses sleight of hand to get you to pick the card he wants. The charge is that Socrates is putting words into his interlocutors’ mouths, the result being a one-sided conversation that simply goes where Socrates wanted it to go. They are not making progress together by comparing their answers; rather, we are just watching the Socrates show.
Socrates’ questions to the slave are “pushy” in the sense that they are informed by Socrates’ own mathematical reasoning and intelligence. Are they leading questions? Although it is possible that the slave is simply telling Socrates what he wanted to hear, that is not a necessary, or the only, interpretation of the exchange. Another interpretation is possible, because we can imagine ourselves in the slave’s shoes, and imagine ourselves being brought, by this kind of conversational exchange, to see that the double square comes from the diagonal. The slave’s answers strike us as answers we might give—and not only because Socrates pressured us to do so. Importantly, this is a function of how Socrates conducted the conversation: he asks the questions in the right order, so that it makes sense to answer as the slave does.
There is certainly no guarantee that two people with different answers will make headway; in most cases of divergent opinion, neither even attempts to refute the other and the disagreement goes nowhere. Socrates’ claim is not that disagreements must or even typically do lead to intellectual progress, but that progress is possible, so long as one person asks pushy questions and the other gives inquisitive answers. Even so, readers have been inclined to wonder whether there is some fancy footwork going on in this part of the Meno; they worry that Socrates’ success with the slave is a function of some feature peculiar to mathematics, and that the same success cannot be found in ethics.
It seems important to the success of the geometrical demonstration that the rightness and wrongness of a prospective answer is available to the learner in a specific way. Socrates seems to be relying on the “Aha!” character of mathematics, where, when confronted with a better answer, you can see that it is a better answer. Something clicks into place. Even if it is the first time you are approaching a new type of mathematical puzzle, you do not need to rely on the authority of your math teacher to inform you which answers are wrong, and which are right. You can, with a little work, see it for yourself.
Compare that example with the predicament of someone who is, for the first time, looking into the question of when Napoleon was born. Wrong answers don’t “feel” wrong to him; he doesn’t say, “I should’ve seen that it can’t be 1768!” When he encounters the correct answer, he does not have the experience of its suddenly falling into place, of saying “Of course! 1769!” This power to recognize that the thing in front of you is (or in the case of wrong answers, is not) the very thing you were looking for—Socrates calls it “recollection”—is central to the kind of demonstration Socrates is putting on. Recall Meno’s challenge:
How will you look for it, Socrates, when you do not know at all what it is? How will you aim to search for something you do not know at all? If you should meet with it, how will you know that this is the thing that you did not know?17
Without answering how, Socrates can show Meno that it is possible to know that this is the thing you did not know. The experience that “this is the thing I did not know” is real, because we have it when we learn math. We also have it outside of math, when we remember something. For example, if there was a word I was trying to remember, and then it suddenly it comes to mind, I say “Aha! that’s it!” Someone who once knew the year of Napoleon’s birth might experience a burst of recognition when presented with 1769. Socrates is inclined to assimilate these two facts, and posit that even in the case of math we are “recognizing” something we saw earlier—in a past life. He claims to have heard from priestesses and poets that the soul is immortal, and that our current life represents a reincarnation. This would explain our ability to do math, and it should make us optimistic about virtue:
The soul is immortal, has been born often, and has seen all things here and in the underworld, there is nothing which it has not learned; so it is in no way surprising that it can recollect the things it knew before, both about virtue and other things. As the whole of nature is akin, and the soul has learned everything, nothing prevents a man, after recalling one thing only—a process people call learning—discovering everything else for himself, if he is brave and does not tire of the search, for searching and learning are, as a whole, recollection.18
Socrates is saying that in our pre-lives, before we were born, we knew things that we can now hope to recover—with an “Aha!” experience—if we search for them. It makes sense to search; we can be optimistic of success. But what if you do not share Socrates’ commitment to reincarnation, or his inclination to defer to priestesses and poets? If you don’t happen to believe that the soul is immortal, that it lived for an infinitely long period before the time you were born, and that during that period it acquired knowledge of all things, do you have any reason to think that inquiry will work out?
The Meno marks the opening of thousands of years of philosophical inquiry into the special “Aha!” character of the kind of knowledge that Socrates claims we can recollect from our pre-lives. Later philosophers speak of this kind of knowledge as “a priori knowledge”—a phrase denoting what we know prior to experience—or “innate ideas,” or “relations of ideas.” They want to hold on to Socrates’ notion that there is some distinct kind of knowledge at play in (for instance) geometry, access to which does not seem to depend on one’s particular life-experiences, but they do not think one must characterize the activation of such knowledge as remembering what one saw in a past life.
If we set aside the peculiar details of Socrates’ story about pre-life, and rely just on the philosophical theory of a priori knowledge, will that reassure our skeptic? Not necessarily. First of all, some people are just as skeptical about a priori knowledge as reincarnation. The philosopher W. V. O. Quine famously denied the existence of a priori knowledge; and even those who don’t deny it outright might be inclined to limit its scope to math and logic. What guarantee do we have that ethics lies inside the space of a priori knowledge? Aren’t there a lot of reasons to doubt the existence of common ground between finding the double square and finding virtue?
These are good questions, but if they are meant as an attack on Socrates, they miss the mark. After the encounter with the slave, Socrates refers back to his claims about the soul’s pre-life and says:
I do not insist that my argument is right in all other respects, but I would contend at all costs both in word and deed as far as I could that we will be better men, braver and less idle, if we believe that one must search for the things one does not know, rather than if we believe that it is not possible to find out what we do not know and that we must not look for it.19
It turns out that Socrates is willing to set aside not only the specifics of the theory of recollection, but even the existence of a special category of a priori knowledge. Both of those are ways to flesh out a positive response to Meno’s paradox, but Socrates’ real commitment is to the positive character of that response rather than to details about what happened in our past life or whether there is such a thing as knowledge held independently of experience. That is why Socrates is less concerned than subsequent philosophers have been to produce a theory about what ethical knowledge shares with the other sorts of knowledge—mathematical, logical, conceptual—that are usually recognized as a priori. Socrates’ point is: Whatever it is that you think is necessary to assume in order to be able to believe in the possibility of searching for the answers to questions—which is to say real questions, by contrast with those that are really problems in question clothing—assume that. If you just believe that “one must search for things one does not know,” you don’t need to commit in advance to any particular theory about how recognition experiences are generated in us.
Socrates and Plato and Aristotle lived in a culture where the closest thing to the idea of what is “your own” or “native” to you or yours “by right” was the idea that it had been yours in the past. Hence the role of “autochthony”—the notion that the citizens of a given city had at some point been born from its soil—in the myths of many ancient societies, and hence the importance placed on myths and origin stories more generally. Aristotle thought that every species of organism stretched back eternally into the past. It makes sense that someone coming from such an intellectual culture, when faced with the demand to flesh out the idea of the mind’s coming home to an answer it can recognize as its own, adopts the language of memory and origins. If Socrates were living in our more dynamic world*—where the understanding of life is informed by evolutionary science, where nations both have been and are increasingly expected to be shaped by mass migration, and where culture is continually subject to upheavals by new technology—Socrates might well choose to speak of the mind’s destiny rather than its memories, of the future of the soul rather than its past. Speaking only for myself, I will say that I prefer to think of inquiry in terms of the aspiration to arrive at a new and better understanding—it will still need to be true that one recognizes it as such!—than in terms of gravitating back to one’s forgotten origins. (I admit that it is not obvious how aspirational search enables us to recognize what we find as what we were after all along; I wrote a book in order to explain this.)20 In any case, Socrates makes it clear that he is, at least in principle, friendly to emendations about his theory of the pre-birth lives of our souls.
That is because, in the final count, his commitment is not to the correctness of some poet’s tale, nor to the existence of a distinct and unified category of items that can be known independently of experience, but rather to the possibility that there are real, genuine questions, and that improving our answers to these questions is a project worthy of our efforts. The point of the slave demonstration is not to claim that ethics is somehow “like math,” except in the broadest terms: both ethics and math are sites of questions that cannot be unmasked as problems. Yes, it is true that many people experience math exclusively as a set of problems we muscle through in order to please some teacher or to proceed with some technical project, but that is not what math is for mathematicians. The image of mathematics as a closed subject in which we grind out proofs according to established rules, or perform calculations in accordance with a fixed algorithm, is a distortion many of us absorb in high school. For those who devote themselves to the study of mathematics, it is a creative activity full of surprises—such as the fact that the line that produces the double square is not commensurable with the side of the original square. Even if many of us do not approach mathematics in a spirit of real inquiry, it can be approached in that way. Mathematics is a site not only of problems, but also of questions.
Both math and ethics feature questions. The difference is that while a mathematical question can become untimely for the mathematician who has invested herself in it, many ethical questions are untimely for everyone. We can’t avoid assuming we already have the answers to questions about how to live our lives. It follows that, like it or not, you are already on the hunt. You don’t get to choose to put yourself in that situation, you already are in that situation; you only get to choose how courageously, energetically, and persistently you search.
Think of the slave. We have no reason to believe he was possessed of any fancy theory about the existence of a priori knowledge or that he knew poetry about past lives. He did not ask for and did not receive any assurance that his search was going to go anywhere, or that he would recognize the answer when he saw it. And yet he proceeded anyway, without advance guarantees, bravely stepping forward into the mathematical unknown, making mistakes, recovering from them, and in the end achieving real progress. What Socrates demonstrates, with the slave’s help, is that that is a way a person can be. Socrates is asking Meno to be inspired by the courage of his slave: Be bold and inquire.

Xenophon recounts the fate of Meno in terms that rival Alcibiades’: as a general under Cyrus, Meno showed himself to be greedy, treacherous, and incompetent.21 He dies young, after being tortured for a year. If the conversation that Plato describes actually took place—and there is some reason to doubt that it did—it may well have represented the best hours of Meno’s life.
The cases of Clitophon, Alcibiades, and Meno should be set alongside those of Socrates’ more successful long-term associates, such as Plato, Xenophon, Theaetetus, and all the participants in the Phaedo (we will meet them in chapter 11). Socrates did not always fail to have a positive impact on the lives around him. Nonetheless, he very clearly did fail sometimes, and Plato wanted to draw those failures to our attention. If Socrates’ interlocutors have a problem sustaining Socratic optimism about the process of inquiry, I anticipate that the reader of this book—even if, as I hope, her life never sinks to the depths of a Meno or an Alcibiades—will also have such a problem. She wants to be able to believe in philosophical progress, but she is not sure that it has anything positive, anything substantive, to offer her. And so, this is the moment to point out that it already has.
V. What Is Thinking?
We can summarize the conclusions of the three chapters of part two, including this chapter, as follows: The Socratic method is inquisitive refutation, refutation cures normative self-blindness, inquiry allows us to ask questions (as opposed to solving problems). These claims, taken together, add up to an answer to the question with which this chapter began: What is thinking?
I am going to define thinking by describing the paradigmatic case, and then I will explain how various kinds of peripheral cases are related to it.
Thinking is, paradigmatically, a social quest for better answers to the sorts of questions that show up for us already answered. It is a quest because it has a built-in endpoint: knowledge. It is social because it operates by resolving disagreements between people. Thinking begins when Socrates, or someone like him, recognizes that his account of justice, or piety, or love is not as good as it could be—which is to say, that it does not qualify as knowledge. This realization prompts him to ask another person for help inquiring into questions such as, “Is it beneficial to be just?” “Who is worthy of love?” and “What is piety?” Socrates plays the role of Clifford, using his answer to examine the one provided by his interlocutor, who plays the role of James. If the interlocutor’s first attempt at an answer is refuted, he tries another, and then another. If one of the interlocutor’s answers holds up against Socratic pressure, they come to agree on that; otherwise—and this is what we see in Plato’s dialogues—it doesn’t, and the process of refutation draws Socrates’ answer out of him, which becomes the shared conclusion. Either way, the two parties come to agree. This does not mean that the quest is completed: both parties can go on to subject what they have agreed on to further tests of the same kind in future disagreements with others. Each time the answer passes, it becomes more firmly “tied down” with the very arguments used to explain its preferability.
This is thinking. It is completed when one arrives at an answer that is perfectly stable. The arguments with which it has been definitively “tied down” can then be conveyed to others, and this is why, if one has knowledge, one can teach it to others. Thinking is the road from ignorance about the most important things to knowledge about them.
Here is another way to put my definition: Thinking is using the Socratic method to inquire into untimely questions. But we can also use the Socratic method to inquire into other sorts of questions, as in the case of the slave and the double square. We can call that “thinking,” too, with the understanding that we are referencing its resemblance to the paradigmatic case. We can also use the Socratic method when what we have on our hands is not a question but a problem, because any problem can, in the right social context, be turned into a question: “What is the solution to this problem?” If the parties pursue the answer to this question using inquisitive refutation, we can call that conversation “thinking” as well. Finally, in the usage of “thinking” that diverges most from the core of my definition, we can use the word “thinking” to describe a process that is not conversational at all—perhaps it takes place in someone’s head, or on a sheet of paper—but has the potential to be integrated into a conversation, because it stands open to the sorts of corrections and clarifications that are associated with Socratic refutation. A dream sequence would not qualify, but a chain of reasoning would, and so would an arithmetical calculation, or even an idea for the plot of a novel.
This definition of thinking inverts the usual order of importance between the inner and the outer: the standard approach to thinking privileges what is private and unvoiced and “in the head” as the core case, so that what happens in conversation counts as thinking only insofar as it is an outer echo of an inner event: “thinking out loud.” I could not have opened this book with the definition of thinking I have just provided, because some readers would have immediately rejected it for failing to correspond to ordinary usage, while others would have too freely accepted it, on the grounds that they do not mind my using the word “thinking” however I see fit. The first set of readers would have anticipated a dictionary definition, which is a summary of our linguistic practices in relation to a word, while the second set would have assumed I was offering a stipulative definition, of the sort that might appear in the opening of a proof: “Let A represent . . . ” If you are giving a dictionary definition, you are beholden to ordinary usage, whereas if you are giving a stipulative definition, you get free rein to use any word to mean anything you like, as long as you are clear about what stands for what.
My definition of thinking is not a dictionary definition, and it is not a stipulative definition; rather, it is a Socratic definition. A Socratic definition must come at the end, and not the beginning, of a process of inquiry: it is the upshot of having figured out what something really is. (By contrast, my definition of the phrase “untimely question” [see chapter 2, here] was stipulative, an invention of my own. I introduced it early in the book, not in order to explain anything, but simply in order to have a convenient handle by which to refer to something that I would go on to explain.)
Unlike stipulative definitions, a Socratic definition can be the target of objections: it is possible to claim that the definition is somehow mistaken, that we ought to emend it or discard it altogether. Unlike in the case of dictionary definitions, you cannot object to a Socratic definition merely by pointing to linguistic conventions. The fact that it stands in some tension to how we usually talk won’t necessarily constitute an objection to a Socratic definition, because a Socratic definition is itself the product of arguments, and those arguments give you leverage to criticize how we usually talk.
The argument for the definition I have given can be stated in two premises: First, in order for someone to be thinking, they must keep an open mind and inquire, moving toward what’s true and away from what’s false. If a series of images flash before your eyes, or follow one another in your daydreams or night dreams, that is not yet thinking—thinking requires subjecting such representations to some minimal standards of thoughtfulness. Second, thinking must, at least in principle, be capable of processing any kind of thought. Unlike “multiplying,” or “remembering,” or “updating,” or “analyzing,” or “planning,” terms that reference specific forms of thinking, thinking itself is an all-purpose activity, accommodating all possible thoughts. Thinking must be the biggest possible tent.
The three chapters in part two have argued that it is the Socratic method that allows us to think about untimely questions in an open-minded, inquisitive, and truth-directed manner.† But the Socratic method is hospitable to narrower forms of thought as well: an interlocutor is free to introduce the results of memory, or analysis, or multiplication into the conversation, as the slave does, when he uses multiplication to find the area of various squares. In one dialogue, Socrates and his interlocutor venture into the interpretation of poetry. There is no algorithm that can be used to answer an untimely question, because an untimely question is not a problem. But any algorithm can, at least in principle, be subjected to the checking procedure of the Socratic method. We can ask, of the algorithm, “Was it used correctly?” or “Should it have been used in the first place?” or “What was it used for?” and we can pursue this inquiry in an open-minded, truth-oriented, and inquisitive way. More generally: anything that you could potentially disagree with in that open-minded, truth oriented, and inquisitive way can be subjected to the Socratic method.
Imagine that there is something you want to think about, because it is desperately important to you to arrive at a better understanding, but you don’t have any antecedently vouchsafed procedure for thinking about it. There is no mechanism you can rely on to check your thinking against it, no process to ensure that your thinking is proceeding in a productive, correct fashion instead of veering wildly off course. You don’t have an algorithm or decision procedure to keep you honest. Are you lost? No. Even in this situation, you can still think about what you need to think about, you are not left out in the cold, because even when there is no existing problem-solving mechanism you can rely on, there is still—other people. The Socratic method is how you think about things that you couldn’t think about if it were not for the presence of other people, which is to say, it is how you think about just anything. The method that allows you to think about anything, leaving nothing behind, in its wake, as unthinkable—that method is rightly called “thinking.”
On this definition, if I multiply 4 × 5 and get 20, it is not obvious that what I have done counts as thinking. I do not think this is an absurd claim. Return to the question at the opening of this chapter, a question that animates many people in our world today: “will computers ever be able to think?” The reason this strikes people as a difficult question is also a reason to hesitate over whether 4 × 5 = 20 is thinking. Someone who is convinced that deploying an algorithm such as multiplication amounts to thinking must concede not only that nonhuman calculators think, but that they are much better at it than we are.
On a Socratic account, the use of an algorithm—for example, multiplication—counts as thinking insofar as it is, at least in principle, subject to questioning. Multiplication is thinking if it is possible for someone to call into question whether the multiplication was done correctly, to request an explanation of why multiplication was used, and to potentially convince the one using it that an alternative arithmetic operation—or none at all—might have been a better choice. The algorithmic activity of a handheld calculator is not embedded in this sort of broader intellectual openness to questioning and challenge, but if a nonhuman computational device—such as a large language model—developed to the point where it were, Socrates would be happy to say that it is thinking. The fact that it is silicon-based instead of being realized in neuronal tissue would be entirely irrelevant, from a Socratic point of view.
Socrates would thus accept a modified version of the Turing test. On Turing’s version, a computer counts as thinking if it seems more human, to the evaluator, than the actual human being that the computer is being compared to. This test would not satisfy Socrates. He would point out that even in his time, it was possible to produce convincing imitations of humans: painted statues, for instance. To count as thinking, Socrates will require that the computer fool us in a specific way: by playing either the role of James, or the role of Clifford, well enough to help us inquire into some untimely question. In order to qualify as a thinker, it is not enough that the computer imitate a human being. It has to imitate a human being who is, in the paradigmatic sense of the word, thinking.
Part three of this book is devoted to showing you the concrete fruits of thinking, in the Socratic sense, not in the area of geometry but in what I believe to be the three most difficult areas of human life: romantic love, facing one’s own death, and the minefield of problems that goes under the heading of “politics.” You may not be as inclined to agree with Socrates’ conclusions about politics, love, and death as you are to agree with his conclusions about geometry, but you will have an opportunity to see the Socratic philosophical machinery sink its teeth into the mess of everyday life.
Inquire, with an open mind, seeking the truth and avoiding falsity. We have explored why using this method is not as straightforward as it initially appeared. Now we will see where it can take us.