11
Thermodynamics: Biochemical Flux
The general struggle for existence of animate beings is therefore not a struggle for raw materials … nor for energy … but a struggle for entropy.
—Ludwig Boltzmann43
What organisms feed on is negative entropy.
—Erwin Schrödinger362
Prior chapters emphasized abstract problems. How do changing environmental factors alter the fitness costs and benefits of traits? How do those fitness costs and benefits shape organismal design?
The remaining chapters link those abstract questions to the biochemistry of microbial metabolism. New comparative predictions follow.
This chapter reviews thermodynamics. The first section begins with free energy, the force that drives biochemical reactions. Free energy measures the production of entropy. Negative entropy in food provides the source for the catabolic increase in entropy, fueling life.
The second section analyzes metabolic reaction rates. Enzymes enhance biochemical flux by lowering the free energy barrier of intermediates. The lowered barrier reduces the resistance against reaction. Biochemical flux equals the free energy driving force divided by the resistance barrier against flux.
The third section links biochemical flux to design. Increased driving force trades off greater flux against lower metabolic efficiency. Reduced resistance trades off greater flux against the cost of catalysis. The costs and benefits of adjusting force or resistance shape metabolism.
Subsequent chapters build on these principles to develop comparative predictions for metabolic design.
11.1 Entropy Production
We have constantly stressed that thermodynamic systems do not tend toward states of lower energy. Therefore the tendency to fall to lower free energy must not be interpreted literally in terms of falling down in energy. The Universe falls upward in entropy: that is the only law of spontaneous change. The free energy is, in fact, just a disguised form of the total entropy of the Universe …even though it carries the name “energy.”
—Peter Atkins18
Textbooks emphasize that free energy drives chemical reactions. A reaction proceeds if the inputs have greater free energy than the outputs. The greater the drop in free energy, the faster the reaction will be. Organisms must acquire free energy from their food and use up that free energy to drive their metabolic processes.
The confusion arises because free energy does not measure energy, it measures entropy. Total energy is always conserved. The cause of change is always an increase in total entropy.
In many chemical applications, it is sufficient to calculate free energy without understanding its meaning. But a clear conceptual view helps to understand broader problems of metabolic design.
This section reviews entropy production, the force that drives chemical reactions. Sections 11.2 and 11.3 link entropy change to tradeoffs between reaction rate and metabolic efficiency.
CHANGE IN FREE ENERGY MEASURES CHANGE IN ENTROPY
[T]he natural cooling of a hot body to the temperature of its environment can be readily accounted for by the jostling, purposeless wandering of atoms and quanta that we call the dispersal of energy. …All chemical reactions are elaborations of cooling, even those that power the body and the brain.
—Peter Atkins18
Food provides chemical bonds with concentrated energy. Breaking the food’s chemical bonds disperses the energy. Dispersing energy increases entropy. Increasing entropy is a general kind of cooling.
We can think of the chemical bonds in food as storing negative entropy. The amount of negative entropy is the potential to produce entropy by dispersing the energy contained in the chemical bonds. Organisms feed on negative entropy.362
To analyze metabolism, we must track the flow of entropy between the chemical reactions and the environment. In chemistry, we typically partition the world into the system on which we focus and the surrounding world. We call the surrounding world the bath because we think of the system as an isolated container floating in a large bath with constant temperature and pressure.
If the system produces heat, the bath soaks up and disperses that heat. The temperature in the system remains constant at the external bath’s temperature. If the system cools, then the bath transmits heat to the system, maintaining uniform temperature. Similarly, pressure in the system equilibrates with the large external bath.
The total entropy is the bath’s entropy plus the system’s entropy,
St = Sb + Ss.
By the Second Law of thermodynamics, the change in entropy is never negative,
ΔSt = ΔSb + ΔSs ≥ 0. (11.1)
In this setup, the system exchanges heat energy with the bath. Total energy never changes. But energy can change location or form.
The dispersal of heat energy from the system to the bath, ΔHb, moves concentrated energy from the system to dispersed energy in the bath. Energy is more dispersed in the bath because the bath is very large and disperses the energy widely, with essentially no change in temperature. As heat energy disperses, it cools and increases in entropy.
The transfer of heat energy to the bath and its dispersal raises the entropy of the bath by

in which T is temperature.
Combining the prior equations yields the total change in entropy,
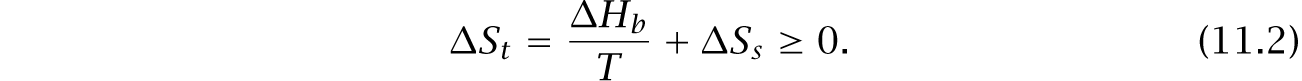
A reaction proceeds when total entropy increases, ΔSt > 0. The change in total entropy depends on the heat produced by the reaction and dissipated through the bath, ΔHb∕T, plus any change in the internal entropy of the system, ΔSs.
The heat term is negative when a reaction sucks up heat, causing heat to flow from the bath to the system. The internal system entropy term is negative when the reaction creates products with less entropy than the initial reactants. The reaction proceeds only when the overall total entropy increases.
The entropy expression in eqn 11.2 is equivalent to the classic expression for Gibbs free energy used in all textbooks on chemistry. I show the equivalence because it is important to understand that entropy is the ultimate driver for the reactions of metabolism.
I noted above that the transfer of heat energy to the bath raises the entropy of the bath by ΔSb = ΔHb/T. Energy has units in joules, J. Entropy has units J K−1, in which K is temperature in kelvins. Thus, we can write the change in heat energy in terms of the change in entropy as ΔH = TΔS.
Because energy is conserved, the change in the heat energy of the bath must be equal and opposite to the change in the heat energy of the system. Thus ΔHb = − ΔHs, and

We can combine eqns 11.1 and 11.3 to write the total change in entropy required for a reaction to proceed as

Multiplying by − T changes the units of the terms to energy and reverses the direction of change required for a reaction to proceed,
ΔG = ΔHs − TΔSs < 0, (11.5)
in which ΔG = − TΔSt is the change in the Gibbs free energy. The word energy is misleading because total energy can never change. The change in Gibbs free energy quantifies the energy that is free and available to do work, not the change in energy.
A decrease in free energy is actually an increase in entropy. It is the increase in entropy that determines the capacity to do work.
For example, concentrated energy in a chemical bond can be relatively “hot” compared with its surrounding environment. As the “heat” disperses and cools, the heat flow can potentially be captured to do work. Dispersed energy is cold and cannot do work.
An ordered system tends to increase in entropy toward its naturally disordered maximum entropy equilibrium. Work gets done when one can capture the dissipation of an ordered disequilibrium in one system to drive the increasingly ordered disequilibrium of another system.
THE ESSENTIAL COUPLING OF DISEQUILIBRIA
The central lesson of the Second Law is that natural processes are accompanied by an increase in the entropy of the Universe. A coupling of two processes may cause one of them to go in an unnatural direction if enough chaos is generated by the other to increase the chaos of the world overall.
—Peter Atkins18
Metabolism couples chemical reactions. One reaction moves a system toward its equilibrium, producing entropy as it dissipates the disequilibrium. The partner reaction is driven away from its natural equilibrium, decreasing entropy.
As digestion breaks down the chemical bonds in food, the increase in entropy can be coupled to reactions that drive the production of ATP. The increasing disequilibrium of ATP against ADP stores negative entropy in a usable form, a battery that can be tapped to do work.
Metabolic reactions dissipate the ATP–ADP disequilibrium to increase entropy. That increase in entropy drives the coupled entropy-decreasing reactions that build the ordered molecules needed for growth and other life processes.47,86,181,182,201
Entropy-producing and entropy-decreasing reactions must be directly and necessarily coupled. The paired reactions proceed only if their combined change produces entropy. Understanding the molecular escapement mechanisms that couple reactions poses one of the great problems of modern biology.47,58,59
Consider two coupled reactions. The first reaction breaks down a food molecule into two parts,
Food → PartA + PartB,
producing entropy ΔS1 > 0. The second reaction drives the production of ATP, increasing the disequilibrium of ATP relative to its components ADP and Pi, as
ADP + Pi → ATP.
Increasing disequilibrium reduces entropy, ΔS2 < 0, or, equivalently, increases negative entropy. The paired reactions when coupled should be thought of as a single process that, mechanistically, necessarily combines the two half-reactions,
Food + ADP + Pi → PartA + PartB + ATP.
The process proceeds if the total entropy change is greater than zero, ΔS1 + ΔS2 > 0, or equivalently, ΔS1 > − ΔS2. Here, − ΔS2, the negative entropy captured in the driven reaction producing ATP, must be less than ΔS1, the entropy produced in the driver reaction digesting the food.
If the reactions are not coupled, the second reaction producing ATP cannot proceed. Instead, the first reaction disperses the concentrated energy in the food, increasing entropy by ΔS1. Typically, that entropy increase associates with the dissipation of heat. The heat spreads out through the bath and is lost.
When the reactions are coupled, some of the entropy produced by the driver reaction is stored as negative entropy in the driven reaction. The fraction of entropy captured by the driven reaction provides a measure of efficiency,

Because the total entropy produced by the combined reactions must be greater than zero, ΔS1 + ΔS2 > 0, some of the entropy produced must escape unused. In every metabolic reaction, the organism loses some of its negative entropy.
ENTROPY CHANGE IN THE DISSIPATION OF DISEQUILIBRIUM
Entropy change drives reactions. Total entropy change arises from the combined move toward equilibrium in the driver reaction and move away from equilibrium in the driven reaction. This subsection describes the relation between entropy and equilibrium. I use ATP as an example.
The terminal phosphate bond in ATP is commonly described as a high-energy bond. However, when ATP is at equilibrium with its components, the forward and back reactions
ADP + Pi ↔ ATP
happen at equal rates. There is no change in entropy or free energy in either direction.
ATP at equilibrium with ADP cannot drive other reactions. It is not the energy in the phosphate bond that drives reactions. Instead, it is the dissipation of the ATP–ADP disequilibrium toward its equilibrium that drives coupled reactions away from their equilibrium.
The classic textbook expression for free energy in terms of disequilibrium highlights the key concepts. Consider the reaction
A + B ↔ C.
As a reaction proceeds from its initial concentrations toward its equilibrium, the change in free energy is proportional to
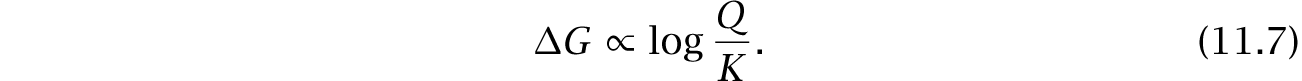
The reaction quotient, Q, is the ratio of the product concentration to the reactant concentrations,

The equilibrium constant, K, expresses the reaction quotient at equilibrium,

The expression log Q/K measures disequilibrium. Thus, the change in free energy measures the size of the initial disequilibrium that dissipates as the system moves to its equilibrium.
The greater the initial disequilibrium of a driver reaction, the more free energy (negative entropy) is available to drive other reactions.
The further a driven reaction is pushed away its equilibrium, the more free energy must be expended by the driving reaction.
At equilibrium, a system has no free energy to drive other reactions, no matter how much energy is concentrated in its chemical bonds.
THERMODYNAMIC DRIVING FORCE AND REACTION RATE
This subsection relates the change in free energy to the rate of reaction. The key point is that faster reaction rate trades off against lower efficiency. Reduced efficiency means more free energy is dissipated as heat, decreasing the free energy available to drive other reactions.
A negative change in free energy drives a reaction forward, toward its equilibrium. The greater the decrease in free energy, the faster the forward reaction proceeds relative to the reverse reaction,

in which J + is the forward reaction flux, and J − is the reverse reaction flux. The decrease in free energy, − ΔG, is the driving force of the reaction.
Section 11.2 links the driving force to the overall reaction rate. Here, I focus on the consequences of a greater driving force for the associated flux ratio, J+/J−. An increased flux ratio corresponds to a faster net forward reaction rate but does not tell us the overall rate.
Greater loss of free energy, − ΔG, increases the flux ratio, J+/J−, and drives the net forward reaction faster. Loss of free energy relates to gain in entropy. The additional entropy increase corresponds to a greater dissipation of concentrated and ordered energy. Dissipated energy typically flows away as lost heat, which cannot be used to do work.
In other words, an increased reaction rate burns more fuel. Here, burning fuel means dissipating negative entropy as heat. That lost heat cannot drive other reactions or do work.
Typically, organisms couple driving reactions that increase entropy by ΔS1 to driven processes that decrease entropy by − ΔS2. In eqn 11.6, the efficiency − ΔS2/ΔS1 expresses the fraction of the entropy produced by the driver reaction that is captured by the driven reaction in useful work or in the building of ordered molecules.
These results link rate and efficiency. For coupled reactions, the closer to zero the total amount of entropy produced, ΔSt = ΔS1 + ΔS2 > 0, the more efficiently the driven process captures the available potential from the driver reaction.
Greater efficiency means that − ΔS2 is closer to ΔS1. The smaller the difference, the less the total free energy decrease of the coupled reactions,
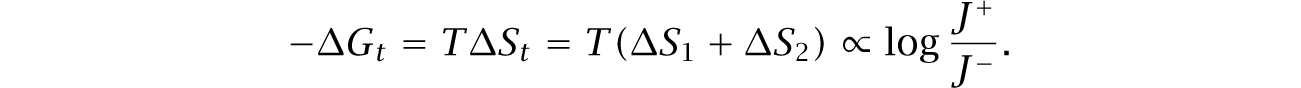
The smaller the free energy decrease, the slower the net forward reaction flux tends to be.
Maximum efficiency occurs as the entropy captured by the driven reaction approaches the entropy produced by the driver reaction, − ΔS2→ΔS1, causing ΔGt→0. As the free energy change becomes small and efficiency increases, the net forward reaction flux of the overall coupled reaction declines toward zero. Reaction rate trades off against efficiency.
FREE ENERGY AND ENTROPY
As noted below eqn 11.5, the total entropy change and the free energy change express the same quantity in slightly different ways as

The standard in chemistry is to use the term free energy when discussing entropy changes in reactions.
Free energy is a useful perspective because the quantity is the degree to which energy is concentrated or ordered and, through the dissipation or disordering of that energy, work can be done. The work may be used to drive other reactions or to do physical work.
Because free energy is the standard term, and also a useful one, I will switch freely between that term and the more causally meaningful entropy descriptions.
11.2 Force and Resistance Determine Flux
Analyses of biochemical reactions often focus on free energy change as the thermodynamic driving force. However, biochemical flux also depends on the resistance that acts against reactions,

Biochemical flux is analogous to electric flux in Ohm’s law, in which the electric flux (current) equals the electric potential force (voltage) divided by the resistance.215,314 High voltage with no wire connecting the poles produces no current. A chemical reaction with a large driving force but high resistance proceeds slowly or not at all.
For example, combining hydrogen and oxygen yields water. The reaction causes a large drop in free energy and thus has a powerful thermodynamic driving force. Yet, at standard ambient temperature, nothing happens when one mixes the two gases.
The oxygen-hydrogen reaction intermediate significantly reduces entropy at ambient temperature and thus does not easily form. A reaction intermediate with a large reduction in entropy corresponds to a high activation energy, creating a resistant barrier to reaction.
Organisms modulate chemical flux by altering resistance or force. Catalysts reduce resistance, which increases flux by lowering the activation energy. Adding reactants or removing products raises the forward driving force, which enhances forward flux.
Changing the flux of a reaction alters the tendency for molecular transformation versus stability. Metabolic transformation moves the negative entropy in food into the highly ordered molecules needed for life. Stability protects those useful ordered forms from their intrinsic tendency to decay. Organisms control transformation and stability by modulating the driving force and the resistance of reactions.
11.3 Mechanisms of Metabolic Flux Control
Three mechanisms alter metabolic flux.100 Each mechanism creates tradeoffs between flux and efficiency. Later chapters show how those tradeoffs shape metabolic design (Fig. 11.1).
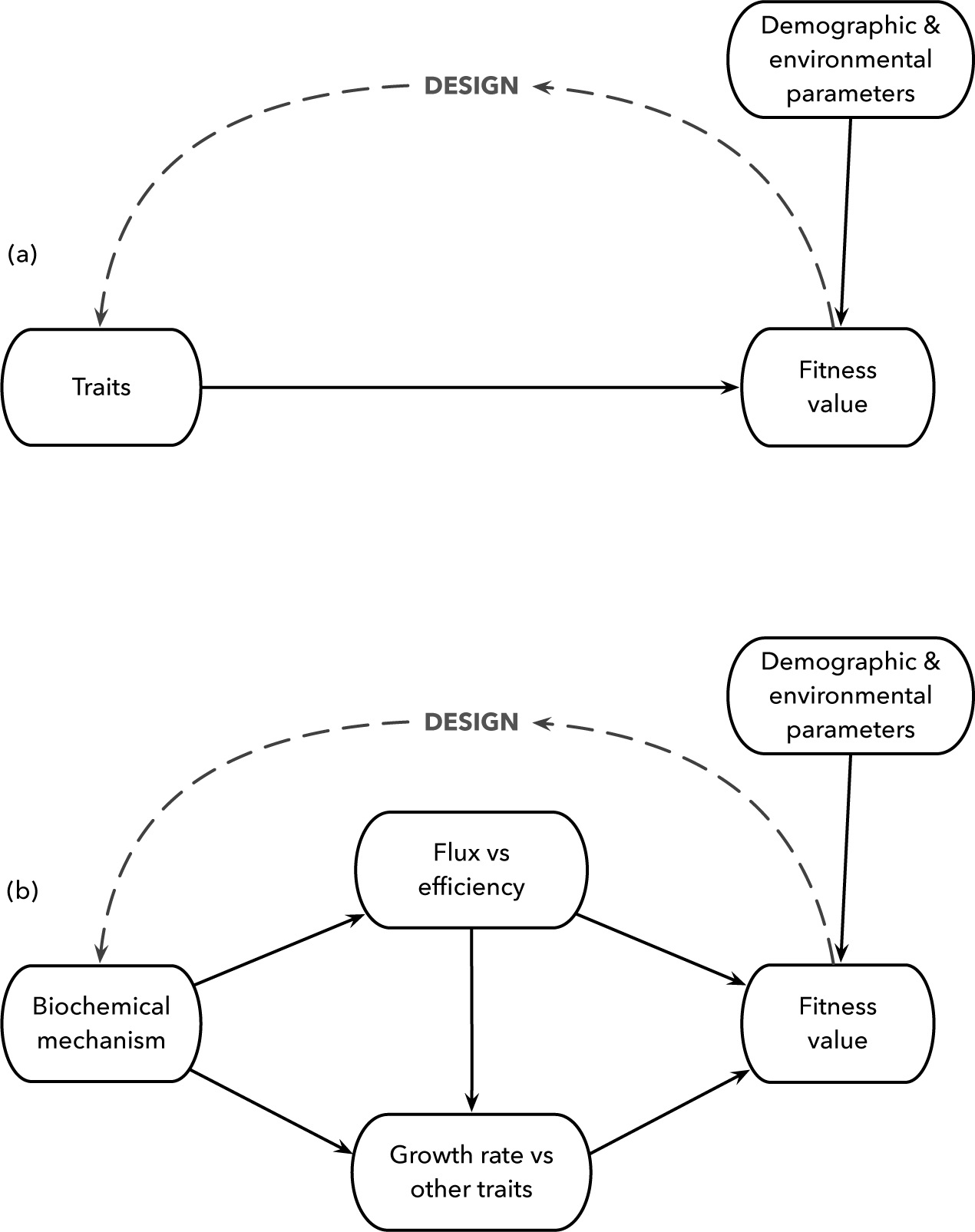
Figure 11.1 Relating mechanism to the study of organismal design. (a) The abstract problem and associated comparative predictions. Traits influence reproduction and fitness. Demographic and environmental parameters alter the fitness value of traits. Fitness value feeds back by natural selection to change traits over time, influencing organismal design. (b) For biochemical aspects of metabolism, we may consider particular mechanisms that influence trait expression and the associated tradeoffs that follow.
SHORT TIMESCALE
On short timescales, changing the metabolite concentrations alters the free energy driving force. When the initial driving force is weak, modest changes in metabolite concentrations can significantly increase the driving force. Greater driving force increases flux and reduces efficiency. Lower efficiency means greater dissipation of metabolic heat and less entropic driving force available to do beneficial work.
Lost benefits include storing less negative entropy in an ATP–ADP disequilibrium, building fewer useful molecules, or doing less physical work by molecular motors.
By contrast, altering metabolite concentrations to lower the driving force enhances efficiency, potentially providing more free energy to build molecules or do physical work. However, the extra usable free energy typically comes more slowly because low driving force associates with reduced reaction rate.
INTERMEDIATE TIMESCALE
On intermediate timescales, modifying enzymes alters the resistance against reactions. Organisms modify enzyme molecules by adding, removing, or changing small pieces. Such covalent modifications of existing enzymes can change their catalytic action. The catalytic change in reaction rate may increase or decrease resistance, providing a mechanism to control metabolic flux via reaction kinetics.
Cells often modulate reactions by covalent changes, catalyzed by widely deployed enzymes. Covalent changes may be faster and the costs of modification may be lower than controlling reaction resistance by building or destroying enzymes.
LONG TIMESCALE
On long timescales, synthesis and degradation change enzyme concentrations. More enzyme lowers resistance and increases flux. Enzymes may be complex molecules that are costly to build and slow to deploy.
For reactions with low driving force, significantly increasing net flux requires a large change in resistance and thus a large and costly change in enzyme concentration. When possible, changes in metabolite concentrations may be more effective and less costly.
For reactions with high driving force, small changes in enzyme concentration significantly alter net flux. That sensitivity to enzyme concentration allows rapid control of flux. However, the high driving force is metabolically inefficient, typically providing benefit only when conditions favor rapid flux.
Metabolite concentration and enzyme activity control force, resistance, and flux. Other mechanisms may affect flux. For example, the surrounding environment in which metabolites float influences entropy, diffusion, interference, and reactivity.86
Alternative control mechanisms have different consequences for flux and timescale of action. Costs and benefits arise from changes in flux, speed of adjustment, and thermodynamic efficiency.