Syntax. BETA.DIST(x;alpha;beta;cumulative;A;B)
Definition. This function returns the values of the cumulative beta distribution function. The beta distribution is usually used to examine the variance of processes across samples. For example, you can calculate the percentage of time people spend every day on their computers.
Arguments
x (required). The value between A and B at which to evaluate the function
alpha (required). A parameter of the distribution
beta (required). A parameter of the distribution
cumulative (required). The logical value that represents the type of the function
A (optional). The lower limit of the interval for x
B (optional). The upper limit of the interval for x
Note
If one of the arguments isn’t a numeric value, the BETA.DIST() function returns the #VALUE! error. If alpha or beta is less than or equal to 0, the BETA.DIST() function returns the #NUM! error.
If x is smaller than A or greater than B, or A equals B, the BETA.DIST() function returns the #NUM! error.
If you don’t enter values for A and B, the BETA.DIST() function uses the standard distribution, A = 0 and B = 1.
Background. BETA.DIST() calculates the probability of a value (x) given the beta distribution shape parameters (see Figure 12-10). The value x should lie between 0 and 1 unless upper and lower values are given. Either the probability or the cumulative probability will be returned.
See Also
You will find more information about beta distributions in the discussion of the BETA.INV()/BETAINV() function.
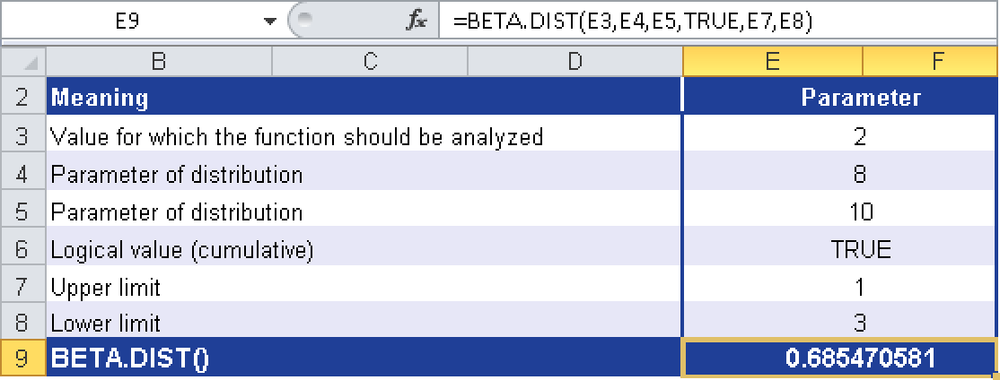
Example. To practice calculating BETA.DIST(), use the following values:
2 = the value at which to evaluate the function
8 = parameter of the distribution
10 = parameter of the distribution
TRUE = cumulative, the logical value of the function
1 = lower limit
3 = upper limit
Figure 12-11 shows the calculation of BETA.DIST().
The BETA.DIST() function is described by the shape parameters 8 and 10. In the range 1 to 3, what is the cumulative probability of a value of 2? The BETA.DIST() function returns a value of 0.68547.