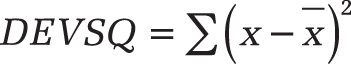DEVSQ()

Syntax. DEVSQ(number1,number2,...)

Definition. This function returns the sum of squares of deviations of data points from their sample mean.

Arguments

• number1 (required) and number2 (optional). At least one and up to 255 arguments (30 in Excel 2003 and earlier versions) for which you want to calculate the sum of squared deviations. You can also use a single array or a reference to an array instead of arguments separated by commas.

Note

Arguments can be numbers, array names, or references to cells containing numbers.

If an array or a reference argument contains text, logical values, or empty cells, those values are ignored. However, cells with the value 0 are included.

Background. In general, correlations between variables are defined by coefficients. Based on the regression calculation, you can also estimate models for interval-scaled variables. A model is the mathematical core of a theory. A model allows the prediction of the dependent variable based on the independent variable. In this way, linear correlations can be defined. This means that the higher the count of the x-values is, the higher (or lower) the y-values. The correlation x to y can also be illustrated with a straight line. More complex models are also possible.

The quality of the regression is usually described by r².

See Also

You will find more information about r² in the descrpiton of RSQ().

The average is the best y forecast value regarding the quality of the regression. The deviation from the average is also called forecast error. To calculate the average deviation, you can use the VAR.S() function.

The DEVSQ() function calculates the sum of the squared deviations from the sample mean. The equation for the sum of the squared deviation is:

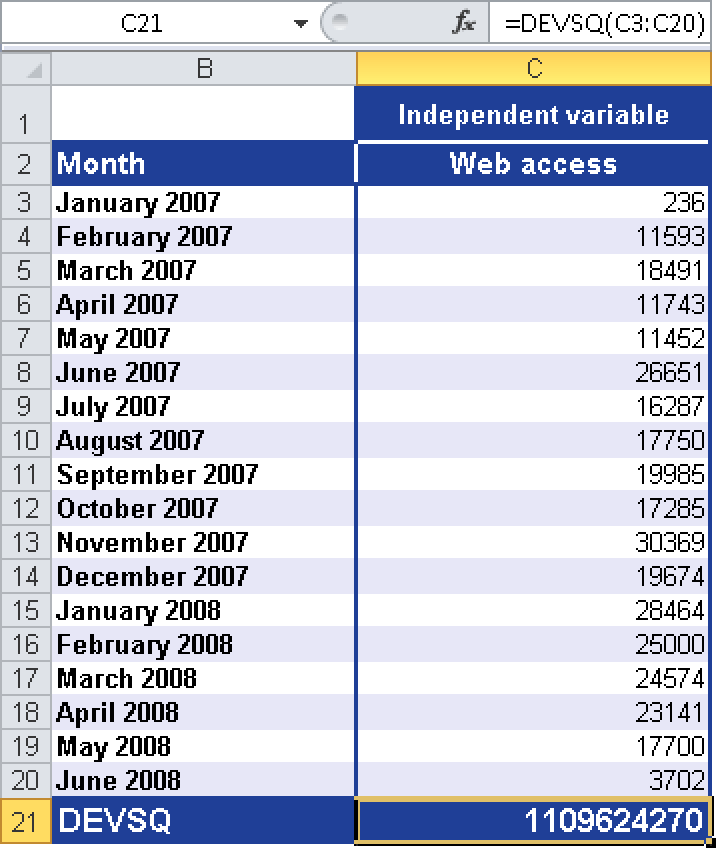
Example. You are still busy with analyzing the website and want to further calculate the correlation between the website visits and the online orders. You work on the website visits—the independent variable y. You want to calculate the sum of the squared deviations from the sample mean and use the DEVSQ() function. Figure 12-37 shows the solution.

Figure 12-37. The sum of the squared deviations from the sample mean.

The DEVSQ() function returns 1,109,624,270 for the website visits. This value matches the sum of the squared deviations from the sample mean.

See Also

AVEDEV(), STDEV.S(), STDEVP(), VAR.P(), VAR.S()

Sample Files

Use the DEVSQ worksheet in the Regression.xls or Regression.xlsx sample file. The sample files are found in the Chapter12 folder. For more information about the sample files, see the section titled Using the Sample Files.