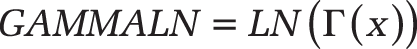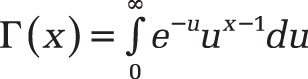Syntax. GAMMALN(x)
Definition. This function returns the natural logarithm of the gamma function (Γ(x)).
Arguments
x (required). The value for which you want to calculate GAMMALN()
Note
If x isn’t a numeric expression, the GAMMALN() function returns the #VALUE! error. If x is less than or equal to 0, the function returns the #NUM! error.
The number e raised to the GAMMALN(i) power, where i is an integer, returns the same result as (i – 1).
Background. The GAMMALN() function returns the natural logarithm of the gamma function.
See Also
You will find more information about gamma distributions in the description of GAMMA.DIST().
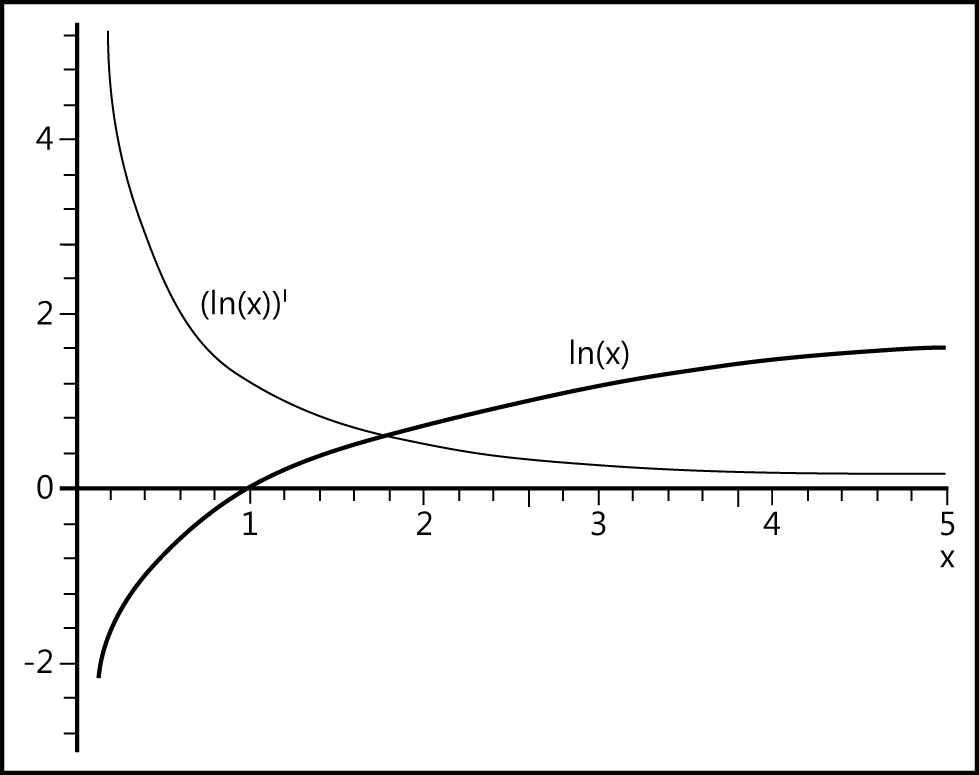
The logarithm of a number is the exponent by which a fixed number, the base, has to be raised to produce that number. The following logarithms exist:
Natural logarithm to base e (Euler’s number = 2.72)
Logarithm to base 10
Logarithm to base 2
The logarithm (to base b) of a number y is the number by which base b has to be raised to produce number y. Therefore, the logarithm is an exponent, and the logarithm function is the inverse function of the exponential function (see Figure 12-66).
GAMMALN() is calculated as follows:
where
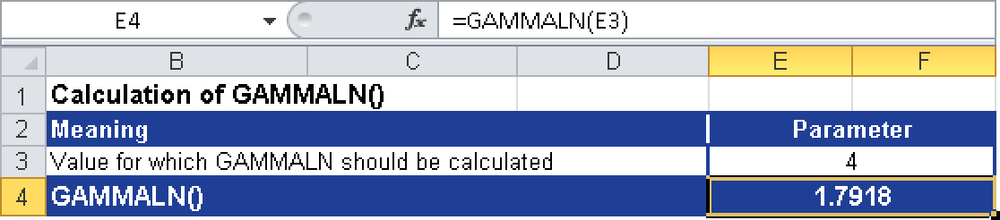
Example. Assume that you want to calculate GAMMALN() given the value 4. Figure 12-67 shows the calculation of GAMMALN().
The GAMMALN() function returns the natural logarithm, 1.7918, for the gamma function based on the parameters shown in Figure 12-67.