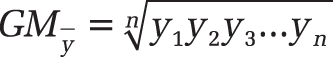Syntax. GEOMEAN(number1,number2,...)
Definition. This function returns the geometric mean of a set of positive numbers. For example, you can use GEOMEAN() to calculate the average growth rate for an interest calculation with variable rates.
The geometric mean is calculated as the n-th root from the product of all values where n is the number of values.
Arguments
number1 (required) and number2 (optional). At least one and up to 255 arguments (30 in Excel 2003 and earlier versions) for which you want to calculate the geometric mean. You can also use a single array or a reference to an array instead of arguments separated by commas.
Note
Arguments can be numbers, names, arrays, or references containing numbers.
If an array or a reference argument contains text, logical values, or empty cells, those values are ignored. However, cells with the value 0 are included. If one of the numbers is less than or equal to 0, the function returns the #NUM! error.
The equation for the geometric mean is:
Background. The geometric mean is mostly used for increase and decrease processes where the increase (or decrease) is not a fixed value but rather a percentage.
If you use the arithmetic average to examine a sales trend over a certain amount of time, the results won’t be sufficient. In this case, the geometric mean is the better choice.
Example. You are the executive manager of the controlling department of a software company and want to know whether sales have increased. If they have, you also want to know the average percentage of the sales increase.
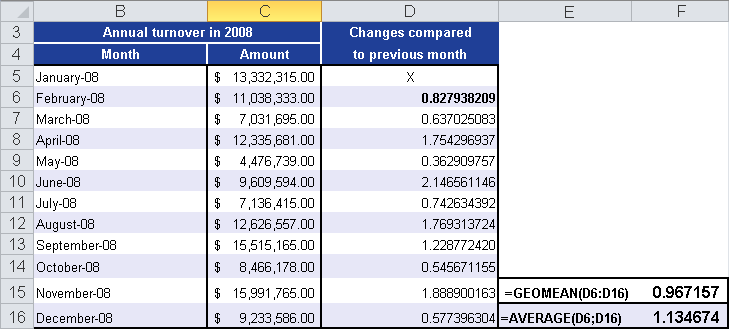
You use the GEOMEAN() function because the arithmetic average would return the wrong result, as shown in Figure 12-68.
First you calculate the monthly growth factor by dividing the monthly results by the results of the previous month. Then you calculate the geometric mean based on these results to get an average indicating the percentage of the sales of the previous month over the entire time period. The result is the average growth factor of the sales increase.
If you calculate the arithmetic average and the geometric mean, you get two results that don’t seem to be very different. The difference becomes clear if you try to derive a general definition from these values. The geometric mean indicates an average of 97 percent for the sales of the previous month since January 2008, and the arithmetic average shows an average of 113 percent. This means that there was no average increase but a decrease of 1 minus 0.967157.