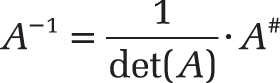Syntax. MINVERSE(array)
Definition. This function returns the inverse of an array.
Argument
array (required) A numeric array with an equal number of rows and columns
Background. Inverse arrays are generally used for solving equations involving several variables. For an array to be inverted, it has to be a square array. The array cannot be a singular array—that is, an array whose determinant ≠ 0 (see the description of the MDETERM() function earlier in this chapter).
The inverse of an array is indicated by –1 (array A becomes A–1). The equation Ax=b becomes x=A–1b.
The inverse can be calculated by using the following methods:
Gaussian elimination method The Gaussian elimination method is often used to manually calculate inverses. A detailed description is outside the scope of this book. You will find more information in specialist literature.
Cramer’s rule Cramer’s rule is interesting for theoretical purposes only because of its complexity. However, for dimensions <=3, you can use Cramer’s rule to quickly get a result. You will find more information in specialist literature.
The formula
This requires the determinant det(A) and the complementary array A#.
An array can be any of the following:
A cell range (such as A1:C3)
An array constant (such as {1.2.3;4.5.6;7.8.9}
A name for the cell range or the array constant
If the cells in the array are empty or contain text, the MINVERSE() function returns the #VALUE! error. If the array does not have an equal number of rows and columns, the MINVERSE() function returns the #VALUE! error.
Because MINVERSE() returns an array, the formula has to be entered as array formula (with Ctrl+Shift+Enter).
MINVERSE() is calculated with an accuracy of approximately 16 digits, which may lead to a small numeric error when the rounding is not accurate.
Some square arrays cannot be inverted, in which case MINVERSE() returns the #NUM! error. The determinant for a noninvertable matrix is zero.
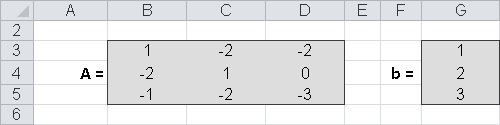
Example. Figure 16-16 shows the variables for the following equation:
Ax = b
Solution:
Change the formula: x = A–1b
Check whether the equation can be solved. To do so, use the MDETERM() function to calculate the determinant for array A. If the determinant is not equal to zero, the equation can be solved.
The formula for the determinant is:
=MDETERM(B3:D5).Result: The determinant of A is –1.
Because the determinant of A is not equal to zero, there is a solution for array A.
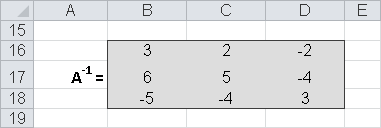
Calculate of the inverse element of A = A–1
To do this, you specify the following array formula for array A (see Figure 16-17) in the cell range (B9:D11):
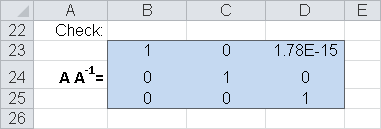
{=MINVERSE(B3:D5}.Check that the inverse array is correct. Do so by multiplying A by A–1. The formula is:
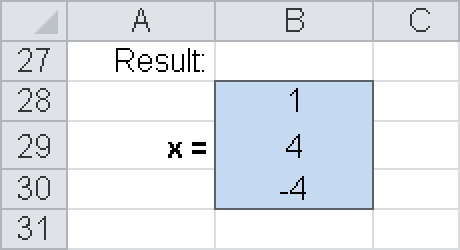
{=MMULT(B3:D5;B9:D11)}.The result has to be an unit array (see Figure 16-18).Finally, A–1 is multiplied by b. The formula is
{=MMULT(B9:D11;G3:G5)}and the result is x (see Figure 16-19).