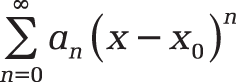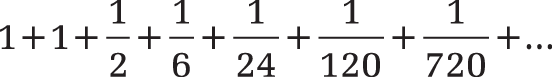Syntax. SERIESSUM(x,n,m,coefficients)
Definition. SERIESSUM(x,n,m,{a1,a2,a3,a4,...,ak}) returns the sum of a power series:
y = a1xn + a2xn+m + a3xn+2m + a4xn+3m +...+ akxn+km
The number of values in coefficients determines the number of terms in the power series.
Arguments
x (required) The value of the independent variable for the power series.
n (required) The power of x in the first term.
m (required) The increment for n.
coefficients (required) An array of coefficients of the power series. The number of values in coefficients determines the number of terms in the power series. For example, if there are three values in coefficients, then there will be three terms in the power series.
Background. A power series is an infinite series in the form:
an (where 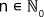 ) is any series of real or complex numbers. The value x0 is the expansion point of the power series.
) is any series of real or complex numbers. The value x0 is the expansion point of the power series.
Examples. Many functions can be approximated by using the expansion point of the power series. The accuracy of the result depends on the number of terms in the power series: the more terms, the more accurate the result.
Example 1
=SERIESSUM(1,0,1,{1,1,0.5,0.16666667,0.04166667,0,00833333,0.00019841})returns 2.71686508. This function uses:
x = 1
n = 0
m = 1
a1 = 1
a2 = 1
a3 = 0.5 =1/2!
a4 = 0.16666667 = 1/3!
a5 = 0.04166667 = 1/4!
a6 = 0.00833333 = 1/5!
a7 = 0.00019841 = 1/6!
These are the first seven terms in the series:
to calculate Euler’s number e.
Example 2
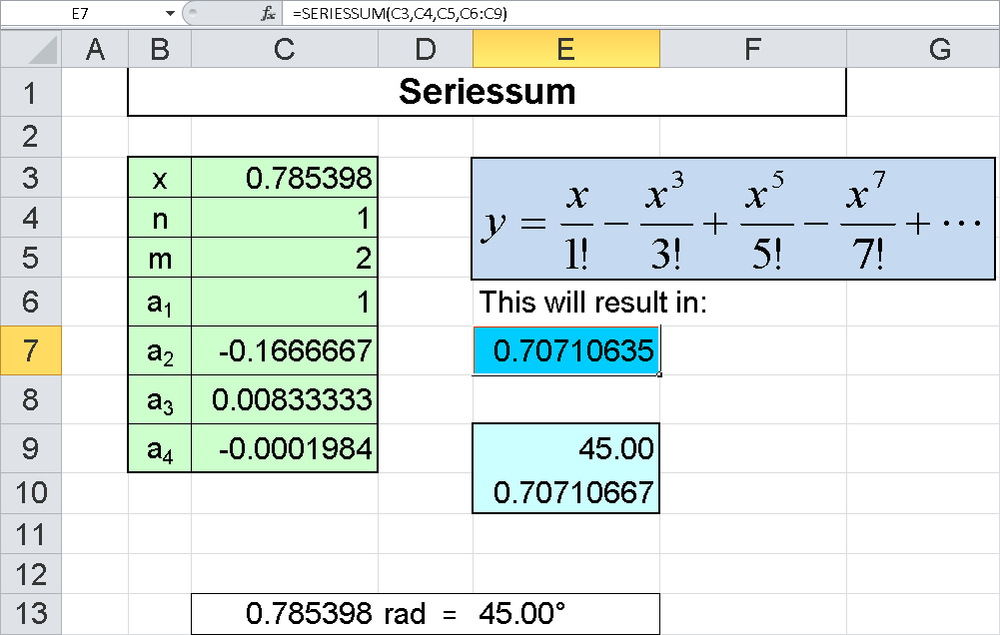
This example evaluates the power series shown in Figure 16-24.
Cell E7 contains the result returned by the function based on the specified arguments in the range B3:C9.
Cell E9 contains the formula
=DEGREES(B3)
which converts x in B3 to degrees (45°). Therefore, B3 has to contain a radian measure. Cell D10 contains the formula
=SIN(B3)
which calculates the sine based on 45°. The result matches the value returned by the SERIESSUM() function up to six decimal places.