This section introduces two mathematical functions that work like switches. Unlike most of the Excel functions (such as sine), which deliver a result value from an original value with no surprises, the saltus functions recognize only two result values: 0 and 1. Depending on the amount of the original value, they toggle between 0 and 1. The DELTA() function only recognizes one instance for which it returns 1. Otherwise, it always returns 0. The GESTEP() function, however, continuously toggles between 0 and 1, when the original value reaches or crosses a fixed minimum (a threshold).
The Dirac delta function δ(x) is the mathematical ancestor of these Excel functions. Like the two Excel functions, it belongs to the saltus functions. The saltus functions as they are taught in mathematics change their result value at a certain location (or at several locations) without transition by jumping, and are therefore not continuous at this location.
The definition range of the Dirac delta function spans from x = –∞ to x = +∞, and at the location x = 0 it becomes infinite (not 1!). It is used, for example, in mechanics and electricity to represent momentary impulses.
Syntax. DELTA(Number1,Number2)
Definition. The DELTA() function checks whether two numbers are equal. The function returns 1 if Number1 and Number2 are exactly the same; otherwise it returns 0 (zero).
Arguments
Number1 (required) and Number2 (optional) Any two real numbers. If the argument Number2 is omitted, it is assumed to be zero.
Background. If the second (optional) argument for this function is omitted or is set to equal 0, you have almost the direct equivalent of the Dirac delta function: The DELTA() function returns for every value of Number1 the value 0, but when Number1 is 0, it returns the value 1. Actually, this last value should not be 1 but ∞ (infinity) instead. However, because calculation systems cannot display the value ∞, programmers have set the value 1 as the result value of this function (see also the introduction for the Saltus functions in Functions for Higher Mathematics).
It does the same as the IF() function when that function is written as follows:
IF(Number1=Number2,1,0)
The advantages of the DELTA() function over the IF() function are a simpler syntax, better overview, and faster execution speed.
Examples. You can use this function to filter a group of values. For example, you can use addition with several DELTA() functions to calculate how many equal number pairs you have.
Example 1. =DELTA(A1,C3) returns 1 if the contents of the cells A1 and C3 are equal; otherwise it returns 0.
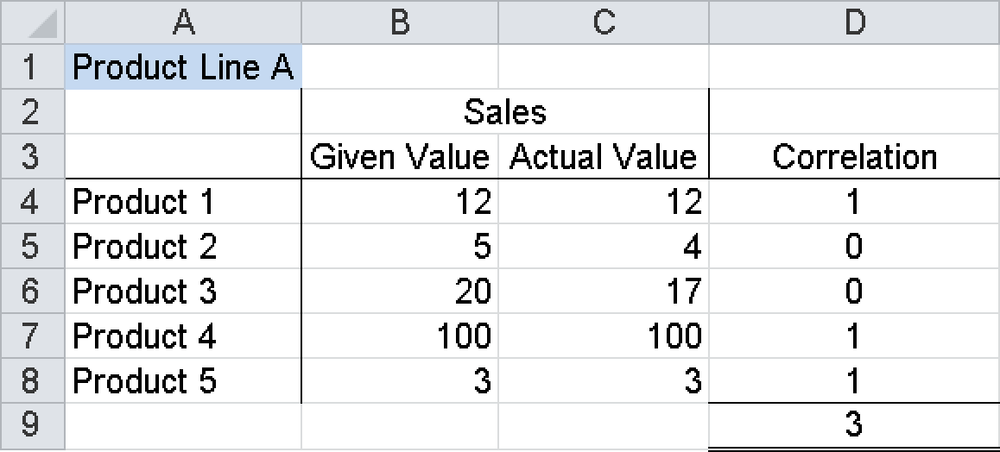
Example 2. A completely finished and packed assortment must consist of five products, each with a different and sometimes varying number of pieces. In addition, the packaging progress of the assortment must be displayed in a clear format in an Excel table. The accordance between nominal and current value can be done easily with the DELTA() function. In the Excel worksheet in Figure 17-19, you get only the value 5 (the number of the different products in the assortment) in cell D9 when all nominal and current values are identical.
You would have reached a similar result with the function GESTEP(), shown in GESTEP(). The disadvantage of that function, however, would be that an overcompliance could not be distinguished, whereas with the DELTA() function you could account for this situation. For example, if you change the value in cell C4 in the worksheet in Figure 17-19 from 12 to 13, the result of the DELTA() function in cell D4 will also be changed to 0.
Note
When looking at this simple example, one might get the idea that using the DELTA() function is superfluous, because upon entering the values it is easy to see at first glance whether the match has been achieved. However, in everyday professional life it is rare that data entry and data evaluation fall on the same location, date, and time. The values in cells B4 through C8 could easily have been linked to this table from other Excel workbooks (perhaps over a network). The person who enters the data is not necessarily the one who has to evaluate it. Therefore, the DELTA() function highlights the deciding factor for the user of the worksheet. (Beyond that, imagine processing the data for 30,000 products.)
Syntax. GESTEP(Number,Step)
Definition. GESTEP() returns the value 1 if the argument Number is greater than or equal to the argument Step; otherwise it returns 0 (zero).
Arguments
Number (required) The value to be checked against Step.
Step (optional) The threshold value. If no value is specified for Step, GESTEP() works with zero.
Background. You can use this function to filter a group of values. For example, you can add several GESTEP() functions to calculate how many values are larger than a threshold value. (See also the introduction to the Saltus functions in Functions for Complex Numbers.)
This function does the same as the IF() function, when that function is written as follows:
=IF(Number>=Step,1,0)
The advantages of the GESTEP() function over the IF() function are a simpler syntax, better overview, and faster execution speed.
Examples. The following examples illustrate GESTEP().
Example 1
=GESTEP(2,5)returns0.=GESTEP(5,5)returns1.=GESTEP(8,5)returns1.
Example 2. A school class enters into a sporting competition for the long jump (see Figure 17-20). The coach wants to know which jumps reach or surpass a certain minimum. The range E6:G16 contains the formulas that use the GESTEP() function to compare the respective jump length in the range B6:D16 to the given minimum of 3.80 yd in cell E5 (named minJump).