. 4 .
È una bella giornata estiva. Passeggiamo tranquilli lungo un sentiero di montagna quando un paesaggio particolarmente suggestivo attira la nostra attenzione. Ci togliamo dal collo la macchina fotografica e la puntiamo su un vecchio albero frondoso dietro il quale appare un monte con un bel picco bianco.
L’obiettivo luminosissimo che ci siamo appena regalati – un 50 mm, f/14 – sembra perfetto. Riusciamo a vedere con nitidezza tutti i soggetti inquadrati nel mirino: l’albero con i rami annodati in primo piano e la montagna innevata sullo sfondo. Siccome è una bella giornata soleggiata impostiamo la velocità di scatto a 1/500, anzi a 1/1000 per essere più sicuri. Premiamo il pulsante e proseguiamo contenti.
Ora il sentiero sale ripido e tortuoso. Ehi, e quello cos’è? Uno stambecco! Il magnifico animale salta allegro di roccia in roccia a pochi metri da noi. Peccato che una nuvola abbia coperto il sole. Ma non ci perdiamo d’animo; con la macchina sempre carica riduciamo la velocità dell’otturatore a 1/60 di secondo e scattiamo una decina di foto. Almeno una verrà! Sorridendo al pensiero di quando le mostreremo ad amici e parenti, riprendiamo a camminare sereni come scoiattoli.
Dopo qualche giorno andiamo a ritirare le foto stampate. Con trepidazione apriamo la busta e… il sorriso sulle labbra si distorce in una smorfia di dolore; gli occhi prima si spalancano, poi si appannano, mentre un leggero tremito affiora alle nostre narici.
I paesaggi appaiono tutti sfocati. In alcuni la montagna risulta coperta da una macchia che potrebbe essere l’albero, in altri si notano addirittura i dettagli delle foglie, ma sembra che dietro all’albero qualcuno abbia steso un telone marrone. E lo stambecco? La sua presenza è testimoniata solo da una striscia indistinguibile che attraversa tutte le foto. Eppure l’esposizione e i colori sono perfetti…
Seguitiamo a girare e rigirare tra le mani le stampe, decisi a riportare indietro quel dannato obiettivo, sicuramente responsabile di cotanto scempio, mentre le nostre lacrime sbiadiscono gli azzurri del cielo e il verde dei prati.
L’ottica è la branca della fisica che studia i fenomeni luminosi e che, quindi, si occupa essenzialmente di raggi solari, di lampade, di specchi, di lenti e di occhi. Tutti questi argomenti possono essere affrontati da diversi punti di vista, in funzione dell’aspetto che maggiormente si desidera mettere in evidenza. In particolare, esistono tre diversi approcci teorici allo studio della luce:
La teoria elettromagnetica della luce, elaborata dallo scienziato scozzese James Clerk Maxwell nella seconda metà dell’Ottocento, è uno dei grandi monumenti della fisica moderna. È una teoria complessa e completa, in grado di spiegare in modo rigoroso ed estremamente preciso quasi tutti i fenomeni luminosi che si possono osservare in natura. Per comprendere la gran parte delle manifestazioni ottiche più comuni, tuttavia, non è necessario ricorrere ai suoi sofisticati strumenti. Perciò in questo capitolo utilizzeremo le approssimazioni offerte dall’ottica geometrica e ondulatoria, rimandando al capitolo 6 i doverosi approfondimenti dedicati alla vera natura della luce.
Per il momento è sufficiente sapere che è la stessa natura dei raggi infrarossi, di quelli ultravioletti, delle onde radio, dei raggi X e gamma: come loro, infatti, la luce visibile è composta da radiazioni elettromagnetiche, onde periodiche che si propagano anche nel vuoto. L’unica cosa che distingue la luce visibile dalle altre onde elettromagnetiche è il fatto che i nostri occhi sono in grado di percepirla.
Come abbiamo osservato nel capitolo dedicato al suono, le onde periodiche si caratterizzano in base alla loro frequenza. Le radiazioni elettromagnetiche, in particolare, hanno frequenze che vanno dalle poche migliaia di hertz delle onde radio più lunghe fino ai miliardi di miliardi di hertz (e oltre) dei raggi gamma. All’interno di questo amplissimo spettro elettromagnetico, tuttavia, l’occhio umano è sensibile solo alle onde con frequenze comprese all’incirca tra 400.000 e 800.000 GHz (si legge gigahertz e vale un miliardo di hertz). Questa è la luce visibile, una minuscola finestra di frequenze elettromagnetiche attraverso cui scrutiamo il mondo. A ciascuna frequenza visibile corrisponde un colore, e la luce che vediamo comunemente – quella che proviene da sorgenti naturali come il Sole o artificiali come le lampadine – è una miscela di queste radiazioni, cioè di questi colori. Ma non tutti gli occhi sono uguali, come vedremo nel paragrafo 4.6.
A differenza della teoria elettromagnetica della luce, l’ottica geometrica non si basa su un’interpretazione fisica della reale natura della luce. È invece un insieme di semplici leggi matematiche che riescono a spiegare egregiamente i fenomeni ottici più comuni.
Queste leggi sono governate da quattro assunti fondamentali:
Per facilitare i ragionamenti e consentire un’interpretazione chiara e convincente dei fenomeni legati alla propagazione della luce, in ottica geometrica si considera un raggio luminoso come una linea retta. Possiamo pensare a un binario rettilineo, che parte da una stazione e termina chissà dove.
Vediamo gli oggetti che ci circondano perché questi emettono in ogni direzione una parte della luce che li colpisce. D’altro canto, se un oggetto si trova dove lo vediamo, è perché la luce che emette arriva a noi seguendo un cammino rettilineo. Per afferrare un libro da uno scaffale, allunghiamo la mano seguendo una linea ipotetica che va dal libro ai nostri occhi (il cervello apporta poi le dovute correzioni dovute al fatto che la mano non è alla stessa altezza degli occhi): questa linea altro non è che il raggio luminoso.
Proviamo a pensare a che cosa potrebbe succedere se la luce non si propagasse in modo rettilineo. In un bar, ad esempio, inzupperemmo la brioche nel cappuccino della signora a fianco oppure rischieremmo di infilare il cucchiaino nell’occhio del barista invece che nella zuccheriera.
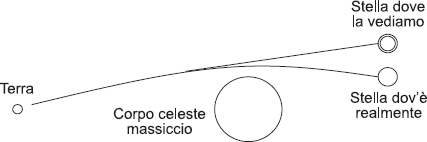
«Ma se l’ottica geometrica è un’approssimazione matematica, significa che in realtà le cose non vanno proprio così. O no?» potrebbe obiettare qualcuno. E in effetti questa persona avrebbe proprio ragione. Ma continuando a semplificare, possiamo affermare che la luce non si propaga in maniera rigorosamente rettilinea perché, essendo costituita da particelle elementari di energia, è soggetta a fenomeni gravitazionali. Ciò vuol dire che quando i raggi luminosi emessi da una stella passano vicino a un altro corpo celeste ne vengono attirati come pagliuzze di ferro da una calamita. Più è grande la massa di questo corpo, più i raggi luminosi si incurvano (fino al paradosso che, se la luce viene attratta da un buco nero, vi entra per non uscirvi più).
Sorvolando sulle potenziali implicazioni filosofiche, potremmo affermare che nello spazio le cose non sono là dove effettivamente le vediamo. Nella vita quotidiana, però, dove abbiamo a che fare con dimensioni e masse molto meno astronomiche, questo aspetto può essere benissimo ignorato.

Fig. 4.1 La forza di gravità incurva i raggi luminosi.
Un’altra importante ipotesi su cui si basa l’ottica geometrica è l’indipendenza dei raggi luminosi: quando due o più raggi vengono a contatto non subiscono alcuna alterazione fisica, né di traiettoria né di intensità. Per verificarlo è sufficiente munirsi di due torce elettriche e intrecciare i fasci emessi. Noteremo subito che… non succede niente. Questa, che a prima vista potrebbe sembrare una grossa banalità, si traduce in un errore scientifico quando si analizza il fenomeno a livello microscopico, come vedremo nel paragrafo dedicato alla diffrazione.
L’ipotesi dell’indipendenza dei raggi di luce ha però permesso agli scienziati di interpretare fenomeni ottici come la riflessione o la rifrazione senza che le approssimazioni introdotte generassero errori significativi.
Le regole del biliardo non sono difficili: o si manda in buca la propria biglia, oppure si prova a colpire la biglia avversaria affinché vada sui birilli a fare punti. Nonostante ciò, padroneggiare il gioco è tutt’altro che semplice. Come sanno bene gli esperti, la strategia di un bravo giocatore consiste nell’impedire che l’avversario riesca a colpire direttamente le biglie (ovvero nell’«impallarlo», come si dice in gergo). Di conseguenza, capita spesso di dover sfruttare i rimbalzi sulle sponde. Per questo è fondamentale sapere che, se si colpisce la biglia senza imprimerle effetti particolari, essa si comporterà in base a una legge molto semplice, una legge geometrica schematizzata nella figura 4.2: rispetto alla retta perpendicolare al piano della sponda (detta anche retta normale), l’angolo formato dalla traiettoria con cui la palla giungerà sulla sponda (αi) sarà sempre uguale all’angolo formato dalla traiettoria con cui la palla sarà respinta dalla sponda (αr).
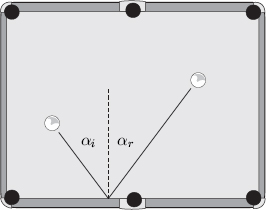
Fig. 4.2 La legge della riflessione si applica al biliardo e ai raggi luminosi.
Un fenomeno analogo accade quando la luce viene riflessa da un corpo la cui superficie è liscia e lucida come quella di uno specchio. In questo caso si può affermare che l’angolo compreso tra il raggio incidente e la normale alla superficie riflettente ha la medesima ampiezza di quello compreso tra la normale e il raggio riflesso. In termini più sintetici, l’angolo di incidenza è uguale all’ angolo di riflessione:

Ovviamente, se la traiettoria del raggio incidente coincide con la normale alla superficie, anche la traiettoria del raggio riflesso coinciderà con questa (dato che i due angoli di incidenza e di riflessione risultano nulli: 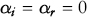 ).
).
È grazie ai fenomeni della riflessione e della propagazione rettilinea della luce che la mattina riusciamo a pettinarci. I raggi luminosi che provengono dal nostro viso colpiscono lo specchio e ritornano indietro verso i nostri occhi, dandoci l’impressione di avere davanti a noi una persona che ci somiglia moltissimo. Moltissimo, ma non completamente. A ben guardare, in effetti, presenta una simmetria destra-sinistra opposta rispetto alla nostra (basta vedere che non tiene il pettine con la stessa mano con cui lo teniamo noi!). Ciò significa, tra l’altro, che specchiandoci non riusciamo mai a vederci come siamo realmente o, meglio, come ci vedono gli altri.
Occorre comunque sottolineare che il motivo per cui riusciamo a specchiarci è dovuto a un insieme di fattori concomitanti.
Fig. 4.3 Se la luce si propagasse lungo un’unica direzione, potremmo vedere soltanto i nostri occhi riflessi nello specchio.
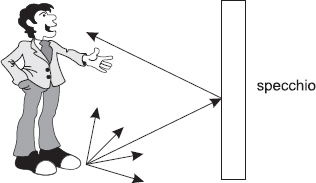
Fig. 4.4 Poiché la luce si propaga in tutte le direzioni, nello specchio riusciamo a vedere la nostra figura intera.
Naturalmente non tutti i corpi riflettono la luce come fanno gli specchi; alcuni, quelli che chiamiamo trasparenti, si fanno attraversare dai raggi luminosi, mentre altri assorbono tutta la luce che li colpisce e per questo ci appaiono neri. Ma la grande maggioranza dei corpi interagisce con la luce incidente in maniera molto più complessa, restituendoci l’immagine di un mondo dotato di infiniti colori, gradi di lucentezza e sfumature. Tra i vari fenomeni ottici che producono questa varietà, uno dei più importanti è la diffusione della luce.
La campagna è gialla di grano. Sul limitare del campo un bambino seduto su un covone guarda pensieroso la falce impugnata dal padre. Ogni volta che sibila roteando tra le spighe recise e svolazzanti, la sua lama scintilla nella luce del sole calante. Il padre si ferma per tergere il sudore dalla fronte. Poggia le mani sul manico di legno e si rivolge al bimbo, che sembra preoccupato e nello stesso tempo divertito.
« Ehilà, Giacomino. Che ti succede? Vuoi dare uno mano a tuo padre? Dai che non si fatica tanto…»
«Laggiù, dove tramonta il sole. Guarda papà…»
«Bello, eh? Che rosso stasera! »
«È troppo rosso papà. Dopodomani piove».
«Ma guarda Giacomino che il nonno dice sempre rosso di sera bel tempo si spera… non lo sai? »
« No, papà. Le cose sono diverse da come le racconta il nonno. È troppo rosso. È per la diffusione della luce. Ce l’ha detto il maestro» risponde Giacomino agitando il dito avanti e indietro.
«Ma dai, Giacomino… vuoi dire che adesso mi vieni a spiegare pure come fa il cielo a essere blu, le nuvole bianche e il tramonto rosso? »
«Perché, non lo sai?» ridacchia il bambino guardando con divertimento il padre che si rimette al lavoro di buona lena.
«Giacomino, cosa vuoi che ne sappia? È rosso perché deve essere rosso. Se il tramonto fosse blu sarebbe… sbagliato. È sempre stato così». Il padre continua a falciare, poi si ferma e, memore della soluzione trovata dal figlio al problema delle uova mischiate, accosta la falce al carro. «E va bene. Stiamo a sentire anche ’sta lezioncina» dice con un bel sorriso stampato sul volto abbronzato e le mani sui fianchi.
« Allora, devi sapere che l’aria è composta da tante particelle. Alcune sono piccoline e altre sono più grandi. Per esempio, la polvere e la sabbia sono fatte da corpuscoli molto più grandi delle molecole di aria e la luce…» Giacomino, ormai in piedi sul covone, rallenta il ritmo perché il padre ha cominciato ad aprire la bocca per lo sconcerto.
«E la luce? Dai Giacomino, che fa notte».
«E la luce puoi fare finta che è un’onda, anzi, è fatta da un mucchio di onde con lunghezze diverse. Ci sono le onde blu che sono le più corte, quelle rosse che sono le più lunghe, e quelle gialle e verdi che stanno in mezzo… Mi sono spiegato, papà? »
«Dai che vai forte Giacomino» dice orgoglioso il padre. «Ho capito quasi tutto. Continua».
«Dunque. Fammi ricordare… Ah, ecco. La luce si riflette, come fa adesso sulla falce, e si rifrange, come quando passa dentro quel secchio d’acqua. Allora, quello che succede è che tutte quelle particelle che stanno nell’aria, le molecole e le polveri, un po’ la riflettono e un po’ la rifrangono. Chiaro? »
Il padre tira fuori il fazzolettone a quadri e se lo passa sulla fronte. Con calma lo ripiega e fa un cenno al figlio che prosegue.
«Il maestro dice che questo fenomeno si chiama diffusione. Il punto è che questa diffusione dipende dal colore della luce. Ricordati che dire colore è come dire lunghezza dell’onda luminosa».
« Va bene, me lo ricordo. Luce blu, onda corta. Luce rossa, onda lunga».
« Esatto. Se le particelle dell’aria sono piccoline, la diffusione avviene per la luce di colore blu. Se le particelle sono un po’ più grandi, la diffusione maggiore accade per la luce rossa. Quando invece le particelle sono abbastanza grandi, come le goccioline che formano le nuvole, tutti i colori sono diffusi nello stesso modo e la luce è bianca».
«Aspetta un attimo! Vuoi dire che quando l’aria è tersa, senza nebbia né polvere, la luce blu è quella più diffusa ed è per questo che il cielo è blu? »
«Bravo papà. Ed è sempre per questo che quando il sole è basso sull’orizzonte il cielo diventa rosso. Perché i raggi del sole attraversano una maggiore quantità di aria e quasi tutta la luce blu viene diffusa prima di raggiungere i nostri occhi, mentre quella rossa riesce a passare senza troppi disturbi ».
«Ho capito. Quindi se il tramonto è troppo rosso…»
« Ci sei arrivato, papà. Se il tramonto è troppo rosso vuol dire che si è alzato un sacco di polvere da quella parte, e che riesce a passare e a essere diffusa solo la luce più rossa».
« E allora meno male che abbiamo ancora un giorno per falciare, Giacomino. Se ho capito bene, laggiù dove tramonta il sole il vento sta alzando un gran polverone. Il tramonto infatti stasera è troppo rosso. Magari domani sarà ancora bello, ma dopo… chissà. Magari hai ragione tu».
Avrete sicuramente notato che un cucchiaino immerso in un bicchiere pieno d’acqua appare diviso in due (vedi la figura 4.5). Se poi aggiungete dello zucchero all’acqua, il cucchiaino sembrerà ancora più spezzato.
Questo curioso effetto è dovuto al fatto che la direzione con cui si propaga la luce all’interno di un mezzo trasparente (come l’aria o l’acqua) dipende dalla materia di cui il mezzo è costituito. Di conseguenza, quando un raggio luminoso passa da un mezzo a un altro di diversa consistenza, il suo percorso subisce una deviazione in corrispondenza della superficie che separa i due mezzi.
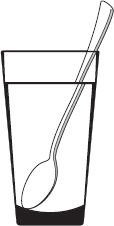
Fig. 4.5 Quando si immerge un cucchiaino in un bicchiere d’acqua, la rifrazione ne spezza l’immagine.
Un tale comportamento, detto rifrazione della luce, sembrerebbe mettere in crisi quanto abbiamo detto fino a ora sulla propagazione rettilinea dei raggi luminosi. E infatti questa riflessione la fecero anche molti fisici. Analizzando il fenomeno con accuratezza, René Descartes (lo stesso degli assi cartesiani, ricordate?) si accorse che esso si manifesta in base a delle regole precise.
In particolare, Descartes notò che il rapporto tra i valori di una particolare funzione dei due diversi angoli che il raggio incidente (αi nella figura 4.6) e quello rifratto (αn) formano con la retta perpendicolare al piano di separazione è uguale a un valore costante che dipende dalla natura dei due mezzi in cui la luce si propaga.

Tale costante è denominata indice di rifrazione del secondo mezzo rispetto al primo e venne formalizzata da Descartes con la pubblicazione, nel 1637, di un saggio sulla natura della luce intitolato La diottrica, che significa proprio studio della rifrazione della luce.
L’indice di rifrazione n relativo a due mezzi trasparenti può essere determinato conoscendo le proprietà ottiche di ciascuno dei due mezzi. Se l’angolo di rifrazione αn è minore di quello di incidenza αi, si dice che il secondo mezzo (nel nostro caso, l’acqua) è più rifrangente del primo (nel nostro caso, l’aria).
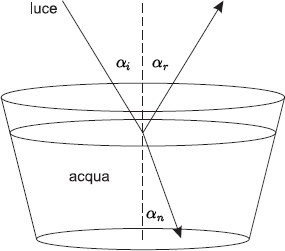
Fig. 4.6 In corrispondenza della superficie di separazione tra due mezzi trasparenti, un raggio luminoso subisce una deviazione che si può esprimere come il rapporto tra l’angolo di incidenza αi e quello di rifrazione αn.
In generale i mezzi più densi sono anche più rifrangenti. La tabella 4.1 riporta gli indici di rifrazione per alcune sostanze rispetto al vuoto, posto quello del vuoto uguale a 1. Come si può vedere, gli indici di rifrazione dei gas sono molto vicini all’unità, mentre quelli dei liquidi e dei solidi variano da 1,3 a oltre 2.
Una simpatica applicazione della legge della rifrazione è un vecchio trucco che si faceva a scuola, ma che si può riesumare quando una serata tra amici langue. Il successo è assicurato.
Per andare al cinema è ormai tardi. Un gioco di società? Siamo troppo stanchi per «Il paroliere» e troppo poco fisionomisti per « Indovina chi ». Di accendere la televisione per imbatterci nell’ennesimo, noiosissimo quiz non se ne parla neppure. Che cosa c’è di meglio, allora, di una sana e innocente scommessa?
Chiedete a qualcuno di scrivere una parola su un foglio, di metterlo sul tavolo di fronte a voi (senza che possiate leggerlo, naturalmente) e di appoggiarci sopra un bicchiere vuoto. Poi lanciate la sfida: «Scommettiamo che riesco a leggere quello che avete scritto senza muovermi da questa poltrona e senza farmelo suggerire da qualcuno? »
Tabella 4.1
| Sostanza | Indice di rifrazione |
| Idrogeno | 1,0001 |
| Aria | 1,0003 |
| Ghiaccio | 1,31 |
| Acqua | 1,33 |
| Alcol etilico | 1,36 |
| Olio d’oliva | 1,45 |
| Vetro comune | 1,52 |
| Zucchero | 1,54 |
| Diamante | 2,42 |
Se nessuno accetta la scommessa andate a casa e cambiate compagnia. Ma nel caso contrario pregate un amico di versare lentamente dell’acqua nel bicchiere. Che cosa succede? Quando nel bicchiere c’è l’acqua, i raggi riflessi dalla scritta subiscono una deviazione dovuta, come abbiamo appena visto, alla rifrazione nel passaggio acqua-aria. Grazie a questa deviazione, alcuni raggi che prima non giungevano ai nostri occhi ora ci permettono di leggere la parola e di incassare la posta della scommessa.
C’è un bel film del 1933, tratto da un romanzo di H.G. Wells, nel quale il solito scienziato matto si iniettava un siero che aveva la proprietà di renderlo invisibile.
Tra le nebbie nicotiniche di un’auletta di fisica spesso fra gli studenti si accendevano, oltre a quantità inverosimili di sigarette, interminabili e dotte dissertazioni: Come fa l’Enterprise a viaggiare a velocità maggiori di quelle della luce? Si arriverà mai a costruire un computer come Hal 9000? Sono possibili i viaggi nel tempo? Come diavolo faceva l’Uomo Invisibile a essere invisibile?
Su quest’ultima questione, avendo tutti visto più volte il film, dibattemmo a lungo e concludemmo che l’unica spiegazione intelligente poteva essere la seguente.
Per essere effettivamente invisibile, l’Uomo Invisibile doveva avere un indice di rifrazione uguale a quello dell’aria, in modo che i raggi luminosi che provenivano, ad esempio, dal muro dove era appoggiato, non fossero né assorbiti né rifratti. Infatti, se tale indice fosse stato superiore a 1 (quello dell’aria, appunto), si sarebbe prodotta una rifrazione dei raggi, con un effetto di distorsione ottica.
«Ecco perché ogni tanto nel film si vedevano delle immagini tremolanti!» ridacchiò alla fine qualcuno, rischiando di essere picchiato.

Foto dell’uomo invisibile
Scena: interno, giorno.
Il Lettore è seduto. Tiene in grembo un libro. Sembra immerso nella lettura.
Lettore: «In fondo in fondo, non è malaccio questo capitolo sull’ottica. Ma quando arriva un bell’esperimento? D’accordo gli specchi e i cucchiaini nell’acqua. Però son tutte cose che già sapevo. Vorrei qualcosa di un po’ più originale, qualcosa di stimolante… E se provassi io?»
Il Lettore si alza, prende una torcia elettrica e una sottile lastra di plastica scura al centro della quale c’è un minuscolo forellino.
Lettore: «Dunque, vediamo. Se punto la torcia elettrica su questo forellino, considerato che la luce si propaga in linea retta, su quella parete lontana dovrei vedere proiettata la sagoma del buco, una macchiolina chiara che dovrebbe avere le sue stesse dimensioni, dato che la luce che lo oltrepassa prosegue appunto diritta, o almeno credo… Mah! La cosa migliore è provare. Ecco qua. Ora accendo la torcia e sul muro compare… Ehi, e quello cos’è? »
Sul muro compaiono una serie di cerchi concentrici luminosi e scuri alternati.
Lettore: «Che diavoleria è mai questa? Imbroglio! Inganno! »
No, nessun inganno. Quella strana immagine sul muro è una conseguenza della natura ondulatoria della luce.
L’ottica ondulatoria si basa sull’ipotesi che la luce si propaghi tramite delle onde simili a quelle sonore o alle increspature che si formano sulla superficie di uno stagno. Questa teoria è nata proprio per riuscire a spiegare in termini semplici quei fenomeni che l’ottica geometrica non riusciva a interpretare.
Ciò che il nostro ipotetico lettore ha scoperto in modo del tutto casuale, come del resto accade spesso per le grandi scoperte scientifiche, è proprio la natura ondulatoria della luce. La strana immagine del forellino proiettata sul muro è infatti il risultato di due fenomeni comuni a qualsiasi tipo di onda: la diffrazione e l’interferenza. Sull’interferenza torneremo tra breve. Adesso occupiamoci della diffrazione.
Quando un’onda, quale che sia la sua natura, incontra un ostacolo o i bordi di un’apertura, tende ad aggirarli, a incurvarsi attorno a essi. Consideriamo ancora un esempio acustico. Immaginiamo di essere all’esterno di un locale da cui proviene della musica. L’esperienza ci dice che le onde sonore ci raggiungono anche se non stiamo davanti alla porta del locale. Senza la diffrazione questo non sarebbe possibile. La porta lascerebbe infatti passare solo un fascio rettilineo di onde, così che al di fuori di quel fascio non si sentirebbe nulla. Invece, proprio perché le onde si incurvano attorno ai bordi della porta, il suono che la attraversa si propaga su un’area molto più ampia. Lo stesso accade con le onde luminose.
Tuttavia, perché l’entità della diffrazione sia significativa, le dimensioni dell’apertura che la provoca non devono essere troppo grandi rispetto alla lunghezza dell’onda che la attraversa. Per questo una porta aperta diffrange le onde sonore, che hanno lunghezze comprese tra alcuni centimetri e alcuni metri. Ma siccome la luce visibile ha lunghezze d’onda nell’ordine dei decimillesimi di millimetro, per poter osservare la sua diffrazione è necessario farla passare attraverso un’apertura molto più piccola di una porta, ad esempio un forellino il cui diametro non superi qualche decimo di millimetro. In questo caso, dopo averlo attraversato, un fascio di luce incidente si allargherà, proiettando sulla parete un dischetto di dimensioni molto maggiori.
Come si interpreta la diffrazione da un punto di vista fisico? Diffrangere significa letteralmente spezzare in più parti, e in effetti è proprio come se, attraversando un’apertura sufficientemente piccola, un’onda si rompesse, dividendosi in tante onde secondarie che si propagano all’interno di un cono. Tenendo conto di questo fatto, l’alternarsi di cerchi scuri e luminosi concentrici nell’immagine del forellino proiettata sulla parete si spiega allora come prodotto dell’interferenza tra le onde che si creano a causa della diffrazione.
Dell’interferenza abbiamo già parlato nel paragrafo 3.5, ricordate? Quando due onde si sovrappongono, possono sommarsi oppure cancellarsi a vicenda. Ed è esattamente questo che accade alle onde che si formano in corrispondenza del forellino a causa della diffrazione: in alcuni dei punti della parete su cui si proietta l’immagine del forellino, queste onde secondarie si sommano, dando origine a zone luminose, mentre in altri punti si cancellano, dando origine a zone scure. Il risultato è un disco luminoso centrale circondato da una serie di anelli chiari e scuri alternati.
All’inizio di questo capitolo abbiamo accennato al fatto che la normale luce visibile emessa dal Sole o da una lampadina – la luce bianca, come è spesso chiamata – è una miscela di onde elettromagnetiche di diverse frequenze a ognuna delle quali corrisponde un colore. Ciò vuol dire che nella luce di una lampadina c’è un po’ di blu, di rosso, di giallo e così via.
Quello che non abbiamo ancora detto è che, proprio a causa della natura ondulatoria della luce, quando un fascio luminoso attraversa la superficie di separazione tra due mezzi trasparenti, ciascuno dei colori che lo compongono viene deviato di un angolo diverso. In altre parole, l’entità della rifrazione dipende dalla lunghezza d’onda della luce che attraversa i due mezzi. E questo che ci permette di scomporre un raggio di luce bianca nelle sue componenti di colore facendolo passare attraverso un prisma di vetro (agli appassionati di rock verrà subito in mente la copertina di un famoso disco dei Pink Floyd). Entrando e uscendo dal prisma, infatti, il raggio subisce una doppia rifrazione che lo disperde su una larga banda in cui compaiono in successione tutti i colori dello spettro, dal rosso al violetto (vedi la figura 4.7). Se l’indice di rifrazione del prisma fosse lo stesso per tutti i colori, l’unica cosa che vedremmo sarebbe la deviazione del raggio di luce bianca incidente.
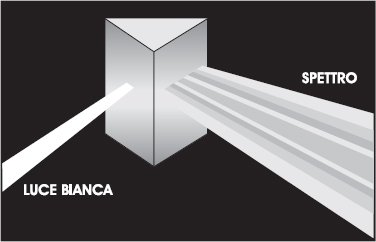
Fig. 4.7 Un prisma di vetro scompone un raggio di luce bianca producendo uno spettro di colori.
L’arcobaleno è una magnifica manifestazione naturale di questo fenomeno fisico: la luce del Sole viene intercettata dalle goccioline d’acqua che dopo un temporale rimangono in sospensione nell’aria, e queste gocce si comportano come tanti piccoli prismi, facendo deviare, nel passaggio della luce solare dall’aria all’acqua e poi di nuovo all’aria, le varie frequenze di angoli differenti.
«Bello! Ma oltre all’arcobaleno? Non c’è una qualche applicazione pratica della rifrazione? Magari una di quelle che cambiano il modo di vedere il mondo? »
Certo non chiedete poco. Ma forse…
La lente è un oggetto trasparente con due facce levigate, almeno una delle quali è curva, ed è in questo semplice strumento che il genio dell’uomo ha messo in pratica le leggi della rifrazione.
Le lenti si dividono in due gruppi: quelle che fanno convergere in un punto un fascio di raggi luminosi paralleli sono chiamate convergenti, mentre quelle che disperdono il fascio di luce in una regione più ampia sono chiamate divergenti (figura 4.8).

Fig. 4.8 Sagome di lenti convergenti (a sinistra) e divergenti (a destra). Notate che le lenti convergenti sono più spesse al centro, mentre le lenti divergenti sono più spesse ai bordi.
Una lente convergente concentra i raggi paralleli al suo asse ottico in un punto definito fuoco della lente (vedi la figura 4.9). Sono le lenti di questo tipo, più spesse al centro che ai bordi, che permettono di accendere il falò per cuocere il pesce pescato nell’isola dopo un naufragio. L’unica precauzione è quella di porre i legnetti esattamente nel fuoco della lente.
La distanza tra il centro della lente e il fuoco viene chiamata distanza o lunghezza focale, e dipende dalla curvatura delle sue superfici e dall’indice di rifrazione del materiale di cui è fatta. A parità di indice di rifrazione la lunghezza focale è tanto più piccola quanto più la lente è bombata e viceversa (vedi le figure 4.9 e 4.10).
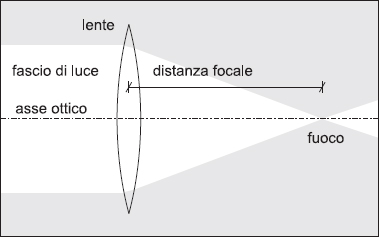
Fig. 4.9 Schema ottico di una lente convergente.
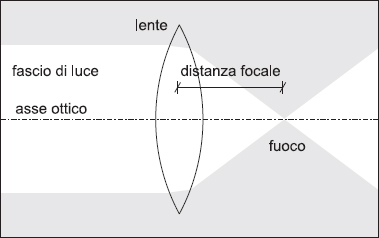
Fig. 4.10 Questa lente convergente, del tutto simile a quella della figura 4.9 ma più bombata, ha una distanza focale minore.
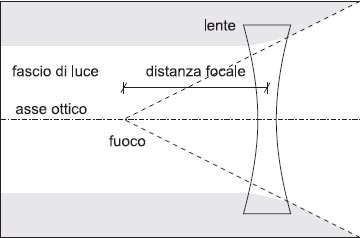
Fig. 4.11 Schema ottico di una lente divergente. Notate che nel fuoco della lente non convergono i raggi luminosi che la attraversano, ma i loro prolungamenti immaginari (a tratteggio nel disegno).
Quando invece è più sottile al centro che ai bordi, una lente è divergente. In questo caso il fuoco è il punto in cui convergono i prolungamenti immaginari dei raggi luminosi deviati dalla lente (vedi la figura 4.11). Perciò è impossibile accendere un falò con una lente divergente.
Tutti gli appassionati di fotografia ne converranno: gli obiettivi sono l’applicazione più piacevole delle lenti. Con una leggera astrazione, possiamo assimilare il sistema composto da obiettivo, pellicola e corpo macchina a un tubo dentro il quale passa dell’acqua che riempie un secchio. Per riempire il secchio in una data quantità di tempo possiamo utilizzare un tubo di piccolo diametro molto inclinato, così che l’acqua scenda più velocemente, oppure un tubo meno inclinato ma di grande diametro, in cui l’acqua scenderà più lentamente ma in maggiore quantità. In questo modello l’acqua è la luce, il secchio è la pellicola, il tempo in cui lo si deve riempire è l’esposizione corretta e… il tubo è il nostro prezioso obiettivo. Variare l’apertura agendo sul diaframma dell’obiettivo significa allora modificare il diametro del tubo, mentre variare la velocità di scatto significa modificarne l’inclinazione (a una minore inclinazione corrisponderà, ovviamente, una maggiore velocità di esposizione, cioè un tempo di posa più breve).
Gli obiettivi solitamente sono composti da una serie di lenti accostate che, grazie alla rifrazione, sono in grado di proiettare un’immagine sulla pellicola fotografica. I parametri che possono permettere di scegliere un obiettivo in maniera saggia (tralasciando il prezzo, che spesso dipende dalla marca, dal negozio e perfino dalla città) sono essenzialmente tre: il numero di lenti, la focale e la luminosità.
1. Numero di lenti – La prima domanda che ci viene in mente è: «Perché gli obiettivi hanno tante lenti? Non ne basterebbe una sola convergente? »
In effetti basterebbe, e la prima macchina fotografica aveva certamente una sola lente, ma abbiamo visto che un fascio luminoso viene rifratto in maniera diversa in funzione delle sue componenti di colore e questo, nelle lenti, dà luogo a ciò che si chiama aberrazione cromatica. La luce che attraversa una lente vicino ai bordi forma degli aloni colorati e per evitarlo (o meglio per ridurre il fenomeno, dato che eliminarlo del tutto è impossibile) si ricorre a un complesso di lenti accostate l’una all’altra, lenti che sono diverse per curvatura, per spessore e per le proprietà ottiche del vetro di cui sono fatte. Ormai è abbastanza frequente leggere sui dépliant delle macchine fotografiche economiche «obiettivo acromatico», il che significa che è stata corretta l’aberrazione per due frequenze di colore. Più rari – e cari – sono gli obiettivi apocromatici in cui la correzione è stata effettuata per tre frequenze.
Insomma, il numero di lenti contenute in un obiettivo è senza dubbio un parametro significativo per valutarne la qualità.
2. Focale – Scegliere l’obiettivo della focale giusta è fondamentale. Sappiamo tutti molto bene che se vogliamo fotografare un soggetto lontano abbiamo bisogno di un teleobiettivo, mentre se vogliamo fotografare un bella piazza ci conviene usare un grandangolo, ma che vuol dire? Molto spesso si pensa che un 50 mm sia un obiettivo « normale » e che un 135 mm sia un tele. È proprio così?
Il 50 mm è l’obiettivo di tutti i giorni, quello più flessibile, quello per cui siamo sicuri che le nostre fotografie saranno una rappresentazione fedele dei soggetti così come li vedevamo a occhio nudo. Proviamo a capire perché.
La focale di un obiettivo altro non è, ovviamente, che la sua lunghezza focale, ovvero la distanza del fuoco dal suo sistema di lenti. Se usiamo una reflex per pellicole di formato 24 × 36, la lunghezza focale di un obiettivo da 50 mm coincide approssimativamente con la diagonale di un negativo. Ricordate il teorema di Pitagora? La somma dei quadrati dei due lati del negativo è (241 + 362) mm2, la cui radice quadrata fa circa 43 mm. Ciò significa che l’immagine inquadrata da un 50 mm avrà dimensioni tali da riempire all’incirca la superficie della pellicola (sarà appena un po’ più grande, in realtà). Se però usassimo una reflex 6 × 6, il nostro obiettivo « normale » dovrebbe avere una focale di 85 mm e se usassimo una 6 × 9 addirittura di 110 mm!
Forse stiamo centrando… l’obiettivo. Abbiamo individuato la lunghezza focale che ci serve e abbiamo scartato gli obiettivi con una sola lente per evitare il problema delle aberrazioni cromatiche. Ma c’è un altro parametro fondamentale da considerare prima dell’acquisto: la luminosità.
3. Luminosità – La luminosità di un obiettivo viene espressa come il rapporto tra la sua lunghezza focale e la sua apertura, cioè il massimo diametro utile attraverso cui la luce può entrare. Perciò, quando leggiamo che un obiettivo ha luminosità f/2, vuol dire che la sua apertura è la metà della sua lunghezza focale. Gli obiettivi fotografici più luminosi hanno un indice f/1,4, mentre la luminosità di un teleobiettivo amatoriale va di solito da f/3,5 a f/5,6. Per dire una banalità, gli obiettivi più luminosi sono migliori di quelli meno luminosi e di conseguenza anche più cari. La spiegazione risiede nel fatto che i primi sono più difficili da costruire: poiché hanno un’apertura maggiore, la luce colpisce anche la parte esterna delle loro lenti, così occorre correggere maggiormente le aberrazioni cromatiche, il che significa dover utilizzare un maggior numero di lenti, e di migliore qualità.
Ecco fatto. Abbiamo individuato l’obiettivo giusto, abbiamo sborsato una cifra che ci pare abbastanza onesta e siamo usciti soddisfatti dal negozio. Ora per poter fare delle ottime foto mancano solo un corpo macchina e un rullino…
In effetti non è proprio così; come direbbero i matematici, è una condizione necessaria ma non sufficiente. Ritorniamo alla piccola disavventura fotografica descritta nel prologo e vediamo quali sono stati gli errori commessi.
Da un punto di vista meramente tecnico (tempo d’esposizione, messa a fuoco, inquadratura) sembrava tutto perfetto, però ci sono una serie di fattori che sono stati trascurati. Ad esempio, se si utilizzano basse velocità di scatto per riprendere soggetti in movimento, nello spazio di tempo in cui la pellicola si impressiona quei soggetti si saranno spostati e sulla foto comparirà una scia. Il che va benissimo se vogliamo dare l’idea di velocità come nelle foto che pubblicizzano auto da corsa, ma non funziona per immortalare uno stambecco nel bel mezzo di un balzo plastico.
Se invece si tiene molto aperto il diaframma dell’obiettivo per raccogliere la massima quantità di luce nel minor tempo possibile, si avrà una scarsa profondità di campo, il che significa che sarà a fuoco solo ciò che si trova più o meno alla stessa distanza del soggetto principale della foto. Per aumentare la profondità di campo ed evitare che lo sfondo oppure gli oggetti in primo piano risultino sfocati, è necessario chiudere il diaframma. (La ragione è la stessa per cui tendiamo istintivamente a strizzare gli occhi quando vogliamo vedere meglio qualcosa lontano). Certo, per ottenere un suggestivo effetto di tridimensionalità, come accade ad esempio in quelle foto pubblicitarie di profumi dove nella macchia sullo sfondo si intuisce la torre Eiffel, una bassa profondità di campo è utile. Ma se si vuole un’immagine «da cartolina» con un bell’albero in primo piano e una montagna innevata sullo sfondo, è necessario impostare un diaframma piccolo.
La tabella che segue non è rigorosa ma può fornire dei riferimenti utili per decidere quale velocità di scatto e quale diaframma impostare in situazioni diverse.
Tabella 4.2
| Velocità di scatto | Situazione/problemi |
| Pose di un secondo o più | Indispensabile per foto notturne, utilizzando il cavalletto per creare suggestivi effetti di luce |
| Fino a 1/60 di secondo | Anche un leggero tremolio delle mani farà risultare la foto mossa |
| Da 1/60 fino a 1/250 | Va bene per paesaggi e per oggetti in movimento lontani |
| Da 1/500 in poi | Si può usare per fotografie al Gran premio di Formula 1 |
| Diaframma | Situazione/problemi |
| Da 1,4 a 3,5 | Sarà a fuoco solo il soggetto che abbiamo puntato |
| Da 3,5 fino a 5,6 | Sono i diaframmi più usati. Offrono un buon compromesso tra luminosità e profondità di campo |
| = 8 | È il diaframma usato per i primi piani. L’obiettivo dà il massimo senza aberrazioni |
| Da 11 a 32 | Con questi siamo sicuri che soggetti da pochi metri all’infinito sono a fuoco |
Gli strumenti ottici sono combinazioni di specchi e lenti disposti in modo tale da aumentare la funzionalità dell’occhio, correggendo difetti della vista oppure potenziandola in modo da permetterci di vedere oggetti molto lontani o molto piccoli. In questo paragrafo daremo una brevissima descrizione di tre semplici strumenti ottici il cui funzionamento si basa sulle proprietà rifrattive delle lenti.
Per comprendere le figure che accompagnano le descrizioni, bisogna tenere presenti le regole di base della costruzione geometrica delle immagini: un raggio di luce parallelo all’asse ottico viene deviato in modo da passare per il fuoco di una lente dopo averla attraversata, mentre un raggio che passa per il centro di una lente non subisce alcuna deviazione. Notate anche che nelle figure i prolungamenti immaginari dei raggi luminosi sono disegnati a tratteggio.
La lente d’ingrandimento è senza dubbio il più semplice degli strumenti ottici. È composta infatti da un’unica lente convergente di piccola lunghezza focale. È proprio la lunghezza focale ridotta che consente di formare un’immagine ingrandita di un oggetto posto tra la lente e il suo fuoco (vedi la figura 4.12).
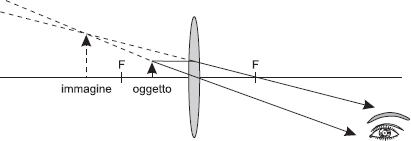
Fig. 4.12 Lo schema ottico di una lente d’ingrandimento.
Il microscopio è formato da due lenti convergenti. La lente a cui si accosta l’occhio per guardare nello strumento prende il nome di oculare, mentre l’altra, più vicina all’oggetto da osservare, è l’obiettivo del microscopio. Quando si pone un oggetto in prossimità del fuoco dell’obiettivo si ottiene un’immagine capovolta e ingrandita che viene raddrizzata e ulteriormente ingrandita dall’oculare (figura 4.13).
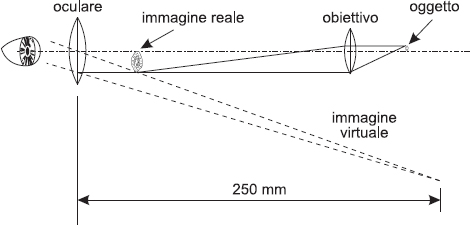
Fig. 4.13 Lo schema ottico di un microscopio. Notate che l’oculare ingrandisce l’immagine prodotta dall’obiettivo.
Anche il cannocchiale è composto da un oculare e da un obiettivo, ma la disposizione delle lenti è tale per cui lo strumento permette di osservare oggetti lontani. L’immagine catturata dall’obiettivo si forma vicino al fuoco dell’oculare ed è molto piccola e capovolta. Dopodiché l’oculare ingrandisce quest’immagine.
La differenza fondamentale tra il microscopio e il cannocchiale è data dalla diversa lunghezza focale degli obiettivi, che è molto piccola nel primo e maggiore nel secondo. L’ingrandimento I di un cannocchiale è dato dal rapporto delle lunghezze focali dell’obiettivo e dell’oculare, cioè:
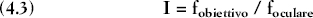
Quindi un telescopio amatoriale con un obiettivo di 800 mm di focale e un oculare di 20 mm di focale consente di osservare la Luna ingrandita di 40 volte.
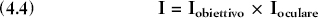
Perciò, se sull’oculare di un microscopio è scritto 10 x e sull’obiettivo 20 ×, un oggetto osservato attraverso lo strumento risulterà ingrandito 200 volte.
«Sistema di messa a fuoco automatica e pressoché istantanea, sensibilità alle variazioni di luminosità superiore a qualsiasi apparecchio digitale, percezione dei colori superiore a qualsiasi scheda grafica, sensibilità assoluta alla luce nell’ordine dei millesimi di lux».
Non è la pubblicità di qualche nuovo giocattolo elettronico nato in un laboratorio di Taiwan; sono alcune caratteristiche dei nostri occhi, o meglio della nostra vista con la sua sofisticata strumentazione.
Gli occhi sono dei veri e propri strumenti ottici come il microscopio o il binocolo, ma di gran lunga più complessi. Tralasciando per ora l’argomento della sensibilità alla luce (ce ne occuperemo alla fine del capitolo) vediamo alcuni dettagli tecnici.
Queste sono caratteristiche del sistema visivo umano, ma vi ricordate che nella premessa di questo capitolo abbiamo detto che non tutti gli occhi sono uguali? L’apparato visivo dei serpenti, ad esempio, si è evoluto in maniera molto diversa da quello dei mammiferi. Si dice che i serpenti siano quasi ciechi, ma non è del tutto vero: da un certo punto di vista ci vedono molto meglio di noi. Alle specie che vivono nel deserto e cacciano nelle ore notturne non serve tanto distinguere il colore del manto di un roditore, quanto piuttosto individuare la sua posizione nell’oscurità. A questo scopo la natura ha fornito queste specie di due recettori, posti vicino agli occhi, che sono sensibili all’infrarosso. La radiazione infrarossa è quella parte della radiazione elettromagnetica che si colloca appena al di fuori della finestra del visibile, giusto oltre il rosso e che, come abbiamo visto nel capitolo 2, viene emessa da tutti i corpi caldi. Poiché dopo il tramonto il corpo del roditore è molto più caldo del deserto, grazie a questa « seconda vista » il serpente riesce a individuarlo anche da molto lontano, esattamente come James Bond riesce a individuare le spie nemiche nel bosco grazie al suo speciale binocolo a infrarossi.
Osservate la figura 4.14 e immaginate che sia una di quelle illustrazioni che compaiono nel libretto di istruzioni di un apparecchio fotografico per descriverne le varie componenti. Assurdo, vero? Eppure le analogie tra l’occhio umano e una macchina fotografica sono sorprendentemente numerose.
L’apertura da cui la luce entra nell’occhio, la pupilla, viene regolata dall’iride, che si stringe o si allarga in funzione della quantità di luce che la colpisce, proprio come il diaframma di un obiettivo fotografico. E questo che ci permette di vedere bene sia su una spiaggia assolata sia nella penombra di una stanza semibuia, anche se in condizioni estreme all’iride occorre un po’ di tempo per allargarsi o restringersi (lo sanno bene i guerrieri ninja, che quando entrano in un ambiente oscuro stanno fermi qualche minuto per adattarsi).
Poi c’è il cristallino, una lente convergente di forma biconvessa che focalizza i raggi luminosi sulla retina. Il cristallino è in grado di mettere a fuoco in successione un oggetto a dieci centimetri e uno a centinaia di metri in una frazione di secondo. Roba da far impallidire qualunque azienda giapponese che produce macchine fotografiche.
Ma mentre in un apparecchio fotografico si mette a fuoco l’immagine variando la distanza focale tra lente e pellicola, nell’occhio è la forma stessa della lente a variare. Modificando la morfologia del cristallino, e quindi la curvatura delle sue superfici, si aumenta oppure si diminuisce il suo potere di convergenza. Questo processo è regolato dal corpo ciliare, un anello di fibre muscolari disposte intorno al cristallino. Quando l’occhio guarda un oggetto in lontananza, le fibre del corpo ciliare sono rilassate e il cristallino assume una forma appiattita (la sua curvatura è minima). Quando invece l’occhio guarda un oggetto vicino, il corpo ciliare entra in azione, facendo assumere al cristallino una forma più bombata (la sua curvatura aumenta). In realtà, il processo di rifrazione dei raggi luminosi nell’occhio è molto più complesso. Vi partecipano anche la cornea, cioè la porzione anteriore della membrana che circonda il globo oculare, e due fluidi trasparenti: l’umor acqueo, contenuto in una piccola sacca che separa il cristallino dalla cornea, e l’umor vitreo, che riempie la cavità interna dell’occhio (vedi la figura 4.14).
Dopo aver attraversato la cornea, l’umor acqueo, il cristallino e l’umor vitreo, i raggi luminosi provenienti dall’oggetto osservato convergono sulla retina che, grazie a milioni di minuscoli sensori chiamati coni e bastoncelli, rileva qualche miliardo di sfumature di grigi e di colore. Nella nostra analogia, la retina rappresenta insomma l’equivalente della pellicola fotografica. In realtà è una sottile membrana trasparente che riveste la superficie interna del globo oculare e trasforma l’immagine in segnali elettrici. Tramite il nervo ottico questi segnali vengono inviati ai centri visivi del cervello, che li elaborano e li trasformano nella nostra percezione finale dell’immagine.
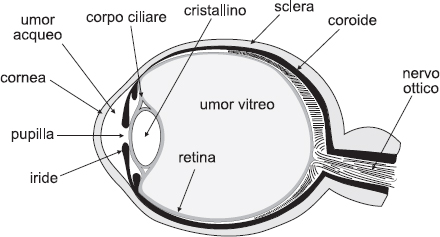
Fig. 4.14 Le componenti essenziali dell’occhio umano.
In definitiva, l’occhio è uno strumento… ottico. Ma se vogliamo restare nel paragone con strumentazioni moderne come quelle che si vedono nelle vetrine dei negozi specializzati, dobbiamo aggiungere che è decisamente riduttivo paragonarlo a un telescopio o a un binocolo, o anche all’obiettivo di una macchina digitale di ultima generazione. Ciò che lo differenzia da questi strumenti è, potremmo dire, il suo software. Ad esempio, l’immagine che si compone sulla retina è rovesciata: senza un « programma » opportuno il mondo ci apparirebbe capovolto. E non solo. Lo stesso software ci dota di un sofisticatissimo sistema antivibrazione. Pensate a cosa vedrebbe un atleta durante una corsa a ostacoli se non ci fosse un computer che a ogni sobbalzo riaggiusta l’immagine in modo da farla vedere là dov’è realmente in quell’istante.
Riassumendo, per guardare intorno a noi abbiamo a disposizione uno strumento davvero straordinario, costituito da lenti a curvatura variabile, da una pellicola sensibile (molto sensibile), da un sistema di fibre ottiche (o meglio nervose) in cui passano i segnali e da un microprocessore all’avanguardia. E a questo apparato hardware è associato un software che i migliori programmatori di Silicon Valley nemmeno si sognano.
Però, c’è sempre un però: tutti gli strumenti meccanici prima o poi si starano. Accade alla bilancia che teniamo in bagno, all’igrometro appeso al muro, ma anche all’acceleratore di particelle del CERN a Ginevra e al telescopio spaziale Hubble. Perché non dovrebbe succedere la stessa cosa ai nostri occhi? E infatti spesso succede, purtroppo.
I più comuni «problemi di taratura» degli occhi sono la miopia, l’ipermetropia, l’astigmatismo e la presbiopia. Come se non bastasse, spesso l’astigmatismo si presenta insieme alla miopia o all’ipermetropia. Esaminiamo molto rapidamente in che cosa consistono questi quattro difetti visivi.
Nell’occhio miope l’immagine di oggetti lontani non si forma sulla retina ma prima, o perché la lunghezza focale massima del cristallino è comunque troppo corta oppure (più spesso) perché il globo oculare ha una forma allungata. Il difetto si riduce man mano che si osservano oggetti più vicini, fino a scomparire quando l’oggetto osservato si trova a una distanza sufficientemente piccola dall’occhio.
Nell’occhio ipermetrope, al contrario, l’immagine si forma sempre dietro la retina, sia quando l’oggetto osservato è vicino sia quando è lontano. Il difetto può essere causato da un cristallino con una lunghezza focale ridotta o, più di frequente, da un globo oculare schiacciato. A differenza di quanto accade con la miopia, avvicinarsi all’oggetto da osservare non migliora la situazione.
L’astigmatismo è provocato di solito da una cornea di forma non perfettamente simmetrica. Poiché infatti, come abbiamo visto, anche la cornea contribuisce al processo rifrattivo di messa a fuoco da parte dell’occhio, ogni irregolarità nella sua curvatura si ripercuote sulla formazione delle immagini.
Con il passare del tempo e con l’usura, i meccanismi di regolazione di uno strumento spesso tendono a indurirsi, a perdere di efficacia. Succede anche ai nostri occhi. Dopo una quarantina d’anni che li usiamo, il cristallino subisce una riduzione progressiva dell’elasticità, così che i muscoli del corpo ciliare non riescono più a modificarne la forma oltre un certo limite. È questa la causa della presbiopia. In un occhio presbite gli oggetti osservati da vicino risultano sfocati perché il potere di accomodazione del cristallino si è ridotto e le immagini si formano dietro la retina. La visione di oggetti lontani, invece, non ne soffre, dato che in tal caso la messa fuoco non richiede di modificare la forma del cristallino.
La miopia compensa parzialmente gli effetti della presbiopia, ritardandone spesso l’insorgenza (in effetti non è insolito vedere un miope che per leggere si toglie gli occhiali). Riuscite a spiegarvi perché?
Si sa, il modo più semplice, sicuro ed efficace per rimediare ai difetti visivi che abbiamo descritto nel paragrafo precedente è quello di porre davanti agli occhi delle lenti correttive. Se una persona è miope, ad esempio, un paio di occhiali con lenti divergenti (o un paio di lenti a contatto divergenti) aumenterà la lunghezza focale dei suoi cristallini, permettendole così di mettere a fuoco le immagini di oggetti lontani. Oggi esiste l’alternativa della chirurgia laser, è vero, ma in ogni caso è necessario intervenire dall’esterno per correggere i difetti di visione.
Tuttavia, questo non significa che non possiamo cercare di preservare quanto meglio sia possibile la nostra vista con… un buon allenamento.
Anche chi non soffre di difetti visivi congeniti o acquisiti in giovane età, infatti, tende a subire un progressivo decadimento della funzionalità degli occhi a causa dell’invecchiamento e dello stile di vita che conduce. Ad esempio, studi recenti hanno dimostrato che la vita in città ha effetti negativi sulla visione perché ci abitua a mettere a fuoco quasi sempre oggetti relativamente vicini. Se perdiamo la capacità di far spaziare lo sguardo verso tramonti lontani o montagne innevate, i nostri occhi si impigriscono e perdono elasticità. Considerando che nell’occhio ci sono muscoli e altri tessuti che si contraggono e si adattano alle diverse condizioni, degli esercizi specifici possono essere utili per correggere o prevenire difetti della vista di leggera entità.
Ecco un esempio di esercizio di rilassamento yoga. Dopo aver sfregato le mani per riscaldare i palmi, chiudete gli occhi e appoggiatevele sopra, toccando leggermente le ossa intorno agli occhi, ma senza sfiorare le palpebre. Inspirate ed espirate visualizzando immagini lontane come una barca in mezzo al mare o un uccello posato sul ramo di un albero. Restate così per almeno un paio di minuti.
Questo esercizio serve invece a distendere e a rafforzare i muscoli dell’occhio, ed è utile nel caso in cui soffriate di miopia o di ipermetropia. Mettetevi comodamente seduti su una poltrona. Rilassatevi con tre inspirazioni profonde e mettete a fuoco un oggetto sulla parete di fronte a voi. Senza modificare la messa a fuoco, distendete quasi completamente le braccia, con le mani chiuse a pugno e gli indici alzati quasi davanti agli occhi (le braccia sono davanti a voi, leggermente flesse, e gli indici sono a circa 30 cm l’uno dall’altro). Dopo qualche secondo vi accorgerete che tra le due dita ne è comparsa una terza. Mettetela a fuoco senza spostare lo sguardo (è più facile di quel che pensiate). Cercate di tenerla a fuoco mentre fate variare lentamente sia la distanza tra le due dita reali sia quella che le separa dai vostri occhi.
La percezione dei colori è una questione soggettiva. In un certo senso potremmo dire che i colori che percepiamo non sono proprietà intrinseche dei corpi ma sensazioni che vengono elaborate dal nostro sistema nervoso.
Abbiamo visto che sulla retina ci sono milioni di sensori, cellule specializzate chiamate coni e bastoncelli. Questi fotorecettori raccolgono le informazioni luminose provenienti dall’esterno e le trasformano in impulsi nervosi che poi il cervello elabora. I coni, in particolare, sono i fotorecettori destinati alla visione a colori. Pur essendo strutturalmente tutti uguali (il nome « cono » deriva dalla loro forma) esistono tre tipi di coni, ognuno con caratteristiche differenti: i coni S sono sensibili alle lunghezze d’onda corte (blu e violetto), i coni M a quelle medie (verde e giallo) e i coni L a quelle lunghe (rosso). La radiazione luminosa che colpisce la retina stimola i fotorecettori corrispondenti a queste tre lunghezze d’onda, innescando un processo che porterà al cervello l’informazione globale sul colore e sulla sua intensità.
Nel 1986 ci fu una grande nevicata a Roma e le strade si riempirono di gente con sci da fondo, bambini con Io slittino, cani sanbernardo con tanto di cognac attaccato al collo. Anche la facoltà di fisica non fu immune dalla carnevalata. Si vedevano entrare studenti e professori con occhiali gialli. Qualcuno aveva montato dei fendinebbia perfino sulla bici.
Fu in una delle solite riunioni tra una lezione e l’altra che uno studente sollevò la questione: perché quando c’è nebbia oppure nevica si accendono delle luci gialle e in montagna si usano occhiali con le lenti gialle? Le risposte furono delle più varie: « È solo una moda lanciata negli anni Sessanta da Brigitte Bardot », «Macché! È perché le lenti gialle riescono ad attraversare la nebbia come la vista di Superman attraversa i vestiti delle donne » e via sproloquiando. La spiegazione è molto più semplice.
Come possiamo vedere nella figura 4.15, i nostri occhi non hanno la stessa sensibilità a tutte le frequenze della luce visibile. Ai due estremi dello spettro (rosso e violetto) la sensibilità è minima, mentre raggiunge il picco massimo al centro, proprio in corrispondenza del giallo. In altre parole, il giallo è il colore che ci appare più luminoso di tutti gli altri. Perciò, se con delle lenti colorate rendiamo giallo il mondo che ci sta intorno, i particolari ci appariranno più nitidi. La nebbia non scomparirà e la visibilità resterà comunque di trenta metri come ci dice la radio, ma il contorno del TIR con rimorchio che ci taglia la strada sarà percepito con maggior facilità dal nostro sistema visivo.
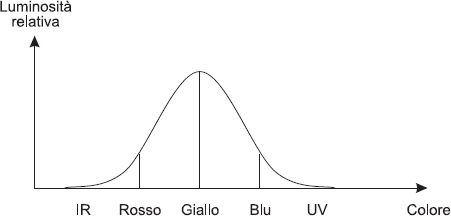
Fig. 4.15 La sensibilità dell’occhio umano varia con il colore della luce, ovvero con la sua frequenza, ed è massima in corrispondenza del giallo.
Il sistema visivo umano è uno strumento quasi perfetto, e rappresenta sicuramente il più complesso dei nostri sensi (non a caso è il più recente dal punto di vista dell’evoluzione). In particolare, quello che abbiamo definito il software degli occhi, l’insieme dei processi cerebrali che integrano i segnali luminosi provenienti dall’esterno in un’immagine dotata di significato, è di una complessità e di una sofisticatezza incredibili. Tuttavia, così come gli apparati informatici più perfetti presentano sempre qualche falla (un «baco», come direbbe qualche hacker), anche il nostro sistema visivo può essere raggirato.
La percezione è il passo successivo all’acquisizione: dopo che gli occhi hanno convertito gli stimoli luminosi in segnali neurali, il cervello deve elaborarli per ricostruire l’immagine corrispondente. Ma come vengono riconosciuti gli oggetti?
Quando osserviamo un cane, lo vediamo nella sua essenza, nella sua interezza, e non come insieme di zampe, muso, coda, orecchie che, inseriti al posto giusto, formano una cosa che rassomiglia molto al nostro cane. Questa è la prima routine del software: percepiamo le informazioni che ci provengono dal mondo non come fatti isolati ma raggruppandoli in contesti significativi in base a delle regole.
Il problema è che, come tutti sanno, fatta una regola si trova l’inganno!
Le immagini che vediamo non sono le stesse che potrebbe registrare in condizioni analoghe una comune cinepresa, ma sono il frutto di una complessa elaborazione compiuta dal nostro cervello sugli impulsi che il nervo ottico gli trasmette.
Prendiamo ad esempio una fotografia. L’immagine è bidimensionale, eppure riusciamo a vedere (a immaginare) che la cima innevata è sullo sfondo, lo stambecco saltella a qualche decina di metri da noi mentre l’albero è un po’ più vicino. Il nostro cervello, abituato a lavorare su immagini tridimensionali, ha aggiunto profondità alla fotografia e ci ha regalato l’emozione di ricostruire la scena com’era nella realtà.
Ma proprio per questo è sufficiente disegnare due linee rette divergenti per ingannarlo – e ingannarci – producendo un effetto di profondità inesistente. Se si inseriscono sapientemente tra le due rette degli oggetti identici tra loro, come gli omini della figura 4.16, questi ci appariranno di dimensioni diverse. Ciò accade perché il cervello crede che gli omini vicini alla intersezione delle linee (a destra nella figura) siano più lontani, e quindi più alti di quelli che si trovano a sinistra. Questo tipo di inganno ottico è noto con il nome di illusione di Ponzo.
Nella figura 4.17 è riportato un tipo di illusione simile, osservato già nel 1861 da Ewald Hering. Qui l’effetto prospettico dato dalle linee divergenti fa apparire incurvate le due linee al centro, che in realtà sono diritte e parallele.
Il nostro cervello non si limita però solo a farci vedere male le cose che ci sono: a volte si diverte anche a farci vedere cose che non ci sono. La figura 4.18 mostra una famosa illusione studiata dallo psicologo Gaetano Kanitsa. L’immagine che appare è quella di un triangolo bianco appoggiato su tre dischi neri. Questa visione è però soltanto l’effetto di un’estrapolazione dovuta al modo particolare in cui sono disposti i tre dischetti intagliati. In realtà il triangolo non esiste: se si modifica la posizione dei dischetti, svanisce. Nella figura 4.19 si può notare come questo triangolo inesistente sia percepito con tanto realismo da riuscire addirittura a generare l’illusione di Ponzo. La lineetta a sinistra sembra infatti più lunga di quella a destra, mentre in realtà è di dimensioni identiche.

Fig. 4.16
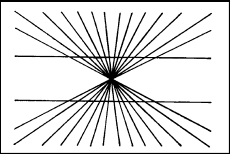
Fig. 4.17

Fig. 4.18
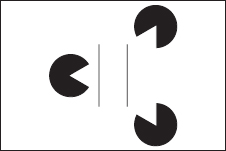
Fig. 4.19
Come se questo non bastasse, talvolta il cervello non ci fa vedere cose che ci sono. Ad esempio, riuscite a riconoscere la parola scritta nella figura 4.20? Abituati a leggere nero su bianco, in prima istanza non distinguiamo altro che dei pittogrammi indecifrabili. Solo se ci sforziamo di leggere bianco su nero riusciremo a vedere chiaramente la scritta «esse».
E quale parola è contenuta nella lisca di pesce della figura 4.21? Finché non copriamo con un foglio la metà inferiore del disegno, difficilmente riusciremo a separare la scritta nume dalla sua immagine riflessa, a causa della nostra istintiva tendenza a considerare i segni contigui come parte di un’unica forma.
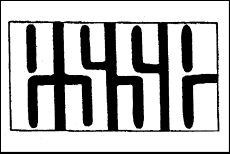
Fig. 4.20

Fig. 4.21
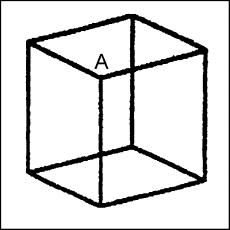
Fig. 4.22
Fig. 4.23
Ma le illusioni ottiche sono davvero tantissime. La figura 4.22 ne riporta una molto famosa, che fu segnalata nel 1832 dal geologo Louis Albert Necker. Se si fissa l’immagine del cubo tratteggiato nella figura (noto come cubo di Necker), il vertice contrassegnato con la lettera A apparirà ora come il più vicino, ora come il più lontano. In questo caso il cervello, non disponendo di informazioni precise sulla reale posizione del cubo nello spazio, è costretto a prendere in considerazione entrambe le ipotesi, oscillando senza sosta da una all’altra. La figura 4.23 è invece uno studio preparatorio per una litografia di Maurits Cornelis Escher intitolata Belvedere. Qui il celebre artista olandese, ingrossando i contorni di un cubo di Necker, realizza una figura impossibile, che si può disegnare nel piano ma è inconcepibile nello spazio.
Nella figura 4.24 è riprodotta infine una caricatura del disegnatore inglese W.E. Hill pubblicata a puro scopo di divertimento nel 1915 sulla rivista «Puck», con il titolo Mia moglie e mia suocera. L’illusione, oggi considerata un classico, fu oggetto di approfonditi studi da parte dello psicologo Edwin G. Boring nel 1930. Guardando il disegno, l’immagine che viene percepita è in genere quella di una bella damina girata di tre quarti. Se però si sposta lo sguardo leggermente verso il basso, il mento della fanciulla si trasforma in un grosso naso e davanti ai nostri occhi si materializza il profilo di una vecchia pensosa. Come nel caso del cubo di Necker, si può notare che se si fissa a lungo la figura la nostra percezione salta di continuo da un’interpretazione all’altra.

Fig. 4.24
Cinquanta gradi all’ombra, la nostra jeep si è rotta venti chilometri fa, altri dieci ci separano da El-Hamrala, il villaggio più vicino. Per completare l’opera, solo adesso ci accorgiamo che la nostra borraccia ha un buco sul fondo. Per fortuna vediamo un’oasi a un centinaio di metri davanti a noi. Ma… sarà vera o è solo un miraggio?
I miraggi! Il contrario di ciò che è vero. Il chiosco di bibite gelate che vede Paperino perso nel deserto. L’oasi che rinfranca gli animi e poi disattende le speranze man mano che ci si avvicina all’ombra delle sue palme. L’immagine di ciò che non è.
Niente di più falso. I miraggi sono la più bella dimostrazione della legge di rifrazione e non dell’inganno ottico!
Chi passasse per il deserto tunisino (a poco più di un’ora d’aereo da Roma!) e percorresse di giorno lo Chott El Jerid – una distesa di sabbia e sale con temperature infernali – vedrebbe, a destra e sinistra della lunga lingua d’asfalto che lo attraversa, una piacevole distesa d’acqua azzurrina. Ma fermarsi per mettere a mollo i piedi sarebbe solo tempo sprecato: l’unica frescura certa è quella garantita dal condizionatore della jeep. Quell’acqua non esiste, è l’immagine riflessa del cielo. E un miraggio.
I miraggi sono un fenomeno molto complesso. Ne esistono di vari tipi, e ognuno richiederebbe una trattazione separata. Facendo delle semplificazioni e senza addentrarci nei dettagli, possiamo dire che i miraggi si verificano in presenza di strati d’aria adiacenti a temperature molto diverse tra loro. Nei deserti, ad esempio, l’aria vicino al suolo si riscalda velocemente, così che la sua temperatura è maggiore di quella degli strati soprastanti (specialmente di mattina). In queste condizioni la densità dell’aria aumenta con la quota, al contrario di ciò che succede normalmente (di solito, tanto più si sale quanto più rarefatta diventa l’aria, come ben sanno gli amanti della montagna). Ma dato che, come abbiamo visto nel paragrafo 4.3.4, l’indice di rifrazione è maggiore per i corpi più densi, anch’esso aumenta con la quota. Perciò i raggi luminosi provenienti da un oggetto che si trova sopra l’orizzonte vengono rifratti in modo tale che la loro curvatura fa comparire un’immagine virtuale dell’oggetto, come se questo si riflettesse sul terreno.
Quanta luce è necessaria per fare una ripresa in una stanza? E quante lampade bisogna accendere per illuminare adeguatamente un salone? A queste domande risponde la fotometria, definendo delle grandezze che ci permettono di misurare la luce.
Ecco una prima definizione fotometrica: «L’intensità della luce emessa da una sorgente in una data direzione si misura in candele ». Ai non giovanissimi (come si usa dire al giorno d’oggi) verrà in mente che quando si andavano a comprare le lampadine per casa, il negoziante chiedeva: « Da quante candele la vuoi? »
La candela è indipendente dalla distanza a cui è posta la sorgente luminosa. È cioè una proprietà della lampadina, proprio come i 700 watt di potenza di un forno a microonde sono una proprietà del forno.
Quanto vale una candela? Non è facilissimo da dire e forse non è nemmeno così importante saperlo (in effetti oggi ci si basa su altre grandezze per decidere quale lampadina comprare), ma se proprio siete curiosi «La candela è l’intensità luminosa, in una data direzione, di una sorgente che emette luce monocromatica di frequenza pari a 1,54 × 1014 hertz con un’intensità energetica di 1/683 watt su steradiante». Lo ammetterete, si poteva vivere bene anche senza saperlo!
Ma il punto non è questo. Il punto è che tale definizione non serve a stabilire quanta luce deve cadere su un oggetto perché possiamo fotografarlo, né quante lampade occorrano per illuminare adeguatamente una cucina o una camera operatoria. Ci dice soltanto che una lampada da 10 candele è più luminosa di una da 5. Ma se la seconda è dotata di un concentratore ed è posta a 50 centimetri dall’oggetto da illuminare, risulterà più idonea dell’altra appesa a un soffitto alto quattro metri e lasciata libera di irradiare in tutte le direzioni.
Perciò è più utile considerare la quantità di energia luminosa che viene irradiata entro un dato angolo. Questa quantità viene espressa in lumen. Probabilmente vorrete anche qui la definizione. Eccovi accontentati: « Il lumen è il flusso luminoso emesso nell’angolo solido unitario da una sorgente che abbia l’intensità di una candela ». Ancora buio pesto, vero?
Allora facciamo un altro piccolo passo e definiamo un’ultima grandezza che dà informazioni sull’illuminamento, ovvero sulla quantità di luce che cade su una data superficie. Questa grandezza è il lux, ed è uguale a un lumen al metro quadrato: 1 lux = 1 lumen/m2.
L’illuminamento è funzione dell’intensità della sorgente luminosa, della distanza di questa dalla superficie irradiata e dalla frequenza della luce emessa (poiché, come sappiamo, l’occhio umano è più sensibile a certe lunghezze d’onda della luce e meno ad altre).
Gli esposimetri delle macchine fotografiche misurano proprio l’illuminamento in lux. Lo si può verificare puntandone uno su un muro bianco illuminato da una torcia. Se si riportano su un grafico i valori registrati dallo strumento, si nota subito che variano in funzione della distanza della torcia dal muro. Se poi si ripete l’esperimento ponendo dei fogli trasparenti e colorati tra la torcia e il muro, si può verificare come la curva dei valori forniti dall’esposimetro cambi con il colore della luce. Ovviamente si deve tener conto dell’assorbimento, dato che i fogli colorati non sono perfettamente trasparenti.
Nel 1999 è entrata in vigore una direttiva comunitaria che impone l’etichetta ecologica per le lampadine. Quindi, come già accadeva per altri elettrodomestici, adesso è obbligatorio dichiarare la reale efficienza energetica delle lampadine in vendita, così che il consumatore possa scegliere con maggiore consapevolezza che cosa acquistare.
Sulle nuove etichette compare, sotto la voce «Energy», una scala di efficienza energetica composta da sette lettere dell’alfabeto (dalla A alla G), ognuna delle quali rappresenta un consumo crescente di energia elettrica.
La differenza di consumo tra i diversi tipi di lampadine è davvero notevole. Una lampada fluorescente da 20 watt ad accensione elettronica, ad esempio, illumina quanto una tradizionale lampadina da 100 watt. Infatti la luce emessa dalla prima è pari a 1240 lumen, contro i soli 160 lumen prodotti da una lampadina tradizionale da 20 watt.
E un minor consumo di energia si traduce naturalmente in un risparmio sulla bolletta elettrica. Ipotizzando un funzionamento medio di 2000 ore all’anno, la lampada tradizionale da 100 watt consuma 200 kilowattora di energia. La lampada a fluorescenza compatta da 20 watt ne consuma invece circa 40. Questo significa che, a parità di luce fornita, la lampada a fluorescenza ci costa sulla bolletta ben cinque volte meno.
Nella tabella 4.3 abbiamo messo a confronto i valori riportati sull’etichetta di una lampadina a basso consumo di ultima generazione con quelli relativi a una lampadina a incandescenza che fornisce un’illuminazione simile.
Se calcoliamo l’efficienza come il rapporto tra la luce emessa e l’energia assorbita nell’unità di tempo (cioè la potenza), risulta che la lampadina a basso consumo è ben sei volte più efficiente della tradizionale lampadina a incandescenza!
Tabella 4.3
| Lampadina a incandescenza | Lampada a basso consumo | |
| Potenza | 60 watt | 11 watt |
| Durata | 1000 ore | 10.000 ore |
| Energy | — | A |
| Lumen | 900 | 990 |
| Efficienza | 15 lumen/watt | 90 lumen/watt |
Per farvi un’idea dell’entità del risparmio che queste lampade permettono di realizzare, sappiate che nel settore domestico le spese per l’illuminazione possono raggiungere anche il 16 per cento dei consumi totali di elettricità.
Scegliere con oculatezza quali lampade comprare per la nostra casa in modo da ottenere un’illuminazione ottimale con un minor consumo di energia è dunque molto importante. Naturalmente oltre ai consumi e all’efficienza bisogna considerare la quantità e la qualità della luce fornita. Per questo è utile avere qualche informazione sulle caratteristiche fondamentali di alcuni tipi di lampade che si trovano in commercio.
Ora che conosciamo il consumo di ciascun tipo di lampada e le caratteristiche qualitative della luce che forniscono, resta un’ultima cosa da stabilire prima dell’acquisto: di quanti lux abbiamo bisogno per illuminare la cucina o il soggiorno. La tabella 4.4 non è rigorosissima, ma può aiutarci.
Tabella 4.4
| Locale | Superficie in m2 | Tipo di lampade e posizione | Lux |
| Cucina | 10 | Alogene direzionali / LBC / Lampade al neon sul soffitto | 150 |
| Soggiorno | 25 | Piantana alogena / Lampadine a incandescenza sul soffitto | 250 |
| Camera da letto | 16 | Lampadine a incandescenza sul soffitto | 150 |
| Sala operatoria | – | Lampade scialitiche (che non producono ombre) direzionate sul soggetto | > 104 |