Chapter 4
Batch Cryptography
4.1 Introduction
From Chapter 1, we know the new direction of modern cryptography — Batch Cryptography, which can process the decryption, key agreement, and signature/verification in a batch way, instead of one by one. In this chapter, we give the formal definitions and concrete schemes as well as the related theories in mathematics. Batch cryptography focuses on the global efficiency and security. It includes batch decryption, batch key agreement and batch signature/verification. To the best of our knowledge, it is the first effort towards introducing batch cryptography.
The remainder of this chapter is organized as follows. A brief review on related work of batch signature/verification schemes as well as their security models and schemes are given in Section 4.2. Batch decryption and batch key agreement are introduced in Section 4.3. Batch RSA is considered as an important case of batch cryptography. New batch RSA schemes based on Diophantine equations are presented in Section 4.4. To implement these new schemes, we employ some related mathematical theory and techniques for solving these Diophantine equations in Section 4.5. Finally, a conclusion of the chapter is presented in Section 4.6.
4.2 Aggregate Signature and Batch Verification
Aggregate signature was first introduced by Boneh et al. [38] for batch verification, which was based on the short signature [41] with efficiently computable bilinear maps in 2003. An aggregate signature scheme is a special digital signature that supports aggregation which can be informally defined as follows: given b signatures on b distinct messages from b distinct users, it is possible to aggregate all these signatures  1,
1,  2, …,
2, …,  b into a single compact signature which convinces the verifier that the b users indeed signed the b original messages in a batch way (i.e., user i signed message mi for i = 1, 2,…, b). Moreover, the aggregation can be performed incrementally. That is, signatures
b into a single compact signature which convinces the verifier that the b users indeed signed the b original messages in a batch way (i.e., user i signed message mi for i = 1, 2,…, b). Moreover, the aggregation can be performed incrementally. That is, signatures  1,
1,  2 can be aggregated into
2 can be aggregated into  12 which can then be further aggregated with
12 which can then be further aggregated with  3 to obtain
3 to obtain  123.
123.

Lysyanskaya et al. [205] use certified trapdoor permutations which permits only sequential aggregation, i.e., the b-th signer must aggregate its own signature into the aggregate signature formed by the first b–1 signers. Lu et al. [203] present the first aggregate signature scheme that is provably secure without random oracles. The signatures are sequentially constructed. However, unlike the scheme of Lysyanskaya et al. [205], a verifier need not know the order in which the aggregate signature was created. Additionally, these signatures are shorter than those of Lysyanskaya et al. [205] and can be verified more efficiently than those of Boneh et al. [38]. Ahn et al. [3] modify the stateful signatures of Hohenberger and Waters [146] by removing the chameleon hash and present a surprisingly efficient synchronized aggregate signature scheme which is secure under the computational Diffie–Hellman (CDH) assumption in the standard model.
In the batch verification, Naccache et al. [219] gave the first efficient batch verifier for DSA signatures in 1994; however, an interactive batch verifier presented in an early version of their paper was broken by Lim and Lee [196]. In 1995, Laih and Yen [302] proposed a new method for batch verification of DSA and RSA signatures, but the RSA batch verifier was broken five years later by Boyd and Pavlovski [45]. In 1998, Harn presented two batch verification techniques for DSA [137] and RSA [138] but both were later broken [45, 152, 153]. In the same year, Bellare et al. [21] took the first systematic look at batch verification and presented three generic methods for batching modular exponentiations, called the random subset test, the small exponents test, and the bucket test which are similar to the ideas from Laih and Yen [302]. Later, Cheon and Lee [83] introduced two new methods called the sparse exponents test and the complex exponents test, which they claim to be about twice as fast as the small exponents test. In 2000, Boyd and Pavlovski [45] proposed some attacks against different batch verification schemes most of which were based on the small exponents test and related tests, and repaired some broken schemes based on the small exponents test. In 2001, Hoshino et al. [148] pointed out that the problem discovered by Boyd and Pavlovski [45] was only critical for batch verification such as the zero-knowledge proofs. Other schemes for batch verification based on bilinear maps were proposed [304, 308, 309] but all were later broken by Cao et al. [67]. In 2006, a method was proposed for identifying invalid signatures in RSA-type batch signatures [180], but Stanek [262] showed that this method is awed. Ferrara et al. [110] gave performance measurements for the schemes herein, and also showed how to batch verify other types of signatures, such as group and ring signatures. Law and Matt [178] pointed out that some identity-based signature schemes batch well, and gave methods for identifying invalid signatures in a batch. Because the goals of batch verification and aggregate signature are slightly different, it is important to clarify these distinct notions. Informally, batch verification’s goal is to verify b distinct signatures quickly, while the goal in aggregate signatures is to compress these signatures.
4.2.1 Definitions
We follow [38] for formalizing the aggregate signature in the chosen-key security model. For the convenience of our presentation, the attacker is also called an adversary or a forger.
Definition 4.2.1. The adversary A is given a single public key, called challenge public key. A’s goal is the existential forgery of an aggregate signature. A is granted the power to choose all public keys except the challenge public key and access to a signing oracle on the challenge public key. A’s advantage, denoted AdvAggSigA, is defined to be the probability of success in the following game:
• Setup. A is provided with a public key pk1, generated at random.
• Queries. A requests hash values of messages and signatures with pk1 on messages of his choice.
• Response. Finally, A outputs b – 1 additional public keys pk2,…, pkb. These keys, along with the initial key pk1, will be included in A’s forged aggregate. A also outputs messages m1, m2,…, mb, and an aggregate signature  , where
, where  is signed by the b users and each user signs on the corresponding message.
is signed by the b users and each user signs on the corresponding message.
The aggregate signature  is called nontrivial if A did not request a signature on m1 under pk1. We define that A wins if
is called nontrivial if A did not request a signature on m1 under pk1. We define that A wins if  is nontrivial valid aggregate signature on messages m1, m2,…, mb under keys pk1, pk2,…, pkb. The probability is over the coin tosses of the key-generation algorithm and of A.
is nontrivial valid aggregate signature on messages m1, m2,…, mb under keys pk1, pk2,…, pkb. The probability is over the coin tosses of the key-generation algorithm and of A.
Definition 4.2.2. An adversary A (t, qH, qS, bmax,  )-breaks an aggregate signature scheme in the chosen-key model if: A runs in time at most t; A makes at most qH queries to the hash function and at most qS queries to the signing oracle; AdvAggSigA is at least
)-breaks an aggregate signature scheme in the chosen-key model if: A runs in time at most t; A makes at most qH queries to the hash function and at most qS queries to the signing oracle; AdvAggSigA is at least 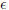 ; and the forged aggregate signature is signed by at most bmax users. An aggregate signature scheme is (t, qH, qS, bmax,
; and the forged aggregate signature is signed by at most bmax users. An aggregate signature scheme is (t, qH, qS, bmax, 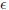 )-secure against existential forgery in the chosen-key model if no forger (t, qH, qS, bmax,
)-secure against existential forgery in the chosen-key model if no forger (t, qH, qS, bmax, 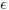 )-breaks it.
)-breaks it.
Recall that a digital signature scheme is a tuple of algorithms (Gen, Sign, Verify) that also is correct and secure. The correctness property states that for all Gen(1l  (pk; sk), the algorithm Verify (pk, m, Sign(sk, m)) = 1.
(pk; sk), the algorithm Verify (pk, m, Sign(sk, m)) = 1.
Definition 4.2.3 (Camenisch et al. [60]). Let l be the security parameter. Suppose (Gen, Sign, Verify) is a signature scheme and (pk1, sk1),…, (pkb, skb) are independently generated according to Gen (1l). We define a probabilistic batch verification algorithm (Batch) as follows:
• Batch((pk1, m1,  1), …, (pkb, mb,
1), …, (pkb, mb,  b)) = 1 provided Verify(pki, mi,
b)) = 1 provided Verify(pki, mi,  i) = 1 for all i = 1, 2,…, b.
i) = 1 for all i = 1, 2,…, b.
• Batch((pk1, m1,  1),…, (pkb, mb,
1),…, (pkb, mb,  b)) = 0 except with probability negligible in
b)) = 0 except with probability negligible in 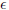 , taken over the randomness of Batch, provided Verify(pki, mi,
, taken over the randomness of Batch, provided Verify(pki, mi,  i) = 0 for any i = 1, 2,…, b.
i) = 0 for any i = 1, 2,…, b.
Definition 4.2.4 (Gentry and Ramzan [121]). The security model for identity based aggregate signature (IBAS) is defined as follows:
• Setup: The adversary A is given public key pk of the Private Key Generation (PKG), an integer bmax, and any other needed parameters.
• Queries: Proceeding adaptively, A may choose identities IDi and request the private key ski. Also, A may request an IBAS  S on (pk, S, {mi}k-1i=1) where S = {IDi}k-1i=1. We require that A has not to make a query (pk, S’, {mi}k-1i=1) where IDi
S on (pk, S, {mi}k-1i=1) where S = {IDi}k-1i=1. We require that A has not to make a query (pk, S’, {mi}k-1i=1) where IDi 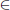 S
S  S’ and m’i
S’ and m’i  mi.
mi.
• Response: For some (pk, {IDi}bi=1, {mi}bi=1) with b ≤ bmax, A outputs an IBAS  1.
1.
We call that the signature is nontrivial, where for some i, 1 ≤ i ≤ b, A did not request the private key for IDi and did not request a signature including the pair (IDi, mi). We define that A wins if  b is a nontrivial valid signature on (pk, {IDi}bi=1, {mi}bi=1)
b is a nontrivial valid signature on (pk, {IDi}bi=1, {mi}bi=1)
Definition 4.2.5. An IBAS adversary A (t, 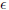 , bmax, qH, qE, qS)-breaks an IBAS scheme in the above model if: for the integer bmax as above, A runs in time at most t; A makes at most qH hash function queries, qE private key extraction queries, and at most qS signing oracle queries; and AdvIBASA is at least
, bmax, qH, qE, qS)-breaks an IBAS scheme in the above model if: for the integer bmax as above, A runs in time at most t; A makes at most qH hash function queries, qE private key extraction queries, and at most qS signing oracle queries; and AdvIBASA is at least 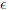 . An IBAS scheme is (t,
. An IBAS scheme is (t,  , bmax, qH, qE, qS)-secured against existential forgery if no adversary (t,
, bmax, qH, qE, qS)-secured against existential forgery if no adversary (t, 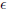 , bmax, qH, qE, qS)-breaks it.
, bmax, qH, qE, qS)-breaks it.
4.2.2 Aggregate Signature
Aggregation is obtained by combining the resulting b signatures { 1,
1,  2,…,
2,…,  b} into one aggregate signature
b} into one aggregate signature  :
:
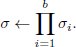
We introduce aggregate signature scheme given by Boneh et al.’s [38] as follows:
• Setup: Let e : G1 x G2  GT, where g generates the group G2 of prime order q.
GT, where g generates the group G2 of prime order q.
• Gen: Chooses a random sk 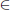 Zq and outputs pk = gsk.
Zq and outputs pk = gsk.
• Sig: A signature on message m is  = H(m)sk, where H is a hash function H : {0, 1}*
= H(m)sk, where H is a hash function H : {0, 1}*  G1.
G1.
• Ver: To verify signature  on message m, one checks that e(
on message m, one checks that e( , g)
, g)  e(H(m), pk).
e(H(m), pk).
Batch verification is very simple. What we need to do are the following two steps: checking that the mi’s are mutually distinct and ensuring that

where hi = h(mi). Equality (4.1) holds because

In the special case when all b signatures are issued by the same public key pk0 (same signer), the verification is faster only for 2 pairings. One needs to verify that
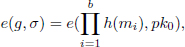
where m1, m2,…, mb are the signed messages.
However, Camenisch et al. [60] pointed out that the aggregate scheme in [38] is not a batch verification scheme since, for any a  1
1 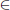 G1, the two invalid message-signature pairs P1 = (m1, a
G1, the two invalid message-signature pairs P1 = (m1, a  H(m1)sk) and P2 = (m2, a−1
H(m1)sk) and P2 = (m2, a−1  H(m2)sk) will verify under Definition 4.2.3.
H(m2)sk) will verify under Definition 4.2.3.
4.2.3 Identity-Based Aggregate Signature
In 2006, Gentry and Ramzan [121] gave the first identity-based aggregate signature (IBAS) as follows:
• Setup: It generates groups G1 and G2 of prime order q and an admissible pairing e : G1 x G1  G2; chooses an arbitrary generator P
G2; chooses an arbitrary generator P  G1. In addition, it chooses three cryptographic hash functions H1, H2 : {0, 1}*
G1. In addition, it chooses three cryptographic hash functions H1, H2 : {0, 1}*  G1, and H3 : {0, 1}*
G1, and H3 : {0, 1}*  Z*q. After setting the system parameters, PKG picks a random number skPKG
Z*q. After setting the system parameters, PKG picks a random number skPKG  Z*q as its secret key and sets its public key as Ppub = skPKG
Z*q as its secret key and sets its public key as Ppub = skPKG  P. The system parameters are params = (G1, G2, q, e, P, Ppub, H1, H2, H3). The sytem’s secret is skPKG.
P. The system parameters are params = (G1, G2, q, e, P, Ppub, H1, H2, H3). The sytem’s secret is skPKG.
• Extract:

where Q0IDi = H1(IDi||0) and Q1IDi = H1(IDi||1).
• Individual Signing:
(1) Choose a unique string ω and compute Pω = H2(ω)  G1;
G1;
(2) Compute ci = H3(mi, IDi, ω)  Z*q;
Z*q;
(3) Generate a random number ri, where ri  Z*q;
Z*q;
(4) Compute signature Sigi = (ω, Ui, Vi) for message mi, where

• Aggregate: Anyone can aggregate a collection of individual signatures that use the same string ω. Signatures Sigi = (Ui, Vi) where 0 ≤ i ≤ N can be aggregated to Sig = (U, V) where U =  bi=0 Ui and V =
bi=0 Ui and V =  bi=0 Vi.
bi=0 Vi.
• Verification:
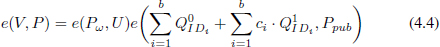

Figure 4.1: Individual decryption model
where ci = H3(mi, IDi, ω). The batch verification equality (4.4) holds because:
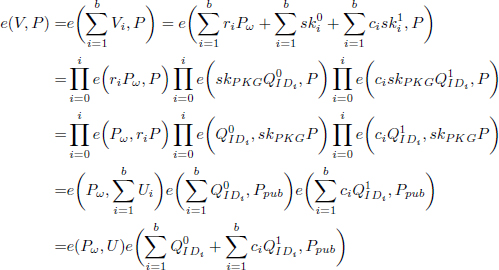
4.3 Batch Decryption and Batch Key Agreement
In the above sections, we focus on signature aggregation and batch verification. From now on, we focus our attention to batch decryption and key agreement schemes. In batch decryption, batch RSA based on the RSA scheme is a frequently used example to explain this concept. Batch RSA was first proposed by Fiat [111] in 1989 and later developed by Boneh and Shacham [43] in 2002. It is designed to speed up RSA decryption and signing algorithms. Batch RSA has many applications. Since it was proposed, it has attracted many researchers and industry engineers. Shacham and Boneh [242] improved performance of SSL based on batch RSA. Yacobi and Beller [298] applied the mathematical ideas of batch RSA to DH-based schemes. They proposed a batch Diffie-Hellman key agreement scheme. Figure 4.1 gives an individual decryption model where messages are encrypted by the different public keys and sent to decryption module individually and the decryption operations are performed one by one. Thus, the total cost is n times individual decryption in the dotted line box (we assume that it is a server) in Figure 4.1.
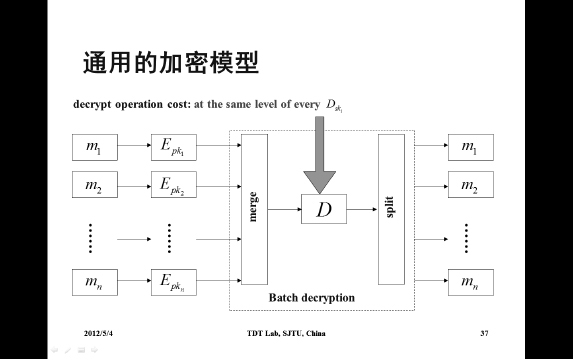
Figure 4.2: Universal batch decryption model
We are trying to find a way to improve the efficiency by a batch model instead of this individual decryption model. Figure 4.2 gives a universal batch decryption model where the messages are encrypted by the different public keys and sent to decryption module individually. The decryption module first merges these ciphertexts, decrypts using its secret key only once, and splits to individual plaintexts.
Batch RSA can do a number of RSA decryptions for approximately the cost of a single decryption.
For the integrally introducing batch RSA, we first give the RSA scheme and then give Fiat’s batch RSA and Boneh and Shacham’s batch RSA.
4.3.1 Review of RSA
RSA [233] is the most widely deployed public key cryptosystem. It is used for securing web traffic, e-mail, and some wireless devices. Since RSA is based on arithmetic modulo large integer numbers it might be slow in constrained environments. For example, 1024-bit RSA decryption on a small handheld device such as the PalmPilot III can take as long as 30 seconds. Similarly, on a heavily loaded web server, RSA decryption significantly reduces the number of SSL requests per second that the server can handle. Typically, one improves performance of RSA using special-purpose hardware. Current RSA coprocessors can perform as many as 10,000 RSA decryptions per second (using a 1024-bit modulus) and even faster processors are coming out.
The RSA encryption scheme can be summarized as follows. The public key is the pair (N, e), where N is the product of two large primes p and q, and e is chosen to be coprime to Euler’s function φ(N). The private key is d where d  e−1 (mod φ(N)).
e−1 (mod φ(N)).
To encrypt a message m, one computes the ciphertext c as follows:

To decrypt the ciphertext c, one computes
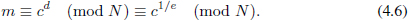
Thus, every decryption consists of one full-sized modular exponentiation.
Later, Quisquater and Couvreur [230] suggested the use of the Chinese Remainder Theorem (CRT) in order to make the decryption run slightly faster. It is standard practice to employ the Chinese Remainder Theorem for RSA decryption. Rather than compute 
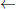 cd mod N, the decryptor evaluates:
cd mod N, the decryptor evaluates:

and

Here, dp  d (mod p – 1) and dq
d (mod p – 1) and dq  d (mod q – 1). Then the decryptor uses the CRT to calculate m from mp and mq. This is approximately four times faster than evaluating cd (mod N) directly.
d (mod q – 1). Then the decryptor uses the CRT to calculate m from mp and mq. This is approximately four times faster than evaluating cd (mod N) directly.
Generally speaking, a small value of e is chosen, which is coprime to φ(N), and d will be O(φ(N)). In fact, if d was too small (less than exponential in the security parameter), it would allow the cryptanalyst to attack the scheme. Weiner [296] gives attacks on the short private key d of RSA.
Problem 4.3.1. How to cut down the cost of decryption with a batch of ciphertext?
Fiat’s batch RSA gives us the first answer to this problem.
4.3.2 Batch RSA
Fiat’s batch RSA [111] can be shown in Figure 4.3. Let e1, e2,…, eb be b different encryption exponents, coprime to φ(N) and to each other where N is defined as in the RSA scheme. Let be O bits long. Given ciphertext c1, c2,…, cb related to plaintext m1, m2,…, mb, our goal is to generate the b roots (decryptions):

Figure 4.3: Batch RSA decryption


Let T be a binary tree with leaves labeled e1, e2,…, eb. Let di denote the depth of the leaf labeled ei, T should be constructed so that W = 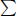 bi=1 di log ei is minimized similar to the Huffman code tree construction. For the main result of O(log2 N) multiplications per RSA operation, Fiat’s scheme could simply assume that T is a full binary tree. In practice, there is some advantage in using a tree that minimizes the sum of weight times path length because the work performed is proportional to the sum W above. Note that W = O(log b log e). Finally, Fiat shows that the number of multiplications required to compute the b roots above is O(W + log N).
bi=1 di log ei is minimized similar to the Huffman code tree construction. For the main result of O(log2 N) multiplications per RSA operation, Fiat’s scheme could simply assume that T is a full binary tree. In practice, there is some advantage in using a tree that minimizes the sum of weight times path length because the work performed is proportional to the sum W above. Note that W = O(log b log e). Finally, Fiat shows that the number of multiplications required to compute the b roots above is O(W + log N).
In Fiat’s scheme, the first goal is to generate the product:
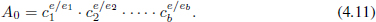
Fiat also shows that this requires O(W) multiplications. Use the binary tree T as a guide, working from the leaves to the root. Every internal node takes the recursive result from the left branch (L) raises it to the power ER where ER is the product of the labels associated with leaves on the right branch. Similarly, each node takes the result from the right branch (R) and raises it to the power EL, which is the product of the labels on the left branch. Each node saves the intermediate results LER and REL (required later). The result associated with this node is LER  REL. The product A0 is simply the result associated with the root.
REL. The product A0 is simply the result associated with the root.
Second, it extracts the e-th root of the product A0:

This involves O(log N) modular multiplications which is equivalent to one RSA decryption.
Third, the factors of A are the roots. The next goal is to break the product A into two subproducts, the breakup is implied by the structure of the binary tree T used to generate the product C. The scheme repeats this recursively to break up the product into its b factors.
Let e1, e2,…, ek be the labels associated with the left branch of the root of the binary tree T. Define an exponent X by means of the Chinese Remainder Theorem (CRT):
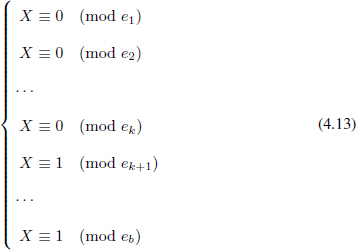
There is a unique solution for X modulo e =  bi=1 ei by CRT. By (4.13), let
bi=1 ei by CRT. By (4.13), let

and

where X1, X2 are positive integers. Let P1 =  ki=1 ei and P2 =
ki=1 ei and P2 =  bi=k+1 ei, then X = P1
bi=k+1 ei, then X = P1  X1 and X – 1 = P2
X1 and X – 1 = P2  X2. Compute
X2. Compute
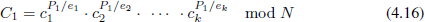
and
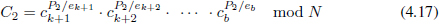
Note that C1 and C2 have been computed, as the left and right branch values of the root, during the tree-based computation of A0.
Raise A to the X-th power modulo N, it follows from
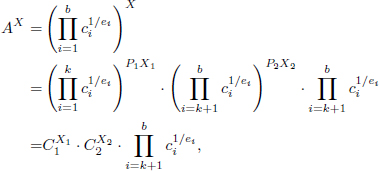
that Q2 =  bk+1 c1/eii, and so Q1 =
bk+1 c1/eii, and so Q1 =  ki=1 c1/eii since Q1 = A/Q2. After that, it recursively breaks up the two products Q1 and Q2, respectively, until each c1/eii is obtained. Thus, the overall number of multiplications is O(W). The number of modular divisions required is O(b).
ki=1 c1/eii since Q1 = A/Q2. After that, it recursively breaks up the two products Q1 and Q2, respectively, until each c1/eii is obtained. Thus, the overall number of multiplications is O(W). The number of modular divisions required is O(b).
To summarize this method, we introduce the following theorem.
Theorem 4.3.2 (Fiat [111]). Let e1, e2,…, eb be b different encryption exponents, relatively prime to φ(N) and to each other. Given the ciphertexts c1, c2,…, cb, we can generate the b roots

in O(log b( bi=1 log ei) + log N) modular multiplications and O(b) modular divisions.
bi=1 log ei) + log N) modular multiplications and O(b) modular divisions.
Fiat’s batch RSA gave an example when using small public exponents e1 and e2, it decrypts two ciphertexts for approximately the price of one decryption.
Suppose c1 is a ciphertext obtained by encrypting some plaintext m1 using the public key (N, 3), and c2 is a ciphertext for some m2 using (N, 5). To decrypt, they must compute c1/31 and c1/52 (mod N). Fiat observed that by setting

one obtains

and

Hence, at the cost of computing a single 15th root and some additional arithmetic, it is able to decrypt both c1 and c2. Computing a 15th root is considered to take the same time as a single RSA decryption in this case.
Boneh and Shacham [43] generalized (4.19) and (4.20) to
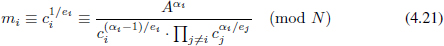
where αi satisfies

where 1 ≤ i,j ≤ b.
This method requires b different modular inversions whereas Fiat’s tree-based method requires 2b modular inversions, but fewer auxiliary multiplications. Thus, Boneh and Shacham give an improvement to Fiat’s scheme. However, in Boneh and Shacham’s scheme, it is still required to solve the systems of linear congruences Equations (4.22) with b modular inversions. In addition, it is not easy to implement in hardware using these different public keys (e1, e2,…, eb) as the modular equipped in advance in the chip based systems. Thus, we leave the following problems:
Problem 4.3.3. For each b, how to obtain all αi’s satisfying Equation (4.22) without any modular operation?
Problem 4.3.4. Are there any other methods to split the plaintext directly like Equation (4.21)?
Once Problem 4.3.3 is solved, we can directly obtain mi satisfying Equation (4.21) using only one modular N, which allows us to implement batch RSA in hardware easily. If the answer to Problem 4.3.4 is positive, we can get more methods to split plaintext to individual. We will discuss it in Section 4.4.
4.3.3 Batch Key Agreement
In this section, we consider a star-like network to present the batch key agreement. For example, in a personal communication system network, the central server, through the ports, agrees upon a session key with each of the users. Each port holds a secret key that is used to establish a secret channel in the network.
Yacobi and Beller [298] proposed a solution, in which each of the users picks a random number, encrypts it with the public key of the corresponding port, and sends it to the counterpart port. The central server decrypts the received ciphertext, and uses the random numbers or their hash values as session keys. Yacobi and Beller [298] summarized the difference between RSA-based and DH-based key exchange. The basic DH scheme was first proposed in [99], which makes the key exchanged individually and needs b operations when the number of the users is b. Yacobi and Beller [298] presented a batch RSA key agreement as follows:
• First, the central server with b ports communicates with the users. The central server generates a public/private key pair for each port. The modulus is a composite N, which is the product of two large primes p and q. Each port’s public key ei is chosen to be prime to Euler’s function φ(N) and pairwise coprime. The private key is di, where di  e−1i (mod φ(N)).
e−1i (mod φ(N)).
• Second, when b users want to agree on session keys individually with the central server, each user needs to find an available port and encrypts a chosen random number using the port’s public key ei.
• Third, when the central server receives the ciphertexts from each port i, it takes one decryption similar to the batch RSA decryption in the above section and gets the random numbers that could finally generate the session keys.
4.4 Batch RSA’s Implementation Based on Diophantine Equations
In this section, we introduce our batch RSA implementation based on Diophantine Equations. Our implementation of batch RSA reduces b – 1 modular inversion computation compared with Fiat’s batch RSA and Boneh and Shacham’s implementations. Furthermore, our implementation is more suitable for hardware circuits. If we apply this algorithm to a hardware circuit for batch RSA decryption, our implementation requires only one circuit module to do modular operations for N, while each of the other two implementations requires b different modules to do modular operations, which is difficult to be written into chips in advance and varies for every decryption.
4.4.1 Implementation Based on Plus-Type Equations
We find that the solutions of the Diophantine equation

can be used to implement batch RSA so that the plaintexts can be constructed directly and the whole decryption only uses modular N. We call Equation (4.23) a Plus-Type Diophantine Equation or Plus-Type Equation. For convenience, throughout this book, Equation (4.23) with n unknown variables is denoted as Equation (4.23)n.
Our new implementation of batch RSA contains three algorithms: KeyGen, Encrypt, and Decrypt. The essence of the new implementation is in the decryption algorithm.
• KeyGen: This algorithm follows Fiat’s batch RSA key generation algorithm except choosing the public keys e1, e2,…, eb from solutions of Equation (4.23)n, that is, {e1, e2,…, eb}  {x1, x2,…, xn}.
{x1, x2,…, xn}.
• Encrypt: This algorithm is same as in Fiat’s batch RSA.
• Decrypt: This algorithm consists of three steps:
– “Merge": The algorithm evaluates A0 =  1≤i≤b ce/eii mod N. This computation can be finished by Fiat’s optimized algorithm [111].
1≤i≤b ce/eii mod N. This computation can be finished by Fiat’s optimized algorithm [111].
– “One decrypt": The algorithm evaluates one full-scale modular exponentiation A  Ad0 mod N.
Ad0 mod N.
– “Split": The essence of our implementation is

where 1 ≤ i ≤ b, and it outputs1
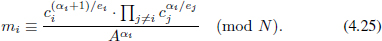
Remark 4.4.1. In our decrypt algorithm, after the plaintext (m1, m2,…, mb-1) are decrypted, the final mb can be calculated by

where the computation can be reduced.
Remark 4.4.2. If the public keys e1, e2,…, eb are chosen arbitrarily (not from the solution (x1, x2,…, xn) of Equation (4.23)n), Equation (4.25) also satisfies when αi satisfies

Theorem 4.4.3 (Correctness). The above scheme is correct.
Proof. From A = Ad0 mod N, we have

Since (x1,…, xn) is a solution of Equation (4.23)n, we have

and  1≤k≤n xk/xi
1≤k≤n xk/xi  0 (mod xj) (for all i, j such that 1 ≤ i ≤ n, 1 ≤ j ≤ n, j
0 (mod xj) (for all i, j such that 1 ≤ i ≤ n, 1 ≤ j ≤ n, j  i). Hence ei\αi + 1 and ej\αi (for all i, j such that 1 ≤ i ≤ b, 1 ≤ j ≤ b, j
i). Hence ei\αi + 1 and ej\αi (for all i, j such that 1 ≤ i ≤ b, 1 ≤ j ≤ b, j 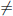 i). In Equation (4.25), all the modular exponentiations are integer exponentiations. Therefore, it follows from a direct computation that mi
i). In Equation (4.25), all the modular exponentiations are integer exponentiations. Therefore, it follows from a direct computation that mi  c1/eii (mod N), where 1 ≤ i ≤ n.
c1/eii (mod N), where 1 ≤ i ≤ n. 
For a simple example, we choose a solution (2, 3, 7) of Equation (4.23)3 and take 3 and 7 as the public keys e1 and e2, respectively. Thus,

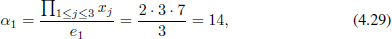
and
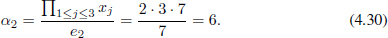
Thus, we can get mi as follows:
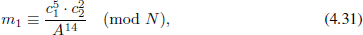
and

In fact, mb can be obtained through Remark 4.4.1. As shown in the above example, if we compute m2 first and then compute m1 = A/m2, we can finish the split (decryption) efficiently. Therefore, we give a new method to compute αi without any modular operation and a new method to split the plaintext. And so, the answer to Problem 4.3.4 is “YES”. As far as Problem 4.3.3 is concerned, for arbitrary positive integer b, we are able to find many αi’s. Furthermore, if b is not greater than 8, we are able to find all αi’s. We will introduce our work towards these problems in detail in Section 4.5.
Here, we would like to point out the differences among Fiat’s RSA, Boneh and Shacham’s Batch RSA and our implementation. The advantage of our implementation is that there is only one modular, mod N, while both Fiat’s batch RSA and Boneh and Shacham’s implementation require at least b modulars.
Fiat’s batch RSA: In KeyGen, {e1,…, eb} are randomly picked. In Decrypt, Fiat’s tree-based method requires 2b + 1 modulars. k is chosen so that 1 ≤ k ≤ b. Let P1 =  1≤i≤k ei, P2 =
1≤i≤k ei, P2 =  k<i≤b ei, X1 = P−11 mod P2, X2 = P1 X1-1/P2. Then compute
k<i≤b ei, X1 = P−11 mod P2, X2 = P1 X1-1/P2. Then compute

and
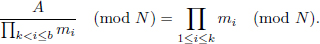
This process is done recursively until m1, m2,…, mb are calculated.
Boneh and Shacham’s improvement: In Decrypt, αi is obtained from Equations (4.22). Then m1,…, mb-1 are evaluated by Equation (4.21). mb is calculated by mb = A/ 1≤j<bmj mod N. The evaluation of α1, α2,…, αb requires b modulars.
1≤j<bmj mod N. The evaluation of α1, α2,…, αb requires b modulars.
Our implementation: α1, α2,…, αb are evaluated directly from the solution of Equation (4.23). Therefore, b – 1 modulars are reduced. Furthermore, we get the plaintext mi from Equation (4.21).
4.4.2 A Concrete Example Based on Plus-Type Equations
We give a concrete example to explain our algorithm to show its advantage.
KeyGen: Let the batch size b = 7. Randomly choose two 512-bit primes p and q:
p =10117548898104292384286149905619010120991278203895691114024386173114298 44196706850901843445909220802938862195711111823138805089269233175589739 8024486601967,
q =11942104782310447106884510125435655207765533763318483151065949254099976 07148379656268155866005262065749842699695077677106764786988072219334757 0651658382099.
Let N = p  q.
q.
N =12082482908131106460128885334610470733722100002825862245001246171456821 80012763601040492827413417501769408868451698340800241737759849184798713 84311467341679006113447482380675139998093264657381057047502767534877118 98885364204757448057797883429393903920166667955622009797159159329896972 3360357448012917410988733.
We also randomly choose a solution (x1, x2, …, x8) of Equation (4.23)8 where

Choose the public keys as a subset of {x1, x2, …, x8}, for example,
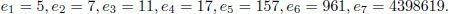
We compute
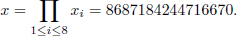
Thus, the public key is (N, b = 7, e1, …, e7, x). We compute the private key d  (
( 1≤i≤7 ei) (mod φ(N)). d is as follows:
1≤i≤7 ei) (mod φ(N)). d is as follows:
d =51876628765295878339434317579819334450607160465137205859602663251881894 76248150332865697383721278328392362980310483479730993621055438208436678 79229731524489835689222861536030650222353925195560713659815910775865522 82418304145301163771498370785315888078449179919532145099665908400332933 900700629001536377165451.
Encrypt: In this algorithm, we randomly choose a set of plaintexts as follows:
m1 =42216335483922430422828646305226638636955551187036758338218940369050771 71838777670539200939753400187558122765253611872592118414072653271581340 49557150686378816189760567012318705743611765112882799638223233870402496 60612305070655416046124619992356068472712803701841057530336101962637429 708518613124606072032913,
m2 =11515339478373653799409100162804092001627376847524519454456897879722755 72450525649782084136951971592156312409505014881084133776507758249194091 01745183559536347953424619444068351729672938002818082476781228433719588 49030458058556915325246572500148818313879322593916775020883447348607809 3654331805097407477851212,
m3 =47564196149813970007363884131737190884763138301794058772403642723080473 12035300434644530039033892729163849746746554561004845842905132968056260 46689776922999970386770238498695474858361140251559169316946590930490790 74855077783622152296547567667859890106605979365108882896772768642533878 129671533527391835259813,
m4 =47076113695544237253122064671136422055958210860752623025678325581081815 84726955718832078797363240141336812574782622687307406041247418256240938 54400992362572138986858352204679423469820466914319036593211022030949477 53860823597327978844407313209862946613671724072935020256407939759987354 078957243653508906462050,
m5 =30568044214000539098104805334573980758657958880378082233476394264866596 11473267935711445240332623905770776659086150428617242444099500783232312 04676910816693107200514851741175379334306919644777051154134292280179732 07188602119552456911467534569434906151478718718595432509630542457525910 131946213578956292963396,
m6 =41377747175811034232018876246074059499644813172580074927939214929882998 79343270705904474700195302890675803041195770969714258620664937410522441 78736605455167725304146829924000744594614850114240963709159146374669699 62099112312462790622604288246922576918641763721175549148057922321723822 247230264707138113937042,
and
m7 =18771896161902354107492151420608960655175748847557766591096333115544693 88639115772459886403263920691549973938090162854541237354779139974823373 22150711283782344174258728142522160188013242155927394712955764457748723 37172809149112059845297173025509381745188281479782761341318653942719134 671008123932040544891767.
Since the ciphertext ci is computed as follows ci = meii (mod N), where 1 ≥ i ≥ 7. The ciphertexts are
c1 =32162445244401743657170446510623926600937713705351525278004836278347467 78927818565931306900626346594961086912725141809256522635855273218400519 72284664046732942258138795733271680027669332436406173493987951365152414 60797459530585405018120324737308623849797695612736566101235396092740354 722520913907481538932914,
c2 =11126467052899354989487810154732066615105697509420849586673823566312709 37106371291521967449468618459618164119164667029310985402655564125542964 94010110454544233209099018186584811824903310123116178433727720898855237 28984076826348484900130452142401788332892321945373838606441449511625255 9429226960199357541705876,
c3 =42702738253874326011706347202093584148640737529891335287560057328232353 12936031281751279979434019357164808476168319559847561796277935971011335 12500689235545118116809962307591329406164127984458850739739240726187291 08244500104462787099197514522083354004527717032842340463375898989280266 039035464356357669755894,
c4 =12040562557445113732473911652223993486907469290295457468128810943319836 89865239881378622819502882220194632147152122716053991772220199156765230 27510298197878920424163371390730684468025560664928791033866500650711867 64062267173825842140914417574375291482513842223759443700367430229129300 5181012290132879477619117,
c5 =66699227296798574343397095996822802356352501707241226477647274006905968 10673854955408065485554029221240872924799602606228672828557689341973222 51563295263105644219421197195443848039478669501756964029791476750411047 04900146183224578433038704943628899192782802758784232421703243761756962 894634288996400822908449,
c6 =35842810907626545862969792069041104823971684976414879250901086369792821 45580427757242397757516407715510081504624842581515104846891405331533253 61167679156090524981249642173885098604795315049563957046069182482249951 05623301480564801725462585729948675579745223831303862071442959713127023 481367052128284782369023,
and
c7 =47155671451031215409844124716042641165572494776610186942841230939281162 67241186266669860841735961194282501443823932882005051795195976808037886 40329386789302925870414294037418371443238801520123232628229674559133870 46744561955317811032439098967200824031961905675407869670714450791407371 569282383073692093702050.
Decrypt: In this algorithm, we first merge these ciphertexts to evaluate A0 by Fiat’s method.
A0 =52359866444019503369219138689244129876435136131866887023807097362559424 85204585255108074606984294095293919326326201521808678582533044952634349 94510658185476933422534369085535424171842256268376777043427683909828453 16021327514525201378524377441114039247482047879358064064184921287633493 11895521745079888137070,
After that, we take one decryption which does a full-scale modular exponentiation A  Ad0 (mod N):
Ad0 (mod N):
A =97020381281501165266847566088201413180464241138685997123851463155123151 43976735868920221887471189785523640074792116012536463406101039184891861 98642917692578018622021094482005608364078487921673756050283179384743906 97318487470321735651171108807814620809108832763769829503607711597977756 914765803133937106665598.
Finally, from Equation (4.24), we split the plaintext using the following α2.
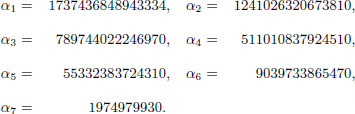
We get the plaintext from Equation (4.25).

We can find that m’1 = m1, which shows the correctness of our implementation. Note that m2, m3, …, m7 can be computed in the same way from Equation (4.25) and Equation (4.26). In fact, we compute m2, m3, …, m7 first and then compute m1 as Remark 4.4.1, we can finish the split (decryption) efficiently.
4.4.3 Implementation Based on Minus-Type Equations
We find that the solutions of the following Diophantine Equation

can also be used to implement batch RSA so that αi, which satisfies Equation (4.22), can be constructed directly and the whole decryption only uses modular N. We call Equation (4.33) the Minus-Type Diophantine Equation or Minus-Type Equation. For convenience, throughout this book, Equation (4.33) with n unknown variables is denoted as Equation (4.33)n.
Our new implementation of batch RSA also contains three algorithms: KeyGen, Encrypt, and Decrypt. The essence of the implementation is in the decryption algorithm. Algorithm KeyGen and Encrypt are the same as our implementation based on the Plus-Type Equations.
Decrypt: This algorithm takes a public key (N, b, e1, e2, …, eb, x =  1≤i≤nxi), a private key d, and ciphertexts c1, c2, …, cb as input. It evaluates A0
1≤i≤nxi), a private key d, and ciphertexts c1, c2, …, cb as input. It evaluates A0  1≤i≤bcie/ei (mod N) by the methods proposed by Fiat, and A
1≤i≤bcie/ei (mod N) by the methods proposed by Fiat, and A  Ad0 (mod N). Obviously
Ad0 (mod N). Obviously
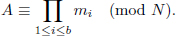
Then it evaluates
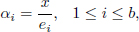
and it outputs
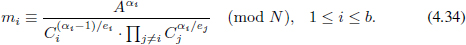
Remark 4.4.4. In our decrypt algorithm, after the plaintext (m1, m2, …, mb–1) are decrypted, the final mb can be calculated by

where computation can be reduced.
In our implementation, b – 1 modulars are reduced, compared with Fiat’s batch RSA and Boneh and Shacham’s improvement. Since (x1, x2, …, xn) is a solution of Equation (4.33)n and {e1, e2, …, eb}  {x1, x2, …, xn}, α1, α2, …, αb are evaluated by αi =
{x1, x2, …, xn}, α1, α2, …, αb are evaluated by αi =  1 ≤j≤nxj/ej without modular inversion. Therefore, there is only one kind of modular operations, which is “mod N.” If we make a hardware circuit for batch RSA decryption, then our implementation requires one circuit module doing modular operations, and other two implementations both require b modules doing modular operations. Our implementation is more suitable for hardware circuit.
1 ≤j≤nxj/ej without modular inversion. Therefore, there is only one kind of modular operations, which is “mod N.” If we make a hardware circuit for batch RSA decryption, then our implementation requires one circuit module doing modular operations, and other two implementations both require b modules doing modular operations. Our implementation is more suitable for hardware circuit.
Theorem 4.4.5 (Correctness). The above scheme is correct.
Proof. See the proof of Theorem 4.4.3.
For a simple example, we choose a solution (2, 3, 11, 13) of Equation (4.33)4 and take 3,11, and 13 as the public keys e1, e2, and e3, respectively.
First, we have

and

and

Second, we can get αi:
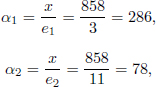
and

Third, we can get mi:

m2 and m3 can be obtained in the same way.
4.4.4 A Concrete Example Based on Minus-Type Equations
We explain the implementation by a concrete example.
KeyGen: Let the batch size b = 4. We choose p = 107 and q = 83. Let N = p  q = 8881. From the solution {x1 = 2, x2 = 3, x3 = 11, x4 = 17, x5 = 59} of Equation (4.33))5, we choose the public key as follows: e1 = 3, e2 = 11, e3 = 17, and e4 = 59. Let e =
q = 8881. From the solution {x1 = 2, x2 = 3, x3 = 11, x4 = 17, x5 = 59} of Equation (4.33))5, we choose the public key as follows: e1 = 3, e2 = 11, e3 = 17, and e4 = 59. Let e =  1≤i≤b ei = 33099 and x =
1≤i≤b ei = 33099 and x =  1≤i≤5 xi = 66198. The private key is d = e−1 (mod φ(N))
1≤i≤5 xi = 66198. The private key is d = e−1 (mod φ(N))  4083.
4083.
Encrypt: Suppose the plaintexts are m1 = 1000, m2 = 2000, m3 = 3000, and m4 = 4000. We compute the ciphertexts c1 = 8281, c2 = 1316, c3 = 4824, and c4 = 169.

Then the algorithm outputs:

where it shows that m’1 = m1. Note that m’2, m’3, and m’4 can be computed in the same way:

Obviously, m’2 = m’2, m’3 = m3, and m’4 = m4.
4.5 Solving the Diophantine Equations
4.5.1 Plus-Type Equations
Algorithms for Solving the Plus-Type Equations
Equation (4.23) is a special case of the problem of expressing 1 as the sum of distinct unit fractions. Equation (4.23) also provides solutions to Znám’s problem: find all sequences {N1, …, Nk} of integers ≥ 2 with the property that for each i, Ni properly divides 1 +  1≤j≤k,j
1≤j≤k,j Nj. In the past forty years, many mathematical researchers have worked on this equation [50, 51, 53, 57, 58, 74–76, 109, 169, 263, 264, 267, 268, 270]. In recent years, applications of Equation (4.23) are also found in the graph theory [52, 58], differential geometry [49, 51], and computation theory [103].
Nj. In the past forty years, many mathematical researchers have worked on this equation [50, 51, 53, 57, 58, 74–76, 109, 169, 263, 264, 267, 268, 270]. In recent years, applications of Equation (4.23) are also found in the graph theory [52, 58], differential geometry [49, 51], and computation theory [103].
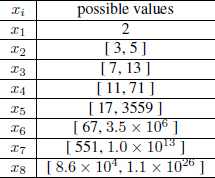
However, it is impossible to solve the Plus-Type Equation when n ≥ by hand. See Table 4.1 for the known possible value intervals for each variable (n = 8).
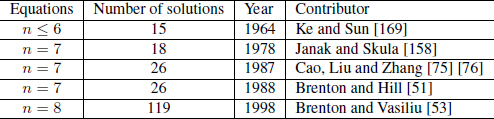
Table 4.1: The known possible values
Although the following results are known, Equation (4.23)8 has not been solved completely until our work was published. Table 4.2 gives the number of solutions for n ≤ 8 in previous works. We have presented an algorithm to solve Equation (4.23) by elliptic curve method. We found all of the 122 solutions for n = 8 in November, 2008. The computation was carried out on one personal computer with 2.3 GHz CPU and lasted 21 days. We have provided the algorithm and all 122 solutions. Although we have not solved Equation (4.23) for all the solutions when n = 9, we have generated solutions based on known solutions [70]. We have found 411 solutions for n = 9, and 2318 solutions for n = 10. Since our method is universal, it could be used to find a number of solutions for n > 10.
Table 4.2: The number of solutions for n ≥ 8 for Equation (4.23)n
Now, we introduce the algorithm to solve Equation (4.23). Firstly, we state some lemmas about Equation (4.23). Then we present the outline and the pseudo codes of the algorithm. Finally we propose a new theorem.
Lemma 4.5.1. Suppose that (x1, x2, …, xn) is a solution of Equation (4.23)n. Then x1, x2, …, xn are pairwise coprime.
Proof. See [51].
Lemma 4.5.2 (Sun and Cao [268]). Let (x1(j), x2(j), …, xn–1(j)) be the j-th solution of Equation (4.23)n–1, 1 ≤ j ≤ Ω(n – 1). Put

Then
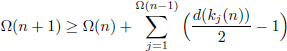
where d(kj(n)) denotes the number of different positive factors of kj(n).
Proof. The proof consists of two steps:
Step 1: Let (x1, x2, …, xn) be any solution of Equation (4.23)n. Put xn+1 =  1≤i≤n xi + 1. By a direct computation, (x1, x2, …, xn+1) is a solution of Equation (4.23)n+1. Hence, Ω(n + 1) ≥ Ω(n).
1≤i≤n xi + 1. By a direct computation, (x1, x2, …, xn+1) is a solution of Equation (4.23)n+1. Hence, Ω(n + 1) ≥ Ω(n).
Step 2: Let (x1(j), x2(j), …, xn–1(j)) be as above. Let k be one positive factor of kj(n), such that 1 < k <  kj(n). Put
kj(n). Put
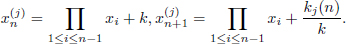
By a direct computation, it is proved that ((x1(j), x2(j), …, xn+1(j)) is a solution of Equation (4.23)n+1. For each j, 1 ≥ j ≥ Ω(n – 1), the number of k satisfying 1 < k  kj(n) is d(kj(n))/2 – 1. Hence, we can generate
kj(n) is d(kj(n))/2 – 1. Hence, we can generate  Ω(n–1)j=1 (d(kj(n))/2 – 1) solutions of Equation (4.23)n+1. These solutions are all different from the solutions generated in Step 1, since x(j)n
Ω(n–1)j=1 (d(kj(n))/2 – 1) solutions of Equation (4.23)n+1. These solutions are all different from the solutions generated in Step 1, since x(j)n  1≤i≤n–1 xi + 1. Therefore, Ω(n + 1) ≥ Ω(n) +
1≤i≤n–1 xi + 1. Therefore, Ω(n + 1) ≥ Ω(n) +  Ω(n–1)j=1 (d(kj(n))/2 – 1).
Ω(n–1)j=1 (d(kj(n))/2 – 1).
Lemma 4.5.3. Suppose 2 ≤ x1 < … < xn–2 and x1, x2, …, xn–2 are pairwise coprime. Put

Let P and Q be positive integers such that PQ = A2 + B, P < Q. Put

If B|A + P and B|A + Q, (x1, x2, …, xn) is a solution to Equation (4.23)n.
Proof. This lemma is proved by a direct computation.
Lemma 4.5.4. Put x1 = A, where A is an arbitrary positive integer. For 1 ≤ i < n, let xi+1 be the minimum positive integer such that xi+1 > xi and xi+1 is coprime to all x1, x2, …, xi. If
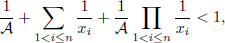
there is no solution of Equation (4.23)n with x1 = A.
Proof. Suppose there is one solution of Equation (4.23)n with x1 = A. For 1 ≤ i < n, xi+1 is the minimum positive integer such that xi+1 > xi and xi+1 is coprime to x1, x2, …, xi.
For all solutions (A, x2, x*3, …, x*n) of Equation (4.23)n, we have

It is a contradiction.
Algorithm Outline-Direct Finding Algorithms
Let (x1, x2, …, xn) be a solution of Equation (4.23)n.
• First we calculate the lower bound of x1, L1, and the upper bound of x1, U1.
Let x1 be A, and xi+1 be the minimum positive integer such that xi+1 > xi, and xi+1 is coprime to x1, x2, …, xi, 1 ≤ i < n. If  1≤i≤n 1/xi +
1≤i≤n 1/xi +  1≤i≤n 1/xi ≥ 1, then A
1≤i≤n 1/xi ≥ 1, then A  [L1, U1] by Lemma 4.5.17.
[L1, U1] by Lemma 4.5.17.
For example, for Equation (4.23)8, we fix x1 = 2 and then we get x2 = 3, x3 = 5, x4 = 7, x5 = 11, x6 = 13, x7 = 17, and x8 = 19. From
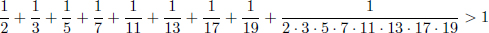
we have 2  [L1, U1].
[L1, U1].
• Then for all values of x1 over the range [L1, U1], we calculate the lower bound of x2, L2, and the upper bound of x2, U2. In this way we fix (x1, x2, …, xi), then we calculate Li+1 and Ui+1, 1 ≤ i < n – 1.
– From
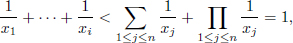
we have

Hence,
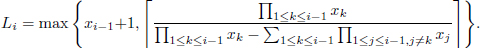
– It follows from

that
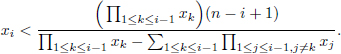
Therefore,

– When (x1, x2, …, xi-1) are fixed, put xi = Ui and let xj(i < j ≤ n) be the minimum positive integer such that xj is coprime to x1, …, xj-1 and xj > xj-1. Then 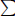 1≤i≤n 1/xi +
1≤i≤n 1/xi +  1≤i≤n 1/xi ≥ 1. We can further reduce Ui based on this fact.
1≤i≤n 1/xi ≥ 1. We can further reduce Ui based on this fact.
• After all the lower/upper bounds of (x1, x2, …, xn-2) are calculated, for all values of xi over the range [Li, Ui] (1 ≤ i ≤ n – 2), put A = 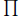 1≤i≤n-2 xi, B = A –
1≤i≤n-2 xi, B = A – 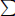 1≤i≤n-2 A/xi. Factorize A2 + B. For all positive integers P and Q such that PQ = A2 + B, P < Q, put xn-1 = A+P/B, xn = A+Q/B. If both xn-1 and xn are integers, (x1, x2, …, xn) is a solution of Equation (4.23)n.
1≤i≤n-2 A/xi. Factorize A2 + B. For all positive integers P and Q such that PQ = A2 + B, P < Q, put xn-1 = A+P/B, xn = A+Q/B. If both xn-1 and xn are integers, (x1, x2, …, xn) is a solution of Equation (4.23)n.
There are many methods to factorize A2 + B, such as general number field sieve, multiple polynomial quadratic sieve, elliptic curve method, and quantum algorithm. The general number field sieve [56,88] is the most efficient algorithm known for factoring integers larger than 100 digits. Its complexity is LN[1/3, c], where LN[c1, c2] = O(e(c2+o(1))(log N)c1 (log log N)1 – c1), and N is the integer to be factorized. The complexity of multiple polynomial quadratic sieve is LN[1/2, 1]. The elliptic curve method [103] is the most suitable method for finding small factors. Its running time is dominated by the size of the smallest factor, while the complexity of the first two methods is both determined by the size of the number to be factored.
In our algorithm, integers are factorized by the elliptic curve method. Other methods also work well.
We present the pseudo codes of algorithm for further explanation.




Remark 4.5.5. The complete solutions of Equation (4.23) can be found by running Algorithm Search 1 (depth = 1).
Remark 4.5.6. Algorithm search can be further optimized. The computation amount of decomposing an integer is about 60,000 times as the computation amount of computing xn based on (x1, …, xn-1). Hence, we factorize A2 + B to get xn-1, xn only if Un-1 - Ln-1 > 120, 000.
Remark 4.5.7. We apply the computer program in [4] to factorization. We would like to thank D. Alpern again.
The computer program examines all possible tuple (x1, …, x6), and executes the factorization to find x7 and x8 for each tuple. The maximum value to be factorized is about 1026, which can be factorized efficiently by elliptic curve method. Elliptic curve method is a randomized method. It may fail to factorize by treating a composite number as a prime. We make sure that this method is always successful when the computer continues searching for the solutions.
Theorem 4.5.8. Equation (4.23)8 has only 122 solutions. There is only one solution such that x1, …, x8 are all primes: 2, 3, 11, 23, 31, 47059, 2217342227, 1729101023519.
All these 122 solutions can be found in Appendix A.
We propose a new method, which can generate solutions of Equation (4.23)n+3 from solutions of Equation (4.23)n [68–70]. We call it Gap-three extension algorithm. See the following pseudo codes.


The correctness of this method is based on the following lemma.
Lemma 4.5.9 (Cao [70]). Let (x1, x2, …, xn-2) be a solution of Equation (4.23)n-2.
Put N =  1≤i≤n-2 xi. Then
1≤i≤n-2 xi. Then

is a solution of Equation (4.23)n+1, where xn-1, xn, xn+1 are integers satisfying xn-1 < xn < xn+1 and t, k are positive integers. Moreover, N, k, t are pairwise coprime. If 2|N, k  t
t  1 (mod 4).
1 (mod 4).
Proof. The proof consists of the following steps:
Step 1: By a direct computation, it is easy to check that (x1, x2, …, xn+1) is a solution of Equation (4.23)n+1.
Step 2: Set y = xn-1, z = xn, w = xn+1. Then from

we have

Therefore,

Hence,

Let d denote gcd(N, k). Then z  w
w  k
k  0 (mod d), and N
0 (mod d), and N  (N + k)
(N + k)  w + N
w + N  (N + k)
(N + k)  z + 1
z + 1  1 (mod d). Therefore, d|1. Hence, N and k are coprime.
1 (mod d). Therefore, d|1. Hence, N and k are coprime.
Step 3: Let d’ denote gcd(k, t). From w  Z, we have t|[N
Z, we have t|[N  (N + k)(N + N2+t)/k)+1]. Hence, d’|[N
(N + k)(N + N2+t)/k)+1]. Hence, d’|[N  (N + k)(N + N2+t/k) + 1]. From d’|k, we get d’|[N2(N + N2+t)/k) + 1]. Since N2+t/k
(N + k)(N + N2+t/k) + 1]. From d’|k, we get d’|[N2(N + N2+t)/k) + 1]. Since N2+t/k  Z, we have k|(N2 + t). Therefore d’|N2. It follows that d’|1. Hence, k and t are coprime.
Z, we have k|(N2 + t). Therefore d’|N2. It follows that d’|1. Hence, k and t are coprime.
Step 4: Let d” denote gcd(N, t). From
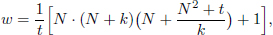
it follows that

Since d“|(wt) and d“|N, we have d“|1. Therefore, N and t are coprime.
It follows from Steps 2, 3, and 4 that N, k, and t are pairwise coprime.
Step 5: Assume that 2|N. Since t|[N  (N + k)
(N + k)  (N + N2+t/k) + 1] and 2|N, we have 2
(N + N2+t/k) + 1] and 2|N, we have 2  t. From k|(N2 + t), we have 2
t. From k|(N2 + t), we have 2  k. From (k, t) = 1, we get (-t/k) = 1. Then from t|[N
k. From (k, t) = 1, we get (-t/k) = 1. Then from t|[N  (N + k)
(N + k)  (N + N2+t/k) + 1], we have t|[N
(N + N2+t/k) + 1], we have t|[N  (N + k)
(N + k)  (nk + N2 + t) + k], i.e., t|[N2
(nk + N2 + t) + k], i.e., t|[N2  (N + k)2 + k]. Therefore (-k/t) = 1. We have,
(N + k)2 + k]. Therefore (-k/t) = 1. We have,

Thus,


Now we propose the following new theorem.
Theorem 4.5.10. Let Ω(k) denote the number of solutions of Equation (4.23)k. We have

where A(n + 1) = 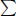 Ω(n+1)j=1 (d(kj(n+2))/2 - 1), d(kj(n + 2)) is defined in Lemma 4.5.2, B(n) denotes the number of solutions found by the Algorithm 2 based on n, restricted by t > 1 and k > 1,
Ω(n+1)j=1 (d(kj(n+2))/2 - 1), d(kj(n + 2)) is defined in Lemma 4.5.2, B(n) denotes the number of solutions found by the Algorithm 2 based on n, restricted by t > 1 and k > 1,  (n + 2) denotes the number of solutions generated as follows: (x1, x2, …, xn+2) be a solution of Equation (4.23)n+2 satisfying that (x1, x2, …, xn+1) is not a solution of Equation (4.23)n+1, and C = (
(n + 2) denotes the number of solutions generated as follows: (x1, x2, …, xn+2) be a solution of Equation (4.23)n+2 satisfying that (x1, x2, …, xn+1) is not a solution of Equation (4.23)n+1, and C = (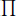 1≤i≤n+1 xi)2 + 1. Let k be a factor of C, such that 1 < k <
1≤i≤n+1 xi)2 + 1. Let k be a factor of C, such that 1 < k < 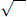 C. Put
C. Put

Then

is a solution of Equation (4.23)n+3.
Proof. Let S(k) be the set of all solutions of Equation (4.23)k. In fact there are at least four different methods to generate solutions of Equation (4.23)n+3 listed in Table 4.6. Methods 3 and 4 are from [70]. They are used firstly to generate solutions of Equation (4.23) when n = 9, 10 in Theorems 4.5.11 and 4.5.12.
Table 4.6: Four methods to generate solutions of Equation (4.23)n+3

We prove that the solutions generated by the four methods are all different. The proof consists of the following three steps.
Step 1: It follows from Lemma 4.5.2 that the solutions generated by Method 2 are different from Method 1.
Step 2: The solutions generated by Method 3 are all different from Method 1. Because t > 1, xn+3 <  1≤i≤n+2 xi + 1 in Method 3, while xn+3 =
1≤i≤n+2 xi + 1 in Method 3, while xn+3 =  1≤i≤n+2 xi + 1 in Method 1.
1≤i≤n+2 xi + 1 in Method 1.
The solutions generated by Method 3 are also different from Method 2. Since k > 1, (x1, x2, …, xn+1)  S(n + 1) in Method 3, while (x1, x2, …, xn+1)
S(n + 1) in Method 3, while (x1, x2, …, xn+1) 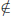 S(n + 1) in Method 2.
S(n + 1) in Method 2.
Step 3: The solutions generated by Method 4 are all different from Methods 2 and 3, because (x1, x2, …, xn+1)  S(n + 1), (x1, x2, …, xn)
S(n + 1), (x1, x2, …, xn) 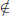 S(n) in Method 4, but (x1, x2, …, xn+1)
S(n) in Method 4, but (x1, x2, …, xn+1)  S(n + 1) in Method 2, (x1, x2, …, xn)
S(n + 1) in Method 2, (x1, x2, …, xn)  S(n) in Method 3.
S(n) in Method 3.
The solutions generated by Method 4 are also different from Method 1. Since k > 1, xn+3 <  1≤i≤n+2 xi + 1 in Method 4, while xn+3 =
1≤i≤n+2 xi + 1 in Method 4, while xn+3 =  1≤i≤n+2 xi + 1 in Method 1.
1≤i≤n+2 xi + 1 in Method 1.
Therefore, we have Ω(n + 3) ≥ Ω(n + 2) + A(n + 1) + B(n) +  (n + 2).
(n + 2).
We found 411 solutions of Equation (4.23)9. The number of solutions found by each method is listed in the following Table 4.7
Table 4.7: Solutions found in Equation (4.23)9.

Because of space limitations, these solutions are listed in http://tdt.sjtu.edu.cn/9plus.html and solutions found by different methods are also listed separately there.
Theorem 4.5.12. There are at least 2318 solutions of Equation (4.23)10.
We also found 2318 solutions of Equation (4.23)10. The number of solutions found by each method is listed in Table 4.8
Table 4.8: Solutions found in Equation (4.23)10.

These solutions are listed in http://tdt.sjtu.edu.cn/10plus.html. Solutions found by different methods are also listed separately there.
4.5.2 Minus-Type Equations
Similar to the Plus-Type Equations, we propose a fast algorithm to solve Equation (4.33) in this section.
Algorithms for Solving the Minus-Type Equations
Traditional algorithms to solve Equation (4.33) have high computational complexity. Our algorithm is based on factorizing integers using the elliptic curve method. The elliptic curve method is a fast, sub-exponential running time algorithm. We found all 550 solutions for n = 8, and we list them in this section. But the computation amount for n = 9 is beyond our computational capacity. We cannot solve Equation (4.33) for n = 9 directly. Therefore, we propose new methods to generate solutions from known solutions of Equation (4.23) with less variables. We have found 1547 solutions for n = 9 and 18984 solutions for n = 10. Due to space limitations, these solutions are published at webpage http://tdt.sjtu.edu.cn/9minus.html and http://tdt.sjtu.edu.cn/10minus.html. These solutions can be used in the new batch RSA implementation.
Table 4.9: Research results about Equation (4.33)

Equation (4.33) also helps to find Giuga numbers. A number K is a Giuga number if and only if p|(K/p - 1) for all prime divisors p of K, or 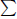 p|K 1/p -
p|K 1/p -  p|K 1/p
p|K 1/p  N [124]. Giuga numbers are named after Giuga [124], who formulated a conjecture on primality in 1950: N is prime if and only if
N [124]. Giuga numbers are named after Giuga [124], who formulated a conjecture on primality in 1950: N is prime if and only if 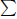 k=1N - 1 kN - 1
k=1N - 1 kN - 1  1 (mod N). In 1996, Borwein et al. [44] published 11 Giuga numbers. Then Hogan and Mangilin found the 12th Giuga number [58], and Girgensohn found another one [58] in 2000. Sloane presented 13 Giuga numbers [261]. We prove that there are only 12 Giuga numbers with less than eight distinct prime factors, through the complete solutions of Equation (4.33) for n ≤ 8, which are listed in Appendix B and Appendix C. The basic idea is that the equation
1 (mod N). In 1996, Borwein et al. [44] published 11 Giuga numbers. Then Hogan and Mangilin found the 12th Giuga number [58], and Girgensohn found another one [58] in 2000. Sloane presented 13 Giuga numbers [261]. We prove that there are only 12 Giuga numbers with less than eight distinct prime factors, through the complete solutions of Equation (4.33) for n ≤ 8, which are listed in Appendix B and Appendix C. The basic idea is that the equation

is a special case of Equation (4.33).  1≤i≤n xi is a Giuga number if and only if (x1, x2, …, xn) is a solution of Equation (4.33)n and x1, x2, …, xn are all primes.
1≤i≤n xi is a Giuga number if and only if (x1, x2, …, xn) is a solution of Equation (4.33)n and x1, x2, …, xn are all primes.
In the following section, we propose a fast algorithm to solve Equation (4.33) and a method to generate new solutions of Equation (4.33) from known solutions of Equation (4.23). We first state some useful lemmas.
Lemma 4.5.13. If(x1, x2, …, xn) is a solution of Equation (4.33), then x1, x2, …, xn are pairwise coprime.
Proof. For any i, j, 1 ≤ i < j ≤ n, put d = gcd(xi, xj). We have
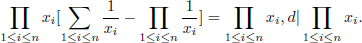
Therefore,

Hence, d|1, and so d = 1. This completes the proof.
Lemma 4.5.14. If (x1, x2, …, xn) is a solution of Equation (4.33), then
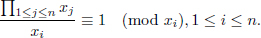
Proof. By a direct computation, it is easy to prove the lemma.
Lemma 4.5.15 (Sun and Cao [266]). Let (x1(j), (x2(j), …, x(n-1(j)) be the j-th solution of Equation (4.23)n-1, 1 ≤ j ≤ Ω(n - 1). Put lj(n) = ( 1≤i≤n-1 xi(j))2 - 1. We have
1≤i≤n-1 xi(j))2 - 1. We have
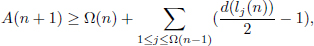
where d(lj(n)) denote the number of different positive factors of lj(n).
Proof. The proof consists of two steps (Cao [70]):
Step 1: Let k be a positive factor of lj(n) satisfying 1 < k <  lj(n). Put
lj(n). Put

Direct computation shows that (x1, x2, …, xn+1) is a solution of Equation (4.33)n+1. The number of k such that 1 < k <  lj(n) is d(lj(n))/2 - 1. Therefore, we can construct
lj(n) is d(lj(n))/2 - 1. Therefore, we can construct  1≤j≤Ω(n-1)(d(lj (n))/2 -1) solutions of Equation (4.33)n+1, and all of the solutions satisfy xn+1
1≤j≤Ω(n-1)(d(lj (n))/2 -1) solutions of Equation (4.33)n+1, and all of the solutions satisfy xn+1  1≤i≤n xi - 1.
1≤i≤n xi - 1.
Step 2: Let (x1, x2, …, xn) be a solution of Equation (4.23)n. Put xn+1 =  1≤i≤n xi - 1. Then (x1, x2, …, xn+1) is a solution of Equation (4.33)n+1. Since xn+1 =
1≤i≤n xi - 1. Then (x1, x2, …, xn+1) is a solution of Equation (4.33)n+1. Since xn+1 =  1≤i≤n xi - 1, this solution is different from any other solutions generated in step 1. Therefore, A(n + 1) ≥ Ω(n) +
1≤i≤n xi - 1, this solution is different from any other solutions generated in step 1. Therefore, A(n + 1) ≥ Ω(n) + 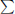 1≤j≤Ω(n-1)(d(lj (n))/2 - 1).
1≤j≤Ω(n-1)(d(lj (n))/2 - 1).
Lemma 4.5.16. For any solution (x1, x2, …, xn) of Equation (4.23)n, put
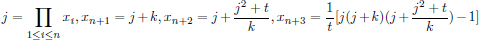
where k, t are positive integers. If xn+1 < xn+2 < xn+3 and xn+1, xn+2, xn+3  Z, then (x1, x2, …, xn+3) is a solution of Equation (4.33)n+3, and
Z, then (x1, x2, …, xn+3) is a solution of Equation (4.33)n+3, and
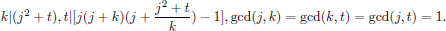
Moreover, 2|j implies (i) the Jacobi symbol (k/t) = 1; (ii) k  1 (mod 4) or k
1 (mod 4) or k  t
t  3 (mod 4).
3 (mod 4).
Proof. Assume that (x1, x2, …, xn) is a solution of Equation (4.23)n. j =  1≤i≤n xi, xn+1 = j + k, xn+2 = j + j2+t/k, xn+3 = 1/t [j(j + k)(j + j2+t/k) - 1], where k, and t are positive integers. Assume that xn+1 < xn+2 < xn+3 and xn+1, xn+2, xn+3
1≤i≤n xi, xn+1 = j + k, xn+2 = j + j2+t/k, xn+3 = 1/t [j(j + k)(j + j2+t/k) - 1], where k, and t are positive integers. Assume that xn+1 < xn+2 < xn+3 and xn+1, xn+2, xn+3  Z. Direct computation shows that (x1, x2, …, xn+3) is a solution of Equation (4.33)n+3. Put y = xn+1, z = xn+2, w = xn+3. We have
Z. Direct computation shows that (x1, x2, …, xn+3) is a solution of Equation (4.33)n+3. Put y = xn+1, z = xn+2, w = xn+3. We have
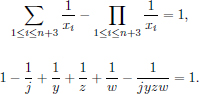
Therefore, zwj + ywj + yzj - 1 = yzw.
Let d denote gcd(j, k), we have d|y since y = j + k. Therefore d|yzw, and so d|1.
Let d’ denote gcd(k, t). Since t|[j(j + k)(j + j2+t/k) - 1], we have

From d’|k, we get

Therefore d’|j2. We have d’|1.
Let d” denote gcd(j, t). From wt = j(j + k)(j + j2+t/k) - 1, and d“|j, d“|wt, it follows that d” = 1.
Hence, gcd(j, k) = gcd(k, t) = gcd(j, t) = 1.
Assume that 2|j. Since t|[j(j + k)(j + j2+t/k) - 1], we have 2  t. From k|(j2 + t) we have 2
t. From k|(j2 + t) we have 2  k. Then from k|(j2 + t) we have
k. Then from k|(j2 + t) we have

Hence j2(j + k)2  k (mod t). We have
k (mod t). We have

Hence, k  1 (mod 4) or k
1 (mod 4) or k  t
t  3 (mod 4).
3 (mod 4).
Lemma 4.5.17. A is any positive integer. Put x1 = A. For 1 < i ≤ n, let xi be the minimum positive integer satisfying xi > xi-1 and xi is coprime to all x1, x2, …, xi-1. If 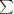 1≤i≤n 1/xi -
1≤i≤n 1/xi -  1≤i≤n 1/xi < 1, there is no solution of Equation (4.33)n with x1 = A.
1≤i≤n 1/xi < 1, there is no solution of Equation (4.33)n with x1 = A.
Proof. Suppose there is one solution of Equation (4.33)n with x1 = A, which is (A, x2*, …, xn*). For 1 < i ≤ n, since xi is the minimum positive integer satisfying xi > xi-1 and xi is coprime to all x1, x2, …, xi-1. We have

This completes the proof.
Lemma 4.5.18. Suppose 2 ≤ x1 < … < xn-2 and x1, x2, …, xn-2 are pairwise coprime. Put
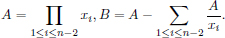
Let P and Q be positive integers such that PQ = A2 - B, P < Q. Put

If xn-2 < xn-1, xn-1  Z and xn
Z and xn  Z, then (x1, x2, …, xn) is a solution of Equation (4.33)n.
Z, then (x1, x2, …, xn) is a solution of Equation (4.33)n.
Proof. By a direct computation, it is easy to prove the lemma.
Let (x1, x2, …, xn) be a solution of Equation (4.33)n.
• First, we calculate L1 (the lower bound of x1) and U1 (the upper bound of x1).
Let x1 be A, and let xi+1 be the minimum positive integer such that xi+1 > xi and xi+1 are coprimes to any of x1, x2, …, xi, 1 ≤ i < n. If 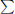 1≤i≤n 1/xi -
1≤i≤n 1/xi -  1≤i≤n 1/xi ≥ 1, then A
1≤i≤n 1/xi ≥ 1, then A  [L1, U1] by Lemma 4.5.17.
[L1, U1] by Lemma 4.5.17.
For example, for Equation (4.33)8, we fix A = 2, then we get x1 = 2, x2 = 3, x3 = 5, x4 = 7, x5 = 11, x6 = 13, x7 = 17, and x8 = 19.

We fix A = 3, then we get x1 = 3, x2 = 4, x3 = 5, x4 = 7, x5 = 11, x6 = 13, x7 = 17, and x8 = 19.

We fix A = 4, then we get x1 = 4, x2 = 5, x3 = 7, x4 = 9, x5 = 11, x6 = 13, x7 = 17, and x8 = 19.

Hence, L1 = 2, U1 = 3.
• Then for all values of x1, x2,…, xi, xj  [Lj, Uj], 1 ≤ j ≤ i, we calculate Li+1 and Ui+1, 1 ≤ i < n – 1.
[Lj, Uj], 1 ≤ j ≤ i, we calculate Li+1 and Ui+1, 1 ≤ i < n – 1.
– From

we have

Hence,
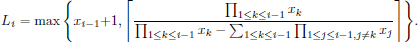
– It follows from

that
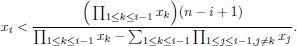
Therefore,

– When (x1, x2,…, xi-1) are fixed, we set xi = Ui and we let xj(i < j ≤ n) be the minimum positive integer such that xj is coprime to any of x1, x2,…, xj-1 and xj > xj-1. Then

We can reduce Ui based on this fact.
• When (x1, x2,…, xn-2) are fixed, calculate xn-1, xn by Lemma 4.5.18. Put

Factorize A2 – B. For all positive integers P and Q such that PQ = A2 – B, P < Q, put

If xn-2 < xn-1, xn-1  Z and xn
Z and xn  Z, then (x1, x2,…, xn) is a solution of Equation (4.33)n.
Z, then (x1, x2,…, xn) is a solution of Equation (4.33)n.
The pseudo codes of the above algorithms are listed as follows:




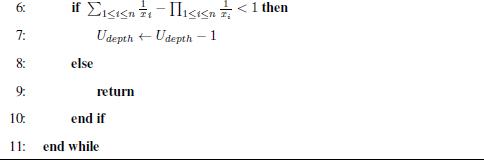
Remark 4.5.19. The complete solutions of Equation (4.33) are found by running Algorithm Search2(depth = 1).
Remark 4.5.20. Algorithm Search2 can be further optimized. The computation amount of factoring an integer is about 60,000 times as that of computing xn from (x1, x2,…, xn-1). Hence, we factorize A2 – B to get xn-1, xn only if Un-1 – Ln-1 > 120,000.
Remark 4.5.21. The integer factorization algorithm is based on Alpern’s [4] contribution.
The new solutions of Minus-type Equation (4.33) can be extracted from the solutions of Plus-type Equation (4.23). The following four methods generate new solutions from known solutions of Equation (4.23).
• Method 1: Gap-one extension. For each solution (x1, x2,…, xn) of Equation (4.23)n, we set xn+1 = 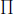 1≤i≤n xi – 1, then (x1, x2,…, xn+1) is a solution of Equation (4.33)n+1.
1≤i≤n xi – 1, then (x1, x2,…, xn+1) is a solution of Equation (4.33)n+1.
• Method 2: Gap-two extension. For each solution (x1, x2,…, xn) of Equation (4.23)n, we set J = 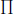 1≤i≤n xi, C = J2 – 1. Then we factor C. For each positive factor k of C, we set
1≤i≤n xi, C = J2 – 1. Then we factor C. For each positive factor k of C, we set

If xn < xn+1 < xn+2, then (x1, x2,…, xn+2) is a solution of Equation (4.33)n+2.
• Method 3: Gap-three extension. For each solution (x1, x2,…, xn) of Equation (4.23)n, put J =  1≤i≤n xi. For each odd integer t > 0, one factors J2 + t. For each positive factor k of J2 + t, put
1≤i≤n xi. For each odd integer t > 0, one factors J2 + t. For each positive factor k of J2 + t, put

Then (x1, x2,…, xn+3) is probably a solution of Equation (4.33)n+3.
• Method 4: Gap-two extension+. Randomly choose (x1, x2,…, xn), such that x1, x2,…, xn are pairwise coprime, 2 ≤ x1 < … < xn. Let

For all P,Q such that 1 ≤ P < Q, PQ = A2 – B, let
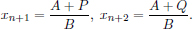
If xn < xn+1, xn+1  Z and xn+2
Z and xn+2  Z, then (x1, x2,…, xn+2) is a solution of Equation (4.33)n+2.
Z, then (x1, x2,…, xn+2) is a solution of Equation (4.33)n+2.
All the solutions of Minus-Type Equations for n ≤ 7 are listed in Appendix B. We also have the following results:
Theorem 4.5.22. The number of the complete solutions of Equation (4.33)8 is 550 (listed in Appendix C).
Each solution of Equation (4.33)n in which x1, x2,…, xn are all primes corresponding to a Giuga number  1≤i≤n xi. Therefore, this corollary can be verified by all solutions of Equation (4.33)n for n ≤ 8, which are listed in Appendices B and C. Giuga numbers with no more than eight distinct prime factors are:
1≤i≤n xi. Therefore, this corollary can be verified by all solutions of Equation (4.33)n for n ≤ 8, which are listed in Appendices B and C. Giuga numbers with no more than eight distinct prime factors are:

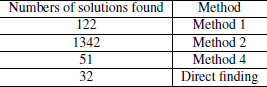
Theorem 4.5.24. Equation (4.33)9 has at least 1547 solutions. These solutions are available at http://tdt.sjtu.edu.cn/9minus.html
Proof. The number of solutions found by each method are listed in Table 4.12.
Table 4.12: Numbers of solutions of Equation (4.33)9 found
Theorem 4.5.25. Equation (4.33)10 has at least 18984 solutions. These solutions are available at http://tdt.sjtu.edu.cn/10minus.html
Proof. From the known 411 solutions of Equation (4.23)9, we can find 411 solutions of Equation (4.33)10 by the Method 1 (Gap-one extension). The others are from the Method 2 (Gap-two extension).
4.6 Notes
In this chapter, we have introduced a new direction of modern cryptography—Batch Cryptography, which includes the batch encryption/decryption, batch key agreement, and batch signature/verification. We implemented batch RSA schemes based on the Diophantine Equations (Plus-Type Equations and Minus-Type Equations), and gave the methods to solve these Diophantine equations2.
There are some interesting problems in batch cryptography which are still open. For instance,
1. How to design aggregate signature and batch verification schemes without extra requirements, such that they are secure in the standard model?
Researches in the batch cryptography are focusing on the aggregate signature and batch verification, which are secure in the random oracle model. In order to make them secure in the standard model, it is usual to introduce extra requirements. However, it remains open to construct a practical aggregation scheme in the standard model without extra requirements such as timing, interactive restrictions, or requiring each user to be able to prove knowledge of his/her secret key. It is also open to explore other relaxations of the full aggregation model.
2. How to design batch encryption schemes based on other assumptions such as quadratic residue, discrete logarithm, and pairing based assumptions?
Almost all existing researches are focusing on the batch RSA. To avoid putting all eggs in one basket, it is better to design new feasible batch cryptographic algorithms based on quadratic residues or discrete logarithm problem. Besides, there is no formal security proof for the batch RSA. This is still an open problem.
3. How to design batch key exchange/agreement protocols?
So far, the batch key exchange/agreement has attracted little attention. In the special case where there are many sends and only one receiver, each sender sends the ciphertext of a random number to the receiver under the receiver’s public key. Then, the receiver is able to batch decrypt them and establish a secure channel with each sender. To design batch key exchange/agreement protocols becomes more complicated if the attackers exist and the property of entity authentication is required.
4. How to combine batch technique with other cryptographic algorithms?
In this chapter, we only considered batch algorithms without combining them with other algorithms, such as proxy re-encryption/re-signature and attribute-based encryption/signature. It must be interesting to construct cryptographic algorithms using batch techniques to improve the efficiency as well as the security.
5. How to find all the solutions of the Plus-Type Equations and Minus-Type Equations with n = 9, 10, which can be used as the public keys in batch RSA? Furthermore, how to find the solutions to these equations when the right side of these equations is 2, not 1?
We have given the new implementation of batch RSA. It requires only one modular, N. This implementation is more suitable to construct hardware circuits for batch RSA decryption. This implementation is based on the Diophantine Equations  1≤i≤N 1/xi ±
1≤i≤N 1/xi ±  1≤i≤N 1/xi = 1, 2 ≤ x1 < x2 <
1≤i≤N 1/xi = 1, 2 ≤ x1 < x2 <  < xN. All solutions to these equations for N ≤ 8 are known, but the complete solutions for N ≤ 9 are unknown.
< xN. All solutions to these equations for N ≤ 8 are known, but the complete solutions for N ≤ 9 are unknown.
 1,
1,  2, …,
2, …,  b into a single compact signature which convinces the verifier that the b users indeed signed the b original messages in a batch way (i.e., user i signed message mi for i = 1, 2,…, b). Moreover, the aggregation can be performed incrementally. That is, signatures
b into a single compact signature which convinces the verifier that the b users indeed signed the b original messages in a batch way (i.e., user i signed message mi for i = 1, 2,…, b). Moreover, the aggregation can be performed incrementally. That is, signatures  1,
1,  2 can be aggregated into
2 can be aggregated into  12 which can then be further aggregated with
12 which can then be further aggregated with  3 to obtain
3 to obtain  123.
123.
 )-breaks an aggregate signature scheme in the chosen-key model if: A runs in time at most t; A makes at most qH queries to the hash function and at most qS queries to the signing oracle; AdvAggSigA is at least
)-breaks an aggregate signature scheme in the chosen-key model if: A runs in time at most t; A makes at most qH queries to the hash function and at most qS queries to the signing oracle; AdvAggSigA is at least 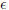 ; and the forged aggregate signature is signed by at most bmax users. An aggregate signature scheme is (t, qH, qS, bmax,
; and the forged aggregate signature is signed by at most bmax users. An aggregate signature scheme is (t, qH, qS, bmax, 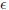 )-secure against existential forgery in the chosen-key model if no forger (t, qH, qS, bmax,
)-secure against existential forgery in the chosen-key model if no forger (t, qH, qS, bmax, 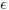 )-breaks it.
)-breaks it. (pk; sk), the algorithm Verify (pk, m, Sign(sk, m)) = 1.
(pk; sk), the algorithm Verify (pk, m, Sign(sk, m)) = 1.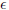 , taken over the randomness of Batch, provided Verify(pki, mi,
, taken over the randomness of Batch, provided Verify(pki, mi, 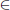 S
S  S’ and m’i
S’ and m’i  mi.
mi.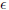 , bmax, qH, qE, qS)-breaks an IBAS scheme in the above model if: for the integer bmax as above, A runs in time at most t; A makes at most qH hash function queries, qE private key extraction queries, and at most qS signing oracle queries; and AdvIBASA is at least
, bmax, qH, qE, qS)-breaks an IBAS scheme in the above model if: for the integer bmax as above, A runs in time at most t; A makes at most qH hash function queries, qE private key extraction queries, and at most qS signing oracle queries; and AdvIBASA is at least 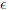 . An IBAS scheme is (t,
. An IBAS scheme is (t,  , bmax, qH, qE, qS)-secured against existential forgery if no adversary (t,
, bmax, qH, qE, qS)-secured against existential forgery if no adversary (t, 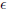 , bmax, qH, qE, qS)-breaks it.
, bmax, qH, qE, qS)-breaks it.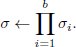
 GT, where g generates the group G2 of prime order q.
GT, where g generates the group G2 of prime order q.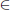 Zq and outputs pk = gsk.
Zq and outputs pk = gsk. G1.
G1. e(H(m), pk).
e(H(m), pk).

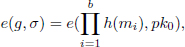
 1
1  G1, the two invalid message-signature pairs P1 = (m1, a
G1, the two invalid message-signature pairs P1 = (m1, a  H(m1)sk) and P2 = (m2, a−1
H(m1)sk) and P2 = (m2, a−1  H(m2)sk) will verify under Definition 4.2.3.
H(m2)sk) will verify under Definition 4.2.3. G2; chooses an arbitrary generator P
G2; chooses an arbitrary generator P  G1. In addition, it chooses three cryptographic hash functions H1, H2 : {0, 1}*
G1. In addition, it chooses three cryptographic hash functions H1, H2 : {0, 1}*  G1, and H3 : {0, 1}*
G1, and H3 : {0, 1}*  Z*q. After setting the system parameters, PKG picks a random number skPKG
Z*q. After setting the system parameters, PKG picks a random number skPKG  Z*q as its secret key and sets its public key as Ppub = skPKG
Z*q as its secret key and sets its public key as Ppub = skPKG  P. The system parameters are params = (G1, G2, q, e, P, Ppub, H1, H2, H3). The sytem’s secret is skPKG.
P. The system parameters are params = (G1, G2, q, e, P, Ppub, H1, H2, H3). The sytem’s secret is skPKG.
 G1;
G1; Z*q;
Z*q; Z*q;
Z*q;
 bi=0 Ui and V =
bi=0 Ui and V =  bi=0 Vi.
bi=0 Vi.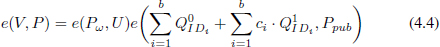

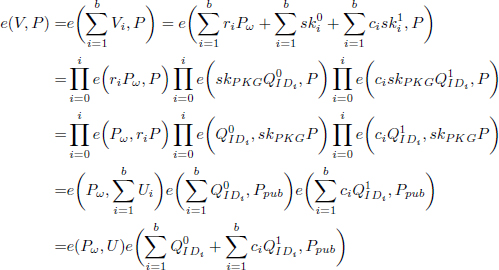

 e−1 (mod φ(N)).
e−1 (mod φ(N)).
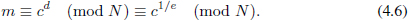
 cd mod N, the decryptor evaluates:
cd mod N, the decryptor evaluates:

 d (mod p – 1) and dq
d (mod p – 1) and dq  d (mod q – 1). Then the decryptor uses the CRT to calculate m from mp and mq. This is approximately four times faster than evaluating cd (mod N) directly.
d (mod q – 1). Then the decryptor uses the CRT to calculate m from mp and mq. This is approximately four times faster than evaluating cd (mod N) directly.


 bi=1 di log ei is minimized similar to the Huffman code tree construction. For the main result of O(log2 N) multiplications per RSA operation, Fiat’s scheme could simply assume that T is a full binary tree. In practice, there is some advantage in using a tree that minimizes the sum of weight times path length because the work performed is proportional to the sum W above. Note that W = O(log b log e). Finally, Fiat shows that the number of multiplications required to compute the b roots above is O(W + log N).
bi=1 di log ei is minimized similar to the Huffman code tree construction. For the main result of O(log2 N) multiplications per RSA operation, Fiat’s scheme could simply assume that T is a full binary tree. In practice, there is some advantage in using a tree that minimizes the sum of weight times path length because the work performed is proportional to the sum W above. Note that W = O(log b log e). Finally, Fiat shows that the number of multiplications required to compute the b roots above is O(W + log N).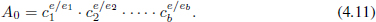
 REL. The product A0 is simply the result associated with the root.
REL. The product A0 is simply the result associated with the root.
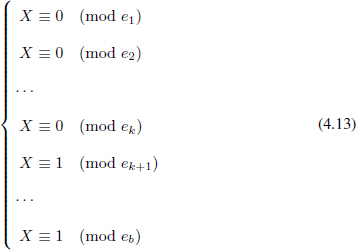
 bi=1 ei by CRT. By
bi=1 ei by CRT. By 

 ki=1 ei and P2 =
ki=1 ei and P2 =  bi=k+1 ei, then X = P1
bi=k+1 ei, then X = P1  X1 and X – 1 = P2
X1 and X – 1 = P2  X2. Compute
X2. Compute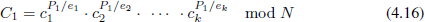
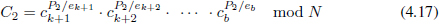
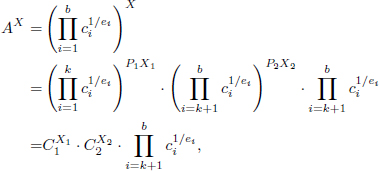
 bk+1 c1/eii, and so Q1 =
bk+1 c1/eii, and so Q1 =  ki=1 c1/eii since Q1 = A/Q2. After that, it recursively breaks up the two products Q1 and Q2, respectively, until each c1/eii is obtained. Thus, the overall number of multiplications is O(W). The number of modular divisions required is O(b).
ki=1 c1/eii since Q1 = A/Q2. After that, it recursively breaks up the two products Q1 and Q2, respectively, until each c1/eii is obtained. Thus, the overall number of multiplications is O(W). The number of modular divisions required is O(b).
 bi=1 log ei) + log N) modular multiplications and O(b) modular divisions.
bi=1 log ei) + log N) modular multiplications and O(b) modular divisions.


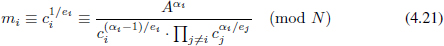

 e−1i (mod φ(N)).
e−1i (mod φ(N)).
 {x1, x2,…, xn}.
{x1, x2,…, xn}. 1≤i≤b ce/eii mod N. This computation can be finished by Fiat’s optimized algorithm [111].
1≤i≤b ce/eii mod N. This computation can be finished by Fiat’s optimized algorithm [111]. Ad0 mod N.
Ad0 mod N.
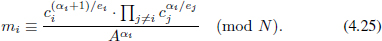




 1≤k≤n xk/xi
1≤k≤n xk/xi  0 (mod xj) (for all i, j such that 1 ≤ i ≤ n, 1 ≤ j ≤ n, j
0 (mod xj) (for all i, j such that 1 ≤ i ≤ n, 1 ≤ j ≤ n, j  i). Hence ei\αi + 1 and ej\αi (for all i, j such that 1 ≤ i ≤ b, 1 ≤ j ≤ b, j
i). Hence ei\αi + 1 and ej\αi (for all i, j such that 1 ≤ i ≤ b, 1 ≤ j ≤ b, j  i). In
i). In  c1/eii (mod N), where 1 ≤ i ≤ n.
c1/eii (mod N), where 1 ≤ i ≤ n. 

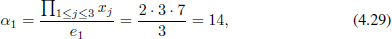
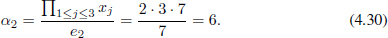
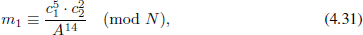

 1≤i≤k ei, P2 =
1≤i≤k ei, P2 =  k<i≤b ei, X1 = P−11 mod P2, X2 = P1 X1-1/P2. Then compute
k<i≤b ei, X1 = P−11 mod P2, X2 = P1 X1-1/P2. Then compute
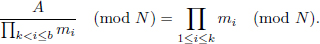
 1≤j<bmj mod N. The evaluation of α1, α2,…, αb requires b modulars.
1≤j<bmj mod N. The evaluation of α1, α2,…, αb requires b modulars. q.
q.
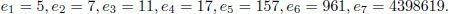
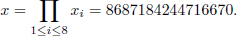
 (
( 1≤i≤7 ei) (mod φ(N)). d is as follows:
1≤i≤7 ei) (mod φ(N)). d is as follows: Ad0 (mod N):
Ad0 (mod N):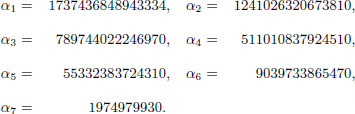


 1≤i≤nxi), a private key d, and ciphertexts c1, c2, …, cb as input. It evaluates A0
1≤i≤nxi), a private key d, and ciphertexts c1, c2, …, cb as input. It evaluates A0  1≤i≤bcie/ei (mod N) by the methods proposed by Fiat, and A
1≤i≤bcie/ei (mod N) by the methods proposed by Fiat, and A  Ad0 (mod N). Obviously
Ad0 (mod N). Obviously
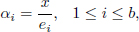
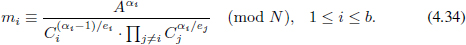

 {x1, x2, …, xn}, α1, α2, …, αb are evaluated by αi =
{x1, x2, …, xn}, α1, α2, …, αb are evaluated by αi =  1 ≤j≤nxj/ej without modular inversion. Therefore, there is only one kind of modular operations, which is “mod N.” If we make a hardware circuit for batch RSA decryption, then our implementation requires one circuit module doing modular operations, and other two implementations both require b modules doing modular operations. Our implementation is more suitable for hardware circuit.
1 ≤j≤nxj/ej without modular inversion. Therefore, there is only one kind of modular operations, which is “mod N.” If we make a hardware circuit for batch RSA decryption, then our implementation requires one circuit module doing modular operations, and other two implementations both require b modules doing modular operations. Our implementation is more suitable for hardware circuit.


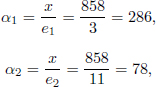


 q = 8881. From the solution {x1 = 2, x2 = 3, x3 = 11, x4 = 17, x5 = 59} of
q = 8881. From the solution {x1 = 2, x2 = 3, x3 = 11, x4 = 17, x5 = 59} of  1≤i≤b ei = 33099 and x =
1≤i≤b ei = 33099 and x =  1≤i≤5 xi = 66198. The private key is d = e−1 (mod φ(N))
1≤i≤5 xi = 66198. The private key is d = e−1 (mod φ(N))  4083.
4083.


 1≤j≤k,j
1≤j≤k,j Nj. In the past forty years, many mathematical researchers have worked on this equation [50, 51, 53, 57, 58, 74–76, 109, 169, 263, 264, 267, 268, 270]. In recent years, applications of
Nj. In the past forty years, many mathematical researchers have worked on this equation [50, 51, 53, 57, 58, 74–76, 109, 169, 263, 264, 267, 268, 270]. In recent years, applications of 


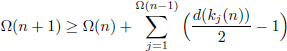
 1≤i≤n xi + 1. By a direct computation, (x1, x2, …, xn+1) is a solution of
1≤i≤n xi + 1. By a direct computation, (x1, x2, …, xn+1) is a solution of  kj(n). Put
kj(n). Put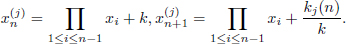
 kj(n) is d(kj(n))/2 – 1. Hence, we can generate
kj(n) is d(kj(n))/2 – 1. Hence, we can generate  Ω(n–1)j=1 (d(kj(n))/2 – 1) solutions of
Ω(n–1)j=1 (d(kj(n))/2 – 1) solutions of  1≤i≤n–1 xi + 1. Therefore, Ω(n + 1) ≥ Ω(n) +
1≤i≤n–1 xi + 1. Therefore, Ω(n + 1) ≥ Ω(n) +  Ω(n–1)j=1 (d(kj(n))/2 – 1).
Ω(n–1)j=1 (d(kj(n))/2 – 1).

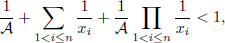

 1≤i≤n 1/xi +
1≤i≤n 1/xi +  1≤i≤n 1/xi ≥ 1, then A
1≤i≤n 1/xi ≥ 1, then A  [L1, U1] by Lemma 4.5.17.
[L1, U1] by Lemma 4.5.17.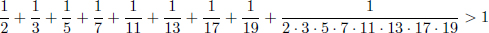
 [L1, U1].
[L1, U1].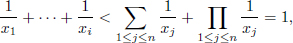

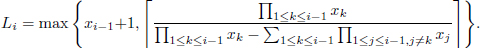

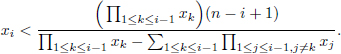

 1≤i≤n 1/xi +
1≤i≤n 1/xi +  1≤i≤n 1/xi ≥ 1. We can further reduce Ui based on this fact.
1≤i≤n 1/xi ≥ 1. We can further reduce Ui based on this fact. 1≤i≤n-2 xi, B = A –
1≤i≤n-2 xi, B = A –  1≤i≤n-2 A/xi. Factorize A2 + B. For all positive integers P and Q such that PQ = A2 + B, P < Q, put xn-1 = A+P/B, xn = A+Q/B. If both xn-1 and xn are integers, (x1, x2, …, xn) is a solution of
1≤i≤n-2 A/xi. Factorize A2 + B. For all positive integers P and Q such that PQ = A2 + B, P < Q, put xn-1 = A+P/B, xn = A+Q/B. If both xn-1 and xn are integers, (x1, x2, …, xn) is a solution of 





 1≤i≤n-2 xi. Then
1≤i≤n-2 xi. Then
 t
t  1 (mod 4).
1 (mod 4).



 w
w  k
k  0 (mod d), and N
0 (mod d), and N  (N + k)
(N + k)  w + N
w + N  (N + k)
(N + k)  z + 1
z + 1  1 (mod d). Therefore, d|1. Hence, N and k are coprime.
1 (mod d). Therefore, d|1. Hence, N and k are coprime. Z, we have t|[N
Z, we have t|[N  (N + k)(N + N2+t)/k)+1]. Hence, d’|[N
(N + k)(N + N2+t)/k)+1]. Hence, d’|[N  (N + k)(N + N2+t/k) + 1]. From d’|k, we get d’|[N2(N + N2+t)/k) + 1]. Since N2+t/k
(N + k)(N + N2+t/k) + 1]. From d’|k, we get d’|[N2(N + N2+t)/k) + 1]. Since N2+t/k  Z, we have k|(N2 + t). Therefore d’|N2. It follows that d’|1. Hence, k and t are coprime.
Z, we have k|(N2 + t). Therefore d’|N2. It follows that d’|1. Hence, k and t are coprime.

 (N + k)
(N + k)  (N + N2+t/k) + 1] and 2|N, we have 2
(N + N2+t/k) + 1] and 2|N, we have 2  t. From k|(N2 + t), we have 2
t. From k|(N2 + t), we have 2  k. From (k, t) = 1, we get (-t/k) = 1. Then from t|[N
k. From (k, t) = 1, we get (-t/k) = 1. Then from t|[N  (N + k)
(N + k)  (N + N2+t/k) + 1], we have t|[N
(N + N2+t/k) + 1], we have t|[N  (N + k)
(N + k)  (nk + N2 + t) + k], i.e., t|[N2
(nk + N2 + t) + k], i.e., t|[N2  (N + k)2 + k]. Therefore (-k/t) = 1. We have,
(N + k)2 + k]. Therefore (-k/t) = 1. We have,



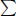 Ω(n+1)j=1 (d(kj(n+2))/2 - 1), d(kj(n + 2)) is defined in Lemma 4.5.2, B(n) denotes the number of solutions found by the Algorithm 2 based on n, restricted by t > 1 and k > 1,
Ω(n+1)j=1 (d(kj(n+2))/2 - 1), d(kj(n + 2)) is defined in Lemma 4.5.2, B(n) denotes the number of solutions found by the Algorithm 2 based on n, restricted by t > 1 and k > 1,  (n + 2) denotes the number of solutions generated as follows: (x1, x2, …, xn+2) be a solution of
(n + 2) denotes the number of solutions generated as follows: (x1, x2, …, xn+2) be a solution of  1≤i≤n+1 xi)2 + 1. Let k be a factor of C, such that 1 < k <
1≤i≤n+1 xi)2 + 1. Let k be a factor of C, such that 1 < k <  C. Put
C. Put


 1≤i≤n+2 xi + 1 in Method 3, while xn+3 =
1≤i≤n+2 xi + 1 in Method 3, while xn+3 =  1≤i≤n+2 xi + 1 in Method 1.
1≤i≤n+2 xi + 1 in Method 1. S(n + 1) in Method 3, while (x1, x2, …, xn+1)
S(n + 1) in Method 3, while (x1, x2, …, xn+1)  S(n + 1) in Method 2.
S(n + 1) in Method 2. S(n + 1), (x1, x2, …, xn)
S(n + 1), (x1, x2, …, xn)  S(n) in Method 4, but (x1, x2, …, xn+1)
S(n) in Method 4, but (x1, x2, …, xn+1)  S(n + 1) in Method 2, (x1, x2, …, xn)
S(n + 1) in Method 2, (x1, x2, …, xn)  S(n) in Method 3.
S(n) in Method 3. 1≤i≤n+2 xi + 1 in Method 4, while xn+3 =
1≤i≤n+2 xi + 1 in Method 4, while xn+3 =  1≤i≤n+2 xi + 1 in Method 1.
1≤i≤n+2 xi + 1 in Method 1. (n + 2).
(n + 2).


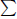 p|K 1/p -
p|K 1/p -  p|K 1/p
p|K 1/p  N [124]. Giuga numbers are named after Giuga [124], who formulated a conjecture on primality in 1950: N is prime if and only if
N [124]. Giuga numbers are named after Giuga [124], who formulated a conjecture on primality in 1950: N is prime if and only if 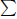 k=1N - 1 kN - 1
k=1N - 1 kN - 1  1 (mod N). In 1996, Borwein et al. [44] published 11 Giuga numbers. Then Hogan and Mangilin found the 12th Giuga number [58], and Girgensohn found another one [58] in 2000. Sloane presented 13 Giuga numbers [261]. We prove that there are only 12 Giuga numbers with less than eight distinct prime factors, through the complete solutions of
1 (mod N). In 1996, Borwein et al. [44] published 11 Giuga numbers. Then Hogan and Mangilin found the 12th Giuga number [58], and Girgensohn found another one [58] in 2000. Sloane presented 13 Giuga numbers [261]. We prove that there are only 12 Giuga numbers with less than eight distinct prime factors, through the complete solutions of 
 1≤i≤n xi is a Giuga number if and only if (x1, x2, …, xn) is a solution of
1≤i≤n xi is a Giuga number if and only if (x1, x2, …, xn) is a solution of 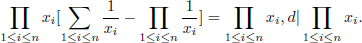

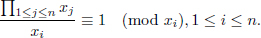
 1≤i≤n-1 xi(j))2 - 1. We have
1≤i≤n-1 xi(j))2 - 1. We have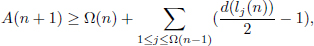
 lj(n). Put
lj(n). Put
 lj(n) is d(lj(n))/2 - 1. Therefore, we can construct
lj(n) is d(lj(n))/2 - 1. Therefore, we can construct  1≤j≤Ω(n-1)(d(lj (n))/2 -1) solutions of
1≤j≤Ω(n-1)(d(lj (n))/2 -1) solutions of  1≤i≤n xi - 1.
1≤i≤n xi - 1. 1≤i≤n xi - 1. Then (x1, x2, …, xn+1) is a solution of
1≤i≤n xi - 1. Then (x1, x2, …, xn+1) is a solution of  1≤i≤n xi - 1, this solution is different from any other solutions generated in step 1. Therefore, A(n + 1) ≥ Ω(n) +
1≤i≤n xi - 1, this solution is different from any other solutions generated in step 1. Therefore, A(n + 1) ≥ Ω(n) + 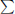 1≤j≤Ω(n-1)(d(lj (n))/2 - 1).
1≤j≤Ω(n-1)(d(lj (n))/2 - 1).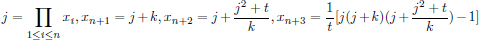
 Z, then (x1, x2, …, xn+3) is a solution of
Z, then (x1, x2, …, xn+3) is a solution of 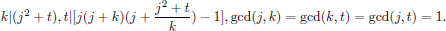
 1 (mod 4) or k
1 (mod 4) or k  t
t  3 (mod 4).
3 (mod 4). 1≤i≤n xi, xn+1 = j + k, xn+2 = j + j2+t/k, xn+3 = 1/t [j(j + k)(j + j2+t/k) - 1], where k, and t are positive integers. Assume that xn+1 < xn+2 < xn+3 and xn+1, xn+2, xn+3
1≤i≤n xi, xn+1 = j + k, xn+2 = j + j2+t/k, xn+3 = 1/t [j(j + k)(j + j2+t/k) - 1], where k, and t are positive integers. Assume that xn+1 < xn+2 < xn+3 and xn+1, xn+2, xn+3  Z. Direct computation shows that (x1, x2, …, xn+3) is a solution of
Z. Direct computation shows that (x1, x2, …, xn+3) is a solution of 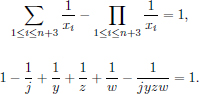


 t. From k|(j2 + t) we have 2
t. From k|(j2 + t) we have 2  k. Then from k|(j2 + t) we have
k. Then from k|(j2 + t) we have
 k (mod t). We have
k (mod t). We have
 1 (mod 4) or k
1 (mod 4) or k  t
t  3 (mod 4).
3 (mod 4).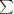 1≤i≤n 1/xi -
1≤i≤n 1/xi -  1≤i≤n 1/xi < 1, there is no solution of
1≤i≤n 1/xi < 1, there is no solution of 
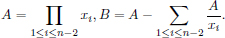

 Z and xn
Z and xn  Z, then (x1, x2, …, xn) is a solution of
Z, then (x1, x2, …, xn) is a solution of 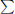 1≤i≤n 1/xi -
1≤i≤n 1/xi -  1≤i≤n 1/xi ≥ 1, then A
1≤i≤n 1/xi ≥ 1, then A  [L1, U1] by Lemma 4.5.17.
[L1, U1] by Lemma 4.5.17.


 [Lj, Uj], 1 ≤ j ≤ i, we calculate Li+1 and Ui+1, 1 ≤ i < n – 1.
[Lj, Uj], 1 ≤ j ≤ i, we calculate Li+1 and Ui+1, 1 ≤ i < n – 1.

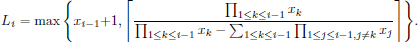

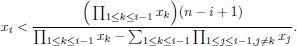




 Z and xn
Z and xn  Z, then (x1, x2,…, xn) is a solution of
Z, then (x1, x2,…, xn) is a solution of 



 1≤i≤n xi – 1, then (x1, x2,…, xn+1) is a solution of
1≤i≤n xi – 1, then (x1, x2,…, xn+1) is a solution of  1≤i≤n xi, C = J2 – 1. Then we factor C. For each positive factor k of C, we set
1≤i≤n xi, C = J2 – 1. Then we factor C. For each positive factor k of C, we set
 1≤i≤n xi. For each odd integer t > 0, one factors J2 + t. For each positive factor k of J2 + t, put
1≤i≤n xi. For each odd integer t > 0, one factors J2 + t. For each positive factor k of J2 + t, put

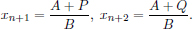
 Z and xn+2
Z and xn+2  Z, then (x1, x2,…, xn+2) is a solution of
Z, then (x1, x2,…, xn+2) is a solution of  p|K 1/p –
p|K 1/p –  p|K 1/p
p|K 1/p  N [124]. If n has no more than 8 distinct prime factors, then K is a Giuga number if and only if
N [124]. If n has no more than 8 distinct prime factors, then K is a Giuga number if and only if  p|K 1/p –
p|K 1/p –  p|K 1/p = 1, since
p|K 1/p = 1, since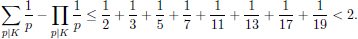
 1≤i≤n xi. Therefore, this corollary can be verified by all solutions of
1≤i≤n xi. Therefore, this corollary can be verified by all solutions of 

 1≤i≤N 1/xi ±
1≤i≤N 1/xi ±  1≤i≤N 1/xi = 1, 2 ≤ x1 < x2 <
1≤i≤N 1/xi = 1, 2 ≤ x1 < x2 <  < xN. All solutions to these equations for N ≤ 8 are known, but the complete solutions for N ≤ 9 are unknown.
< xN. All solutions to these equations for N ≤ 8 are known, but the complete solutions for N ≤ 9 are unknown.