The method of first and ultimate ratios, for use in demonstrating what follows
Lemma 1
Quantities, and also ratios of quantities, which in aany finite timea constantly tend
to equality, and which before the end of that time approach so close to one another
that their difference is less than any given quantity, become ultimately equal.
If you deny this, blet them become ultimately unequal, andb let their ultimate difference be D. Then they cannot approach so close to equality that their difference is less than the given difference D, contrary to the hypothesis.
Lemma 2
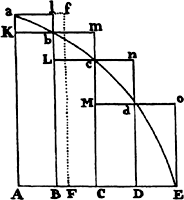
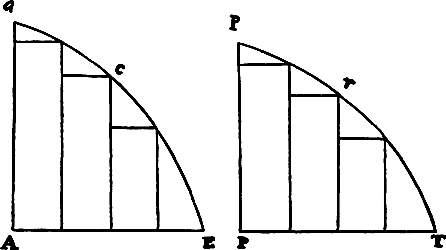
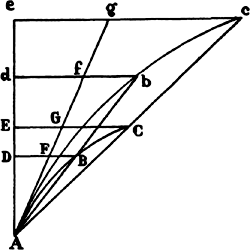
If in any figure AacE, comprehended by the straight lines Aa and AE and the
curve acE, any number of parallelograms Ab, Bc, Cd, . . . are inscribed upon
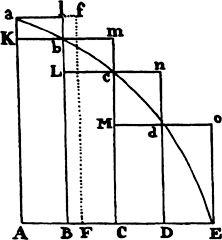 equal bases AB, BC, CD, . . . and have sides Bb,
Cc, Dd, . . . parallel to the side Aa of the figure;
and if the parallelograms aKbl, bLcm, cMdn, . . . are
completed; if then the width of these
parallelograms is diminished and their number increased
indefinitely, I say that the ultimate ratios which the
inscribed figure AKbLcMdD, the circumscribed
figure AalbmcndoE, and the curvilinear figure
AabcdE have to one another are ratios of equality.
equal bases AB, BC, CD, . . . and have sides Bb,
Cc, Dd, . . . parallel to the side Aa of the figure;
and if the parallelograms aKbl, bLcm, cMdn, . . . are
completed; if then the width of these
parallelograms is diminished and their number increased
indefinitely, I say that the ultimate ratios which the
inscribed figure AKbLcMdD, the circumscribed
figure AalbmcndoE, and the curvilinear figure
AabcdE have to one another are ratios of equality.
For the difference of the inscribed and circumscribed figures is the sum of the parallelograms Kl, Lm, Mn, and Do, that is (because they all have equal bases), the rectangle having as base Kb (the base of one of them) and as altitude Aa (the sum of the altitudes), that is, the rectangle ABla. But this rectangle, because its width AB is diminished indefinitely, becomes less than any given rectangle. Therefore (by lem. 1) the inscribed figure and the circumscribed figure and, all the more, the intermediate curvilinear figure become ultimately equal. Q.E.D.
Lemma 3
The same ultimate ratios are also ratios of equality when the widths AB, BC,
CD, . . . of the parallelograms are unequal and are all diminished indefinitely.
For let AF be equal to the greatest width,
 and let the parallelogram FAaf be completed.
This parallelogram will be greater than the
difference of the inscribed and the circumscribed
figures; but if its width AF is diminished
indefinitely, it will become less than any given
rectangle. Q.E.D.
and let the parallelogram FAaf be completed.
This parallelogram will be greater than the
difference of the inscribed and the circumscribed
figures; but if its width AF is diminished
indefinitely, it will become less than any given
rectangle. Q.E.D.
COROLLARY 1. Hence the ultimate sum of the vanishing parallelograms coincides with the curvilinear figure in its every part.
COROLLARY 2. And, all the more, the rectilinear figure that is comprehended by the chords of the vanishing arcs ab, be, cd, . . . coincides ultimately with the curvilinear figure.
COROLLARY 3. And it is the same for the circumscribed rectilinear figure that is comprehended by the tangents of those same arcs.
COROLLARY 4. And therefore these ultimate figures (with respect to their perimeters acE) are not rectilinear, but curvilinear limits of rectilinear figures.
Lemma 4
If in two figures AacE and PprT two series of parallelograms are inscribed (as
above) and the number of parallelograms in both series is the same; and if when
their widths are diminished indefinitely, the ultimate ratios of the parallelograms
in one figure to the corresponding parallelograms in the other are the same; then
I say that the two figures AacE and PprT are to each other in that same ratio.
For as the individual parallelograms in the one figure are to the corresponding individual parallelograms in the other, so (by composition [or componendo]) will the sum of all the parallelograms in the one become to the sum of all the parallelograms in the other, and so also the one figure to the other—the first figure, of course, being (by lem. 3) to the first sum, and the second figure to the second sum, in a ratio of equality. Q.E.D.
COROLLARY. Hence, if two quantities of any kind are divided in any way into the same number of parts, and these parts—when their number is increased and their size is diminished indefinitely—maintain a given ratio to one another, the first to the first, the second to the second, and so on in sequence, then the wholes will be to each other in the same given ratio. For if the parallelograms in the figures of this lemma are taken in the same proportion to one another as those parts, the sums of the parts will always be as the sums of the parallelograms; and therefore, when the number of parts and parallelograms is increased and their size diminished indefinitely, the sums of the parts will be in the ultimate ratio of a parallelogram in one figure to a corresponding parallelogram in the other, that is (by hypothesis), in the ultimate ratio of part to part.
Lemma 5
All the mutually corresponding sides—curvilinear as well as rectilinear—of similar
figures are proportional, and the areas of such figures are as the squares of their
sides.
Lemma 6
If any arc ACB, given in position, is subtended by the chord AB and at some point
 A, in the middle of the continuous
curvature, is touched by the straight
line AD, produced in both directions,
and if then points A and B approach
each other and come together, I say
that the angle BAD contained by the
chord and the tangent will be
indefinitely diminished and will ultimately
vanish.
A, in the middle of the continuous
curvature, is touched by the straight
line AD, produced in both directions,
and if then points A and B approach
each other and come together, I say
that the angle BAD contained by the
chord and the tangent will be
indefinitely diminished and will ultimately
vanish.
For aif that angle does not vanish, the angle contained by the arc ACB and the tangent AD will be equal to a rectilinear angle, and therefore the curvature at point A will not be continuous, contrary to the hypothesis.a
Lemma 7
With the same suppositions, I say that the ultimate ratios of the arc, the chord,
and the tangent to one another are ratios of equality.
For while point B approaches point A, let AB and AD be understood
always to be produced to the distant points b and d; and let bd be drawn
parallel to secant BD. And let arc Acb be always similar to arc ACB. Then as
 points A and B come together, the angle
dAb will vanish (by lem. 6), and thus the
straight lines Ab and Ad (which are
always finite) and the intermediate arc Acb
will coincide and therefore will be equal. Hence, the straight lines AB and
AD and the intermediate arc ACB (which are always proportional to the
lines Ab and Ad and the arc Acb respectively) will also vanish and will
have to one another an ultimate ratio of equality. Q.E.D.
points A and B come together, the angle
dAb will vanish (by lem. 6), and thus the
straight lines Ab and Ad (which are
always finite) and the intermediate arc Acb
will coincide and therefore will be equal. Hence, the straight lines AB and
AD and the intermediate arc ACB (which are always proportional to the
lines Ab and Ad and the arc Acb respectively) will also vanish and will
have to one another an ultimate ratio of equality. Q.E.D.
COROLLARY 1. Hence, if BF is drawn through B parallel to the tangent and always cutting at F any straight line AF passing through A, then BF will ultimately have a ratio of equality to the vanishing arc ACB, because, if parallelogram AFBD is completed, BF always has a ratio of equality to AD.
COROLLARY 2. And if through B and A additional straight lines BE, BD, AF, and AG are drawn cutting the tangent AD and its parallel BF, the ultimate ratios of all the abscissas AD, AE, BF, and BG and of the chord and arc AB to one another will be ratios of equality.
COROLLARY 3. And therefore all these lines can be used for one another interchangeably in any argumentation concerning ultimate ratios.
Lemma 8
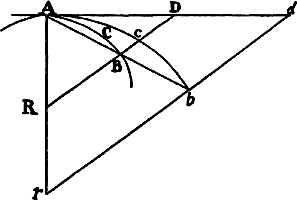
If the given straight lines AR and BR, together with the arc ACB, its chord AB,
and the tangent AD, constitute three triangles RAB, RACB, and RAD, and if
then points A and B approach each other, I say that the triangles as they vanish
are similar in their ultimate form, and that their ultimate ratio is one of equality.
For while point B approaches
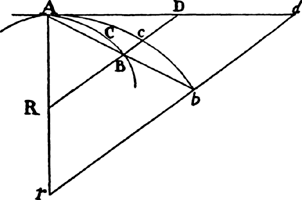 point A, let AB, AD, and AR be
understood always to be produced
to the distant points b, d, and r, and
rbd to be drawn parallel to RD;
and let arc Acb be always similar
to arc ACB. Then as points A and
B come together, the angle bAd will
vanish, and therefore the three triangles rAb, rAcb, and rAd, which are
always finite, will coincide and on that account are similar and equal. Hence
also RAB, RACB, and RAD, which will always be similar and proportional
to these, will ultimately become similar and equal to one another. Q.E.D.
point A, let AB, AD, and AR be
understood always to be produced
to the distant points b, d, and r, and
rbd to be drawn parallel to RD;
and let arc Acb be always similar
to arc ACB. Then as points A and
B come together, the angle bAd will
vanish, and therefore the three triangles rAb, rAcb, and rAd, which are
always finite, will coincide and on that account are similar and equal. Hence
also RAB, RACB, and RAD, which will always be similar and proportional
to these, will ultimately become similar and equal to one another. Q.E.D.
COROLLARY. And hence those triangles can be used for one another interchangeably in any argumentation concerning ultimate ratios.
Lemma 9
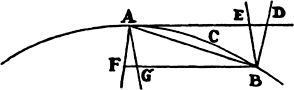
If the straight line AE and the curve ABC, both given in position, intersect each
other at a given angle A, and if BD and CE are drawn as ordinates to the straight
line AE at another given angle and meet the curve in B and C, and if then points
B and C simultaneously approach point A, I say that the areas of the triangles
ABD and ACE will ultimately be to each other as the squares of the sides.
For while points B and C approach point A, let AD be understood always
to be produced to the distant points d and e, so that Ad and Ae are
 proportional to AD and AE; and erect ordinates
db and ec parallel to ordinates DB
and EC and meeting AB and AC, produced,
at b and c. Understand the curve
Abc to be drawn similar to ABC, and
the straight line Ag to be drawn touching
both curves at A and cutting the ordinates
DB, EC, db, and ec at F, G, f, and g.
Then, with the length Ae remaining the
same, let points B and C come together
with point A; and as the angle cAg
vanishes, the curvilinear areas Abd and Ace will coincide with the rectilinear
areas Afd and Age, and thus (by lem. 5) will be in the squared ratio of the
sides Ad and Ae. But areas ABD and ACE are always proportional to these
areas, and sides AD and AE to these sides. Therefore areas ABD and ACE
also are ultimately in the squared ratio of the sides AD and AE. Q.E.D.
proportional to AD and AE; and erect ordinates
db and ec parallel to ordinates DB
and EC and meeting AB and AC, produced,
at b and c. Understand the curve
Abc to be drawn similar to ABC, and
the straight line Ag to be drawn touching
both curves at A and cutting the ordinates
DB, EC, db, and ec at F, G, f, and g.
Then, with the length Ae remaining the
same, let points B and C come together
with point A; and as the angle cAg
vanishes, the curvilinear areas Abd and Ace will coincide with the rectilinear
areas Afd and Age, and thus (by lem. 5) will be in the squared ratio of the
sides Ad and Ae. But areas ABD and ACE are always proportional to these
areas, and sides AD and AE to these sides. Therefore areas ABD and ACE
also are ultimately in the squared ratio of the sides AD and AE. Q.E.D.
Lemma 10
The spaces which a body describes when urged by any
afinitea force,
bwhether
that force is determinate and immutable or is continually increased or continually
decreased,b are at the very beginning of the motion in the squared ratio of the
times.
Let the times be represented by lines AD and AE, and the generated velocities by ordinates DB and EC; then the spaces described by these velocities will be as the areas ABD and ACE described by these ordinates, that is, at the very beginning of the motion these spaces will be (by lem. 9) in the squared ratio of the times AD and AE. Q.E.D.
COROLLARY 1. And hence it is easily concluded that when bodies describe similar parts of similar figures in proportional times, the errors that are generated by any equal forces similarly applied to the bodies, and that are measured by the distances of the bodies from those points on the similar figures at which the same bodies would arrive in the same proportional times without these forces, are very nearly as the squares of the times in which they are generated.
COROLLARY 2. But the errors that are generated by proportional forces similarly applied to similar parts of similar figures are as the forces and the squares of the times jointly.
Lemma 11
In all curves having a finite curvature at the point of contact, the vanishing
subtense of the angle of contact is ultimately in the squared ratio of the subtense
of the conterminous arc.
CASE 1. Let AB be the arc, AD its tangent, BD the subtense of the angle
of contact perpendicular to the tangent [angle BAD], and [the line] AB the
 subtense [i.e., the conterminous chord] of the arc [AB].
Erect BG and AG perpendicular to this subtense AB
and tangent AD and meeting in G; then let points D,
B, and G approach points d, b, and g, and let J be
the intersection of lines BG and AG, which ultimately
occurs when points D and B reach A. It is evident that
the distance GJ can be less than any assigned distance.
And (from the nature of the circles passing through
points A, B, G and a, b, g) AB2 is equal to AG × BD,
and Ab2 is equal to Ag × bd, and thus the ratio of AB2
to Ab2 is compounded of the ratios of AG to Ag and
BD to bd. But since GJ can be taken as less than any assigned length, it can
happen that the ratio of AG to Ag differs from the ratio of equality by less
than any assigned difference, and thus that the ratio of AB2 to Ab2 differs
from the ratio of BD to bd by less than any assigned difference. Therefore,
by lem. 1, the ultimate ratio of AB2 to Ab2 is the same as the ultimate ratio
of BD to bd. Q.E.D.
subtense [i.e., the conterminous chord] of the arc [AB].
Erect BG and AG perpendicular to this subtense AB
and tangent AD and meeting in G; then let points D,
B, and G approach points d, b, and g, and let J be
the intersection of lines BG and AG, which ultimately
occurs when points D and B reach A. It is evident that
the distance GJ can be less than any assigned distance.
And (from the nature of the circles passing through
points A, B, G and a, b, g) AB2 is equal to AG × BD,
and Ab2 is equal to Ag × bd, and thus the ratio of AB2
to Ab2 is compounded of the ratios of AG to Ag and
BD to bd. But since GJ can be taken as less than any assigned length, it can
happen that the ratio of AG to Ag differs from the ratio of equality by less
than any assigned difference, and thus that the ratio of AB2 to Ab2 differs
from the ratio of BD to bd by less than any assigned difference. Therefore,
by lem. 1, the ultimate ratio of AB2 to Ab2 is the same as the ultimate ratio
of BD to bd. Q.E.D.
CASE 2. Now let BD be inclined to AD at any given angle, and the ultimate ratio of BD to bd will always be the same as before and thus the same as AB2 to Ab2. Q.E.D.
CASE 3. And even when angle D is not given, if the straight line BD converges to a given point or is drawn according to any other specification, still the angles D and d (constructed according to the specification common to both) will always tend to equality and will approach each other so closely that their difference will be less than any assigned quantity, and thus will ultimately be equal, by lem. 1; and therefore lines BD and bd are in the same ratio to each other as before. Q.E.D.
COROLLARY 1. Hence, since tangents AD and Ad, arcs AB and Ab, and their sines BC and bc become ultimately equal to chords AB and Ab, their squares will also be ultimately as the subtenses BD and bd.
COROLLARY 4. The rectilinear triangles ADB and
 Adb are ultimately in the cubed ratio of the sides
AD and Ad, and in the sesquialteral ratio [i.e., as
the 3/2 power] of the sides DB and db, inasmuch as
these triangles are in a ratio compounded of the ratios
of AD and DB to Ad and db. So also the triangles
ABC and Abc are ultimately in the cubed ratio of the
sides BC and bc. bThe ratio that I call sesquialteral
is the halved of the tripled, namely, the one that is
compounded of the simple and the halved.b
Adb are ultimately in the cubed ratio of the sides
AD and Ad, and in the sesquialteral ratio [i.e., as
the 3/2 power] of the sides DB and db, inasmuch as
these triangles are in a ratio compounded of the ratios
of AD and DB to Ad and db. So also the triangles
ABC and Abc are ultimately in the cubed ratio of the
sides BC and bc. bThe ratio that I call sesquialteral
is the halved of the tripled, namely, the one that is
compounded of the simple and the halved.b
COROLLARY 5. And since DB and db are ultimately parallel and in the squared ratio of AD and Ad, the ultimate curvilinear areas ADB and Adb will be (from the nature of the parabola) two-thirds of the rectilinear triangles ADB and Adb; and the segments AB and Ab will be thirds of these same triangles. And hence these areas and segments will be in the cubed ratio of both of the tangents AD and Ad and of the chords AB and Ab and their arcs.
Scholium
But we suppose throughout that the angle of contact is neither infinitely
greater nor infinitely less than the angles of contact that circles contain with
their tangents, that is, that the curvature at point A is neither infinitely
small nor infinitely great—in other words, that the distance AJ is of a finite
magnitude. For DB can be taken proportional to AD3, in which case no
circle can be drawn through point A between tangent AD and curve AB,
and accordingly the angle of contact will be infinitely less than those of
circles. And, similarly, if DB is made successively proportional to AD4, AD5,
AD6, AD7, . . . , there will be a sequence of angles of contact going on to
infinity, any succeeding one of which is infinitely less than the preceding
one. And if DB is made successively proportional to AD2, AD3/2, AD4/3,
AD5/4, AD6/5, AD7/6, . . . , there will be another infinite sequence of angles
of contact, the first of which is of the same kind as those of circles, the second
infinitely greater, and any succeeding one infinitely greater than the preceding
one. Moreover, between any two of these angles a sequence of intermediate
angles, going on to infinity in both directions, can be inserted, any succeeding
one of which will be infinitely greater or smaller than the preceding one—as,
for example, if between the terms AD2 and AD3 there were inserted
the sequence AD13/6, AD11/5, AD9/4, AD7/3, AD5/2, AD8/3, AD11/4, AD14/5,
AD17/6, . . . . And again, between any two angles of this sequence a new
sequence of intermediate angles can be inserted, differing from one another
by infinite intervals. And nature knows no limit.
What has been demonstrated concerning curved lines and the [plane] surfaces comprehended by them is easily applied to curved surfaces and their solid contents. In any case, I have presented these lemmas before the propositions in order to avoid the tedium of working out clengthyc proofs by reductio ad absurdum in the manner of the ancient geometers. Indeed, proofs are rendered more concise by the method of indivisibles. But since the hypothesis of indivisibles is dproblematicald and this method is therefore accounted less geometrical, I have preferred to make the proofs of what follows depend on the ultimate sums and ratios of vanishing quantities and the first sums and ratios of nascent quantities, that is, on the limits of such sums and ratios, and therefore to present proofs of those limits beforehand as briefly as I could. For the same result is obtained by these as by the method of indivisibles, and we shall be on safer ground using principles that have been proved. Accordingly, whenever in what follows I consider quantities as consisting of particles or whenever I use curved line-elements [or minute curved lines] in place of straight lines, I wish it always to be understood that I have in mind not indivisibles but evanescent divisibles, and not sums and ratios of definite parts but the limits of such sums and ratios, and that the force of such proofs always rests on the method of the preceding lemmas.
It may be objected that there is no such thing as an ultimate proportion of vanishing quantities, inasmuch as before vanishing the proportion is not ultimate, and after vanishing it does not exist at all. But by the same argument it could equally be contended that there is no ultimate velocity of a body reaching a certain place at which the motion ceases; for before the body arrives at this place, the velocity is not the ultimate velocity, and when it arrives there, there is no velocity at all. But the answer is easy: to understand the ultimate velocity as that with which a body is moving, neither before it arrives at its ultimate place and the motion ceases, nor after it has arrived there, but at the very instant when it arrives, that is, the very velocity with which the body arrives at its ultimate place and with which the motion ceases. And similarly the ultimate ratio of vanishing quantities is to be understood not as the ratio of quantities before they vanish or after they have vanished, but the ratio with which they vanish. Likewise, also, the first ratio of nascent quantities is the ratio with which they begin to exist [or come into being]. And the first and the ultimate sum is the sum with which they begin and cease to exist (or to be increased or decreased). There exists a limit which their velocity can attain at the end of the motion, but cannot exceed. This is their ultimate velocity. And it is the same for the limit of all quantities and proportions that come into being and cease existing. And since this limit is certain and definite, the determining of it is properly a geometrical problem. But everything that is geometrical is legitimately used in determining and demonstrating whatever else may be geometrical.
It can also be contended that if the ultimate ratios of vanishing quantities are given, their ultimate magnitudes will also be given; and thus every quantity will consist of indivisibles, contrary to what Euclid had proved concerning incommensurables in the tenth book of his Elements. But this objection is based on a false hypothesis. Those ultimate ratios with which quantities vanish are not actually ratios of ultimate quantities, but limits which the ratios of quantities decreasing without limit are continually approaching, and which they can approach so closely that their difference is less than any given quantity, but which they can never exceed and can never reach before the quantities are decreased indefinitely. This matter will be understood more clearly in the case of quantities that are indefinitely great. If two quantities whose difference is given are increased indefinitely, their ultimate ratio will be given, namely the ratio of equality, and yet the ultimate or maximal quantities of which this is the ratio will not on this account be given. Therefore, whenever, to make things easier to comprehend, I speak in what follows of quantities as minimally small or vanishing or ultimate, take care not to understand quantities that are determinate in magnitude, but always think of quantities that are to be decreased without limit.
Proposition 1a, Theorem 1
The areas which bodies bmade to move in orbitsb describe by radii drawn to an
unmoving center of forces lie in unmoving planes and are proportional to the
times.
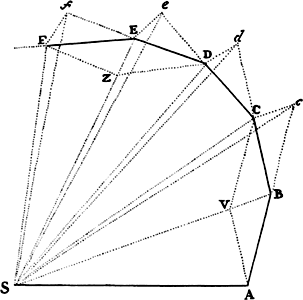
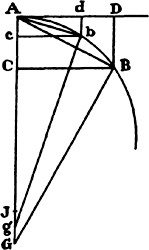
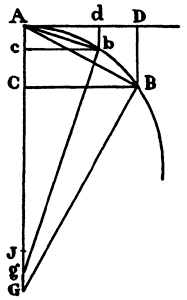
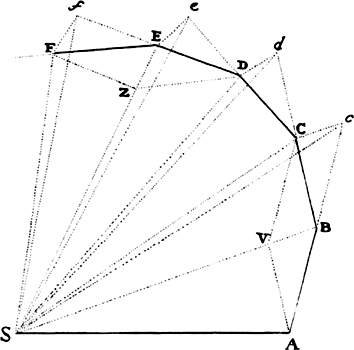
Let the time be divided into equal parts, and in the first part of the time let a body by its inherent force describe the straight line AB. In the second part of the time, if nothing hindered it, this body would (by law 1) go straight on to c, describing line Bc equal to AB, so that—when radii AS, BS, and cS were drawn to the center—the equal areas ASB and BSc would be described. But when the body comes to B, let a centripetal force act with a single but great impulse and make the body deviate from the straight line Bc and proceed in the straight line BC. Let cC be drawn parallel to BS and meet BC at C; then, when the second part of the time has been completed, the body (by corol. 1 of the laws) will be found at C in the same plane as triangle ASB. Join SC; and because SB and Cc are parallel, triangle SBC will be equal to triangle SBc and thus also to triangle SAB. By a similar argument, if the centripetal force acts successively at C, D, E, . . . , making the body in each of the individual particles of time describe the individual straight lines CD, DE, EF, . . . , all these lines will lie in the same plane; and triangle SCD will be equal to triangle SBC, SDE to SCD, and SEF to SDE. Therefore, in equal times equal areas are described in an unmoving plane; and by composition [or componendo], any sums SADS and SAFS of the areas are to each other as the times of description. Now let the number of triangles be increased and their width decreased indefinitely, and their ultimate perimeter ADF will (by lem. 3, corol. 4) be a curved line; and thus the centripetal force by which the body is continually drawn back from the tangent of this curve will act uninterruptedly, while any areas described, SADS and SAFS, which are always proportional to the times of description, will be proportional to those times in this case. Q.E.D.
Proposition 2, Theorem 2
Every body that moves in some curved line described in a plane and, by a radius
drawn to a point, either unmoving or moving uniformly forward with a rectilinear
motion, describes areas around that point proportional to the times, is urged by a
centripetal force tending toward that same point.
CASE 1. For every body that moves in a curved line is deflected from a rectilinear course by some force acting upon it (by law 1). And that force by which the body is deflected from a rectilinear course and in equal times is made to describe, about an immobile point S, the equal minimally small triangles SAB, SBC, SCD, . . . , acts in place B along a line parallel to cC (by book 1, prop. 40, of the Elements, and law 2), that is, along the line BS; and in place C, the force acts along a line parallel to dD, that is, along the line SC, . . . . Therefore it always acts along lines tending toward that unmoving point S. Q.E.D.
CASE 2. And, by corol. 5 of the laws, it makes no difference whether the surface on which the body describes a curvilinear figure is at rest or whether it moves uniformly straight forward, together with the body, the figure described, and the point S.
aCOROLLARY 1. bIn nonresisting spaces or mediums, if the areas are not proportional to the times, the forces do not tend toward the point where the radii meet but deviate forward [or in consequentia] from it, that is, in the direction toward which the motion takes place, provided that the description of the areas is accelerated; but if it is retarded, they deviate backward [or in antecedentia, i.e., in a direction contrary to that in which the motion takes place].b
COROLLARY 2. cIn resisting mediums also, if the description of areas is accelerated, the directions of the forces deviate from the point where the radii meet in the direction toward which the motion takes place.a c
Scholium
A body can be urged by a centripetal force compounded of several forces.
In this case the meaning of the proposition is that the force which is
compounded of all the forces tends toward point S. Further, if some force acts
continually along a line perpendicular to the surface described, it will cause
the body to deviate from the plane of its motion, but it will neither increase
nor decrease the quantity of the surface-area described and is therefore to be
ignored in the compounding of forces.
Scholium
Since the uniform description of areas indicates the center toward which that
force is directed by which a body is most affected and by which it is drawn
away from rectilinear motion and kept in orbit, why should we not in what
follows use uniform description of areas as a criterion for a center about
which all orbital motion takes place in free spaces?
Proposition 4, Theorem 4
The centripetal forces of bodies that describe different circles with uniform motion
tend toward the centers of those circles and are to one another as the squares of
the arcs described in the same time divided by the radii of the circles.
aThese forces tend toward the centers of the circles by prop. 2 and prop. 1, corol. 2, and are to another as the versed sines of the arcs described in minimally small equal times, by prop. 1, corol. 4, that is, as the squares of those arcs divided by the diameters of the circles, by lem. 7; and therefore, since these arcs are as the arcs described in any equal times and the diameters are as their radii, the forces will be as the squares of any arcs described in the same time divided by the radii of the circles. Q.E.D.a
bCOROLLARY 1. cSince those arcs are as the velocities of the bodies, the centripetal forces will be in a ratio compounded of the squared ratio of the velocities directly and the simple ratio of the radii inversely.c
COROLLARY 2. dAnd since the periodic times are in a ratio compounded of the ratio of the radii directly and the ratio of the velocities inversely, the centripetal forces are in a ratio compounded of the ratio of the radii directly and the squared ratio of the periodic times inversely.d
COROLLARY 4. eIf both the periodic times and the velocities are as the square roots of the radii, the centripetal forces will be equal to one another; and conversely.e
COROLLARY 5. fIf the periodic times are as the radii, and therefore the velocities are equal, the centripetal forces will be inversely as the radii; and conversely.f
COROLLARY 6. gIf the periodic times are as the 3/2 powers of the radii, and therefore the velocities are inversely as the square roots of the radii, the centripetal forces will be inversely as the squares of the radii; and conversely.bg
Scholium
iThe case of corol. 6 holds for the heavenly bodies (as our compatriots Wren,
Hooke, and Halley have also found out independently). Accordingly, I have
decided that in what follows I shall deal more fully with questions relating to
the centripetal forces that decrease as the squares of the distances from centers
[i.e., centripetal forces that vary inversely as the squares of the distances].
Further, with the help of the preceding proposition and its corollaries the proportion of a centripetal force to any known force, such as that of gravity, may also be determined. jFor if a body revolves by the force of its gravity in a circle concentric with the earth, this gravity is its centripetal force. Moreover, by prop. 4, corol. 9, both the time of one revolution and the arc described in any given time are given from the descent of heavy bodies.j And by propositions of this sort Huygens in his excellent treatise On the Pendulum Clock compared the force of gravity with the centrifugal forces of revolving bodies.
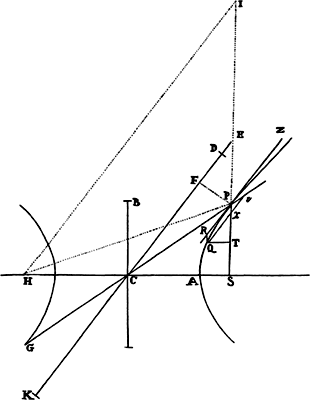
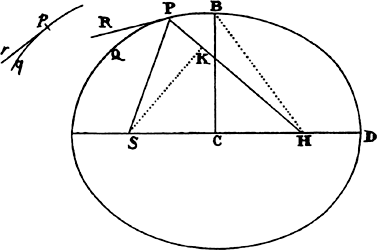
Proposition 5, Problem 1
Given, in any places, the velocity with which a body describes a given curve when
acted on by forces tending toward some common center, to find that center.
Let the curve so described be touched in three points P, Q, and R by three
straight lines PT, TQV, and VR, meeting in T and V. Erect PA, QB, and
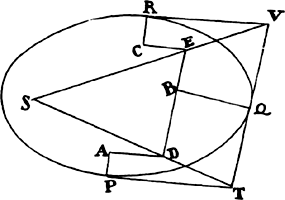 RC perpendicular to the tangents and
inversely proportional to the velocities
of the body at the points P, Q, and
R from which the perpendiculars are
erected—that is, so that PA is to QB
as the velocity at Q to the velocity at
P, and QB to RC as the velocity at R
to the velocity at Q. Through the ends
A, B, and C of the perpendiculars draw AD, DBE, and EC at right angles
to those perpendiculars, and let them meet in D and E; then TD and VE,
when drawn and produced, will meet in the required center S.
RC perpendicular to the tangents and
inversely proportional to the velocities
of the body at the points P, Q, and
R from which the perpendiculars are
erected—that is, so that PA is to QB
as the velocity at Q to the velocity at
P, and QB to RC as the velocity at R
to the velocity at Q. Through the ends
A, B, and C of the perpendiculars draw AD, DBE, and EC at right angles
to those perpendiculars, and let them meet in D and E; then TD and VE,
when drawn and produced, will meet in the required center S.
For the perpendiculars dropped from center S to tangents PT and QT are (by prop. 1, corol. 1) inversely as the velocities of the body at points P and Q, and therefore, by the construction, as the perpendiculars AP and BQ directly, that is, as the perpendiculars dropped from point D to the tangents. Hence it is easily gathered that points S, D, and T are in one straight line. And, by a similar argument, the points S, E, and V are also in one straight line; and therefore the center S is at the point where the straight lines TD and VE meet. Q.E.D.
Proposition 6a, Theorem 5
bIf in a nonresisting space a body revolves in any orbit about an immobile center
and describes any just-nascent arc in a minimally small time, and if the sagitta of
the arc is understood to be drawn so as to bisect the chord and, when produced,
to pass through the center of forces, the centripetal force in the middle of the arc
will be as the sagitta directly and as the time twice [i.e., as the square of the time]
inversely.
This proposition is also easily proved by lem. 10, corol. 4.
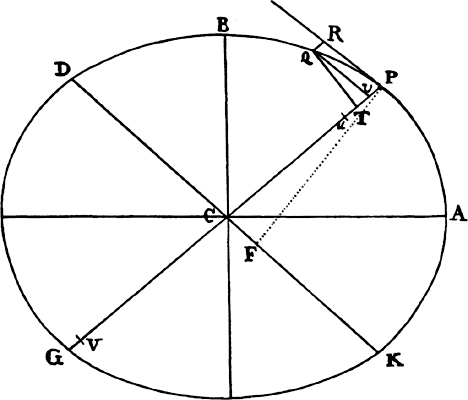
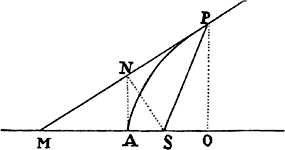
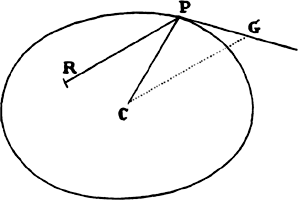
Proposition 7, Problem 2
Let a body revolve in the circumference of a circle; it is required to find the law
of the centripetal force tending toward any given point.
Let VQPA be the
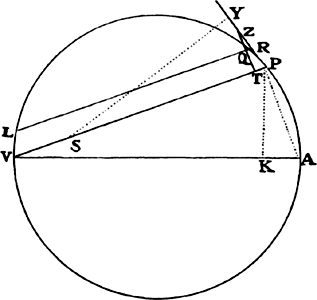 circumference of the circle, S the given
point toward which the force
tends as to its center, P the body
revolving in the circumference, Q
the place to which it will move
next, and PRZ the tangent of
the circle at the previous place.
Through point S draw chord PV;
and when the diameter VA of
the circle has been drawn, join
AP; and to SP drop perpendicular
QT, which when produced meets the tangent PR at Z; and finally through
point Q draw LR parallel to SP and meeting both the circle at L and the
tangent PZ at R. Then because the triangles ZQR, ZTP, and VPA are
similar, RP2 (that is, QR × RL) will be to QT2 as AV2 to PV2. And therefore
circumference of the circle, S the given
point toward which the force
tends as to its center, P the body
revolving in the circumference, Q
the place to which it will move
next, and PRZ the tangent of
the circle at the previous place.
Through point S draw chord PV;
and when the diameter VA of
the circle has been drawn, join
AP; and to SP drop perpendicular
QT, which when produced meets the tangent PR at Z; and finally through
point Q draw LR parallel to SP and meeting both the circle at L and the
tangent PZ at R. Then because the triangles ZQR, ZTP, and VPA are
similar, RP2 (that is, QR × RL) will be to QT2 as AV2 to PV2. And therefore
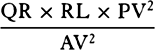 is equal to QT2. Multiply these equals by
is equal to QT2. Multiply these equals by 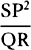 and, the
points P and Q coming together, write PV for RL. Thus
and, the
points P and Q coming together, write PV for RL. Thus 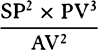 will
become equal to
will
become equal to 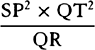 . Therefore (by prop. 6, corols. 1 and 5), the
centripetal force is inversely as
. Therefore (by prop. 6, corols. 1 and 5), the
centripetal force is inversely as 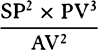 , that is (because AV2 is given),
inversely as the square of the distance or altitude SP and the cube of the
chord PV jointly. Q.E.I.
, that is (because AV2 is given),
inversely as the square of the distance or altitude SP and the cube of the
chord PV jointly. Q.E.I.
Draw SY perpendicular to the tangent PR produced; then, because
triangles SYP and VPA are similar, AV will be to PV as SP to SY, and thus
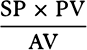 will be equal to SY, and
will be equal to SY, and 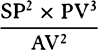 will be equal to SY2 × PV.
And therefore (by prop. 6, corols. 3 and 5), the centripetal force is inversely
as
will be equal to SY2 × PV.
And therefore (by prop. 6, corols. 3 and 5), the centripetal force is inversely
as 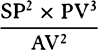 , that is, because AV is given, inversely as SP2 × PV3. Q.E.I.
, that is, because AV is given, inversely as SP2 × PV3. Q.E.I.
COROLLARY 1. Hence, if the given point S to which the centripetal force always tends is located in the circumference of this circle, say at V, the centripetal force will be inversely as the fifth power of the altitude SP.
COROLLARY 2. The force by which body
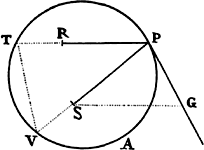 P revolves in the circle APTV around the
center of forces S is to the force by which the
same body P can revolve in the same circle
and in the same periodic time around any
other center of forces R as RP2 × SP to the
cube of the straight line SG, which is drawn
from the first center of forces S to the tangent
of the orbit PG and is parallel to the distance of the body from the second
center of forces. For by the construction of this proposition the first force is
to the second force as RP2 × PT3 to SP2 × PV3, that is, as SP × RP2 to
P revolves in the circle APTV around the
center of forces S is to the force by which the
same body P can revolve in the same circle
and in the same periodic time around any
other center of forces R as RP2 × SP to the
cube of the straight line SG, which is drawn
from the first center of forces S to the tangent
of the orbit PG and is parallel to the distance of the body from the second
center of forces. For by the construction of this proposition the first force is
to the second force as RP2 × PT3 to SP2 × PV3, that is, as SP × RP2 to
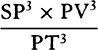 , or (because the triangles PSG and TPV are similar) to SG3.
, or (because the triangles PSG and TPV are similar) to SG3.
COROLLARY 3. The force by which body P revolves in any orbit around the center of forces S is to the force by which the same body P can revolve in the same orbit and in the same periodic time around any other center of forces R as the solid SP × RP2—contained under the distance of the body from the first center of forces S and the square of its distance from the second center of forces R—to the cube of the straight line SG, which is drawn from the first center of forces S to the tangent of the orbit PG and is parallel to the distance RP of the body from the second center of forces. For the forces in this orbit at any point of it P are the same as in a circle of the same curvature.
Proposition 8, Problem 3
Let a body move in the semicircle PQA; it is required to find the law of the
centripetal force for this effect, when the centripetal force tends toward a point S
so distant that all the lines PS and RS drawn to it can be considered parallel.
From the center C of the semicircle
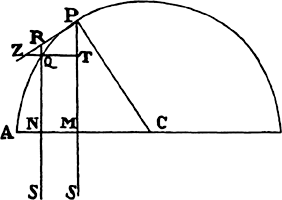 draw the semidiameter CA, intersecting
those parallels perpendicularly at M and
N, and join CP. Because triangles CPM,
PZT, and RZQ are similar, CP2 is to
PM2 as PR2 to QT2, and from the
nature of a circle PR2 is equal to the
rectangle QR × (RN + QN), or, the points
P and Q coming together, to the rectangle QR × 2PM. Therefore, CP2 is
to PM2 as QR × 2PM to QT2, and thus
draw the semidiameter CA, intersecting
those parallels perpendicularly at M and
N, and join CP. Because triangles CPM,
PZT, and RZQ are similar, CP2 is to
PM2 as PR2 to QT2, and from the
nature of a circle PR2 is equal to the
rectangle QR × (RN + QN), or, the points
P and Q coming together, to the rectangle QR × 2PM. Therefore, CP2 is
to PM2 as QR × 2PM to QT2, and thus 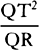 is equal to
is equal to 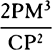 , and
, and
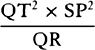 is equal to
is equal to 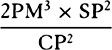 . Therefore (by prop. 6, corols. 1 and
5), the centripetal force is inversely as
. Therefore (by prop. 6, corols. 1 and
5), the centripetal force is inversely as 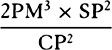 , that is
, that is  neglecting the
determinatea ratio
neglecting the
determinatea ratio 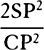
 , inversely as PM3. Q.E.I.
, inversely as PM3. Q.E.I.
The same is easily gathered also from the preceding proposition.
Scholium
And by a not very different argument, a body will be found to move in an
ellipse, or even in a hyperbola
or a parabola, under the action of a centripetal
force that is inversely as the cube of the ordinate tending toward an extremely
distant center of forces.
Proposition 9, Problem 4
Let a body revolve in a spiral PQS intersecting all its radii SP, SQ, . . . , at a
given angle; it is required to find the law of the centripetal force tending toward
the center of the spiral.
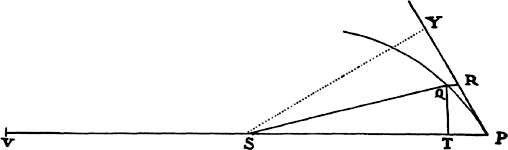
Let the indefinitely small angle PSQ be given, and because all the angles
are given, the species [i.e., the ratio of all the parts] of the figure SPRQT
will be given. Therefore, the ratio 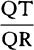 is given, and
is given, and 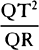 is as QT, that is
(because the species of the figure is given), as SP. Now change the angle PSQ
in any way, and the straight line QR subtending the angle of contact QPR
will be changed (by lem. 11) as the square of PR or QT. Therefore,
is as QT, that is
(because the species of the figure is given), as SP. Now change the angle PSQ
in any way, and the straight line QR subtending the angle of contact QPR
will be changed (by lem. 11) as the square of PR or QT. Therefore, 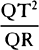 will remain the same as before, that is, as SP. And therefore
will remain the same as before, that is, as SP. And therefore 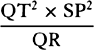 is
as SP3, and thus (by prop. 6, corols. 1 and 5) the centripetal force is inversely
as the cube of the distance SP. Q.E.I.
is
as SP3, and thus (by prop. 6, corols. 1 and 5) the centripetal force is inversely
as the cube of the distance SP. Q.E.I.
The perpendicular SY dropped to the tangent, and the chord PV of the circle cutting the spiral concentrically, are to the distance SP in given ratios; and thus SP3 is as SY2 × PV, that is (by prop. 6, corols. 3 and 5), inversely as the centripetal force.
Lemma 12
All the parallelograms described about any conjugate diameters of a given ellipse
or hyperbola are equal to one another.
This is evident from the Conics.
Proposition 10, Problem 5
Let a body revolve in an ellipse; it is required to find the law of the centripetal
force tending toward the center of the ellipse.
Let CA and CB be the semiaxes of the ellipse, GP and DK other
conjugate diameters, PF and QT perpendiculars to those diameters, Qv an
ordinate to diameter GP; then, if parallelogram QvPR is completed, the rectangle
Pv × vG will (from the Conicsa) be to Qv2 as PC2 to CD2, and (because
triangles QvT and PCF are similar) Qv2 is to QT2 as PC2 to PF2, and,
when these ratios are combined, the rectangle Pv × vG is to QT2 as PC2 to
CD2 and PC2 to PF2; that is, vG is to 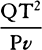 as PC2 to
as PC2 to 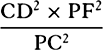 . Write
QR for Pv and (by lem. 12) BC × CA for CD × PF, and also (points P
and Q coming together) 2PC for vG, and, multiplying the extremes and
means together,
. Write
QR for Pv and (by lem. 12) BC × CA for CD × PF, and also (points P
and Q coming together) 2PC for vG, and, multiplying the extremes and
means together, 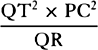 will become equal to
will become equal to 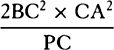 . Therefore
(by prop. 6, corol. 5), the centripetal force is as
. Therefore
(by prop. 6, corol. 5), the centripetal force is as 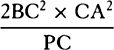 inversely, that
is (because 2BC2 × CA2 is given), as
inversely, that
is (because 2BC2 × CA2 is given), as 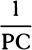 inversely, that is, as the distance PC
directly. Q.E.I.
inversely, that is, as the distance PC
directly. Q.E.I.
On the straight line PG take a point u on the other side of point T,
so that Tu is equal to Tv; then take uV such that it is to vG as DC2 is to
PC2. And since (from the Conics) Qv2 is to Pv × vG as DC2 to PC2, Qv2
will be equal to Pv × uV. Add the rectangle uP × Pv to both sides, and the
square of the chord of arc PQ will come out equal to the rectangle VP × Pv;
and therefore a circle that touches the conic section at P and passes through
point Q will also pass through point V. Let points P and Q come together,
and the ratio of uV to vG, which is the same as the ratio of DC2 to PC2,
will become the ratio of PV to PG or PV to 2PC; and therefore PV will
be equal to 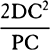 . Accordingly, the force under the action of which body P
revolves in the ellipse will (by prop. 6, corol. 3) be as
. Accordingly, the force under the action of which body P
revolves in the ellipse will (by prop. 6, corol. 3) be as 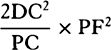 inversely,
that is (because 2DC2 × PF2 is given), as PC directly. Q.E.I.
inversely,
that is (because 2DC2 × PF2 is given), as PC directly. Q.E.I.
COROLLARY 1. Therefore, the force is as the distance of the body from the center of the ellipse; and, conversely, if the force is as the distance, the body will move in an ellipse having its center in the center of forces, or perhaps it will move in a circle, into which an ellipse can be changed.
COROLLARY 2. And the periodic times of the revolutions made in all ellipses universally around the same center will be equal. For in similar ellipses those times are equal (by prop. 4, corols. 3 and 8), while in ellipses having a common major axis they are to one another as the total areas of the ellipses directly and the particles of the areas described in the same time inversely; that is, as the minor axes directly and the velocities of bodies in their principal vertices inversely; that is, as those minor axes directly and the ordinates to the same point of the common axis inversely; and therefore (because of the equality of the direct and inverse ratios) in the ratio of equality.
Scholium
If the center of the ellipse goes off to infinity, so that the ellipse turns into
a parabola, the body will move in this parabola, and the force, now tending
toward an infinitely distant center, will prove to be uniform. This is Galileo’s
theorem. And if (by changing the inclination of the cutting plane to the
cone) the parabolic section of the cone turns into a hyperbola, the body will
move in the perimeter of the hyperbola, with the centripetal force turned
into a centrifugal force. And just as in a circle or an ellipse, if the forces
tend toward a figure’s center located in the abscissa, and if the ordinates are
increased or decreased in any given ratio or even if the angle of the inclination
of the ordinates to the abscissa is changed, these forces are always increased
or decreased in the ratio of the distances from the center, provided that the
periodic times remain equal; so also in all figures universally, if the ordinates
are increased or decreased in any given ratio or the angle of inclination of
the ordinates is changed in any way while the periodic time remains the
same, the forces tending toward any center located in the abscissa are, for
each individual ordinate, increased or decreased in the ratio of the distances
from the center.
The motion of bodies in eccentric conic sections
Proposition 11a Problem 6
Let a body revolve in an ellipse; it is required to find the law of the centripetal
force tending toward a focus of the ellipse.
Let S be a focus of the ellipse. Draw SP cutting both the diameter DK
of the ellipse in E and the ordinate Qv in x, and complete the parallelogram
QxPR. It is evident that EP is equal to the semiaxis major AC because when
line HI is drawn parallel to EC from the other focus H of the ellipse, ES
and EI are equal because CS and CH are equal; so that EP is the half-sum
of PS and PI, that is (because HI and PR are parallel and angles IPR and
HPZ are equal), the half-sum of PS and PH (which taken together equal
the whole axis 2AC). Drop QT perpendicular to SP, and if L denotes the
principal latus rectum of the ellipse 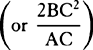 , L × QR will be to L × Pv
as QR to Pv, that is, as PE or AC to PC; and L × Pv will be to Gv × vP as
L to Gv; andb Gv × vP will be to Qv2 as PC2 to CD2; and (by lem. 7, corol.
2) the ratio of Qv2 to Qx2, with the points Q and P coming together, is the
ratio of equality; and Qx2 or Qv2 is to QT2 as EP2 to PF2, that is, as CA2 to
PF2 or (by lem. 12) as CD2 to CB2. And when all these ratios are combined,
L × QR will be to QT2 as AC × L × PC2 × CD2, or as 2CB2 × PC2 × CD2
to PC × Gv × CD2 × CB2, or as 2PC to Gv. But with the points Q and P
coming together, 2PC and Gv are equal. Therefore, L × QR and QT2, which
are proportional to these, are also equal. Multiply these equals by
, L × QR will be to L × Pv
as QR to Pv, that is, as PE or AC to PC; and L × Pv will be to Gv × vP as
L to Gv; andb Gv × vP will be to Qv2 as PC2 to CD2; and (by lem. 7, corol.
2) the ratio of Qv2 to Qx2, with the points Q and P coming together, is the
ratio of equality; and Qx2 or Qv2 is to QT2 as EP2 to PF2, that is, as CA2 to
PF2 or (by lem. 12) as CD2 to CB2. And when all these ratios are combined,
L × QR will be to QT2 as AC × L × PC2 × CD2, or as 2CB2 × PC2 × CD2
to PC × Gv × CD2 × CB2, or as 2PC to Gv. But with the points Q and P
coming together, 2PC and Gv are equal. Therefore, L × QR and QT2, which
are proportional to these, are also equal. Multiply these equals by 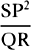 , and
L × SP2 will become equal to
, and
L × SP2 will become equal to 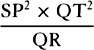 . Therefore (by prop. 6, corols. 1
and 5) the centripetal force is inversely as L × SP2, that is, inversely as the
square of the distance SP. Q.E.I.
. Therefore (by prop. 6, corols. 1
and 5) the centripetal force is inversely as L × SP2, that is, inversely as the
square of the distance SP. Q.E.I.
The force which tends toward the center of the ellipse, and by which
body P can revolve in that ellipse, is (by prop. 10, corol. 1) as the distance CP
of the body from the center C of the ellipse; hence, if CE is drawn parallel to
the tangent PR of the ellipse and if CE and PS meet at E, then the force by
which the same body P can revolve around any other point S of the ellipse
will (by prop. 7, corol. 3) be as 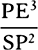 ; that is, if point S is a focus of the ellipse,
and therefore PE is given, this force will be inversely as SP2. Q.E.I.
; that is, if point S is a focus of the ellipse,
and therefore PE is given, this force will be inversely as SP2. Q.E.I.
This solution could be extended to the parabola and the hyperbola as concisely as in prop. 10, but because of the importance of this problem and its use in what follows, it will not be too troublesome to confirm each of these other cases by a separate demonstration.
Proposition 12, Problem 7
Let a body move in a hyperbola; it is required to find the law of the centripetal
force tending toward the focus of the figure.
Let CA and CB be the semiaxes of the hyperbola, PG and KD other
conjugate diameters, PF a perpendicular to the diameter KD, and Qv an
ordinate to the diameter GP. Draw SP cutting diameter DK in E and ordinate
Qv in x, and complete the parallelogram QRPx. It is evident that EP is
equal to the transverse semiaxis AC, because when line HI is drawn parallel
to EC from the other focus H of the hyperbola, ES and EI are equal because
CS and CH are equal; so that EP is the half-difference of PS and PI, that
is (because IH and PR are parallel and the angles IPR and HPZ are equal),
of PS and PH, the difference of which equals the whole axis 2AC. Drop
QT perpendicular to SP. Then, if L denotes the principal latus rectum of
the hyperbola 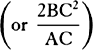 , L × QR will be to L × Pv as QR to Pv, or Px
to Pv, that is (because the triangles Pxv and PEC are similar), as PE to PC,
or AC to PC. L × Pv will also be to Gv × Pv as L to Gv; and (from the
nature of conics) the rectangle Gv × vP will be to Qv2 as PC2 to CD2; and
(by lem. 7, corol. 2) the ratio of Qv2 to Qx2, the points Q and P coming
together, comes to be the ratio of equality; and Qx2 or Qv2 is to AT2 as EP2
to PF2, that is, as CA2 to PF2, or (by lem. 12) as CD2 to CB2; and if all these
ratios are combined, L × QR will be to QT2 as AC × L × PC2 × CD2 or
2CB2 × PC2 × CD2 to PC × Gv × CD2 × CB2, or as 2PC to Gv. But, the points
P and Q coming together, 2PC and Gv are equal. Therefore, L × QR and
QT2, which are proportional to these, are also equal. Multiply these equals by
, L × QR will be to L × Pv as QR to Pv, or Px
to Pv, that is (because the triangles Pxv and PEC are similar), as PE to PC,
or AC to PC. L × Pv will also be to Gv × Pv as L to Gv; and (from the
nature of conics) the rectangle Gv × vP will be to Qv2 as PC2 to CD2; and
(by lem. 7, corol. 2) the ratio of Qv2 to Qx2, the points Q and P coming
together, comes to be the ratio of equality; and Qx2 or Qv2 is to AT2 as EP2
to PF2, that is, as CA2 to PF2, or (by lem. 12) as CD2 to CB2; and if all these
ratios are combined, L × QR will be to QT2 as AC × L × PC2 × CD2 or
2CB2 × PC2 × CD2 to PC × Gv × CD2 × CB2, or as 2PC to Gv. But, the points
P and Q coming together, 2PC and Gv are equal. Therefore, L × QR and
QT2, which are proportional to these, are also equal. Multiply these equals by
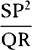 , and L × SP2 will become equal to
, and L × SP2 will become equal to 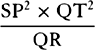 . Therefore (by prop. 6,
corols. 1 and 5), the centripetal force is inversely as L × SP2, that is, inversely
as the square of the distance SP. Q.E.I.
. Therefore (by prop. 6,
corols. 1 and 5), the centripetal force is inversely as L × SP2, that is, inversely
as the square of the distance SP. Q.E.I.
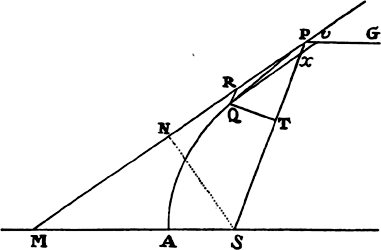
Find the force that tends from the center C of the hyperbola. This will
come out proportional to the distance CP. And hence (by prop. 7, corol. 3)
the force tending toward the focus S will be as 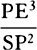 , that is, because PE is
given, inversely as SP2. Q.E.I.
, that is, because PE is
given, inversely as SP2. Q.E.I.
It is shown in the same way that if this centripetal force is turned into a centrifugal force, a body will move in the opposite branch of the hyperbola.
Lemma 13
In a parabola the latus rectum belonging to any vertex is four times the distance
of that vertex from the focus of the figure.
This is evident from the Conics.
Lemma 14
A perpendicular dropped from the focus of a parabola to its tangent is a mean
proportional between the distance of the focus from the point of contact and its
distance from the principal vertex of the figure.
For let AP be the parabola, S its focus, A the principal vertex, P the
point of contact, PO an ordinate to the principal diameter, PM a tangent
 meeting the principal diameter in M,
and SN a perpendicular line from
the focus to the tangent. Join AN,
and because MS and SP, MN and
NP, and MA and AO are equal, the
straight lines AN and OP will be
parallel; and hence triangle SAN will
be right-angled at A and similar to the equal triangles SNM and SNP;
therefore, PS is to SN as SN to SA. Q.E.D.
meeting the principal diameter in M,
and SN a perpendicular line from
the focus to the tangent. Join AN,
and because MS and SP, MN and
NP, and MA and AO are equal, the
straight lines AN and OP will be
parallel; and hence triangle SAN will
be right-angled at A and similar to the equal triangles SNM and SNP;
therefore, PS is to SN as SN to SA. Q.E.D.
COROLLARY 1. PS2 is to SN2 as PS to SA.
COROLLARY 2. And because SA is given, SN2 is as PS.
COROLLARY 3. And the point where any tangent PM meets the straight line SN, which is drawn from the focus perpendicular to that tangent, occurs in the straight line AN, which touches the parabola in the principal vertex.
Proposition 13, Problem 8
Let a body move in the perimeter of a parabola; it is required to find the law of
the centripetal force tending toward a focus of the figure.
Let the construction be the same as in lem. 14, and let P be the body in
the perimeter of the parabola; from the place Q into which the body moves
next, draw QR parallel and QT perpendicular to SP and draw Qv parallel
to the tangent and meeting both the diameter PG in v and the distance SP
in x. Now, because triangles Pxv and SPM are similar and the sides SM
and SP of the one are equal, the sides Px or QR and Pv of the other are
equal. But from the Conics the square of the ordinate Qv is equal to the
rectangle contained by the latus rectum and the segment Pv of the diameter,
that is (by lem. 13), equal to the rectangle 4PS × Pv, or 4PS × QR, and, the
points P and Q coming together, the ratio of Qv to Qx (by lem. 7, corol.
2) becomes the ratio of equality. Therefore, in this case Qx2 is equal to the
rectangle 4PS × QR. Moreover (because triangles QxT and SPN are similar),
Qx2 is to QT2 as PS2 to SN2, that is (by lem. 14, corol. 1), as PS to SA,
that is, as 4PS × QR to 4SA × QR, and hence (by Euclid’s Elements, book
5, prop. 9) QT2 and 4SA × QR are equal. Multiply these equals by 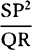 ,
and
,
and 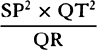 will become equal to SP2 × 4SA; and therefore (by prop.
6, corols. 1 and 5) the centripetal force is inversely as SP2 × 4SA, that is,
because 4SA is given, inversely as the square of the distance SP. Q.E.I.
will become equal to SP2 × 4SA; and therefore (by prop.
6, corols. 1 and 5) the centripetal force is inversely as SP2 × 4SA, that is,
because 4SA is given, inversely as the square of the distance SP. Q.E.I.
COROLLARY 1. From the last three propositions it follows that if any body P departs from the place P along any straight line PR with any velocity whatever and is at the same time acted upon by a centripetal force that is inversely proportional to the square of the distance of places from the center, this body will move in some one of the conics having a focus in the center of forces; and conversely. For if the focus and the point of contact and the position of the tangent are given, a conic can be described that will have a given curvature at that point. But the curvature is given from the given centripetal force and velocity of the body; and two different orbits touching each other cannot be described with the same centripetal force and the same velocity.
COROLLARY 2. If the velocity with which the body departs from its place
P is such that the line-element PR can be described by it in some minimally
small particle of time, and if the centripetal force is able to move the same
body through space QR in that same time, this body will move in some
conic whose principal latus rectum is the quantity 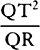 which ultimately
results when the line-elements PR and QR are diminished indefinitely. In
these corollaries I include the circle along with the ellipse, but not for the
case where the body descends straight down to a center.
which ultimately
results when the line-elements PR and QR are diminished indefinitely. In
these corollaries I include the circle along with the ellipse, but not for the
case where the body descends straight down to a center.
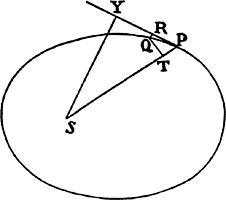
Proposition 14, Theorem 6
If several bodies revolve about a common center and the centripetal force is
inversely as the square of the distance of places from the center, I say that the
principal latera recta of the orbits are as the squares of the areas which the bodies
describe in the same time by radii drawn to the center.
For (by prop. 13, corol. 2) the latus rectum L is equal to the
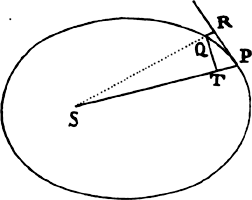 quantity
quantity 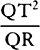 that results ultimately when points
P and Q come together. But the minimally
small line QR is in a given time as the generating
centripetal force, that is (by hypothesis),
inversely as SP2. Therefore,
that results ultimately when points
P and Q come together. But the minimally
small line QR is in a given time as the generating
centripetal force, that is (by hypothesis),
inversely as SP2. Therefore, 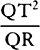 is as
QT2 × SP2, that is, the latus rectum L is as
the square of the area QT × SP. Q.E.D.
is as
QT2 × SP2, that is, the latus rectum L is as
the square of the area QT × SP. Q.E.D.
COROLLARY. Hence the total area of the ellipse and, proportional to it, the rectangle contained by the axes is as the square root of the latus rectum and as the periodic time. For the total area is as the area QT × SP, which is described in a given time, multiplied by the periodic time.
Proposition 15, Theorem 7
Under the same suppositions as in prop. 14, I say that the squares of the periodic
times in ellipses are as the cubes of the major axes.
For the minor axis is a mean proportional between the major axis and the latus rectum, and thus the rectangle contained by the axes is as the square root of the latus rectum and as the 3/2 power of the major axis. But this rectangle (by prop. 14, corol.) is as the square root of the latus rectum and as the periodic time. Take away from both sides [i.e., divide through by] the square root of the latus rectum, and the result will be that the squares of the periodic times are as the cubes of the major axes. Q.E.D.
COROLLARY. Therefore the periodic times in ellipses are the same as in circles whose diameters are equal to the major axes of the ellipses.
Proposition 16, Theorem 8
Under the same suppositions as in prop. 15, if straight lines are drawn to the bodies
in such a way as to touch the orbits in the places where the bodies are located,
and if perpendiculars are dropped from the common focus to these tangents, I say
that the velocities of the bodies are inversely as the perpendiculars and directly as
the square roots of the principal latera recta.
From focus S to tangent PR drop
 perpendicular SY, and the velocity of body P
will be inversely as the square root of
perpendicular SY, and the velocity of body P
will be inversely as the square root of 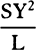 .
For this velocity is as the minimally small
arc PQ described in a given particle of time,
that is (by lem. 7), as the tangent PR, that
is—because the proportion of PR to QT is
as SP to SY—as
.
For this velocity is as the minimally small
arc PQ described in a given particle of time,
that is (by lem. 7), as the tangent PR, that
is—because the proportion of PR to QT is
as SP to SY—as 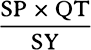 , or as SY inversely and SP × QT directly; and
SP × QT is as the area described in the given time, that is (by prop. 14), as
the square root of the latus rectum. Q.E.D.
, or as SY inversely and SP × QT directly; and
SP × QT is as the area described in the given time, that is (by prop. 14), as
the square root of the latus rectum. Q.E.D.
COROLLARY 1. The principal latera recta are as the squares of the perpendiculars and as the squares of the velocities.
COROLLARY 2. The velocities of bodies at their greatest and least distances from the common focus are inversely as the distances and directly as the square roots of the principal latera recta. For the perpendiculars are now the distances themselves.
COROLLARY 3. And thus the velocity in a conic, at the greatest or least distance from the focus, is to the velocity with which the body would move in a circle, at the same distance from the center, as the square root of the principal latus rectum is to the square root of twice that distance.
COROLLARY 4. The velocities of bodies revolving in ellipses are, at their mean distances from the common focus, the same as those of bodies revolving in circles at the same distances, that is (by prop. 4, corol. 6), inversely as the square roots of the distances. For the perpendiculars now coincide with the semiaxes minor, and these are as mean proportionals between the distances and the latera recta. Compound this ratio [of the semiaxes] inversely with the square root of the ratio of the latera recta directly, and it will become the square root of the ratio of the distances inversely.
COROLLARY 5. In the same figure, or even in different figures whose principal latera recta are equal, the velocity of a body is inversely as the perpendicular dropped from the focus to the tangent.
COROLLARY 6. In a parabola the velocity is inversely as the square root of the distance of the body from the focus of the figure; in an ellipse the velocity varies in a ratio that is greater than this, and in a hyperbola in a ratio that is less. For (by lem. 14, corol. 2) the perpendicular dropped from the focus to the tangent of a parabola is as the square root of that distance. In a hyperbola the perpendicular is smaller, and in an ellipse greater, than in this ratio.
COROLLARY 7. In a parabola the velocity of a body at any distance from the focus is to the velocity of a body revolving in a circle at the same distance from the center as the square root of the ratio of 2 to 1; in an ellipse it is smaller and in a hyperbola greater than in this ratio. For by corol. 2 of this proposition the velocity in the vertex of a parabola is in this ratio, and—by corol. 6 of this proposition and by prop. 4, corol. 6—the same proportion is kept at all distances. Hence, also, in a parabola the velocity everywhere is equal to the velocity of a body revolving in a circle at half the distance; in an ellipse it is smaller and in a hyperbola greater.
COROLLARY 8. The velocity of a body revolving in any conic is to the velocity of a body revolving in a circle at a distance of half the principal latus rectum of the conic as that distance is to the perpendicular dropped from the focus to the tangent of the conic. This is evident by corol. 5.
COROLLARY 9. Hence, since (by prop. 4, corol. 6) the velocity of a body revolving in this circle is to the velocity of a body revolving in any other circle inversely in the ratio of the square roots of the distances, it follows from the equality of the ratios [or ex aequo] that the velocity of a body revolving in a conic will have the same ratio to the velocity of a body revolving in a circle at the same distance that a mean proportional between that common distance and half of the principal latus rectum of the conic has to the perpendicular dropped from the common focus to the tangent of the conic.
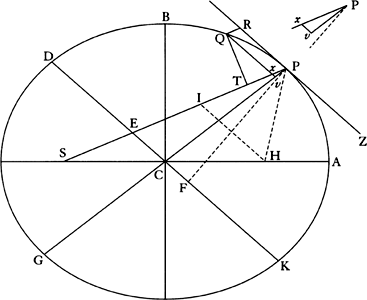
Proposition 17, Problem 9
Supposing that the centripetal force is inversely proportional to the square of the
distance of places from the center and that the absolute quantity of this force is
known, it is required to find the line which a body describes when going forth
from a given place with a given velocity along a given straight line.
Let the centripetal force tending toward a point S be such that a body p revolves by its action in any given orbit pq, and let its velocity in the place p be found out. Let body P go forth from place P along line PR with a given velocity and thereupon be deflected from that line into a conic PQ under the compulsion of the centripetal force. Therefore the straight line PR will touch this conic at P. Let some straight line pr likewise touch the orbit pq at p, and if perpendiculars are understood to be dropped from S to these tangents, the principal latus rectum of the conic will (by prop. 16, corol. 1) be to the principal latus rectum of the orbit in a ratio compounded of the squares of the perpendiculars and the squares of the velocities and thus is given. Let L be the latus rectum of the conic. The focus S of the conic is also given. Let angle RPH be the complement of angle RPS to two right angles [i.e., the supplement of angle RPS]; then the line PH, on which the other focus H is located, will be given in position. Drop the perpendicular SK to PH and understand the conjugate semiaxis BC to be erected; then SP2 − 2KP × PH + PH2 = SH2 = 4CH2 = 4BH2 − 4BC2 = (SP + PH)2 − L × (SP + PH) = SP2 + 2SP × PH + PH2 − L × (SP + PH). Add to each side 2(KP × PH) − SP2 − PH2 + L × (SP + PH), and L × (SP + PH) will become = 2(SP × PH) + 2(KP × PH), or SP + PH will be to PH as 2SP + 2KP to L. Hence PH is given in length as well as in position. Specifically, if the velocity of the body at P is such that the latus rectum L is less than 2SP + 2KP, PH will lie on the same side of the tangent PR as the line PS; and thus the figure will be an ellipse and will be given from the given foci S and H and the given principal axis SP + PH. But if the velocity of the body is so great that the latus rectum L is equal to 2SP + 2KP, the length PH will be infinite; and accordingly the figure will be a parabola having its axis SH parallel to the line PK, and hence will be given. But if the body goes forth from its place P with a still greater velocity, the length PH will have to be taken on the other side of the tangent; and thus, since the tangent goes between the foci, the figure will be a hyperbola having its principal axis equal to the difference of the lines SP and PH, and hence will be given. For if the body in these cases revolves in a conic thus found, it has been demonstrated in props. 11, 12, and 13 that the centripetal force will be inversely as the square of the distance of the body from the center of forces S; and thus the line PQ is correctly determined, which a body will describe under the action of such a force, when it goes forth from a given place P with a given velocity along a straight line PR given in position. Q.E.F.
COROLLARY 1. Hence in every conic, given the principal vertex D, the latus rectum L, and a focus S, the other focus H is given when DH is taken to DS as the latus rectum is to the difference between the latus rectum and 4DS. For the proportion SP + PH to PH as 2SP + 2KP to L in the case of this corollary becomes DS + DH to DH as 4DS to L and, by separation [or dividendo], becomes DS to DH as 4DS − L to L.
COROLLARY 2. Hence, given the velocity of a body in the principal vertex D, the orbit will be found expeditiously, namely, by taking its latus rectum to twice the distance DS as the square of the ratio of this given velocity to the velocity of a body revolving in a circle at a distance DS (by prop. 16, corol. 3), and then taking DH to DS as the latus rectum to the difference between the latus rectum and 4DS.
COROLLARY 3. Hence also, if a body moves in any conic whatever and is forced out of its orbit by any impulse, the orbit in which it will afterward pursue its course can be found. For by compounding the body’s own motion with that motion which the impulse alone would generate, there will be found the motion with which the body will go forth from the given place of impulse along a straight line given in position.
COROLLARY 4. And if the body is continually perturbed by some force impressed from outside, its trajectory can be determined very nearly, by noting the changes which the force introduces at certain points and estimating from the order of the sequence the continual changes at intermediate places.a
Scholium
If a body P, under the action of a centripetal force tending toward any given
 point R, moves in the perimeter of any
given conic whatever, whose center is
C, and the law of the centripetal force
is required, let CG be drawn parallel to
the radius RP and meeting the tangent
PG of the orbit at G; then the force
(by prop. 10, corol. 1 and schol.; and
prop. 7, corol. 3) will be as
point R, moves in the perimeter of any
given conic whatever, whose center is
C, and the law of the centripetal force
is required, let CG be drawn parallel to
the radius RP and meeting the tangent
PG of the orbit at G; then the force
(by prop. 10, corol. 1 and schol.; and
prop. 7, corol. 3) will be as 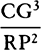 .
.
To find elliptical, parabolic, and hyperbolic orbits, given a focus
Lemma 15
If from the two foci S and H of any ellipse or hyperbola two straight lines SV
and HV are inclined to any third point V, one of the lines HV being equal to the
principal axis of the figure, that is, to the axis on which the foci lie, and the other
line SV being bisected in T by TR perpendicular to it, then the perpendicular
TR will touch the conic at some point; and conversely, if TR touches the conic,
HV will be equal to the principal axis of the figure.
For let the perpendicular TR cut the straight
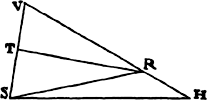 line HV (produced, if need be) in R; and join SR.
Because TS and TV are equal, the straight lines
SR and VR and the angles TRS and TRV will
be equal. Hence the point R will be on the conic, and the perpendicular TR
will touch that conic, and conversely. Q.E.D.
line HV (produced, if need be) in R; and join SR.
Because TS and TV are equal, the straight lines
SR and VR and the angles TRS and TRV will
be equal. Hence the point R will be on the conic, and the perpendicular TR
will touch that conic, and conversely. Q.E.D.
Proposition 18, Problem 10
Given a focus and the principal axes, to describe elliptical and hyperbolic
trajectories that will pass through given points and will touch straight lines given in
position.
Let S be the common focus of the figures, AB the length of the
principal axis of any trajectory, P a point through which the trajectory ought to
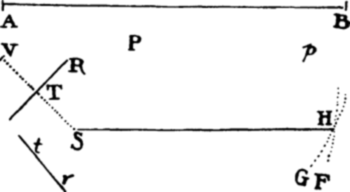 pass, and TR a straight line which it ought
to touch. Describe the circle HG with P as
center and AB − SP as radius if the orbit is
an ellipse, or AB + SP if it is a hyperbola.
Drop the perpendicular ST to the tangent
TR and produce ST to V so that TV is
equal to ST, and with center V and radius AB describe the circle FH. By
this method, whether two points P and p are given, or two tangents TR
and tr, or a point P and a tangent TR, two circles are to be described. Let
H be their common intersection, and with foci S and H and the given axis,
describe the trajectory. I say that the problem has been solved. For the trajectory
described (because PH + SP in an ellipse, or PH − SP in a hyperbola,
is equal to the axis) will pass through point P and (by lem. 15) will touch
the straight line TR. And by the same argument, this trajectory will pass
through the two points P and p or will touch the two straight lines TR and
tr. Q.E.F.
pass, and TR a straight line which it ought
to touch. Describe the circle HG with P as
center and AB − SP as radius if the orbit is
an ellipse, or AB + SP if it is a hyperbola.
Drop the perpendicular ST to the tangent
TR and produce ST to V so that TV is
equal to ST, and with center V and radius AB describe the circle FH. By
this method, whether two points P and p are given, or two tangents TR
and tr, or a point P and a tangent TR, two circles are to be described. Let
H be their common intersection, and with foci S and H and the given axis,
describe the trajectory. I say that the problem has been solved. For the trajectory
described (because PH + SP in an ellipse, or PH − SP in a hyperbola,
is equal to the axis) will pass through point P and (by lem. 15) will touch
the straight line TR. And by the same argument, this trajectory will pass
through the two points P and p or will touch the two straight lines TR and
tr. Q.E.F.
Proposition 19, Problem 11
To describe about a given focus a parabolic trajectory that will pass through given
points and will touch straight lines given in position.
Let S be the focus, P a given point, and TR a tangent of the trajectory
to be described. With center P and radius PS describe the circle FG. Drop
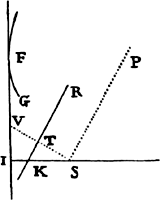 the perpendicular ST from the focus to the tangent
and produce ST to V, so that TV is equal to ST.
In the same manner, if a second point p is given,
a second circle fg is to be described; or if a second
tangent tr is given, or a second point v is to be found,
then the straight line IF is to be drawn touching the
two circles FG and fg if the two points P and p are
given, or passing through the two points V and v if
the two tangents TR and tr are given, or touching the circle FG and passing
through the point V if the point P and tangent TR are given. To FI drop
the perpendicular SI, and bisect it in K; and with axis SK and principal
vertex K describe a parabola. I say that the problem has been solved. For,
because SK and IK are equal, and SP and FP are equal, the parabola will
pass through point P; and (by lem. 14, corol. 3) because ST and TV are equal
and the angle STR is a right angle, the parabola will touch the straight line
TR. Q.E.F.
the perpendicular ST from the focus to the tangent
and produce ST to V, so that TV is equal to ST.
In the same manner, if a second point p is given,
a second circle fg is to be described; or if a second
tangent tr is given, or a second point v is to be found,
then the straight line IF is to be drawn touching the
two circles FG and fg if the two points P and p are
given, or passing through the two points V and v if
the two tangents TR and tr are given, or touching the circle FG and passing
through the point V if the point P and tangent TR are given. To FI drop
the perpendicular SI, and bisect it in K; and with axis SK and principal
vertex K describe a parabola. I say that the problem has been solved. For,
because SK and IK are equal, and SP and FP are equal, the parabola will
pass through point P; and (by lem. 14, corol. 3) because ST and TV are equal
and the angle STR is a right angle, the parabola will touch the straight line
TR. Q.E.F.
Proposition 20, Problem 12
To describe about a given focus any trajectory, given in species [i.e., of given
eccentricity], that will pass through given points and will touch straight lines
given in position.
CASE 1. Given a focus S, let it be required to describe a trajectory ABC
through two points B and C. Since the trajectory is given in species, the
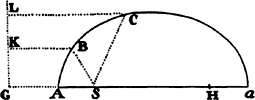 ratio of the principal axis to the distance
between the foci will be given. Take KB
to BS in this ratio and also LC to CS.
With centers B and C and radii BK and
CL, describe two circles, and drop the
perpendicular SG to the straight line KL, which touches those circles in K
and L, and cut SG in A and a so that GA is to AS, and Ga to aS, as
KB is to BS; and describe a trajectory with axis Aa and vertices A and a.
I say that the problem has been solved. For let H be the other focus of the
figure described, and since GA is to AS as Ga to aS, then by separation
[or dividendo] Ga − GA or Aa to aS − AS or SH will be in the same
ratio and thus in the ratio which the principal axis of the figure that was
to be described has to the distance between its foci; and therefore the figure
described is of the same species as the one that was to be described. And
since KB to BS and LC to CS are in the same ratio, this figure will pass
through the points B and C, as is manifest from the Conics.
ratio of the principal axis to the distance
between the foci will be given. Take KB
to BS in this ratio and also LC to CS.
With centers B and C and radii BK and
CL, describe two circles, and drop the
perpendicular SG to the straight line KL, which touches those circles in K
and L, and cut SG in A and a so that GA is to AS, and Ga to aS, as
KB is to BS; and describe a trajectory with axis Aa and vertices A and a.
I say that the problem has been solved. For let H be the other focus of the
figure described, and since GA is to AS as Ga to aS, then by separation
[or dividendo] Ga − GA or Aa to aS − AS or SH will be in the same
ratio and thus in the ratio which the principal axis of the figure that was
to be described has to the distance between its foci; and therefore the figure
described is of the same species as the one that was to be described. And
since KB to BS and LC to CS are in the same ratio, this figure will pass
through the points B and C, as is manifest from the Conics.
CASE 2. Given a focus S, let it be required to describe a trajectory which
somewhere touches the two straight lines TR and tr. Drop the perpendiculars
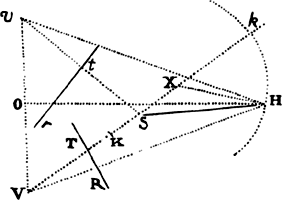 ST and St from the focus to the tangents
and produce ST and St to V and v, so
that TV and tv are equal to TS and tS.
Bisect Vv in O, and erect the indefinite
perpendicular OH, and cut the straight
line VS, indefinitely produced, in K and
k, so that VK is to KS and Vk to kS as
the principal axis of the trajectory to be
described is to the distance between the foci. On the diameter Kk describe a
circle cutting OH in H; and with foci S and H and a principal axis equal to
VH, describe a trajectory. I say that the problem has been solved. For bisect
Kk in X, and draw HX, HS, HV, and Hv. Since VK is to KS as Vk to
kS and, by composition [or componendo], as VK + Vk to KS + kS and,
by separation [or dividendo], as Vk − VK to kS − KS, that is, as 2VX to
2KX and 2KX to 2SX and thus as VX to HX and HX to SX, the triangles
VXH and HXS will be similar, and therefore VH will be to SH as VX to
XH and thus as VK to KS. Therefore the principal axis VH of the trajectory
which has been described has the same ratio to the distance SH between its
foci as the principal axis of the trajectory to be described has to the distance
between its foci and is therefore of the same species. Besides, since VH and
vH are equal to the principal axis and since VS and vS are perpendicularly
bisected by the straight lines TR and tr, it is clear (from lem. 15) that these
straight lines touch the trajectory described. Q.E.F.
ST and St from the focus to the tangents
and produce ST and St to V and v, so
that TV and tv are equal to TS and tS.
Bisect Vv in O, and erect the indefinite
perpendicular OH, and cut the straight
line VS, indefinitely produced, in K and
k, so that VK is to KS and Vk to kS as
the principal axis of the trajectory to be
described is to the distance between the foci. On the diameter Kk describe a
circle cutting OH in H; and with foci S and H and a principal axis equal to
VH, describe a trajectory. I say that the problem has been solved. For bisect
Kk in X, and draw HX, HS, HV, and Hv. Since VK is to KS as Vk to
kS and, by composition [or componendo], as VK + Vk to KS + kS and,
by separation [or dividendo], as Vk − VK to kS − KS, that is, as 2VX to
2KX and 2KX to 2SX and thus as VX to HX and HX to SX, the triangles
VXH and HXS will be similar, and therefore VH will be to SH as VX to
XH and thus as VK to KS. Therefore the principal axis VH of the trajectory
which has been described has the same ratio to the distance SH between its
foci as the principal axis of the trajectory to be described has to the distance
between its foci and is therefore of the same species. Besides, since VH and
vH are equal to the principal axis and since VS and vS are perpendicularly
bisected by the straight lines TR and tr, it is clear (from lem. 15) that these
straight lines touch the trajectory described. Q.E.F.
CASE 3. Given a focus S, let it be required to describe a trajectory which
will touch the straight line TR in a given point R. Drop the perpendicular
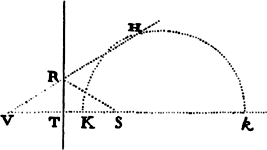 ST to the straight line TR and
produce ST to V so that TV is equal to
ST. Join VR and cut the straight line
VS, indefinitely produced, in K and k
so that VK is to SK and Vk to Sk
as the principal axis of the ellipse to
be described is to the distance between
the foci; and after describing a circle on the diameter Kk, cut the straight
line VR, produced, in H, and with foci S and H and a principal axis equal
to the straight line VH, describe a trajectory. I say that the problem has
been solved. For, from what has been demonstrated in case 2, it is
evident that VH is to SH as VK to SK and thus as the principal axis of
the trajectory which was to be described to the distance between its foci, and
therefore the trajectory which was described is of the same species as the
one which was to be described, while it is evident from the Conics that
the straight line TR by which the angle VRS is bisected touches the
trajectory at point R. Q.E.F.
ST to the straight line TR and
produce ST to V so that TV is equal to
ST. Join VR and cut the straight line
VS, indefinitely produced, in K and k
so that VK is to SK and Vk to Sk
as the principal axis of the ellipse to
be described is to the distance between
the foci; and after describing a circle on the diameter Kk, cut the straight
line VR, produced, in H, and with foci S and H and a principal axis equal
to the straight line VH, describe a trajectory. I say that the problem has
been solved. For, from what has been demonstrated in case 2, it is
evident that VH is to SH as VK to SK and thus as the principal axis of
the trajectory which was to be described to the distance between its foci, and
therefore the trajectory which was described is of the same species as the
one which was to be described, while it is evident from the Conics that
the straight line TR by which the angle VRS is bisected touches the
trajectory at point R. Q.E.F.
CASE 4. About a focus S let it be now required to describe a trajectory APB which touches the straight line TR and passes through any point P outside the given tangent and which is similar to the figure apb described with principal axis ab and foci s and h. Drop the perpendicular ST to the tangent TR and produce ST to V so that TV is equal to ST. Next make the angles hsq and shq equal to the angles VSP and SVP; and with center q and a radius that is to ab as SP to VS, describe a circle cutting the figure apb in p. Join sp and draw SH such that it is to sh as SP is to sp and makes the angle PSH equal to the angle psh and the angle VSH equal to the angle psq. Finally with foci S and H and with principal axis AB equaling the distance VH, describe a conic. I say that the problem has been solved. For if SV is drawn such that it is to sp as sh is to sq, and makes the angle vsp equal to the angle hsq and the angle vsh equal to the angle psq, the triangles svh and spq will be similar, and therefore vh will be to pq as sh is to sq, that is (because the triangles VSP and bsq are similar), as VS is to SP or ab to pq. Therefore vh and ab are equal. Furthermore, because the triangles VSH and vsh are similar, VH is to SH as vh to sh; that is, the axis of the conic just described is to the distance between its foci as the axis ab to the distance sh between the foci; and therefore the figure just described is similar to the figure apb. But because the triangle PSH is similar to the triangle psh, this figure passes through point P; and since VH is equal to the axis of this figure and VS is bisected perpendicularly by the straight line TR, the figure touches the straight line TR. Q.E.F.
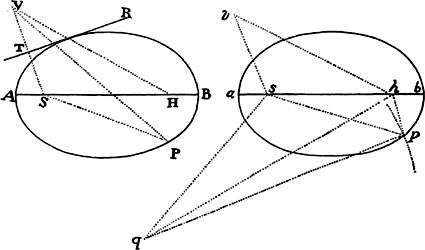
Lemma 16
From three given points to draw three slanted straight lines to a fourth point,
which is not given, when the differences between the lines either are given or
are nil.
CASE 1. Let the given points be A, B,
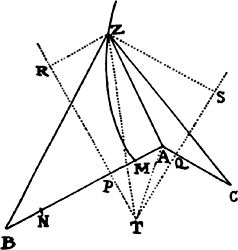 and C, and let the fourth point be Z, which
it is required to find; because of the given
difference of the lines AZ and BZ, point
Z will be located in a hyperbola whose foci
are A and B and whose principal axis is
the given difference. Let the axis be MN.
Take PM to MA as MN is to AB, and let
PR be erected perpendicular to AB and let
ZR be dropped perpendicular to PR; then,
from the nature of this hyperbola, ZR will
be to AZ as MN is to AB. By a similar process, point Z will be located in
another hyperbola, whose foci are A and C and whose principal axis is the
difference between AZ and CZ; and QS can be drawn perpendicular to AC,
whereupon, if the normal ZS is dropped to QS from any point Z of this
hyperbola, ZS will be to AZ as the difference between AZ and CZ is to AC.
Therefore the ratios of ZR and ZS to AZ are given, and consequently the
ratio of ZR and ZS to each other is given; and thus if the straight lines RP
and SQ meet in T, and TZ and TA are drawn, the figure TRZS will be
given in species, and the straight line TZ, in which point Z is somewhere
located, will be given in position. The straight line TA will also be given, as
will also the angle ATZ; and because the ratios of AZ and TZ to ZS are
given, their ratio to each other will be given; and hence the triangle ATZ,
whose vertex is the point Z, will be given. Q.E.I.
and C, and let the fourth point be Z, which
it is required to find; because of the given
difference of the lines AZ and BZ, point
Z will be located in a hyperbola whose foci
are A and B and whose principal axis is
the given difference. Let the axis be MN.
Take PM to MA as MN is to AB, and let
PR be erected perpendicular to AB and let
ZR be dropped perpendicular to PR; then,
from the nature of this hyperbola, ZR will
be to AZ as MN is to AB. By a similar process, point Z will be located in
another hyperbola, whose foci are A and C and whose principal axis is the
difference between AZ and CZ; and QS can be drawn perpendicular to AC,
whereupon, if the normal ZS is dropped to QS from any point Z of this
hyperbola, ZS will be to AZ as the difference between AZ and CZ is to AC.
Therefore the ratios of ZR and ZS to AZ are given, and consequently the
ratio of ZR and ZS to each other is given; and thus if the straight lines RP
and SQ meet in T, and TZ and TA are drawn, the figure TRZS will be
given in species, and the straight line TZ, in which point Z is somewhere
located, will be given in position. The straight line TA will also be given, as
will also the angle ATZ; and because the ratios of AZ and TZ to ZS are
given, their ratio to each other will be given; and hence the triangle ATZ,
whose vertex is the point Z, will be given. Q.E.I.
CASE 2. If two of the three lines, say AZ and BZ, are equal, draw the straight line TZ in such a way that it bisects the straight line AB; then find the triangle ATZ as above.
CASE 3. If all three lines are equal, point Z will be located in the center of a circle passing through points A, B, and C. Q.E.I.
The problem dealt with in this lemma is also solved by means of Apollonius’s book On Tangencies, restored by Viète.
Proposition 21, Problem 13
To describe about a given focus a trajectory that will pass through given points
and will touch straight lines given in position.
Let a focus S, a point P, and a tangent TR be given; the second focus
H is to be found. Drop the perpendicular ST to the tangent and produce
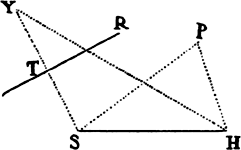 ST to Y so that TY is equal to ST, and YH
will be equal to the principal axis. Join SP
and also HP, and SP will be the difference
between HP and the principal axis. In this
way, if more tangents TR or more points P
are given, there will always be the same
number of lines YH or PH, which can be drawn
from the said points Y or P to the focus H, and which either are equal to the
axes or differ from them by given lengths SP and so either are equal to one
another or have given differences; and hence, by lem. 16, that second focus
H is given. And once the foci are found, together with the length of the axis
(which length is either YH, or PH + SP if the trajectory is an ellipse, but
PH − SP if the trajectory is a hyperbola), the trajectory is found. Q.E.I.
ST to Y so that TY is equal to ST, and YH
will be equal to the principal axis. Join SP
and also HP, and SP will be the difference
between HP and the principal axis. In this
way, if more tangents TR or more points P
are given, there will always be the same
number of lines YH or PH, which can be drawn
from the said points Y or P to the focus H, and which either are equal to the
axes or differ from them by given lengths SP and so either are equal to one
another or have given differences; and hence, by lem. 16, that second focus
H is given. And once the foci are found, together with the length of the axis
(which length is either YH, or PH + SP if the trajectory is an ellipse, but
PH − SP if the trajectory is a hyperbola), the trajectory is found. Q.E.I.
Scholium
When the trajectory is a hyperbola, I do not include the opposite branch of
the hyperbola as part of the trajectory. For a body going on with an
uninterrupted motion cannot pass from one branch of a hyperbola into the
other.
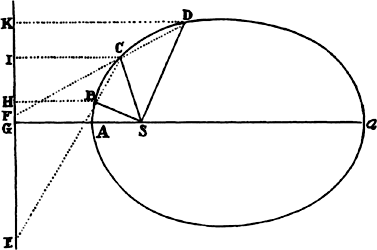
The case in which three points are given is solved more speedily as follows: Let the points B, C, and D be given. Join BC and also CD and produce them to E and F so that EB is to EC as SB to SC and FC is to FD as SC to SD. Draw EF, and drop the normals SG and BH to EF produced, and on GS indefinitely produced take GA to AS and Ga to aS as HB is to BS; then A will be the vertex and Aa the principal axis of the trajectory. According as GA is greater than, equal to, or less than AS, this trajectory will be an ellipse, a parabola, or a hyperbola, with point a in the first case falling on the same side of the line GF as point A, in the second case going off to infinity, in the third falling on the other side of the line GF. For if the perpendiculars CI and DK are dropped to GF, IC will be to HB as EC to EB, that is, as SC to SB; and by alternation [or alternando], IC will be to SC as HB to SB or as GA to SA. And by a similar argument it will be proved that KD is to SD in the same ratio. Therefore points B, C, and D lie in a conic described about the focus S in such a way that all the straight lines drawn from the focus S to the individual points of the conic are to the perpendiculars dropped from the same points to the straight line GF in that given ratio.
By a method that is not very different, the eminent geometer La Hire presents a solution of this problem in his Conics, book 8, prop. 25.
To find orbits when neither focus is given
Lemma 17
If four straight lines PQ, PR, PS, and PT are drawn at given angles from any
point P of a given conic to the four indefinitely produced sides AB, CD, AC, and
DB of some quadrilateral ABDC inscribed in the conic, one line being drawn to
each side, the rectangle PQ × PR of the lines drawn to two opposite sides will
be in a given ratio to the rectangle PS × PT of the lines drawn to the other two
opposite sides.
CASE 1. Let us suppose first that the lines drawn to opposite sides are
parallel to either one of the other sides, say PQ and PR parallel to side
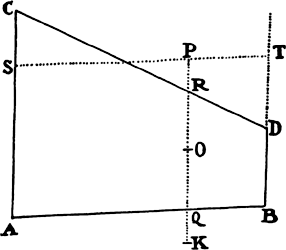 AC, and PS and PT parallel to side AB.
In addition, let two of the opposite sides,
say AC and BD, be parallel to each other.
Then the straight line which bisects those
parallel sides will be one of the diameters
of the conic and will bisect RQ also. Let
O be the point in which RQ is bisected,
and PO will be an ordinate to that
diameter. Produce PO to K so that OK is
equal to PO, and OK will be the ordinate on the opposite side of the
diameter. Therefore, since points A, B, P, and K are on the conic and PK cuts AB
at a given angle, the rectangle PQ × QK will be to the rectangle AQ × QB
in a given ratio (by book 3, props. 17, 19, 21, and 23, of the Conics of
Apollonius). But QK and PR are equal, inasmuch as they are differences of the
equal lines OK and OP, and OQ and OR, and hence also the rectangles
PQ × QK and PQ × PR are equal, and therefore the rectangle PQ × PR
is to the rectangle AQ × QB, that is, to the rectangle PS × PT, in a given
ratio. Q.E.D.
AC, and PS and PT parallel to side AB.
In addition, let two of the opposite sides,
say AC and BD, be parallel to each other.
Then the straight line which bisects those
parallel sides will be one of the diameters
of the conic and will bisect RQ also. Let
O be the point in which RQ is bisected,
and PO will be an ordinate to that
diameter. Produce PO to K so that OK is
equal to PO, and OK will be the ordinate on the opposite side of the
diameter. Therefore, since points A, B, P, and K are on the conic and PK cuts AB
at a given angle, the rectangle PQ × QK will be to the rectangle AQ × QB
in a given ratio (by book 3, props. 17, 19, 21, and 23, of the Conics of
Apollonius). But QK and PR are equal, inasmuch as they are differences of the
equal lines OK and OP, and OQ and OR, and hence also the rectangles
PQ × QK and PQ × PR are equal, and therefore the rectangle PQ × PR
is to the rectangle AQ × QB, that is, to the rectangle PS × PT, in a given
ratio. Q.E.D.
CASE 2. Let us suppose now that the opposite sides AC and BD of the
quadrilateral are not parallel. Draw Bd parallel to AC, meeting the straight
line ST in t and the conic in d. Join Cd cutting PQ in r; and draw DM
parallel to PQ, cutting Cd in M and AB in N. Now, because triangles BTt
and DBN are similar, Bt or PQ is to Tt as DN to NB. So also Rr is to
AQ or PS as DM to AN. Therefore, multiplying the antecedents by the
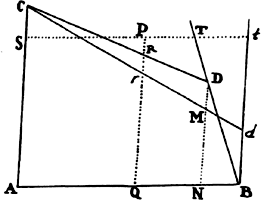 antecedents and the consequents by the
consequents, the rectangle PQ × Rr is
to the rectangle PS × Tt as the rectangle
ND × DM is to the rectangle AN × NB,
and (by case 1) as the rectangle PQ ×
Pr is to the rectangle PS × Pt, and by
separation [or dividendo] as the rectangle
PQ × PR is to the rectangle PS × PT. Q.E.D.
antecedents and the consequents by the
consequents, the rectangle PQ × Rr is
to the rectangle PS × Tt as the rectangle
ND × DM is to the rectangle AN × NB,
and (by case 1) as the rectangle PQ ×
Pr is to the rectangle PS × Pt, and by
separation [or dividendo] as the rectangle
PQ × PR is to the rectangle PS × PT. Q.E.D.
CASE 3. Let us suppose finally that the four lines PQ, PR, PS, and PT
are not parallel to the sides AC and AB, but are inclined to them in any
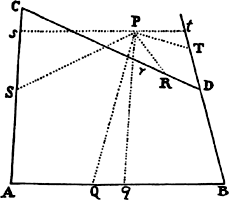 way whatever. In place of these lines draw
Pq and Pr parallel to AC, and Ps and Pt
parallel to AB; then because the angles of
the triangles PQq, PRr, PSs, and PTt are
given, the ratios of PQ to Pq, PR to Pr,
PS to Ps, and PT to Pt will be given, and
thus the compound ratios of PQ × PR to
Pq × Pr, and PS × PT to Ps × Pt. But,
by what has been demonstrated above, the
ratio of Pq × Pr to Ps × Pt is given, and therefore also the ratio of PQ × PR
to PS × PT. Q.E.D.
way whatever. In place of these lines draw
Pq and Pr parallel to AC, and Ps and Pt
parallel to AB; then because the angles of
the triangles PQq, PRr, PSs, and PTt are
given, the ratios of PQ to Pq, PR to Pr,
PS to Ps, and PT to Pt will be given, and
thus the compound ratios of PQ × PR to
Pq × Pr, and PS × PT to Ps × Pt. But,
by what has been demonstrated above, the
ratio of Pq × Pr to Ps × Pt is given, and therefore also the ratio of PQ × PR
to PS × PT. Q.E.D.
Lemma 18
With the same suppositions as in lem. 17, if the rectangle PQ × PR of the lines
drawn to two opposite sides of the quadrilateral is in a given ratio to the rectangle
PS × PT of the lines drawn to the other two sides, the point P from which the
lines are drawn will lie on a conic circumscribed about the quadrilateral.
Suppose that a conic is described through points A, B, C, D, and some
one of the infinite number of points P, say p; I say that point P always
lies on this conic. If you deny it, join AP cutting this conic in some point
other than P, if possible, say in b. Therefore, if from these points p and
b the straight lines pq, pr, ps, pt and bk, bn, bf, bd are drawn at given
angles to the sides of the quadrilateral, then bk × bn will be to bf × bd
as (by lem. 17) pq × pr is to ps × pt, and as (by hypothesis) PQ × PR is
to PS × PT. Also, because the quadrilaterals bkAf and PQAS are
similar, bk is to bf as PQ to PS. And therefore, if the terms of the previous
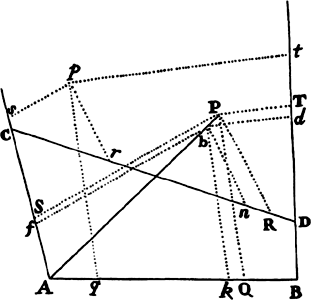 proportion are divided by the
corresponding terms of this one, bn will
be to bd as PR to PT. Therefore
the angles of the quadrilateral Dnbd
are respectively equal to the angles of
quadrilateral DRPT and the
quadrilaterals are similar, and consequently
their diagonals Db and DP coincide.
And thus b falls upon the
intersection of the straight lines AP and
DP and accordingly coincides with
point P. And therefore point P, wherever it is taken, falls on the assigned
conic. Q.E.D.
proportion are divided by the
corresponding terms of this one, bn will
be to bd as PR to PT. Therefore
the angles of the quadrilateral Dnbd
are respectively equal to the angles of
quadrilateral DRPT and the
quadrilaterals are similar, and consequently
their diagonals Db and DP coincide.
And thus b falls upon the
intersection of the straight lines AP and
DP and accordingly coincides with
point P. And therefore point P, wherever it is taken, falls on the assigned
conic. Q.E.D.
COROLLARY. Hence if three straight lines PQ, PR, and PS are drawn at given angles from a common point P to three other straight lines given in position, AB, CD, and AC, one line being drawn to each of the other lines, and if the rectangle PQ × PR of two of the lines drawn is in a given ratio to the square of the third line PS, then the point P, from which the straight lines are drawn, will be located in a conic which touches lines AB and CD at A and C, and conversely. For let line BD coincide with line AC, while the position of the three lines AB, CD, and AC remains the same, and let line PT also coincide with line PS; then the rectangle PS × PT will come to be PS2, and the straight lines AB and CD, which formerly cut the curve in points A and B, C and D, can no longer cut the curve in those points which now coincide, but will only touch it.
Scholium
The term “conic” [or “conic section”] is used in this lemma in an extended
sense, so as to include both a rectilinear section passing through the vertex
of a cone and a circular section parallel to the base. For if point p falls on a
straight line which joins points A and D or C and B, the conic section will
turn into twin straight lines, one of which is the straight line on which point
p falls and the other the straight line which joins the other two of the four
points.
If two opposite angles of the quadrilateral, taken together, are equal to
two right angles, and the four lines PQ, PR, PS, and PT are drawn to its
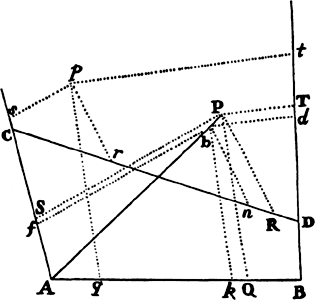 sides either perpendicularly or at any
equal angles, and the rectangle PQ ×
PR of two of the lines drawn is equal
to the rectangle PS × PT of the other
two, the conic will turn out to be a
circle. The same will happen if the
four lines are drawn at any angles and
the rectangle PQ × PR of two of the
lines drawn is to the rectangle PS ×
PT of the other two as the rectangle
of the sines of the angles S and T, at
which the last two lines PS and PT are drawn, is to the rectangle of the
sines of the angles Q and R, at which the first two lines PQ and PR are
drawn.
sides either perpendicularly or at any
equal angles, and the rectangle PQ ×
PR of two of the lines drawn is equal
to the rectangle PS × PT of the other
two, the conic will turn out to be a
circle. The same will happen if the
four lines are drawn at any angles and
the rectangle PQ × PR of two of the
lines drawn is to the rectangle PS ×
PT of the other two as the rectangle
of the sines of the angles S and T, at
which the last two lines PS and PT are drawn, is to the rectangle of the
sines of the angles Q and R, at which the first two lines PQ and PR are
drawn.
In the other cases the locus of point P will be some one of the three figures that are commonly called conic sections [or conics]. In place of the quadrilateral ABCD, however, there can be substituted a quadrilateral whose two opposite sides decussate each other as diagonals do. But also, one or two of the four points A, B, C, and D can go off to infinity, and in this way the sides of the figure which converge to these points can turn out to be parallel, in which case the conic will pass through the other points and will go off to infinity in the direction of the parallels.
Lemma 19
To find a point P such that if four straight lines PQ, PR, PS, and PT are drawn
from it at given angles to four other straight lines AB, CD, AC, and BD given in
position, one line being drawn from the point P to each of the four other straight
lines, the rectangle PQ × PR of two of the lines drawn will be in a given ratio
to the rectangle PS × PT of the other two.
Let lines AB and CD, to which the two straight lines PQ and PR
containing one of the rectangles are drawn, meet the other two lines
given in position in the points A, B, C, and D. From some one of
them A draw any straight line AH, in which you wish point P to be
found. Let this line AH cut the opposite lines BD and CD—that is,
BD in H and CD in I—and because all the angles of the figure are
given, the ratios of PQ to PA and PA to PS, and consequently the ratio
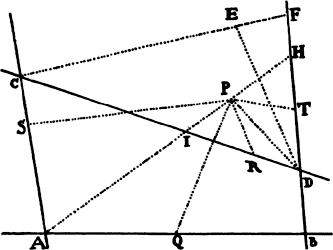 of PQ to PS, will be given. On
eliminating this ratio of PQ to PS
from the given ratio of PQ × PR
to PS × PT, the ratio of PR to PT
will be given; and when the given
ratios of PI to PR and PT to PH
are combined, the ratio of PI to
PH, and thus the point P, will be
given. Q.E.I.
of PQ to PS, will be given. On
eliminating this ratio of PQ to PS
from the given ratio of PQ × PR
to PS × PT, the ratio of PR to PT
will be given; and when the given
ratios of PI to PR and PT to PH
are combined, the ratio of PI to
PH, and thus the point P, will be
given. Q.E.I.
COROLLARY 1. Hence also a tangent can be drawn to any point D of the locus of the infinite number of points P. For when points P and D come together—that is, when AH is drawn through the point D—the chord PD becomes a tangent. In this case the ultimate ratio of the vanishing lines IP and PH will be found as above. Therefore, draw CF parallel to AD and meeting BD in F and being cut in E in that ultimate ratio; then DE will be a tangent, because CF and the vanishing line IH are parallel and are similarly cut in E and P.
COROLLARY 2.a Hence also, the
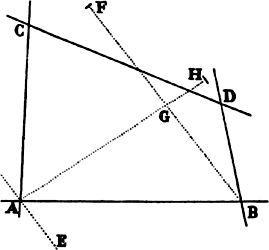 locus of all the points P can be
determined. Through any one of the points
A, B, C, D—say A—draw the
tangent AE of the locus, and through any
other point B draw BF parallel to the
tangent and meeting the locus in F.
The point F will be found by means
of lem. 19. Bisect BF in G, and the
indefinite line AG, when drawn, will
be the position of the diameter to which BG and FG are ordinates. Let
this line AG meet the locus in H, and AH will be the diameter or
latus transversum [i.e., transverse diameter] to which the latus rectum will be
as BG2 to AG × GH. If AG nowhere meets the locus, the line AH
being indefinitely produced, the locus will be a parabola, and its latus rectum
corresponding to the diameter AG will be
locus of all the points P can be
determined. Through any one of the points
A, B, C, D—say A—draw the
tangent AE of the locus, and through any
other point B draw BF parallel to the
tangent and meeting the locus in F.
The point F will be found by means
of lem. 19. Bisect BF in G, and the
indefinite line AG, when drawn, will
be the position of the diameter to which BG and FG are ordinates. Let
this line AG meet the locus in H, and AH will be the diameter or
latus transversum [i.e., transverse diameter] to which the latus rectum will be
as BG2 to AG × GH. If AG nowhere meets the locus, the line AH
being indefinitely produced, the locus will be a parabola, and its latus rectum
corresponding to the diameter AG will be 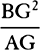 . But if AG does meet the
locus somewhere, the locus will be a hyperbola when points A and H are
situated on the same side of G, and an ellipse when G is between points
A and H, unless angle AGB happens to be a right angle and additionally
BG2 is equal to the rectangle AG × GH, in which case the locus will be
a circle.
. But if AG does meet the
locus somewhere, the locus will be a hyperbola when points A and H are
situated on the same side of G, and an ellipse when G is between points
A and H, unless angle AGB happens to be a right angle and additionally
BG2 is equal to the rectangle AG × GH, in which case the locus will be
a circle.
And thus there is exhibited in this corollary not an [analytical] computation but a geometrical synthesis, such as the ancients required, of the classical problem of four lines, which was begun by Euclid and carried on by Apollonius.
Lemma 20
If any parallelogram ASPQ touches a conic in points A and P with two of its
opposite angles A and P, and if the sides AQ and AS, indefinitely produced, of
one of these angles meet the said conic in B and C, and if from the meeting
points B and C two straight lines BD and CD are drawn to any fifth point D
of the conic, meeting the other two indefinitely produced sides PS and PQ of the
parallelogram in T and R; then PR and PT, the parts cut off from the sides, will
always be to each other in a given ratio. And conversely, if the parts which are
cut off are to each other in a given ratio, the point D will touch a conic passing
through the four points A, B, C, and P.
CASE 1. Join BP and also
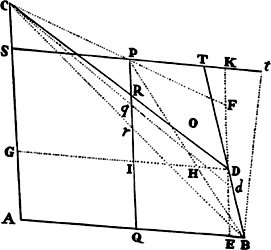 CP, and from point D draw two
straight lines DG and DE, the
first of which (DG) is parallel to
AB and meets PB, PQ, and CA
at H, I, and G, while the second
(DE) is parallel to AC and meets
PC, PS, and AB at F, K, and E;
then (by lem. 17) the rectangle
DE×DF will be to the rectangle
DG × DH in a given ratio. But
PQ is to DE (or IQ) as PB to
HB and thus as PT to DH; and by alternation [or alternando] PQ is to PT
as DE to DH. Additionally, PR is to DF as RC to DC and hence as (IG
or) PS to DG; and by alternation [or alternando] PR is to PS as DF to DG;
and when the ratios are combined, the rectangle PQ × PR comes to be to the
rectangle PS × PT as the rectangle DE × DF to the rectangle DG × DH,
and hence in a given ratio. But PQ and PS are given, and therefore the ratio
of PR to PT is given. Q.E.D.
CP, and from point D draw two
straight lines DG and DE, the
first of which (DG) is parallel to
AB and meets PB, PQ, and CA
at H, I, and G, while the second
(DE) is parallel to AC and meets
PC, PS, and AB at F, K, and E;
then (by lem. 17) the rectangle
DE×DF will be to the rectangle
DG × DH in a given ratio. But
PQ is to DE (or IQ) as PB to
HB and thus as PT to DH; and by alternation [or alternando] PQ is to PT
as DE to DH. Additionally, PR is to DF as RC to DC and hence as (IG
or) PS to DG; and by alternation [or alternando] PR is to PS as DF to DG;
and when the ratios are combined, the rectangle PQ × PR comes to be to the
rectangle PS × PT as the rectangle DE × DF to the rectangle DG × DH,
and hence in a given ratio. But PQ and PS are given, and therefore the ratio
of PR to PT is given. Q.E.D.
CASE 2. But if PR and PT are supposed in a given ratio to each other, then on working backward with a similar argument, it will follow that the rectangle DE × DF is to the rectangle DG × DH in a given ratio and consequently that point D (by lem. 18) lies in a conic passing through points A, B, C, and P. Q.E.D.
COROLLARY 1. Hence, if BC is drawn cutting PQ in r, and if Pt is taken on PT in the ratio to Pr which PT has to PR, Bt will be a tangent of the conic at point B. For conceive of point D as coming together with point B in such a way that, as chord BD vanishes, BT becomes a tangent; then CD and BT will coincide with CB and Bt.
COROLLARY 2. And vice versa, if Bt is a tangent and BD and CD meet in any point D of the conic, PR will be to PT as Pr to Pt. And conversely, if PR is to PT as Pr to Pt, BD and CD will meet in some point D of the conic.
COROLLARY 3. One conic does not intersect another conic in more than four points. For, if it can be done, let two conics pass through five points A, B, C, P, and O, and let the straight line BD cut these conics in points D and d, and let the straight line Cd cut PQ in q. Then PR is to PT as Pq to PT; hence PR and Pq are equal to each other, contrary to the hypothesis.
Lemma 21
If two movable and infinite straight lines BM and CM, drawn through given
points B and C as poles, describe by their meeting-point M a third straight line
MN given in position, and if two other infinite straight lines BD and CD are
drawn, making given angles MBD and MCD with the first two lines at those
given points B and C; then I say that the point D, where these two lines BD and
CD meet, will describe a conic passing through points B and C. And conversely, if
the point D, where the straight lines BD and CD meet, describes a conic passing
through the given points B, C, and A, and the angle DBM is always equal to the
given angle ABC, and the angle DCM is always equal to the given angle ACB;
then point M will lie in a straight line given in position.
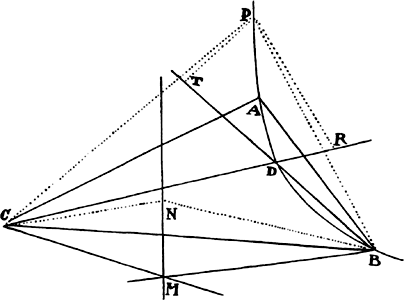
For let point N be given in the straight line MN; and when the movable point M falls on the stationary point N, let the movable point D fall on the stationary point P. Draw CN, BN, CP, and BP, and from point P draw the straight lines PT and PR meeting BD and CD in T and R and forming an angle BPT equal to the given angle BNM, and an angle CPR equal to the given angle CNM. Since therefore (by hypothesis) angles MBD and NBP are equal, as are also angles MCD and NCP, take away the angles NBD and NCD that are common, and there will remain the equal angles NBM and PBT, NCM and PCR; and therefore triangles NBM and PBT are similar, as are also triangles NCM and PCR. And therefore PT is to NM as PB to NB, and PR is to NM as PC to NC. But the points B, C, N, and P are stationary. Therefore, PT and PR have a given ratio to NM and accordingly a given ratio to each other; and thus (by lem. 20) the point D, the perpetual meeting-point of the movable straight lines BT and CR, lies in a conic passing through points B, C, and P. Q.E.D.
And conversely, if the movable point D lies in a conic passing through the given points B, C, and A; and if angle DBM is always equal to the given angle ABC, and the angle DCM is always equal to the given angle ACB; and if, when point D falls successively on any two stationary points p and P of the conic, the movable point M falls successively on the two stationary points n and N; then through these same points n and N draw the straight line nN, and this will be the perpetual locus of the movable point M. For, if it can be done, let point M move in some curved line. Then the point D will lie in a conic passing through the five points B, C, A, p, and P when the point M perpetually lies in a curved line. But from what has already been demonstrated, point D will also lie in a conic passing through the same five points B, C, A, p, and P when point M perpetually lies in a straight line. Therefore, two conics will pass through the same five points, contrary to lem. 20, corol. 3. Therefore, it is absurd to suppose the point M to be moving in a curved line. Q.E.D.
Proposition 22, Problem 14
To describe a trajectory through five given points.
Let five points A, B, C, P, and D be given. From one of them A to any other two B and C (let B and C be called poles), draw the straight lines AB and AC, and parallel to these draw TPS and PRQ through the fourth point P. Then from the two poles B and C draw two indefinite lines BDT and CRD through the fifth point D, BDT meeting the line TPS (just drawn) in T, and CRD meeting PRQ in R. Finally, draw the straight line tr parallel to TR, and cut off from the straight lines PT and PR any straight lines Pt and Pr proportional to PT and PR; then, if through their ends t and r and poles B and C the lines Bt and Cr are drawn meeting in d, that point d will be located in the required trajectory. For that point d (by lem. 20) lies in a conic passing through the four points A, B, C, and P; and, the lines Rr and Tt vanishing, point d coincides with point D. Therefore, the conic section passes through the five points A, B, C, P, and D. Q.E.D.
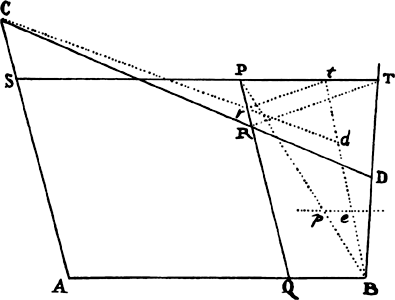
Join any three of the given points, A, B, and C; and, rotating the angles ABC and ACB, given in magnitude, around two of these points B and C as poles, apply the legs BA and CA first to point D and then to point P, and note the points M and N in which the other legs BL and CL cross in each case. Draw the indefinite straight line MN, and rotate these movable angles around their poles B and C in such a way that the intersection of the legs BL and CL or BM and CM (which now let be m) always falls on that indefinite straight line MN; and the intersection of the legs BA and CA or BD and CD (which now let be d) will trace out the required trajectory PADdB. For point d (by lem. 21) will lie in a conic passing through points B and C: and when point m approaches points L, M, and N, point d (by construction) will approach points A, D, and P. Therefore a conic will be described passing through the five points A, B, C, P, and D. Q.E.F.
COROLLARY 1. Hence a straight line can readily be drawn that will touch the required trajectory in any given point B. Let point d approach point B, and the straight line Bd will come to be the required tangent.
COROLLARY 2. Hence also the centers, diameters, and latera recta of the trajectories can be found, as in lem. 19, corol. 2.
Scholium
The first of the constructions of prop. 22 will become a little simpler by
joining BP, producing it if necessary, and in it taking Bp to BP as PR is to
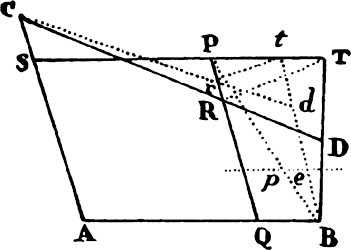 PT, and then drawing through
p the indefinite straight line pe
parallel to SPT and in it always
taking pe equal to Pr, and then
drawing the straight lines Be and
Cr meeting in d. For since the
ratios Pr to Pt, PR to PT, pB to
PB, and pe to Pt are equal, pe
and Pr will always be equal. By
this method the points of the trajectory are found most readily, unless you
prefer to describe the curve mechanically, as in the second construction.
PT, and then drawing through
p the indefinite straight line pe
parallel to SPT and in it always
taking pe equal to Pr, and then
drawing the straight lines Be and
Cr meeting in d. For since the
ratios Pr to Pt, PR to PT, pB to
PB, and pe to Pt are equal, pe
and Pr will always be equal. By
this method the points of the trajectory are found most readily, unless you
prefer to describe the curve mechanically, as in the second construction.
Proposition 23, Problem 15
To describe a trajectory that will pass through four given points and touch a
straight line given in position.
CASE 1. Let the tangent HB, the point of contact B, and three other points C, D, and P be given. Join BC, and by drawing PS parallel to the straight line BH, and PQ parallel to the straight line BC, complete the parallelogram BSPQ. Draw BD cutting SP in T, and CD cutting PQ in R. Finally, by drawing any line tr parallel to TR, cut off Pr and Pt from PQ and PS in such a way that Pr and Pt are proportional respectively to PR and PT; then draw Cr and Bt, and their meeting-point d (by lem. 20) will always fall on the trajectory to be described.
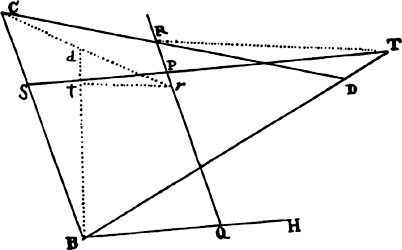
Revolve the angle CBH, given in
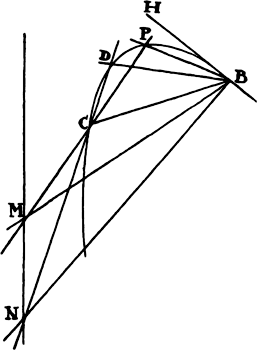 magnitude, about the pole B, and revolve about the
pole C any rectilinear radius DC, produced
at both ends. Note the points M and N at
which the leg BC of the angle cuts that
radius when the other leg BH meets the same
radius in points P and D. Then draw the
indefinite line MN, and let that radius CP or
CD and the leg BC of the angle meet
perpetually in the line MN; and the meeting-point
of the other leg BH with the radius will trace
out the required trajectory.
magnitude, about the pole B, and revolve about the
pole C any rectilinear radius DC, produced
at both ends. Note the points M and N at
which the leg BC of the angle cuts that
radius when the other leg BH meets the same
radius in points P and D. Then draw the
indefinite line MN, and let that radius CP or
CD and the leg BC of the angle meet
perpetually in the line MN; and the meeting-point
of the other leg BH with the radius will trace
out the required trajectory.
For if, in the constructions of prop. 22, point A approaches point B, lines CA and CB will coincide, and line AB in its ultimate position will come to be the tangent BH; and therefore the constructions set forth in prop. 22 will come to be the same as the constructions described in this proposition. Therefore, the meeting-point of the leg BH with the radius will trace out a conic passing through points C, D, and P and touching the straight line BH in point B. Q.E.F.
CASE 2. Let four points B, C, D, and P be given, situated outside the
tangent HI. Join them in pairs by the lines BD and CP coming together in
G and meeting the tangent in H and I. Cut the tangent in A in such a way
that HA is to IA as the rectangle of the mean proportional between CG
and GP and the mean proportional between BH and HD is to the rectangle
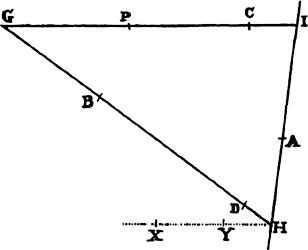 of the mean proportional between
DG and GB and the mean
proportional between PI and IC, and A will
be the point of contact. For if HX,
parallel to the straight line PI, cuts
the trajectory in any points X and Y,
then (from the Conics) point A will
have to be so placed that HA2 is to
AI2 in a ratio compounded of the
ratio of the rectangle XH × HY to the product BH × HD, or of the rectangle
CG × GP to the rectangle DG × GD, and of the ratio of the rectangle
BH × HD to the rectangle PI × IC. And once the point of contact A has
been found, the trajectory will be described as in the first case. Q.E.F.
of the mean proportional between
DG and GB and the mean
proportional between PI and IC, and A will
be the point of contact. For if HX,
parallel to the straight line PI, cuts
the trajectory in any points X and Y,
then (from the Conics) point A will
have to be so placed that HA2 is to
AI2 in a ratio compounded of the
ratio of the rectangle XH × HY to the product BH × HD, or of the rectangle
CG × GP to the rectangle DG × GD, and of the ratio of the rectangle
BH × HD to the rectangle PI × IC. And once the point of contact A has
been found, the trajectory will be described as in the first case. Q.E.F.
But point A can be taken either between points H and I or outside them, and accordingly two trajectories can be described as solutions to the problem.
Proposition 24, Problem 16
To describe a trajectory that will pass through three given points and touch two
straight lines given in position.
Let tangents HI and KL and points B, C, and D be given. Through
any two of the points, B and D, draw an indefinite straight line BD
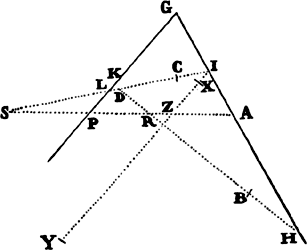 meeting the tangents in points H
and K. Then, likewise, through any
two other points, C and D, draw the
indefinite straight line CD meeting
the tangents in points I and L. Cut
BD in R and CD in S in such a way
that HR will be to KR as the mean
proportional between BH and HD
is to the mean proportional between
BK and KD and that IS will be to LS as the mean proportional between
CI and ID is to the mean proportional between CL and LD. And cut these
lines at will either between points K and H, and between I and L, or outside
them; then draw RS cutting the tangents in A and P, and A and P will be
the points of contact. For if A and P are supposed to be the points of contact
situated anywhere on the tangents, and if through any one of the points
H, I, K, and L, say I, situated in either tangent HI, the straight line IY is
drawn parallel to the other tangent KL and meeting the curve in X and Y;
and if in this line, IZ is taken so as to be the mean proportional between IX
and IY; then, from the Conics, the rectangle XI × IY or IZ2 will be to LP2
as the rectangle CI × ID to the rectangle CL × LD, that is (by construction),
as SI2 to SL2, and thus IZ will be to LP as SI to SL. Therefore the points
S, P, and Z lie in one straight line. Furthermore, since the tangents meet in
G, the rectangle XI × IY or IZ2 will be to IA2 (from the Conics) as GP2 to
GA2, and hence IZ will be to IA as GP to GA. Therefore, the points P, Z,
and A lie in one straight line, and thus the points S, P, and A are in one
straight line. And by the same argument it will be proved that the points
R, P, and A are in one straight line. Therefore the points of contact A and
P lie in the straight line RS. And once these points have been found, the
trajectory will be described as in prop. 23, case 1. Q.E.F.
meeting the tangents in points H
and K. Then, likewise, through any
two other points, C and D, draw the
indefinite straight line CD meeting
the tangents in points I and L. Cut
BD in R and CD in S in such a way
that HR will be to KR as the mean
proportional between BH and HD
is to the mean proportional between
BK and KD and that IS will be to LS as the mean proportional between
CI and ID is to the mean proportional between CL and LD. And cut these
lines at will either between points K and H, and between I and L, or outside
them; then draw RS cutting the tangents in A and P, and A and P will be
the points of contact. For if A and P are supposed to be the points of contact
situated anywhere on the tangents, and if through any one of the points
H, I, K, and L, say I, situated in either tangent HI, the straight line IY is
drawn parallel to the other tangent KL and meeting the curve in X and Y;
and if in this line, IZ is taken so as to be the mean proportional between IX
and IY; then, from the Conics, the rectangle XI × IY or IZ2 will be to LP2
as the rectangle CI × ID to the rectangle CL × LD, that is (by construction),
as SI2 to SL2, and thus IZ will be to LP as SI to SL. Therefore the points
S, P, and Z lie in one straight line. Furthermore, since the tangents meet in
G, the rectangle XI × IY or IZ2 will be to IA2 (from the Conics) as GP2 to
GA2, and hence IZ will be to IA as GP to GA. Therefore, the points P, Z,
and A lie in one straight line, and thus the points S, P, and A are in one
straight line. And by the same argument it will be proved that the points
R, P, and A are in one straight line. Therefore the points of contact A and
P lie in the straight line RS. And once these points have been found, the
trajectory will be described as in prop. 23, case 1. Q.E.F.
In this proposition and in prop. 23, case 2, the constructions are the same whether or not the straight line XY cuts the trajectory in X and Y, and they do not depend on this cut. But once the constructions have been demonstrated for the case in which the straight line does cut the trajectory, the constructions for the case in which it does not cut the trajectory also can be found; and for the sake of brevity I do not take the time to demonstrate them further.
Lemma 22
To change figures into other figures of the same class.
Let it be required to transmute any figure HGI. Draw at will two parallel
straight lines AO and BL cutting in A and B any third line AB, given in
position; and from any point G of the figure draw to the straight line AB
any other straight line GD parallel to OA. Then from some point O, given
in line OA, draw to the point D the straight line OD meeting BL at d,
and from the meeting-point erect the straight line dg containing any given
angle with the straight line BL and having the same ratio to Od that DG
has to OD; and g will be the point in the new figure hgi corresponding to
point G. By the same method, each of the points in the first figure will yield
a corresponding point in the new figure. Therefore, suppose point G to be
running through all the points in the first figure with a continual motion;
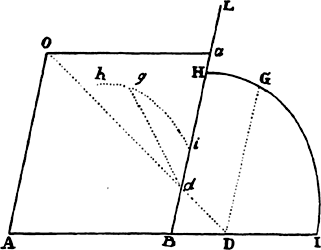 then point g—also with a
continual motion—will run through all
the points in the new figure and
will describe that figure. For the
sake of distinction let us call DG
the first ordinate, dg the new
ordinate, AD the first abscissa, ad
the new abscissa, O the pole, OD
the abscinding radius, OA the first
ordinate radius, and Oa (which completes the parallelogram OAba) the new
ordinate radius.
then point g—also with a
continual motion—will run through all
the points in the new figure and
will describe that figure. For the
sake of distinction let us call DG
the first ordinate, dg the new
ordinate, AD the first abscissa, ad
the new abscissa, O the pole, OD
the abscinding radius, OA the first
ordinate radius, and Oa (which completes the parallelogram OAba) the new
ordinate radius.
I say now that if point G traces a straight line given in position, point
g will also trace a straight line given in position. If point G traces a conic,
point g will also trace a conic. I here count a circle among the conic sections.
Further, if point G traces a curved line of the third analytic order, point g
will likewise trace a curved line of the third order; and so on with curves of
higher orders, the two curved lines which points G and g trace will always
be of the same analytic order. For as ad is to OA, so are Od to OD, dg to
DG, and AB to AD; and hence AD is equal to 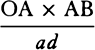 , and DG is equal
to
, and DG is equal
to 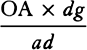 . Now, if point G traces a straight line and consequently, in
any equation which gives the relation between the abscissa AD and the
ordinate DG, the indeterminate lines AD and DG rise to only one dimension,
and if in this equation
. Now, if point G traces a straight line and consequently, in
any equation which gives the relation between the abscissa AD and the
ordinate DG, the indeterminate lines AD and DG rise to only one dimension,
and if in this equation 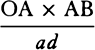 is written for AD and
is written for AD and 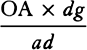 for DG, then the result will be a new equation in which the new abscissa
ad and the new ordinate dg will rise to only one dimension and which
therefore designates a straight line. But if AD and DG or either one of
them rose to two dimensions in the first equation, then ad and dg will
also rise to two dimensions in the second equation. And so on for three or
more dimensions. The indeterminates ad and dg in the second equation,
and AD and DG in the first, will always rise to the same number of dimensions,
and therefore the lines which points G and g trace are of the same
analytic order.
for DG, then the result will be a new equation in which the new abscissa
ad and the new ordinate dg will rise to only one dimension and which
therefore designates a straight line. But if AD and DG or either one of
them rose to two dimensions in the first equation, then ad and dg will
also rise to two dimensions in the second equation. And so on for three or
more dimensions. The indeterminates ad and dg in the second equation,
and AD and DG in the first, will always rise to the same number of dimensions,
and therefore the lines which points G and g trace are of the same
analytic order.
I say further that if some straight line touches a curved line in the first figure, this straight line—after being transferred into the new figure in the same manner as the curve—will touch that curved line in the new figure; and conversely. For if any two points of the curve approach each other and come together in the first figure, the same points—after being transferred—will approach each other and come together in the new figure; and thus the straight lines by which these points are joined will simultaneously come to be tangents of the curves in both figures.
The demonstrations of these assertions could have been composed in a more geometrical style. But I choose to be brief.
Therefore, if one rectilinear figure is to be transmuted into another, it is only necessary to transfer the intersections of the straight lines of which it is made up and to draw straight lines through them in the new figure. But if it is required to transmute a curvilinear figure, then it is necessary to transfer the points, tangents, and other straight lines which determine the curved line. Moreover, this lemma is useful for solving more difficult problems by transmuting the proposed figures into simpler ones. For any converging straight lines are transmuted into parallels by using for the first ordinate radius any straight line that passes through the meeting-point of the converging lines; and this is so because the meeting-point goes off this way to infinity, and lines that nowhere meet are parallel. Moreover, after the problem is solved in the new figure, if this figure is transmuted into the first figure by the reverse procedure, the required solution will be obtained.
This lemma is useful also for solving solid problems. For whenever two conics occur by whose intersection a problem can be solved, either one of them, if it is a hyperbola or parabola, can be transmuted into an ellipse; then the ellipse is easily changed into a circle. Likewise, in constructing plane problems, a straight line and a conic are turned into a straight line and a circle.
Proposition 25, Problem 17
To describe a trajectory that will pass through two given points and touch three
straight lines given in position.
Through the meeting-point of any two tangents with each other and
the meeting-point of a third tangent with the straight line that passes
through two given points, draw an indefinite straight line; and using it
as the first ordinate radius, transmute the figure, by lem. 22, into a new
figure. In this figure the two tangents will come to be parallel to each
other, and the third tangent will become parallel to the straight line passing
through the two given points. Let hi and kl be the two parallel tangents,
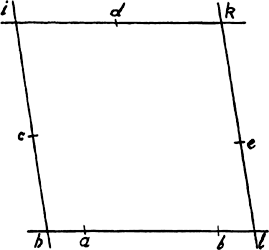 ik the third tangent, and hl the
straight line parallel to it, passing
through the points a and b through
which the conic ought to pass in
this new figure and completing the
parallelogram hikl. Cut the straight
lines hi, ik, and kl in c, d, and e, so
that hc is to the square root of the
rectangle ah × hb, and ic is to id,
and ke is to kd, as the sum of the
straight lines hi and kl is to the sum of three lines, of which the first is
the straight line ik and the other two are the square roots of the rectangles
ah × hb and al × lb; then c, d, and e will be the points of contact. For,
from the Conics, hc2 is to the rectangle ah × hb in the same ratio as ic2 to
id2, and ke2 to kd2, and el2 to the rectangle al × lb; and therefore hc is
to the square root of ah × hb, and ic is to id, and ke is to kd, and el is
to the square root of al × lb, as the square root of that ratio and hence,
by composition [or componendo], in the given ratio of all the antecedents
hi and kl to all the consequents, which are the square root of the rectangle
ah × hb, the straight line ik, and the square root of the rectangle al × lb [i.e.,
in the given ratio of hi + kl to √(ah × hb) + ik + √(al × lb)]. Therefore,
the points of contact c, d, and e in the new figure are obtained from that
given ratio. By the reverse procedure of lem. 22, transfer these points to
the first figure, and there (by prop. 22) the trajectory will be described. Q.E.F.
ik the third tangent, and hl the
straight line parallel to it, passing
through the points a and b through
which the conic ought to pass in
this new figure and completing the
parallelogram hikl. Cut the straight
lines hi, ik, and kl in c, d, and e, so
that hc is to the square root of the
rectangle ah × hb, and ic is to id,
and ke is to kd, as the sum of the
straight lines hi and kl is to the sum of three lines, of which the first is
the straight line ik and the other two are the square roots of the rectangles
ah × hb and al × lb; then c, d, and e will be the points of contact. For,
from the Conics, hc2 is to the rectangle ah × hb in the same ratio as ic2 to
id2, and ke2 to kd2, and el2 to the rectangle al × lb; and therefore hc is
to the square root of ah × hb, and ic is to id, and ke is to kd, and el is
to the square root of al × lb, as the square root of that ratio and hence,
by composition [or componendo], in the given ratio of all the antecedents
hi and kl to all the consequents, which are the square root of the rectangle
ah × hb, the straight line ik, and the square root of the rectangle al × lb [i.e.,
in the given ratio of hi + kl to √(ah × hb) + ik + √(al × lb)]. Therefore,
the points of contact c, d, and e in the new figure are obtained from that
given ratio. By the reverse procedure of lem. 22, transfer these points to
the first figure, and there (by prop. 22) the trajectory will be described. Q.E.F.
But according as points a and b lie between points h and l or lie outside them, points c, d, and e must be taken either between points h, i, k, and l, or outside them. If either one of the points a and b falls between points h and l, and the other outside, the problem is impossible.
Proposition 26, Problem 18
To describe a trajectory that will pass through a given point and touch four straight
lines given in position.
From the common intersection of any two of the tangents to the
common intersection of the other two, draw an indefinite straight line; then,
using this as the first ordinate radius, transmute the figure (by lem. 22) into
 a new figure; then the tangents, which
formerly met in the first ordinate radius,
will now come to be parallel in pairs. Let
those tangents be hi and kl, ik and hl,
forming the parallelogram hikl. And let
p be the point in this new figure
corresponding to the given point in the first
figure. Through the center O of the figure
draw pq, and, on Oq being equal to
Op, q will be another point through which the conic must pass in this new
figure. By the reverse procedure of lem. 22 transfer this point to the first
figure, and in that figure two points will be obtained through which the
trajectory is to be described. And that trajectory can be described through these
same points by prop. 25.
a new figure; then the tangents, which
formerly met in the first ordinate radius,
will now come to be parallel in pairs. Let
those tangents be hi and kl, ik and hl,
forming the parallelogram hikl. And let
p be the point in this new figure
corresponding to the given point in the first
figure. Through the center O of the figure
draw pq, and, on Oq being equal to
Op, q will be another point through which the conic must pass in this new
figure. By the reverse procedure of lem. 22 transfer this point to the first
figure, and in that figure two points will be obtained through which the
trajectory is to be described. And that trajectory can be described through these
same points by prop. 25.
Lemma 23
If two straight lines AC and BD, given in position, terminate at the given points
A and B and have a given ratio to each other; and if the straight line CD, by
which the indeterminate points C and D are joined, is cut in K in a given ratio;
I say that point K will be located in a straight line given in position.
For let the straight lines AC and BD meet in E, and in BE take BG
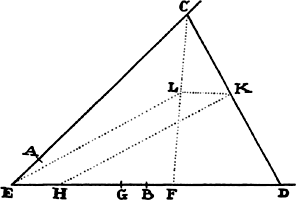 to AE as BD is to AC, and let FD
always be equal to the given line
EG; then, by construction, EC will
be to GD, that is, to EF, as AC to
BD, and thus in a given ratio, and
therefore the species of the triangle
EFC will be given. Cut CF in L
so that CL is to CF in the ratio of
CK to CD; then, because that ratio
is given, the species of the triangle EFL will also be given, and accordingly
point L will be located in the straight line EL given in position. Join LK,
and the triangles CLK and CFD will be similar; and because FD and the
ratio of LK to FD are given, LK will be given. Take EH equal to LK, and
ELKH will always be a parallelogram. Therefore, point K is located in the
side HK, given in position, of the parallelogram. Q.E.D.
to AE as BD is to AC, and let FD
always be equal to the given line
EG; then, by construction, EC will
be to GD, that is, to EF, as AC to
BD, and thus in a given ratio, and
therefore the species of the triangle
EFC will be given. Cut CF in L
so that CL is to CF in the ratio of
CK to CD; then, because that ratio
is given, the species of the triangle EFL will also be given, and accordingly
point L will be located in the straight line EL given in position. Join LK,
and the triangles CLK and CFD will be similar; and because FD and the
ratio of LK to FD are given, LK will be given. Take EH equal to LK, and
ELKH will always be a parallelogram. Therefore, point K is located in the
side HK, given in position, of the parallelogram. Q.E.D.
COROLLARY. Because the species of the figure EFLC is given, the three straight lines EF, EL, and EC (that is, GD, HK, and EC) have given ratios to one another.
Lemma 24
If three straight lines, two of which are parallel and given in position, touch any
conic section, I say that the semidiameter of the section which is parallel to the
two given parallel lines is a mean proportional between their segments that are
intercepted between the points of contact and the third tangent.
Let AF and GB be two parallel
 lines touching the conic ADB
in A and B; and let EF be a third
straight line touching the conic in
I and meeting the first tangents
in F and G; and let CD be the
semidiameter of the figure parallel
to the tangents; then I say that
AF, CD, and BG are continually
proportional.
lines touching the conic ADB
in A and B; and let EF be a third
straight line touching the conic in
I and meeting the first tangents
in F and G; and let CD be the
semidiameter of the figure parallel
to the tangents; then I say that
AF, CD, and BG are continually
proportional.
For if the conjugate diameters AB and DM meet the tangent FG in E and H and cut each other in C, and the parallelogram IKCL is completed, then, from the nature of conics, EC will be to CA as CA to CL, and by separation [or dividendo] as EC − CA to CA − CL, or EA to AL; and by composition [or componendo], EA will be to EA + AL or EL as EC to EC + CA or EB; and therefore, because the triangles EAF, ELI, ECH, and EBG are similar, AF will be to LI as CH to BG. And likewise, from the nature of conics, LI or CK is to CD as CD to CH and therefore from the equality of the ratios in inordinate proportion [or ex aequo perturbate] AF will be to CD as CD to BG. Q.E.D.
COROLLARY 1. Hence if two tangents FG and PQ meet the parallel tangents AF and BG in F and G, P and Q, and cut each other in O; then, from the equality of the ratios in inordinate proportion [or ex aequo perturbate] AF will be to BQ as AP to BG, and by separation [or dividendo] as FP to GQ, and thus as FO to OG.
COROLLARY 2. Hence also, two straight lines PG and FQ drawn through points P and G, F and Q, will meet in the straight line ACB that passes through the center of the figure and the points of contact A and B.
Lemma 25
If the indefinitely produced four sides of a parallelogram touch any conic and are
intercepted at any fifth tangent, and if the intercepts of any two conterminous sides
are taken so as to be terminated at opposite corners of the parallelogram; I say
that either intercept is to the side from which it is intercepted as the part of the
other conterminous side between the point of contact and the third side is to the
other intercept.
Let the four sides ML, IK, KL, and MI of the parallelogram MLIK touch the conic section in A, B, C, and D, and let a fifth tangent FQ cut those sides in F, Q, H, and E; and take the intercepts ME and KQ of the sides MI and KI or the intercepts KH and MF of the sides KL and ML; I say that ME is to MI as BK to KQ, and KH is to KL as AM to MF. For by lem. 24, corol. 1, ME is to EI as AM or BK to BQ, and by composition [or componendo] ME is to MI as BK to KQ. Q.E.D. Likewise, KH is to HL as BK or AM to AF, and by separation [or dividendo] KH is to KL as AM to MF. Q.E.D.
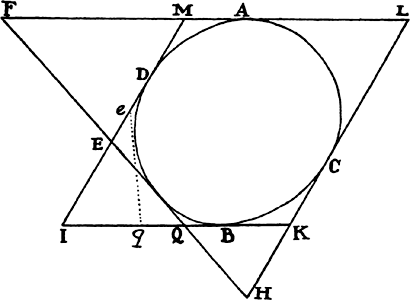
COROLLARY 1. Hence if the parallelogram IKLM is given, described about a given conic, the rectangle KQ × ME will be given, as will also the rectangle KH × MF equal to it. For those rectangles are equal because the triangles KQH and MFE are similar.
COROLLARY 2. And if a sixth tangent eq is drawn meeting the tangents KI and MI at q and e, the rectangle KQ × ME will be equal to the rectangle Kq × Me, and KQ will be to Me as Kq to ME, and by separation [or dividendo] as Qq to Ee.
COROLLARY 3. Hence also, if Eq and eQ are drawn and bisected and a straight line is drawn through the points of bisection, this line will pass through the center of the conic. For since Qq is to Ee as KQ to Me, the same straight line will (by lem. 23) pass through the middle of all the lines Eq, eQ, and MK, and the middle of the straight line MK is the center of the section.
Proposition 27, Problem 19
To describe a trajectory that will touch five straight lines given in position.
Let the tangents ABG, BCF, GCD, FDE, and EA be given in position. Bisect in M and N the diagonals AF and BE of the quadrilateral figure ABFE formed by any four of those tangents, and (by lem. 25, corol. 3) the straight line MN drawn through the points of bisection will pass through the center of the trajectory. Again, bisect in P and Q the diagonals (as I call them) BD and GF of the quadrilateral figure BGFD formed by any other four tangents; then the straight line PQ drawn through the points of bisection will pass through the center of the trajectory. Therefore, the center will be given at the meeting-point of the bisecting lines. Let that center be O. Parallel to any tangent BC draw KL at such a distance that the center O is located midway between the parallels, and KL so drawn will touch the trajectory to be described. Let this line KL cut any other two tangents GCD and FDE in L and K. Through the meeting-points C and K, F and L, of these nonparallel tangents CL and FK with the parallels CF and KL, draw CK and FL meeting in R, and the straight line OR, drawn and produced, will cut the parallel tangents CF and KL in the points of contact. This is evident by lem. 24, corol. 2. By the same method other points of contact may be found, and then finally the trajectory may be described by the construction of prop. 22. Q.E.F.
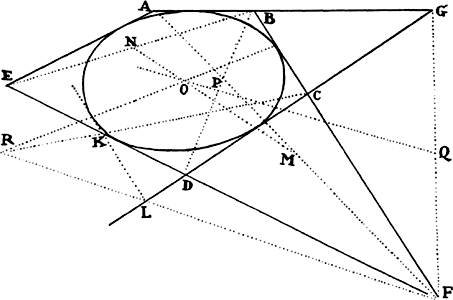
Scholium
What has gone before includes problems in which either the centers or
the asymptotes of trajectories are given. For when points and tangents are
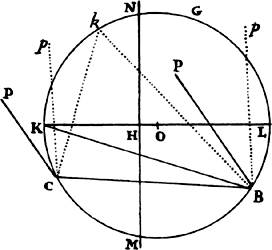 given together with the center, the same
number of other points and tangents are
given equally distant from the center on
its other side. Moreover, an asymptote
is to be regarded as a tangent, and its
infinitely distant end-point (if it is
permissible to speak of it in this way) as
a point of contact. Imagine the point of
contact of any tangent to go off to
infinity, and the tangent will be turned into
an asymptote, and the constructions of the preceding problems will be turned
into constructions in which the asymptote is given.
given together with the center, the same
number of other points and tangents are
given equally distant from the center on
its other side. Moreover, an asymptote
is to be regarded as a tangent, and its
infinitely distant end-point (if it is
permissible to speak of it in this way) as
a point of contact. Imagine the point of
contact of any tangent to go off to
infinity, and the tangent will be turned into
an asymptote, and the constructions of the preceding problems will be turned
into constructions in which the asymptote is given.
After the trajectory has been described, its axes and foci may be found by the following method. In the construction and figure of lem. 21 make the legs BP and CP (by the meeting of which the trajectory was there described) of the mobile angles PBN and PCN be parallel to each other, and let them—while maintaining that position—revolve about their poles B and C in that figure. Meanwhile, let the circle BGKC be described by the point K or k in which the other legs CN and BN of those angles meet. Let the center of this circle be O. From this center to the ruler MN, at which those other legs CN and BN met while the trajectory was being described, drop the normal OH meeting the circle in K and L. And when those other legs CK and BK meet in K, the point that is nearer to the ruler, the first legs CP and BP will be parallel to the major axis and perpendicular to the minor axis; and the converse will occur if the same legs meet in the farther point L. Hence, if the center of a trajectory is given, the axes will be given. And when these are given, the foci are apparent.
But the squares of the axes are to
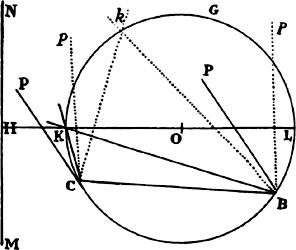 each other as KH to LH, and hence
it is easy to describe a trajectory,
given in species, through four given
points. For if two of the given points
constitute the poles C and B, a third
will give the mobile angles PCK and
PBK; and once these are given, the
circle BGKC can be described. Then,
because the species of the trajectory
is given, the ratio of OH to OK, and thus OH itself, will be given. With
center O and radius OH describe another circle, and the straight line that
touches this circle and passes through the meeting-point of the legs CK and
BK when the first legs CP and BP meet in the fourth given point will be
that ruler MN by means of which the trajectory will be described. Hence, in
turn, a quadrilateral given in species can (except in certain impossible cases)
also be inscribed in any given conic.
each other as KH to LH, and hence
it is easy to describe a trajectory,
given in species, through four given
points. For if two of the given points
constitute the poles C and B, a third
will give the mobile angles PCK and
PBK; and once these are given, the
circle BGKC can be described. Then,
because the species of the trajectory
is given, the ratio of OH to OK, and thus OH itself, will be given. With
center O and radius OH describe another circle, and the straight line that
touches this circle and passes through the meeting-point of the legs CK and
BK when the first legs CP and BP meet in the fourth given point will be
that ruler MN by means of which the trajectory will be described. Hence, in
turn, a quadrilateral given in species can (except in certain impossible cases)
also be inscribed in any given conic.
There are also other lemmas by means of which trajectories given in species can be described if points and tangents are given. An example: if a straight line, drawn through any point given in position, intersects a given conic in two points, and the distance between the intersections is bisected, the point of bisection will lie on another conic that is of the same species as the first one and that has its axes parallel to the axes of the first. But I pass quickly to what is more useful.
Lemma 26
To place the three corners of a triangle given in species and magnitude on three
straight lines given in position and not all parallel, with one corner on each line.
aThree indefinite straight lines, AB, AC, and BC, are given in position,
and it is required to place triangle DEF in such a way that its corner D
touches line AB, corner E line AC, and corner F line BC.a On DE, DF, and
 EF describe three segments DRE,
DGF, and EMF of circles,
containing angles equal respectively to
angles BAC, ABC, and ACB. And
let these segments be described on
those sides of the lines DE, DF,
and EF that will make the letters
DRED go round in the same order
as the letters BACB, the letters
DGFD in the same order as ABCA, and the letters EMFE in the same
order as ACBA; then complete these segments into full circles. Let the first
two circles cut each other in G, and let their centers be P and Q. Joining GP
and also PQ, take Ga to AB as GP is to PQ; and with center G and radius
Ga describe a circle that cuts the first circle DGE in a. Join aD cutting the
second circle DFG in b, and aE cutting the third circle EMF in c. And
now the figure ABCdef may be constructed similar and equal to the figure
abcDEF. This being done, the problem is solved.
EF describe three segments DRE,
DGF, and EMF of circles,
containing angles equal respectively to
angles BAC, ABC, and ACB. And
let these segments be described on
those sides of the lines DE, DF,
and EF that will make the letters
DRED go round in the same order
as the letters BACB, the letters
DGFD in the same order as ABCA, and the letters EMFE in the same
order as ACBA; then complete these segments into full circles. Let the first
two circles cut each other in G, and let their centers be P and Q. Joining GP
and also PQ, take Ga to AB as GP is to PQ; and with center G and radius
Ga describe a circle that cuts the first circle DGE in a. Join aD cutting the
second circle DFG in b, and aE cutting the third circle EMF in c. And
now the figure ABCdef may be constructed similar and equal to the figure
abcDEF. This being done, the problem is solved.
For draw Fc meeting aD in n, and join aG, bG, QG, QD, and PD. By construction, angle EaD is equal to angle CAB, and angle acF is equal to angle ACB, and thus the angles of triangle anc are respectively equal to the angles of triangle ABC. Therefore angle anc or FnD is equal to angle ABC, and hence equal to angle FbD; and therefore point n coincides with point b. Further, angle GPQ, which is half of angle GPD at the center, is equal to angle GaD at the circumference; and angle GQP, which is half of angle GQD at the center, is equal to the supplement of angle GbD at the circumference, and hence equal to angle Gba; and therefore triangles GPQ and Gab are similar, and Ga is to ab as GP to PQ, that is (by construction), as Ga to AB. And thus ab and AB are equal; and therefore triangles abc and ABC, which we have just proved to be similar, are also equal. Hence, since in addition the corners D, E, and F of the triangle DEF touch the sides ab, ac, and bc respectively of the triangle abc, the figure ABCdef can be completed similar and equal to the figure abcDEF; and by its completion the problem will be solved. Q.E.F.
COROLLARY. Hence a straight line can be drawn whose parts given in length will lie between three straight lines given in position. Imagine that triangle DEF, with point D approaching side EF and sides DE and DF placed in a straight line, is changed into a straight line whose given part DE is to be placed between the straight lines AB and AC given in position and whose given part DF is to be placed between the straight lines AB and BC given in position; then, by applying the preceding construction to this case, the problem will be solved.
Proposition 28, Problem 20
To describe a trajectory given in species and magnitude, whose given parts will lie
between three straight lines given in position.
Let it be required to describe a trajectory that is similar and equal to the curved line DEF and that will be cut by three straight lines AB, AC, and BC, given in position, into parts similar and equal to the given parts DE and EF of this curved line.
Draw the straight lines DE, EF, and DF, place one of the corners D, E, and F of this triangle DEF on each of those straight lines given in position (by lem. 26); then about the triangle describe a trajectory similar and equal to the curve DEF. Q.E.F.
Lemma 27
To describe a quadrilateral given in species, whose corners will lie on four straight
lines, given in position, which are not all parallel and do not all converge to a
common point—each corner lying on a separate line.
Let four straight lines ABC, AD, BD, and CE
 be given in position, the first of which cuts the
second in A, cuts the third in B, and cuts the fourth
in C; let it be required to describe a quadrilateral
fghi which is similar to the quadrilateral FGHI
and whose corner f, equal to the given corner F,
touches the straight line ABC, and whose other corners
g, h, and i, equal to the other given corners
G, H, and I, touch the other lines AD, BD, and
CE respectively. Join FH, and on FG, FH, and
FI describe three segments of circles, FSG, FTH,
and FVI, of which the first (FSG) contains an
angle equal to angle BAD, the
second (FTH) contains an angle equal
to angle CBD, and the third (FVI)
contains an angle equal to angle
ACE. The segments ought,
moreover, to be described on those sides
of the lines FG, FH, and FI that
will make the circular order of the
letters FSGF the same as that of
the letters BADB, and will make
the letters FTHF go round in the
same order as CBDC, and the letters
FVIF in the same order as ACEA.
be given in position, the first of which cuts the
second in A, cuts the third in B, and cuts the fourth
in C; let it be required to describe a quadrilateral
fghi which is similar to the quadrilateral FGHI
and whose corner f, equal to the given corner F,
touches the straight line ABC, and whose other corners
g, h, and i, equal to the other given corners
G, H, and I, touch the other lines AD, BD, and
CE respectively. Join FH, and on FG, FH, and
FI describe three segments of circles, FSG, FTH,
and FVI, of which the first (FSG) contains an
angle equal to angle BAD, the
second (FTH) contains an angle equal
to angle CBD, and the third (FVI)
contains an angle equal to angle
ACE. The segments ought,
moreover, to be described on those sides
of the lines FG, FH, and FI that
will make the circular order of the
letters FSGF the same as that of
the letters BADB, and will make
the letters FTHF go round in the
same order as CBDC, and the letters
FVIF in the same order as ACEA.
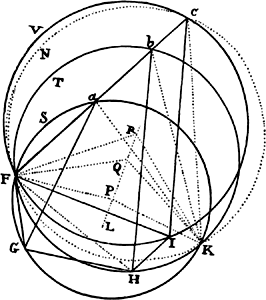 Complete the segments into whole circles, and let P be the center of the
first circle FSG, and Q the center of the second circle FTH. Join PQ and
produce it in both directions; and in it take QR in the ratio to PQ that BC
has to AB. And take QR on the side of the point Q which makes the order
of the letters P, Q, and R the same as that of the letters A, B, and C; and
then with center R and radius RF describe a fourth circle FNc cutting the
third circle FVI in c. Join Fc cutting the first circle in a and the second
in b. Draw aG, bH, and cI, and the figure ABCfghi can be constructed
similar to the figure abcFGHI. When this is done, the quadrilateral fghi
will be the very one which it was required to construct.
Complete the segments into whole circles, and let P be the center of the
first circle FSG, and Q the center of the second circle FTH. Join PQ and
produce it in both directions; and in it take QR in the ratio to PQ that BC
has to AB. And take QR on the side of the point Q which makes the order
of the letters P, Q, and R the same as that of the letters A, B, and C; and
then with center R and radius RF describe a fourth circle FNc cutting the
third circle FVI in c. Join Fc cutting the first circle in a and the second
in b. Draw aG, bH, and cI, and the figure ABCfghi can be constructed
similar to the figure abcFGHI. When this is done, the quadrilateral fghi
will be the very one which it was required to construct.
For let the first two circles FSG and FTH intersect each other in K. Join PK, QK, RK, aK, bK, and cK, and produce QP to L. The angles FaK, FbK, and FcK at the circumferences are halves of the angles FPK, FQK, and FRK at the centers, and hence are equal to the halves LPK, LQK, and LRK of these angles. Therefore, the angles of figure PQRK are respectively equal to the angles of figure abcK, and the figures are similar; and hence ab is to bc as PQ to QR, that is, as AB to BC. Besides, the angles fAg, fBh, and fCi are (by construction) equal to the angles FaG, FbH, and FcI. Therefore, ABCfghi, a figure similar to the figure abcFGHI, can be completed. When this is done, the quadrilateral fghi will be constructed similar to the quadrilateral FGHI with its corners f, g, h, and i touching the straight lines ABC, AD, BD, and CE. Q.E.F.
COROLLARY. Hence a straight line can be drawn whose parts, intercepted in a given order between four straight lines given in position, will have a given proportion to one another. Increase the angles FGH and GHI until the straight lines FG, GH, and HI lie in a single straight line; and by constructing the problem in this case, a straight line fghi will be drawn, whose parts fg, gh, and hi, intercepted between four straight lines given in position, AB and AD, AD and BD, BD and CE, will be to one another as the lines FG, GH, and HI, and will keep the same order with respect to one another. But the same thing is done more expeditiously as follows.
Produce AB to K and BD to L so that BK is to AB as HI to GH, and DL to BD as GI to FG; and join KL meeting the straight line CE in i. Produce iL to M, so that LM is to iL; as GH to HI; and draw MQ parallel to LB and meeting the straight line AD in g, and draw gi cutting AB and BD in f and h. I declare it done.
For let Mg cut the straight line AB in Q, and let AD cut the straight line KL in S, and draw AP parallel to BD and meeting iL in P; then gM will be to Lh (gi to hi, Mi to Li, GI to HI, AK to BK) and AP to BL in the same ratio. Cut DL in R so that DL is to RL in that same ratio; then, because gS to gM, AS to AP, and DS to DL are proportional, from the equality of the ratios [or ex aequo] ASa will be to BL, and DS to RL, as gS to Lh, and by a mixture of operations BL − RL will be to Lh − BL as AS − DS to gS − AS. That is, BR will be to Bh as AD to Ag and thus as BD to gQ. And by alternation [or alternando] BR is to BD as Bh to gQ or as fh to fg. But by construction the line BL was cut in D and R in the same ratio as the line FI in G and H; and therefore BR is to BD as FH to FG. As a result, fh is to fg as FH to FG. Therefore, since gi is also to hi as Mi to Li, that is, as GI to HI, it is evident that the lines FI and fi are similarly cut in g and h, G and H. Q.E.F.
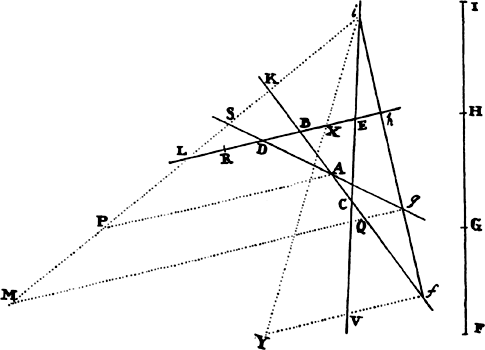
In the construction of this corollary, after LK is drawn cutting CE in i, it is possible to produce iE to V, so that EV is to Ei as FH to HI, and then to draw Vf parallel to BD. It comes to the same thing if with center i and radius IH a circle is described cutting BD in X, and if iX is produced to Y, so that iY is equal to IF, and if Yf is drawn parallel to BD.
Other solutions of this problem were devised some time ago by Wren and Wallis.
Proposition 29, Problem 21
To describe a trajectory, given in species, which four straight lines given in position
will cut into parts given in order, species, and proportion.
Let it be required to describe a trajectory that is similar to the curved line FGHI and whose parts, similar and proportional to the parts FG, GH, and HI of the curve, are intercepted between the straight lines AB and AD, AD and BD, BD and CE given in position, the first part between the first two lines, the second between the second two lines, and the third between the third two lines. After drawing the straight lines FG, GH, HI, and FI, describe (by lem. 27) a quadrilateral fghi that is similar to the quadrilateral FGHI and whose corners f, g, h, and i touch the straight lines AB, AD, BD, and CE, given in position, each corner touching a separate line in the order stated. Then about this quadrilateral describe a trajectory exactly similar to the curved line FGHI.
Scholium
This problem can also be constructed as follows. After joining FG, GH, HI,
and FI, produce GF to V, join FH and IG, and make angles CAK and
DAL equal to angles FGH and VFH. Let AK and AL meet the straight
line BD in K and L, and from these points draw KM and LN, of which
KM makes an angle AKM equal to angle GHI and is to AK as HI is to
GH, and LN makes an angle ALN equal to angle FHI and is to AL as HI
to FH. And draw AK, KM, AL, and LN on those sides of the lines AD,
AK, and AL that will make the letters CAKMC, ALKA, and DALND go
round in the same order as the letters FGHIF; and draw MN meeting the
straight line CE in i. Make angle iEP equal to the angle IGF, and let PE
be to Ei as FG to GI; and through P draw PQf, which with the straight
line ADE contains the angle PQE equal to the angle FIG and meets the
straight line AB in f; and join fi. Now draw PE and PQ on those sides of
the lines CE and PE that will make the circular order of the letters PEiP
and PEQP the same as that of the letters FGHIF; and then, if on line fi a
quadrilateral fghi similar to the quadrilateral FGHI is constructed (with the
same order of the letters), and a trajectory given in species is circumscribed
about the quadrilateral, the problem will be solved.
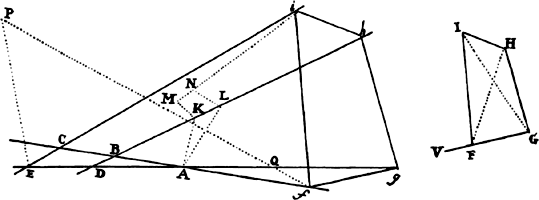
So much for the finding of orbits. It remains to determine the motions of bodies in the orbits that have been found.
To find motions in given orbits
Proposition 30, Problem 22
If a body moves in a given parabolic trajectory, to find its position at an assigned
time.
Let S be the focus and A the principal vertex of the parabola, and
let 4AS × M be equal to the parabolic area APS to be cut off, which
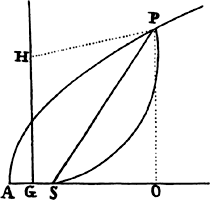 either was described by the radius SP after the
body’s departure from the vertex or is to be
described by that radius before the body’s arrival
at the vertex. The quantity of that area to be
cut off can be found from the time, which is
proportional to it. Bisect AS in G, and erect
the perpendicular GH equal to 3M, and a
circle described with center H and radius HS will
cut the parabola in the required place P. For,
when the perpendicular PO has been dropped to the axis and PH has
been drawn, then AG2 + GH2
(= HP2 = (AO − AG)2 + (PO − GH)2) =
AO2 + PO2 − 2GA × AO − 2GH × PO + AG2 + GH2. Hence 2GH × PO
(= AO2 + PO2 − 2GA × AO) = AO2 + ¾PO2. For AQ2 write
either was described by the radius SP after the
body’s departure from the vertex or is to be
described by that radius before the body’s arrival
at the vertex. The quantity of that area to be
cut off can be found from the time, which is
proportional to it. Bisect AS in G, and erect
the perpendicular GH equal to 3M, and a
circle described with center H and radius HS will
cut the parabola in the required place P. For,
when the perpendicular PO has been dropped to the axis and PH has
been drawn, then AG2 + GH2
(= HP2 = (AO − AG)2 + (PO − GH)2) =
AO2 + PO2 − 2GA × AO − 2GH × PO + AG2 + GH2. Hence 2GH × PO
(= AO2 + PO2 − 2GA × AO) = AO2 + ¾PO2. For AQ2 write 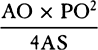 ,
and if all the terms are divided by 3PO and multiplied by 2AS, it will result
that 4/3GH × AS
,
and if all the terms are divided by 3PO and multiplied by 2AS, it will result
that 4/3GH × AS  = ⅙AO × PO + ½AS × PO
= ⅙AO × PO + ½AS × PO  × PO =
× PO =
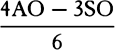 × PO = area (APO − SPO)
× PO = area (APO − SPO) = area APS. But GH was 3M,
and hence 4/3GH × AS is 4AS × M. Therefore, the area APS that was cut
off is equal to the area 4AS × M that was to be cut off. Q.E.D.
= area APS. But GH was 3M,
and hence 4/3GH × AS is 4AS × M. Therefore, the area APS that was cut
off is equal to the area 4AS × M that was to be cut off. Q.E.D.
COROLLARY 1. Hence GH is to AS as the time in which the body described the arc AP is to the time in which it described the arc between the vertex A and a perpendicular erected from the focus S to the axis.
COROLLARY 2. And if a circle ASP continually passes through the moving body P, the velocity of point H is to the velocity which the body had at the vertex A as 3 to 8, and thus the line GH is also in this ratio to the straight line which the body could describe in the time of its motion from A to P with the velocity which it had at the vertex A.
COROLLARY 3. Hence also, conversely, the time can be found in which the body described any assigned arc AP. Join AP and at its midpoint erect a perpendicular meeting the straight line GH in H.
Lemma 28
No oval figure exists whose area, cut off by straight lines at will, can in general be
found by means of equations finite in the number of their terms and dimensions.
Within an oval let any point be given about which, as a pole, a straight line revolves continually with uniform motion, and meanwhile in that straight line let a mobile point go out from the pole and proceed always with the velocity that is as the square of that straight line within the oval. By this motion that point will describe a spiral with an infinite number of gyrations. Now, if the portion of the area of the oval cut off by that straight line can be found by means of a finite equation, there will also be found by the same equation the distance of the point from the pole, a distance that is proportional to this area, and thus all the points of the spiral can be found by means of a finite equation; and therefore the intersection of any straight line, given in position, with the spiral can also be found by means of a finite equation. But every infinitely produced straight line cuts a spiral in an infinite number of points; and the equation by which some intersection of two lines [i.e., curved lines] is found gives all their intersections by as many roots [as there are intersections] and therefore rises to as many dimensions as there are intersections. Since two circles cut each other in two points, one intersection will not be found except by an equation of two dimensions, by which the other intersection may also be found. Since two conics can have four intersections, one of these intersections cannot generally be found except by an equation of four dimensions, by means of which all four of the intersections may be found simultaneously. For if those intersections are sought separately, since they all have the same law and condition, the computation will be the same in each case, and therefore the conclusion will always be the same, which accordingly must comprehend all the intersections together and give them indiscriminately. Hence also the intersections of conics and of curves of the third power, because there can be six such intersections, are found simultaneously by equations of six dimensions; and intersections of two curves of the third power, since there can be nine of them, are found simultaneously by equations of nine dimensions. If this did not happen necessarily, all solid problems might be reduced to plane problems, and higher than solid to solid problems. I am speaking here of curves with a power that cannot be reduced. For if the equation by which the curve is defined can be reduced to a lower power, the curve will not be simple, but will be compounded of two or more curves whose intersections can be found separately by different computations. In the same way, the pairs of intersections of straight lines and conics are always found by equations of two dimensions; the trios of intersections of straight lines and of irreducible curves of the third power, by equations of three dimensions; the quartets of intersections of straight lines and of irreducible curves of the fourth power, by equations of four dimensions; and so on indefinitely. Therefore, the intersections of a straight line and of a spiral, which are infinite in number (since this curve is simple and cannot be reduced to more curves), require equations infinite in the number of their dimensions and roots, by which all the intersections can be given simultaneously. For they all have the same law and computation. For if a perpendicular is dropped from the pole to the intersecting straight line, and the perpendicular, together with the intersecting straight line, revolves about the pole, the intersections of the spiral will pass into one another, and the one that was the first or the nearest to the pole will be the second after one revolution, and after two revolutions will be third, and so on; nor will the equation change in the meantime except insofar as there is a change in the magnitude of the quantities by which the position of the intersecting line is determined. Hence, since the quantities return to their initial magnitudes after each revolution, the equation will return to its original form, and thus one and the same equation will give all the intersections and therefore will have an infinite number of roots by which all of the intersections can be given. Therefore, it is not possible for the intersection of a straight line and a spiral to be found universally by means of a finite equation, and on that account no oval exists whose area, cut off by prescribed straight lines, can universally be found by such an equation.
By the same argument, if the distance between the pole and the point by which the spiral is described is taken proportional to the intercepted part of the perimeter of the oval, it can be proved that the length of the perimeter cannot universally be found by a finite equation. aBut here I am speaking of ovals that are not touched by conjugate figures extending out to infinity.a
COROLLARY. Hence the area of an ellipse that is described by a radius drawn from a focus to a moving body cannot be found, from a time that has been given, by means of a finite equation, and therefore cannot be determined by describing geometrically rational curves. I call curves “geometrically rational” when all of their points can be determined by lengths defined by equations, that is, by involved ratios of lengths, and I call the other curves (such as spirals, quadratrices, and cycloids) “geometrically irrational.” For lengths that are or are not as integer to integer (as in book 10 of the Elements) are arithmetically rational or irrational. Therefore I cut off an area of an ellipse proportional to the time by a geometrically irrational curve as follows.
Proposition 31a, Problem 23
If a body moves in a given elliptical trajectory, to find its position at an assigned
time.
Let A be the principal vertex of the ellipse APB, S a focus, and O the center, and let P be the position of the body. Produce OA to G so that OG is to OA as OA to OS. Erect the perpendicular GH, and with center O and radius OG describe the circle GEF; then, along the rule GH as a base let the wheel GEF move progressively forward, revolving about its own axis, while the point A on the wheel describes the cycloid ALI. When this has been done, take GK so that it will have the same ratio to the perimeter GEFG of the wheel as the time in which the body, in moving forward from A, described the arc AP has to the time of one revolution in the ellipse. Erect the perpendicular KL meeting the cycloid in L; and when LP has been drawn parallel to KG, it will meet the ellipse in the required position P of the body.
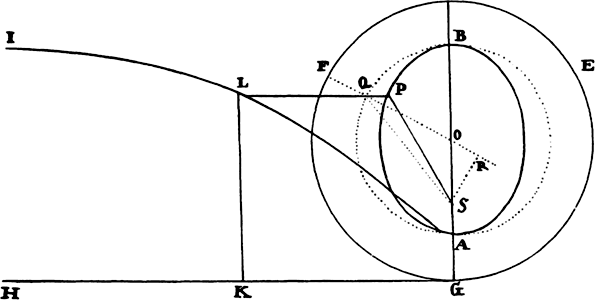
For with center O and radius OA describe the semicircle AQB, and let LP, produced if necessary, meet the arc AQ in Q, and join SQ and also OQ. Let OQ meet the arc EFG in F, and drop the perpendicular SR to OQ. Area APS is as area AQS, that is, as the difference between sector OQA and triangle OQS, or as the difference of the rectangles ½OQ × AQ and ½OQ × SR, that is, because ½OQ is given, as the difference between the arc AQ and the straight line SR, and hence (because of the equality of the given ratios of SR to the sine of the arc AQ, OS to OA, OA to OG, AQ to GF, and so by separation [or dividendo] AQ − SR to GF − the sine of the arc AQ) as GK, the difference between the arc GF and the sine of the arc AQ. Q.E.D.
Scholium
But the description of this curve is difficult; hence it is preferable to use a
solution that is approximately true. Find a certain angle B that is to the angle
of 57.29578° (which an arc equal to the radius subtends) as the distance SH
between the foci is to the diameter AB of the ellipse; and also find a certain
length L that is to the radius in the inverse of that ratio. Once these have
been found, the problem can thereupon be solved by the following analysis.
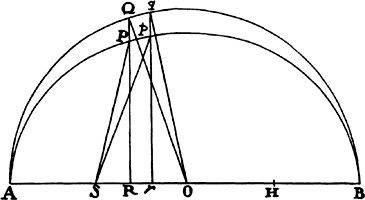
By any construction, or by making any kind of guess, find the body’s position P very close to its true position p. Then, when the ordinate PR has been dropped to the axis of the ellipse, the ordinate RQ of the circumscribed circle AQB will be given from the proportion of the diameters of the ellipse, where the ordinate RQ is the sine of the angle AOQ (AO being the radius) and cuts the ellipse in P. It is sufficient to find this angle AOQ approximately by a rough numerical calculation. Also find the angle proportional to the time, that is, the angle that is to four right angles as the time in which the body described the arc Ap is to the time of one revolution in the ellipse. Let that angle be N. Then take an angle D that will be to angle B as the sine of angle AOQ is to the radius, and also take an angle E that will be to angle N − AOQ + D as the length L is to this same length L minus the cosine of angle AOQ when that angle is less than a right angle, but plus that cosine when it is greater. Next take an angle F that will be to angle B as the sine of angle AOQ + E is to the radius, and take an angle G that will be to angle N − AOQ − E + F as the length L is to this same length minus the cosine of angle AOQ + E when that angle is less than a right angle, and plus that cosine when it is greater. Thirdly, take an angle H that will be to angle B as the sine of angle AOQ + E + G is to the radius, and take an angle I that will be to angle N − AOQ − E − G + H as the length L is to this same length L minus the cosine of angle AOQ + E + G when that angle is less than a right angle, but plus that cosine when it is greater. And so on indefinitely. Finally take angle AOq equal to angle AOQ + E + G + I + · · · . And from its cosine Or and ordinate pr, which is to its sine qr as the minor axis of the ellipse to the major axis, the body’s corrected place p will be found. If the angle N − AOQ + D is negative, the + sign of E must everywhere be changed to −, and the − sign to +. The same is to be understood of the signs of G and I when the angles N − AOQ − E + F and N − AOQ − E − G + H come out negative. But the infinite series AOQ + E + G + I + · · · converges so very rapidly that it is scarcely ever necessary to proceed further than the second term E. And the computation is based on this theorem: that the area APS is as the difference between the arc AQ and the straight line dropped perpendicularly from the focus S to the radius OQ.
In the case of a hyperbola the problem is solved by a similar computation.
Let O be its center, A a vertex, S a focus, and OK an asymptote. Find
the quantity of the area to be cut off, which is proportional to the time.
Let this quantity be A, and guess the position of the straight line SP that
cuts off an approximately true area APS. Join OP, and from A and P to
the asymptote OK draw AI and PK parallel to the second asymptote; then
a table of logarithms will give the area AIKP and the equal area OPA,
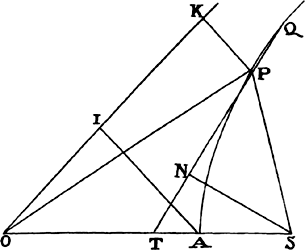 which, on being subtracted from the
triangle OPS, will leave the cut-off
area APS. Divide 2APS − 2A or
2A − 2APS (twice the difference of
the area A to be cut off and the
cut-off area APS) by the line SN,
which is perpendicular to the
tangent TP from the focus S, so as to
obtain the length of the chord PQ.
Now, draw the chord PQ between
A and P if the cut-off area APS is greater than the area A to be cut off, but
otherwise draw PQ on the opposite side of point P, and then the point Q
will be a more accurate position of the body. And by continually repeating
the computation, a more and more accurate position will be obtained.
which, on being subtracted from the
triangle OPS, will leave the cut-off
area APS. Divide 2APS − 2A or
2A − 2APS (twice the difference of
the area A to be cut off and the
cut-off area APS) by the line SN,
which is perpendicular to the
tangent TP from the focus S, so as to
obtain the length of the chord PQ.
Now, draw the chord PQ between
A and P if the cut-off area APS is greater than the area A to be cut off, but
otherwise draw PQ on the opposite side of point P, and then the point Q
will be a more accurate position of the body. And by continually repeating
the computation, a more and more accurate position will be obtained.
And by these computations a general analytical solution of the problem is
achieved. But the particular computation that follows is more suitable for
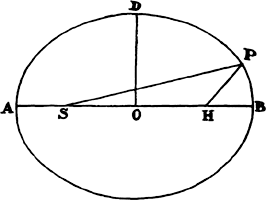 astronomical purposes. Let AO, OB, and OD
be the semiaxes of the ellipse, and L its
latus rectum, and D the difference between
the semiaxis minor OD and half of the
latus rectum ½L; find an angle Y, whose
sine is to the radius as the rectangle of that
difference D and the half-sum of the axes
AO+OD is to the square of the major axis
AB; and find also an angle Z, whose sine is to the radius as twice the
rectangle of the distance SH between the foci and the difference D is to three times
the square of the semiaxis major AO. Once these angles have been found,
the position of the body will thereupon be determined as follows: Take an
angle T proportional to the time in which arc BP was described, or equal to
the mean motion (as it is called); and an angle V (the first equation of the
mean motion) that shall be to angle Y (the greatest first equation) as the sine
of twice angle T is to the radius; and an angle X (the second equation) that
shall be to angle Z (the greatest second equation) as the cube of the sine of
angle T is to the cube of the radius. Then take the angle BHP (the equated
mean motion) equal either to the sum T + X + V of angles T, X, and V if
angle T is less than a right angle, or to the difference T + X − V if angle
T is greater than a right angle and less than two right angles; and if HP
meets the ellipse in P, SP (when drawn) will cut off the area BSP very nearly
proportional to the time.
astronomical purposes. Let AO, OB, and OD
be the semiaxes of the ellipse, and L its
latus rectum, and D the difference between
the semiaxis minor OD and half of the
latus rectum ½L; find an angle Y, whose
sine is to the radius as the rectangle of that
difference D and the half-sum of the axes
AO+OD is to the square of the major axis
AB; and find also an angle Z, whose sine is to the radius as twice the
rectangle of the distance SH between the foci and the difference D is to three times
the square of the semiaxis major AO. Once these angles have been found,
the position of the body will thereupon be determined as follows: Take an
angle T proportional to the time in which arc BP was described, or equal to
the mean motion (as it is called); and an angle V (the first equation of the
mean motion) that shall be to angle Y (the greatest first equation) as the sine
of twice angle T is to the radius; and an angle X (the second equation) that
shall be to angle Z (the greatest second equation) as the cube of the sine of
angle T is to the cube of the radius. Then take the angle BHP (the equated
mean motion) equal either to the sum T + X + V of angles T, X, and V if
angle T is less than a right angle, or to the difference T + X − V if angle
T is greater than a right angle and less than two right angles; and if HP
meets the ellipse in P, SP (when drawn) will cut off the area BSP very nearly
proportional to the time.
This technique seems expeditious enough because it is sufficient to find the first two or three figures of the extremely small angles V and X (reckoned in seconds, if it is agreeable). This technique is also accurate enough for the theory of the planets. For even in the orbit of Mars itself, whose greatest equation of the center is ten degrees, the error will hardly exceed one second. But when the angle BHP of equated mean motion has been found, the angle BSP of true motion and the distance SP are readily found by the very well known method.
So much for the motion of bodies in curved lines. It can happen, however, that a moving body descends straight down or rises straight up; and I now go on to expound what relates to motions of this sort.
The rectilinear ascent and descent of bodies
Proposition 32a, Problem 24
Given a centripetal force inversely proportional to the square of the distance of
places from its center, to determine the spaces which a body in falling straight
down describes in given times.
CASE 1. If the body does not fall perpendicularly, it will (by prop. 13,
corol. 1) describe some conic having a focus coinciding with the center of
 forces. Let the conic be ARPB, and its focus S. And
first, if the figure is an ellipse, on its major axis AB
describe the semicircle ADB, and let the straight line
DPC pass through the falling body and be perpendicular
to the axis; and when DS and PS have been
drawn, area ASD will be proportional to area ASP
and thus also to the time. Keeping the axis AB fixed,
continually diminish the width of the ellipse, and area
ASD will always remain proportional to the time.
Diminish that width indefinitely; and, the orbit APB
now coming to coincide with the axis AB, and the
focus S with the terminus B of the axis, the body will descend in the straight
line AC, and the area ABD will become proportional to the time. Therefore
forces. Let the conic be ARPB, and its focus S. And
first, if the figure is an ellipse, on its major axis AB
describe the semicircle ADB, and let the straight line
DPC pass through the falling body and be perpendicular
to the axis; and when DS and PS have been
drawn, area ASD will be proportional to area ASP
and thus also to the time. Keeping the axis AB fixed,
continually diminish the width of the ellipse, and area
ASD will always remain proportional to the time.
Diminish that width indefinitely; and, the orbit APB
now coming to coincide with the axis AB, and the
focus S with the terminus B of the axis, the body will descend in the straight
line AC, and the area ABD will become proportional to the time. Therefore
 the space AC will be given, which the body in
falling perpendicularly from place A describes in a
given time, provided that area ABD is taken
proportional to that time and the perpendicular DC
is dropped from point D to the straight line AB. Q.E.I.
the space AC will be given, which the body in
falling perpendicularly from place A describes in a
given time, provided that area ABD is taken
proportional to that time and the perpendicular DC
is dropped from point D to the straight line AB. Q.E.I.
CASE 2. If the figure RPB is a hyperbola, describe the rectangular hyperbola BED on the same principal diameter AB; and since the areas CSP, CBfP, and SPfB are respectively to the areas CSD, CBED, and SDEB in the given ratio of the distances CP and CD, and the area SPfB is proportional to the time in which body P will move through the arc PfB, the area SDEB will also be proportional to that same time. Diminish the latus rectum of the hyperbola RPB indefinitely, keeping the principal diameter fixed, and the arc PB will coincide with the straight line CB, and the focus S with the vertex B, and the straight line SD with the straight line BD. Accordingly, the area BDEB will be proportional to the time in which body C, falling straight down, describes the line CB. Q.E.I.
CASE 3. And by a similar argument, let the
 figure RPB be a parabola and let another parabola
BED with the same principal vertex B be described
and always remain given, while the latus rectum of
the first parabola (in whose perimeter the body P
moves) is diminished and reduced to nothing, so
that this parabola comes to coincide with the line
CB; then the parabolic segment BDEB will become proportional to the time
in which the body P or C will descend to the center S or B. Q.E.I.
figure RPB be a parabola and let another parabola
BED with the same principal vertex B be described
and always remain given, while the latus rectum of
the first parabola (in whose perimeter the body P
moves) is diminished and reduced to nothing, so
that this parabola comes to coincide with the line
CB; then the parabolic segment BDEB will become proportional to the time
in which the body P or C will descend to the center S or B. Q.E.I.
Proposition 33, Theorem 9
Supposing what has already been found, I say that the velocity of a falling body
at any place C is to the velocity of a body describing a circle with center B and
radius BC as the square root of the ratio of AC (the distance of the body from the
further vertex A of the circle or rectangular hyperbola) to ½AB (the principal
semidiameter of the figure).
Bisect AB, the common diameter of both figures RPB and DEB, in
O; and draw the straight line PT touching the figure RPB in P and also
cutting the common diameter AB (produced if necessary) in T, and let SY be
perpendicular to this straight line and BQ be perpendicular to this diameter,
and take the latus rectum of the figure RPB to be L. It is established by
prop. 16, corol. 9, that at any place P the velocity of a body moving about
the center S in the [curved] line RPB is to the velocity of a body describing a
circle about the same center with the radius SP as the square root of the ratio
of the rectangle ½L × SP to SY2. But from the Conics, AC × CB is to CP2
as 2AO to L, and thus 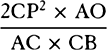 is equal to L. Therefore, the velocities
are to each other as the square root of the ratio of
is equal to L. Therefore, the velocities
are to each other as the square root of the ratio of 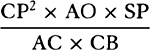 to SY2.
Further, from the Conics, CO is to BO as BO to TO, and by composition [or
componendo] or by separation [or dividendo], as CB to BT. Hence, either
by separation or by composition, BO ∓ CO becomes to BO as CT to BT,
that is, AC to AO as CP to BQ; and hence
to SY2.
Further, from the Conics, CO is to BO as BO to TO, and by composition [or
componendo] or by separation [or dividendo], as CB to BT. Hence, either
by separation or by composition, BO ∓ CO becomes to BO as CT to BT,
that is, AC to AO as CP to BQ; and hence 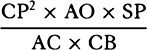 is equal to
is equal to
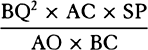 . Now let the width CP of the figure RPB be diminished
indefinitely, in such a way that point P comes to coincide with point C and
point S with point B and the line SP with the line BC and the line SY with
the line BQ; then the velocity of the body now descending straight down in
the line CB will become to the velocity of a body describing a circle with
center B and radius BC as the square root of the ratio of
. Now let the width CP of the figure RPB be diminished
indefinitely, in such a way that point P comes to coincide with point C and
point S with point B and the line SP with the line BC and the line SY with
the line BQ; then the velocity of the body now descending straight down in
the line CB will become to the velocity of a body describing a circle with
center B and radius BC as the square root of the ratio of 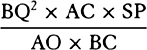 to SY2, that is (neglecting the ratios of equality SP to BC and BQ2 to SY2),
as the square root of the ratio of AC to AO or ½AB. Q.E.D.
to SY2, that is (neglecting the ratios of equality SP to BC and BQ2 to SY2),
as the square root of the ratio of AC to AO or ½AB. Q.E.D.
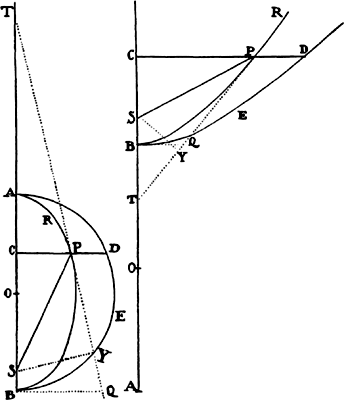
COROLLARY 1. When the points B and S come to coincide, TC becomes to TS as AC to AO.
COROLLARY 2. A body revolving in any circle at a given distance from the center will, when its motion is converted to an upward motion, ascend to twice that distance from the center.
Proposition 34, Theorem 10
If the figure BED is a parabola, I say that the velocity of a
falling body at any
place C is equal to the velocity with which a body can uniformly describe a circle
with center B and a radius equal to one-half of BC.
For at any place P the velocity of a body describing the parabola RPB
about the center S is (by prop. 16, corol. 7) equal to the velocity of a body
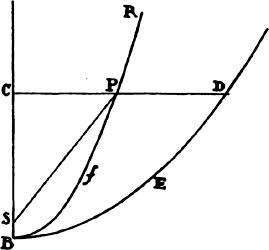 uniformly describing a circle about the
same center S with a radius equal to half
of the interval SP. Let the width CP of
the parabola be diminished indefinitely,
so that the parabolic arc PfB will come
to coincide with the straight line CB, the
center S with the vertex B, and the
interval SP with the interval BC, and the
proposition will be established. Q.E.D.
uniformly describing a circle about the
same center S with a radius equal to half
of the interval SP. Let the width CP of
the parabola be diminished indefinitely,
so that the parabolic arc PfB will come
to coincide with the straight line CB, the
center S with the vertex B, and the
interval SP with the interval BC, and the
proposition will be established. Q.E.D.
Proposition 35, Theorem 11
Making the same suppositions, I say that the area of the figure DES described by
the indefinite radius SD is equal to the area that a body revolving uniformly in
orbit about the center S can describe in the same time by a radius equal to half
of the latus rectum of the figure DES.
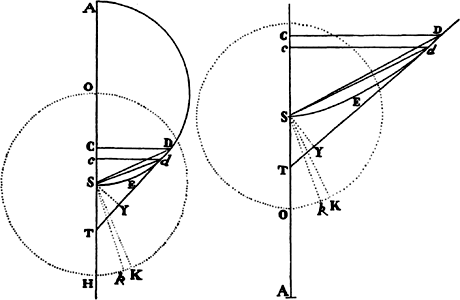
For suppose that body C falling in a minimally small particle of time describes the line-element Cc while another body K, revolving uniformly in the circular orbit OKk about the center S, describes the arc Kk. Erect the perpendiculars CD and cd meeting the figure DES in D and d. Join SD, Sd, SK, and Sk, and draw Dd meeting the axis AS in T, and drop the perpendicular SY to Dd.
CASE 1. Now, if the figure DES is a circle or a rectangular hyperbola, bisect its transverse diameter AS in O, and SO will be half of the latus rectum. And since TC is to TD as Cc to Dd, and TD to TS as CD to SY, from the equality of the ratios [or ex aequo] TC will be to TS as CD × Cc to SY × Dd. But (by prop. 33, corol. 1) TC is to TS as AC to AO, if, say, in the coming together of points D and d the ultimate ratios of the lines are taken. Therefore, AC is to AO or SK as CD × Cc is to SY × Dd. Further, the velocity of a descending body at C is to the velocity of a body describing a circle about the center S with radius SC as the square root of the ratio of AC to AO or SK (by prop. 33). And this velocity is to the velocity of a body describing the circle OKk as the square root of the ratio of SK to SC (by prop. 4, corol. 6), and from the equality of the ratios [or ex aequo] the first velocity is to the ultimate velocity, that is, the line-element Cc is to the arc Kk, as the square root of the ratio of AC to SC, that is, in the ratio of AC to CD. Therefore, CD × Cc is equal to AC × Kk, and thus AC is to SK as AC × Kk to SY × Dd, and hence SK × Kk is equal to SY × Dd, and ½SK × Kk is equal to ½SY × Dd, that is, the area KSk is equal to the area SDd. Therefore, in each particle of time, particles KSk and SDd of the two areas are generated such that, if their magnitude is diminished and their number increased indefinitely, they obtain the ratio of equality; and therefore (by lem. 4, corol.), the total areas generated in the same times are always equal. Q.E.D.
CASE 2. But if the figure DES is
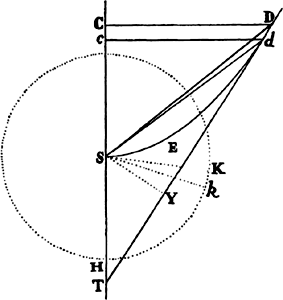 a parabola, then it will be found that,
as above, CD × Cc is to SY × Dd
as TC to TS, that is, as 2 to 1, and
thus ¼CD × Cc will be equal to
½SY × Dd. But the velocity of the
falling body at C is equal to the
velocity with which a circle can be
described uniformly with the radius
½SC (by prop. 34). And this velocity
is to the velocity with which a circle
can be described with the radius SK, that is, the line-element Cc is to the
arc Kk (by prop. 4, corol. 6), as the square root of the ratio of SK to ½SC,
that is, in the ratio of SK to ½CD. And therefore ½SK × Kk is equal to
¼CD × Cc and thus equal to ½SY × Dd; that is, the area KSk is equal to
the area SDd, as above. Q.E.D.
a parabola, then it will be found that,
as above, CD × Cc is to SY × Dd
as TC to TS, that is, as 2 to 1, and
thus ¼CD × Cc will be equal to
½SY × Dd. But the velocity of the
falling body at C is equal to the
velocity with which a circle can be
described uniformly with the radius
½SC (by prop. 34). And this velocity
is to the velocity with which a circle
can be described with the radius SK, that is, the line-element Cc is to the
arc Kk (by prop. 4, corol. 6), as the square root of the ratio of SK to ½SC,
that is, in the ratio of SK to ½CD. And therefore ½SK × Kk is equal to
¼CD × Cc and thus equal to ½SY × Dd; that is, the area KSk is equal to
the area SDd, as above. Q.E.D.
Proposition 36, Problem 25
To determine the times of descent of a body falling from a given place A.
Describe a semicircle ADS with diameter AS (the
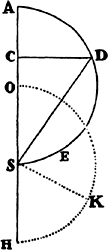 distance of the body from the center at the beginning of the
descent), and about the center S describe a semicircle OKH
equal to ADS. From any place C of the body erect the
ordinate CD. Join SD, and construct the sector OSK equal
to the area ASD. It is evident by prop. 35 that the body
in falling will describe the space AC in the same time in
which another body, revolving uniformly in orbit about the
center S, can describe the arc OK. Q.E.F.
distance of the body from the center at the beginning of the
descent), and about the center S describe a semicircle OKH
equal to ADS. From any place C of the body erect the
ordinate CD. Join SD, and construct the sector OSK equal
to the area ASD. It is evident by prop. 35 that the body
in falling will describe the space AC in the same time in
which another body, revolving uniformly in orbit about the
center S, can describe the arc OK. Q.E.F.
Proposition 37, Problem 26
To define the times of the ascent or descent of a body projected upward or
downward from a given place.
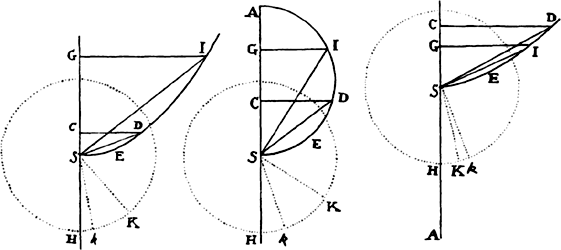
Let the body depart from the given place G along the line GS with any velocity whatever. Take GA to ½AS as the square of the ratio of this velocity to the uniform velocity in a circle with which the body could revolve about the center S at the given interval (or distance) SG. If that ratio is as 2 to 1, point A is infinitely distant, in which case a parabola is to be described with vertex S, axis SG, and any latus rectum, as is evident by prop. 34. But if that ratio is smaller or greater than the ratio of 2 to 1, then in the former case a circle, and in the latter case a rectangular hyperbola, must be described on the diameter SA, as is evident by prop. 33. Then, with center S and a radius equaling half of the latus rectum, describe the circle HkK, and to the place G of the descending or ascending body and to any other place C, erect the perpendiculars GI and CD meeting the conic or the circle in I and D. Then joining SI and SD, let the sectors HSK and HSk be made equal to the segments SEIS and SEDS, and by prop. 35 the body G will describe the space GC in the same time as the body K can describe the arc Kk. Q.E.F.
Proposition 38, Theorem 12
Supposing that the centripetal force is proportional to the height or distance of
places from the center, I say that the times of falling bodies, their velocities, and
the spaces described are proportional respectively to the arcs, the right sines, and
the versed sines.
Let a body fall from any place A along the
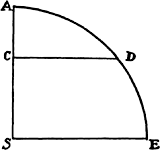 straight line AS; and with center of forces S and
radius AS describe the quadrant AE of a circle,
and let CD be the right sine of any arc AD; then
the body A, in the time AD, will in falling describe
the space AC and at place C will acquire the
velocity CD.
straight line AS; and with center of forces S and
radius AS describe the quadrant AE of a circle,
and let CD be the right sine of any arc AD; then
the body A, in the time AD, will in falling describe
the space AC and at place C will acquire the
velocity CD.
This is demonstrated from prop. 10 in the same way that prop. 32 was demonstrated from prop. 11.
COROLLARY 1. Hence the time in which one body, falling from place A, arrives at the center S is equal to the time in which another body, revolving, describes the quadrantal arc ADE.
COROLLARY 2. Accordingly, all the times are equal in which bodies fall from any places whatever as far as to the center. For all the periodic times of revolving bodies are (by prop. 4, corol. 3) equal.
Proposition 39, Problem 27
Suppose a centripetal force of any kind, and grant the quadratures of curvilinear
figures; it is required to find, for a body ascending straight up or descending straight
down, the velocity in any of its positions and the time in which the body will reach
any place; and conversely.
Let a body E fall from any place A whatever in the straight line ADEC,
and let there be always erected from the body’s place E the perpendicular
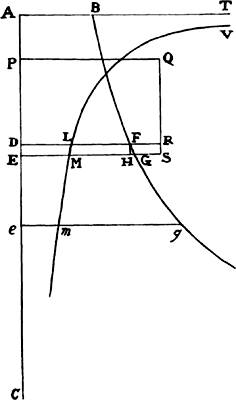 EG, proportional to the centripetal force
in that place tending toward the center C;
and let BFG be the curved line which the
point G continually traces out. At the very
beginning of the motion let EG coincide
with the perpendicular AB; then the
velocity of the body in any place E will be
as the straight line whose square is equal
to the curvilinear area ABGE. Q.E.I.
EG, proportional to the centripetal force
in that place tending toward the center C;
and let BFG be the curved line which the
point G continually traces out. At the very
beginning of the motion let EG coincide
with the perpendicular AB; then the
velocity of the body in any place E will be
as the straight line whose square is equal
to the curvilinear area ABGE. Q.E.I.
In EG take EM inversely proportional to the straight line whose square is equal to the area ABGE, and let VLM be a curved line which the point M continually traces out and whose asymptote is the straight line AB produced; then the time in which the body in falling describes the line AE will be as the curvilinear area ABTVME. Q.E.I.
For in the straight line AE take a minimally small line DE of a given
length, and let DLF be the location of the line EMG when the body was at
D; then, if the centripetal force is such that the straight line whose square
is equal to the area ABGE is as the velocity of the descending body, the
area itself will be as the square of the velocity, that is, if V and V + I are
written for the velocities at D and E, the area ABFD will be as V2, and
the area ABGE as V2 + 2VI + I2, and by separation [or dividendo] the area
DFGE will be as 2VI + I2, and thus 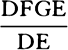 will be as
will be as 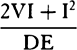 , that is,
if the first ratios of nascent quantities are taken, the length DF will be as
the quantity
, that is,
if the first ratios of nascent quantities are taken, the length DF will be as
the quantity 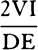 , and thus also as half of that quantity, or
, and thus also as half of that quantity, or 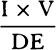 . But the
time in which the body in falling describes the line-element DE is as that
line-element directly and the velocity V inversely, and the force is as the
increment I of the velocity directly and the time inversely, and thus—if the
first ratios of nascent quantities are taken—as
. But the
time in which the body in falling describes the line-element DE is as that
line-element directly and the velocity V inversely, and the force is as the
increment I of the velocity directly and the time inversely, and thus—if the
first ratios of nascent quantities are taken—as 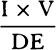 , that is, as the length
DF. Therefore a force proportional to DF or EG makes the body descend
with the velocity that is as the straight line whose square is equal to the area
ABGE. Q.E.D.
, that is, as the length
DF. Therefore a force proportional to DF or EG makes the body descend
with the velocity that is as the straight line whose square is equal to the area
ABGE. Q.E.D.
Moreover, since the time in which any line-element DE of a given length is described is as the velocity inversely, and hence inversely as the straight line whose square is equal to the area ABFD, and since DL (and hence the nascent area DLME) is as the same straight line inversely, the time will be as the area DLME, and the sum of all the times will be as the sum of all the areas, that is (by lem. 4, corol.), the total time in which the line AE is described will be as the total area ATVME. Q.E.D.
COROLLARY 1. Let P be the place from which a body must fall so that, under the action of some known uniform centripetal force (such as gravity is commonly supposed to be), it will acquire at place D a velocity equal to the velocity that another body, falling under the action of any force whatever, acquired at the same place D. In the perpendicular DF take DR such that it is to DF as that uniform force is to the other force at the place D. Complete the rectangle PDRQ and cut off the area ABFD equal to it. Then A will be the place from which the other body fell.
For, when the rectangle DRSE has been completed, the area ABFD is
to the area DFGE as V2 to 2VI and hence as ½V to I, that is, as half of
the total velocity to the increment of the velocity of the body falling under
the action of the nonuniform force; and similarly, the area PQRD is to the
area DRSE as half of the total velocity is to the increment of the velocity of
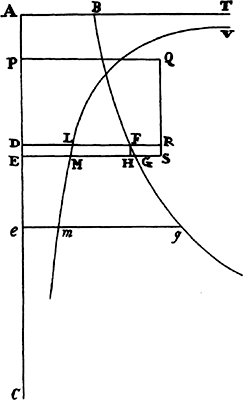 the body falling under the action of the
uniform force, and those increments
(because the nascent times are equal) are
as the generative forces, that is, as the
ordinates DF and DR, and thus as the
nascent areas DFGE and DRSE. Therefore,
the total areas ABFD and PQRD
will then from the equality of the ratios
[or ex aequo] be to each other as halves
of the total velocities and therefore are
equal because the velocities are equal.
the body falling under the action of the
uniform force, and those increments
(because the nascent times are equal) are
as the generative forces, that is, as the
ordinates DF and DR, and thus as the
nascent areas DFGE and DRSE. Therefore,
the total areas ABFD and PQRD
will then from the equality of the ratios
[or ex aequo] be to each other as halves
of the total velocities and therefore are
equal because the velocities are equal.
COROLLARY 2. Hence if any body is projected with a given velocity either upward or downward from any place D and the law of centripetal force is given, the velocity of the body at any other place e will be found by erecting the ordinate eg and taking that velocity at place e to the velocity at place D as the straight line whose square is equal to the rectangle PQRD, either increased by the curvilinear area DFge (if place e is lower than place D) or diminished by DFge (if place e is higher), is to the straight line whose square is equal to the rectangle PQRD alone.
COROLLARY 3. The time, also, will be determined by erecting the ordinate em inversely proportional to the square root of PQRD ± DFge, and by taking the time in which the body described the line De to the time in which the other body fell under the action of a uniform force from P and (by so falling) reached D as the curvilinear area DLme to the rectangle 2PD × DL. For the time in which the body descending under the action of a uniform force described the line PD is to the time in which the same body described the line PE as the square root of the ratio of PD to PE, that is (the line-element DE being just now nascent), in the ratio of PD to PD + ½DE or 2PD to 2PD + DE and by separation [or dividendo] to the time in which the same body described the line-element DE as 2PD to DE, and thus as the rectangle 2PD × DL to the area DLME; and the time in which each of the two bodies described the line-element DE is to the time in which the second body with nonuniform motion described the line De as the area DLME to the area DLme, and from the equality of the ratios [or ex aequo] the first time is to the ultimate time as the rectangle 2PD × DL to the area DLme.
To find the orbits in which bodies revolve when acted upon by any centripetal forces
Proposition 40, Theorem 13
If a body, under the action of any centripetal force, moves in any way whatever,
and another body ascends straight up or descends straight down, and if their
velocities are equal in some one instance in which their distances from the center
are equal, their velocities will be equal at all equal distances from the center.
Let some body descend from A through D and E to the center C, and
let another body move from V in the curved line VIKk. With center C and
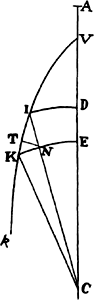 any radii describe the concentric circles DI and EK meeting
the straight line AC in D and E and the curve VIK in
I and K. Join IC meeting KE in N, and to IK drop the
perpendicular NT, and let the interval DE or IN between
the circumferences of the circles be minimally small, and
let the bodies have equal velocities at D and I. Since the
distances CD and CI are equal, the centripetal forces at D
and I will be equal. Represent these forces by the equal
line-elements DE and IN; then, if one of these forces IN is (by
corol. 2 of the laws) resolved into two, NT and IT, the
force NT, acting along the line NT perpendicular to the
path ITK of the body, will in no way change the velocity of
the body in that path but will only draw the body back from
a rectilinear path and make it turn aside continually from the tangent of the
orbit and move forward in the curvilinear path ITKk. That whole force
will be spent in producing this effect, while the whole of the other force IT,
acting along the body’s path, will accelerate the body and in a given minimally
small time will generate an acceleration proportional to itself. Accordingly,
the accelerations of the bodies at D and I that are made in equal times (if
the first ratios of the nascent lines DE, IN, IK, IT, and NT are taken) are
as the lines DE and IT, but in unequal times they are as those lines and the
times jointly. Now, the times in which DE and IK are described are as the
described paths DE and IK (because the velocities are equal), and hence
the accelerations in the path of the bodies along the lines DE and IK are
jointly as DE and IT, DE and IK, that is, as DE2 and the rectangle IT × IK.
But the rectangle IT × IK is equal to IN2, that is, equal to DE2, and therefore
the accelerations generated in the passing of the bodies from D and I to E
and K are equal. Therefore the velocities of the bodies at E and K are equal,
and by the same argument they will always be found equal at subsequent
equal distances. Q.E.D.
any radii describe the concentric circles DI and EK meeting
the straight line AC in D and E and the curve VIK in
I and K. Join IC meeting KE in N, and to IK drop the
perpendicular NT, and let the interval DE or IN between
the circumferences of the circles be minimally small, and
let the bodies have equal velocities at D and I. Since the
distances CD and CI are equal, the centripetal forces at D
and I will be equal. Represent these forces by the equal
line-elements DE and IN; then, if one of these forces IN is (by
corol. 2 of the laws) resolved into two, NT and IT, the
force NT, acting along the line NT perpendicular to the
path ITK of the body, will in no way change the velocity of
the body in that path but will only draw the body back from
a rectilinear path and make it turn aside continually from the tangent of the
orbit and move forward in the curvilinear path ITKk. That whole force
will be spent in producing this effect, while the whole of the other force IT,
acting along the body’s path, will accelerate the body and in a given minimally
small time will generate an acceleration proportional to itself. Accordingly,
the accelerations of the bodies at D and I that are made in equal times (if
the first ratios of the nascent lines DE, IN, IK, IT, and NT are taken) are
as the lines DE and IT, but in unequal times they are as those lines and the
times jointly. Now, the times in which DE and IK are described are as the
described paths DE and IK (because the velocities are equal), and hence
the accelerations in the path of the bodies along the lines DE and IK are
jointly as DE and IT, DE and IK, that is, as DE2 and the rectangle IT × IK.
But the rectangle IT × IK is equal to IN2, that is, equal to DE2, and therefore
the accelerations generated in the passing of the bodies from D and I to E
and K are equal. Therefore the velocities of the bodies at E and K are equal,
and by the same argument they will always be found equal at subsequent
equal distances. Q.E.D.
But also by the same argument bodies that have equal velocities and are equally distant from the center will be equally retarded in ascending to equal distances. Q.E.D.
COROLLARY 1. Hence if a body either oscillates while hanging by a thread or is compelled by any very smooth and perfectly slippery impediment to move in a curved line, and another body ascends straight up or descends straight down, and their velocities are equal at any identical height, their velocities at any other equal heights will be equal. For the thread of the pendent body or the impediment of an absolutely slippery vessel produces the same effect as the transverse force NT. The body is neither retarded nor accelerated by these, but only compelled to depart from a rectilinear course.
COROLLARY 2. Now let the quantity P be the greatest distance from the center to which a body, either oscillating or revolving in any trajectory whatever, can ascend when projected upward from any point of the trajectory with the velocity that it has at that point. Further, let the quantity A be the distance of the body from the center at any other point of the orbit. And let the centripetal force be always as any power An−1 of A, the index n − 1 being any number n diminished by unity. Then the velocity of the body at every height A [i.e., distance A] will be as √(Pn − An) and therefore is given. For the velocity of a body ascending straight up and descending straight down is (by prop. 39) in this very ratio.
Proposition 41a, Problem 28
Supposing a centripetal force of any kind and granting the quadratures of curvilinear
figures, it is required to find the trajectories in which bodies will move and
also the times of their motions in the trajectories so found.
Let any force tend toward a center C; and let it be required to find the
trajectory VIKk. Let the circle VR be given, described about the center C
with any radius CV; and about the same center let there be described any
other circles ID and KE cutting the trajectory in I and K and cutting the
straight line CV in D and E. Then draw the straight line CNIX cutting
the circles KE and VR in N and X, and also draw the straight line CKY
meeting the circle VR in Y. Let the points I and K be very close indeed
to each other, and let the body proceed from V through I and K to k; and
let point A be the place from which another body must fall so as to acquire
at place D a velocity equal to the velocity of the first body at I. And with
everything remaining as it was in prop. 39, the line-element IK, described in
a given minimally small time, will be as the velocity and hence as the straight
line whose square equals the area ABFD, and the triangle ICK proportional
to the time will be given; and therefore KN will be inversely as the height
IC, that is, if some quantity Q is given and the height IC is called A, as
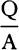 . Let us denote this quantity
. Let us denote this quantity 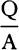 by Z, and let us suppose the magnitude
of Q to be such that in some one case √ABFD is to Z as IK is to KN,
and in every case √ABFD will be to Z as IK to KN and ABFD to Z2 as
IK2 to KN2, and by separation [or dividendo] ABFD − Z2 will be to Z2 as
IN2 to KN2, and therefore √(ABFD − Z2) will be to Z, or
by Z, and let us suppose the magnitude
of Q to be such that in some one case √ABFD is to Z as IK is to KN,
and in every case √ABFD will be to Z as IK to KN and ABFD to Z2 as
IK2 to KN2, and by separation [or dividendo] ABFD − Z2 will be to Z2 as
IN2 to KN2, and therefore √(ABFD − Z2) will be to Z, or 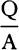 , as IN to
KN, and therefore A × KN will be equal to
, as IN to
KN, and therefore A × KN will be equal to 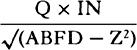 . Hence, since
YX × XC is to A × KN as CX2 to A2, the rectangle XY × XC will be equal
to
. Hence, since
YX × XC is to A × KN as CX2 to A2, the rectangle XY × XC will be equal
to 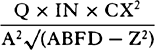 . Therefore, in the perpendicular DF take Db and Dc
always equal respectively to
. Therefore, in the perpendicular DF take Db and Dc
always equal respectively to 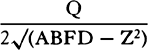 and
and 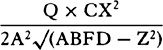 , and
describe the curved lines ab and ac which the points b and c continually trace
out, and from point V erect Va perpendicular to the line AC so as to cut
off the curvilinear areas VDba and VDca, and also erect the ordinates Ez
and Ex. Then, since the rectangle Db × IN or DbzE is equal to half of the
rectangle A × KN or is equal to the triangle ICK, and the rectangle Dc × IN
or DcxE is equal to half of the rectangle YX × XC or is equal to the triangle
XCY—that is, since the nascent particles DbzE and ICK of the areas VDba
and VIC are always equal, and the nascent particles DcxE and XCY of the
areas VDca and VCX are always equal—the generated area VDba will be
equal to the generated area VIC and hence will be proportional to the time,
and the generated area VDca will be equal to the generated sector VCX.
Therefore, given any time that has elapsed since the body set out from place
V, the area VDba proportional to it will be given and hence the body’s
height CD or CI will be given, and the area VDca and, equal to that area,
the sector VCX along with its angle VCI. And given the angle VCI and the
height CI, the place I will be given, in which the body will be found at the
end of that time. Q.E.I.
, and
describe the curved lines ab and ac which the points b and c continually trace
out, and from point V erect Va perpendicular to the line AC so as to cut
off the curvilinear areas VDba and VDca, and also erect the ordinates Ez
and Ex. Then, since the rectangle Db × IN or DbzE is equal to half of the
rectangle A × KN or is equal to the triangle ICK, and the rectangle Dc × IN
or DcxE is equal to half of the rectangle YX × XC or is equal to the triangle
XCY—that is, since the nascent particles DbzE and ICK of the areas VDba
and VIC are always equal, and the nascent particles DcxE and XCY of the
areas VDca and VCX are always equal—the generated area VDba will be
equal to the generated area VIC and hence will be proportional to the time,
and the generated area VDca will be equal to the generated sector VCX.
Therefore, given any time that has elapsed since the body set out from place
V, the area VDba proportional to it will be given and hence the body’s
height CD or CI will be given, and the area VDca and, equal to that area,
the sector VCX along with its angle VCI. And given the angle VCI and the
height CI, the place I will be given, in which the body will be found at the
end of that time. Q.E.I.
COROLLARY 1. Hence the greatest and least heights of bodies (that is, the apsides of their trajectories) can be found expeditiously. For the apsides are those points in which the straight line IC drawn through the center falls perpendicularly upon the trajectory VIK, which happens when the straight lines IK and NK are equal, and thus when the area ABFD is equal to Z2.
COROLLARY 2. The angle KIN, in which the trajectory anywhere cuts the line IC, is also expeditiously found from the given height IC of the body, namely, by taking its sine to the radius as KN to IK, that is, as Z to the square root of the area ABFD.
COROLLARY 3. If with center C
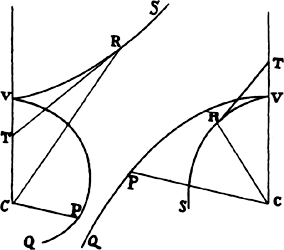 and principal vertex V any conic VRS
is described, and from any point R
of it the tangent RT is drawn so as
to meet the axis CV, indefinitely
produced, at point T; and, joining CR,
there is drawn the straight line CP,
which is equal to the abscissa CT and
makes an angle VCP proportional to
the sector VCR; then, if a centripetal
force inversely proportional to the cube of the distance of places from the
center tends toward that center C, and the body leaves the place V with the
proper velocity along a line perpendicular to the straight line CV, the body
will move forward in the trajectory VPQ which point P continually traces
out; and therefore, if the conic VRS is a hyperbola, the body will descend
to the center. But if the conic is an ellipse, the body will ascend continually
and will go off to infinity.
and principal vertex V any conic VRS
is described, and from any point R
of it the tangent RT is drawn so as
to meet the axis CV, indefinitely
produced, at point T; and, joining CR,
there is drawn the straight line CP,
which is equal to the abscissa CT and
makes an angle VCP proportional to
the sector VCR; then, if a centripetal
force inversely proportional to the cube of the distance of places from the
center tends toward that center C, and the body leaves the place V with the
proper velocity along a line perpendicular to the straight line CV, the body
will move forward in the trajectory VPQ which point P continually traces
out; and therefore, if the conic VRS is a hyperbola, the body will descend
to the center. But if the conic is an ellipse, the body will ascend continually
and will go off to infinity.
And conversely, if the body leaves
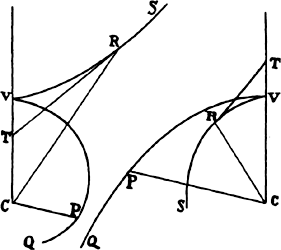 the place V with any velocity and,
depending on whether the body has
begun either to descend obliquely to the
center or to ascend obliquely from it,
the figure VRS is either a hyperbola or
an ellipse, the trajectory can be found
by increasing or diminishing the angle
VCP in some given ratio. But also, if
the centripetal force is changed into a
centrifugal force, the body will ascend obliquely in the trajectory VPQ, which
is found by taking the angle VCP proportional to the elliptic sector VRC and
by taking the length CP equal to the length CT, as above. All this follows
from the foregoing (prop. 41), by means of the quadrature of a certain curve,
the finding of which, as being easy enough, I omit for the sake of brevity.
the place V with any velocity and,
depending on whether the body has
begun either to descend obliquely to the
center or to ascend obliquely from it,
the figure VRS is either a hyperbola or
an ellipse, the trajectory can be found
by increasing or diminishing the angle
VCP in some given ratio. But also, if
the centripetal force is changed into a
centrifugal force, the body will ascend obliquely in the trajectory VPQ, which
is found by taking the angle VCP proportional to the elliptic sector VRC and
by taking the length CP equal to the length CT, as above. All this follows
from the foregoing (prop. 41), by means of the quadrature of a certain curve,
the finding of which, as being easy enough, I omit for the sake of brevity.
Proposition 42, Problem 29
Let the law of centripetal force be given; it is required to find the motion of a
body setting out from a given place with a given velocity along a given straight
line.
With everything remaining as it was in the three preceding propositions, let the body go forth from the place I along the line-element IK, with the velocity which another body, falling from the place P under the action of some uniform centripetal force, could acquire at D; and let this uniform force be to the force with which the first body is urged at I as DR to DF. Let the body go on toward k; and with center C and radius Ck describe the circle ke meeting the straight line PD at e, and erect the ordinates eg, ev, and ew of the curves BFg, abv, and acw. From the given rectangle PDRQ and the given law of the centripetal force acting on the first body, the curved line BFg is given by the construction of prop. 39 and its corol. 1. Then, from the given angle CIK, the proportion of the nascent lines IK and KN is given, and hence, by the construction of prop. 41, the quantity Q is given, along with the curved lines abv and acw; and therefore, when any time Dbve is completed, the body’s height Ce or Ck is given and the area Dcwe and the sector XCy equal to it and the angle ICk and the place k in which the body will then be. Q.E.I.
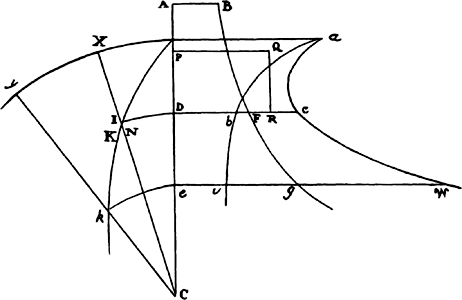
In these propositions we suppose that the centripetal force in receding from the center varies according to any law which can be imagined, but that at equal distances from the center it is everywhere the same. And so far we have considered the motion of bodies in nonmoving orbits. It remains for us to add a few things about the motion of bodies in orbits that revolve about a center of forces.
The motion of bodies in mobile orbits, and the motion of the apsides
Proposition 43, Problem 30
aIt is required to find the force that makes a body capable of moving in any
trajectory that is revolving about the center of forces in the same way as another
body in that same trajectory at rest.a
Let a body P revolve in the orbit VPK given in position, moving
forward from V toward K. From center C continually draw Cp equal to CP
 and making the angle VCp which is
proportional to the angle VCP; and the area that
the line Cp describes will be to the area VCP
that the line CP simultaneously describes as
the velocity of the describing line Cp to the
velocity of the describing line CP, that is, as
the angle VCp to the angle VCP and thus
in a given ratio and therefore proportional
to the time. Since the area that line Cp
describes in the immobile plane is proportional
to the time, it is manifest that the body, under the action of a centripetal
force of just the right quantity, can revolve along with point p in the curved
line that the same point p, in the manner just explained, describes in an
immobile plane. Let the angle VCu be made equal to the angle PCp, and the
line Cu equal to the line CV, and the figure uCp equal to the figure VCP;
then the body, being always at the point p, will move in the perimeter of the
revolving figure uCp, and will describe its arc up in the same time in which
another body P can describe the arc VP, similar and equal to up, in the
figure VPK at rest. Determine, therefore, by prop. 6, corol. 5, the centripetal
force by which a body can revolve in the curved line that point p describes
in an immobile plane, and the problem will be solved. Q.E.F.
and making the angle VCp which is
proportional to the angle VCP; and the area that
the line Cp describes will be to the area VCP
that the line CP simultaneously describes as
the velocity of the describing line Cp to the
velocity of the describing line CP, that is, as
the angle VCp to the angle VCP and thus
in a given ratio and therefore proportional
to the time. Since the area that line Cp
describes in the immobile plane is proportional
to the time, it is manifest that the body, under the action of a centripetal
force of just the right quantity, can revolve along with point p in the curved
line that the same point p, in the manner just explained, describes in an
immobile plane. Let the angle VCu be made equal to the angle PCp, and the
line Cu equal to the line CV, and the figure uCp equal to the figure VCP;
then the body, being always at the point p, will move in the perimeter of the
revolving figure uCp, and will describe its arc up in the same time in which
another body P can describe the arc VP, similar and equal to up, in the
figure VPK at rest. Determine, therefore, by prop. 6, corol. 5, the centripetal
force by which a body can revolve in the curved line that point p describes
in an immobile plane, and the problem will be solved. Q.E.F.
Proposition 44, Theorem 14
The difference between the forces under the action of which two bodies are able
to move equally—one in an orbit that is at rest and the other in an identical orbit
that is revolving—is inversely as the cube of their common height.
Let the parts up and pk of the revolving orbit be similar and equal to the parts VP and PK of the orbit at rest; and let it be understood that the distance between points P and K is minimally small. From point k drop the perpendicular kr to the straight line pC, and produce kr to m so that mr is to kr as the angle VCp to the angle VCP. Since the heights PC and pC, KC and kC, of the bodies are always equal, it is manifest that the increments and decrements of the lines PC and pC are always equal, and hence, if the motions of each of these bodies, when they are at places P and p, are resolved (by corol. 2 of the laws) into two components, of which one is directed toward the center, or along the line PC or pC, and the second is transverse to the first and has a direction along a line perpendicular to PC or pC, the components of motion toward the center will be equal, and the transverse component of motion of body p will be to the transverse component of motion of body P as the angular motion of line pC to the angular motion of line PC, that is, as the angle VCp to the angle VCP. Therefore, in the same time in which body P by the two components of its motion reaches point K, body p by its equal component of motion toward the center will move equally from p toward C and thus, when that time is completed, will be found somewhere on the line mkr (which is perpendicular to the line pC through point k) and by its transverse motion will reach a distance from the line pC that is to the distance from the line PC (which the other body P reaches) as the transverse motion of body p is to the transverse motion of the other body P. Therefore, since kr is equal to the distance from the line PC which body P reaches, and since mr is to kr as the angle VCp to the angle VCP, that is, as the transverse motion of body p to the transverse motion of body P, it is manifest that body p, at the completion of the time, will be found at the place m.
This will be the case when bodies p and P move equally along lines pC and PC and thus are urged along those lines by equal forces. But now, take the angle pCn to the angle pCk as the angle VCp is to the angle VCP, and let nC be equal to kC, and then body p—at the completion of the time—will actually be found at the place n; and thus body p is urged by a greater force than that by which body P is urged, provided that the angle nCp is greater than the angle kCp, that is, if the orbit upk either moves forward [or in consequential or moves backward [or in antecedentia] with a speed greater than twice that with which the line CP is carried forward [or in consequential and it is urged by a smaller force if the orbit moves backward [or in antecedentia] more slowly. And the difference between the forces is as the intervening distance mn through which the body p ought to be carried by the action of that difference in the given space of time.
Understand that a circle is described, with center C and radius Cn or
Ck, cutting in s and t the lines mr and mn produced; then the rectangle
mn × mt will be equal to the rectangle mk × ms, and thus mn will be equal
to 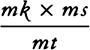 . But since the triangles pCk and pCn are, in a given time, given
in magnitude, kr and mr and their difference mk and sum ms are inversely
as the height pC, and thus the rectangle mk × ms is inversely as the square
of the height pC. Also, mt is directly as ½mt, that is, as the height pC.
These are the first ratios of the nascent lines; and hence
. But since the triangles pCk and pCn are, in a given time, given
in magnitude, kr and mr and their difference mk and sum ms are inversely
as the height pC, and thus the rectangle mk × ms is inversely as the square
of the height pC. Also, mt is directly as ½mt, that is, as the height pC.
These are the first ratios of the nascent lines; and hence 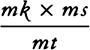 (that is,
the nascent line-element mn and, proportional to it, the difference between
the forces) becomes inversely as the cube of the height pC. Q.E.D.
(that is,
the nascent line-element mn and, proportional to it, the difference between
the forces) becomes inversely as the cube of the height pC. Q.E.D.
COROLLARY 1. Hence the difference of the forces in the places P and
p or K and k is to the force by which a body would be able to revolve
with circular motion from R to K in the same time in which body P in
an immobile orbit describes the arc PK as the nascent line-element mn is to
the versed sine of the nascent arc RK, that is, as 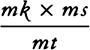 to
to 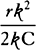 or as
mk × ms to rk2, that is, if the given quantities F and G are taken in the
ratio to each other that the angle VCP has to the angle VCp, as G2 − F2
to F2. And therefore, if with center C and any radius CP or Cp a circular
sector is described equal to the total area VPC which the body P revolving
in an immobile orbit has described in any time by a radius drawn to the
center, the difference between the forces by which body P in an immobile
orbit and body p in a mobile orbit revolve will be to the centripetal force by
which some body, by a radius drawn to the center, would have been able to
describe that sector uniformly in the same time in which the area VPC was
described, as G2 − F2 to F2. For that sector and the area pCk are to each
other as the times in which they are described.
or as
mk × ms to rk2, that is, if the given quantities F and G are taken in the
ratio to each other that the angle VCP has to the angle VCp, as G2 − F2
to F2. And therefore, if with center C and any radius CP or Cp a circular
sector is described equal to the total area VPC which the body P revolving
in an immobile orbit has described in any time by a radius drawn to the
center, the difference between the forces by which body P in an immobile
orbit and body p in a mobile orbit revolve will be to the centripetal force by
which some body, by a radius drawn to the center, would have been able to
describe that sector uniformly in the same time in which the area VPC was
described, as G2 − F2 to F2. For that sector and the area pCk are to each
other as the times in which they are described.
COROLLARY 2. If the orbit VPK is an ellipse having a focus C and an
upper apsis V, and the mobile ellipse upk is supposed similar and equal to
it, so that pC is always equal to PC and the angle VCp is to the angle VCP
in the given ratio of G to F; and if A is written for the height PC or pC,
and 2R is put for the latus rectum of the ellipse; then the force by which
a body can revolve in the mobile ellipse will be as 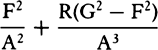 , and
conversely. For let the force by which a body revolves in the unmoving ellipse
be represented by the quantity
, and
conversely. For let the force by which a body revolves in the unmoving ellipse
be represented by the quantity 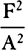 , and then the force at V will be
, and then the force at V will be 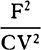 .
But the force by which a body could revolve in a circle at the distance CV
with the velocity that a body revolving in an ellipse has at V is to the force
by which a body revolving in an ellipse is urged at the apsis V as half of the
latus rectum of the ellipse to the semidiameter CV of the circle, and thus
has the value
.
But the force by which a body could revolve in a circle at the distance CV
with the velocity that a body revolving in an ellipse has at V is to the force
by which a body revolving in an ellipse is urged at the apsis V as half of the
latus rectum of the ellipse to the semidiameter CV of the circle, and thus
has the value 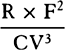 ; and the force that is to this as G2 − F2 to F2 has the
value
; and the force that is to this as G2 − F2 to F2 has the
value 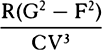 ; and this force (by corol. 1 of this prop.) is the difference
between the forces at V by which body P revolves in the unmoving ellipse
VPK and body p revolves in the mobile ellipse upk. Hence, since (by this
proposition) that difference at any other height A is to itself at the height
CV as
; and this force (by corol. 1 of this prop.) is the difference
between the forces at V by which body P revolves in the unmoving ellipse
VPK and body p revolves in the mobile ellipse upk. Hence, since (by this
proposition) that difference at any other height A is to itself at the height
CV as 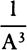 to
to 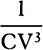 , the same difference at every height A will have the value
, the same difference at every height A will have the value
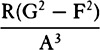 . Therefore, add the excess
. Therefore, add the excess 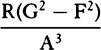 to the force
to the force 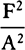 by which
a body can revolve in the immobile ellipse VPK, and the result will be the
total force
by which
a body can revolve in the immobile ellipse VPK, and the result will be the
total force 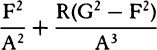 by which a body may be able to revolve in the
same times in the mobile ellipse upk.
by which a body may be able to revolve in the
same times in the mobile ellipse upk.
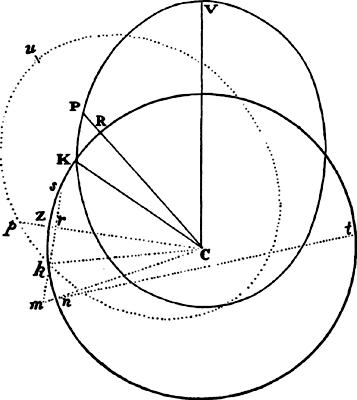
COROLLARY 3. In the same way it will be gathered that if the immobile
orbit VPK is an ellipse having its center at the center C of forces, and a
mobile ellipse upk is supposed similar, equal, and concentric with it; and if
2R is the principal latus rectum of this ellipse, and 2T the principal diameter
or major axis, and the angle VCp is always to the angle VCP as G to F; then
the forces by which bodies can revolve in equal times in the immobile ellipse
and the mobile ellipse will be as 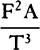 and
and 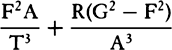 respectively.
respectively.
COROLLARY 4. And universally, if the greatest height CV of a body is
called T; and the radius of the curvature which the orbit VPK has at V (that
is, the radius of a circle of equal curvature) is called R; and the centripetal
force by which a body can revolve in any immobile trajectory VPK at place
V is called 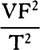 and at other places P is indefinitely styled X, while the
height CP is called A; and if G is taken to F in the given ratio of the angle
VCp to the angle VCP; then the centripetal force by which the same body
can complete the same motions in the same times in the same trajectory upk
which is moving circularly will be as the sum of the forces
and at other places P is indefinitely styled X, while the
height CP is called A; and if G is taken to F in the given ratio of the angle
VCp to the angle VCP; then the centripetal force by which the same body
can complete the same motions in the same times in the same trajectory upk
which is moving circularly will be as the sum of the forces 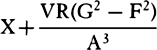 .
.
COROLLARY 5. Therefore, given the motion of a body in any immobile orbit, its angular motion about the center of forces can be increased or diminished in a given ratio, and hence new immobile orbits can be found in which bodies may revolve by new centripetal forces.
COROLLARY 6. Therefore, if on the straight line CV, given in position,
there is erected the perpendicular VP of indeterminate length, and CP is
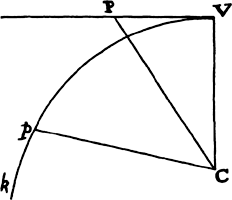 joined, and Cp is drawn equal to it making the
angle VCp that is to the angle VCP in a given
ratio; then the force by which a body can revolve
in the curve Vpk which the point p
continually traces out will be inversely as the cube
of the height Cp. For body P, by its own force
of inertia, and with no other force urging it, can
move forward uniformly in the straight line VP.
Add the force toward the center C, inversely proportional to the cube of the
height CP or Cp, and (by what has just been demonstrated) the rectilinear
motion will be bent into the curved line Vpk. But this curve Vpk is the same
as the curve VPQ found in prop. 41, corol. 3, and (as we said there) bodies
attracted by forces of this kind ascend obliquely in this curve.
joined, and Cp is drawn equal to it making the
angle VCp that is to the angle VCP in a given
ratio; then the force by which a body can revolve
in the curve Vpk which the point p
continually traces out will be inversely as the cube
of the height Cp. For body P, by its own force
of inertia, and with no other force urging it, can
move forward uniformly in the straight line VP.
Add the force toward the center C, inversely proportional to the cube of the
height CP or Cp, and (by what has just been demonstrated) the rectilinear
motion will be bent into the curved line Vpk. But this curve Vpk is the same
as the curve VPQ found in prop. 41, corol. 3, and (as we said there) bodies
attracted by forces of this kind ascend obliquely in this curve.
Proposition 45, Problem 31
It is required to find the motions of
the apsides of orbits that differ very little from
circles.
This problem is solved arithmetically by taking the orbit that is described
in an immobile plane by a body revolving in a mobile ellipse (as in prop. 44,
corol. 2 or 3) and making it approach the form of the orbit whose apsides are
required, and by seeking the apsides of the orbit which that body describes
in an immobile plane. Orbits will acquire the same shape if the centripetal
forces with which those orbits are described, when compared with each other,
are made proportional at equal heights. Let point V be the upper apsis, and
write T for the greatest height CV, A for any other height CP or Cp, and
X for the difference CV — CP of the heights; then the force by which a body
moves in an ellipse revolving about its own focus C (as in corol. 2)—and
which in corol. 2 was as 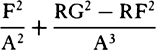 ,
that is, as
,
that is, as 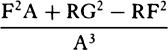 will, when T − X is substituted for A, be as
will, when T − X is substituted for A, be as 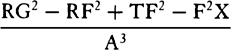 .
Any other centripetal force is similarly to be reduced to a fraction whose
denominator is A3; and the numerators are to be made analogous [i.e., made
proportional in the same degree] by bringing together homologous terms [i.e.,
corresponding terms, or terms of the same degree]. All of this will be clarified
by the following examples.
.
Any other centripetal force is similarly to be reduced to a fraction whose
denominator is A3; and the numerators are to be made analogous [i.e., made
proportional in the same degree] by bringing together homologous terms [i.e.,
corresponding terms, or terms of the same degree]. All of this will be clarified
by the following examples.
EXAMPLE 1. Let us suppose the centripetal force to be uniform and thus
as 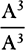 , or (writing T − X for A in the numerator) as
, or (writing T − X for A in the numerator) as
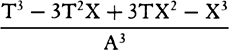 ;
and by bringing together the corresponding [or homologous] terms of the
numerators (namely, given ones with given ones, and ones not given with
ones not given), RG2 − RF2 + TF2 to T3 will come to be as -F2X to
−3T2X + 3TX2 − X3 or as −F2 to −3T2 + 3TX − X2. Now, since the orbit
is supposed to differ very little from a circle, let the orbit come to coincide
with a circle; and because R and T become equal and X is diminished
indefinitely, the ultimate ratios will be RG2 to T3 as −F2 to −3T2, or G2 to
T2 as F2 to 3T2, and by alternation [or alternando] G2 to F2 as T2 to 3T2,
that is, as 1 to 3; and therefore G is to F, that is, the angle VCp is to the
angle VCP, as 1 to √3. Therefore, since a body in an immobile ellipse, in
descending from the upper apsis to the lower apsis, completes the angle VCP
(so to speak) of 180 degrees, another body in the mobile ellipse (and hence
in the immobile orbit with which we are dealing) will, in descending from
the upper apsis to the lower apsis, complete the angle VCp of
;
and by bringing together the corresponding [or homologous] terms of the
numerators (namely, given ones with given ones, and ones not given with
ones not given), RG2 − RF2 + TF2 to T3 will come to be as -F2X to
−3T2X + 3TX2 − X3 or as −F2 to −3T2 + 3TX − X2. Now, since the orbit
is supposed to differ very little from a circle, let the orbit come to coincide
with a circle; and because R and T become equal and X is diminished
indefinitely, the ultimate ratios will be RG2 to T3 as −F2 to −3T2, or G2 to
T2 as F2 to 3T2, and by alternation [or alternando] G2 to F2 as T2 to 3T2,
that is, as 1 to 3; and therefore G is to F, that is, the angle VCp is to the
angle VCP, as 1 to √3. Therefore, since a body in an immobile ellipse, in
descending from the upper apsis to the lower apsis, completes the angle VCP
(so to speak) of 180 degrees, another body in the mobile ellipse (and hence
in the immobile orbit with which we are dealing) will, in descending from
the upper apsis to the lower apsis, complete the angle VCp of  degrees;
this is so because of the similarity of this orbit, which the body describes
under the action of a uniform centripetal force, to the orbit which a body
completing its revolutions in a revolving ellipse describes in a plane at rest.
By the above collation of terms, these orbits are made similar, not universally
but at the time when they very nearly approach a circular form. Therefore
a body revolving with uniform centripetal force in a very nearly circular
orbit will always complete an angle of
degrees;
this is so because of the similarity of this orbit, which the body describes
under the action of a uniform centripetal force, to the orbit which a body
completing its revolutions in a revolving ellipse describes in a plane at rest.
By the above collation of terms, these orbits are made similar, not universally
but at the time when they very nearly approach a circular form. Therefore
a body revolving with uniform centripetal force in a very nearly circular
orbit will always complete an angle of  degrees between the upper apsis
and the lower apsis, or 103°55′23″ at the center, arriving at the lower apsis
from the upper apsis when it has completed this angle once, and returning
from the lower to the upper apsis when it has completed the same angle
again, and so on without end.
degrees between the upper apsis
and the lower apsis, or 103°55′23″ at the center, arriving at the lower apsis
from the upper apsis when it has completed this angle once, and returning
from the lower to the upper apsis when it has completed the same angle
again, and so on without end.
EXAMPLE 2. Let us suppose the centripetal force to be as the height A
raised to any power, as An−3 (that is, 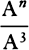 ), where n − 3 and n signify any
indices of powers whatsoever—integral or fractional, rational or irrational,
positive or negative. On reducing the numerator An = (T − X)n to an
indeterminate series by our method of converging series, the result is Tn −
nXTn−1 +
), where n − 3 and n signify any
indices of powers whatsoever—integral or fractional, rational or irrational,
positive or negative. On reducing the numerator An = (T − X)n to an
indeterminate series by our method of converging series, the result is Tn −
nXTn−1 + 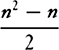 X2Tn−2 · · · . And by collating the terms of this with the
terms of the other numerator RG2 − RF2 + TF2 − F2X, the result is that
RG2 − RF2 + TF2 is to Tn as −F2 to −nTn−1 +
X2Tn−2 · · · . And by collating the terms of this with the
terms of the other numerator RG2 − RF2 + TF2 − F2X, the result is that
RG2 − RF2 + TF2 is to Tn as −F2 to −nTn−1 + 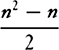 XTn−2 · · ·. And after
taking the ultimate ratios that result when the orbits approach circular form,
RG2 will be to Tn as −F2 to
−nTn−1, or G2 to Tn−1 as
F2 to nTn−1, and
by alternation [or alternando] G2 is to F2 as Tn−1 to nTn−1, that is, as 1 to
n; and therefore G is to F, that is, the angle VCp is to the angle VCP as 1
to √n. Therefore, since the angle VCP, completed in the descent of a body
from the upper apsis to the lower apsis in an ellipse, is 180 degrees, the angle
VCp, completed in the descent of a body from the upper apsis to the lower
apsis in the very nearly circular orbit which any body describes under the
action of a centripetal force proportional to An−3, will be equal to an angle
of
XTn−2 · · ·. And after
taking the ultimate ratios that result when the orbits approach circular form,
RG2 will be to Tn as −F2 to
−nTn−1, or G2 to Tn−1 as
F2 to nTn−1, and
by alternation [or alternando] G2 is to F2 as Tn−1 to nTn−1, that is, as 1 to
n; and therefore G is to F, that is, the angle VCp is to the angle VCP as 1
to √n. Therefore, since the angle VCP, completed in the descent of a body
from the upper apsis to the lower apsis in an ellipse, is 180 degrees, the angle
VCp, completed in the descent of a body from the upper apsis to the lower
apsis in the very nearly circular orbit which any body describes under the
action of a centripetal force proportional to An−3, will be equal to an angle
of 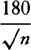 degrees; and when this angle is repeated, the body will return from
the lower apsis to the upper apsis, and so on without end.
degrees; and when this angle is repeated, the body will return from
the lower apsis to the upper apsis, and so on without end.
For example, if the centripetal force is as the distance of the body from
the center, that is, as A or 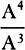 , n will be equal to 4 and √n will be equal
to 2; and therefore the angle between the upper apsis and the lower apsis
will be equal to
, n will be equal to 4 and √n will be equal
to 2; and therefore the angle between the upper apsis and the lower apsis
will be equal to  or 90°. Therefore, at the completion of a quarter of a
revolution the body will arrive at the lower apsis, and at the completion of
another quarter the body will arrive at the upper apsis, and so on by turns
without end. This is also manifest from prop. 10. For a body urged by this
centripetal force will revolve in an immobile ellipse whose center is in the
center of forces. But if the centripetal force is inversely as the distance, that
is, directly as
or 90°. Therefore, at the completion of a quarter of a
revolution the body will arrive at the lower apsis, and at the completion of
another quarter the body will arrive at the upper apsis, and so on by turns
without end. This is also manifest from prop. 10. For a body urged by this
centripetal force will revolve in an immobile ellipse whose center is in the
center of forces. But if the centripetal force is inversely as the distance, that
is, directly as 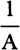 or
or 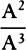 , n will be equal to 2, and thus the angle between the
upper and the lower apsis will be
, n will be equal to 2, and thus the angle between the
upper and the lower apsis will be 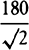 degrees, or 127°16′45″, and therefore
a body revolving under the action of such a force will—by the continual
repetition of this angle—go alternately from the upper apsis to the lower
and from the lower to the upper forever. Further, if the centripetal force
is inversely as the fourth root of the eleventh power of the height, that is,
inversely as A11/4 and thus directly as
degrees, or 127°16′45″, and therefore
a body revolving under the action of such a force will—by the continual
repetition of this angle—go alternately from the upper apsis to the lower
and from the lower to the upper forever. Further, if the centripetal force
is inversely as the fourth root of the eleventh power of the height, that is,
inversely as A11/4 and thus directly as 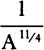 or as
or as 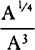 , n will be equal to
¼, and
, n will be equal to
¼, and 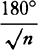 will be equal to 360°; and therefore a body, setting out from
the upper apsis and continually descending from then on, will arrive at the
lower apsis when it has completed an entire revolution, and then, completing
another entire revolution by continually ascending, will return to the upper
apsis; and so on by turns forever.
will be equal to 360°; and therefore a body, setting out from
the upper apsis and continually descending from then on, will arrive at the
lower apsis when it has completed an entire revolution, and then, completing
another entire revolution by continually ascending, will return to the upper
apsis; and so on by turns forever.
EXAMPLE 3. Let m and n be any indices of powers of the height, and
let b and c be any given numbers, and let us suppose that the centripetal
force is as 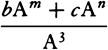 , that is, as
, that is, as 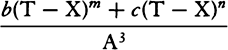 or (again by our
method of converging series) as
or (again by our
method of converging series) as
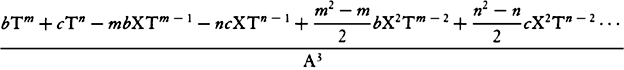 then, if the terms of the numerators are collated, the result will be RG2 −
RF2 + TF2 to bTm + cTn as −F2 to
−mbTm−1 − ncTn−1 +
then, if the terms of the numerators are collated, the result will be RG2 −
RF2 + TF2 to bTm + cTn as −F2 to
−mbTm−1 − ncTn−1 + 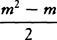 bXTm−2 +
bXTm−2 +
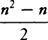 cXTn−2 · · · . And after taking the ultimate ratios that result when
the orbits approach circular form, G2 will be to bTm−1 + cTn−1 as F2 to
mbTm−1 + ncTn−1, and by alternation [or alternando] G2 will be to F2 as
bTm−1 + cTn−1 to mbTn−1 + ncTn−1. This proportion, if the greatest height
CV or T is expressed arithmetically by unity, becomes G2 to F2 as b + c to
mb + nc and thus as 1 to
cXTn−2 · · · . And after taking the ultimate ratios that result when
the orbits approach circular form, G2 will be to bTm−1 + cTn−1 as F2 to
mbTm−1 + ncTn−1, and by alternation [or alternando] G2 will be to F2 as
bTm−1 + cTn−1 to mbTn−1 + ncTn−1. This proportion, if the greatest height
CV or T is expressed arithmetically by unity, becomes G2 to F2 as b + c to
mb + nc and thus as 1 to 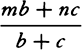 . Hence G is to F, that is, the angle VCp
is to the angle VCP, as 1 to
. Hence G is to F, that is, the angle VCp
is to the angle VCP, as 1 to 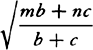 . And therefore, since the angle VCP
between the upper apsis and the lower apsis in the immobile ellipse is 180
degrees, the angle VCp between the same apsides, in the orbit described by
a body under the action of a centripetal force proportional to the quantity
. And therefore, since the angle VCP
between the upper apsis and the lower apsis in the immobile ellipse is 180
degrees, the angle VCp between the same apsides, in the orbit described by
a body under the action of a centripetal force proportional to the quantity
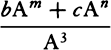 , will be equal to an angle of
, will be equal to an angle of 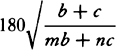 degrees. And by the
same argument, if the centripetal force is as
degrees. And by the
same argument, if the centripetal force is as 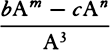 , the angle between
the apsides will be found to be
, the angle between
the apsides will be found to be 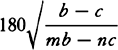 degrees. And the problem
will be resolved in just the same way in more difficult cases. The quantity
to which the centripetal force is proportional must always be resolved into
converging series having the denominator A3. Then the ratio of the given
part of the numerator (resulting from that operation) to its other part, which
is not given, is to be made the same as the ratio of the given part of this
numerator RG2 − RF2 + TF2 − F2X to its other part, which is not given;
and when the superfluous quantities are taken away and unity is written for
T, the proportion of G to F will be obtained.
degrees. And the problem
will be resolved in just the same way in more difficult cases. The quantity
to which the centripetal force is proportional must always be resolved into
converging series having the denominator A3. Then the ratio of the given
part of the numerator (resulting from that operation) to its other part, which
is not given, is to be made the same as the ratio of the given part of this
numerator RG2 − RF2 + TF2 − F2X to its other part, which is not given;
and when the superfluous quantities are taken away and unity is written for
T, the proportion of G to F will be obtained.
COROLLARY 1. Hence, if the centripetal force is as some power of the
height, that power can be found from the motion of the apsides, and conversely.
That is, if the total angular motion with which the body returns to
the same apsis is to the angular motion of one revolution, or 360 degrees, as
some number m to another number n, and the height is called A, the force
will be as the power of the height 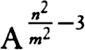 whose index is
whose index is 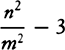 . This is
manifest by the instances in ex. 2. Hence it is clear that the force, in receding
from the center, cannot decrease in a ratio greater than that of the cube of
the height; if a body revolving under the action of such a force and setting
out from an apsis begins to descend, it will never reach the lower apsis or
minimum height but will descend all the way to the center, describing that
curved line which we treated in prop. 41, corol. 3. But if the body, on setting
out from an apsis, begins to ascend even the least bit, it will ascend
indefinitely and will never reach the upper apsis. For it will describe the curved
line treated in the above-mentioned corol. 3 and in prop. 44, corol. 6. So also,
when the force, in receding from the center, decreases in a ratio greater than
that of the cube of the height, a body setting out from an apsis (depending
on whether it begins to descend or to ascend) either will descend all the way
to the center or will ascend indefinitely. But if the force, in receding from
the center, either decreases in a ratio less than that of the cube of the height
or increases in any ratio of the height whatever, the body will never descend
all the way to the center, but will at some time reach a lower apsis; and
conversely, if a body descending and ascending alternately from apsis to apsis
never gets to the center, either the force in receding from the center will be
increased or it will decrease in a ratio less than that of the cube of the height;
and the more swiftly the body returns from apsis to apsis, the farther the
ratio of the forces will recede from that of the cube.
. This is
manifest by the instances in ex. 2. Hence it is clear that the force, in receding
from the center, cannot decrease in a ratio greater than that of the cube of
the height; if a body revolving under the action of such a force and setting
out from an apsis begins to descend, it will never reach the lower apsis or
minimum height but will descend all the way to the center, describing that
curved line which we treated in prop. 41, corol. 3. But if the body, on setting
out from an apsis, begins to ascend even the least bit, it will ascend
indefinitely and will never reach the upper apsis. For it will describe the curved
line treated in the above-mentioned corol. 3 and in prop. 44, corol. 6. So also,
when the force, in receding from the center, decreases in a ratio greater than
that of the cube of the height, a body setting out from an apsis (depending
on whether it begins to descend or to ascend) either will descend all the way
to the center or will ascend indefinitely. But if the force, in receding from
the center, either decreases in a ratio less than that of the cube of the height
or increases in any ratio of the height whatever, the body will never descend
all the way to the center, but will at some time reach a lower apsis; and
conversely, if a body descending and ascending alternately from apsis to apsis
never gets to the center, either the force in receding from the center will be
increased or it will decrease in a ratio less than that of the cube of the height;
and the more swiftly the body returns from apsis to apsis, the farther the
ratio of the forces will recede from that of the cube.
For example, if by alternate descent and ascent a body returns from
upper apsis to upper apsis in 8 or 4 or 2 or 1½ revolutions, that is, if m is to
n as 8 or 4 or 2 or 1½ to 1, and therefore
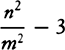 has the value 1/64 − 3 or
1/16 − 3 or ¼ − 3 or 4/9 − 3, the force will be as A1/64−3 or
A1/16−3 or A¼−3 or
A4/9−3, that is, inversely as A3−1/64 or
A3−1/16 or A3−¼ or
A3−4/9. If the body
returns in each revolution to the same unmoving apsis, m will be to n as 1
to 1, and thus
has the value 1/64 − 3 or
1/16 − 3 or ¼ − 3 or 4/9 − 3, the force will be as A1/64−3 or
A1/16−3 or A¼−3 or
A4/9−3, that is, inversely as A3−1/64 or
A3−1/16 or A3−¼ or
A3−4/9. If the body
returns in each revolution to the same unmoving apsis, m will be to n as 1
to 1, and thus 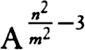 will be equal to A−2 or
will be equal to A−2 or 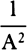 ; and therefore the decrease
in force will be as the square of the height, as has been demonstrated in
the preceding propositions. If the body returns to the same apsis in
three-quarters or two-thirds or one-third or one-quarter of a single revolution, m
will be to n as ¾ or ⅔ or ⅓ or ¼ to 1, and so
; and therefore the decrease
in force will be as the square of the height, as has been demonstrated in
the preceding propositions. If the body returns to the same apsis in
three-quarters or two-thirds or one-third or one-quarter of a single revolution, m
will be to n as ¾ or ⅔ or ⅓ or ¼ to 1, and so 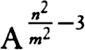 will be equal to
A16/9−3 or A9/4−3
or A9−3 or A16−3; and therefore the force will be either
inversely as A11/9 or A¾, or directly as A6 or A13. Finally, if the body in
proceeding from upper apsis to upper apsis completes an entire revolution
and an additional three degrees (and therefore, during each revolution of
the body, that apsis moves three degrees forward [or in consequential]), m
will be to n as 363° to 360° or as 121 to 120, and thus
will be equal to
A16/9−3 or A9/4−3
or A9−3 or A16−3; and therefore the force will be either
inversely as A11/9 or A¾, or directly as A6 or A13. Finally, if the body in
proceeding from upper apsis to upper apsis completes an entire revolution
and an additional three degrees (and therefore, during each revolution of
the body, that apsis moves three degrees forward [or in consequential]), m
will be to n as 363° to 360° or as 121 to 120, and thus 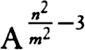 will be equal
to
will be equal
to 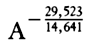 , and therefore the centripetal force will be inversely as
, and therefore the centripetal force will be inversely as 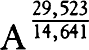 or
inversely as
or
inversely as 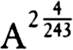 approximately. Therefore the centripetal force decreases in
a ratio a little greater than that of the square, but 59¾ times closer to that
of the square than to that of the cube.
approximately. Therefore the centripetal force decreases in
a ratio a little greater than that of the square, but 59¾ times closer to that
of the square than to that of the cube.
COROLLARY 2. Hence also if a body, under the action of a centripetal
force that is inversely as the square of the height, revolves in an ellipse
having a focus in the center of forces, and any other extraneous force is
added to or taken away from this centripetal force, the motion of the apsides
that will arise from that extraneous force can be found out (by instances in
ex. 3), and conversely. For example, if the force under the action of which
the body revolves in the ellipse is as 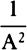 and the extraneous force which has
been taken away is as cA, and hence the remaining force is as
and the extraneous force which has
been taken away is as cA, and hence the remaining force is as 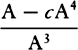 , then
(as in ex. 3) b will be equal to 1, m will be equal to 1, and n will be equal
to 4, and therefore the angle of the revolution between apsides will be equal
to an angle of
, then
(as in ex. 3) b will be equal to 1, m will be equal to 1, and n will be equal
to 4, and therefore the angle of the revolution between apsides will be equal
to an angle of 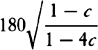 degrees. Let us suppose the extraneous force to
be 357.45 times less than the other force under the action of which the body
revolves in the ellipse, that is, let us suppose c to be
degrees. Let us suppose the extraneous force to
be 357.45 times less than the other force under the action of which the body
revolves in the ellipse, that is, let us suppose c to be 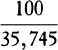 , A or T being
equal to 1, and then
, A or T being
equal to 1, and then 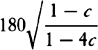 will come to be
will come to be 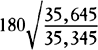 , or 180.7623,
that is, 180°45′44″. Therefore a body, setting out from the upper apsis, will
reach the lower apsis by an angular motion of 180°45′44″ and will return to
upper apsis if this angular motion is doubled; and thus in each revolution
the upper apsis will move forward through 1°31′28″. aThe [advance of the]
the apsis of the moon is about twice as swift.a
, or 180.7623,
that is, 180°45′44″. Therefore a body, setting out from the upper apsis, will
reach the lower apsis by an angular motion of 180°45′44″ and will return to
upper apsis if this angular motion is doubled; and thus in each revolution
the upper apsis will move forward through 1°31′28″. aThe [advance of the]
the apsis of the moon is about twice as swift.a
So much concerning the motion of bodies in orbits whose planes pass through the center of forces. It remains for us to determine additionally those motions which occur in planes that do not pass through the center of forces. For writers who deal with the motion of heavy bodies are wont to consider the oblique ascents and descents of weights in any given planes as well as perpendicular ascents and descents, and there is equal justification for considering here the motion of bodies that tend to centers under the action of any forces whatever and are supported by eccentric planes. We suppose, however, that these planes are highly polished and absolutely slippery, so as not to retard the bodies. Further, in these demonstrations, in place of the planes on which bodies rest and which they touch by resting on them, we even make use of planes parallel to them, in which the centers of the bodies move and by so moving describe orbits. And by the same principle we then determine the motions of bodies performed in curved surfaces.
The motion of bodies on given surfaces and the oscillating motion of asimple pendulumsa
Proposition 46, Problem 32
Suppose a centripetal force of any kind, and let there be given both the center
of force and any plane in which a body revolves, and grant the quadratures of
curvilinear figures; it is required to find the motion of a body setting out from a
given place with a given velocity along a given straight line in that plane.
Let S be the center of force, SC the least distance of this center from the given plane, P a body setting out from place P along the straight line PZ, Q the same body revolving in its trajectory, and PQR the required trajectory described in the given plane. Join CQ and also QS, and if SV is taken in QS and is proportional to the centripetal force by which the body is drawn toward the center S, and VT is drawn parallel to CQ and meeting SC in T, then the force SV will be resolved (by corol. 2 of the laws) into the forces ST and TV, of which ST, by drawing the body along a line perpendicular to the plane, does not at all change the body’s motion in this plane. But the other force TV, by acting along the position of the plane, draws the body directly toward [i.e., along a line directed toward] the given point C in the plane and thus causes the body to move in this plane just as if the force ST were removed and as if the body revolved in free space about the center C under the action of the force TV alone. But, given the centripetal force TV under the action of which the body Q revolves in free space about the given center C, there are also given (by prop. 42) not only the trajectory PQR described by the body, but also the place Q in which the body will be at any given time, and finally the velocity of the body in that place Q; and conversely. Q.E.I.
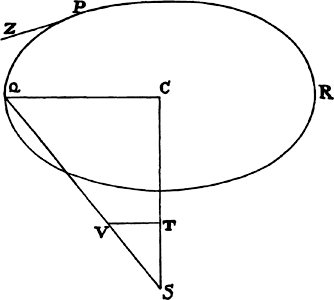
Proposition 47, Theorem 15
Suppose that a centripetal force is proportional to the distance of a body from a
center; then all bodies revolving in any planes whatever will describe ellipses and
will make their revolutions in equal times; and bodies that move in straight lines,
by oscillating to and fro, will complete in equal times their respective periods of
going and returning.
For, under the same conditions as in prop. 46, the force SV, by which the body Q revolving in any plane PQR is drawn toward the center S, is as the distance SQ; and thus—because SV and SQ, TV and CQ are proportional—the force TV, by which the body is drawn toward the given point C in the plane of the orbit, is as the distance CQ. Therefore, the forces by which bodies that are in the plane PQR are drawn toward point C are, in proportion to the distances, equal to the forces by which bodies are drawn from all directions toward the center S; and thus in the same times the bodies will move in the same figures in any plane PQR about the point C as they would move in free spaces about the center S; and hence (by prop. 10, corol. 2, and prop. 38, corol. 2) in times which are always equal, they will either describe ellipses [i.e., complete a whole revolution in such ellipses] in that plane about the center C or will complete periods of oscillating to and fro in straight lines drawn through the center C in that plane. Q.E.D.
Scholium
The ascents and descents of bodies in curved surfaces are very closely related
to the motions just discussed. Imagine that curved lines are described in a
plane, that they then revolve around any given axes passing through the
center of force and describe curved surfaces by this revolution, and then that
bodies move in such a way that their centers are always found in these
surfaces. If those bodies, in ascending and descending obliquely, oscillate to and
fro, their motions will be made in planes passing through the axis and hence
in curved lines by whose revolution those curved surfaces were generated. In
these cases, therefore, it is sufficient to consider the motion in those curved
lines.
Proposition 48, Theorem 16
If a wheel stands upon the outer surface of a globe at right angles to that surface
and, rolling as wheels do, moves forward in a great circle [in the globe’s surface],
the length of the curvilinear path traced out by any given point in the perimeter
[or rim] of the wheel from the time when that point touched the globe (a curve
which may be called a cycloid or epicycloid) will be to twice the versed sine of
half the arc [of the rim of the wheel] which during the time of rolling has been
in contact with the globe’s surface as the sum of the diameters of the globe and
wheel is to the semidiameter of the globe.
Proposition 49, Theorem 17
If a wheel stands upon the inner surface of a hollow globe at right angles to
that surface and, rolling as wheels do, moves forward in a great circle [in the
globes surface], the length of the curvilinear path traced out by any given point
in the perimeter [or rim] of the wheel from the time when that point touched the
globe will be to twice the versed sine of half the arc [of the rim of the wheel]
which during the time of rolling has been in contact with the globe’s surface as
the difference of the diameters of the globe and wheel is to the semidiameter of
the globe.
Let ABL be the globe, C its center, BPV the wheel standing upon it, E the center of the wheel, B the point of contact, and P the given point in the perimeter of the wheel. Imagine that this wheel proceeds in the great circle ABL from A through B toward L and, while rolling, rotates in such a way that the arcs AB and PB are always equal to each other and that the given point P in the perimeter of the wheel is meanwhile describing the curvilinear path AP. Now, let AP be the whole curvilinear path described since the wheel was in contact with the globe at A, and the length AP of this path will be to twice the versed sine of the arc ½PB as 2CE to CB. For let the straight line CE (produced if need be) meet the wheel in V, and join CP, BP, EP, VP, and drop the normal VF to CP produced. Let PH and VH, meeting in H, touch the circle in P and V, and let PH cut VF in G, and drop the normals GI and HK to VP. With the same center C and with any radius whatever describe the circle nom cutting the straight line CP in n, the wheel’s perimeter BP in o, and the curvilinear path AP in m; and with center V and radius Vo describe a circle cutting VP produced in q.
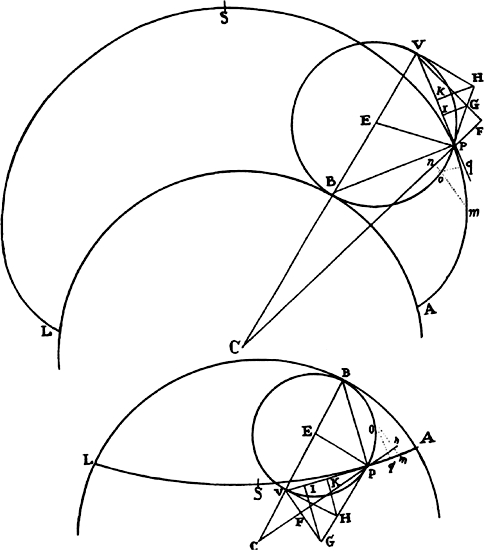
Since the wheel, in rolling, always revolves about the point of contact B, it is manifest that the straight line BP is perpendicular to the curved line AP described by the wheel’s point P, and therefore that the straight line VP will touch this curve in point P. Let the radius of the circle nom be gradually increased or decreased, and so at last become equal to the distance CP; then, because the evanescent figure Pnomq and the figure PFGVI are similar, the ultimate ratio of the evanescent line-elements Pm, Pn, Po, and Pq, that is, the ratio of the instantaneous changes of the curve AP, the straight line CP, the circular arc BP, and the straight line VP, will be the same as that of the lines PV, PF, PG, and PI respectively. But since VF is perpendicular to CF, and VH is perpendicular to CV, and the angles HVG and VCF are therefore equal, and the angle VHG is equal to the angle CEP (because the angles of the quadrilateral HVEP are right angles at V and P), the triangles VHG and CEP will be similar; and hence it will come about that EP is to CE as HG to HV or HP and as KI to KP, and by composition [or componendo] or by separation [or dividendo] CB is to CE as PI to PK, and—by doubling of the consequents—CB is to 2CE as PI to PV and as Pq to Pm. Therefore the decrement of the line VP, that is, the increment of the line BV − VP, is to the increment of the curved line AP in the given ratio of CB to 2CE, and therefore (by lem. 4, corol.) the lengths BV − VP and AP, generated by those increments, are in the same ratio. But since BV is the radius, VP is the cosine of the angle BVP or ½BEP, and therefore BV − VP is the versed sine of the same angle; and therefore in this wheel, whose radius is ½BV, BV − VP will be twice the versed sine of the arc ½BP. And thus AP is to twice the versed sine of the arc ½BP as 2CE to CB. Q.E.D.
For the sake of distinction, we shall call the curved line AP in prop. 48 a cycloid outside the globe, and the curved line AP in prop. 49 a cycloid inside the globe.
COROLLARY 1. Hence, if an entire cycloid ASL is described and is bisected in S, the length of the part PS will be to the length VP (which is twice the sine of the angle VBP, where EB is the radius) as 2CE to CB, and thus in a given ratio.
COROLLARY 2. And the length of the semiperimeter AS of the cycloid will be equal to a straight line that is to the diameter BV of the wheel as 2CE to CB.
Proposition 50, Problem 33
To make a pendulum bob oscillate in a given cycloid.
Within a globe QVS described with center C, let the cycloid QRS be given, bisected in R and with its end-points Q and S meeting the surface of the globe on the two sides. Draw CR bisecting the arc QS in O, and produce CR to A, so that CA is to CO as CO to CR. Describe an outer globe DAF with center C and radius CA; and inside this globe let two half-cycloids AQ and AS be described by means of a wheel whose diameter is AO, and let these two half-cycloids touch the inner globe at Q and S and meet the outer globe in A. Let a body T hang from the point A by a thread APT equal to the length AR, and let this body T oscillate between the two half-cycloids AQ and AS in such a way that each time the pendulum departs from the perpendicular AR, the upper part AP of the thread comes into contact with that half-cycloid APS toward which the motion is directed, and is bent around it as an obstacle, while the other part PT of the thread, to which the half-cycloid is not yet exposed, stretches out in a straight line; then the weight T will oscillate in the given cycloid QRS. Q.E.F.
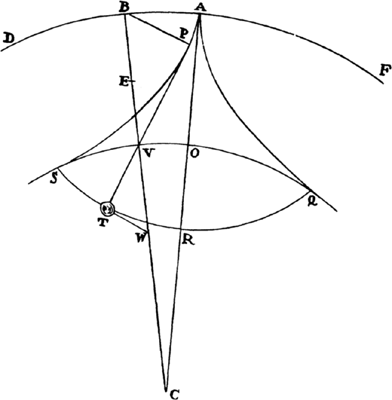
For let the thread PT meet the cycloid QRS in T and the circle QOS in V, and draw CV; and from the end-points P and T of the straight part PT of the thread, erect BP and TW perpendicular to PT, meeting the straight line CV in B and W. It is evident, from the construction and the generation of the similar figures AS and SR, that the perpendiculars PB and TW cut off from CV the lengths VB and VW equal respectively to OA and OR, the diameters of the wheels. Therefore, TP is to VP (which is twice the sine of the angle VBP, where ½BV is the radius) as BW to BV, or AO + OR to AO, that is (since CA is proportional to CO, CO to CR, and by separation [or dividendo] AO to OR), as CA + CO to CA, or, if BV is bisected in E, as 2CE to CB. Accordingly (by prop. 49, corol. 1), the length of the straight part PT of the thread is always equal to the arc PS of the cycloid, and the whole thread APT is always equal to the half-arc APS of the cycloid, that is (by prop. 49, corol. 2), to the length AR. And therefore, conversely, if the thread always remains equal to the length AR, point T will move in the given cycloid QRS. Q.E.D.
COROLLARY. The thread AR is equal to the half-cycloid AS and thus has the same ratio to the semidiameter AC of the outer globe that the half-cycloid SR, similar to it, has to the semidiameter CO of the inner globe.
Proposition 51, Theorem 18
If a centripetal force tending from all directions to the center C of a globe is in
each individual place as the distance of that place from the center; and if, under
the action of this force alone, the body T oscillates (in the way just described)
in the perimeter of the cycloid QRS; then I say that the times of the oscillations,
however unequal the oscillations may be, will themselves be equal.
For let the perpendicular CX fall to the indefinitely produced tangent
TW of the cycloid and join CT. Now the centripetal force by which the
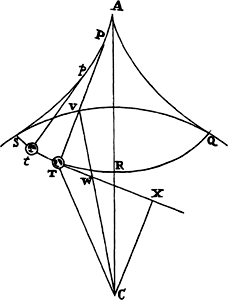 body T is impelled toward C is as
the distance CT, and CT may be
resolved (by corol. 2 of the laws)
into the components CX and TX,
of which CX (by impelling the
body directly from P) stretches the
thread PT and is wholly nullified
by the resistance of the thread and
produces no other effect, while the
other component TX (by urging
the body transversely or toward X)
directly accelerates the motion of
the body in the cycloid; hence it
is manifest that the body’s
acceleration, which is proportional to
this accelerative force, is at each
individual moment as the length TX, that is (because CV and WV—and
TX and TW, proportional to them—are given), as the length TW, that is
(by prop. 49, corol. 1), as the length of the arc of the cycloid TR. Therefore,
if the two pendulums APT and Apt are drawn back unequally from the
perpendicular [or vertical] AR and are let go simultaneously, their
accelerations will always be as the respective arcs to be described TR and tR. But
the parts of these arcs described at the beginning of the motion are as the
accelerations, that is, as the whole arcs to be described at the beginning,
and therefore the parts that remain to be described and the subsequent
accelerations proportional to these parts are also as the whole arcs, and so on.
Therefore the accelerations—and hence the velocities generated, the parts of
the arcs described with these velocities, and the parts to be so described—are
always as the whole arcs; and therefore the parts to be described, preserving
a given ratio to one another, will vanish simultaneously, that is, the two
oscillating bodies will arrive at the same time at the perpendicular [or
vertical] AR. And since, conversely, the ascents of the pendulums, made
from the lowest place R through the same cycloidal arcs with a reverse
motion, are retarded in individual places by the same forces by which their
descents were accelerated, it is evident that the velocities of the ascents and
descents made through the same arcs are equal and hence occur in equal
times; and therefore, since the two parts RS and RQ of the cycloid, each
lying on a different side of the perpendicular [or vertical], are similar and
equal, the two pendulums will always make their whole oscillations as well
as their half-oscillations in the same times. Q.E.D.
body T is impelled toward C is as
the distance CT, and CT may be
resolved (by corol. 2 of the laws)
into the components CX and TX,
of which CX (by impelling the
body directly from P) stretches the
thread PT and is wholly nullified
by the resistance of the thread and
produces no other effect, while the
other component TX (by urging
the body transversely or toward X)
directly accelerates the motion of
the body in the cycloid; hence it
is manifest that the body’s
acceleration, which is proportional to
this accelerative force, is at each
individual moment as the length TX, that is (because CV and WV—and
TX and TW, proportional to them—are given), as the length TW, that is
(by prop. 49, corol. 1), as the length of the arc of the cycloid TR. Therefore,
if the two pendulums APT and Apt are drawn back unequally from the
perpendicular [or vertical] AR and are let go simultaneously, their
accelerations will always be as the respective arcs to be described TR and tR. But
the parts of these arcs described at the beginning of the motion are as the
accelerations, that is, as the whole arcs to be described at the beginning,
and therefore the parts that remain to be described and the subsequent
accelerations proportional to these parts are also as the whole arcs, and so on.
Therefore the accelerations—and hence the velocities generated, the parts of
the arcs described with these velocities, and the parts to be so described—are
always as the whole arcs; and therefore the parts to be described, preserving
a given ratio to one another, will vanish simultaneously, that is, the two
oscillating bodies will arrive at the same time at the perpendicular [or
vertical] AR. And since, conversely, the ascents of the pendulums, made
from the lowest place R through the same cycloidal arcs with a reverse
motion, are retarded in individual places by the same forces by which their
descents were accelerated, it is evident that the velocities of the ascents and
descents made through the same arcs are equal and hence occur in equal
times; and therefore, since the two parts RS and RQ of the cycloid, each
lying on a different side of the perpendicular [or vertical], are similar and
equal, the two pendulums will always make their whole oscillations as well
as their half-oscillations in the same times. Q.E.D.
COROLLARY. The force by which body T is accelerated or retarded in any place T of the cycloid is to the total weight of body T in the highest place S or Q as the arc TR of the cycloid to its arc SR or QR.
Proposition 52, Problem 34
To determine both the velocities of pendulums in individual places and the times
in which complete oscillations, as well as the separate parts of oscillations, are
completed.
With any center G and with a radius GH equal to the arc RS of the cycloid, describe the semicircle HKM bisected by the semidiameter GK. And if a centripetal force proportional to the distances of places from the center tends toward that center G, and if in the perimeter HIK that force is equal to the centripetal force in the perimeter of the globe QOS tending toward its center, and if, at the same time that the pendulum T is let go from its highest place S, some other body L falls from H to G; then, since the forces by which the bodies are urged are equal at the beginning of the motion, and are always proportional to the spaces TR and LG which are to be described, and are therefore equal in the places T and L if TR and LG are equal, it is evident that the two bodies describe the equal spaces ST and HL at the beginning of the motion and thus will proceed thereafter to be equally urged and to describe equal spaces. Therefore (by prop. 38), the time in which the body describes the arc ST is to the time of one oscillation as the arc HI (the time in which the body H will reach L) to the semiperiphery HKM (the time in which the body H will reach M). And the velocity of the pendulum bob at the place T is to its velocity at the lowest place R (that is, the velocity of body H in the place L to its velocity in the place G, or the instantaneous increment of the line HL to the instantaneous increment of the line HG, where the arcs HI and HK increase with a uniform flow) as the ordinate LI to the radius GK, or as √(SR2 − TR2) to SR. Hence, since in unequal oscillations arcs proportional to the total arcs of the oscillations are described in equal times, both the velocities and the arcs described in all oscillations universally can be found from the given times. As was first to be found.
Now let simple pendulums oscillate in different cycloids described within
different globes, whose absolute forces are also different; and if the absolute
force of any globe QOS is called V, the accelerative force by which the
pendulum is urged in the circumference of this globe, when it begins to move
directly toward its center, will be jointly as the distance of the pendulum bob
from that center and the absolute force of the globe, that is, as CO × V.
Therefore the line-element HY (which is as this accelerative force CO × V)
will be described in a given time; and if the normal YZ is erected so as to
meet the circumference in Z, the nascent arc HZ will denote that given time.
But this nascent arc HZ is as the square root of the rectangle GH × HY, and
thus as √(GH × CO × V). Hence the time of a complete oscillation in the
cycloid QRS (since it is directly as the semiperiphery HKM, which denotes
that complete oscillation, and inversely as the arc HZ, which similarly denotes
the given time) will turn out to be as GH directly and √(GH × CO × V)
inversely, that is, because GH and SR are equal, as 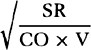 , or (by
prop. 50, corol.) as
, or (by
prop. 50, corol.) as 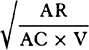 . Therefore the oscillations in all globes and
cycloids, made with any absolute forces whatever, are as the square root of
the length of the thread directly and as the square root of the distance
between the point of suspension and the center of the globe inversely and also
as the square root of the absolute force of the globe inversely. Q.E.I.
. Therefore the oscillations in all globes and
cycloids, made with any absolute forces whatever, are as the square root of
the length of the thread directly and as the square root of the distance
between the point of suspension and the center of the globe inversely and also
as the square root of the absolute force of the globe inversely. Q.E.I.
COROLLARY 1. Hence also the times of bodies oscillating, falling, and
revolving can be compared one with another. For if the diameter of the
wheel by which a cycloid is described within a globe is made equal to the
semidiameter of the globe, the cycloid will turn out to be a straight line
passing through the center of the globe, and the oscillation will now be a
descent and subsequently an ascent in this straight line. Hence the time of
the descent from any place to the center is given, as well as the time (equal
to that time of descent) in which a body, by revolving uniformly about the
center of the globe at any distance, describes a quadrantal arc. For this time
(by the second case [that is, according to the second paragraph above]) is to
the time of a half-oscillation in any cycloid QRS as 1 to 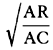 .
.
COROLLARY 2. Hence also there follows what Wren and Huygens discovered about the common cycloid. For if the diameter of the globe is increased indefinitely, its spherical surface will be changed into a plane, and the centripetal force will act uniformly along lines perpendicular to this plane, and our cycloid will turn into a common cycloid. But in that case the length of the arc of the cycloid between that plane and the describing point will come out equal to four times the versed sine of half of the arc of the wheel between that same plane and the describing point, as Wren discovered; and a pendulum between two cycloids of this sort will oscillate in a similar and equal cycloid in equal times, as Huygens demonstrated. But also the descent of heavy bodies during the time of one oscillation will be the descent which Huygens indicated.
Moreover, the propositions that we have demonstrated fit the true constitution of the earth, insofar as wheels, moving in the earth’s great circles, describe cycloids outside this globe by the motion of nails fastened in their perimeters; and pendulums suspended lower down in mines and caverns of the earth must oscillate in cycloids within globes in order that all their oscillations may be isochronous. For gravity (as will be shown in book 3) decreases in going upward from the surface of the earth as the square of the distance from the earth’s center, and in going downward from the surface is as the distance from that center.
Proposition 53, Problem 35
Granting the quadratures of curvilinear figures, it is required to find the forces by
whose action bodies moving in given curved lines will make oscillations that are
always isochronous.
Let a body T oscillate in any
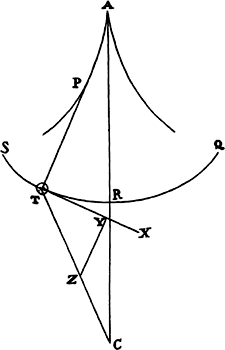 curved line STRQ whose axis is AR
passing through the center of forces C.
Draw TX touching that curve in any
place T of the body, and on this
tangent TX take TY equal to the arc TR.
[This may be done] since the length
of that arc can be known from the
quadratures of figures by commonly
used methods. From point Y draw the
straight line YZ perpendicular to the
tangent. Draw CT meeting the
perpendicular in Z, and the centripetal force
will be proportional to the straight line
TZ. Q.E.I.
curved line STRQ whose axis is AR
passing through the center of forces C.
Draw TX touching that curve in any
place T of the body, and on this
tangent TX take TY equal to the arc TR.
[This may be done] since the length
of that arc can be known from the
quadratures of figures by commonly
used methods. From point Y draw the
straight line YZ perpendicular to the
tangent. Draw CT meeting the
perpendicular in Z, and the centripetal force
will be proportional to the straight line
TZ. Q.E.I.
For if the force by which the body is drawn from T toward C is represented by the straight line TZ taken proportional to it, this will be resolved into the forces TY and YZ, of which YZ, by drawing the body along the length of the thread PT, does not change its motion at all, while the other force TY directly accelerates or directly retards its motion in the curve STRQ. Accordingly, since this force is as the projection TR to be described, the body’s accelerations or retardations in describing proportional parts of two oscillations (a greater and a lesser oscillation) will always be as those parts, and will therefore cause those parts to be described simultaneously. And bodies that in the same time describe parts always proportional to the wholes will describe the wholes simultaneously. Q.E.D.
COROLLARY 1. Hence, if body T, hanging by a rectilinear thread AT
from the center A, describes the circular arc STRQ and meanwhile is urged
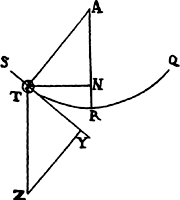 downward along parallel lines by some force that
is to the uniform force of gravity as the arc TR
to its sine TN, the times of any single oscillations
will be equal. For, because TZ and AR are
parallel, the triangles ATN and ZTY will be similar;
and therefore TZ will be to AT as TY to TN;
that is, if the uniform force of gravity is
represented by the given length AT, the force TZ, by
the action of which the oscillations will turn out
to be isochronous, will be to the force of gravity AT as the arc TR (equal to
TY) to the sine TN of that arc.
downward along parallel lines by some force that
is to the uniform force of gravity as the arc TR
to its sine TN, the times of any single oscillations
will be equal. For, because TZ and AR are
parallel, the triangles ATN and ZTY will be similar;
and therefore TZ will be to AT as TY to TN;
that is, if the uniform force of gravity is
represented by the given length AT, the force TZ, by
the action of which the oscillations will turn out
to be isochronous, will be to the force of gravity AT as the arc TR (equal to
TY) to the sine TN of that arc.
COROLLARY 2. And therefore in [pendulum] clocks, if the forces impressed by the mechanism upon the pendulum to maintain the motion can be compounded with the force of gravity in such a way that the total force downward is always as the line that arises from dividing the rectangle of the arc TR and the radius AR by the sine TN, all the oscillations will be isochronous.
Proposition 54, Problem 36
Granting the quadratures of curvilinear figures, to find the times in which bodies
under the action of any centripetal force will descend and ascend in any curved
lines described in a plane passing through the center of forces.
Let a body descend from any place S through any curved line STtR
given in a plane passing through the center of forces C. Join CS and divide
it into innumerable equal parts, and let Dd be some one of those parts. With
center C and radii CD and Cd, describe the circles DT and dt, meeting the
curved line STtR in T and t. Then, since both the law of centripetal force
and the height CS from which the body has fallen are given, the velocity
of the body at any other height CT will be given (by prop. 39). Moreover,
the time in which the body describes the line-element Tt is as the length
of this line-element (that is, as the secant of the angle tTC) directly and as
the velocity inversely. Let the ordinate DN be proportional to this time and
perpendicular to the straight line CS through point D; then, because Dd is
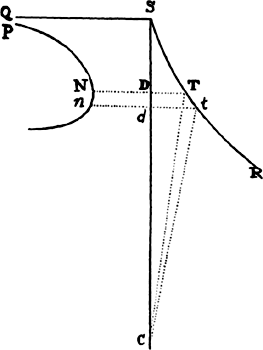 given, the rectangle Dd × DN, that is,
the area DNnd, will be proportional
to that same time. Therefore if PNn is
the curved line that point N continually
traces out, aand its asymptote is the
straight line SQ standing perpendicularly
upon the straight line CS,a the area
SQPND will be proportional to the time
in which the body, by descending, has
described the line ST; and accordingly,
when that area has been found, the time
will be given. Q.E.I.
given, the rectangle Dd × DN, that is,
the area DNnd, will be proportional
to that same time. Therefore if PNn is
the curved line that point N continually
traces out, aand its asymptote is the
straight line SQ standing perpendicularly
upon the straight line CS,a the area
SQPND will be proportional to the time
in which the body, by descending, has
described the line ST; and accordingly,
when that area has been found, the time
will be given. Q.E.I.
Proposition 55, Theorem 19
If a body moves in any curved surface whose axis passes through a center of
forces, and a perpendicular is dropped from the body to the axis, and a straight
line parallel and equal to the perpendicular is drawn from any given point of the
axis; I say that the parallel will describe an area proportional to the time.
Let BKL be the curved surface, T the body revolving in it, STR the
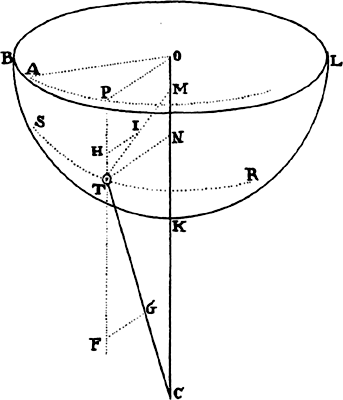 trajectory which the body
describes in it, S the beginning of
the trajectory, OMK the axis of
the curved surface, TN the
perpendicular straight line dropped
from the body to the axis; and let
OP be the straight line parallel
and equal to TN and drawn
from a point O that is given in
the axis, AP the path described
by point P in the plane AOP
of the revolving line OP, A
the beginning of the projection
(corresponding to point S); and
let TC be a straight line drawn
from the body to the center, TG the part of TC that is proportional to
the centripetal force by which the body is urged toward the center C, TM
a straight line perpendicular to the curved surface, TI the part of TM
proportional to the force of pressure by which the body urges the surface
and is in turn urged by the surface toward M; and let PTF be a straight line
parallel to the axis and passing through the body, and GF and IH straight
lines dropped perpendicularly from the points G and I to the parallel
PHTF. I say now that the area AOP, described by the radius OP from the
beginning of the motion, is proportional to the time. For the force TG (by
corol. 2 of the laws) is resolved into the forces TF and FG, and the force
TI into the forces TH and HI. But the forces TF and TH, by acting along
the line PF perpendicular to the plane AOP, change the body’s motion only
insofar as it is perpendicular to this plane. And therefore the body’s motion,
insofar as it takes place in the position of the plane—that is, the motion of
point P, by which the projection AP of the trajectory is described in this
plane—is the same as if the forces TF and TH were taken away and the
body were acted on by the forces FG and HI alone; that is, it is the same
as if the body were to describe the curve AP in the plane AOP under the
action of a centripetal force tending toward the center O and equal to the
sum of the forces FG and HI. But by the action of such a force the area
AOP is (by prop. 1) described proportional to the time.a Q.E.D.
trajectory which the body
describes in it, S the beginning of
the trajectory, OMK the axis of
the curved surface, TN the
perpendicular straight line dropped
from the body to the axis; and let
OP be the straight line parallel
and equal to TN and drawn
from a point O that is given in
the axis, AP the path described
by point P in the plane AOP
of the revolving line OP, A
the beginning of the projection
(corresponding to point S); and
let TC be a straight line drawn
from the body to the center, TG the part of TC that is proportional to
the centripetal force by which the body is urged toward the center C, TM
a straight line perpendicular to the curved surface, TI the part of TM
proportional to the force of pressure by which the body urges the surface
and is in turn urged by the surface toward M; and let PTF be a straight line
parallel to the axis and passing through the body, and GF and IH straight
lines dropped perpendicularly from the points G and I to the parallel
PHTF. I say now that the area AOP, described by the radius OP from the
beginning of the motion, is proportional to the time. For the force TG (by
corol. 2 of the laws) is resolved into the forces TF and FG, and the force
TI into the forces TH and HI. But the forces TF and TH, by acting along
the line PF perpendicular to the plane AOP, change the body’s motion only
insofar as it is perpendicular to this plane. And therefore the body’s motion,
insofar as it takes place in the position of the plane—that is, the motion of
point P, by which the projection AP of the trajectory is described in this
plane—is the same as if the forces TF and TH were taken away and the
body were acted on by the forces FG and HI alone; that is, it is the same
as if the body were to describe the curve AP in the plane AOP under the
action of a centripetal force tending toward the center O and equal to the
sum of the forces FG and HI. But by the action of such a force the area
AOP is (by prop. 1) described proportional to the time.a Q.E.D.
COROLLARY. By the same argument, if a body, acted on by forces tending toward two or more centers in any one given straight line CO, described any curved line ST in free space, the area AOP would always be proportional to the time.
Proposition 56, Problem 37
Granting the quadratures of curvilinear figures, and given both the law of
centripetal force tending toward a given center and a curved surface whose axis passes
through that center, it is required to find the trajectory that a body will describe
in that same surface when it has set out from a given place with a given velocity,
in a given direction in that surface.
Assuming the same constructions as in prop. 55, let body T go forth
from the given place S, along a straight line given in position, in the required
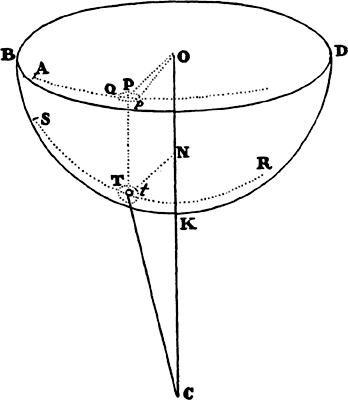 trajectory STR, and let the
projection of this trajectory in the
plane BLO be AP. And since the
velocity of the body is given at
the height SC, its velocity at any
other height TC will be given.
With this velocity, let the body in
a given minimally small time
describe the particle Tt of its
trajectory, and let Pp be its projection
described in the plane AOP. Join
Op, and let the projection (in the
plane AOP) of the little circle
described with center T and radius
Tt in the curved surface be the ellipse pQ. Then, because the little circle
Tt is given in magnitude, and its distance TN or PO from the axis CO is
given, the ellipse pQ will be given in species and in magnitude, as well as
in its position with respect to the straight line PO. And since the area POp
is proportional to the time and therefore given because the time is given, the
angle POp will be given. And hence the common intersection p of the ellipse
and the straight line Op will be given, along with the angle OPp in which
the projection APp of the trajectory cuts the line OP. And accordingly (by
consulting prop. 41 with its corol. 2) the way of determining the curve APp
is readily apparent. Then, erecting perpendiculars to the plane AOP one by
one, from the points P of the projection, so as to meet the curved surface in
T, the points T of the trajectory will be given one by one. Q.E.I.
trajectory STR, and let the
projection of this trajectory in the
plane BLO be AP. And since the
velocity of the body is given at
the height SC, its velocity at any
other height TC will be given.
With this velocity, let the body in
a given minimally small time
describe the particle Tt of its
trajectory, and let Pp be its projection
described in the plane AOP. Join
Op, and let the projection (in the
plane AOP) of the little circle
described with center T and radius
Tt in the curved surface be the ellipse pQ. Then, because the little circle
Tt is given in magnitude, and its distance TN or PO from the axis CO is
given, the ellipse pQ will be given in species and in magnitude, as well as
in its position with respect to the straight line PO. And since the area POp
is proportional to the time and therefore given because the time is given, the
angle POp will be given. And hence the common intersection p of the ellipse
and the straight line Op will be given, along with the angle OPp in which
the projection APp of the trajectory cuts the line OP. And accordingly (by
consulting prop. 41 with its corol. 2) the way of determining the curve APp
is readily apparent. Then, erecting perpendiculars to the plane AOP one by
one, from the points P of the projection, so as to meet the curved surface in
T, the points T of the trajectory will be given one by one. Q.E.I.
The motion of bodies drawn to one another by centripetal forces
Up to this point, I have been setting forth the motions of bodies attracted toward an immovable center, such as, however, hardly exists in the natural world. For attractions are always directed toward bodies, and—by the third law—the actions of attracting and attracted bodies are always mutual and equal; so that if there are two bodies, neither the attracting nor the attracted body can be at rest, but both (by corol. 4 of the laws) revolve about a common center of gravity as if by a mutual attraction; and if there are more than two bodies that either are all attracted by and attract a single body or all attract one another, these bodies must move with respect to one another in such a way that the common center of gravity either is at rest or moves uniformly straight forward. For this reason I now go on to set forth the motion of bodies that attract one another, considering centripetal forces as attractions, although perhaps—if we speak in the language of physics—they might more truly be called impulses. For here we are concerned with mathematics; and therefore, putting aside any debates concerning physics, we are using familiar language so as to be more easily understood by mathematical readers.
Proposition 57, Theorem 20
Two bodies that attract each other describe similar figures about their common
center of gravity and also about each other.
For the distances of these bodies from their common center of gravity are inversely proportional to the masses of the bodies and therefore in a given ratio to each other and, by composition [or componendo], in a given ratio to the total distance between the bodies. These distances, moreover, rotate about their common end-point with an equal angular motion because, since they always lie in the same straight line, they do not change their inclination toward each other. And straight lines that are in a given ratio to each other and that rotate about their end-points with an equal angular motion describe entirely similar figures about the end-points in planes that, along with these end-points, either are at rest or move with any motion that is not angular. Accordingly, the figures described by the rotation of these distances are similar. Q.E.D.
Proposition 58, Theorem 21
If two bodies attract each other with any forces whatever and at the same time
revolve about their common center of gravity, I say that by the action of the same
forces there can be described around either body if unmoved a figure similar and
equal to the figures that the bodies so moving describe around each other.
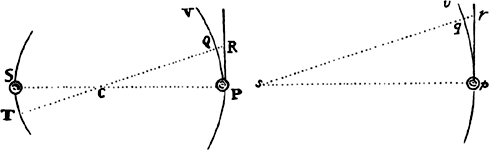
Let bodies S and P revolve about their common center of gravity C, going from S to T and from P to Q. From a given point s let sp and sq be drawn always equal and parallel to SP and TQ; then the curve pqv, which the point p describes by revolving around the motionless point s, will be similar and equal to the curves that bodies S and P describe around each other; and accordingly (by prop. 57) this curve pqv will be similar to the curves ST and PQV, which the same bodies describe around their common center of gravity C; and this is so because the proportions of the lines SC, CP, and SP or sp to one another are given.
CASE 1. The common center of gravity C (by corol. 4 of the laws) either is at rest or moves uniformly straight forward. Let us suppose first that it is at rest, and at s and p let two bodies be placed, a motionless one at s and a moving one at p, similar and equal to bodies S and P. Then let the straight lines PR and pr touch the curves PQ and pq in P and p, and let CQ and sq be produced to R and r. Then, because the figures CPRQ and sprq are similar, RQ will be to rq as CP to sp and thus in a given ratio. Accordingly, if the force with which body P is attracted toward body S, and therefore toward the intermediate center C, were in that same given ratio to the force with which body p is attracted toward center s, then in equal times these forces would always attract the bodies from the tangents PR and pr to the arcs PQ and pq through the distances RQ and rq proportional to them; and therefore the latter force would cause body p to revolve in orbit in the curve pqv, which would be similar to the curve PQV, in which the former force causes body P to revolve in orbit, and the revolutions would be completed in the same times. But those forces are not to each other in the ratio CP to sp but are equal to each other (because bodies S and s, P and p are similar and equal, and distances SP and sp are equal); therefore, the bodies will in equal times be equally drawn away from the tangents; and therefore, for the second body p to be attracted through the greater distance rq, a greater time is required, which is as the square root of the distances, because (by lem. 10) the spaces described at the very beginning of the motion are as the squares of the times. Therefore, let the velocity of body p be supposed to be to the velocity of body P as the square root of the ratio of the distance sp to the distance CP, so that the arcs pq and PQ, which are in a simple ratio, are described in times which are as the square roots of the distances. Then bodies P and p, being always attracted by equal forces, will describe around the centers C and s at rest the similar figures PQV and pqv, of which pqv is similar and equal to the figure that body P describes around the moving body S. Q.E.D.
CASE 2. Let us suppose now that the common center of gravity, along with the space in which the bodies are moving with respect to each other, is moving uniformly straight forward; then (by corol. 6 of the laws) all motions in this space will occur as in case 1. Hence the bodies will describe around each other figures which are the same as before and which therefore will be similar and equal to the figure pqv. Q.E.D.
COROLLARY 1. Hence (by prop. 10) two bodies, attracting each other with forces proportional to their distance, describe concentric ellipses, both around their common center of gravity and also around each other; and, conversely, if such figures are described, the forces are proportional to the distance.
COROLLARY 2. And (by props. 11, 12, and 13) two bodies, under the action of forces inversely proportional to the square of the distance, describe—around their common center of gravity and also around each other—conics having their focus in that center about which the figures are described. And, conversely, if such figures are described, the centripetal forces are inversely proportional to the square of the distance.
COROLLARY 3. Any two bodies revolving in orbit around a common center of gravity describe areas proportional to the times, by radii drawn to that center and also to each other.
Proposition 59, Theorem 22
The periodic time of two bodies S and P revolving about their common center of
gravity C is to the periodic time of one of the two bodies P, revolving in orbit
about the other body S which is without motion, and describing a figure similar
and equal to the figures that the bodies describe around each other, as the square
root of the ratio of the mass of the second body S to the sum of the masses of the
bodies S + P.
For, from the proof of prop. 58, the times in which any similar arcs PQ and pq are described are as the square roots of the distances CP and SP or sp, that is, as the square root of the ratio of body S to the sum of the bodies S + P [or, as √S to √(S + P)]. And by composition [or componendo] the sums of the times in which all the similar arcs PQ and pq are described, that is, the whole times in which the whole similar figures are described, are in that same ratio. Q.E.D.
Proposition 60, Theorem 23
If two bodies S and P, attracting each other with forces inversely proportional to
the square of the distance, revolve about a common center of gravity, I say that
the principal axis of the ellipse which one of the bodies P describes by this motion
about the other body S will be to the principal axis of the ellipse which the same
body P would be able to describe in the same periodic time about the other body
S at rest as the sum of the masses of the two bodies S + P is to the first of two
mean proportionals between this sum and the mass of the other body S.a
For if the ellipses so described were equal to each other, the periodic times would (by prop. 59) be as the square root of the mass of body S is to the square root of the sum of the masses of the bodies S + P. Let the periodic time in the second ellipse be decreased in this same ratio, and then the periodic times will become equal; but the principal axis of the second ellipse (by prop. 15) will be decreased as the 3/2 power of the former ratio, that is, in the ratio of which the ratio S to S + P is the cube; and therefore the principal axis of the second ellipse will be to the principal axis of the first ellipse as the first of two mean proportionals between S + P and S to S + P. And inversely, the principal axis of the ellipse described about the body in motion will be to the principal axis of the ellipse described about the body not in motion as S + P to the first of two mean proportionals between S + P and S. Q.E.D.
Proposition 61, Theorem 24
If two bodies, attracting each other with any kind of forces and not otherwise acted
on or impeded, move in any way whatever, their motions will be the same as if
they were not attracting each other but were each being attracted with the same
forces by a third body set in their common center of gravity. And the law of the
attracting forces will be the same with respect to the distance of the bodies from
that common center and with respect to the total distance between the bodies.
For the forces with which the bodies attract each other, in tending toward the bodies, tend toward a common center of gravity between them and therefore are the same as if they were emanating from a body between them. Q.E.D.
And since there is given the ratio of the distance of either of the two bodies from that common center to the distance between the bodies, there will also be given the ratio of any power of one such distance to the same power of the other distance, as well as the ratio that any quantity derived in any manner from one such distance together with given quantities has to another quantity derived in the same manner from the other distance together with the same number of given quantities having that given ratio of distances to the former ones. Accordingly, if the force with which one body is attracted by the other is directly or inversely as the distance of the bodies from each other or as any power of this distance or finally as any quantity derived in any manner from this distance and given quantities, the same force with which the same body is attracted to the common center of gravity will be likewise directly or inversely as the distance of the attracted body from that common center or as the same power of this distance or finally as a quantity derived in the same manner from this distance and analogous given quantities. That is, the law of the attracting force will be the same with respect to either of the distances. Q.E.D.
Proposition 62, Problem 38
To determine the motions of two bodies that attract each other with forces inversely
proportional to the square of the distance and are let go from given places.
These bodies will (by prop. 61) move just as if they were being attracted by a third body set in their common center of gravity; and by hypothesis, that center will be at rest at the very beginning of the motion and therefore (by corol. 4 of the laws) will always be at rest. Accordingly, the motions of the bodies are (by prop. 36) to be determined just as if they were being urged by forces tending toward that center, and the motions of the bodies attracting each other will then be known. Q.E.I.
Proposition 63, Problem 39
To determine the motions of two bodies that attract each other with forces inversely
proportional to the square of the distance and that set out from given places with
given velocities along given straight lines.
From the given motions of the bodies at the beginning the uniform motion of the common center of gravity is given, as well as the motion of the space that moves along with this center uniformly straight forward, and also the initial motions of the bodies with respect to this space. Now (by corol. 5 of the laws and prop. 61), the subsequent motions take place in this space just as if the space itself, along with that common center of gravity, were at rest, and as if the bodies were not attracting each other but were being attracted by a third body situated in that center. Therefore the motion of either body in this moving space, setting out from a given place with a given velocity along a given straight line and pulled by a centripetal force tending toward that center, is to be determined (by props. 17 and 37), and at the same time the motion of the other body about the same center will be known. This motion is to be compounded with that uniform progressive motion (found above) of the system of the space and bodies revolving in it, and the absolute motion of the bodies in an unmoving space will be known. Q.E.I.
Proposition 64, Problem 40
If the forces with which bodies attract one another increase in the simple ratio of
the distances from the centers, it is required to find the motions of more than two
bodies in relation to one another.
Suppose first that two bodies T and L have a common center of gravity D. These bodies will (by prop. 58, corol. 1) describe ellipses that have their centers at D and that have magnitudes which become known by prop. 10.
Now let a third body S attract the first two bodies T and L with
accelerative forces ST and SL, and let it be attracted by those bodies in turn.
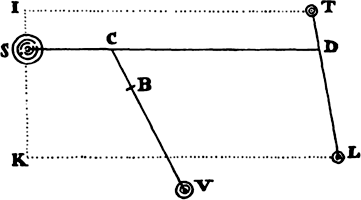 The force ST (by corol. 2 of the
laws) is resolved into forces SD
and DT, and the force SL into
forces SD and DL. Moreover, the
forces DT and DL, which are as
their sum TL and therefore as
the accelerative forces with which
bodies T and L attract each other, when added respectively to those forces
of bodies T and L, compose forces proportional to the distances DT and
DL, as before, but greater than those former forces, and therefore (by prop.
10, corol. 1, and prop. 4, corols. 1 and 8) they cause those bodies to describe
ellipses as before, but with a swifter motion. The remaining accelerative
forces, each of which is SD, by attracting those bodies T and L equally
and along lines TI and LK (which are parallel to DS) with motive actions
SD × T and SD × L (which are as the bodies), do not at all change the
situations of those bodies in relation to one another, but make them equally
approach line IK, which is to be conceived as drawn through the middle of
body S, perpendicular to the line DS. That approach to line IK, however,
will be impeded by causing the system of bodies T and L on one side and
body S on the other to revolve in orbit with just the right velocities about
a common center of gravity C. Body S describes an ellipse about that same
point C with such a motion, because the sum of the motive forces SD × T
and SD × L, which are proportional to the distance CS, tends toward the
center C; and because CS and CD are proportional, point D will describe
a similar ellipse directly opposite. But bodies T and L, being attracted
respectively by motive forces SD × T and SD × L equally and along the
parallel lines TI and LK (as has been said), will (by corols. 5 and 6 of the
laws) proceed to describe their own ellipses about the moving center D, as
before. Q.E.I.
The force ST (by corol. 2 of the
laws) is resolved into forces SD
and DT, and the force SL into
forces SD and DL. Moreover, the
forces DT and DL, which are as
their sum TL and therefore as
the accelerative forces with which
bodies T and L attract each other, when added respectively to those forces
of bodies T and L, compose forces proportional to the distances DT and
DL, as before, but greater than those former forces, and therefore (by prop.
10, corol. 1, and prop. 4, corols. 1 and 8) they cause those bodies to describe
ellipses as before, but with a swifter motion. The remaining accelerative
forces, each of which is SD, by attracting those bodies T and L equally
and along lines TI and LK (which are parallel to DS) with motive actions
SD × T and SD × L (which are as the bodies), do not at all change the
situations of those bodies in relation to one another, but make them equally
approach line IK, which is to be conceived as drawn through the middle of
body S, perpendicular to the line DS. That approach to line IK, however,
will be impeded by causing the system of bodies T and L on one side and
body S on the other to revolve in orbit with just the right velocities about
a common center of gravity C. Body S describes an ellipse about that same
point C with such a motion, because the sum of the motive forces SD × T
and SD × L, which are proportional to the distance CS, tends toward the
center C; and because CS and CD are proportional, point D will describe
a similar ellipse directly opposite. But bodies T and L, being attracted
respectively by motive forces SD × T and SD × L equally and along the
parallel lines TI and LK (as has been said), will (by corols. 5 and 6 of the
laws) proceed to describe their own ellipses about the moving center D, as
before. Q.E.I.
Now let a fourth body V be added, and by a similar argument it will be concluded that this point and point C describe ellipses about B, the common center of gravity of all the bodies, while the motions of the former bodies T, L, and S about centers D and C remain the same as before, but accelerated. And by the same method it will be possible to add more bodies. Q.E.I.
These things are so, even if bodies T and L attract each other with accelerative forces that are greater or less than those by which they attract the rest of the bodies in proportion to the distance. Let the mutual accelerative attractions of all the bodies to one another be as the distances multiplied by the attracting bodies; then, from what has gone before, it will be easily deduced that all the bodies describe different ellipses in equal periodic times about B, the common center of gravity of them all, in a motionless plane. Q.E.I.
Proposition 65, Theorem 25
More than two bodies whose forces decrease as the squares of the distances from
their centers are able to move with respect to one another in ellipses and, by radii
drawn to the foci, are able to describe areas proportional to the times very nearly.
In prop. 64 the case was demonstrated in which the several motions occur exactly in ellipses. The more the law of force departs from the law there supposed, the more the bodies will perturb their mutual motions; nor can it happen that bodies will move exactly in ellipses while attracting one another according to the law here supposed, except by maintaining a fixed proportion of distances one from another. In the following cases, however, the orbits will not be very different from ellipses.
CASE 1. Suppose that several lesser bodies revolve about some very much greater one at various distances from it, and that absolute forces proportional to these bodies [i.e., their masses] tend toward each and every one of them. Then, since the common center of gravity of them all (by corol. 4 of the laws) either is at rest or moves uniformly straight forward, let us imagine that the lesser bodies are so small that the greater body never is sensibly distant from this center. In this case, the greater body will—without any sensible error—either be at rest or move uniformly straight forward, while the lesser ones will revolve about this greater one in ellipses and by radii drawn to it will describe areas proportional to the times, except insofar as there are errors introduced either by a departure of the greater body from that common center of gravity or by the mutual actions of the lesser bodies on one another. The lesser bodies, however, can be diminished until that departure and the mutual actions are less than any assigned values, and therefore until the orbits square with ellipses and the areas correspond to the times without any error that is not less than any assigned value. Q.E.O.
CASE 2. Let us now imagine a system of lesser bodies revolving in the way just described around a much greater one, or any other system of two bodies revolving around each other, to be moving uniformly straight forward and at the same time to be urged sideways by the force of another very much greater body, situated at a great distance. Then, since the equal accelerative forces by which the bodies are urged along parallel lines do not change the situations of the bodies in relation to one another, but cause the whole system to be transferred simultaneously, while the motions of the parts with respect to one another are maintained; it is manifest that no change whatsoever of the motion of the bodies attracted among themselves will result from their attractions toward the greater body, unless such a change comes either from the inequality of the accelerative attractions or from the inclination to one another of the lines along which the attractions take place. Suppose, therefore, that all the accelerative attractions toward the greater body are with respect to one another inversely as the squares of the distances; then by increasing the distance of the greater body until the differences (with respect to their length) among the straight lines drawn from this body to the other bodies and their inclinations with respect to one another are less than any assigned values, the motions of the parts of the system with respect to one another will persevere without any errors that are not less than any assigned values. And since, because of the slight distance of those parts from one another, the whole system is attracted as if it were one body, that system will be moved by this attraction as if it were one body; that is, by its center of gravity it will describe about the greater body some conic (namely, a hyperbola or parabola if the attraction is weak, an ellipse if the attraction is stronger) and by a radius drawn to the greater body will describe areas proportional to the times without any errors except the ones that may be produced by the distances between the parts, and these are admittedly slight and may be diminished at will. Q.E.O.
By a similar argument one can go on to more complex cases indefinitely.
COROLLARY 1. In case 2, the closer the greater body approaches to the system of two or more bodies, the more the motions of the parts of the system with respect to one another will be perturbed, because the inclinations to one another of the lines drawn from this great body to those parts are now greater, and the inequality of the proportion is likewise greater.
COROLLARY 2. But these perturbations will be greatest if the accelerative attractions of the parts of the system toward the greater body are not to one another inversely as the squares of the distances from that greater body, especially if the inequality of this proportion is greater than the inequality of the proportion of the distances from the greater body. For if the accelerative force, acting equally and along parallel lines, in no way perturbs the motions of the parts of the system with respect to one another, it will necessarily cause a perturbation to arise when there is an inequality in its action, and such perturbation will be greater or less according as this inequality is greater or less. The excess of the greater impulses acting on some bodies, but not acting on others, will necessarily change the situation of the bodies with respect to one another. And this perturbation, added to the perturbation that arises from the inclination and inequality of the lines, will make the total perturbation greater.
COROLLARY 3. Hence, if the parts of this system—without any significant perturbation—move in ellipses or circles, it is manifest that these parts either are not urged at all (except to a very slight degree indeed) by accelerative forces tending toward other bodies, or are all urged equally and very nearly along parallel lines.
Proposition 66a, Theorem 26
Let three bodies—whose forces decrease as the squares of the distances—attract
one another, and let the accelerative attractions of any two toward the third be
to each other inversely as the squares of the distances, and let the two lesser
ones revolve about the greatest. Then I say that if that greatest body is moved
by these attractions, the inner body [of the two revolving bodies] will describe
about the innermost and greatest body, by radii drawn to it, areas more nearly
proportional to the times and a figure more closely approaching the shape of an
ellipse (having its focus in the meeting point of the radii) than would be the case if
that greatest body were not attracted by the smaller ones and were at rest, or if it
were much less or much more attracted and were acted on either much less or much
more.
This is sufficiently clear from the demonstration of the second corollary of prop. 65, but it is proved as follows by a more lucid and more generally convincing argument.
CASE 1. Let the lesser bodies P and S revolve in the same plane about a greatest body T, and let P describe the inner orbit PAB, and S the outer orbit ESE. Let SK be the mean distance between bodies P and S, and let the accelerative attraction of body P toward S at that mean distance be represented by that same line SK. Let SL be taken to SK as SK2 to SP2, and SL will be the accelerative attraction of body P toward S at any distance SP. Join PT, and parallel to it draw LM meeting ST in M; then the attraction SL will be resolved (by corol. 2 of the laws) into attractions SM and LM. And thus body P will be urged by a threefold accelerative force. One such force tends toward T and arises from the mutual attraction of bodies T and P. By this force alone (whether T is motionless or is moved by this attraction), body P must, by a radius PT, describe around body T areas proportional to the times and must also describe an ellipse whose focus is in the center of body T. This is clear from prop. 11 and prop. 58, corols. 2 and 3.
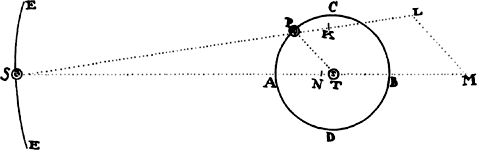
The second force is that of the attraction LM, which (since it tends from P to T) will, when added to the first of these forces, coincide with it and will thus cause areas to be described that are still proportional to the times, by prop. 58, corol. 3. But since this force is not inversely proportional to the square of the distance PT, it will, together with the first force, compose a force differing from this proportion—and the more so, the greater the proportion of this force is to that first force, other things being equal. Accordingly, since (by prop. 11 and by prop. 58, corol. 2) the force by which an ellipse is described about the focus T must tend toward that focus and be inversely proportional to the square of the distance PT, that composite force, by differing from this proportion, will cause the orbit PAB to deviate from the shape of an ellipse having its focus in T, and the more so the greater the difference from this proportion; and the difference from this proportion will be greater according as the proportion of the second force LM to the first force is greater, other things being equal.
But now the third force SM, by attracting body P along a line parallel to ST, will, together with the former forces, compose a force which is no longer directed from P to T and which deviates from this direction the more, the greater the proportion of this third force is to the former forces, other things being equal; and this compound force therefore will make body P describe, by a radius TP, areas no longer proportional to the times and will make the divergence from this proportionality be the greater, the greater the proportion of this third force is to the other forces. This third force will increase the deviation of the orbit PAB from the aforesaid elliptical shape for two reasons: not only is this force not directed from P to T, but also it is not inversely proportional to the square of the distance PT. Once these things have been understood, it is manifest that the areas will be most nearly proportional to the times when this third force is least, the other forces remaining the same as they were; and that the orbit PAB approaches closest to the aforesaid elliptical shape when both the second force and the third (but especially the third force) are least, the first force remaining the same as it was.
Let the accelerative attraction of body T toward S be represented by line SN; and if the accelerative attractions SM and SN were equal, they would, by attracting bodies T and P equally and along parallel lines, not at all change the situation of those two bodies with respect to each other. In this case, their motions with respect to each other would (by corol. 6 of the laws) be the same as it would be without these attractions. And for the same reason, if the attraction SN were smaller than the attraction SM, it would take away the part SN of the attraction SM, and only the part MN would remain, by which the proportionality of the times and areas and the elliptical shape of the orbit would be perturbed. And similarly, if the attraction SN were greater than the attraction SM, the perturbation of the proportionality and of the orbit would arise from the difference MN alone. Thus SM, the third attraction above, is always reduced by the attraction SN to the attraction MN, the first and second attractions remaining completely unchanged; and therefore the areas and times approach closest to proportionality, and the orbit PAB approaches closest to the aforesaid elliptical shape, when the attraction MN is either null or the least possible—that is, when the accelerative attractions of bodies P and T toward body S approach as nearly as possible to equality, in other words, when the attraction SN is neither null nor less than the least of all the attractions SM, but is a kind of mean between the maximum and minimum of all those attractions SM, that is, not much greater and not much smaller than the attraction SK. Q.E.D.
CASE 2. Now let the lesser bodies P and S revolve about the greatest body T in different planes; then the force LM, acting along a line PT situated in the plane of orbit PAB, will have the same effect as before, and will not draw body P away from the plane of its orbit. But the second force NM, acting along a line that is parallel to ST (and therefore, when body S is outside the line of the nodes, is inclined to the plane of orbit PAB), besides the perturbation of its motion in longitude, already set forth above, will introduce a perturbation of the motion in latitude, by attracting body P out of the plane of its orbit. And this perturbation, in any given situation of bodies P and T with respect to each other, will be as the generating force MN, and therefore becomes least when MN is least, that is (as I have already explained), when the attraction SN is not much greater and not much smaller than the attraction SK. Q.E.D.
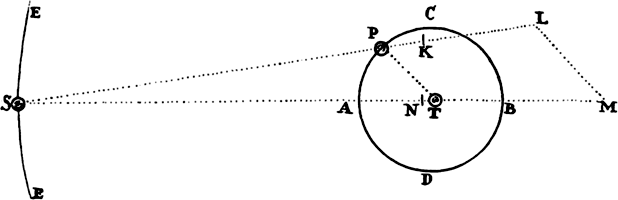
COROLLARY 1. Hence it is easily gathered that if several lesser bodies P, S, R, . . . revolve about a greatest body T, the motion of the innermost body P will be least perturbed by the attractions of the outer bodies when the greatest body T is attracted and acted on as much by the other bodies (according to the ratio of the accelerative forces) as the other bodies are by one another.
COROLLARY 2. In a system of three bodies T, P, and S, if the accelerative attractions of any two toward the third are to each other inversely as the squares of the distances, body P will describe, by a radius PT, an area about body T more swiftly near their conjunction A and their opposition B than near the quadratures C and D. For every force by which body P is urged and body T is not, and which does not act along line PT, accelerates or retards the description of areas, according as its direction is forward and direct [or in consequentia] or retrograde [or in antecedentia]. Such is the force NM. In the passage of body P from C to A, this force is directed forward [or in consequentia] and accelerates the motion; afterward, as far as D, it is retrograde [or in antecedentia] and retards the motion; then forward up to B, and finally retrograde in passing from B to C.
COROLLARY 3. And by the same argument it is evident that body P, other things being the same, moves more swiftly in conjunction and opposition than in the quadratures.
COROLLARY 4. The orbit of body P, other things being the same, is more curved in the quadratures than in conjunction and opposition. For swifter bodies are deflected less from a straight path. And besides, in conjunction and opposition the force KL, or NM, is opposite to the force with which body T attracts body P and therefore diminishes that force, while body P will be deflected less from a straight path when it is less urged toward body T.
COROLLARY 5. Accordingly, body P, other things being the same, will recede further from body T in the quadratures than in conjunction and opposition. These things are so if the motion of [i.e., change in] eccentricity is neglected. For if the orbit of body P is eccentric, its eccentricity (as will shortly be shown in corol. 9 of this proposition) will come out greatest when the apsides are in the syzygies; and thus it can happen that body P, arriving at the upper apsis, may be further away from body T in the syzygies than in the quadratures.
COROLLARY 6. Since the centripetal force of the central body T, which keeps body P in its orbit, is increased in the quadratures by the addition of the force LM and is diminished in the syzygies by the subtraction of the force KL and, because of the magnitude of the force KL [which is greater than LM], is more diminished than increased; and since that centripetal force (by prop. 4, corol. 2) is in a ratio compounded of the simple ratio of the radius TP directly and the squared ratio of the periodic time inversely [i.e., the force is directly as the radius and inversely as the square of the periodic time], it is evident that this compound ratio is diminished by the action of the force KL, and therefore that the periodic time (assuming the radius TP of the orbit to remain unchanged) is increased as the square root of the ratio in which that centripetal force is diminished. It is therefore further evident that, assuming this radius to be increased or diminished, the periodic time is increased more or diminished less than as the 3/2 power of this radius, by prop. 4, corol. 6. If the force of the central body were gradually to weaken, body P, attracted always less and less, would continually recede further and further from the center T; and on the contrary, if the force were increased, body P would approach nearer and nearer. Therefore, if the action of the distant body S, whereby the force is diminished, is alternately increased and diminished, radius TP will at the same time also be alternately increased and diminished, and the periodic time will be increased and diminished in a ratio compounded of the 3/2 power of the ratio of the radius and the square root of the ratio in which the centripetal force of the central body T is diminished or increased by the increase or decrease of the action of the distant body S.
COROLLARY 7. From what has gone before, it follows also that with respect to angular motion the axis of the ellipse described by body P, or the line of the apsides, advances and regresses alternately, but nevertheless advances more than it regresses and is carried forward [or in consequentia] by the excess of its direct forward motion. For the force whereby body P is urged toward body T in the quadratures, when the force MN vanishes, is compounded of the force LM and the centripetal force with which body T attracts body P. If the distance PT is increased, the first force LM is increased in about the same ratio as this distance, and the latter force is decreased as the square of that ratio, and so the sum of these forces is decreased in a less than squared ratio of the distance PT, and therefore (by prop. 45, corol. 1) causes the auge, or upper apsis, to regress. But in conjunction and opposition the force whereby body P is urged toward body T is the difference between the force by which body T attracts body P and the force KL; and that difference, because the force KL is increased very nearly in the ratio of the distance PT, decreases in a ratio of the distance PT that is greater than the square of the distance PT, and so (by prop. 45, corol. 1) causes the upper apsis to advance. In places between the syzygies and quadratures the motion of the upper apsis depends on both of these causes jointly, so that according to the excess of the one or the other it advances or regresses. Accordingly, since the force KL in the syzygies is roughly twice as large as the force LM in the quadratures, the excess will have the same sense as the force KL and will carry the upper apsis forward [or in consequentia]. The truth of this corollary and its predecessor will be easily understood by supposing that a system of two bodies T and P is surrounded on all sides by more bodies S, S, S, . . . that are in an orbit ESE. For by the actions of these bodies, the action of T will be diminished on all sides and will decrease in a ratio greater than the square of the distance.
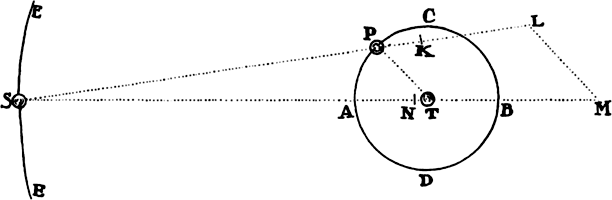
COROLLARY 8. Since, however, the advance or retrogression of the apsides depends on the decrease of the centripetal force, a decrease occurring in a ratio of the distance TP that is either greater or less than the square of the ratio of the distance TP, in the passage of the body from the lower to the upper apsis, and also depends on a similar increase in its return to the lower apsis, and therefore is greatest when the proportion of the force in the upper apsis to the force in the lower apsis differs most from the ratio of the inverse squares of the distances, it is manifest that KL or NM − LM, the force that subtracts, will cause the apsides to advance more swiftly in their syzygies and that LM, the force that adds, will cause them to recede more slowly in their quadratures. And because of the length of time in which the swiftness of the advance or slowness of the retrogression is continued, this inequality becomes by far the greatest.
COROLLARY 9. If a body, by the action of a force inversely proportional to the square of its distance from a center, were to revolve about this center in an ellipse, and if then, in its descent from the upper apsis or auge to the lower apsis, that force—because of the continual addition of a new force—were increased in a ratio that is greater than the square of the diminished distance, it is manifest that that body, being always impelled toward the center by the continual addition of that new force, would incline toward this center more than if it were urged only by a force increasing as the square of the diminished distance, and therefore would describe an orbit inside the elliptical orbit and in its lower apsis would approach nearer to the center than before. Therefore by the addition of this new force, the eccentricity of the orbit will be increased. Now if, during the receding of the body from the lower to the upper apsis, the force were to decrease by the same degrees by which it had previously increased, the body would return to its former distance; and so, if the force decreases in a greater ratio, the body, now attracted less, will ascend to a greater distance, and thus the eccentricity of its orbit will be increased still more. And therefore, if the ratio of the increase and decrease of the centripetal force is increased in each revolution, the eccentricity will always be increased; and contrariwise, the eccentricity will be diminished if that ratio decreases.
Now, in the system of bodies T, P, and S, when the apsides of the orbit PAB are in the quadratures, this ratio of the increase and decrease is least, and it becomes greatest when the apsides are in the syzygies. If the apsides are in the quadratures, the ratio near the apsides is smaller and near the syzygies is greater than the squared ratio of the distances, and from that greater ratio arises the forward or direct motion of the upper apsis, as has already been stated. But if one considers the ratio of the total increase or decrease in the forward motion between the apsides, this ratio is smaller than the squared ratio of the distances. The force in the lower apsis is to the force in the upper apsis in a ratio that is less than the squared ratio of the distance of the upper apsis from the focus of the ellipse to the distance of the lower apsis from that same focus; and conversely, when the apsides are in the syzygies, the force in the lower apsis is to the force in the upper apsis in a ratio greater than that of the squares of the distances.
For the forces LM in the quadratures, added to the forces of body T, compose forces in a smaller ratio, and the forces KL in the syzygies, subtracted from the forces of body T, leave forces in a greater ratio. Therefore, the ratio of the total decrease and increase during the passage between apsides is least in the quadratures and greatest in the syzygies; and therefore, during the passage of the apsides from quadratures to syzygies, this ratio is continually increased and it increases the eccentricity of the ellipse; and in the passage from syzygies to quadratures, this ratio is continually diminished and it diminishes the eccentricity.
COROLLARY 10. To give an account of the errors in latitude, let us imagine that the plane of the orbit EST remains motionless; then from the cause of errors just expounded, it is manifest that of the forces NM and ML (which are the entire cause of these errors) the force ML, always acting in the plane of the orbit PAB, never perturbs the motions in latitude. It is likewise manifest that when the nodes are in the syzygies, the force NM, also acting in the same plane of the orbit, does not perturb these motions; but when the nodes are in the quadratures, this force perturbs those motions to the greatest extent, and—by continually attracting body P away from the plane of its orbit—diminishes the inclination of the plane during the passage of the body from quadratures to syzygies and increases that inclination in turn during the passage from syzygies to quadratures. Hence it happens that when the body is in the syzygies the inclination turns out to be least of all, and it returns approximately to its former magnitude when the body comes to the next node. But if the nodes are situated in the octants after the quadratures, that is, between C and A, or D and B, it will be understood from what has just been explained that in the passage of body P from either node to a position 90 degrees from there, the inclination of the plane is continually diminished; then, in its passage through the next 45 degrees to the next quadrature, the inclination is increased; and afterward, in its next passage through another 45 degrees to the next node, it is diminished. Therefore, the inclination is diminished more than it is increased, and hence it is always less in each successive node than in the immediately preceding one. And by a similar reasoning, it follows that the inclination is increased more than it is diminished when the nodes are in the other octants between A and B, or B and C. Thus, when the nodes are in the syzygies, the inclination is greatest of all. In the passage of the nodes from syzygies to quadratures, the inclination is diminished in each appulse of the body to the nodes, and it becomes least of all when the nodes are in the quadratures and the body is in the syzygies; then it increases by the same degrees by which it had previously decreased, and at the appulse of the nodes to the nearest syzygies it returns to its original magnitude.
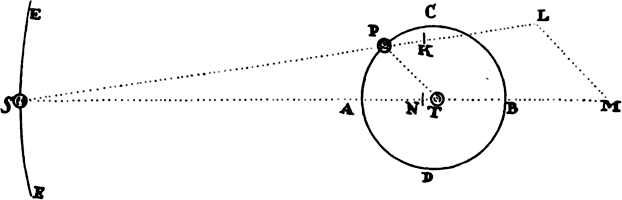
COROLLARY 11. When the nodes are in the quadratures, the body P is continually attracted away from the plane of its orbit in the direction toward S, during its passage from the node C through the conjunction A to the node D, and in the opposite direction in its passage from node D through opposition B to node C; hence it is manifest that the body, in its motion from node C, continually recedes from the first plane CD of its orbit until it has reached the next node; and therefore at this node, being at the greatest distance from that first plane CD, it passes through EST, the plane of the orbit, not in the other node D of that plane but in a point that is closer to body S and which accordingly is a new place of the node, behind its former place. By a similar argument the nodes will continue to recede in the passage of the body from this node to the next node. Hence the nodes, when situated in the quadratures, continually recede; in the syzygies, when the motion in latitude is not at all perturbed, the nodes are at rest; in the intermediate places, since they share in both conditions, they recede more slowly; and therefore, since the nodes always either have a retrograde motion or are stationary, they are carried backward [or in antecedentia] in each revolution.
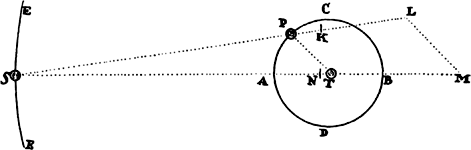
COROLLARY 12. All the errors described in these corollaries are slightly greater in the conjunction of bodies P and S than in their opposition; and this occurs because then the generating forces NM and ML are greater.
COROLLARY 13. And since the proportions in these corollaries do not depend on the magnitude of the body S, all the preceding statements are valid when the magnitude of body S is assumed to be so great that the system of two bodies T and P will revolve about it. And from this increase of body S, and consequently the increase of its centripetal force (from which the errors of body P arise), all those errors will—at equal distances—come out greater in this case than in the other, in which body S revolves around the system of bodies P and T.
COROLLARY 14.b When body S is extremely far away, the forces NM and ML are very nearly as the force SK and the ratio of PT to ST jointly (that is, if both the distance PT and the absolute force of body S are given, as ST3 inversely), and those forces NM and ML are the causes of all the errors and effects that have been dealt with in the preceding corollaries; hence it is manifest that all these effects—if the system of bodies T and P stays the same and only the distance ST and the absolute force of body S are changed—are very nearly in a ratio compounded of the direct ratio of the absolute force of body S and the inverse ratio of the cube of the distance ST. Accordingly, if the system of bodies T and P revolves about the distant body S, those forces NM and ML and their effects will (by prop. 4, corols. 2 and 6) be inversely as the square of the periodic time. And hence also, if the magnitude of body S is proportional to its absolute force, those forces NM and ML and their effects will be directly as the cube of the apparent diameter of the distant body S when looked at from body T, and conversely. For these ratios are the same as the above-mentioned compounded ratio.
COROLLARY 15. If the magnitudes of the orbits ESE and PAB are changed, while their forms and their proportions and inclinations to each other remain the same, and if the forces of bodies S and T either remain the same or are changed in any given ratio, then these forces (that is, the force of body T, by whose action body P is compelled to deflect from a straight path into an orbit PAB; and the force of body S, by whose action that same body P is compelled to deviate from that orbit) will always act in the same way and in the same proportion; thus it will necessarily be the case that all the effects will be similar and proportional and that the times for these effects will be proportional as well—that is, all the linear errors will be as the diameters of the orbits, the angular errors will be the same as before, and the times of similar linear errors or of equal angular errors will be as the periodic times of the orbits.
COROLLARY 16. And hence, if the forms of the orbits and their inclination to each other are given, and the magnitudes, forces, and distances of the bodies are changed in any way, then from the given errors and given times of errors in one case there can be found the errors and times of errors in any other case very nearly. This may be done more briefly, however, by the following method. The forces NM and ML, other things remaining the same, are as the radius TP, and their periodic effects are (by lem. 10, corol. 2) jointly as the forces and the square of the periodic time of body P. These are the linear errors of body P, and hence the angular errors as seen from the center T (that is, the motions of the upper apsis and of the nodes, as well as all the apparent errors in longitude and latitude) are in any revolution of body P very nearly as the square of the time of revolution. Let these ratios be compounded with the ratios of corol. 14; then in any system of bodies T, P, and S, in which P revolves around T which is near to it and T revolves around a distant S, the angular errors of body P, as seen from the center T, will—in each revolution of that body P—be as the square of the periodic time of body P directly and the square of the periodic time of body T inversely. And thus the mean motion of the upper apsis will be in a given ratio to the mean motion of the nodes, and each of the two motions will be as the periodic time of body P directly and the square of the periodic time of body T inversely. By increasing or decreasing the eccentricity and inclination of the orbit PAB, the motions of the upper apsis and of the nodes are not changed sensibly, except when the eccentricity and inclination are too great.
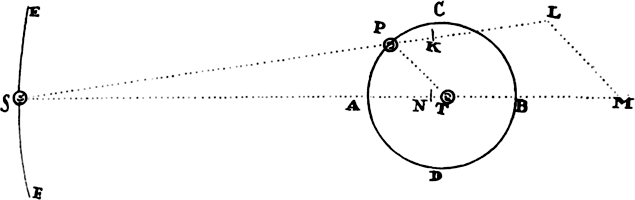
COROLLARY 17. Since, however, the line LM is sometimes greater and sometimes less than the radius PT, let the mean force LM be represented by that radius PT; then this force will be to the mean force SK or SN (which can be represented by ST) as the length PT to the length ST. But the mean force SN or ST by which body T is kept in its orbit around S is to the force by which body P is kept in its orbit around T in a ratio compounded of the ratio of the radius ST to the radius PT and the square of the ratio of the periodic time of body P around T to the periodic time of body T around S. And from the equality of the ratios [or ex aequo] the mean force LN is to the force by which a body P is kept in its orbit around T (or by which the same body P could revolve in the same periodic time around any immobile point T at a distance PT) in the same squared ratio of the periodic times. Therefore, if the periodic times are given, along with the distance PT, the mean force LM is also given; and if the force LM is given, the force MN is also given very nearly by the proportion of lines PT and MN.
COROLLARY 18. Let us imagine many fluid bodies to move around body T at equal distances from it according to the same laws by which body P revolves around the same body T; then let a ring—fluid, round, and concentric to body T—be produced by making these individual fluid bodies come into contact with one another; these individual parts of the ring, carrying out all their motions according to the law of body P, will approach closer to body T and will move more swiftly in the conjunction and opposition of themselves and body S than in the quadratures. The nodes of this ring, or its intersections with the plane of the orbit of body S or T, will be at rest in the syzygies, but outside the syzygies they will move backward [or in antecedentia], and do so most swiftly in the quadratures and more slowly in other places. The inclination of the ring will also vary, and its axis will oscillate in each revolution; and when a revolution has been completed, it will return to its original position except insofar as it is carried around by the precession of the nodes.
COROLLARY 19. Now imagine the globe T, which consists of nonfluid matter, to be so enlarged as to extend out to this ring, and to have a channel to contain water dug out around its whole circumference; and imagine this new globe to revolve uniformly about its axis with the same periodic motion. This water, being alternately accelerated and retarded (as in the previous corollary), will be swifter in the syzygies and slower in the quadratures than the surface of the globe itself, and thus will ebb and flow in the channel just as the sea does. If the attraction of body S is taken away, the water—now revolving about the quiescent center of the globe—will acquire no motion of ebb and flow. This is likewise the case for a globe advancing uniformly straight forward and meanwhile revolving about its own center (by corol. 5 of the laws), and also for a globe uniformly attracted away from a rectilinear path (by corol. 6 of the laws). But let body S now draw near, and by its nonuniform attraction of the water, the water will soon be disturbed. For its attraction of the nearer water will be greater and that of the more distant water will be smaller. Moreover, the force LM will attract the water downward in the quadratures and will make it descend as far as the syzygies, and the force KL will attract this same water upward in the syzygies and will prevent its further descent and will make it ascend as far as the quadratures, except insofar as the motion of ebb and flow is directed by the channel of water and is somewhat retarded by friction.
COROLLARY 20. If the ring now becomes hard and the globe is diminished, the motion of ebb and flow will cease; but the oscillatory motion of the inclination and the precession of the nodes will remain. Let the globe have the same axis as the ring and complete its revolutions in the same times, and let its surface touch the inside of the ring and adhere to it; then, with the globe participating in the motion of the ring, the structure of the two will oscillate and the nodes will regress. For the globe, as will be shown presently, is susceptible to all impressions equally. The greatest angle of inclination of the ring alone, with the globe removed, occurs when the nodes are in the syzygies. From there in the forward motion of the nodes to the quadratures it endeavors to diminish its inclination and by that endeavor impresses a motion upon the whole globe. The globe keeps this impressed motion until the ring removes this motion by an opposite endeavor and impresses a new motion in the opposite direction; and in this way the greatest motion of the decreasing inclination occurs when the nodes are in the quadratures, and the least angle of inclination occurs in the octants after the quadratures; and the greatest motion of reclination occurs in the syzygies, and the greatest angle in the next octants. And this is likewise the case for a globe which has no such ring and which in the regions of the equator is either a little higher than near the poles or consists of matter a little denser. For that excess of matter in the regions of the equator takes the place of a ring. And although, by increasing the centripetal force of this globe in any way whatever, all its parts are supposed to tend downward, as the gravitating parts of the earth do, nevertheless the phenomena of this corollary and of corol. 19 will scarcely be changed on that account, except that the places of the greatest and least height of the water will be different. For the water is now sustained and remains in its orbit not by its own centrifugal force but by the channel in which it is flowing. And besides, the force LM attracts the water downward to the greatest degree in the quadratures, and the force KL or NM − LM attracts the same water upward to the greatest degree in the syzygies. And these forces conjoined cease to attract the water downward and begin to attract the water upward in the octants before the syzygies, and they cease to attract the water upward and begin to attract the water downward in the octants after the syzygies. As a result, the greatest height of the water can occur very nearly in the octants after the syzygies, and the least height can occur very nearly in the octants after the quadratures, except insofar as the motion of ascent or descent impressed on the water by these forces either perseveres a little longer because of the inherent force of the water or is stopped a little more swiftly because of the impediments of the channel.
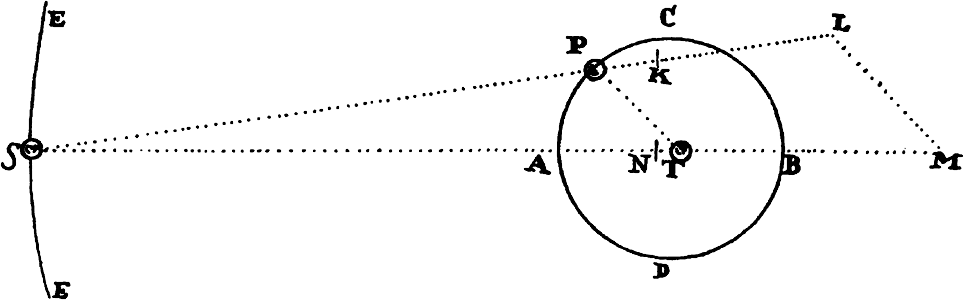
COROLLARY 21. In the same way that the excess matter of a globe near its equator makes the nodes regress (and thus the retrogression is increased by increase of equatorial matter and is diminished by its diminution and is removed by its removal), it follows that if more than the excess matter is removed, that is, if the globe near the equator is made either more depressed or more rare than near the poles, there will arise a motion of the nodes forward [or in consequentia].
COROLLARY 22. And thus, in turn, from the motion of the nodes the constitution of a globe can be found. That is to say, if a globe constantly preserves the same poles and there occurs a motion backward [or in antecedentia], there is an excess of matter near the equator; if there occurs a motion forward [or in consequentia], there is a deficiency. Suppose that a uniform and perfectly spherical globe is at first at rest in free space; then is propelled by any impetus whatever delivered obliquely upon its surface, from which it takes on a motion that is partly circular [i.e., rotational] and partly straight forward. Because the globe is indifferent to all axes passing through its center and does not have a greater tendency to turn around any one axis or an axis at any particular inclination, it is clear that the globe, by its own force alone, will never change its axis and the inclination of the axis. Now let the globe be impelled obliquely by any new impulse whatever, delivered to that same part of the surface as before; then, since the effect of an impulse is in no way changed by its being delivered sooner or later, it is manifest that the same motion will be produced by these two impulses being successively impressed as if they had been impressed simultaneously, that is, the resultant motion will be the same as if the globe had been impelled by a simple force compounded of these two (by corol. 2 of the laws), and hence will be a simple motion about an axis of a given inclination. This is likewise the case for a second impulse impressed in any other place on the equator of the first motion; and also for a first impulse impressed in any place on the equator of the motion which the second impulse would generate without the first, and hence for both impulses impressed in any places whatever. These two impulses will generate the same circular motion as if they had been impressed together and all at once in the place of intersection of the equators of the motions which each of them would generate separately. Therefore a homogeneous and perfect globe does not retain several distinct motions but compounds all the motions impressed on it and reduces them to one; and insofar as it can in and of itself, it always rotates with a simple and uniform motion about a single axis of a given and always invariable inclination. A centripetal force cannot change either this inclination of the axis or the velocity of rotation.
If a globe is thought of as divided into two hemispheres by any plane passing through the center of the globe and the center toward which a force is directed, that force will always urge both hemispheres equally and therefore will not cause the globe—as regards its motion of rotation—to incline in any direction. Let some new matter, heaped up in the shape of a mountain, be added to the globe anywhere between the pole and the equator; then this matter, by its continual endeavor to recede from the center of its motion, will disturb the motion of the globe and will make its poles wander over its surface and continually describe circles about themselves and the point opposite to them. And this tremendous wandering of the poles will not be corrected, save by placing the mountain either in one of the two poles, in which case (by corol. 21) the nodes of the equator will advance, or on the equator, in which case (by corol. 20) the nodes will regress, or finally by placing on the other side of the axis some additional matter by which the mountain is balanced in its motion, and in this way the nodes will either advance or regress, according as the mountain and this new matter are closer to a pole or to the equator.
Proposition 67, Theorem 27
With the same laws of attraction being supposed, I say that with respect to the
common center of gravity O of the inner bodies P and T, the outer body S—by
radii drawn to that center—describes areas more nearly proportional to the times,
and an orbit more closely approaching the shape of an ellipse having its focus in
that same center, than it can describe about the innermost and greatest body T by
radii drawn to that body.
For the attractions of body S toward
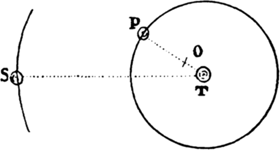 T and P compose its absolute attraction,
which is directed more toward the common
center of gravity O of bodies T and P than
toward the greatest body T, and which is
more nearly inversely proportional to the
square of the distance SO than to the square of the distance ST, as will
easily be seen by anyone carefully considering the matter.
T and P compose its absolute attraction,
which is directed more toward the common
center of gravity O of bodies T and P than
toward the greatest body T, and which is
more nearly inversely proportional to the
square of the distance SO than to the square of the distance ST, as will
easily be seen by anyone carefully considering the matter.
Proposition 68, Theorem 28
With the same laws of attraction being supposed, I say that with respect to the
common center of gravity O of the inner bodies P and T, the outer body S—by
radii drawn to that center—describes areas more nearly proportional to the times,
and an orbit more closely approaching the shape of an ellipse having its focus in
the same center, if the innermost and greatest body is acted on by these attractions
just as the others are, than would be the case if it is either not attracted and
is at rest or is much more or much less attracted or much more or much less
moved.
This is demonstrated in almost the same way as prop. 66, but the proof is more prolix and I therefore omit it. The following considerations should suffice.
From the demonstration of the last
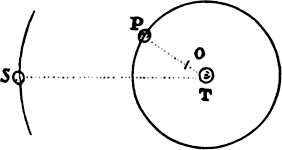 proposition it is apparent that the center
toward which body S is urged by both
forces combined is very near to the
common center of gravity of the other bodies P
and T. If this center were to coincide with
the common center of those two bodies, and the common center of gravity of
all three bodies were to be at rest, body S on the one hand and the common
center of the other two bodies on the other would describe exact ellipses
about the common center of them all which is at rest. This is clear from the
second corollary of prop. 58 compared with what is demonstrated in props.
64 and 65. Such an exact elliptical motion is perturbed somewhat by the
distance of the center of the two bodies from the center toward which the
third body S is attracted. Let a motion be given, in addition, to the common
center of the three, and the perturbation will be increased. Accordingly, the
perturbation is least when the common center of the three is at rest, that is,
when the innermost and greatest body T is attracted by the very same law
as the others; and it always becomes greater when the common center of the
three bodies, by a diminution of the motion of body T, begins to be moved
and thereupon acted on more and more.
proposition it is apparent that the center
toward which body S is urged by both
forces combined is very near to the
common center of gravity of the other bodies P
and T. If this center were to coincide with
the common center of those two bodies, and the common center of gravity of
all three bodies were to be at rest, body S on the one hand and the common
center of the other two bodies on the other would describe exact ellipses
about the common center of them all which is at rest. This is clear from the
second corollary of prop. 58 compared with what is demonstrated in props.
64 and 65. Such an exact elliptical motion is perturbed somewhat by the
distance of the center of the two bodies from the center toward which the
third body S is attracted. Let a motion be given, in addition, to the common
center of the three, and the perturbation will be increased. Accordingly, the
perturbation is least when the common center of the three is at rest, that is,
when the innermost and greatest body T is attracted by the very same law
as the others; and it always becomes greater when the common center of the
three bodies, by a diminution of the motion of body T, begins to be moved
and thereupon acted on more and more.
COROLLARY. And hence, if several lesser bodies revolve about a greatest one, it can be found that the orbits described will approach closer to elliptical orbits, and the descriptions of areas will become more uniform, if all the bodies attract and act on one another by accelerative forces that are directly as their absolute forces and inversely as the squares of the distances, and if the focus of each orbit is located in the common center of gravity of all the inner bodies (that is to say, with the focus of the first and innermost orbit in the center of gravity of the greatest and innermost body; the focus of the second orbit in the common center of gravity of the two innermost bodies; the focus of the third in the common center of gravity of the three inner bodies; and so on), than if the innermost body is at rest and is set at the common focus of all the orbits.
Proposition 69, Theorem 29
If, in a system of several bodies A, B, C, D, . . . , some body A attracts all the
others, B, C, D, . . . , by accelerative forces that are inversely as the squares of
the distances from the attracting body; and if another body B also attracts the rest
of the bodies A, C, D, . . . , by forces that are inversely as the squares of the
distances from the attracting body; then the absolute forces of the attracting bodies
A and B will be to each other in the same ratio as the bodies [i.e., the masses] A
and B themselves to which those forces belong.
For, at equal distances, the accelerative attractions of all the bodies B, C, D, . . . toward A are equal to one another by hypothesis; and similarly, at equal distances, the accelerative attractions of all the bodies toward B are equal to one another. Moreover, at equal distances, the absolute attractive force of body A is to the absolute attractive force of body B as the accelerative attraction of all the bodies toward A is to the accelerative attraction of all the bodies toward B at equal distances; and the accelerative attraction of body B toward A is also in the same proportion to the accelerative attraction of body A toward B. But the accelerative attraction of body B toward A is to the accelerative attraction of body A toward B as the mass of body A is to the mass of body B, because the motive forces—which (by defs. 2, 7, and 8) are as the accelerative forces and the attracted bodies jointly—are in this case (by the third law of motion) equal to each other. Therefore the absolute attractive force of body A is to the absolute attractive force of body B as the mass of body A is to the mass of body B. Q.E.D.
COROLLARY 1. Hence if each of the individual bodies of the system A, B, C, D, . . . , considered separately, attracts all the others by accelerative forces that are inversely as the squares of the distances from the attracting body, the absolute forces of all those bodies will be to one another in the ratios of the bodies [i.e., the masses] themselves.
COROLLARY 2. By the same argument, if each of the individual bodies of the system A, B, C, D, . . . , considered separately, attracts all the others by accelerative forces that are either inversely or directly as any powers whatever of the distances from the attracting body, or that are defined in terms of the distances from each one of the attracting bodies according to any law common to all these bodies; then it is evident that the absolute forces of those bodies are as the bodies [i.e., the masses].
COROLLARY 3. If, in a system of bodies whose forces decrease in the squared ratio of the distances [i.e., vary inversely as the squares of the distances], the lesser bodies revolve about the greatest one in ellipses as exact as they can be, having their common focus in the center of that greatest body, and—by radii drawn to the greatest body—describe areas as nearly as possible proportional to the times, then the absolute forces of those bodies will be to one another, either exactly or very nearly, as the bodies, and conversely. This is clear from the corollary of prop. 68 compared with corol. 1 of this proposition.
Scholium
By these propositions we are directed to the analogy between centripetal
forces and the central bodies toward which those forces tend. For it is
reasonable that forces directed toward bodies depend on the nature and the
quantity of matter of such bodies, as happens in the case of magnetic bodies.
And whenever cases of this sort occur, the attractions of the bodies must be
reckoned by assigning proper forces to their individual particles and then
taking the sums of these forces.
I use the word “attraction” here in a general sense for any endeavor whatever of bodies to approach one another, whether that endeavor occurs as a result of the action of the bodies either drawn toward one another or acting on one another by means of spirits emitted or whether it arises from the action of aether or of air or of any medium whatsoever—whether corporeal or incorporeal—in any way impelling toward one another the bodies floating therein. I use the word “impulse” in the same general sense, considering in this treatise not the species of forces and their physical qualities but their quantities and mathematical proportions, as I have explained in the definitions.
Mathematics requires an investigation of those quantities of forces and their proportions that follow from any conditions that may be supposed. Then, coming down to physics, these proportions must be compared with the phenomena, so that it may be found out which conditions [or laws] of forces apply to each kind of attracting bodies. And then, finally, it will be possible to argue more securely concerning the physical species, physical causes, and physical proportions of these forces. Let us see, therefore, what the forces are by which spherical bodies, consisting of particles that attract in the way already set forth, must act upon one another, and what sorts of motions result from such forces.
The attractive forces of spherical bodies
Proposition 70, Theorem 30
If toward each of the separate points of a spherical surface there tend equal
centripetal forces decreasing as the squares of the distances from the point, I say that
a corpuscle placed inside the surface will not be attracted by these forces in any
direction.
Let HIKL be the spherical surface, and P the corpuscle placed inside.
Through P draw to this surface the two lines HK and IL intercepting
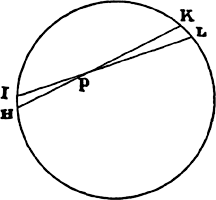 minimally small arcs HI and KL; and because
triangles HPI and LPK are similar (by lem. 7,
corol. 3), those arcs will be proportional to the
distances HP and LP; and any particles of the
spherical surface at HI and KL, terminated
everywhere by straight lines passing through point
P, will be in that proportion squared. Therefore
the forces exerted on body P by these particles of
surface are equal to one another. For they are as the particles directly and the
squares of the distances inversely. And these two ratios, when compounded,
give the ratio of equality. The attractions, therefore, being made equally in
opposite directions, annul each other. And by a similar argument, all the
attractions throughout the whole spherical surface are annulled by opposite
attractions. Accordingly, body P is not impelled by these attractions in any
direction. Q.E.D.
minimally small arcs HI and KL; and because
triangles HPI and LPK are similar (by lem. 7,
corol. 3), those arcs will be proportional to the
distances HP and LP; and any particles of the
spherical surface at HI and KL, terminated
everywhere by straight lines passing through point
P, will be in that proportion squared. Therefore
the forces exerted on body P by these particles of
surface are equal to one another. For they are as the particles directly and the
squares of the distances inversely. And these two ratios, when compounded,
give the ratio of equality. The attractions, therefore, being made equally in
opposite directions, annul each other. And by a similar argument, all the
attractions throughout the whole spherical surface are annulled by opposite
attractions. Accordingly, body P is not impelled by these attractions in any
direction. Q.E.D.
Proposition 71, Theorem 31
With the same conditions being supposed as in prop. 70, I say that a corpuscle
placed outside the spherical surface is attracted to the center of the sphere by a
force inversely proportional to the square of its distance from that same center.
Let AHKB and ahkb be two equal spherical surfaces, described about centers S and s with diameters AB and ab, and let P and p be corpuscles located outside those spheres in those diameters produced. From the corpuscles draw lines PHK, PIL, phk, and pil, so as to cut off from the great circles AHB and ahb the equal arcs HK and hk, and IL and il. And onto these lines drop perpendiculars SD and sd, SE and se, IR and ir, of which SD and sd cut PL and pl at F and f. Also drop perpendiculars IQ and iq onto the diameters. Let angles DPE and dpe vanish; then, because DS and ds, ES and es are equal, lines PE, PF and pe, pf and the line-elements DF and df may be considered to be equal, inasmuch as their ultimate ratio, when angles DPE and dpe vanish simultaneously, is the ratio of equality.
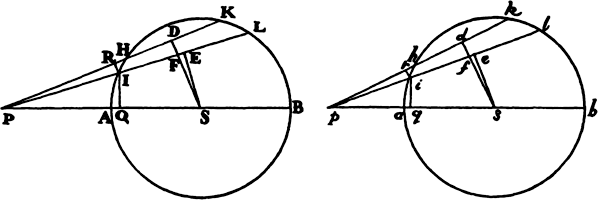
On the basis of these things, therefore, PI will be to PF as RI to DF, and pf to pi as df or DF to ri, and from the equality of the ratios [or ex aequo] PI × pf will be to PF × pi as RI to ri, that is (by lem. 7, corol. 3), as the arc IH to the arc ih. Again, PI will be to PS as IQ to SE, and ps will be to pi as se or SE to iq; and from the equality of the ratios [or ex aequo] PI × ps will be to PS × pi as IQ to iq. And by compounding these ratios, PI2 × pf × ps will be to pi2 × PF × PS as IH × IQ to ih × iq; that is, as the circular surface that the arc IH will describe by the revolution of the semicircle AKB about the diameter AB to the circular surface that the arc ih will describe by the revolution of the semicircle akb about the diameter ab. And the forces by which these surfaces attract the corpuscles P and p (along lines tending to these same surfaces) are (by hypothesis) as these surfaces themselves directly and the squares of the distances of these surfaces from the bodies inversely, that is, as pf × ps to PF × PS.
Now (once the resolution of the forces has been made according to
corol. 2 of the laws), these forces are to their oblique parts, which tend
along the lines PS and ps toward the centers, as PI to PQ and pi to pq;
that is (because the triangles PIQ and PSF, piq and psf are similar), the
forces are to their oblique parts as PS to PF and ps to pf. Hence, from the
equality of the ratios [or ex aequo] the attraction of this corpuscle P toward
S becomes to the attraction of the corpuscle p toward s as 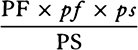 to
to
 , that is, as ps2 to PS2. And by a similar argument, the forces
by which the surface described by the revolution of the arcs KL and kl
attract the corpuscles will be as ps2 to PS2. And the same ratio will hold for
the forces of all the spherical surfaces into which each of the two spherical
surfaces can be divided by taking sd always equal to SD and se equal to
SE. And by composition [or componendo] the forces of the total spherical
surfaces exercised upon the corpuscles will be in the same ratio. Q.E.D.
, that is, as ps2 to PS2. And by a similar argument, the forces
by which the surface described by the revolution of the arcs KL and kl
attract the corpuscles will be as ps2 to PS2. And the same ratio will hold for
the forces of all the spherical surfaces into which each of the two spherical
surfaces can be divided by taking sd always equal to SD and se equal to
SE. And by composition [or componendo] the forces of the total spherical
surfaces exercised upon the corpuscles will be in the same ratio. Q.E.D.
Proposition 72, Theorem 32
If toward each of the separate points of any sphere there tend equal centripetal
forces, decreasing in the squared ratio of the distances from those points, and there
are given both the density of the sphere and the ratio of the diameter of the sphere
to the distance of the corpuscle from the center of the sphere, I say that the force
by which the corpuscle is attracted will be proportional to the semidiameter of the
sphere.
For imagine that two corpuscles are attracted separately by two spheres, one corpuscle by one sphere, and the other corpuscle by the other sphere, and that their distances from the centers of the spheres are respectively proportional to the diameters of the spheres, and that the two spheres are resolved into particles that are similar and similarly placed with respect to the corpuscles. Then the attractions of the first corpuscle, made toward each of the separate particles of the first sphere, will be to the attractions of the second toward as many analogous particles of the second sphere in a ratio compounded of the direct ratio of the particles and the inverse squared ratio of the distances [i.e., the attractions will be to one another as the particles directly and the squares of the distances inversely]. But the particles are as the spheres, that is, they are in the cubed ratio of the diameters, and the distances are as the diameters; and thus the first of these ratios directly combined with the second ratio taken twice inversely becomes the ratio of diameter to diameter. Q.E.D.
COROLLARY 1. Hence, if corpuscles revolve in circles about spheres consisting of equally attractive matter, and their distances from the centers of the spheres are proportional to the diameters of the spheres, the periodic times will be equal.
COROLLARY 2. And conversely, if the periodic times are equal, the distances will be proportional to the diameters. These two corollaries are evident from prop. 4, corol. 3.
COROLLARY 3. If toward each of the separate points of any two similar and equally dense solids there tend equal centripetal forces decreasing in the squared ratio of the distances from those points, the forces by which corpuscles will be attracted by those two solids, if they are similarly situated with regard to them, will be to each other as the diameters of the solids.
Proposition 73, Theorem 33
If toward each of the separate points of any given sphere there tend equal
centripetal forces decreasing in the squared ratio of the distances from those points; I
say that a corpuscle placed inside the sphere is attracted by a force proportional to
the distance of the corpuscle from the center of the sphere.
Let a corpuscle P be placed inside the sphere ABCD, described about
center S; and about the same center S with radius SP, suppose that an inner
 sphere PEQF is described. It is manifest (by
prop. 70) that the concentric spherical surfaces
of which the difference AEBF of the spheres is
composed do not act at all upon body P, their
attractions having been annulled by opposite
attractions. There remains only the attraction of
the inner sphere PEQF. And (by prop. 72) this
is as the distance PS. Q.E.D.
sphere PEQF is described. It is manifest (by
prop. 70) that the concentric spherical surfaces
of which the difference AEBF of the spheres is
composed do not act at all upon body P, their
attractions having been annulled by opposite
attractions. There remains only the attraction of
the inner sphere PEQF. And (by prop. 72) this
is as the distance PS. Q.E.D.
Scholium
The surfaces of which the solids are composed are here not purely
mathematical, but orbs [or spherical shells] so extremely thin that their thickness is
as null: namely, evanescent orbs of which the sphere ultimately consists when
the number of those orbs is increased and their thickness diminished
indefinitely. Similarly, when lines, surfaces, and solids are said to be composed of
points, such points are to be understood as equal particles of a magnitude so
small that it can be ignored.
Proposition 74, Theorem 34
With the same things being supposed as in prop. 73, I say that a corpuscle placed
outside a sphere is attracted by a force inversely proportional to the square of the
distance of the corpuscle from the center of the sphere.
For let the sphere be divided into innumerable concentric spherical surfaces; then the attractions of the corpuscle that arise from each of the surfaces will be inversely proportional to the square of the distance of the corpuscle from the center (by prop. 71). And by composition [or componendo] the sum of the attractions (that is, the attraction of the corpuscle toward the total sphere) will come out in the same ratio. Q.E.D.
COROLLARY 1. Hence at equal distances from the centers of homogeneous spheres the attractions are as the spheres themselves. For (by prop. 72) if the distances are proportional to the diameters of the spheres, the forces will be as the diameters. Let the greater distance be diminished in that ratio; and, the distances having now become equal, the attraction will be increased in that ratio squared, and thus will be to the other attraction in that ratio cubed, that is, in the ratio of the spheres.
COROLLARY 2. At any distances the attractions are as the spheres divided by the squares of the distances.
COROLLARY 3. If a corpuscle placed outside a homogeneous sphere is attracted by a force inversely proportional to the square of the distance of the corpuscle from the center of the sphere, and the sphere consists of attracting particles, the force of each particle will decrease in the squared ratio of the distance from the particle.
Proposition 75, Theorem 35
If toward each of the points of a given sphere there tend equal centripetal forces
decreasing in the squared ratio of the distances from the points, I say that this sphere
will attract any other homogeneous sphere with a force inversely proportional to
the square of the distance between the centers.a
For the attraction of any particle is inversely as the square of its distance from the center of the attracting sphere (by prop. 74), and therefore is the same as if the total attracting force emanated from one single corpuscle situated in the center of this sphere. Moreover, this attraction is as great as the attraction of the same corpuscle would be if, in turn, it were attracted by each of the individual particles of the attracted sphere with the same force by which it attracts them. And that attraction of the corpuscle (by prop. 74) would be inversely proportional to the square of its distance from the center of the sphere; and therefore the sphere’s attraction, which is equal to the attraction of the corpuscle, is in the same ratio. Q.E.D.
COROLLARY 1. The attractions of spheres toward other homogeneous spheres are as the attracting spheres [i.e., as the masses of the attracting spheres] divided by the squares of the distances of their own centers from the centers of those that they attract.
COROLLARY 2. The same is true when the attracted sphere also attracts. For its individual points will attract the individual points of the other with the same force by which they are in turn attracted by them; and thus, since in every attraction the attracting point is as much urged (by law 3) as the attracted point, the force of the mutual attraction will be duplicated, the proportions remaining the same.
COROLLARY 3. Everything that has been demonstrated above concerning the motion of bodies about the focus of conics is valid when an attracting sphere is placed in the focus and the bodies move outside the sphere.
COROLLARY 4. And whatever concerns the motion of bodies around the center of conics applies when the motions are performed inside the sphere.
Proposition 76, Theorem 36
If spheres are in any way nonhomogeneous (as to the density of their matter and
their attractive force) going from the center to the circumference, but are uniform
throughout in every spherical shell at any given distance from the center, and the
attractive force of each point decreases in the squared ratio of the distance of the
attracted body, I say that the total force by which one sphere of this sort attracts
another is inversely proportional to the square of the distance between their centers.
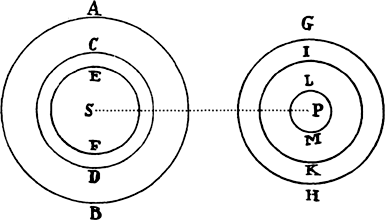
COROLLARY 1. Hence, if many spheres of this sort, similar to one another in all respects, attract one another, the accelerative attraction of any one to any other of them, at any equal distances between the centers, will be as the attracting spheres.
COROLLARY 2. And at any unequal distances, as the attracting sphere divided by the square of the distances between the centers.
COROLLARY 3. And the motive attractions, or the weights of spheres toward other spheres, will—at equal distances from the centers—be as the attracting and the attracted spheres jointly, that is, as the products produced by multiplying the spheres by each other.
COROLLARY 4. And at unequal distances, as those products directly and the squares of the distances between the centers inversely.
COROLLARY 5. These results are valid when the attraction arises from each sphere’s force of attraction being mutually exerted upon the other sphere. For the attraction is duplicated by both forces acting, the proportion remaining the same.
COROLLARY 6. If some spheres of this sort revolve about others at rest, one sphere revolving about each sphere at rest, and the distances between the centers of the revolving spheres and those at rest are proportional to the diameters of those at rest, the periodic times will be equal.
COROLLARY 7. And conversely, if the periodic times are equal, the distances will be proportional to those diameters.
COROLLARY 8. Everything that has been demonstrated above about the motion of bodies around the foci of conics holds when the attracting sphere, of any form and condition that has already been described, is placed in the focus.
COROLLARY 9. As also when the bodies revolving in orbit are also attracting spheres of any condition that has already been described.
Proposition 77, Theorem 37
If toward each of the individual points of spheres there tend centripetal forces
proportional to the distances of the points from attracted bodies, I say that the
composite force by which two spheres will attract each other is as the distance
between the centers of the spheres.
CASE 1. Let AEBF be a sphere, S its center, P an attracted exterior
corpuscle, PASB that axis of the sphere which passes through the center of
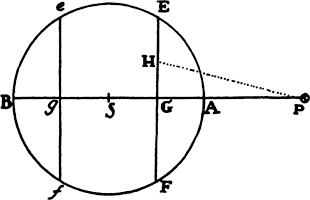 the corpuscle, EF and ef two planes by
which the sphere is cut and which are
perpendicular to this axis and equally
distant on both sides from the center of
the sphere, G and g the intersections
of the planes and the axis, and H any
point in the plane EF. The centripetal
force of point H upon the corpuscle P,
exerted along the line PH, is as the distance PH; and (by corol. 2 of the laws)
along the line PG, or toward the center S, as the length PG. Therefore the
force of all the points in the plane EF (that is, of the total plane) by which the
corpuscle P is attracted toward the center S is as the distance PG multiplied
by the number of such points, that is, as the solid contained by that plane
EF itself and the distance PG [i.e., as the product of the plane EF and the
distance PG]. And similarly the force of the plane ef, by which the corpuscle
P is attracted toward the center S, is as that plane multiplied by its distance
Pg, or as the plane EF equal thereto multiplied by that distance Pg; and the
sum of the forces of both planes is as the plane EF multiplied by the sum of
the distances PG + Pg; that is, as that plane multiplied by twice the distance
PS between the center S and the corpuscle P; that is, as twice the plane EF
multiplied by the distance PS, or as the sum of the equal planes EF + ef
multiplied by that same distance. And by a similar argument, the forces of all
the planes in the whole sphere, equally distant on both sides from the center
of the sphere, are as the sum of those planes multiplied by the distance PS,
that is, as the whole sphere and the distance PS jointly. Q.E.D.
the corpuscle, EF and ef two planes by
which the sphere is cut and which are
perpendicular to this axis and equally
distant on both sides from the center of
the sphere, G and g the intersections
of the planes and the axis, and H any
point in the plane EF. The centripetal
force of point H upon the corpuscle P,
exerted along the line PH, is as the distance PH; and (by corol. 2 of the laws)
along the line PG, or toward the center S, as the length PG. Therefore the
force of all the points in the plane EF (that is, of the total plane) by which the
corpuscle P is attracted toward the center S is as the distance PG multiplied
by the number of such points, that is, as the solid contained by that plane
EF itself and the distance PG [i.e., as the product of the plane EF and the
distance PG]. And similarly the force of the plane ef, by which the corpuscle
P is attracted toward the center S, is as that plane multiplied by its distance
Pg, or as the plane EF equal thereto multiplied by that distance Pg; and the
sum of the forces of both planes is as the plane EF multiplied by the sum of
the distances PG + Pg; that is, as that plane multiplied by twice the distance
PS between the center S and the corpuscle P; that is, as twice the plane EF
multiplied by the distance PS, or as the sum of the equal planes EF + ef
multiplied by that same distance. And by a similar argument, the forces of all
the planes in the whole sphere, equally distant on both sides from the center
of the sphere, are as the sum of those planes multiplied by the distance PS,
that is, as the whole sphere and the distance PS jointly. Q.E.D.
CASE 2. Now let the corpuscle P attract the sphere AEBF. Then by the same argument it can be proved that the force by which that sphere is attracted will be as the distance PS. Q.E.D.
CASE 3. Now let a second sphere be composed of innumerable corpuscles P; then, since the force by which any one corpuscle is attracted is as the distance of the corpuscle from the center of the first sphere and as that same sphere jointly, and thus is the same as if all the force came from one single corpuscle in the center of the sphere, the total force by which all the corpuscles in the second sphere are attracted (that is, by which that whole sphere is attracted) will be the same as if that sphere were attracted by a force coming from one single corpuscle in the center of the first sphere, and therefore is proportional to the distance between the centers of the spheres. Q.E.D.
CASE 4. Let the spheres attract each other mutually; then the force, now duplicated, will keep the former proportion. Q.E.D.
CASE 5. Now let a corpuscle p be placed inside the sphere AEBF. Then,
since the force of the plane ef upon the corpuscle is as the solid contained by
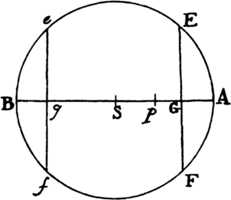 [or the product of] that plane and the distance
pg; and the opposite force of the plane EF is
as the solid contained by [or the product of]
that plane and the distance pG; the force
compounded of the two will be as the difference of
the solids [or the products], that is, as the sum
of the equal planes multiplied by half of the
difference of the distances, that is, as that sum multiplied by pS, the distance
of the corpuscle from the center of the sphere. And by a similar argument,
the attraction of all the planes EF and ef in the whole sphere (that is, the
attraction of the whole sphere) is jointly as the sum of all the planes (or the
whole sphere) and as pS, the distance of the corpuscle from the center of
the sphere. Q.E.D.
[or the product of] that plane and the distance
pg; and the opposite force of the plane EF is
as the solid contained by [or the product of]
that plane and the distance pG; the force
compounded of the two will be as the difference of
the solids [or the products], that is, as the sum
of the equal planes multiplied by half of the
difference of the distances, that is, as that sum multiplied by pS, the distance
of the corpuscle from the center of the sphere. And by a similar argument,
the attraction of all the planes EF and ef in the whole sphere (that is, the
attraction of the whole sphere) is jointly as the sum of all the planes (or the
whole sphere) and as pS, the distance of the corpuscle from the center of
the sphere. Q.E.D.
CASE 6. And if from innumerable corpuscles p a new sphere is composed, placed inside the former sphere AEBF, then it can be proved as above that the attraction, whether the simple attraction of one sphere toward the other, or a mutual attraction of both toward each other, will be as the distance pS between the centers. Q.E.D.
Proposition 78, Theorem 38
If spheres, on going from the center to the circumference, are in any way
nonhomogeneous and nonuniform, but in every concentric spherical shell at any given
distance from the center are homogeneous throughout; and the attracting force of
each point is as the distance of the body attracted; then I say that the total force
by which two spheres of this sort attract each other is proportional to the distance
between the centers of the spheres.
This is demonstrated from prop. 77 in the same way that prop. 76 was demonstrated from prop. 75.
COROLLARY. Whatever was demonstrated above in props. 10 and 64 on the motion of bodies about the centers of conics is valid when all the attractions take place by the force of spherical bodies of the condition already described, and when the attracted bodies are spheres of the same condition.
Scholium
I have now given explanations of the two major cases of attractions, namely,
when the centripetal forces decrease in the squared ratio of the distances or
increase in the simple ratio of the distances, causing bodies in both cases to
revolve in conics, and composing centripetal forces of spherical bodies that
decrease or increase in proportion to the distance from the center according
to the same law—which is worthy of note. It would be tedious to go one by
one through the other cases which lead to less elegant conclusions. I prefer
to comprehend and determine all the cases simultaneously under a general
method as follows.
Lemma 29a
If any circle AEB is described with center S; and then two circles EF and ef are
described with center P, cutting the first circle in E and e, and cutting the line
PS in F and f; and if the perpendiculars ED and ed are dropped to PS; then I
say that if the distance between the arcs EF and ef is supposed to be diminished
indefinitely, the ultimate ratio of the evanescent line Dd to the evanescent line
Ff is the same as that of line PE to line PS.
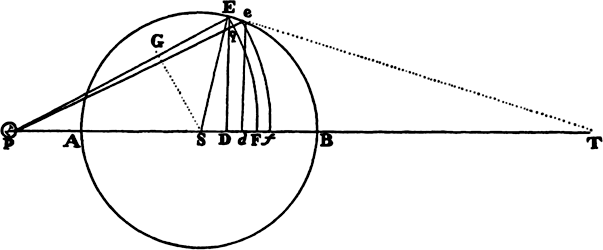
For if line Pe cuts arc EF in q, and the straight line Ee, which coincides with the evanescent arc Ee, when produced meets the straight line PS in T, and the normal SG is dropped from S to PE; then because the triangles DTE, dTe, and DES are similar, Dd will be to Ee as DT to TE, or DE to ES; and because the triangles Eeq and ESG (by sec. 1, lem. 8 and lem. 7, corol. 3) are similar, Ee will be to eq or Ff as ES to SG; and from the equality of the ratios [or ex aequo] Dd will be to Ff as DE to SG—that is (because the triangles PDE and PGS are similar), as PE to PS. Q.E.D.
Proposition 79, Theorem 39
If the surface EFfe, just now vanishing because its width has been indefinitely
diminished, describes by its revolution about the axis PS a concavo-convex spherical
solid, toward each of whose individual equal particles there tend equal centripetal
forces; then I say that the force by which that solid attracts an exterior corpuscle
located in P is in a ratio compounded of the ratio of the solid [or product]
DE2 × Ff and the ratio of the force by which a given particle at the place Ff
would attract the same corpuscle.
For if we first consider the force of the spherical surface FE, which
is generated by the revolution of the arc FE and is cut anywhere by the
line de in r, the annular part of this surface generated by the revolution
of the arc rE will be as the line-element Dd, the radius PE of the sphere
remaining the same (as Archimedes demonstrated in his book on the Sphere
and Cylinder). And the force of that surface, exerted along lines PE or Pr,
placed everywhere in the surface of a cone, will be as this annular part of the
surface—that is, as the line-element Dd or, what comes to the same thing, as
the rectangle of the given radius PE of the sphere and that line-element Dd;
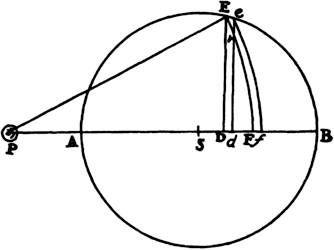 but along the line PS tending toward
the center S, this force will be smaller
in the ratio of PD to PE, and hence
this force will be as PD × Dd. Now
suppose the line DF to be divided into
innumerable equal particles, and let
each of them be called Dd; then the
surface FE will be divided into the
same number of equal rings, whose total forces will be as the sum of all
the products PD × Dd, that is, as ½PF2 − ½PD2, and thus as DE2. Now
multiply the surface FE by the altitude Ff, and the force of the solid EFfe
exerted upon the corpuscle P will become as DE2 × Ff, if there is given the
force that some given particle Ff exerts on the corpuscle P at the distance
PF. But if that force is not given, the force of the solid EFfe will become as
the solid DE2 × Ff and that non-given force jointly. Q.E.D.
but along the line PS tending toward
the center S, this force will be smaller
in the ratio of PD to PE, and hence
this force will be as PD × Dd. Now
suppose the line DF to be divided into
innumerable equal particles, and let
each of them be called Dd; then the
surface FE will be divided into the
same number of equal rings, whose total forces will be as the sum of all
the products PD × Dd, that is, as ½PF2 − ½PD2, and thus as DE2. Now
multiply the surface FE by the altitude Ff, and the force of the solid EFfe
exerted upon the corpuscle P will become as DE2 × Ff, if there is given the
force that some given particle Ff exerts on the corpuscle P at the distance
PF. But if that force is not given, the force of the solid EFfe will become as
the solid DE2 × Ff and that non-given force jointly. Q.E.D.
Proposition 80, Theorem 40
If equal centripetal forces tend toward each of the individual equal particles of
some sphere ABE, described about a center S; and if from each of the individual
points D to the axis AB of the sphere, in which some corpuscle P is located, there
are erected the perpendiculars DE, meeting the sphere in the points E; and if on
these perpendiculars, the lengths DN are taken, which are jointly as the quantity
 and as the force that a particle of the sphere, located on the axis,
exerts at the distance PE upon the corpuscle P; then I say that the total force
with which the corpuscle P is attracted toward the sphere is as the area ANB
comprehended by the axis AB of the sphere and the curved line ANB, which the
point N traces out.
and as the force that a particle of the sphere, located on the axis,
exerts at the distance PE upon the corpuscle P; then I say that the total force
with which the corpuscle P is attracted toward the sphere is as the area ANB
comprehended by the axis AB of the sphere and the curved line ANB, which the
point N traces out.
For, keeping the same constructions as in lem. 29 and prop. 79, suppose
the axis AB of the sphere to be divided into innumerable equal particles Dd,
and the whole sphere to be divided into as many spherical concavo-convex
laminae EFfe; and erect the perpendicular dn. By prop. 79, the force with
which the lamina EFfe attracts the corpuscle P is jointly as DE2 × Ff and
the force of one particle exerted at the distance PE or PF. But Dd is to
Ff (by lem. 29) as PE to PS, and hence Ff is equal to 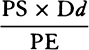 , and
DE2 × Ff is equal to Dd
, and
DE2 × Ff is equal to Dd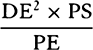 ; and therefore the force of the lamina
EFfe is jointly as Dd
; and therefore the force of the lamina
EFfe is jointly as Dd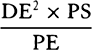 and the force of a particle exerted at the
distance PF; that is (by hypothesis) as DN × Dd, or as the evanescent area
DNnd. Therefore the forces upon body P exerted by all the laminae are
as all the areas DNnd, that is, the total force of the sphere is as the total
area ANB. Q.E.D.
and the force of a particle exerted at the
distance PF; that is (by hypothesis) as DN × Dd, or as the evanescent area
DNnd. Therefore the forces upon body P exerted by all the laminae are
as all the areas DNnd, that is, the total force of the sphere is as the total
area ANB. Q.E.D.
COROLLARY 1. Hence, if the centripetal force tending toward each of
the individual particles always remains the same at all distances, and DN is
taken proportional to 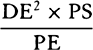 , the total force by which the corpuscle P is
attracted by the sphere will be as the area ANB.
, the total force by which the corpuscle P is
attracted by the sphere will be as the area ANB.
COROLLARY 2. If the centripetal force of the particles is inversely as
the distance of the attracted corpuscle, and DN is taken proportional to
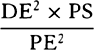 , the force by which the corpuscle P is attracted by the whole
sphere will be as the area ANB.
, the force by which the corpuscle P is attracted by the whole
sphere will be as the area ANB.
COROLLARY 3. If the centripetal force of the particles is inversely as the
cube of the distance of the attracted corpuscle, and DN is taken proportional
to 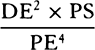 , the force by which the corpuscle is attracted by the whole
sphere will be as the area ANB.
, the force by which the corpuscle is attracted by the whole
sphere will be as the area ANB.
COROLLARY 4. And universally, if the centripetal force tending toward
each of the individual particles of a sphere is supposed to be inversely as the
quantity V, and DN is taken proportional to 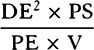 , the force by which
a corpuscle is attracted by the whole sphere will be as the area ANB.
, the force by which
a corpuscle is attracted by the whole sphere will be as the area ANB.
Proposition 81, Problem 41
Under the same conditions as before, it is required to measure the area ANB.
From point P draw the straight line PH touching the sphere in H; and,
having dropped the normal HI to the axis PAB, bisect PI in L; then (by book
2, prop. 12, of Euclid’s Elements) PE2 will be equal to PS2+SE2+2(PS × SD).
Moreover, SE2 or SH2 (because the triangles SPH and SHI are similar) is
equal to the rectangle PS × SI. Therefore PE2 is equal to the rectangle of PS
and PS + SI + 2SD, that is, of PS and 2LS + 2SD, that is, of PS and 2LD.
Further, DE2 is equal to SE2 − SD2, or SE2 − LS2 +2(SL × LD) − LD2, that
is, 2(SL × LD) − LD2 − AL × LB. For LS2 − SE2 or LS2 − SA2 (by book 2,
prop. 6, of the Elements) is equal to the rectangle AL × LB. Write, therefore,
2(SL × LD) − LD2 − AL × LB for DE2; and the quantity 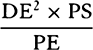 ,
which (according to corol. 4 of the preceding prop. 80) is as the length of
the ordinate DN, will resolve itself into the three parts
,
which (according to corol. 4 of the preceding prop. 80) is as the length of
the ordinate DN, will resolve itself into the three parts 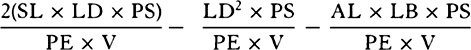 :
where, if for V we write the inverse ratio
of the centripetal force, and for PE the mean proportional between PS and
2LD, those three parts will become ordinates of as many curved lines, whose
areas can be found by ordinary methods. Q.E.F.
:
where, if for V we write the inverse ratio
of the centripetal force, and for PE the mean proportional between PS and
2LD, those three parts will become ordinates of as many curved lines, whose
areas can be found by ordinary methods. Q.E.F.
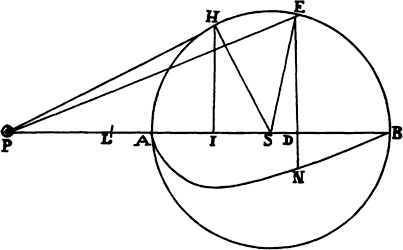
EXAMPLE 1. If the centripetal force tending toward each of the
individual particles of the sphere is inversely as the distance, write the
distance PE in place of V, and then 2PS × LD in place of PE2, and DN
will become as SL − ½LD − 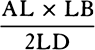 . Suppose DN equal to its double
2SL − LD −
. Suppose DN equal to its double
2SL − LD − 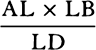 ; and the given part 2SL of that ordinate
; and the given part 2SL of that ordinate
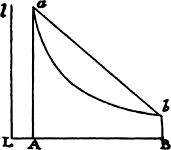 multiplied by the length AB will describe a rectangular
area 2SL × AB, and the indefinite part LD
multiplied perpendicularly by the same length AB in a
continual motion (according to the rule that, while
moving, either by increasing or decreasing, it is
always equal to the length LD) will describe an area
multiplied by the length AB will describe a rectangular
area 2SL × AB, and the indefinite part LD
multiplied perpendicularly by the same length AB in a
continual motion (according to the rule that, while
moving, either by increasing or decreasing, it is
always equal to the length LD) will describe an area
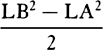 , that is, the area SL × AB, which,
subtracted from the first area 2SL × AB, leaves the area SL × AB. Now the
third part
, that is, the area SL × AB, which,
subtracted from the first area 2SL × AB, leaves the area SL × AB. Now the
third part 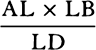 , likewise multiplied perpendicularly by the same length
AB in a local [i.e., continual] motion, will describe a hyperbolic area, which
subtracted from the area SL × AB will leave the required area ANB. Hence,
there arises the following construction of the problem.
, likewise multiplied perpendicularly by the same length
AB in a local [i.e., continual] motion, will describe a hyperbolic area, which
subtracted from the area SL × AB will leave the required area ANB. Hence,
there arises the following construction of the problem.
At points L, A, and B erect perpendiculars Ll, Aa, and Bb, of which Aa is equal to LB, and Bb to LA. With asymptotes Ll and LB, through points a and b describe the hyperbola ab. Then the chord ba, when drawn, will enclose the area aba equal to the required area ANB.
EXAMPLE 2. If the centripetal force tending toward each of the
individual particles of the sphere is inversely as the cube of the distance, or
(which comes to the same thing) as that cube divided by any given plane,
write 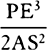 for V, and then 2PS × LD for PE2, and DN will become
as
for V, and then 2PS × LD for PE2, and DN will become
as 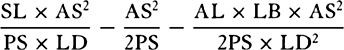 , that is (because PS, AS, and SI
are continually proportional [or PS is to AS as AS to SI]), as
, that is (because PS, AS, and SI
are continually proportional [or PS is to AS as AS to SI]), as 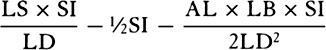 . If the three parts of this quantity are multiplied
by the length AB, the first,
. If the three parts of this quantity are multiplied
by the length AB, the first, 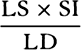 , will generate a hyperbolic area; the
second, ½SI, will generate the area ½AB × SI; the third,
, will generate a hyperbolic area; the
second, ½SI, will generate the area ½AB × SI; the third, 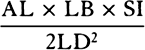 ,
will generate the area
,
will generate the area 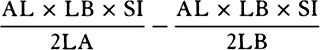 , that is, ½AB × SI.
From the first subtract the sum of the second and third, and the required
area ANB will remain.
, that is, ½AB × SI.
From the first subtract the sum of the second and third, and the required
area ANB will remain.
Hence there arises the following construction
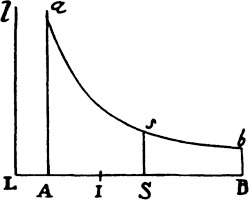 of the problem. At the points L, A, S, and B erect
the perpendiculars Ll, Aa, Ss, and Bb, of which
Ss is equal to SI; and through the point s, with
asymptotes Ll and LB, describe the hyperbola
asb meeting the perpendiculars Aa and Bb in a
and b; then the rectangle 2AS × SI subtracted
from the hyperbolic area AasbB will leave the requirea area ANB.
of the problem. At the points L, A, S, and B erect
the perpendiculars Ll, Aa, Ss, and Bb, of which
Ss is equal to SI; and through the point s, with
asymptotes Ll and LB, describe the hyperbola
asb meeting the perpendiculars Aa and Bb in a
and b; then the rectangle 2AS × SI subtracted
from the hyperbolic area AasbB will leave the requirea area ANB.
EXAMPLE 3. If the centripetal force tending toward each of the
individual particles of the sphere decreases as the fourth power of the distance from
those particles, write 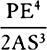 for V, and then √(2PS × LD) for PE, and DN
will become as
for V, and then √(2PS × LD) for PE, and DN
will become as 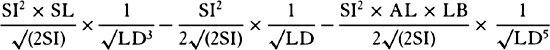 .
Those three parts, multiplied by the length AB, produce three areas,
namely
.
Those three parts, multiplied by the length AB, produce three areas,
namely 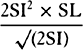 multiplied by
multiplied by 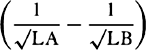 ;
; 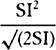 multiplied
by (√LB − √LA); and
multiplied
by (√LB − √LA); and 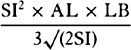 multiplied by
multiplied by 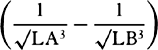 .
And these, after the due reduction, become
.
And these, after the due reduction, become 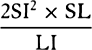 , SI2, and
, SI2, and 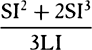 .
And when the latter two quantities are subtracted from the first one, the
result comes out to be
.
And when the latter two quantities are subtracted from the first one, the
result comes out to be 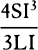 . Accordingly, the total force by which the
corpuscle P is attracted to the center of the sphere is as
. Accordingly, the total force by which the
corpuscle P is attracted to the center of the sphere is as 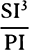 , that is, inversely as
PS3 × PI. Q.E.I.
, that is, inversely as
PS3 × PI. Q.E.I.
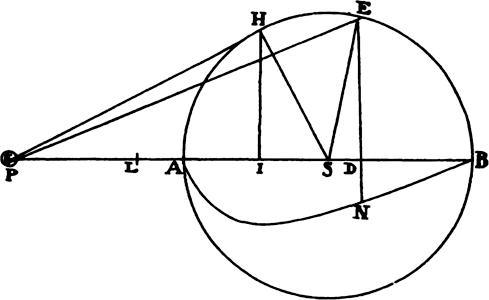
The attraction of a corpuscle located inside a sphere can be determined by the same method, but more expeditiously by means of the following proposition.
Proposition 82, Theorem 41
If—in a sphere described about center S with radius SA−SI, SA, and SP are
taken continually proportional [i.e., SI to SA as SA to SP], I say that the
attraction of a corpuscle inside the sphere at any place I is to its attraction outside
the sphere at place P in a ratio compounded of the square root of the ratio of
the distances IS and PS from the center, and the square root of the ratio of the
centripetal forces, tending at those places P and I toward the center.
If, for example, the centripetal forces of the particles of the sphere are inversely as the distances of the corpuscle attracted by them, the force by which the corpuscle situated at I is attracted by the total sphere will be to the force by which it is attracted at P in a ratio compounded of the square root of the ratio of the distance SI to the distance SP and the square root of the ratio of the centripetal force at place I arising from some particle in the center to the centripetal force at place P arising from the same particle in the center, which is the square root of the ratio of the distances SI and SP to each other inversely. Compounding these two square roots of ratios gives the ratio of equality, and therefore the attractions produced at I and P by the whole sphere are equal. By a similar computation, if the forces of the particles of the sphere are inversely in the squared ratio of the distances, it will be seen that the attraction at I is to the attraction at P as the distance SP is to the semidiameter SA of the sphere. If those forces are inversely in the cubed ratio of the distances, the attractions at I and P will be to each other as SP2 to SA2; if as the inverse fourth power, as SP3 to SA3. Hence, since—in this last case [of the inverse fourth power, as in the final ex. 3 of prop. 81]—the attraction at P was found to be inversely as PS3 × PI, the attraction at I will be inversely as SA3 × PI, that is (because SA3 is given), inversely as PI. And the progression goes on in the same way indefinitely. Moreover, the theorem is demonstrated as follows.
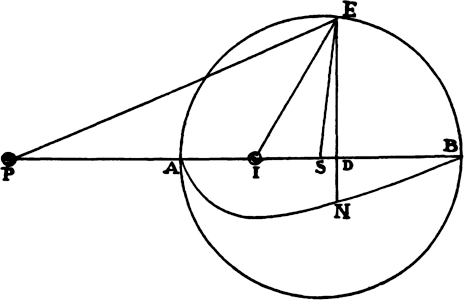
With the same construction and with the corpuscle being in any place
P, the ordinate DN was found to be as 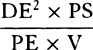 . Therefore, if IE is
drawn, that ordinate for any other place I of the corpuscle will—mutatis
mutandis [i.e., by substituting I for P in the considerations and arguments
that have previously been applied to P]—come out as
. Therefore, if IE is
drawn, that ordinate for any other place I of the corpuscle will—mutatis
mutandis [i.e., by substituting I for P in the considerations and arguments
that have previously been applied to P]—come out as 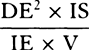 . Suppose
the centripetal forces emanating from any point E of the sphere to be to
each other at the distances IE and PE as PEn to IEn (where let the number
n designate the index of the powers of PE and IE); then those ordinates
will become as
. Suppose
the centripetal forces emanating from any point E of the sphere to be to
each other at the distances IE and PE as PEn to IEn (where let the number
n designate the index of the powers of PE and IE); then those ordinates
will become as 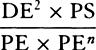 and
and 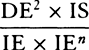 , whose ratio to each other is as
PS × IE × IEn to IS × PE × PEn. Because SI, SE, and SP are continually
proportional, the triangles SPE and SEI are similar, and hence IE becomes
to PE as IS to SE or SA; for the ratio of IE to PE, write the ratio of IS to
SA, and the ratio of the ordinates will come out PS × IEn to SA × PEn. But
PS to SA is the square root of the ratio of the distances PS and SI, and IEn
to PEn (because IE is to PE as IS to SA) is the square root of the ratio of the
forces at the distances PS and IS. Therefore the ordinates, and consequently
the areas that the ordinates describe and the attractions proportional to them,
are in a ratio compounded of the foregoing square-root ratios. Q.E.D.
, whose ratio to each other is as
PS × IE × IEn to IS × PE × PEn. Because SI, SE, and SP are continually
proportional, the triangles SPE and SEI are similar, and hence IE becomes
to PE as IS to SE or SA; for the ratio of IE to PE, write the ratio of IS to
SA, and the ratio of the ordinates will come out PS × IEn to SA × PEn. But
PS to SA is the square root of the ratio of the distances PS and SI, and IEn
to PEn (because IE is to PE as IS to SA) is the square root of the ratio of the
forces at the distances PS and IS. Therefore the ordinates, and consequently
the areas that the ordinates describe and the attractions proportional to them,
are in a ratio compounded of the foregoing square-root ratios. Q.E.D.
Proposition 83, Problem 42
To find the force by which a corpuscle located in the center of a sphere is attracted
toward any segment of it whatever.
Let P be the corpuscle in the center of the sphere, and RBSD a segment
of the sphere contained by the plane RDS and the spherical surface RBS.
Let DB be cut at F by the spherical surface EFG described about the center
P, and divide that segment into the parts BREFGS and FEDG. But
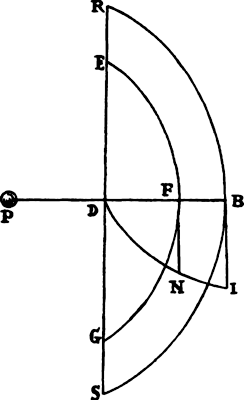 let that surface be taken to be not purely
mathematical, but physical, having a minimally small
thickness. Call that thickness O, and this surface
(by what Archimedes has demonstrated), will be
as PF × DF × O. Let us suppose, additionally, the
attractive forces of the particles of the sphere to
be inversely as that power of the distances whose
index is n; then the force by which the surface
EFG attracts the body P will be (by prop. 79)
as
let that surface be taken to be not purely
mathematical, but physical, having a minimally small
thickness. Call that thickness O, and this surface
(by what Archimedes has demonstrated), will be
as PF × DF × O. Let us suppose, additionally, the
attractive forces of the particles of the sphere to
be inversely as that power of the distances whose
index is n; then the force by which the surface
EFG attracts the body P will be (by prop. 79)
as 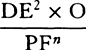 , that is, as
, that is, as 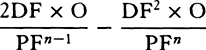 .
Let the perpendicular FN drawn in [the
thickness] O be proportional to this quantity; then the
curvilinear area BDI, as described by the ordinate FN, drawn in a continual
motion, applied to the length DB, will be as the whole force by which the
whole segment RBSD attracts the corpuscle P. Q.E.I.
.
Let the perpendicular FN drawn in [the
thickness] O be proportional to this quantity; then the
curvilinear area BDI, as described by the ordinate FN, drawn in a continual
motion, applied to the length DB, will be as the whole force by which the
whole segment RBSD attracts the corpuscle P. Q.E.I.
Proposition 84, Problem 43
To find the force with which a corpuscle is attracted by a segment of a sphere
when it is located on the axis of the segment beyond the center of the sphere.
Let corpuscle P, located on the
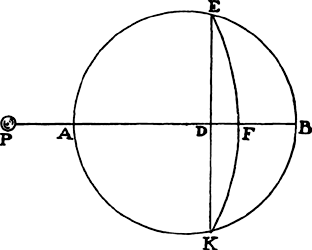 axis ADB of the segment EBK, be
attracted by that segment. About
center P and with radius PE describe the
spherical surface EFK, which divides
the segment into two parts EBKFE
and EFKDE. Find the force of the
first part by prop. 81 and the force of
the second part by prop. 83, and the
sum of these two forces will be the force of the whole segment
EBKDE. Q.E.I.
axis ADB of the segment EBK, be
attracted by that segment. About
center P and with radius PE describe the
spherical surface EFK, which divides
the segment into two parts EBKFE
and EFKDE. Find the force of the
first part by prop. 81 and the force of
the second part by prop. 83, and the
sum of these two forces will be the force of the whole segment
EBKDE. Q.E.I.
Scholium
Now that the attractions of spherical bodies have been explained, it would
be possible to go on to the laws of the attractions of certain other bodies
similarly consisting of attracting particles, but to treat these in particular
cases is not essential to my design. It will be enough to subjoin certain more
general propositions concerning the forces of bodies of this sort and the
motions that arise from such forces, because these propositions are of some use
in philosophical questions [i.e., questions of natural philosophy, or physical
science].
The attractive forces of nonspherical bodies
Proposition 85, Theorem 42
If the attraction of an attracted body is far stronger when it is contiguous to the
attracting body than when the bodies are separated from each other by even a very
small distance, then the forces of the particles of the attracting body decrease, as
the attracted body recedes, in a more than squared ratio of the distances from the
particles.
For if the forces decrease in the squared ratio of the distances from the particles, the attraction toward a spherical body will not be sensibly increased by contact, because (by prop. 74) it is inversely as the square of the distance of the attracted body from the center of the sphere; and still less will it be increased by contact, if the attraction decreases in a smaller ratio as the attracted body recedes. Therefore, this proposition is evident in the case of attracting spheres. It is the same for concave spherical orbsa attracting external bodies. And it is much more established in the case of orbs attracting bodies placed inside of them, since the attractions spreading out through the concavities of the orbs are annulled by opposite attractions (by prop. 70), and therefore the attracting forces are null, even in contact. But if any parts remote from the place of contact are taken away from these spheres and spherical orbs, and new parts are added anywhere away from the place of contact, the shapes of these attracting bodies can be changed at will; and yet the parts added or subtracted will not notably increase the excess of attraction that arises from contact, since they are remote from the place of contact. Therefore the proposition is established concerning bodies of all shapes. Q.E.D.
Proposition 86, Theorem 43
If the forces of the particles composing an attracting body decrease, as an attracted
body recedes, in the cubed or more than cubed ratio of the distances from the
particles, the attraction will be far stronger in contact than when the attracting
body and attracted body are separated from each other by even a very small
distance.
For by the solution of prop. 81 given in exx. 2 and 3, it is established that the attraction is increased indefinitely in the approach of an attracted corpuscle to an attracting sphere of this sort. By the combination of those examples and prop. 82, the same result is easily inferred concerning the attractions of bodies toward concavo-convex orbs whether the attracted bodies are placed outside those orbs or in the cavities inside the orbs. But the proposition will also be established concerning all bodies universally by adding some attractive matter to these spheres and orbs, or taking some away from them, anywhere away from the place of contact, so that the attracting bodies take on any desired shape. Q.E.D.
Proposition 87, Theorem 44
If two bodies, similar to each other and consisting of equally attracting matter,
separately attract corpuscles proportional to those bodies and similarly placed with
respect to them, then the accelerative attractions of the corpuscles toward the whole
bodies will be as the accelerative attractions of those corpuscles toward particles
of those bodies proportional to the wholes and similarly situated in those whole
bodies.
For if the bodies are divided into particles that are proportional to the whole bodies and similarly placed in those whole bodies, then the attraction toward an individual particle of the first body will be to the attraction toward the corresponding individual particle of the second body as the attractions toward any given particles of the first body are to the attractions toward the corresponding particles of the second body, and by compounding, the attraction toward the whole first body will be to the attraction toward the whole second body in that same ratio. Q.E.D.
COROLLARY 1. Therefore, if the attracting forces of the particles, on
increasing the distances of the attracted corpuscles, decrease in the ratio of any
power of those distances, the accelerative attractions toward the whole bodies
will be as the bodies directly and those powers of the distances inversely.
For example, if the forces of the particles decrease in the squared ratio of
the distances from the attracted corpuscles, and the bodies are as A3 and B3,
and thus both the cube roots of the bodies and the distances of the attracted
corpuscles from the bodies are as A and B, the accelerative attractions toward
the bodies will be as 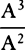 and
and 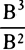 , that is, as those cube roots A and B of the
bodies. If the forces of the particles decrease in the cubed ratio of the distances
from the attracted corpuscles, the accelerative attractions toward the whole
bodies will be as
, that is, as those cube roots A and B of the
bodies. If the forces of the particles decrease in the cubed ratio of the distances
from the attracted corpuscles, the accelerative attractions toward the whole
bodies will be as 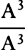 and
and 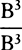 , that is, will be equal. If the forces decrease in
the fourth power of the distance, the attractions toward the bodies will be as
, that is, will be equal. If the forces decrease in
the fourth power of the distance, the attractions toward the bodies will be as
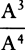 and
and 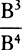 , that is, inversely as the cube roots A and B. And so on.
, that is, inversely as the cube roots A and B. And so on.
COROLLARY 2. Hence, on the other hand, from the forces with which similar bodies attract corpuscles similarly placed with respect to such bodies, there can be gathered the ratio of the decrease of the forces of the attracting particles, as the attracted corpuscle recedes, so long as that decrease is directly or inversely in some ratio of the distances.
Proposition 88, Theorem 45
If the attracting forces of equal particles of any body are as the distances of places
from the particles, the force of the whole body will tend toward its center of
gravity, and will be the same as the force of a globe consisting of entirely similar
and equal matter and having its center in that center of gravity.
Let the particles A and B of the body RSTV attract some corpuscle Z
by forces which, if the particles are equal to each other, are as the distances
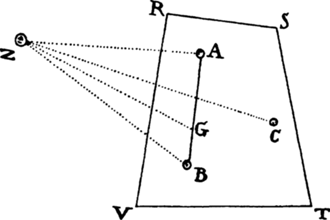 AZ and BZ: but if the particles are
supposed unequal, are as these particles
and their distances AZ and BZ jointly,
or (so to speak) as these particles
multiplied respectively by their distances AZ
and BZ. And let the forces be
represented by those solids [or products]
A × AZ and B × BZ. Join AB, and let
it be cut in G so that AG is to BG as the particle B to the particle A; then
G will be the common center of gravity of the particles A and B. The force
A × AZ (by corol. 2 of the laws) is resolved into the forces A × GZ and
A × AG, and the force B × BZ into the forces B × GZ and B × BG. But
the forces A × AG and B × BG are equal (because A is to B as BG to AG);
and therefore, since they tend in opposite directions, they nullify each other.
There remain the forces A × GZ and B × GZ. These tend from Z toward
the center G and compose the force (A + B) × GZ—that is, the same force
as if the attracting particles A and B were situated in their common center
of gravity G and there composed a globe.
AZ and BZ: but if the particles are
supposed unequal, are as these particles
and their distances AZ and BZ jointly,
or (so to speak) as these particles
multiplied respectively by their distances AZ
and BZ. And let the forces be
represented by those solids [or products]
A × AZ and B × BZ. Join AB, and let
it be cut in G so that AG is to BG as the particle B to the particle A; then
G will be the common center of gravity of the particles A and B. The force
A × AZ (by corol. 2 of the laws) is resolved into the forces A × GZ and
A × AG, and the force B × BZ into the forces B × GZ and B × BG. But
the forces A × AG and B × BG are equal (because A is to B as BG to AG);
and therefore, since they tend in opposite directions, they nullify each other.
There remain the forces A × GZ and B × GZ. These tend from Z toward
the center G and compose the force (A + B) × GZ—that is, the same force
as if the attracting particles A and B were situated in their common center
of gravity G and there composed a globe.
By the same argument, if a third particle C is added, and its force is compounded with the force (A + B) × GZ tending toward the center G, the force thence arising will tend toward the common center of gravity of the globe (at G) and the particle C (that is, toward the common center of gravity of the three particles A, B, and C), and will be the same as if the globe and the particle C were situated in their common center, there composing a greater globe. And so on indefinitely. Therefore the whole force of all the particles of any body RSTV is the same as if that body, while maintaining the same center of gravity, were to assume the shape of a globe. Q.E.D.
COROLLARY. Hence the motion of the attracted body Z will be the same as if the attracting body RSTV were spherical; and therefore, if that attracting body either is at rest or progresses uniformly straight forward, the attracted body will move in an ellipse having its center in the center of gravity of the attracting body.
Proposition 89, Theorem 46
If there are several bodies consisting of equal particles whose forces are as the
distances of places from each individual particle, the force—compounded of the
forces of all these particles—by which any corpuscle is attracted will tend toward
the common center of gravity of the attracting bodies and will be the same as if
those attracting bodies, while maintaining their common center of gravity, were
united together and were formed into a globe.
This is demonstrated in the same way as the preceding proposition.
COROLLARY. Therefore the motion of an attracted body will be the same as if the attracting bodies, while maintaining their common center of gravity, came together and were formed into a globe. And hence, if the common center of gravity of the attracting body either is at rest or progresses uniformly in a straight line, the attracted body will move in an ellipse having its center in the common center of gravity of the attracting bodies.
Proposition 90, Problem 44
If equal centripetal forces, increasing or decreasing in any ratio of the distances,
tend toward each of the individual points of any circle, it is required to find the
force by which a corpuscle is attracted when placed anywhere on the straight line
that stands perpendicularly upon the plane of the circle at its center.
Suppose a circle to be described with center A and any radius AD in a
plane to which the straight line AP is perpendicular; then it is required to
find the force by which any corpuscle P is attracted toward the circle. From
 any point E of the circle, draw the straight
line PE to the attracted corpuscle P. In the
straight line PA take PF equal to PE, and
erect the normal FK so that it will be as the
force by which the point E attracts the
corpuscle P. And let IKL be the curved line
that the point K traces out. Let that line
meet the plane of the circle in L. In PA take
PH equal to PD, and erect the perpendicular
HI meeting the aforesaid curve at I, and
the attraction of the corpuscle P toward the circle will be as the area AHIL
multiplied by the altitude AP. Q.E.I.
any point E of the circle, draw the straight
line PE to the attracted corpuscle P. In the
straight line PA take PF equal to PE, and
erect the normal FK so that it will be as the
force by which the point E attracts the
corpuscle P. And let IKL be the curved line
that the point K traces out. Let that line
meet the plane of the circle in L. In PA take
PH equal to PD, and erect the perpendicular
HI meeting the aforesaid curve at I, and
the attraction of the corpuscle P toward the circle will be as the area AHIL
multiplied by the altitude AP. Q.E.I.
For on AE take the minimally small line Ee. Join Pe, and in PE and
PA take PC and Pf equal to Pe. And since the force by which any point
E of the ring described with center A and radius AE in the aforesaid plane
attracts body [i.e., corpuscle] P toward itself has been supposed to be as FK,
and hence the force by which that point attracts body P toward A is as
 ; and the force by which the whole ring attracts body P toward
A is as the ring and
; and the force by which the whole ring attracts body P toward
A is as the ring and 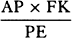 jointly; and that ring is as the rectangle of
the radius AE and the width Ee, and this rectangle (because PE is to AE
as Ee to CE) is equal to the rectangle PE × CE or PE × Ff; it follows that
the force by which that ring attracts body P toward A will be as PE × Ff
and
jointly; and that ring is as the rectangle of
the radius AE and the width Ee, and this rectangle (because PE is to AE
as Ee to CE) is equal to the rectangle PE × CE or PE × Ff; it follows that
the force by which that ring attracts body P toward A will be as PE × Ff
and 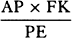 jointly, that is, as the solid [or product] Ff × FK × AP, or
as the area FKkf multiplied by AP. And therefore the sum of the forces
by which all the rings in the circle that is described with center A and
radius AD attract body P toward A is as the whole area AHIKL multiplied
by AP. Q.E.D.
jointly, that is, as the solid [or product] Ff × FK × AP, or
as the area FKkf multiplied by AP. And therefore the sum of the forces
by which all the rings in the circle that is described with center A and
radius AD attract body P toward A is as the whole area AHIKL multiplied
by AP. Q.E.D.
COROLLARY 1. Hence, if the forces of the points decrease in the squared
ratio of the distances, that is, if FK is as 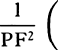 and thus the area AHIKL is
as
and thus the area AHIKL is
as 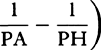 , the attraction of the corpuscle P toward the circle will be as
1 −
, the attraction of the corpuscle P toward the circle will be as
1 − 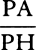 , that is, as
, that is, as 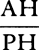 .
.
COROLLARY 2. And universally, if the forces of the points at the distances
D are inversely as any power Dn of the distances  that is, if FK is a
that is, if FK is a 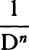 , and
hence the area AHIKL is as
, and
hence the area AHIKL is as 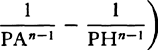 , the attraction of the
corpuscle P toward the circle will be as
, the attraction of the
corpuscle P toward the circle will be as 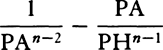 .
.
COROLLARY 3. And if the diameter of the circle is increased indefinitely
and the number n is greater than unity, the attraction of the corpuscle P
toward the whole indefinitely extended plane will be inversely as PAn−2,
because the other term, 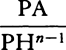 , will vanish.
, will vanish.
Proposition 91, Problem 45
To find the attraction of a corpuscle placed in the axis of a round solid, to each of
whose individual points there tend equal centripetal forces decreasing in any ratio
of the distances.
Let corpuscle P, placed in the axis AB of the solid DECG, be attracted
toward that same solid. Let this solid be cut by any circle RFS
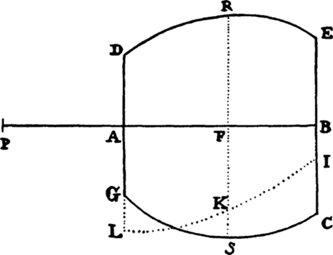 perpendicular to this axis, and in its semidiameter
FS, in a plane PALKB passing through
the axis, take (according to prop. 90) the
length FK proportional to the force by
which the corpuscle P is attracted toward
that circle. Let point K touch the curved
line LKI meeting the planes of the
outermost circles AL and BI at L and I, and
the attraction of the corpuscle P toward the solid will be as the area
LABI. Q.E.I.
perpendicular to this axis, and in its semidiameter
FS, in a plane PALKB passing through
the axis, take (according to prop. 90) the
length FK proportional to the force by
which the corpuscle P is attracted toward
that circle. Let point K touch the curved
line LKI meeting the planes of the
outermost circles AL and BI at L and I, and
the attraction of the corpuscle P toward the solid will be as the area
LABI. Q.E.I.
COROLLARY 1. Hence, if the solid is
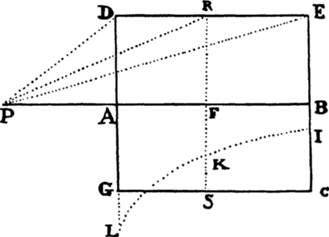 a cylinder described by parallelogram
ADEB revolving about the axis AB,
and the centripetal forces tending
toward each of its individual points are
inversely as the squares of the distances
from the points, the attraction of the
corpuscle P toward this cylinder will be
as AB − PE + PD. For the ordinate FK (by prop. 90, corol. 1) will be as
1 −
a cylinder described by parallelogram
ADEB revolving about the axis AB,
and the centripetal forces tending
toward each of its individual points are
inversely as the squares of the distances
from the points, the attraction of the
corpuscle P toward this cylinder will be
as AB − PE + PD. For the ordinate FK (by prop. 90, corol. 1) will be as
1 − 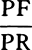 . The unit part of this
. The unit part of this  or the quantity 1 in 1 −
or the quantity 1 in 1 − 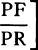 multiplied by
the length AB describes the area 1 × AB, and the other part
multiplied by
the length AB describes the area 1 × AB, and the other part 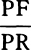 multiplied
by the length PB describes the area 1 × (PE − AD), which can easily be
shown from the quadrature of the curve LKI; and similarly the same part
multiplied
by the length PB describes the area 1 × (PE − AD), which can easily be
shown from the quadrature of the curve LKI; and similarly the same part
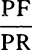 multiplied by the length PA describes the area 1 × (PD − AD), and
multiplied by the difference AB of PB and PA describes the difference of
the areas 1 × (PE − PD). From the first product 1 × AB take away the
last product 1 × (PE − PD), and there will remain the area LABI equal
to 1 × (AB − PE + PD). Therefore the force proportional to this area is as
AB − PE + PD.
multiplied by the length PA describes the area 1 × (PD − AD), and
multiplied by the difference AB of PB and PA describes the difference of
the areas 1 × (PE − PD). From the first product 1 × AB take away the
last product 1 × (PE − PD), and there will remain the area LABI equal
to 1 × (AB − PE + PD). Therefore the force proportional to this area is as
AB − PE + PD.
COROLLARY 2. Hence also the force becomes known by which a spheroid
AGBC attracts any body P, situated outside the spheroid in its axis AB.
Let NKRM be a conic whose ordinate ER, perpendicular to PE, is always
equal to the length of the line PD, which is drawn to the point D in which
the ordinate cuts the spheroid. From the vertices A and B of the spheroid,
erect AK and BM perpendicular to the axis AB of the spheroid and equal
respectively to AP and BP, and therefore meeting the conic in K and M; and
join KM cutting off the segment KMRK from the conic. Let the center of the
spheroid be S, and its greatest semidiameter SC. Then the force by which the
spheroid attracts the body P will be to the force by which a sphere described
with diameter AB attracts the same body as 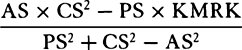 to
to
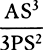 . And by the same mode of computation it is possible to find the forces
of the segments of the spheroid.
. And by the same mode of computation it is possible to find the forces
of the segments of the spheroid.
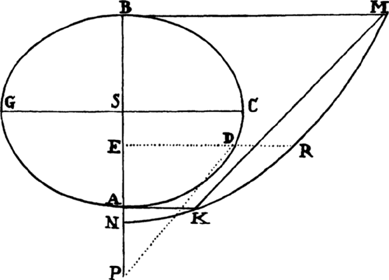
COROLLARY 3. But if the corpuscle is located inside the spheroid and
in its axis, the attraction will be as its distance from the center. This is seen
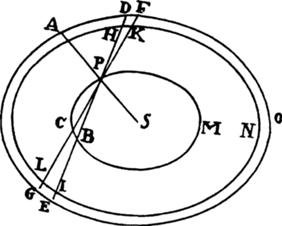 more easily by the following argument,
whether the particle is in the axis or in
any other given diameter. Let AGOF be
the attracting spheroid, S its center, and P
the attracted body. Through that body P
draw both the semidiameter SPA and any
two straight lines DE and FG meeting the
spheroid in D and F on one side and in E
and G on the other; and let PCM and HLN be the surfaces of two inner
spheroids, similar to and concentric with the outer spheroid; and let the first
of these pass through the body P and cut the straight lines DE and FG in
B and C, and let the latter cut the same straight lines in H, I and K, L.
Let all the spheroids have a common axis, and the parts of the straight lines
intercepted on the two sides, DP and BE, FP and CG, DH and IE, FK
and LG will be equal to one another, because the straight lines DE, PB, and
HI are bisected in the same point, as are also the straight lines FG, PC, and
KL. Now suppose that DPF and EPG designate opposite cones described
with the infinitely small vertical angles DPF and EPG, and that the lines
DH and EI also are infinitely small; then the particles of the cones—that
is, the particles DHKF and GLIE—cut off by the surfaces of the spheroids
will (because of the equality of the lines DH and EI) be to each other as the
squares of their distances from the corpuscle P, and therefore will attract the
corpuscle equally. And by a like reasoning, if the spaces DPF and EGCB
are divided into particles by the surfaces of innumerable similar concentric
spheroids, having a common axis, then all of these particles will attract the
body P in opposite directions equally on both sides. Therefore the forces
of the cone DPF and of the conical segment [or truncated cone] EGCB
are equal, and—being opposite—annul each other. And it is the same with
regard to the forces of all the matter outside the innermost spheroid PCBM.
Therefore the body P is attracted only by the innermost spheroid PCBM,
and accordingly (by prop. 72, corol. 3) its attraction is to the force by which
the body A is attracted by the whole spheroid AGOD as the distance PS to
the distance AS. Q.E.D.
more easily by the following argument,
whether the particle is in the axis or in
any other given diameter. Let AGOF be
the attracting spheroid, S its center, and P
the attracted body. Through that body P
draw both the semidiameter SPA and any
two straight lines DE and FG meeting the
spheroid in D and F on one side and in E
and G on the other; and let PCM and HLN be the surfaces of two inner
spheroids, similar to and concentric with the outer spheroid; and let the first
of these pass through the body P and cut the straight lines DE and FG in
B and C, and let the latter cut the same straight lines in H, I and K, L.
Let all the spheroids have a common axis, and the parts of the straight lines
intercepted on the two sides, DP and BE, FP and CG, DH and IE, FK
and LG will be equal to one another, because the straight lines DE, PB, and
HI are bisected in the same point, as are also the straight lines FG, PC, and
KL. Now suppose that DPF and EPG designate opposite cones described
with the infinitely small vertical angles DPF and EPG, and that the lines
DH and EI also are infinitely small; then the particles of the cones—that
is, the particles DHKF and GLIE—cut off by the surfaces of the spheroids
will (because of the equality of the lines DH and EI) be to each other as the
squares of their distances from the corpuscle P, and therefore will attract the
corpuscle equally. And by a like reasoning, if the spaces DPF and EGCB
are divided into particles by the surfaces of innumerable similar concentric
spheroids, having a common axis, then all of these particles will attract the
body P in opposite directions equally on both sides. Therefore the forces
of the cone DPF and of the conical segment [or truncated cone] EGCB
are equal, and—being opposite—annul each other. And it is the same with
regard to the forces of all the matter outside the innermost spheroid PCBM.
Therefore the body P is attracted only by the innermost spheroid PCBM,
and accordingly (by prop. 72, corol. 3) its attraction is to the force by which
the body A is attracted by the whole spheroid AGOD as the distance PS to
the distance AS. Q.E.D.
Proposition 92, Problem 46
Given an attracting body, it is required to find the ratio by which the centripetal
forces tending toward each of its individual points decrease [i.e., decrease as a
function of distance].
From the given body a sphere or cylinder or other regular figure is to be formed, whose law of attraction—corresponding to any ratio of decrease [in relation to distance]—can be found by props. 80, 81, and 91. Then, by making experiments, the force of attraction at different distances is to be found; and the law of attraction toward the whole that is thus revealed will give the ratio of the decrease of the forces of the individual parts, which was required to be found.
Proposition 93, Theorem 47
If a solid, plane on one side but infinitely extended on the other sides, consists of
equal and equally attracting particles, whose forces—in receding from the
solid—decrease in the ratio of any power of the distances that is more than the square;
and if a corpuscle set on either side of the plane is attracted by the force of the
whole solid; then I say that that force of attraction of the solid in receding from
its plane surface will decrease in the ratio of the distance of the corpuscle from
the plane raised to a power whose index is less by 3 units than that of the power
of the distances in the law of attractive force [lit. will decrease in the ratio of the
power whose base is the distance of the corpuscle from the plane and whose index
is less by 3 than the index of the power of the distances].
CASE 1. Let LGl be the plane by which the solid is terminated.
Let the solid lie on the side of this plane toward I, and let it be resolved into
 innumerable planes mHM, nIN,
oKO, . . . parallel to GL. And
first let the attracted body C be
placed outside the solid. Draw
CGHI perpendicular to those
innumerable planes, and let the
forces of attraction of the points
of the solid decrease in the
ratio of a power of the distances
whose index is the number n not
smaller than 3. Therefore (by prop. 90, corol. 3) the force by which any
plane mHM attracts the point C is inversely as CHn−2. In the plane mHM
take the length HM inversely proportional to CHn−2, and that force will be
as HM. Similarly, on each of the individual planes lGL, nIN, oKO, . . . , take
the lengths GL, IN, KO, . . . inversely proportional to CGn−2, CIn−2,
CKn−2, . . . ; then the forces of these same planes will be as the lengths
taken, and thus the sum of the forces will be as the sum of the lengths;
that is, the force of the whole solid will be as the area GLOK produced
infinitely in the direction OK. But that area (by the well-known methods
of quadratures) is inversely as CGn−3, and therefore the force of the whole
solid is inversely as CGn−3. Q.E.D.
innumerable planes mHM, nIN,
oKO, . . . parallel to GL. And
first let the attracted body C be
placed outside the solid. Draw
CGHI perpendicular to those
innumerable planes, and let the
forces of attraction of the points
of the solid decrease in the
ratio of a power of the distances
whose index is the number n not
smaller than 3. Therefore (by prop. 90, corol. 3) the force by which any
plane mHM attracts the point C is inversely as CHn−2. In the plane mHM
take the length HM inversely proportional to CHn−2, and that force will be
as HM. Similarly, on each of the individual planes lGL, nIN, oKO, . . . , take
the lengths GL, IN, KO, . . . inversely proportional to CGn−2, CIn−2,
CKn−2, . . . ; then the forces of these same planes will be as the lengths
taken, and thus the sum of the forces will be as the sum of the lengths;
that is, the force of the whole solid will be as the area GLOK produced
infinitely in the direction OK. But that area (by the well-known methods
of quadratures) is inversely as CGn−3, and therefore the force of the whole
solid is inversely as CGn−3. Q.E.D.
CASE 2. Now let the corpuscle C be placed on the side of the plane lGL
inside the solid, and take the distance CK equal to the distance CG. Then the
 part LGloKO of this solid, terminated by the
parallel planes lGL and oKO, will not attract
the corpuscle C (situated in the middle) in
any direction, the opposite actions of opposite
points annulling each other because of their
equality. Accordingly, corpuscle C is attracted
only by the force of the solid situated beyond
the plane OK. But this force (by case 1) is
inversely as CKn−3, that is (because CG and CK are equal), inversely as
CGn−3. Q.E.D.
part LGloKO of this solid, terminated by the
parallel planes lGL and oKO, will not attract
the corpuscle C (situated in the middle) in
any direction, the opposite actions of opposite
points annulling each other because of their
equality. Accordingly, corpuscle C is attracted
only by the force of the solid situated beyond
the plane OK. But this force (by case 1) is
inversely as CKn−3, that is (because CG and CK are equal), inversely as
CGn−3. Q.E.D.
COROLLARY 1. Hence, if the solid LGIN is terminated on both sides by two infinitely extended and parallel planes LG and IN, its force of attraction becomes known by subtracting from the force of attraction of the whole infinitely extended solid LGKO the force of attraction of the further part NIKO produced infinitely in the direction KO.
COROLLARY 2. If the more distant part of this infinitely extended solid is ignored, since its attraction compared with the attraction of the nearer part is of almost no moment, then the attraction of that nearer part, with an increase of the distance, will decrease very nearly in the ratio of the power CGn−3.
COROLLARY 3. And hence, if any body that is finite and plane on one side attracts a corpuscle directly opposite the middle of that plane, and the distance between the corpuscle and the plane is exceedingly small compared with the dimensions of the attracting body, and the attracting body consists of homogeneous particles whose forces of attraction decrease in the ratio of any power of the distances that is more than the fourth; the force of attraction of the whole body will decrease very nearly in the ratio of a power of that exceedingly small distance, whose index is less by 3 than the index of the stated power. This assertion is not valid for a body consisting of particles whose forces of attraction decrease in the ratio of the third power of the distances, because in this case the attraction of the more distant part of the infinitely extended body in corol. 2 is always infinitely greater than the attraction of the nearer part.
Scholium
If a body is attracted perpendicularly toward a given plane, and the motion of
the body is required to be found from the given law of attraction, the problem
will be solved by seeking (by prop. 39) the motion of the body descending
directly to this plane and by compounding this motion (according to corol. 2
of the laws) with a uniform motion performed along lines parallel to the
same plane. And conversely, if it is required to find the law of an attraction
made toward the plane along perpendicular lines, under the condition that
the attracted body moves in any given curved line whatever, the problem will
be solved by the operations used in the third problem [i.e., prop. 8].
The procedure can be shortened by resolving the ordinates into converging
series. For example, if B is the ordinate to the base A at any given angle,
and is as any power 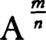 of that base, and the force is required by which a
body that is either attracted toward the base or repelled away from the base
(according to the position of the ordinate) can move in a curved line that the
upper end of the ordinate traces out; I suppose the base to be increased by a
minimally small part O, and I resolve the ordinate
of that base, and the force is required by which a
body that is either attracted toward the base or repelled away from the base
(according to the position of the ordinate) can move in a curved line that the
upper end of the ordinate traces out; I suppose the base to be increased by a
minimally small part O, and I resolve the ordinate 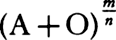 into the infinite
series
into the infinite
series
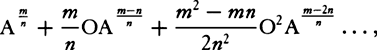 and I suppose the force to be proportional to the term of this series in which
O is of two dimensions, that is, to the term
and I suppose the force to be proportional to the term of this series in which
O is of two dimensions, that is, to the term 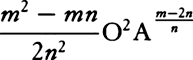 . Therefore the
required force is as
. Therefore the
required force is as 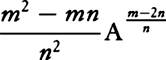 , or, which is the same, as
, or, which is the same, as  .
For example, if the ordinate traces out a parabola, where m = 2 and n = 1,
the force will become as the given quantity 2B°, and thus will be given.
Therefore with a given [i.e., constant] force the body will move in a parabola,
as Galileo demonstrated. But if the ordinate traces out a hyperbola, where
m = 0 − 1 and n = 1, the force will become as 2A−3 or 2B3; and therefore
with a force that is as the cube of the ordinate, the body will move in a
hyperbola. But putting aside propositions of this sort, I go on to certain
others on motion which I have not as yet considered.
.
For example, if the ordinate traces out a parabola, where m = 2 and n = 1,
the force will become as the given quantity 2B°, and thus will be given.
Therefore with a given [i.e., constant] force the body will move in a parabola,
as Galileo demonstrated. But if the ordinate traces out a hyperbola, where
m = 0 − 1 and n = 1, the force will become as 2A−3 or 2B3; and therefore
with a force that is as the cube of the ordinate, the body will move in a
hyperbola. But putting aside propositions of this sort, I go on to certain
others on motion which I have not as yet considered.
The motion of minimally small bodies that are acted on by centripetal forces tending toward each of the individual parts of some great body
Proposition 94, Theorem 48
If two homogeneous mediums are separated from each other by a space terminated
on the two sides by parallel planes, and a body passing through this space is
attracted or impelled perpendicularly toward either medium and is not acted on or
impeded by any other force, and the attraction at equal distances from each plane
(taken on the same side of that plane) is the same everywhere; then I say that the
sine of the angle of incidence onto either plane will be to the sine of the angle of
emergence from the other plane in a given ratio.
CASE 1. Let Aa and Bb be the two parallel planes. Let the body be
incident upon the first plane Aa along line GH, and in all its passage
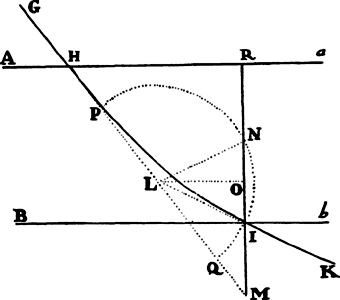 through the intermediate space let
it be attracted or impelled toward
the medium of incidence, and by
this action let it describe the curved
line HI and emerge along the line
IK. To the plane of emergence Bb
erect the perpendicular IM meeting
the line of incidence GH produced
in M and the plane of incidence Aa
in R; and let the line of emergence
KI produced meet HM in L. With
center L and radius LI describe a circle cutting HM in P and Q, as well
as MI produced in N. Then first, if the attraction or impulse is supposed
uniform, the curve HI (from what Galileo demonstrated) will be a parabola,
of which this is a property: that the rectangle of its given latus rectum and
the line IM is equal to HM squared; but also the line HM will be bisected in
L. Hence, if the perpendicular LO is dropped to MI, MO and OR will be
equal; and when the equals ON and OI have been added to these quantities,
the totals MN and IR will become equal. Accordingly, since IR is given,
MN is also given; and the rectangle NM × MI is to the rectangle of the
latus rectum and IM (that is, to HM2) in a given ratio. But the rectangle
NM × MI is equal to the rectangle PM × MQ, that is, to the difference of
the squares ML2 and PL2 or LI2; and HM2 has a given ratio to its fourth
part ML2: therefore the ratio of ML2 − LI2 to ML2 is given, and by
conversion [or convertendo] the ratio LI2 to ML2 is given, and also the square root
of that ratio, LI to ML. But in every triangle LMI, the sines of the angles
are proportional to the opposite sides. Therefore the ratio of the sine of the
angle of incidence LMR to the sine of the angle of emergence LIR is
given. Q.E.D.
through the intermediate space let
it be attracted or impelled toward
the medium of incidence, and by
this action let it describe the curved
line HI and emerge along the line
IK. To the plane of emergence Bb
erect the perpendicular IM meeting
the line of incidence GH produced
in M and the plane of incidence Aa
in R; and let the line of emergence
KI produced meet HM in L. With
center L and radius LI describe a circle cutting HM in P and Q, as well
as MI produced in N. Then first, if the attraction or impulse is supposed
uniform, the curve HI (from what Galileo demonstrated) will be a parabola,
of which this is a property: that the rectangle of its given latus rectum and
the line IM is equal to HM squared; but also the line HM will be bisected in
L. Hence, if the perpendicular LO is dropped to MI, MO and OR will be
equal; and when the equals ON and OI have been added to these quantities,
the totals MN and IR will become equal. Accordingly, since IR is given,
MN is also given; and the rectangle NM × MI is to the rectangle of the
latus rectum and IM (that is, to HM2) in a given ratio. But the rectangle
NM × MI is equal to the rectangle PM × MQ, that is, to the difference of
the squares ML2 and PL2 or LI2; and HM2 has a given ratio to its fourth
part ML2: therefore the ratio of ML2 − LI2 to ML2 is given, and by
conversion [or convertendo] the ratio LI2 to ML2 is given, and also the square root
of that ratio, LI to ML. But in every triangle LMI, the sines of the angles
are proportional to the opposite sides. Therefore the ratio of the sine of the
angle of incidence LMR to the sine of the angle of emergence LIR is
given. Q.E.D.
CASE 2. Now let the body pass successively through several spaces
terminated by parallel planes, AabB, BbcC, . . . , and be acted on by a force
 that is uniform in each of the individual
spaces considered separately but is
different in each of the different spaces. Then
by what has just been demonstrated, the
sine of the angle of incidence upon the first
plane Aa will be to the sine of the angle
of emergence from the second plane Bb in a given ratio; and this sine, which
is the sine of the angle of incidence upon the second plane Bb, will be to
the sine of the angle of emergence from the third plane Cc in a given ratio;
and this sine will be in a given ratio to the sine of the angle of emergence
from the fourth plane Dd; and so on indefinitely. And from the equality
of the ratios [or ex aequo] the sine of the angle of incidence upon the first
plane will be in a given ratio to the sine of the angle of emergence from the
last plane. Now let the distances between the planes be diminished and their
number increased indefinitely, so that the action of attraction or of impulse,
according to any assigned law whatever, becomes continuous; then the ratio
of the sine of the angle of incidence upon the first plane to the sine of the
angle of emergence from the last plane, being always given, will still be given
now. Q.E.D.
that is uniform in each of the individual
spaces considered separately but is
different in each of the different spaces. Then
by what has just been demonstrated, the
sine of the angle of incidence upon the first
plane Aa will be to the sine of the angle
of emergence from the second plane Bb in a given ratio; and this sine, which
is the sine of the angle of incidence upon the second plane Bb, will be to
the sine of the angle of emergence from the third plane Cc in a given ratio;
and this sine will be in a given ratio to the sine of the angle of emergence
from the fourth plane Dd; and so on indefinitely. And from the equality
of the ratios [or ex aequo] the sine of the angle of incidence upon the first
plane will be in a given ratio to the sine of the angle of emergence from the
last plane. Now let the distances between the planes be diminished and their
number increased indefinitely, so that the action of attraction or of impulse,
according to any assigned law whatever, becomes continuous; then the ratio
of the sine of the angle of incidence upon the first plane to the sine of the
angle of emergence from the last plane, being always given, will still be given
now. Q.E.D.
Proposition 95, Theorem 49
With the same suppositions as in prop. 94, I say that the velocity of the body before
incidence is to its velocity after emergence as the sine of the angle of emergence
to the sine of the angle of incidence.
Let AH be taken equal to Id, and erect the perpendiculars AG and dK
meeting the lines of incidence and emergence GH and IK in G and K. In
GH take TH equal to IK, and drop Tv perpendicular to the plane Aa. And
(by corol. 2 of the laws) resolve the motion of the body into two motions, one
 perpendicular, the other parallel, to the
planes Aa, Bb, Cc, . . . . The
[component of the] force of attraction or of
impulse acting along perpendicular lines
does not at all change the motion in the
direction of the parallels; and therefore
the body, by this latter motion, will in
equal times pass through equal distances
along parallels between the line AG and the point H, and between the point
I and the line dK, that is, it will describe the lines GH and IK in equal times.
Accordingly, the velocity before incidence is to the velocity after emergence
as GH to IK or TH; that is, as AH or Id to vH, that is (with respect to the
radius TH or IK), as the sine of the angle of emergence to the sine of the
angle of incidence. Q.E.D.
perpendicular, the other parallel, to the
planes Aa, Bb, Cc, . . . . The
[component of the] force of attraction or of
impulse acting along perpendicular lines
does not at all change the motion in the
direction of the parallels; and therefore
the body, by this latter motion, will in
equal times pass through equal distances
along parallels between the line AG and the point H, and between the point
I and the line dK, that is, it will describe the lines GH and IK in equal times.
Accordingly, the velocity before incidence is to the velocity after emergence
as GH to IK or TH; that is, as AH or Id to vH, that is (with respect to the
radius TH or IK), as the sine of the angle of emergence to the sine of the
angle of incidence. Q.E.D.
Proposition 96, Theorem 50
With the same suppositions, and supposing also that the motion before incidence
is faster than afterward, I say that as a result of achanging the inclinationa of the
line of incidence, the body will at last be reflected, and the angle of reflection will
become equal to the angle of incidence.
For suppose the body to describe parabolic arcs between the parallel
planes Aa, Bb, Cc, . . ., as before; and let those arcs be HP, PQ, QR, . . . . And
 let the obliquity of the line
of incidence GH to the first
plane Aa be such that the sine
of the angle of incidence is to
the radius of the circle whose
sine it is in the ratio which that same sine of the angle of incidence has to
the sine of the angle of emergence from the plane Dd into the space DdeE;
then, because the sine of the angle of emergence will now have become
equal to the radius, the angle of emergence will be a right angle, and hence
the line of emergence will coincide with the plane Dd. Let the body arrive
at this plane at the point R; and since the line of emergence coincides with
that same plane, it is obvious that the body cannot go any further toward
the plane Ee. But neither can it go on in the line of emergence Rd, because
it is continually attracted or impelled toward the medium of incidence.
Therefore, this body will be turned back between the planes Cc and Dd,
describing an arc of the parabola QRq, whose principal vertex (according to
what Galileo demonstrated) is at R, and will cut the plane Cc in the same
angle at q as formerly at Q; and then, proceeding in the parabolic arcs qp,
ph, . . . , similar and equal to the former arcs QP and PH, this body will
cut the remaining planes in the same angles at p, h, . . ., as formerly at P,
H, . . ., and will finally emerge at h with the same obliquity with which
it was incident upon the plane at H. Now suppose the distances between
the planes Aa, Bb, Cc, Dd, Ee, . . . to be diminished and their number
increased indefinitely, so that the action of attraction or impulse, according
to any assigned law whatever, is made to be continuous; then the angle of
emergence, being always equal to the angle of incidence, will still remain
equal to it now. Q.E.D.
let the obliquity of the line
of incidence GH to the first
plane Aa be such that the sine
of the angle of incidence is to
the radius of the circle whose
sine it is in the ratio which that same sine of the angle of incidence has to
the sine of the angle of emergence from the plane Dd into the space DdeE;
then, because the sine of the angle of emergence will now have become
equal to the radius, the angle of emergence will be a right angle, and hence
the line of emergence will coincide with the plane Dd. Let the body arrive
at this plane at the point R; and since the line of emergence coincides with
that same plane, it is obvious that the body cannot go any further toward
the plane Ee. But neither can it go on in the line of emergence Rd, because
it is continually attracted or impelled toward the medium of incidence.
Therefore, this body will be turned back between the planes Cc and Dd,
describing an arc of the parabola QRq, whose principal vertex (according to
what Galileo demonstrated) is at R, and will cut the plane Cc in the same
angle at q as formerly at Q; and then, proceeding in the parabolic arcs qp,
ph, . . . , similar and equal to the former arcs QP and PH, this body will
cut the remaining planes in the same angles at p, h, . . ., as formerly at P,
H, . . ., and will finally emerge at h with the same obliquity with which
it was incident upon the plane at H. Now suppose the distances between
the planes Aa, Bb, Cc, Dd, Ee, . . . to be diminished and their number
increased indefinitely, so that the action of attraction or impulse, according
to any assigned law whatever, is made to be continuous; then the angle of
emergence, being always equal to the angle of incidence, will still remain
equal to it now. Q.E.D.
Scholium
These attractions are very similar to the reflections
and refractions of light
made according to a given ratio of the secants, as Snel discovered, and
consequently according to a given ratio of the sines, as Descartes set forth. For the
fact that light is propagated successively [i.e., in time and not instantaneously]
and comes from the sun to the earth in about seven or eight minutes is now
established by means of the phenomena of the satellites of Jupiter, confirmed
by the observations of various astronomers. Moreover, the rays of light that
are in the air (as Grimaldi recently discovered, on admitting light into a
dark room through a small hole—something I myself have also tried) in
their passing near the edges of bodies, whether opaque or transparent (such
as are the circular-rectangular edges of coins minted from gold, silver, and
bronze, and the sharp edges of knives, stones, or broken glass), are inflected
around the bodies, as if attracted toward them; and those of the rays that
in such passing approach closer to the bodies are inflected the more, as if
more attracted, as I myself have also diligently observed. And those that
pass at greater distances are less inflected, and at still greater distances are
inflected somewhat in the opposite direction and form three bands of colors.
In the figure, s designates the sharp edge
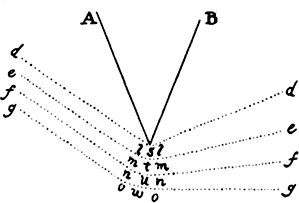 of a knife or of any wedge AsB, and
gowog, fnunf, emtme, and dlsld are
rays, inflected in the arcs owo, nun, mtm,
and lsl toward the knife, more so or less
so according to their distance from the
knife. Moreover, since such an inflection
of the rays takes place in the air outside the knife, the rays which are incident
upon the knife must also be inflected in the air before they reach it. And the
case is the same for those rays incident upon glass. Therefore refraction takes
place not at the point of incidence, but gradually by a continual inflection of
the rays, made partly in the air before the rays touch the glass, and partly (if
I am not mistaken) within the glass after they have entered it, as has been
of a knife or of any wedge AsB, and
gowog, fnunf, emtme, and dlsld are
rays, inflected in the arcs owo, nun, mtm,
and lsl toward the knife, more so or less
so according to their distance from the
knife. Moreover, since such an inflection
of the rays takes place in the air outside the knife, the rays which are incident
upon the knife must also be inflected in the air before they reach it. And the
case is the same for those rays incident upon glass. Therefore refraction takes
place not at the point of incidence, but gradually by a continual inflection of
the rays, made partly in the air before the rays touch the glass, and partly (if
I am not mistaken) within the glass after they have entered it, as has been
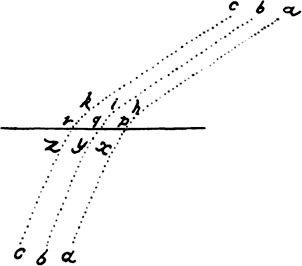 delineated in the rays ckzc, biyb, and ahxa
incident upon the glass at r, q, and p, and
inflected between k and z, i and y, h and
x. Therefore because of the analogy that
exists between the propagation of rays of light
and the motion of bodies, I have decided to
subjoin the following propositions for
optical uses, meanwhile not arguing at all about
the nature of the rays (that is, whether they
are bodies or not), but only determining the trajectories of bodies, which are
very similar to the trajectories of rays.
delineated in the rays ckzc, biyb, and ahxa
incident upon the glass at r, q, and p, and
inflected between k and z, i and y, h and
x. Therefore because of the analogy that
exists between the propagation of rays of light
and the motion of bodies, I have decided to
subjoin the following propositions for
optical uses, meanwhile not arguing at all about
the nature of the rays (that is, whether they
are bodies or not), but only determining the trajectories of bodies, which are
very similar to the trajectories of rays.
Proposition 97, Problem 47
Supposing that the sine of the angle of incidence upon some surface is to the sine
of the angle of emergence in a given ratio, and that the inflection of the paths of
bodies in close proximity to that surface takes place in a very short space, which
can be considered to be a point; it is required to determine the surface that may
make all the corpuscles emanating successively from a given place converge to
another given place.
Let A be the place from
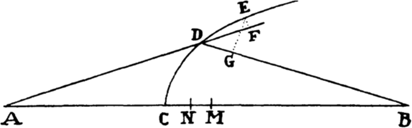 which the corpuscles diverge, B
the place to which they should
converge, CDE the curved line
that—by revolving about the axis
AB—describes the required surface, D and E any two points of that curve,
and EF and EG perpendiculars dropped to the paths AD and DB of the
body. Let point D approach point E; then the ultimate ratio of the line DF
(by which AD is increased) to the line DG (by which DB is decreased) will
be the same as that of the sine of the angle of incidence to the sine of the
angle of emergence. Therefore the ratio of the increase of the line AD to
the decrease of the line DB is given; and as a result, if a point C is taken
anywhere on the axis AB, this being a point through which the curve CDE
should pass, and the increase CM of AC is taken in that given ratio to the
decrease CN of BC, and if two circles are described with centers A and B
and radii AM and BN and cut each other at D, that point D will touch the
required curve CDE, and by touching it anywhere whatever will determine
that curve. Q.E.I.
which the corpuscles diverge, B
the place to which they should
converge, CDE the curved line
that—by revolving about the axis
AB—describes the required surface, D and E any two points of that curve,
and EF and EG perpendiculars dropped to the paths AD and DB of the
body. Let point D approach point E; then the ultimate ratio of the line DF
(by which AD is increased) to the line DG (by which DB is decreased) will
be the same as that of the sine of the angle of incidence to the sine of the
angle of emergence. Therefore the ratio of the increase of the line AD to
the decrease of the line DB is given; and as a result, if a point C is taken
anywhere on the axis AB, this being a point through which the curve CDE
should pass, and the increase CM of AC is taken in that given ratio to the
decrease CN of BC, and if two circles are described with centers A and B
and radii AM and BN and cut each other at D, that point D will touch the
required curve CDE, and by touching it anywhere whatever will determine
that curve. Q.E.I.
COROLLARY 1. But by making point A or B in one case go off indefinitely, in another case move to the other side of point C, all the curves which Descartes exhibited with respect to refractions in his treatises on optics and geometry will be traced out. Since Descartes concealed the methods of finding these, I have decided to reveal them by this proposition.
COROLLARY 2. If a body, incident upon any surface CD along the
straight line AD drawn according to any law, emerges along any other
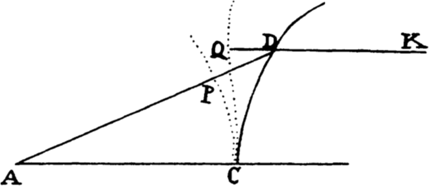 straight line DK; and if from point
C the curved lines CP and CQ,
always perpendicular to AD and DK,
are understood to be drawn; then the
increments of the lines PD and QD,
and hence the lines themselves PD
and QD generated by those increments, will be as the sines of the angles of
incidence and emergence to each other, and conversely.
straight line DK; and if from point
C the curved lines CP and CQ,
always perpendicular to AD and DK,
are understood to be drawn; then the
increments of the lines PD and QD,
and hence the lines themselves PD
and QD generated by those increments, will be as the sines of the angles of
incidence and emergence to each other, and conversely.
Proposition 98, Problem 48
The same conditions being supposed as in prop. 97, and supposing that there
is described about the axis AB any attracting surface CD, regular or irregular,
through which the bodies coming out from a given place A must pass; it is required
to find a second attracting surface EF that will make the bodies converge to a
given place B.
Join AB and let it cut the first surface in C and the second in E, point D being taken in any way whatever. And supposing that the sine of the angle of incidence upon the first surface is to the sine of the angle of emergence from that first surface, and that the sine of the angle of emergence from the second surface is to the sine of the angle of incidence upon the second surface, as some given quantity M is to another given quantity N; produce AB to G so that BG is to CE as M − N to N, and produce AD to H so that AH is equal to AG, and also produce DF to K so that DK is to DH as N to M. Join KB, and with center D and radius DH describe a circle meeting KB produced in L, and draw BF parallel to DL; then the point F will touch the line EF, which—on being revolved about the axis AB—will describe the required surface. Q.E.F
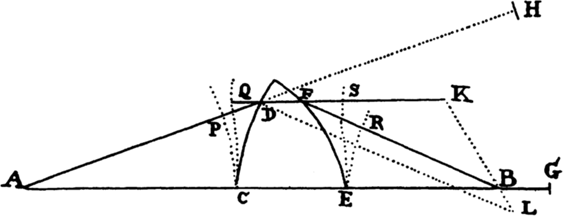
Now suppose the lines CP and CQ to be everywhere perpendicular to AD and DF respectively, and the lines ER and ES to be similarly perpendicular to FB and FD, with the result that QS is always equal to CE; then (by prop. 97, corol. 2) PD will be to QD as M to N, and therefore as DL to DK or FB to FK; and by separation [or dividendo] as DL − FB or PH − PD — FB to FD or FQ — QD, and by composition [or componendo] as PH − FB to FQ, that is (because PH and CG, QS and CE are equal), as CE + BG − FR to CE − FS. But (because BG is proportional to CE and M − N is proportional to N) CE + BG is also to CE as M to N, and thus by separation [or dividendo] FR is to FS as M to N; and therefore (by prop. 97, corol. 2) the surface EF compels a body incident upon it along the line DF to go on in the line FR to the place B. Q.E.D.
Scholium
It would be possible to use the same method for three surfaces or more. But
for optical uses spherical shapes are most suitable. If the objective lenses of
telescopes are made of two lenses that are spherically shaped and water is
enclosed between them, it can happen that errors of the refractions that take
place in the extreme surfaces of the lenses are accurately enough corrected
by the refractions of the water. Such objective lenses are to be preferred to
elliptical and hyperbolical lenses, not only because they can be formed more
easily and more accurately but also because they more accurately refract the
pencils of rays situated outside the axis of the glass. Nevertheless, the differing
refrangibility of different rays [i.e., of rays of different colors] prevents optics
from being perfected by spherical or any other shapes. Unless the errors
arising from this source can be corrected, all labor spent in correcting the
other errors will be of no avail.