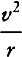 rule is published (from Newton’s “Waste Book”)
in Background, pp. 130–131.
rule is published (from Newton’s “Waste Book”)
in Background, pp. 130–131.* An Index Verborum of the Latin edition of the Principia has been produced by Anne Whitman and I. Bernard Cohen in association with Owen Gingerich and Barbara Welther. This index includes the complete text of the third edition (1726) and also the variant readings as given in the Latin edition of the Principia (edited by Alexandre Koyré, I. Bernard Cohen, and Anne Whitman), published in 1972 by the Harvard University Press and the Cambridge University Press. Thus the Index includes the complete text of the three authorized Latin editions (1687, 1713, 1726) as well as the MS annotations in both Newton’s “annotated” and ‘interleaved” personal copies of the first and second editions. The Index is on deposit in the Burndy Library of the Dibner Institute (Cambridge, Mass.), where it may be consulted. Microfilm copies can be purchased.
Very useful tools for scholars and students are the planned Octavo editions of the first and third Latin editions of Newton’s Principia; the latter will include this English translation. The high-resolution facsimiles on CD-ROM allow readers to view the original book and search the complete Latin texts and translation. For publication information, see the Octavo web site: www.octavo.com.
1. Newton’s objections were not based on the name in terms of its Greek roots or its adequacy or inadequacy to describe the subject matter. Rather, he took umbrage at Leibniz’s having devised a name as if he had been the inventor of the subject, whereas Newton believed that he himself had been the primary creator. In a private memorandum (my Introduction, p. 296, §6), Newton wrote that “Galileo began to consider the effect of Gravity upon Projectiles. Mr. Newton in his Principia Philosophiae improved that consideration into a large science. Mr. Leibnitz christened the child by [a] new name as if it had been his own, calling it Dynamica.” In another such memorandum (ibid., p. 297), he declared that Leibniz “changed the name of vis centripeta used by Newton into that of sollicitatio paracentrica, not because it is a fitter name, but to avoid being thought to build upon Mr. Newton’s foundation.” He also held that Leibniz “has set his mark upon this whole science of forces calling it Dynamick, as if he had invented it himself & is frequently setting his mark upon things by new names & new Notations.”
2. E.g., my Introduction, Westfall’s Never at Rest, Whiteside’s introduction in Math. Papers (vol. 6), Herivel’s Background, and more recently A. Rupert Hall, Isaac Newton: Adventurer in Thought (Oxford and Cambridge, Mass.: Blackwell, 1992).
3. Our source for this anecdote may be found in the notes accumulated by John Conduitt, husband of Newton’s niece and Newton’s successor at the Mint, for a proposed biography of Newton. Conduitt got the story from the mathematician Abraham de Moivre. The main lines of the story are undoubtedly correct, but we may doubt the accuracy of the details, since this is a secondhand record of an event that had happened about half a century earlier. What was the exact question that Halley would have asked Newton?
The question recorded by Conduitt has puzzled critical historians, because it does not have a simple answer. There has even been some speculation whether Halley may have asked Newton for the force acting in the case of an elliptical orbit rather than for the orbit produced by an inverse-square force. It is doubtful whether Conduitt knew enough mathematics to see the difference between the two. But, in fact, there is a real difference. As Newton shows in the Principia, in prop. 11, and as he proved in the drafts of De Motu, an elliptical orbit does imply an inverse-square force. Yet, as readers of the Principia would have been aware, an inverse-square force does not necessarily imply an elliptic orbit, rather a conic section (which can be an ellipse, a parabola, or a hyperbola).
Of course, Halley’s question may have implied (or have been thought by Newton to have implied) an orbit of a planet or possibly a planetary satellite. Since such an orbit is a closed curve, and therefore not a parabola or a hyperbola, Halley’s question to Newton would then have been, in effect, What is the planetary orbit (or closed orbit) produced by an inverse-square force? In this case, the answer would legitimately be the one recorded by Conduitt.
4. The several versions of De Motu may be found (with translations and commentary) in Whiteside’s edition of Math. Papers 6:30–80; the Halls’ Unpublished Sci. Papers, pp. 237–239, 243–292; Herivel’s Background, pp. 256–303; and, earlier, in Rouse Ball’s Essay, pp. 31–56, and in Stephen P. Rigaud, Historical Essay on the First Publication of Sir Isaac Newton’s “Principia” (Oxford: Oxford University Press, 1838; reprint, with an introd. by I. B. Cohen, New York and London: Johnson Reprint Corp., 1972), appendix, no. 1, pp. 1–19. For a facsimile reprint of the MSS of De Motu, see n. 5 below.
5. On this first draft of book 1, see my Introduction, chap. 4 and suppl. 3, where it is referred to as Newton’s Lucasian Lectures (LL) because Newton later deposited this MS in the University Library as if it were the text of his university lectures for 1684 and 1685. This text has been edited and translated by D. T. Whiteside in vol. 6 of Math. Papers, and Whiteside has also prepared a facsimile edition of the whole MS, together with the drafts of De Motu, under the general title The Preliminary Manuscripts for Isaac Newton’s 1687 “Principia,” 1684–1685 (Cambridge and New York: Cambridge University Press, 1989).
6. This early book 1 concluded (as did De Motu) with a brief presentation of motion in resisting fluids, which was later considerably expanded so as to become the first sections of book 2 of the Principia.
7. Pendulums are also discussed in book 1.
8. A new translation of this early version of book 3, by Anne Whitman and I. Bernard Cohen, is scheduled for publication by the University of California Press. In order to distinguish this work from book 3 of the Principia (with its subtitle “De Systemate Mundi”), we have called this early version Essay on the System of the World. A list of the paragraphs that are the same in both versions may be found in a supplement to our edition of the Principia with variant readings, cited in n. 45 below.
9. The books and articles devoted to this topic are so numerous, and continue to appear at so rapid a rate, that it would hardly be practical to cite them all. The most accessible and authoritative presentations are to be found in Curtis Wilson’s “Newt. Achievement” and especially in D. T. Whiteside, “Before the Principia: The Maturing of Newton’s Thoughts on Dynamical Astronomy, 1664–84,” Journal for the History of Astronomy 1 (1970): 5–19; “The Mathematical Principles Underlying Newton’s Principia,” ibid., 116–138. See also my Newt. Revolution, chaps. 4 and 5; R. S. Westfall’s Never at Rest and his earlier Force in Newton’s Physics (London: Macdonald; New York: American Elsevier, 1971), chaps. 7 and 8; Herivel’s Background. A splendid review of this topic is available in Hall, Isaac Newton: Adventurer in Thought, pp. 55–64. A list of other scholars who have made contributions to this subject would include, among others, Bruce Brackenridge, Herman Ehrlichson, J. E. McGuire, and Michael M. Nauenberg.
10. The text of Newton’s early discovery of the 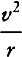 rule is published (from Newton’s “Waste Book”)
in Background, pp. 130–131.
rule is published (from Newton’s “Waste Book”)
in Background, pp. 130–131.
11. This celebrated autobiographical document was first printed in A Catalogue of the Portsmouth Collection of Books and Papers Written by or Belonging to Sir Isaac Newton, the Scientific Portion of Which Has Been Presented by the Earl of Portsmouth to the University of Cambridge, ed. H. R. Luard et al. (Cambridge: Cambridge University Press, 1888), and has been reprinted many times since. A corrected version, taken from the manuscript in the Cambridge University Library (ULC MS Add. 3968, §41, fol. 85) may be found in my Introduction, pp. 290–292.
12. Corresp. 1:300; see A. Rupert Hall, “Newton on the Calculation of Central Forces,” Annals of Science 13 (1957): 62–71.
13. Hall, Isaac Newton: Adventurer in Thought, p. 62. This work gives an excellent critical summary of Newton’s thoughts about celestial motions during the 1660s.
14. For the documents and an analysis, see Hall, “Newton on the Calculation of Central Forces,” pp. 62–71; also Background, pp. 192–198, 68–69; and esp. Never at Rest, pp. 151–152. See, further, Newt. Revolution, esp. pp. 238–240. A splendid review of this subject is available in D. T. Whiteside, “The Prehistory of the Principia from 1664 to 1686,” Notes and Records of the Royal Society of London 45 (1991): 11–61, esp. 18–22.
15. Florian Cajori, “Newton’s Twenty Years’ Delay in Announcing the Law of Gravitation,” in Sir Isaac Newton, 1727–1927: A Bicentenary Evaluation of His Work, ed. Frederic E. Brasch (Baltimore: Williams and Wilkins, 1928), pp. 127–188.
16. The Newton-Hooke correspondence during 1679/80 is to be found in Corresp., vol. 2. See, in this regard, Alexandre Koyré, “An Unpublished Letter of Robert Hooke to Isaac Newton,” Isis 43 (1952): 312–337, reprinted in Koyré’s Newtonian Studies (Cambridge, Mass.: Harvard University Press, 1965), pp. 221–260. Also J. A. Lohne, “Hooke versus Newton: An Analysis of the Documents in the Case of Free Fall and Planetary Motion,” Centaurus 7 (1960): 6–52.
17. Later, Newton quite correctly insisted that Hooke could not prove this assertion. In any event he himself had already been thinking of an inverse-square force.
18. Newton was to prove that this particular conclusion or guess of Hooke’s was wrong. The force on a planet at a point P (see book 1, prop. 1, corol. 1) is inversely proportional to the perpendicular distance from the sun to the tangent to the curve at P. We shall take note, below, that Hooke’s rule, previously stated by Kepler, is true only at the apsides.
19. There has, however, been some consideration given to the possibility that what Newton wrote up at this time was a prototype of the paper he later sent to John Locke.
This work is available, with a commentary by D. T. Whiteside, in Math. Papers, vol. 6, and in Herivel’s Background and the Halls’ edition of Unpubl. Sci. Papers.
20. Never at Rest, p. 387. I have discussed this matter in my Introduction, pp. 49–52, in relation to the question of what Halley asked Newton on the famous visit in the summer of 1684 and what Newton would have replied.
21. Most scholars date the Locke paper after the Principia. An earlier dating was suggested by Herivel in 1961 and reaffirmed in his Background, pp. 108–117. This assigned date was then challenged by the Halls in 1963, and supported by Westfall in 1969, whose arguments were refuted by Whiteside in 1970. See the summary in Westfall’s Never at Rest, pp. 387–388 n. 145.
An admirable discussion of the various attempts to date this work is given in Bruce Brackenridge, “The Critical Role of Curvature in Newton’s Developing Dynamics,” in The Investigation of Difficult Things: Essays on Newton and the History of the Exact Sciences, ed. P. M. Harman and Alan E. Shapiro (Cambridge: Cambridge University Press, 1992), pp. 231–260, esp. 241–242 and n. 35. Brackenridge concludes by agreeing with Whiteside that the date of a “prototype manuscript” on which this tract is based should be fixed at August 1684, shortly after Halley’s visit.
22. Newton to Halley, 27 July 1686, Corresp. 2:447; my Introduction, suppl. 1. My own awareness of the significance of the Hooke-Newton correspondence (in suggesting a fruitful way to analyze celestial orbital motions) derives from a pioneering study by R. S. Westfall, “Hooke and the Law of Universal Gravitation,” The British Journal for the History of Science 3 (1967): 245–261.
23. On the problems of using Kepler’s law of areas and the various approximations used by seventeenth-century astronomers in place of this law, see Curtis Wilson, “From Kepler’s Laws, So-Called, to Universal Gravitation: Empirical Factors,” Archive for History of Exact Sciences 6 (1970): 89–170; and my Newt. Revolution, pp. 224–229.
24. Patri Pugliese, “Robert Hooke and the Dynamics of Motion in the Curved Path,” in Robert Hooke: New Studies, ed. Michael Hunter and Simon Schaffer (London: Boydell Press, 1989), pp. 181–205. See, further, Michael Nauenberg, “Hooke, Orbital Motion, and Newton’s Principia,” American Journal of Physics 62 (1994): 331–350.
25. “Newt. Achievement,” pp. 242–243.
26. Newton to Hooke, 13 December 1679, Corresp. 2:308. Wilson’s suggested reconstruction occurs in “Newt. Achievement,” p. 243.
27. Unpubl. Sci. Papers, pp. 253, 277.
28. Ibid., pp. 256, 281.
29. See D. T. Whiteside’s notes in Math. Papers 5:148–149 n. 152; 6:98–99 n. 16.
30. A quite different reconstruction of Newton’s path to universal gravity has been proposed by George Smith. He suggests: “The ‘one-body’ solutions of the tract ‘De Motu’ expressly entail that the a3/T2 value associated with each celestial central body is a measure of the centripetal tendency toward it. The known values for the Sun, Jupiter, Saturn, and the Earth can then be used, in conjunction with the principle that the center of gravity of the system remains unaffected (corollary 4 of the Laws of Motion), first to conclude independently of any explicit reference to mass that the Copernican system is basically correct (as in the ‘Copernican scholium’ of the revised version of ‘De Motu’), and then to infer that the gravitational force acting celestially is proportional to the masses of the central and orbiting bodies. The final step to universal gravitation then follows along the lines of Propositions 8 and 9 of Book III of the Principia.” See, also, Wilson’s “From Kepler’s Laws” (n. 23 above).
31. Corresp. 2:419–420.
32. These two goals are discussed in my “Newton’s Theory vs. Kepler’s Theory and Galileo’s Theory: An Example of a Difference between a Philosophical and a Historical Analysis of Science,” in The Interaction between Science and Philosophy, ed. Yehuda Elkana (Atlantic Highlands, N.J.: Humanities Press, 1974), pp. 299–388.
33. “Exposition abregée du système du monde, et explication des principaux phénomènes astronomiques tirée des Principes de M. Newton,” suppl. to the marquise du Châtelet’s translation of the Principia (Paris: chez Desaint & Saillant [&] Lambert, 1756), 2:6.
34. Newton was referring to the problem of the gravitational action of a homogeneous sphere on an external particle; see Whiteside’s note in Math. Papers 6:19 n. 59.
35. Newton to Halley, 20 June 1686, Corresp., vol. 2.
36. Ibid. “I do pretend [i.e., claim],” Newton wrote, “to have done as much for the proportion [of the inverse square] as for the ellipsis, and to have as much right to the one from Mr. Hooke and all men, as to the other from Kepler.”
37. See §3.1 below.
38. See my Introduction, suppl. 7.
39. A. N. L. Munby estimated the size of the first edition at some 300 or 400 copies, but this number has recently been increased to perhaps 500. See Whiteside, “The Prehistory of the Principia” (n. 14 above), esp. p. 34. Whiteside reckons that, granting this larger size of the edition, Halley would not have suffered financially by paying the printing costs of the Principia and would even have made not “less than £10 in pocket for all his time and trouble.”
40. Or. the alterations in the poem in successive editions of the Principia, see our Latin edition, cited in n. 45 below.
41. Philosophical Transactions 16, no. 186 (Jan.-Feb.-March 1687): 291–297, reprinted in Isaac Newton’s Papers and Letters on Natural Philosophy, ed. I. B. Cohen and Robert E. Schofield, 2d ed. (Cambridge, Mass.: Harvard University Press, 1978), pp. 405–411.
42. See my Introduction, chap. 7, and esp. Math. Papers, vol. 6.
43. Introduction, p. 193.
44. Ibid., pp. 188–198.
45. Isaac Newton’s “Philosophiae Naturalis Principia Mathematica”: The Third Edition (1726) with Variant Readings, assembled and edited by Alexandre Koyré, I. Bernard Cohen, and Anne Whitman, 2 vols. (Cambridge: Cambridge University Press; Cambridge, Mass.: Harvard University Press, 1972).
46. See D. T. Whiteside’s magisterial discussion of this episode, together with all the relevant documents concerning the stages of alteration of book 2, prop. 10, in Math. Papers 8:50–53, esp. nn. 175, 180, and esp. §6, appendix 2.1.52 in that same volume. See also §7.3 below and my Introduction, §9.4.
47. These props. 34–40 of the first edition (translated by I. Bernard Cohen and Anne Whitman) will be published, together with a commentary by George Smith, in Newton’s Natural Philosophy, ed. Jed Buchwald and I. Bernard Cohen (Cambridge: MIT Press, forthcoming).
48. Unpubl. Sci. Papers, pp. 320–347 (see §9.3 below); Newton to Cotes, 2 Mar. 1712/13. On the production of the second edition, see the texts, notes, and commentaries in Correspondence of Sir Isaac Newton and Professor Cotes, ed. J. Edleston (London: John W. Parker; Cambridge: John Deighton, 1850).
49. See §9.3 below.
50. See §8.2 below.
51. See my Introduction, chap. 6, sec. 6.
52. See §8.14 below.
53. For details see Isaac Newton’s Theory of the Moon’s Motion (1702), introd. I. Bernard Cohen (Folkestone: Dawson, 1975).
54. These four special copies are described in my Introduction; Newton’s MS notes appear in our edition with variant readings (n. 45 above).
55. See my Introduction, chap. 11.
56. See A. Rupert Hall, Philosophers at War: The Quarrel between Newton and Leibniz (Cambridge, London, New York: Cambridge University Press, 1980), and especially Math. Papers, vol. 8.
57. See §2.3 below.
58. See the later Queries of the Opticks and the discussion by Betty Jo Dobbs, Janus Faces (§3.1, n. 10 below).
59. See §9.3 below.
All notes to the translation are keyed to the text by superscript letters. When a note is introduced by two letters, such as “aa,” it refers to that part of the text enclosed between an opening superscript “a” and a final or closing “a.”
These notes are, for the most part, extracts from variant passages or expressions as found in the first two editions. The glosses and explanations of the text are to be found in the Guide, the text of which follows the order of Newton’s presentation in the Principia.
a. Newton’s comparison and contrast between the subject of rational or theoretical mechanics and practical mechanics was a common one at the time of the Principia. Thus John Harris in his Newtonian Lexicon Technicum (London, 1704), citing the authority of John Wallis, made a distinction between the two as follows. One was a “Geometry of Motion,” a “Mathematical Science which shews the Effects of Powers, or moving Forces,” and “demonstrates the Laws of Motion.” The other is “commonly taken for those Handy-crafts, which require as well the Labour of the Hands, as the Study of the Brain.” The subject of the Principia became generally known as “rational mechanics” following Newton’s use of that name in his Preface.
b. Newton would seem to be expressing in Latin more or less the same concept that later appears in English (in query 28 of the Opticks) as “the main Business of natural Philosophy.”
a. Literally, lack of lubricity or slipperiness.
aa. In translating def. 1, we have rendered Newton’s “Quantitas materiae est mensura ejusdem . . .” as “Quantity of matter is a measure of matter . . .” rather than the customary “. . . is the measure . . .” The indefinite article is more in keeping with the Latin usage, with its absence of articles, and accords better with the sense in which we have interpreted this definition. See the Guide, §4.2. It should be noted that the indefinite article permits the possibility of the sense of either a definite or an indefinite article, whereas a definite article precludes the possibility of the sense of an indefinite article.
bb. Ed. 3 reads literally: “Air, if the density is doubled, in a space also doubled, becomes quadruple; in [a space] tripled, sextuple.” The printer’s manuscript for ed. 1 and the printed text of ed. 1 have: “Air twice as dense in twice the space is quadruple.” Newton’s interleaved copy of ed. 1 has: “Air twice as dense in twice the space is quadruple; in three times [the space], sextuple.” Newton’s annotated copy of ed. 1 has first: “Air twice as dense in twice the space becomes quadruple; in three times [the space], sextuple.” This is then deleted and replaced with: “Air, by doubling the density, in the same container becomes double; in a container twice as large, quadruple; in one three times as large, sextuple; and by tripling the density, it becomes triple in the same container and sextuple in a container twice as large,” but the last clause, “and by tripling . . . large,” is then deleted.
The manuscript errata at the end of the annotated copy have: “For this quantity, if the density is given [or fixed], is as the volume and, if the volume is given, is as the density and therefore, if neither is given, is as the product of both. Thus indeed Air, if the density is doubled, in a space also doubled, becomes quadruple; in [a space] tripled, sextuple.” The first sentence, “For this . . . product of both,” and the following two words, “Thus indeed,” are inserted over a caret preceding “Air.”
An interleaf of the interleaved copy of ed. 1 and then the printed text of ed. 2 have exactly the same phrasing as ed. 3.
aa. Newton’s Latin clause is “quantum in se est,” which here means “to the degree that it can of and by itself.” See I. Bernard Cohen, “‘Quantum in se est’: Newton’s Concept of Inertia in Relation to Descartes and Lucretius,” Notes and Records of the Royal Society of London 19 (1964): 131–155.
bb. Newton’s “in directum” (used together with “uniformiter” [“uniformly”]) has the sense of moving straight on, of going continuously straight forward, and therefore in a straight line. In an earlier version, Newton had used the phrase “in linea recta” (“in a right line” or “in a straight line”), but by the time of the Principia he had rejected this expression in favor of “in directum.” For details, see the Guide, §10.2. On Newton’s “vis insita” and our rendition, see the Guide, §4.7.
c. Newton’s interleaved copy of ed. 2 adds the following, which was never printed: “I do not mean Kepler’s force of inertia, by which bodies tend toward rest, but a force of remaining in the same state either of resting or of moving.”
aa. Ed. 1 lacks this.
bb. See the Guide, §2.4.
aa. Newton uses the phrase “seu accurata seu inaequabilis”—literally, “exact or nonuniform.”
aa. See note bb to def. 3.
bb. Ed. 1 and ed. 2 lack the pronoun “illud,” which, by expressing the subject, renders it somewhat more emphatic than it is when conveyed only by the form of the verb (“is compelled”) and which makes more explicit the reference to an antecedent noun (“body”).
cc. Ed. 1 and ed. 2 have “that.”
d. The Latin word is “trochus,” i.e., a top or some kind of spinner.
a. By “body” Newton means quantity of matter or mass (def. 1) and by “motion” he means quantity of motion (def. 2) or momentum.
aa. Ed. 1 and ed. 2 lack this.
bb. Evidently “in natural compositions” or “in natural bodies.”
cc. Ed. 1 lacks this.
d. Newton writes of “instrumentorum” (literally, “equipment”) and of “instrumentis mechanicis” (literally, “mechanical instruments”), as well as “machinae.” See §5.7 of the Guide.
aa. Ed. 1 has “a given time.”
bb. Ed. 1 lacks this.
aa. Ed. 1 has “produce AB to b and AD to d; then, since points A and B come together and thus no part AB of Ab still lies within the curve, it is obvious that this straight line Ab will either coincide with the tangent Ad or be drawn between the tangent and the curve. But the latter case is contrary to the nature of curvature; therefore, the former obtains. Q.E.D.”
aa. Ed. 1 has “regular.”
bb. Ed. 1 lacks this.
cc. Ed. 1 lacks corols. 3–5 and scholium.
aa. Ed. 1 lacks corols. 2 and 3.
bb. Ed. 1 lacks this sentence.
cc. For “lengthy” (Lat. “longas”) ed. 1 and ed. 2 have “complicated” (Lat. “perplexas”), which Newton inserted with his own hand into the manuscript of ed. 1. Motte gives “perplexed,” thus obviously using ed. 2, and Cajori has “involved,” revealing that the Latin text was not consulted at this point. But in A History of the Conceptions of Limits and Fluxions in Great Britain from Newton to Woodhouse (Chicago and London: Open Court Publishing Co., 1919), Cajori notes on p. 5 that “in the third edition ‘longas’ takes the place of ‘perplexas,’” and on p. 8 he uses Thorp’s translation (“long”).
dd. Newton uses the adjective “durior,” which is traditionally translated by “rather harsh.”
a. For a gloss on this proposition see the Guide, §10.8.
bb. In the statement of prop. 1, Newton uses the phrase “in gyros acta”; see the Guide, §2.4.
cc. In ed. 1, corols. 1 and 2 are earlier versions of prop. 2, corols. 1 and 2, and the corols. 1 and 2 of ed. 2 and ed. 3 are lacking.
dd. Ed. 1 lacks corols. 3–6.
aa. In ed. 1, prop. 2 has no corollaries. Corols. 1 and 2 of ed. 2 and ed. 3 are basically revised versions of corols. 1 and 2 to prop. 1 of ed. 1.
bb. Ed. 1 has (as prop. 1, corol. 1): “In nonresisting mediums, if the areas are not proportional to the times, the forces do not tend toward the point where the radii meet.”
cc. Ed. 1 has (as prop. 1, corol. 2): “In all mediums, if the description of areas is accelerated, the forces do not tend toward the point where the radii meet but deviate forward [or in consequentia] from it.”
aa. In both the statement and the demonstration of the proposition and also in the corollaries, ed. 1 lacks letters to designate the two bodies. In Newton’s annotated copy of ed. 1, the letters L and T are added in all of these parts of the proposition. In Newton’s interleaved copy of ed. 1, letters are added in all of these sections but are then deleted from the statement of the proposition, where the letters written in might have first been A and B and then been changed to L and T before being crossed out. In the first sentence of the demonstration in this interleaved copy, the first two letters added at the beginning of the sentence were originally A and B, which were then altered to L and T. It is these letters, L and T, that were added elsewhere and were kept in the demonstration and corollaries.
aa. Ed. 1 has: “Let bodies B and b, revolving in the circumferences of circles BD and bd,
describe arcs BD and bd in the same time. Since by their inherent force alone they would describe
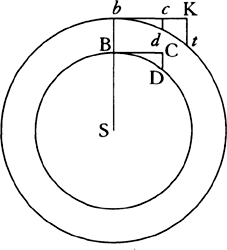 tangents BC and bc equal to these arcs, it is obvious that
centripetal forces are the ones which continually draw the
bodies back from the tangents to the circumferences of the
circles, and thus these forces are to each other in the first ratio
of the nascent spaces CD and cd, and they tend toward the
centers of the circles, by theor. 2, because the areas described
by the radii are supposed proportional to the times. [Newton
is using “first ratio” here in the special sense developed in
sec. 1 above, where he introduces the concept of “first” and
“ultimate” ratio.] Let figure tkb be similar to DCB and, by
lem. 5, line-element CD will be to line-element kt as arc BD
to arc bt, and also, by lem. 11, the nascent line-element tk
will be to the nascent line-element dc as bt2 to bd2 and, from the equality of the ratios [or ex
aequo], the nascent line-element DC will be to the nascent line-element dc as BD × bt to bd2 or,
what comes to the same thing, as BD ×
tangents BC and bc equal to these arcs, it is obvious that
centripetal forces are the ones which continually draw the
bodies back from the tangents to the circumferences of the
circles, and thus these forces are to each other in the first ratio
of the nascent spaces CD and cd, and they tend toward the
centers of the circles, by theor. 2, because the areas described
by the radii are supposed proportional to the times. [Newton
is using “first ratio” here in the special sense developed in
sec. 1 above, where he introduces the concept of “first” and
“ultimate” ratio.] Let figure tkb be similar to DCB and, by
lem. 5, line-element CD will be to line-element kt as arc BD
to arc bt, and also, by lem. 11, the nascent line-element tk
will be to the nascent line-element dc as bt2 to bd2 and, from the equality of the ratios [or ex
aequo], the nascent line-element DC will be to the nascent line-element dc as BD × bt to bd2 or,
what comes to the same thing, as BD × 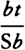 to
to 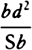 and thus (because the ratios
and thus (because the ratios 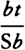 and
and 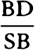 are equal)
as
are equal)
as 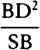 to
to 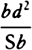 . Q.E.D.”
. Q.E.D.”
Here, as in the very similar earlier formulation of De Motu and in a later handwritten revision of ed. 1, the sentence specifying centrifugal forces has some ambiguity because the grammatical structure can indicate that Newton is redefining these forces whereas the context shows that he is giving one of their properties.
bb. Different versions of corols. 1, 2, 4, 5, and 6 exemplify interesting variations in basic mathematical terminology, as is indicated in the following notes.
cc. In ed. 1 this corollary reads: “Hence the centripetal forces are as the squares of the velocities divided by the radii of the circles.” In manuscript revisions of ed. 1 “Hence” is deleted and the sentence begins with an additional clause: “Whence, since the arcs described in the same time are directly as the velocities and inversely as the periodic times.” Ed. 2 reads: “Therefore, since those arcs are as the velocities of the bodies, the centripetal forces are as the squares of the velocities divided by the radii of the circles; that is, to express it as the geometers do, the forces are in a ratio compounded of the squared ratio of the velocities directly and the simple ratio of the radii inversely.” And then, in ed. 3, Newton decides to eliminate the first formulation and express his result only “as the geometers do.”
dd. In ed. 1 this corollary reads: “And inversely as the squares of the periodic times divided by the radii so are these forces to one another. That is (to express it as the geometers do), these forces are in a ratio compounded of the squared ratio of the velocities directly and the simple ratio of the radii inversely, and also in a ratio compounded of the simple ratio of the radii directly and the squared ratio of the periodic times inversely.” The inversion in the first sentence suggests that originally it was not a full sentence but a continuation from corol. 1, as comparison with the earlier De Motu shows to be true. Ed. 2 reads: “And since the periodic times are in a ratio compounded of the ratio of the radii directly and the ratio of the velocities inversely, the centripetal forces are inversely as the squares of the periodic times divided by the radii of the circles: that is, in a ratio compounded of the ratio of the radii directly and the squared ratio of the periodic times inversely.”
ee. In ed. 1 this corollary reads: “If the squares of the periodic times are as the radii, the centripetal forces are equal, and the velocities are in the halved ratio of the radii, and vice versa.”
ff. In ed. 1 this corollary reads: “If the squares of the periodic times are as the squares of the radii, the centripetal forces are inversely as the radii, and the velocities are equal, and vice versa.” After “of the radii,” handwritten revisions of ed. 1 add “that is, the times [are] as the radii.”
gg. In ed. 1 this corollary reads: “If the squares of the periodic times are as the cubes of the radii, the centripetal forces are inversely as the squares of the radii, but the velocities are in the halved ratio of the radii, and vice versa.”
hh. Ed. 1 lacks corols. 7 and 9, and in corol. 8, which is numbered 7, it lacks “in those figures” in the first sentence and all of the second sentence.
ii. In the printer’s manuscript of ed. 1 the scholium originally consisted of a single sentence, corresponding to the first sentence of ed. 3 but without the parenthesis containing the three proper names. A separate sheet in this manuscript and the printed text of ed. 1 contain the entire scholium, but in the addition to the manuscript the names are listed as Wren, Halley, and Hooke, whereas in ed. 1 they appear in the order retained in ed. 3. We cannot tell by whose authority Hooke’s name was moved to a position before Halley’s, but we can infer that the alteration was made in proof (and so presumably by Halley), since the handwritten addition to the manuscript as sent by Newton to Halley and by Halley to the printer is unaltered. It is very probable that Halley put Hooke’s name ahead of his own because he did not want Hooke to be offended.
jj. Ed. 1 has: “For since the former force, in the time in which a body traverses arc BC, impels the body through space CD, which at the very beginning of the motion is equal to the square of that arc BD divided by the diameter of the circle, and since every body, by the same force continued always in the same direction, describes spaces that are in the squared ratio of the times, that force, in the time in which the revolving body describes any given arc, will cause the body as it advances directly forward to describe a space equal to the square of that arc divided by the diameter of the circle and thus is to the force of gravity as that space is to the space which a heavy body in falling describes in the same time.”
a. For a gloss on this proposition see the Guide, §10.8.
bb. In ed. 1 there is a different prop. 6, with its proof and single unnumbered corollary. In ed. 2
and ed. 3 the statement of this proposition becomes corol. 1 to the new prop. 6 and the single corollary
becomes corol. 5. The proof in ed. 1 reads as follows: “For in the indefinitely small figure QRPT the
nascent line-element QR, if the time is given, is as the centripetal force (by law 2) and, if the force is
given, is as the square of the time (by lem. 10) and thus, if neither is given, is as the centripetal force
and the square of the time jointly, and thus the centripetal force is as the line-element QR directly and
the square of the time inversely. But the time is as the area SPQ, or its double SP × QT, that is, as SP
and QT jointly, and thus the centripetal force is as QR directly and SP2 times QT2 inversely, that is, as
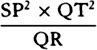 inversely. Q.E.D.” (The figure for prop. 6 in ed. 1 is the same as in eds. 2 and 3, except
that the line PS does not extend below the line SA, so that there is no point V.)
inversely. Q.E.D.” (The figure for prop. 6 in ed. 1 is the same as in eds. 2 and 3, except
that the line PS does not extend below the line SA, so that there is no point V.)
a. CP is the radius of the semicircle, and SP may be considered constant.
a. Concerning this reference to “the Conics,” see the Guide, §10.10.
a. For a gloss on this proposition see the Guide, §10.9.
b. This result is given in prop. 10 with reference to “the Conics”; see the Guide, §10.10.
a. The sense of corol. 4 is that Newton can determine “the changes which the [impressed] force will make at certain points” and, by interpolation, estimate the changes continually made at intermediary points.
a. For Newton’s statement of the reason for including secs. 4 and 5 in book 1, see book 3, prop. 41 (p. 901).
a. In the index prepared by Cotes for ed. 2 and retained in ed. 3, this corollary is keyed under “Problematis” (“of the problem”) and characterized as follows: “Geometrical synthesis of the classical problem of four lines made famous by Pappus and attempted by Descartes through algebraic computation.” As this description makes explicit, Newton’s rejection of “an [analytical] computation” in favor of “a geometrical synthesis” is directed at Descartes, who reduced the four-line locus to a curve defined algebraically by an equation of the second degree. See The Mathematical Papers of Isaac Newton, ed. D. T. Whiteside (Cambridge: Cambridge University Press, 1967–1981), 6:252–254 n. 35, 4:291 n. 17, 4:274–282, esp. 274–276.
aa. In all three editions, and in the preliminary manuscripts (see The Mathematical Papers of Isaac Newton, ed. D. T. Whiteside [Cambridge: Cambridge University Press, 1967–1981], 6:287), there is a minor discrepancy between the text and the accompanying diagram. The text refers (in the opening sentence) to “triangle DEF,” but the corresponding diagram would indicate that this should rather be “triangle def,” and similarly “corner [lit. vertex] D” and “corner F” should be respectively “corner d” and “corner f.” At the end of the paragraph, however, and in the succeeding paragraph, Newton introduces lowercase letters a, b, c for the triangle abc.
aa. This concluding sentence appeared for the first time in ed. 2.
a. In the index prepared by Cotes for ed. 2 and retained in ed. 3, this proposition is keyed under “Problematis” (“of the problem”) and characterized as follows: “Solution of Kepler’s problem by the cycloid and by approximations.”
a. For a gloss on this proposition see the Guide, §10.11.
a. For a gloss on this proposition see the Guide, §10.12.
aa. Newton does not use the word “force” in the statement of prop. 43, but he does so in the conclusion of the demonstration. A literal translation of prop. 43 would read: “It is required to make it happen [or, It is to be effected] that a body may be able to move in any trajectory that is revolving about the center of forces exactly as another body moves in that same trajectory at rest.” The force in question must be centripetal.
aa. Ed. 1 and ed. 2 lack this, but it appears both in the interleaved copy and in the annotated copy of ed. 2. The interleaved copy also has: “Query: Can this motion arise from twice the external force?” See further the Guide to the present translation, §6.10.
aa. We use the term “simple pendulum” in its classical and technical sense. For example, according to Brougham and Routh, “A simple pendulum consists of a material particle suspended from a fixed point by an inflexible inextensible string without weight” (Henry Lord Brougham and E. J. Routh, Analytical View of Sir Isaac Newton’s “Principia” [1855; reprint, with an introd. by I. Bernard Cohen, New York and London: Johnson Reprint Corp., 1972], pp. 240–241). See, further, §7.5 of the Guide.
aa. A clarification by Pemberton after he had called Newton’s attention to the incorrect diagrams in eds. 1 and 2 (cf. The Mathematical Papers of Isaac Newton, ed. D. T. Whiteside [Cambridge: Cambridge University Press, 1967–1981], 6:409, nn. 308–309).
a. In this proposition, Newton’s “vestigium,” literally, “a trace,” has been translated as “projection,” following D. T. Whiteside.
a. That is, as (S + P) to the cube root of S × (S + P)2.
a. In ed. 1, Newton used a different system of letters. In imitation of the usual form of Copernican diagram, the central body was labeled S (for “Sol,” the sun) and the encircling body was P (for “Planeta,” or planet). The next or outer body continued the sequence from P to Q. In ed. 2, as in ed. 3, the central body is T (suggesting “Terra” for the earth), the encircling body is still P (but now secondary planet or planetary satellite), while the outermost or perturbing body is S (suggesting “Sol”). In this way, in ed. 2 and ed. 3, Newton quite properly alerts the reader to the fact that he is basically analyzing mathematically a form of the three-body problem, exemplified by the moon moving in orbit around the earth while being perturbed by the gravitational force of the distant sun. The corollaries will not only serve for the discussion of the moon’s motion in book 3 but also be used in determining the mass of the moon in book 3, prop. 37, corol. 3.
b. For a gloss on this corollary see the Guide, §10.16.
a. Newton writes of a “sphaera quaevis alia similaris,” literally, “any other like [or similar] sphere,” but the context (see prop. 74, corols. 1 and 3) is that of a homogeneous sphere.
aa. The text of this proof has been translated somewhat freely, and in part expanded, for greater ease in comprehension.
a. For a gloss on this lemma see the Guide, §10.13.
a. Here, as elsewhere in the Principia, Newton uses the word “orb” for what we would more precisely call a spherical shell.
aa. The sense of Newton’s “changing the inclination” is that of increasing the angle of incidence.
aa. Ed. 2 has “the excess of this force over the force by which it is resisted at the end of that time.”
a. Ed. 1 and ed. 2 have an additional sentence: “This ratio obtains very nearly when bodies are moving very slowly in mediums having some rigidity.” In Newton’s annotated copy of ed. 2, “very nearly” is changed to “more closely.”
a. Newton’s use of “terminus” and “latus” for “root” is of particular interest in lem. 2 and its cases, corollaries, and scholium. “Radix” appears only twice and is unchanged from edition to edition, but Newton tends to replace the “terminus” (“term,” “root”) of ed. 1 with the “latus” (“side,” “root”) of ed. 2 and ed. 3. In the statement of the lemma, for example, ed. 1 has “momentis Terminorum singulorum generantium” (“the moments of the individual generating terms,” i.e., “the moments of each of the generating roots”) and “eorundem laterum indices dignitatum” (“the exponents of the powers of the same sides,” i.e., “the exponents of the powers of those roots”). Thus “terminus” and “latus” are obviously synonyms. In ed. 2 and ed. 3, however, “laterum” (“sides,” “roots”) is substituted for “Terminorum” (“terms,” “roots”). In the first sentence of the explanation, where ed. 1 has “ex Terminis quibuscunque” (“from any terms,” i.e., “from any roots”), ed. 2 and ed. 3 have “ex lateribus vel terminis quibuscunque” (“from any sides or terms,” i.e., “from any roots or terms”). As the explanation proceeds, ed. 1 has, like ed. 2 and ed. 3, “extractionem radicum” (“extraction of roots”), “contentorum & laterum” (“of products and roots”), “Radices” (“roots”), and “latera quadrata, latera cubica” (“square roots, cube roots”), but ed. 1 has “Termini” and “Terminum” where ed. 2 and ed. 3 have “Lateris” and “latus” in the last sentence of the first paragraph: “And the coefficient of each generating root is the quantity that results from dividing the generated quantity by this root.” In corol. 1, on the other hand, all the editions have “terminus” (with the ordinary sense of “term,” not with the sense of “root”), while all have “latus” (with the sense of “root”) in cases 1 and 2 and corols. 2 and 3. “Terminus” also occurs, in the phrase “in terminis surdis” (“in surd terms”), in the scholium of ed. 1 and ed. 2, which is, as will be seen below, very different from that of ed. 3, where, however, “quantitatibus surdis” (“surd quantities”) is at least comparable, especially since “surdis” (“surd”) appears nowhere else in all the editions of the Principia.
b. In the Latin text of this lemma, Newton referred to roots in two senses. The first occurs in the opening sentence, where he writes of “extraction of roots,” using the Latin term “radix,” or “root.” The second occurs in the next sentence, where he writes of “products, quotients, roots, rectangles, squares, cubes, square roots, cube roots, and the like.” Here both senses of “roots” appear in a single sentence, the first as “radices” (or “roots”), the second as “latera quadrata, latera cubica” (lit. “square sides” and “cubic sides”). In the geometric language of algebra, in which a “rectangle” of A and B indicates the product of two unequal quantities A and B as the area of a rectangle whose sides are A and B, the square root and cube root have similar geometric expression. Thus the square root of A is the side of a square whose area is A, while the cube root of A is the “side” (actually the edge) of a cube whose volume is A.
In his Lexicon Technicum (London, 1704), John Harris explained these two different mathematical senses of the word “root.” An “Unknown Quantity in an Algebraick Equation,” he wrote, “is often called the Root.” This is the sense of the word as it appears in the first sentence of the lemma. But, as Harris explained, a root is also “whatever Quantity being multiplied by it self produces a Square” and when once again “multiplied by that first Quantity produces a Cube, &c.” These, he said, are called “Square, Cube . . . Root.”
Even without any knowledge of the geometric sense of algebra, one might easily guess that Newton is referring to square and cube roots in the phrase “products, quotients, . . . squares, cubes, square sides, cube sides, and the like.” Yet Andrew Motte, in his English translation (London, 1729), rendered these terms literally as “products, quotients, roots, rectangles, squares, cubes, square and cubic sides, and the like,” which was carried over into the Motte-Cajori version. The marquise du Châtelet knew better and in her French translation (Paris, 1756) wrote, just as we would today, of “les produits, les quotiens, les racines, les rectangles, les quarrés, les cubes, les racines quarrées, & les racines cubes.”
cc. Ed. 1 has: “Moments, as soon as they are of finite magnitude, cease to be moments. For being finite is somewhat incompatible with their continual increment or decrement.” When one reads the “somewhat” (“aliquatenus”: “to a certain extent,” “in some respects”) in the second of these sentences, one can understand why Newton decided to revise this portion of his explanation.
dd. In ed. 1 this scholium reads: “In correspondence which I carried on ten years ago with the very able geometer G. W. Leibniz, I indicated that I was in possession of a method of determining maxima and minima, drawing tangents, and performing similar operations, and that the method worked for surd as well as rational terms. I concealed this method under an anagram comprising this sentence: ‘Given an equation involving any number of fluent quantities, to find the fluxions, and vice versa.’ The distinguished gentleman wrote back that he too had come upon a method of this kind, and he communicated his method, which hardly differed from mine except in the forms of words and notations. The foundation of both methods is contained in this lemma.” In ed. 2 the scholium is exactly the same except that “and the concept of the generation of quantities” is added at the end of the penultimate sentence.
For the principal texts with interpretative comments on the Newton-Leibniz controversy over priority in the invention of the calculus, see The Mathematical Papers of Isaac Newton, ed. D. T. Whiteside (Cambridge: Cambridge University Press, 1967–1981), vol. 8, esp. pp. 469–697; also A. Rupert Hall, Philosophers at War: The Quarrel between Newton and Leibniz (Cambridge: Cambridge University Press, 1980).
a. Ed.
1 has two additional corollaries as follows: “Corol. 4. But also the particle of time wherein the
minimally small particle of space NKLO is described in descent is as the rectangle KN × PQ. For since
the space NKLO is as the velocity multiplied by the particle of time, the particle of time will be as that
space divided by the velocity, that is, as the minimally small rectangle KN × KL divided by AP. For KL,
above, was as AP × PQ. Therefore the particle of time is as KN × PQ, or what comes to the same, as
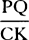 . Q.E.D.”
. Q.E.D.”
“Corollary 5. By the same argument the particle of time wherein the particle of space nklo is described
in ascent is as 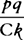 .”
.”
aa. Ed. 1 and ed. 2 have “of the future ascent.”
bb. Ed. 1 and ed. 2 have “of the past descent.”
cc. Ed. 1 and ed. 2 have “the time of the whole future ascent.”
dd. Ed. 1 and ed. 2 have “the time of the whole past descent.”
ee. Ed. 1 and ed. 2 have “the time of the whole future ascent.”
aa. Ed. 1 has: “Let AK be the plane of the horizon, perpendicular to the plane of the figure; ACK a curved line; C a body moving along the line; and FCf a straight line touching it in C. And suppose that body C now goes forward from A to K along the line ACK and now goes back along the same line and that in going forward it is impeded by the medium and in going back is equally assisted, so that in the same places the velocity of the body as it goes forward and back is always the same.
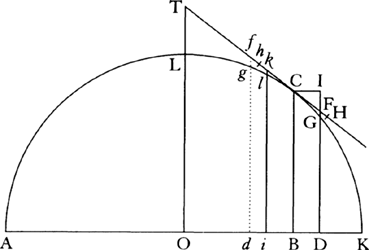
“And in equal times let the body as it goes forward describe the minimally small arc CG, and let
the body as it goes back describe arc Cg, and let CH and Ch be equal rectilinear lengths which bodies
moving away from place C would describe in these times without the actions of the medium and of
gravity, and from points C, G, and g to the horizontal plane AK drop perpendiculars CB, GD, and gd,
letting GD and gd meet the tangent in F and f. Through the resistance of the medium it comes about
that the body as it goes forward describes, instead of length CH, only length CF, and through the force of
gravity the body is transferred from F to G, and thus line-element HF and line-element FG are generated
simultaneously, the first by the force of resistance and the second by the force of gravity. Accordingly (by
book 1, lem. 10), line-element FG is as the force of gravity and the square of the time jointly and thus
(since the gravity is given) as the square of the time, and line-element HF is as the resistance and the
square of the time, that is, as the resistance and line-element FG. And hence the resistance comes to be
as HF directly and FG inversely, or as 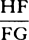 . This is so in the case of nascent line-elements. For in the
case of line-elements of finite magnitude these ratios are not accurate.
. This is so in the case of nascent line-elements. For in the
case of line-elements of finite magnitude these ratios are not accurate.
“And by a similar argument fg is as the square of the time and thus, since the times are equal, is
equal to FG, and the impulse by which the body going back is urged is as 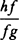 . But the impulse upon
the body as it goes back and the resistance to it as it goes forward are equal at the very beginning of the
motion, and thus also
. But the impulse upon
the body as it goes back and the resistance to it as it goes forward are equal at the very beginning of the
motion, and thus also 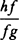 and
and 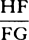 , proportional to them, are equal, and therefore, because fg and FG
are equal, hf and HF are also equal, and thus CF, CH (or Ch), and Cf are in arithmetic progression,
and hence HF is half the difference between Cf and CF, and the resistance, which above was as
, proportional to them, are equal, and therefore, because fg and FG
are equal, hf and HF are also equal, and thus CF, CH (or Ch), and Cf are in arithmetic progression,
and hence HF is half the difference between Cf and CF, and the resistance, which above was as 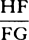 , is
as
, is
as 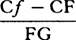 .
.
“But the resistance is as the density of the medium and the square of the velocity. And the velocity is
as the described length CF directly and the time √FG inversely, that is, as 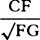 , and thus the square of
the velocity is as
, and thus the square of
the velocity is as 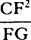 . Therefore the resistance, proportional to
. Therefore the resistance, proportional to 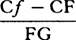 , is as the density of the medium
and
, is as the density of the medium
and 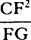 jointly, and hence the density of the medium is as
jointly, and hence the density of the medium is as 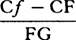 directly and
directly and 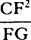 inversely, that
is, as
inversely, that
is, as 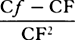 . Q.E.I.
. Q.E.I.
“Corollary 1. And hence it is gathered that if Ck on Cf is taken as equal to CF and the perpendicular
ki is dropped to the horizontal plane AK, cutting the curve ACK in l, the density of the medium will
come to be as 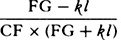 . For fC will be to kC as √fg or √FG to √kl, and by separation [or
dividendo] fk will be to kC, that is, Cf − CF to CF, as √FG + √kl to √kl, that is, if both terms are
multiplied by √FG + √kl, as FG − kl to kl + √(FG × kl), or to FG + kl. For the first ratio of the nascent
quantities kl + √(FG × kl) and FG + kl is that of equality. And so let
. For fC will be to kC as √fg or √FG to √kl, and by separation [or
dividendo] fk will be to kC, that is, Cf − CF to CF, as √FG + √kl to √kl, that is, if both terms are
multiplied by √FG + √kl, as FG − kl to kl + √(FG × kl), or to FG + kl. For the first ratio of the nascent
quantities kl + √(FG × kl) and FG + kl is that of equality. And so let 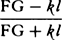 be written for
be written for 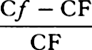 ,
and the density of the medium, which was as
,
and the density of the medium, which was as 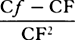 , will turn out to be as
, will turn out to be as 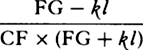 .
.
“Corollary 2. Hence, since 2HF and Cf − CF are equal and FG and kl (because of the ratio of equality) compose 2FG, 2HF will be to CF as FG − kl to 2FG, and hence HF will be to FG, that is, the resistance will be to the gravity, as the rectangle CF × (FG − kl) to 4FG2.”
The demonstration in ed. 1 is incorrect, and the error was brought to Newton’s attention only after the corresponding pages in ed. 2 had been printed off. For details see the Guide to the present translation, §7.3; also The Mathematical Papers of Isaac Newton, ed. D. T. Whiteside (Cambridge: Cambridge University Press, 1967–1981), 8:312–424; The Correspondence of Isaac Newton, vol. 5, ed. A. Rupert Hall and Laura Tilling (Cambridge: published for the Royal Society by Cambridge University Press, 1975); A. Rupert Hall, “Correcting the Principia,” Osiris 13 (1958): 291–326; I. Bernard Cohen, Introduction to Newton’s “Principia” (Cambridge, Mass.: Harvard University Press; Cambridge: Cambridge University Press, 1971), pp. 236–238.
bb. In ed. 1 this is, with some variants, corol. 3.
cc. Ed.
1 has: “Besides, CF is the square root of CI2 and IF2, that is, of BD2 and the square of the
second term. And FG + kl is equal to twice the third term, and FG − kl is equal to twice the fourth. For
the value of DG is converted into the value of il, and the value of FG into the value of kl, by writing Bi
for BD, or −o for +o. Accordingly, since FG is − 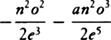 . . . , kl will be
. . . , kl will be 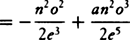 .
And the sum of these is
.
And the sum of these is 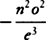 ; the difference,
; the difference, 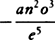 . The fifth and following terms I ignore here as
infinitely less than such as come under consideration in this problem. And so if the series is universally
designated by the terms ∓ Qo − Ro2 − So3 . . . , CF will be equal to
√(o2 + Q2o2), FG + kl will be
equal to 2Ro2, and FG − kl will be equal to 2So3. For CF, FG + kl, and FG − kl, write these values
of theirs, and the density of the medium, which was as
. The fifth and following terms I ignore here as
infinitely less than such as come under consideration in this problem. And so if the series is universally
designated by the terms ∓ Qo − Ro2 − So3 . . . , CF will be equal to
√(o2 + Q2o2), FG + kl will be
equal to 2Ro2, and FG − kl will be equal to 2So3. For CF, FG + kl, and FG − kl, write these values
of theirs, and the density of the medium, which was as  , will now be as
, will now be as 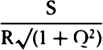 .
Therefore by reducing each problem to a converging series and here writing for Q, R, and S the terms of
the series corresponding to these and then supposing the resistance of the medium in any place G to be
to the gravity as S√(1 + Q2) to 2R2, and the velocity to be the same as that with which a body, departing
from place C along straight line CF, could subsequently move in a parabola having diameter CB and
latus rectum
.
Therefore by reducing each problem to a converging series and here writing for Q, R, and S the terms of
the series corresponding to these and then supposing the resistance of the medium in any place G to be
to the gravity as S√(1 + Q2) to 2R2, and the velocity to be the same as that with which a body, departing
from place C along straight line CF, could subsequently move in a parabola having diameter CB and
latus rectum 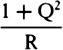 , the problem will be solved.
, the problem will be solved.
“Thus, in now solving the problem, if 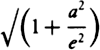 or
or  is written for √(1 + Q2),
is written for √(1 + Q2), 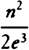 for R, and
for R, and 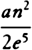 for S, the density of the medium will come out.”
for S, the density of the medium will come out.”
dd. Ed. 1 lacks this.
ee. Ed. 1 has: “and then finally, if a regular curved line NN x N is drawn through them all, this will cut off SX equal to the required length AH. For mechanical purposes it suffices to keep the same lengths AH, AI in all angles HAK. But if the figure must be determined more exactly in order to find the resistance of the medium, these lengths must always be corrected (by rule 4).”
a. Ed. 1 and ed. 2 lack the scholium.
aa. Ed. 1 has: “But the time is as DET or ½BD × ET, and the moments of these areas are as
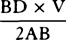 multiplied by the moment of V and ½BD multiplied by the moment of ET, that is, as
multiplied by the moment of V and ½BD multiplied by the moment of ET, that is, as
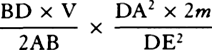 and ½BD × 2m, or as
and ½BD × 2m, or as 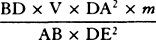 and BD × m. And therefore the
moment of area V2 is to the moment of the difference of areas DET and AKNb as
and BD × m. And therefore the
moment of area V2 is to the moment of the difference of areas DET and AKNb as 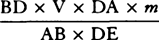 to
to 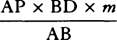 or as
or as 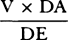 to AP and thus, when V and AP are minimally small, in the ratio of
equality. Therefore the minimally small area
to AP and thus, when V and AP are minimally small, in the ratio of
equality. Therefore the minimally small area 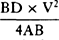 is equal to the minimally small difference of areas
DET and AKNb. Hence, since the spaces described simultaneously in both mediums at the beginning of
the descent or at the end of the ascent approach equality and thus are then to one another as area
is equal to the minimally small difference of areas
DET and AKNb. Hence, since the spaces described simultaneously in both mediums at the beginning of
the descent or at the end of the ascent approach equality and thus are then to one another as area 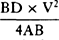 and the difference of areas DET and AKNb, it follows that, because of their analogous increments, in
any equal times they must be to one another as the area
and the difference of areas DET and AKNb, it follows that, because of their analogous increments, in
any equal times they must be to one another as the area 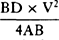 and the difference of areas DET
and AKNb. Q.E.D.” In ed. 2 the passage is the same as in ed. 1 except that AKNb is AbNK and
the first two sentences read: “The moment of this area or of its equivalent,
and the difference of areas DET
and AKNb. Q.E.D.” In ed. 2 the passage is the same as in ed. 1 except that AKNb is AbNK and
the first two sentences read: “The moment of this area or of its equivalent,
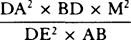 , is to
the moment of the difference of areas DET and AbNK as
, is to
the moment of the difference of areas DET and AbNK as 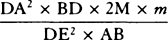 to
to
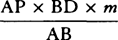 ,
that is, as
,
that is, as 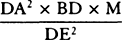 to ½BD × AP, or as
to ½BD × AP, or as
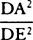 to DAP, and thus, when the areas DET and
DAP are minimally small, in the ratio of equality.” In both eds. 1 and 2 the fraction
to DAP, and thus, when the areas DET and
DAP are minimally small, in the ratio of equality.” In both eds. 1 and 2 the fraction
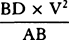 , which
occurs just before this passage, is
, which
occurs just before this passage, is 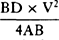 .
.
b. Ed. 1 and ed. 2 lack the scholium.
aa. Ed. 1 has: “In a nonresisting medium, equal areas PSQ, QSr would (by book 1, theor. 1) have
to be described in equal times. From the resistance arises the difference RSr of the areas, and therefore
the resistance is as decrement Rr of line-element Qr compared with the square of the time in which it is
generated. For line-element Rr (by book 1, lem. 10) is as the square of the time. Therefore the resistance
is as 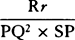 .”
.”
bb. Ed. 1 has: “Hence the times of descent will here be twice as great as those times and so are given.”
a. Here, as elsewhere in the Principia, Newton uses the noun “orbis” (orb) for a spherical shell.
aa. In ed. 1 the order of the two sentences is reversed.
b. Ed. 1 has in addition: “except perhaps through the increase of the intermediate particles by that virtue.”
c. Ed. 1 has in addition: “For example, if each particle by its own force, which is inversely as the distance of places from its center, repels all other particles indefinitely, the forces by which the fluid can be equally compressed and condensed in similar vessels will be as the squares of the diameters of the vessels, and thus the force by which the fluid is compressed in the same vessel will be inversely as the cube root of the fifth power of the density.”
aa. Newton uses the term “corpora funependula,” literally “bodies hanging by a thread [or string],” which we have translated as “simple pendulums”; see the Guide, §7.5.
a. Ed. 1 and ed. 2 have in addition: “which is both more general and more than exact enough for use in natural philosophy.”
aa. Ed. 1 has: “Likewise Fg is to Fh as CF to DF, and from the equality of the ratios in inordinate proportion [or ex aequo perturbate] Fh or MN is to Dd as DK to CF. Take DR to ½aB as DK to CF, and MN will be to Dd as DR to ½aB, and thus the sum of all the MN × ½aB, that is, Aa × ½aB, will be equal to the sum of all the Dd × DR, that is, to area BRrSa, which all the rectangles Dd × DR or DRrd compose. Bisect Aa and aB in P and O, and ½aB or OB will be equal to CP, and thus DR is to DK as CP to CF or CM, and by separation [or dividendo] KR will be to DR as PM to CP. And thus, since point M, when the body is in the midpoint O of the oscillation, falls approximately on point P and in the earlier part of the oscillation is between A and P and in the later part is between P and a, in both cases deviating equally from point P in opposite directions, it follows that point K, at about the midpoint of the oscillation, that is, over against point O, say in point V, will fall on point R and in the earlier part of the oscillation will lie between R and E and in the later part between R and D, in both cases deviating equally from point R in opposite directions. Accordingly, the area which line KR describes will in the earlier part of the oscillation lie outside area BRSa and in the later part within it and will do so within ranges nearly equal to each other on each of the two sides and therefore, when added to area BRSa in the first case and subtracted from it in the second, will result in area BKTa very nearly equal to area BRSa. Therefore the rectangle Aa × ½aB, or AaO, will, since it is equal to area BRSa, also be very nearly equal to area BKTa. Q.E.D.”
a. In ed. 1 the general scholium appears at the end of book 2, sec. 7, with some variations, primarily in the numerical values.
bb. Here Newton makes a puzzling statement, namely, that the diameter of this ball, “about ⅓ or ⅔ inch,” was larger than the one mentioned earlier, which was “about ⅓ inch.” The source of this puzzling “about ⅓ or ⅔ inch” may be seen by comparing the various editions, as is done in our Latin edition. In the printer’s manuscript and in ed. 1, the larger ball is said to have a diameter of “about ⅓ or ⅔ inch,” which in ed. 2 was wrongly printed as “about ⅓ or ⅔ inch.” In Newton’s annotated copy of the Principia, it was noted that this should be corrected to “about ½ or ⅔ inch,” but this was not done in ed. 3.
cc. This reads literally: “the opinion of some is.” Ed. 1 and ed. 2 have: “the most widely accepted opinion of the philosophers of this age is.” The index prepared by Cotes for ed. 2 and retained for ed. 3 keys this opinion under “Materia” (“Matter”) and specifies the “philosophers” (and hence the later “some”) by thus describing the paragraph: “The subtle matter of the Cartesians is subjected to a certain examination.”
a. In ed. 1, sec. 7 is very different. Props. 32–34 (32–35 in ed. 1) underwent partial alteration, including the suppression of the original prop. 34. The remainder of sec. 7 was completely rewritten for ed. 2 and essentially retained, with only minor changes, in ed. 3. For details, see the Guide to the present translation, §7.6.
a. A translation of the versions of book 2, props. 35–40, that appear in the first edition has been made by I. Bernard Cohen and Anne Whitman and will be published, together with a commentary by George Smith, in Newton’s Natural Philosophy, ed. Jed Buchwald and I. Bernard Cohen (Cambridge: MIT Press, forthcoming).
aa. In expt. 13, Newton writes of weights being dropped “a culmine ecclesiae Sancti Pauli, in urbe Londini.” Newton is not referring to St. Paul’s Church in Covent Garden, as is obvious from the fact that the distance through which the weights are let fall is 220 London feet. The only house of worship that tall (about twenty stories) was St. Paul’s Cathedral. That these experiments were conducted in St. Paul’s Cathedral is evident from the fact that in the cathedral there is a balcony, just below the cupola, at a height corresponding to Newton’s 220 London feet. See, below, the note to expt. 14.
bb. Newton here writes of weights dropped “ab altiore loco in templi ejusdem turri rotunda fornicata, nempe ab altitudine pedum 272,” that is, “from a higher place in the round arched tower [i.e., from the lantern at the top of the cupola] of the same cathedral.” This position corresponds to the height given by Newton, 272 feet.
a. Newton evidently is referring to amplitude.
aa. Ed. 1 has: “Mersenne writes in prop. 35 of his Ballistics that he found by making experiments that sound travels 1,150 French toises (that is, 6,900 French feet) in 5 seconds. Hence, since a French foot is to an English foot as 1,068 to 1,000, sound will have to travel 1,474 English feet in the time of 1 second. Mersenne also writes that the eminent geometer Roberval observed during the siege of Thionville that the noise of cannons was heard 13 or 14 seconds after the fire was seen, although he was scarcely half a league away from the cannons. A French league contains 2,500 toises, and thus, according to Roberval’s observation, in the time of 13 or 14 seconds sound traveled 7,500 Paris feet, and in the time of 1 second 560 Paris feet, or about 600 English feet. These observations are very different from one another, and our computation falls in the middle. In the cloister of our college, which is 208 feet long, a sound excited at either end makes a fourfold echo in four returnings. And by making experiments I found that at each returning of the sound a pendulum of about 6 or 7 inches completed an oscillation, starting at the first returning of the sound and completing its oscillation at the second one. I was not able to determine the length of the pendulum exactly enough, but I judged that with a length of 4 inches the oscillations were too fast and that with a length of 9 inches they were too slow. Hence in going and returning the sound traveled 416 feet in a smaller time than that in which a pendulum of 9 inches oscillates and in a greater time than a pendulum of 4 inches, that is, in a smaller time than 28¾ thirds and a greater than 19⅙. And therefore in the time of 1 second the sound travels more than 866 English feet and fewer than 1,272 and thus is faster than according to Roberval’s observation and slower than according to Mersenne’s. Further, by more accurate observations made afterward, I determined that the length of the pendulum ought to be greater than 5½ inches and less than 8 inches and thus that sound in the time of 1 second traveled more than 920 English feet and fewer than 1,085. Therefore the motion of sounds, being between these limits according to the geometrical calculation given above, squares with the phenomena insofar as it has been possible to test it up to now. Accordingly, since this motion depends on the density of the whole air, it follows that sounds consist not in the motion of aether or of some more subtle air but in the agitation of the whole air.
“Certain experiments concerning sound propagated in vessels empty of air seem to contradict this, but vessels can scarcely be emptied of all air; and when they are sufficiently emptied, sounds are noticeably diminished. For example, if only a hundredth of the whole air remains in the vessel, a sound will have to be a hundred times weaker and thus should not be less audible than if someone, hearing the same sound excited in free air, immediately withdrew to ten times the distance from the sonorous body. Two equally sonorous bodies therefore must be compared, of which one is in an emptied vessel and the other is in free air and whose distances from the hearer are as the square roots of the densities of the air, and if the sound of the former body does not exceed the sound of the latter, the objection will cease.
“Once the velocity of sounds has been found, the intervals between the pulses can also be found. Mersenne writes (Harmonics, book 1, prop. 4) that (by making certain experiments which he describes in the same place) he found that a stretched musical string vibrates 104 times in the space of 1 second when it makes a unison with an open four-foot organ pipe or a stopped two-foot pipe, which organists call C fa ut. Accordingly, there are 104 pulses in a space of 968 feet, the distance which sound travels in the time of 1 second, and thus one pulse occupies a space of roughly 9¼ feet, that is, roughly twice the length of the pipe. Hence it is likely that the lengths of the pulses in the sounds of all open pipes are equal to twice the lengths of the pipes.”
a. In props. 51 and 52, Newton is using the word “orb” in two closely related senses. One is that of a series of nested hollow spheres or orbs, much as in the older Aristotelian universe, where the orbits of the planets were considered to be embedded in a set of nesting or concentric hollow spherical shells or orbs. In prop. 52, Newton writes of a set of “innumerable concentric orbs of the same thickness.” In prop. 51, a similar concept is introduced for a cylinder, which Newton says is to be divided into “innumerable concentric solid cylindrical orbs of the same thickness.” Today it would not be usual to call such cylindrical shells “orbs” as Newton did; nevertheless, we have kept Newton’s “orbs” in prop. 51 so as to keep it in harmony with the language of prop. 52.
a. On the use of “orbs” in prop. 52, and in the antecedent prop. 51, see the note to prop. 51.
a. In this introduction to book 3, Newton uses “philosophy” and its adjective “philosophical” to refer to “natural philosophy.” According to John Harris’s Lexicon Technicum (London, 1704), natural philosophy is that “Science which contemplates the Powers of Nature, the Properties of Natural Bodies, and their mutual Action one upon another.” The half title of the third edition of the Principia reads “Newtoni Principia Philosophiae” (“Newton’s Principles of Philosophy”). The dedication page of the Principia, in all editions, refers to the Royal Society as founded “ad philosophiam promovendam” (“for the promotion of philosophy”).
aa. Ed. 1 has nine numbered “Hypotheses,” most of which ed. 2 converts into two categories, now called “Rules for Natural Philosophy” and “Phenomena.” Hyps. 1 and 2 become rules 1 and 2; hyp. 3 is discarded, to be replaced by rule 3; hyp. 4 becomes hyp. 1 and is transferred to a location between prop. 10 and prop. 11; hyps. 5–9 become phen. 1, 3–6, while phen. 2 is new in ed. 2. Ed. 3 further introduces rule 4. These changes may be tabulated as follows:
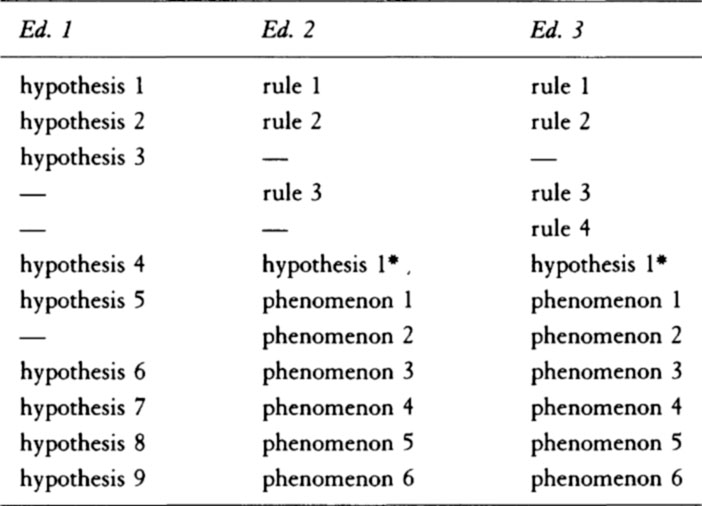
Ed. 2 also has additions of explanatory phrases and sentences, alterations in wording, and, for the phenomena, revisions of numerical data and references to observers. Ed. 3 further expands or adds some explanatory sentences. For details see the Guide to the present translation, §8.2. Cf. also Alexandre Koyré, “Newton’s ‘Regulae Philosophandi,’” in his Newtonian Studies (Cambridge, Mass.: Harvard University Press, 1965), pp. 261–272; I. Bernard Cohen, “Hypotheses in Newton’s Philosophy,” Physis: Rivista internazionale di storia della scienza 8 (1966): 163–184, reprinted in Proceedings of the Boston Colloquium for the Philosophy of Science 1966/1968, ed. Robert S. Cohen and Marx W. Wartofsky, Boston Studies in the Philosophy of Science, vol. 5 (Dordrecht: D. Reidel Publishing Co., 1969), pp. 304–326; I. Bernard Cohen, Introduction to Newton’s “Principia” (Cambridge, Mass.: Harvard University Press; Cambridge: Cambridge University Press, 1971), pp. 23–26, 240–245.
bb. Ed. 1 has: “Hypothesis 3. Every body can be transformed into a body of any other kind and successively take on all the intermediate degrees of qualities.” Cf. prop. 6, corol. 2, below.
aa. Ed. 1 has: “Therefore all bodies universally that are on or near the earth are heavy [or gravitate] toward the earth, and the weights of all bodies that are equally distant from the center of the earth are as the quantities of matter in them. For if the aether or any other body whatever either were entirely devoid of gravity or gravitated less in proportion to the quantity of its matter, then, since it does not differ from other bodies except in the form of its matter, it could by a change of its form be changed by degrees into a body of the same condition as those that gravitate the most in proportion to the quantity of their matter (by hyp. 3), and, on the other hand, the heaviest bodies, through taking on by degrees the form of the other body, could by degrees lose their gravity. And accordingly the weights would depend on the forms of bodies and could be altered with the forms, contrary to what has been proved in corol. 1.”
Some of the handwritten notes to Newton’s copies of ed. 1 show various other alterations that never appeared in printed editions at this point. In one, for example, everything after the first sentence is replaced by “This is evident by hyp. 3, provided that this hypothesis holds here,” while another has the substitution “This follows from the preceding proposition by hyp. 3, provided that this hypothesis holds here.” See further the notes to the Rules and Phenomena above.
bb. In place of corols. 3 and 4, ed. 1 has a single corol. 3: “And thus a vacuum is necessary. For if all spaces were full, the specific gravity of the fluid with which the region of the air would be filled, because of the extreme density of its matter, would not be less than the specific gravity of quicksilver or of gold or of any other body with the greatest density, and therefore neither gold nor any other body could descend in air. For bodies do not ever descend in fluids unless they have a greater specific gravity.”
aa. The text of the first part of corol. 1 as it appears in the later editions—that is, the first two sentences and part of the third sentence up to “of the moon around the earth (27 days, 7 hours, 43 minutes)”— is almost the same as in the version in ed. 1, except that the later editions have a more complete reference to prop. 4 (the addition of “corol. 2”) and have more exact values for the periods of Venus (224 days and 16¾ hours) and of the outermost satellite of Jupiter (16 days and 168/15 hours). In the remainder of the text, however, the later versions are notably different from the earlier one. (For a gloss on this corollary, see the Guide, §8.10.) In ed. 1, corol. 1 reads as follows:
“Corollary 1. Hence the weights of bodies toward different planets can be found and compared one with another. For the weights of equal bodies [i.e., bodies with equal masses] revolving in circles around planets are (by book 1, prop. 4) as the diameters of the circles directly and the squares of the periodic times inversely, and weights at the surfaces of the planets or at any other distances from the center are greater or smaller (by the same proposition) inversely as the squared ratio of the distances. I compared the periodic times of Venus around the sun (224⅔ days), of the outermost circumjovial satellite around Jupiter (16¾ days), of Huygens’s satellite around Saturn (15 days and 22⅔ hours), and of the moon around the earth (27 days, 7 hours, 43 minutes) respectively with the mean distance of Venus from the sun, with the greatest heliocentric elongation of the outermost circumjovial satellite, which (at the mean distance of Jupiter from the sun according to the observations of Flamsteed) is 8′13″, with the greatest heliocentric elongation of the satellite of Saturn (3′20″), and with the distance of the moon from the earth, on the hypothesis that the horizontal solar parallax or the semidiameter of the earth as seen from the sun is about 20″.
In this way I found by calculation that the weights of bodies which are equal and equally distant
from the sun, Jupiter, Saturn, and the earth as directed toward the sun, Jupiter, Saturn, and the earth,
were to one another as 1,  , and
, and
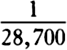 . But the mean apparent semidiameter of the sun is
about 16′6″. From the diameter of the shadow of Jupiter as found by eclipses of the satellites, Flamsteed
determined that the mean apparent diameter of Jupiter as seen from the sun is to the elongation of the
outermost satellite as 1 to 24.9, and since that elongation is 8′13″, the semidiameter of Jupiter as seen from
the sun will be 19¾″. The diameter of Saturn is to the diameter of its ring as 4 to 9, and the diameter of
the ring as seen from the sun (by Flamsteed’s measurement) is 50″, and thus the semidiameter of Saturn
as seen from the sun is 11″. I would prefer to say 10″ or 9″, because the globe of Saturn is somewhat
dilated by a nonuniform refrangibility of light.
. But the mean apparent semidiameter of the sun is
about 16′6″. From the diameter of the shadow of Jupiter as found by eclipses of the satellites, Flamsteed
determined that the mean apparent diameter of Jupiter as seen from the sun is to the elongation of the
outermost satellite as 1 to 24.9, and since that elongation is 8′13″, the semidiameter of Jupiter as seen from
the sun will be 19¾″. The diameter of Saturn is to the diameter of its ring as 4 to 9, and the diameter of
the ring as seen from the sun (by Flamsteed’s measurement) is 50″, and thus the semidiameter of Saturn
as seen from the sun is 11″. I would prefer to say 10″ or 9″, because the globe of Saturn is somewhat
dilated by a nonuniform refrangibility of light.
Thus, when the calculation is made, the true semidiameters of the sun, Jupiter, Saturn, and the earth
to one another come out as 10,000, 1,063, 889, and 208. Whence, because the weights of bodies which
are equal and equally distant from the centers of the sun, Jupiter, Saturn, and the earth are, respectively,
toward the sun, Jupiter, Saturn, and the earth as 1,
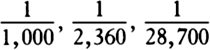 , and because, when the distances
are increased or decreased, the weights are decreased or increased in the squared ratio, [it follows that]
the weights of the same equal bodies toward the sun, Jupiter, Saturn, and the earth at distances of 10,000,
1,063, 889, and 208 from their centers, and hence their weights at the surfaces, will be as 10,000, 804½,
536, and 805½ respectively. We shall show below that the weights of bodies on the surface of the moon
are almost two times less than the weights of bodies on the surface of the earth.”
, and because, when the distances
are increased or decreased, the weights are decreased or increased in the squared ratio, [it follows that]
the weights of the same equal bodies toward the sun, Jupiter, Saturn, and the earth at distances of 10,000,
1,063, 889, and 208 from their centers, and hence their weights at the surfaces, will be as 10,000, 804½,
536, and 805½ respectively. We shall show below that the weights of bodies on the surface of the moon
are almost two times less than the weights of bodies on the surface of the earth.”
bb. In ed. 1, there was an additional corollary numbered 2, so that the corollaries numbered 2, 3, and 4 in the later editions were originally numbered 3, 4, and 5. (For a gloss on this corollary see the Guide, §8.10.) The corol. 2 of the first edition reads as follows:
“Corollary 2. Therefore the weights of equal bodies [i.e., bodies with equal masses], on the surfaces of the earth and of the planets, are almost proportional to the square roots of their apparent diameters as seen from the sun. With respect to the diameter of the earth as seen from the sun there is as yet no agreement. I have taken it to be 40″, because the observations of Kepler, Riccioli, and Vendelin do not permit it to be much greater; the observations of Horrocks and Flamsteed seem to make it a little smaller. And I have preferred to err on the side of excess. But if perhaps that diameter and the gravity on the surface of the earth are a mean among the diameters of the planets and the gravities on their surfaces, then, since the diameters of Saturn, Jupiter, Mars, Venus, and Mercury are about 18″, 39½″, 8″, 28″, 20″, the diameter of the earth will be about 24″ and therefore the parallax of the sun about 12″, as Horrocks, and Flamsteed pretty nearly concluded. But a slightly larger diameter agrees better with the rule of this corollary.” That is, the larger diameter of the earth as seen from the sun, and hence the larger solar parallax, agrees better with the rule about the weights of equal bodies on the surface of the earth and planets being “almost proportional to the square roots of their apparent diameters as seen from the sun.”
cc. In place of this portion of corol. 4, ed. 1 has:
“Corollary 5. The densities of the planets, moreover, are to one another nearly in a ratio compounded
of the ratio of the distance from the sun and the square roots of the diameters of the planets as seen from
the sun. For the densities of Saturn, Jupiter, the earth, and the moon (60, 76, 387, and 700) are almost as
the roots of the apparent diameters (18″, 39½″, 40″, and 11″) divided by the reciprocals of their distances
from the sun 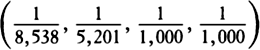 . We said, moreover [utique], in corol. 2, that the gravities
at the surfaces of the planets are approximately as the square roots of their apparent diameters as seen
from the sun; and in lem. 4 [i.e., corol. 4] that the densities are as the gravities divided by the true
diameters; and so the densities are almost as the roots of the apparent diameters multiplied by the true
diameters—that is, inversely as the roots of the apparent diameters divided by the distances of the planets
from the sun. Therefore God placed the planets at different distances from the sun so that each one
might, according to the degree of its density, enjoy a greater or smaller amount of heat from the sun.”
. We said, moreover [utique], in corol. 2, that the gravities
at the surfaces of the planets are approximately as the square roots of their apparent diameters as seen
from the sun; and in lem. 4 [i.e., corol. 4] that the densities are as the gravities divided by the true
diameters; and so the densities are almost as the roots of the apparent diameters multiplied by the true
diameters—that is, inversely as the roots of the apparent diameters divided by the distances of the planets
from the sun. Therefore God placed the planets at different distances from the sun so that each one
might, according to the degree of its density, enjoy a greater or smaller amount of heat from the sun.”
a. For a gloss on this proposition see the Guide, §10.14.
bb. Ed. 1 has: “The solution of this problem requires a complex computation, which is shown more easily by example than by precept. Through making the calculation, therefore, I find, by book 1, prop. 4, that the centrifugal force of the parts of the earth at the equator, arising from the daily motion, is to the force of gravity as 1 to 290⅘.”
cc. Ed. 2 has: “Picard measured an arc of 1°22′55″ between Amiens and Malvoisine and found an arc of one degree to be 57,060 Paris toises. Hence the circumference of the earth is 123,249,600 Paris feet, as above. But since an error of four hundredths of an inch, either in the construction of the instruments or in their application to making observations, is imperceptible and, in the ten-foot sector by which the French observed the latitudes of places, corresponds to four seconds and, in single observations, can fall upon the center of the sector as well as on its circumference, and since errors in smaller arcs are of greater significance, therefore Cassini by the king’s order undertook the measurement of the earth by means of greater intervals between the places (see the History of the Royal Academy of Sciences for the year 1700) and in the process, by using the distance between the Royal Paris Observatory and the village of Collioure in Roussillon and the difference of 6°18′ between the latitudes and supposing that the earth’s shape is spherical, found one degree to be 57,292 toises, nearly as our fellow countryman Norwood had found earlier. For Norwood, in about the year 1635, measured a distance of 905,751 London feet between London and York and observed the difference of latitudes between those places to be 2°28′ and thereby found the measure of one degree to be 367,196 London feet, that is, 57,300 Paris toises. Because of the magnitude of the interval measured by Cassini, I shall use 57,292 toises for the measure of one degree in the middle of that interval, that is, between the latitudes of 45° and 46°. Hence, if the earth is spherical, its semidiameter will be 19,695,539 Paris feet.
“The length of a seconds pendulum oscillating in the latitude of Paris is three Paris feet and 85/9 lines. And the length which a heavy body describes by falling in the time of one second is to half the length of this pendulum or as the square of the ratio of the circumference of the circle to its diameter (as Huygens indicated) and thus is 15 Paris feet, 1 inch, 21/18 lines, or 2,1741/18 lines.”
dd. Ed. 2 has “centripetal.”
ee. Ed. 2 has “centripetal.”
ff. Ed. 1 has “centripetal.”
gg. Ed. 1 and ed. 2 have: “These things are so on the hypothesis that the matter of the planets is uniform. For if the matter is denser at the center than at the circumference, the diameter which is drawn from east to west will be still greater.” In ed. 1 the proposition ends here, but in ed. 2 it continues: “Indeed, Cassini observed long ago that the diameter of Jupiter which lies between its poles is smaller than the other diameter, and it will be apparent from what is said in prop. 20 below that the diameter of the earth between the poles is smaller than the other diameter.”
hh. The Latin text reads “paulo magis ibi decoquuntur,” employing the verb “decoquo,” which could mean, literally, “boil down” or “cook” or “bake.” The problems of interpretation are discussed in the Guide to the present translation, §8.11.
a. See the Guide, §10.15.
bb. In place of the remaining part of this proposition, ed. 1 has: “For example, the latitude of Paris
is 48°45′, that of the island of Gorée near Cape Verde 14°15′, that of Cayenne off the coast of Guiana
about 50°, that of places at the pole 90°. If the arcs of latitude are doubled, they are 97.5°, 28.5°, 10°,
and 180°. The versed sines are 11,305, 1,211, 152, and 2,000. Furthermore, since the gravity at the pole
is to the gravity at the equator as 692 to 689 and the excess of gravity at the pole is to the gravity at
the equator as 3 to 689, the excess of gravity at Paris, on the island of Gorée, and at Cayenne will be to
the gravity at the equator as 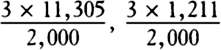 ,
and
,
and 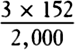 to 689, or as 33,915, 3,633, and 456 to
13,780,000, and therefore the total gravities in these places will be to one another as 13,813,915, 13,783,633,
13,780,456, and 13,780,000. Therefore, since the lengths of pendulums oscillating with equal periods are as
the gravities, and the length of a seconds pendulum at Paris is 3 Paris feet and 17/24 inches, the lengths of
seconds pendulums on the island of Gorée, at Cayenne, and at the equator will be surpassed by the length
of a Paris pendulum by excesses of
to 689, or as 33,915, 3,633, and 456 to
13,780,000, and therefore the total gravities in these places will be to one another as 13,813,915, 13,783,633,
13,780,456, and 13,780,000. Therefore, since the lengths of pendulums oscillating with equal periods are as
the gravities, and the length of a seconds pendulum at Paris is 3 Paris feet and 17/24 inches, the lengths of
seconds pendulums on the island of Gorée, at Cayenne, and at the equator will be surpassed by the length
of a Paris pendulum by excesses of 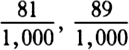 , and
, and 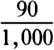 inches. All of these things will be so on the
hypothesis that the earth consists of uniform matter. For if the matter at the center is a little denser than
at the surface, those excesses will be a little greater. The reason is that if the superabundant matter at the
center, by which the density there is rendered greater, is taken away and considered separately, the gravity
toward the rest of the earth, which is uniformly dense, will be inversely as the distance of a weight from
the center, but toward the superabundant matter inversely as the square of the distance from that matter
very nearly. Therefore, gravity at the equator will be less toward that superabundant matter than as in
the above computation, and therefore the earth there, on account of the deficiency of gravity, will rise a
little higher than has been determined above. Indeed, the French by making experiments have already
found that the length of seconds pendulums at Paris is greater than on the island of Gorée by 1/10 of an
inch and greater than at Cayenne by ⅛. These differences are a little greater than the differences
inches. All of these things will be so on the
hypothesis that the earth consists of uniform matter. For if the matter at the center is a little denser than
at the surface, those excesses will be a little greater. The reason is that if the superabundant matter at the
center, by which the density there is rendered greater, is taken away and considered separately, the gravity
toward the rest of the earth, which is uniformly dense, will be inversely as the distance of a weight from
the center, but toward the superabundant matter inversely as the square of the distance from that matter
very nearly. Therefore, gravity at the equator will be less toward that superabundant matter than as in
the above computation, and therefore the earth there, on account of the deficiency of gravity, will rise a
little higher than has been determined above. Indeed, the French by making experiments have already
found that the length of seconds pendulums at Paris is greater than on the island of Gorée by 1/10 of an
inch and greater than at Cayenne by ⅛. These differences are a little greater than the differences 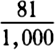 and
and 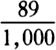 which resulted from the above computation, and therefore (if one can have enough confidence
in these rough observations) the earth will be somewhat higher at the equator than according to the
above calculation and denser at the center than in mines near the surface. If the excess of gravity in these
northern places over the gravity at the equator is finally determined exactly by experiments conducted
with greater diligence, and then its excess is everywhere taken in the ratio of the versed sine of twice the
latitude, then there will be determined a universal measure, an equalizing of the time of equal pendulums
in the different places indicated, and also the proportion of the diameters of the earth and its density at
the center, on the hypothesis that that density, as one goes to the circumference, decreases uniformly. And
indeed this hypothesis, even though it is not exact, can be assumed for undertaking such a calculation.”
which resulted from the above computation, and therefore (if one can have enough confidence
in these rough observations) the earth will be somewhat higher at the equator than according to the
above calculation and denser at the center than in mines near the surface. If the excess of gravity in these
northern places over the gravity at the equator is finally determined exactly by experiments conducted
with greater diligence, and then its excess is everywhere taken in the ratio of the versed sine of twice the
latitude, then there will be determined a universal measure, an equalizing of the time of equal pendulums
in the different places indicated, and also the proportion of the diameters of the earth and its density at
the center, on the hypothesis that that density, as one goes to the circumference, decreases uniformly. And
indeed this hypothesis, even though it is not exact, can be assumed for undertaking such a calculation.”
cc. Ed. 2 has: “and that the inequality of the diameters of the earth can be ascertained more easily and more surely by experiments with pendulums or even by eclipses of the moon than by arcs measured geographically on the meridian.
“These things are so on the hypothesis that the earth consists of uniform matter. For if the matter at the center is a little denser than at the surface, the differences of pendulums and degrees on a meridian will be a little greater than according to the preceding table. The reason is that if superabundant matter at the center, by which the density there is rendered greater, is taken away and regarded separately, the gravity toward the rest of the earth, which is uniformly dense, will be inversely as the distance of a weight from the center; but toward the superabundant matter, it will be inversely as the square of the distance from that matter very nearly. Therefore gravity at the equator is less toward that superabundant matter than according to the above computation, and therefore the earth there, on account of the deficiency of gravity, will rise a little higher, and the excesses of the lengths of pendulums and of the degrees at the poles will be a little greater than has been determined above.”
d. Here ed. 2 has an additional sentence: “But from the slowness of the pendulum clock in Cayenne, the difference of the pendulums is gathered to be 1½ lines.”
ee. Ed. 2 has: “ . . . the difference being about 2 lines or ⅙ of an inch. By the observations of M. Richer made in Cayenne, the difference was 1½ lines. An error of half a line is easily committed. And M. Des Hayes afterward, by his observations made on the same island, corrected the error, finding a difference of 21/18 lines. But also by observations made on the islands of Gorée, Guadeloupe, Martinique, Grenada, St. Kitts, and Santo Domingo and reduced to the equator, that difference came out to be scarcely smaller than 119/20 of a line and scarcely greater than 2½ lines. And the mean quantity between these limits is 29/40 lines. Because of the heat of places in the torrid zone, let us ignore 9/40 of a line, and a difference of 2 lines will remain.
“Therefore, since that difference, by the preceding table, on the hypothesis that the earth consists of
uniformly dense matter, is only 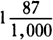 of a line, the excess of the height of the earth at the equator over
its height at the poles, which was 17⅙ miles, being now increased in the ratio of the differences, will
become 317/12 miles. For the slowness of a pendulum at the equator proves the deficiency of the gravity;
and the lighter the matter is, the greater its height must be in order that by its weight it may hold in
equilibrium the matter at the poles.
of a line, the excess of the height of the earth at the equator over
its height at the poles, which was 17⅙ miles, being now increased in the ratio of the differences, will
become 317/12 miles. For the slowness of a pendulum at the equator proves the deficiency of the gravity;
and the lighter the matter is, the greater its height must be in order that by its weight it may hold in
equilibrium the matter at the poles.
“Hence the shape of the earth’s shadow, which is to be determined by eclipses of the moon, will not be entirely circular, but its diameter drawn from east to west will be greater than its diameter drawn from south to north by an excess of about 55″. And the greatest longitudinal parallax of the moon will be a little greater than its greatest latitudinal parallax. And the greatest semidiameter of the earth will be 19,767,630 Paris feet, the least, 19,609,820 feet, and the mean, 19,688,725 feet, very nearly.
“Since one degree by Picard’s measurement is 57,060 toises but by Cassini’s measurement is 57,292
toises, some suspect that each degree, as one goes southward through France, is greater than the preceding
degree by 72 toises more or less, or 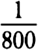 of one degree, the earth being an oblong spheroid whose parts
are highest at the poles. Under this supposition, all bodies at the earth’s poles would be lighter than at the
equator, and the height of the earth at the poles would exceed its height at the equator by nearly 95 miles,
and isochronous pendulums would be longer at the equator than in the Royal Observatory at Paris by an
excess of about half an inch, as will be easily seen by anyone comparing the proportions set forth here with
the proportions set forth in the preceding table. But also the diameter of the earth’s shadow drawn from
south to north would be greater than its diameter drawn from east to west by an excess of 2′46″, or 1/12 of
the moon’s diameter. Experience contradicts all this. Certainly Cassini, in determining that one degree is
57,292 toises, took a mean between all his measurements, on the hypothesis of the equality of degrees. And
although Picard on the northern border of France found a degree to be a little smaller, yet our compatriot
Norwood in more northern reigons, by measuring a greater interval, found a degree to be a little greater
than Cassini had found. And Cassini himself, when he attempted to determine the measurement of one
degree by using a far greater interval, judged Picard’s measurement to be insufficiently certain and exact
because of the smallness of the interval measured. But the differences among the measurements of Cassini,
Picard, and Norwood are nearly imperceptible and could easily have arisen from imperceptible errors in
observations, not to mention the nutation of the earth’s axis.”
of one degree, the earth being an oblong spheroid whose parts
are highest at the poles. Under this supposition, all bodies at the earth’s poles would be lighter than at the
equator, and the height of the earth at the poles would exceed its height at the equator by nearly 95 miles,
and isochronous pendulums would be longer at the equator than in the Royal Observatory at Paris by an
excess of about half an inch, as will be easily seen by anyone comparing the proportions set forth here with
the proportions set forth in the preceding table. But also the diameter of the earth’s shadow drawn from
south to north would be greater than its diameter drawn from east to west by an excess of 2′46″, or 1/12 of
the moon’s diameter. Experience contradicts all this. Certainly Cassini, in determining that one degree is
57,292 toises, took a mean between all his measurements, on the hypothesis of the equality of degrees. And
although Picard on the northern border of France found a degree to be a little smaller, yet our compatriot
Norwood in more northern reigons, by measuring a greater interval, found a degree to be a little greater
than Cassini had found. And Cassini himself, when he attempted to determine the measurement of one
degree by using a far greater interval, judged Picard’s measurement to be insufficiently certain and exact
because of the smallness of the interval measured. But the differences among the measurements of Cassini,
Picard, and Norwood are nearly imperceptible and could easily have arisen from imperceptible errors in
observations, not to mention the nutation of the earth’s axis.”
a. Motte adds, “to the other side of the equator.”
a. That is, if the point d traces out the curve NdGn, or if NdGn is the curve which is the locus of the point d.
b. That is, if the curve NeFn is the locus of point e.
aa. Ed. 1 has: “Up to now no consideration has been taken of the motions of the moon insofar as the eccentricity of the orbit is concerned. By similar computations, I found that the apogee, when it is in conjunction with or in opposition to the sun, moves forward 23′ each day with respect to the fixed stars but, when it is in the quadratures, regresses about 16⅓′ each day and that its mean annual motion is about 40°. By the astronomical tables which the distinguished Flamsteed adapted to the hypothesis of Horrocks, the apogee moves forward in its syzygies with a daily motion of 24′28″ but regresses in the quadratures with a daily motion of 20′12″ and is carried forward [or in consequential with a mean annual motion of 40°41′. The difference between the daily forward motion of the apogee in its syzygies and the daily regressive motion in its quadratures is 4′16″ by the tables but 6⅔′ by our computation, which we suspect ought to be attributed to a fault in the tables. But we do not think that our computation is exact enough either. For by means of a certain calculation the daily forward motion of the apogee in its syzygies and the daily regressive motion in its quadratures came out a little greater. But it seems preferable not to give the computations, since they are too complicated and encumbered by approximations and not exact enough.”
aa. In this proposition and its corollaries there are numerical differences in ed. 1 and sometimes also in ed. 2. The number 4.4815 at the end of the fifth paragraph, giving the ratio of the force of the sun to the force of the moon, was 6⅓ in ed. 1.
bb. The Latin here is “in India orientali,” lit. “in east India.” In Newton’s day the terms “East India” and “East Indies” were collective names applied to the whole area consisting of India, Indochina, Malaya, and the Malay Archipelago (see Oxford English Dictionary, s.vv. “East India” and “East Indies”; Webster’s New Geographical Dictionary, s.v. “East Indies”). Although that usage is now obsolete, modern English provides no alternative collective name for that area, and so we have chosen the rendering “in the East Indies” used by Motte. In modern geographical terms, Cambay is in western India, and Pegu in Burma.
c. For a gloss on this corollary see the Guide, §10.16.
dd. Ed. 1 lacks this.
ee. This is considerably different in ed. 2.
ff. This is very different in ed. 2.
gg. Ed. 2 lacks this.
aa. In ed. 1, with certain variants, lems. 1—3 and hyp. 2 are simply three lemmas, of which the first contains the statement of lem. 1 followed by the demonstration (which is, however, greatly altered in ed. 2 and ed. 3) of lem. 2, the second corresponds to lem. 3, and the third corresponds to hyp. 1.
b. Strictly speaking, a sphere is defined as a solid body all of whose points are equidistant from the center, but the context and the diagram leave no doubt that in lem. 1, Newton’s “sphere Pape” (“sphaera Pape”) is not truly spherical but of an ellipsoidal shape.
c. In moving ahead from lem. 1 to lem. 2, Newton has shifted his vocabulary from “sphere” to “globe.” He now writes of a circle “outside the globe Pape” (“extra globum Pape”), where again the context and the diagram leave no doubt that the “globe Pape” is ellipsoidal.
d. Newton has here changed his terminology, reverting to “sphere.”
e. Note that here Newton makes explicit use of the “method” of fluxions, that is, the calculus.
a. See the notes to lem. 1 and lem. 2.
bb. Ed. 1 has: “This is the precession of the equinoxes that arises from the force of the sun. Now the force of the moon to move the sea was to the force of the sun as 6⅓ to 1, and this force in proportion to its quantity will also increase the precession of the equinoxes. And therefore the precession arising from both causes will now become greater in the ratio of 7⅓ to 1 and thus will be 45ii24iii15iv. This is the motion of the equinoctial points arising from the actions of the sun and the moon on the parts of the earth that lie on the globe Pape. For the earth cannot be inclined in any direction by those actions exerted upon the globe itself. [On Newton’s use of “globe,” see the note to lem. 2.]
“Now let APEp represent the body of the earth, possessing an elliptical shape and consisting of
uniform matter. And if this is divided into innumerable elliptical, concentric, and similar figures APEp,
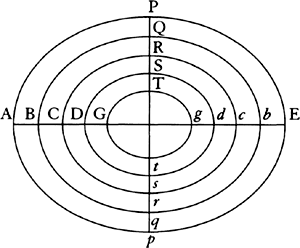 BQbq, CRcr, DSds, . . . , whose diameters are
in a geometric progression, then, since the
figures are similar, the forces of the sun and the
moon under the action of which the equinoctial
points regress would cause those same
equinoctial points of the remaining figures regarded
separately to regress with the same velocity.
And the case is the same for the motion of
the single orbs AQEq, BRbr, CScs, . . . , which
are the differences between those figures.
[Newton here uses the word “orb” (“orbits”) for the
solid we would call an ellipsoid of revolution.]
The equinoctial points of each orb, if it were
alone, would have to regress with the same
velocity. And it does not matter whether any orb
is denser or rarer, provided that it is made up of uniformly dense matter. Hence also if the orbs are
denser at the center than at the circumference, the motion of the equinoxes of the whole earth will be
the same as before, provided that each orb regarded separately consists of uniformly dense matter and
that the shape of the orb is not changed. But if the shapes of the orbs are changed and if the earth now
ascends higher than before at the equator AE because of the density of the matter at the center, the
regression of the equinoxes will be increased as a result of the increase in the height, and will be increased
in single separate orbs in the ratio of the greater height of the matter near the equator of that orb, and in
the whole earth in the ratio of the greater height of the matter near the equator of an orb which is not
the outermost AQEq and not the innermost Gg but some mean orb CScs. Moreover, we have implied
above that the earth is denser at the center and therefore is higher at the equator than at the poles in a
greater ratio than 692 to 689. And the ratio of the greater height can be gathered approximately from the
greater diminution of gravity at the equator than that which ought to follow from a ratio of 692 to 689.
The deviations by which the length of a seconds pendulum oscillating on Gorée Island and on Cayenne
exceeded the length of a pendulum oscillating at Paris in the same time were found by the French to be
1/10 and ⅛ of an inch, which, however, from the proportion of 692 to 689, came out
BQbq, CRcr, DSds, . . . , whose diameters are
in a geometric progression, then, since the
figures are similar, the forces of the sun and the
moon under the action of which the equinoctial
points regress would cause those same
equinoctial points of the remaining figures regarded
separately to regress with the same velocity.
And the case is the same for the motion of
the single orbs AQEq, BRbr, CScs, . . . , which
are the differences between those figures.
[Newton here uses the word “orb” (“orbits”) for the
solid we would call an ellipsoid of revolution.]
The equinoctial points of each orb, if it were
alone, would have to regress with the same
velocity. And it does not matter whether any orb
is denser or rarer, provided that it is made up of uniformly dense matter. Hence also if the orbs are
denser at the center than at the circumference, the motion of the equinoxes of the whole earth will be
the same as before, provided that each orb regarded separately consists of uniformly dense matter and
that the shape of the orb is not changed. But if the shapes of the orbs are changed and if the earth now
ascends higher than before at the equator AE because of the density of the matter at the center, the
regression of the equinoxes will be increased as a result of the increase in the height, and will be increased
in single separate orbs in the ratio of the greater height of the matter near the equator of that orb, and in
the whole earth in the ratio of the greater height of the matter near the equator of an orb which is not
the outermost AQEq and not the innermost Gg but some mean orb CScs. Moreover, we have implied
above that the earth is denser at the center and therefore is higher at the equator than at the poles in a
greater ratio than 692 to 689. And the ratio of the greater height can be gathered approximately from the
greater diminution of gravity at the equator than that which ought to follow from a ratio of 692 to 689.
The deviations by which the length of a seconds pendulum oscillating on Gorée Island and on Cayenne
exceeded the length of a pendulum oscillating at Paris in the same time were found by the French to be
1/10 and ⅛ of an inch, which, however, from the proportion of 692 to 689, came out
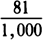 and
and 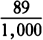 .
Therefore the length of a pendulum on Cayenne is greater than it should be in the ratio of ⅛ to
.
Therefore the length of a pendulum on Cayenne is greater than it should be in the ratio of ⅛ to 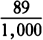 ,
or 1,000 to 712, and on Gorée Island, in the ratio of 1/10 to
,
or 1,000 to 712, and on Gorée Island, in the ratio of 1/10 to
 , or 1,000 to 810. If we take a mean
ratio of 1,000 to 760, the gravity of the earth will have to be diminished at the equator, and its height
increased in the same place, in the ratio of 1,000 to 760 very nearly. Hence the motion of the equinoxes
(as was said above), if increased in the ratio of the height of the earth, not at the outermost orb, not at
the innermost, but at some intermediate orb, that is, not in the greatest ratio of 1,000 to 760, not in the
least ratio of 1,000 to 1,000, but in some mean ratio, say 10 to 8⅓ or 6 to 5, will come out to be 54ii29iii6iv
annually.
, or 1,000 to 810. If we take a mean
ratio of 1,000 to 760, the gravity of the earth will have to be diminished at the equator, and its height
increased in the same place, in the ratio of 1,000 to 760 very nearly. Hence the motion of the equinoxes
(as was said above), if increased in the ratio of the height of the earth, not at the outermost orb, not at
the innermost, but at some intermediate orb, that is, not in the greatest ratio of 1,000 to 760, not in the
least ratio of 1,000 to 1,000, but in some mean ratio, say 10 to 8⅓ or 6 to 5, will come out to be 54ii29iii6iv
annually.
“Again, because of the inclination of the plane of the equator to the plane of the ecliptic, this motion must be diminished, and must be diminished in the ratio of the sine of the complement of the inclination to the radius. For the distance of each terrestrial particle from the plane QR, when the particle is farthest away from the plane of the ecliptic, being (so to speak) in its tropic, is diminished by the inclination of the planes of the ecliptic and the equator to each other, in the ratio of the sine of the complement of the inclination to the radius. And the force of the particle to move the equinoxes is also diminished in the ratio of that distance. The sum of the forces of that same particle is also diminished in the same ratio in places equally distant in both directions from the tropic, as could easily be shown from what has been demonstrated earlier, and therefore the whole force of that particle to move the equinoxes in an entire revolution, as well as the whole force of all the particles, and the motion of the equinoxes arising from that force, is diminished in the same ratio. Therefore since that inclination is 23½°, the motion of 54ii29iii must be diminished in the ratio of the sine of 91,706 (which is the sine of the complement of 23½°) to the radius 100,000. In this way that motion will now become 49ii58iii. Therefore the points of the equinoxes regress with an annual motion (according to our calculation) of 49ii58iii, nearly as the celestial phenomena require. For that annual regression, from the observations of astronomers, is 50ii.”
a. The Latin word “coma” means “head of hair” and is used today to designate the nebulous envelope surrounding the nucleus or head of a comet. Another Latin word for “head of hair” is “capillitium.” In book 3, lem. 4, Newton uses “capillitium” for the “head of hair” of a comet, but in prop. 41 he uses “coma.” We have translated both as “coma,” the term commonly used in English.
a. Here “content” has the sense of Newton’s “solid,” that is, the result of multiplying SB by the square of St.
b. In prop. 41, Newton refers to the line Bi as “[lineam] occultam Bi,” directing that “Per punctum B age occultam Bi,” literally, “Through point B draw the occult line Bi.” In the next sentence, the same adjective, “occult,” is applied to the line Si; in the following sentence, the line σξ is said to be “occult.” (In the first and second editions, there is another “occult” line OD.) In the final paragraph, there is a reference to the “occult” line AC.
In Newton’s day, according to the Oxford English Dictionary, the adjective “occult” was used to denote “a line drawn in the construction of a figure, but not forming part of the finished figure,” and also to denote a dotted line. The diagram for prop. 41 does not show any lines Bi, Si, OD, or AC, but σξ does appear as a dotted line. Accordingly, we have translated “occult” in the sense of “imagined” in the case of lines Si, Bi, and AC, and as “dotted” in the case of line σξ.
Perhaps the reason why Newton has referred to all these lines (both invisible and dotted) as “occult” is that, in the original diagram that he drew for the cutter of the wood block, he did not show σξ as a dotted line. In this case, all of these lines would have been “occult” or hidden from view, invisible and only imagined.
c. Basically, here Newton is determining a comet’s distance from its latitude and longitude as determined by a terrestrial observer. He guesses a position B of the comet in the plane of the ecliptic and then determines the altitude (or distance above the ecliptic), and so can construct a right triangle, of which one side is SB (a line drawn from the sun to the point B on the ecliptic) and other is tB times the tangent of the latitude of the comet (which Newton writes as: the tangent of the latitude of the comet in the second observation to the radius tB).
For an extensive gloss on prop. 41 and on Newton’s theory of comets, see A. N. Kriloff, “On Sir Isaac Newton’s Method of Determining the Parabolic Orbit of a Comet,” Monthly Notices of the Royal Astronomical Society 85 (1925): 640–656; see also the enlightening discussion by S. Chandrasekhar, Newton’s “Principia” for the Common Reader (Oxford: Clarendon Press, 1995), pp. 514–529, especially the diagram on p. 514.
dd. The next eight paragraphs (and the included tables) are not present in ed. 1. They were first published in ed. 2 and considerably revised and expanded in ed. 3.
ee. These two sentences were added in ed. 3.
f. Newton referred to the star
α Virginis in the constellation Virgo as “spica  ” and simply as
“spica.” We have rendered these as “Spica Virginis” and “Spica.”
” and simply as
“spica.” We have rendered these as “Spica Virginis” and “Spica.”
g. See note a on p. 891 above.
hh. The clause in parentheses was added by Newton, as were the following expressions within parentheses.
aa. This paragraph and the accompanying table (on p. 936) appeared for the first time in ed. 3.
a. Ed. 1 lacks the General Scholium, which includes Newton’s famous discussions of God and of hypotheses. This scholium is first printed in ed. 2 but is documented further by its changing versions in five extant earlier holograph drafts and is treated also in contemporaneous correspondence between Newton and Roger Cotes, editor of ed. 2. For details see Unpublished Scientific Papers of Isaac Newton, ed. A. Rupert Hall and Marie Boas Hall (Cambridge: Cambridge University Press, 1962), pp. 348–364; I. Bernard Cohen, Introduction to Newton’s “Principia” (Cambridge, Mass.: Harvard University Press; Cambridge: Cambridge University Press, 1971), pp. 240–245.
bb. Ed. 2 lacks this.
cc. Ed. 2 lacks this.
d. Newton’s note a: “That is, universal ruler.”
e. Newton here uses the word “deitas,” a nonclassical term which signifies the essential nature of the divinity or “god-ness.” Although “Godhead” does fit, the term “godhood” (which is more abstract) may more accurately convey the sense of Newton’s “deitas.”
ff. Ed. 2 lacks this.
g. Newton’s note b, which ed. 2 lacks: “Our fellow countryman Pocock derives the word ‘deus’ from the Arabic word ‘du’ (and in the oblique case ‘di’), which means lord. And in this sense princes are called gods, Psalms 82.6 and John 10.35. And Moses is called a god of his brother Aaron and a god of king Pharaoh (Exod. 4.16 and 7.1). And in the same sense the souls of dead princes were formerly called gods by the heathen, but wrongly because of their lack of dominion.”
hh. Ed. 2 has “space, eternity, and infinity.”
ii. Ed. 2 lacks this.
j. Newton’s note c: “This opinion was held by the ancients: for example, by Pythagoras as cited in Cicero, On the Nature of the Gods, book 1; Thales; Anaxagoras; Virgil, Georgics, book 4, v. 221, and Aeneid, book 6, v. 726; Philo, Allegorical Interpretation, book 1, near the beginning; Aratus in the Phenomena, near the beginning. Also by the sacred writers: for example, Paul in Acts 17.27, 28; John in his Gospel 14.2; Moses in Deuteronomy 4.39 and 10.14; David, Psalms 139.7, 8, 9; Solomon, 1 Kings 8.27; Job 22.12, 13, 14; Jeremiah 23.23, 24. Moreover idolators imagined that the sun, moon, and stars, the souls of men, and other parts of the world were parts of the supreme god and so were to be worshiped, but they were mistaken.” In ed. 2 this note reads: “This opinion was held by the ancients: Aratus in the Phenomena, near the beginning; Paul in Acts 7.27, 28; Moses, Deuteronomy 4.39 and 10.14; David, Psalms 139.7, 8; Solomon, Kings 8.27; Job 22.12; the prophet Jeremiah, 23.23, 24.”
kk. Ed. 2 lacks this.
ll. Ed. 2 has: “For a god.”
mm. Ed. 2 lacks this.
nn. Ed. 2 has “experimental.”
oo. The word “fingo” in Newton’s famous declaration, “Hypotheses non fingo,” appears to be the Latin equivalent of the English word “feign.” Andrew Motte translated “fingo” by “frame,” a verb which at that time could have a pejorative sense. For details see the Guide, §9.1.
pp. The final paragraph of the General Scholium has attracted much scholarly attention, notably in an effort to discern what Newton intended (in the opening and closing sentences) by a “spirit” which may be operative in various types of phenomena. It might even appear that Newton was here introducing a speculation—we dare not call it a hypothesis—although Newton’s actual language indicates that for him there was no question about whether this spirit “really” exists, only about the laws according to which this spirit acts.
A puzzle relating to the interpretation of this “spirit” is the appearance of the qualifying adjectives “electric and elastic,” introduced in the original Motte translation and retained in the Motte-Cajori version. Although these words are not found in either the second or the third Latin editions, they have a Newtonian provenience since they occur in Newton’s personal interleaved copy of the second edition as one of the proposed emendations. Furthermore, thanks to the research of A. Rupert Hall and Marie Boas Hall, we know that the spirit in question is indeed “electrical.” In particular, as Newton worked toward the second edition of the Principia, he composed various drafts of proposed conclusions which, together with other manuscripts, provide evidence for the importance of electrical phenomena in his thinking about gravity during the years 1711–1713. For details see the Guide to the present translation, §9.3.
One possible reason why Newton decided not to insert the qualifying phrase “electric and elastic” into the text of the third edition (1726) is that in his interleaved copy of the second edition he has finally drawn a line through the whole paragraph, showing his intention of deleting it in a third edition. The reason for this decision seems to be that some time after 1713 Newton lost his enthusiasm for electricity as a possible agent in gravitation.
We may readily understand why Newton omitted to carry out either the revision or the proposed cancellation of the final paragraph. By the time that the third edition was fully printed, in about February 1726, Newton and Pemberton had spent several years revising the text and reading the proofs and Newton was within a little more than a year of his death. When Newton reached the last paragraph he was probably so weary that he overlooked his proposed alteration of the conclusion.
The third edition concludes with an “Index Rerum Alphabeticus” (pp. 531–536) and an advertisement of books sold by William and John Innys (pp. 537–538).