Although our senses receive physical information from the world, we interpret those senses in terms of the objects in the world—we see a tree, we feel the wind, we hear a bird. Interpreting that information requires an integration process that takes time. We can trade off time for accuracy if need be.
When you look at a picture (say of a face), your eyes dart from one important feature to the next.1 In part, you need to do this because the photoreceptors in the human eye are more concentrated in the center of your retina than in the periphery, which means that your vision is more accurate (has higher resolutionA) when you are looking directly at something. Every few hundred milliseconds, your eyes make another journey (they saccadeB) to another location. Over the course of a few seconds or minutes, you have integrated the important information about the picture to answer whatever question you had. Where you look, how long you look, and how long your eyes stop at each point depend on the questions you are trying to answer about the picture.C
Experimental studies of decision-making often make the perceptual recognition of the information difficult, which means that one has to integrate information over time.2 Old studies did this because it allowed them to use the reaction time to differentiate between conditions. New studies do this because it allows them to study how the neural firing changes as the subject figures out what to do. Interestingly, because of this, much of the neuroscience literature on “decision-making” is about situation recognition rather than deliberation or the other action-selection processes we have been discussing. In these perceptually difficult tasks (which we discuss in detail later), the hard part is recognizing which situation the cues imply you are in not deciding what to do. Each situation has a single correct outcome. (Compare this to the examples we discussed in Chapter 9 when we talked about people deliberating over job options or over large purchases like cars or houses.) Nevertheless, perceptual categorization is a key part of the decision-making process, and these perceptually difficult tasks have taught us how we integrate information over time.
Computationally, integrating information is most easily understood in terms of the race-to-threshold models.3 In these algorithms, originally used by Alan Turing and the Allies to break the German Enigma code in World War II,D the weight of evidence for each possibility is measured, and when the weight of evidence becomes overwhelming for one possibility over the others (when the weight of evidence for one possibility reaches a threshold), that choice wins and the decision is made.
Let us first look at this in the case of a two-choice forced decision. A two-choice forced decision is one where you must make a decision between two options. There is no third option; not choosing the first option is equivalent to choosing the second. We can measure how much better one option is than the other by measuring the ratio of the weight of evidence for one option over the weight of evidence for the other option. The ratio of the probabilities is convenient to use because any advantage to one side is equivalent to a disadvantage to the other side.
Some readers may recognize this as an odds ratio,4 which is usually written as 1:X, where X measures how much better the second choice is than the first. However, these odds ratios require a lot of division and require that we represent our number from 0 (1:infinity) to infinity (infinity:1). A better option is to take the logarithm of this ratio. The advantage of logarithms is that multiplying two numbers is equivalent to adding their logarithms; similarly, dividing two numbers is equivalent to subtracting their logarithms. The logarithm is a function that translates this ratio into a number from minus infinity to plus infinity. (This turns out to be how much information there is to support one hypothesis over the other.) When the two choices are equal, this difference between the logarithms is zero, and the difference moves away from zero as we gather information. This allows us to define the weight of evidence of choosing left or right as a single number (greater than zero will mean go left, less than zero will mean go right). We simply start at zero and integrate our information over time by moving up with evidence for the first choice and down with evidence for the alternate choice.
This leaves us with three important parameters. First, we have the slope, which is how much to change our ratio with each piece of information supporting one hypothesis over the other. Second, the bias determines where we start our decision from.E Finally, third, there is the stopping condition, which can either be taking the best option after a certain time or (more commonly used in the experimental literature) the odds ratio where we decide that we have enough information—that is, when we have deviated from zero (the two choices being equal) to some threshold (one choice is so much better, we’ll go with that one).
I find the race-to-threshold model extremely intuitive in that it entails weighing the pros and cons of two options and stopping when we’re convinced that one choice is better than the other one. The primary parameters are ones that make sense intuitively—bias is our preference for one choice over the other, slope is how quickly we learn about the options, and the threshold is how sure we want to be before we commit to a choice.
The integration-to-threshold model produces a unique distribution of reaction times because of the way the integration occurs (Figure 11.1).5 It works out to be related to what is known in the engineering fields as a hazard function—How long will it take before something happens?, given that we stop counting the first time it happens. This is used, for example, in measuring the first time something breaks down and has to be repaired (like an airplane).6 It also tracks the physics of a noisy signal crossing an energy barrier.7 Imagine popcorn in a hot-air popcorn popper. We have two cases of a “hazard” function here. First, the popcorn is bouncing around, and some of the popcorn will have enough bounce to get out and over the threshold of the popper on its own. The more the air blows, the more the popcorn bounces (more air = faster slope; getting out of the popper = crossing the threshold). Second, the heat in the popper is making the water inside each kernel of popcorn expand; at some point the water expands enough and blows the kernel open (more heat = faster slope; exploding kernel = crossing the threshold). If the first hazard function occurs before the second, you get unpopped kernels in your bowl.
These theories have been explicitly tested in a number of experimental paradigms. The simplest is the “visual noise” or “television snow” paradigm.F In this paradigm, the subject stares at a black screen on which bright dots are plotted. Some of those dots vanish in the next instant. Other dots move in a random direction. But some of the dots move together in a given direction (say left). The goal is to figure out which direction the subset of coherent dots is going. By varying the proportion of dots moving in the same direction, the experimenter can quantitatively control the speed at which information is provided to the subject. Both humans and monkeys are remarkably sensitive to even very small proportions, being able to easily recognize as few as 10% of the dots moving in the same direction.8

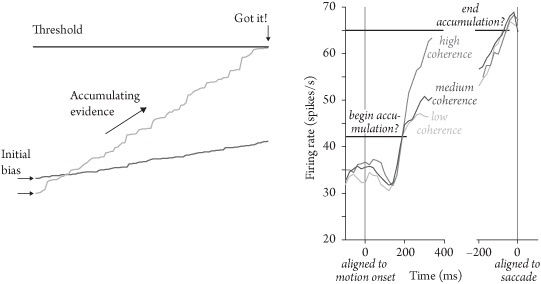
Figure 11.1 INTEGRATION TO THRESHOLD. (Left) Multiple accumulators start with an initial bias, and each races toward threshold by integrating the accumulating evidence at a different rate. The first one to reach threshold wins, and the perception collapses to decision. (Right) Individual neurons in LIP integrate information. All trials start at similar firing rates (there is no initial bias) and end at the same firing rates (on reaching threshold) but integrate at different rates depending on the coherence of the incoming sensory signal. Right panel from Gold and Shadlen (2002), redrawn from Roitman and Shadlen (2002). Reprinted with permission of author and publisher.
This task depends on the primate ability to detect motion. Your brain wants to detect things that move for two reasons. First, if you are moving, then the whole world you see moves in sync. (This is the secret to the illusions of motion that IMAX movies can produce.) But, second, your brain wants to detect other things that move in the world. The ability to detect things that move depends on a brain structure called MT,G which has cells that detect things that move in the visual world, and a structure called LIP,H which has cells that have tuning curves to a given direction and increase their firing rate over time as the monkey watches the screen. (There is a nearby structure called MST,I which detects the first case, where the whole visual world is moving, usually because you are moving within it.) The features of the world detected by cells in MT are good for detecting moving animals and objects. Imagine, for example, a camouflaged animal (like a leopard) moving through a forest. Most of the dots you see would flicker on and off with the wind, but a few of them (the leopard!) would reliably move in the same direction together.
The MT cells provide information about the direction of those moving dots—each cell’s firing rate has a preferred direction and the firing of that cell reflects the proportion of dots moving in that direction against a static background.11 (MST cells also have a preferred firing rate and reflect motion of the entire screen.12)
The LIP cells seem to be integrating the information. (MT projects directly to LIP.) The starting firing rate of an LIP cell reflects the monkey’s initial predictions about whether the dots are going to be moving in that cell’s favorite direction or not (the bias), the speed at which the firing increases reflects the information coming from MT (the slope), and when the LIP cells reach a certain firing rate, the animal reacts (reaching the threshold).13 We can think of this decision as being controlled by two neurons, one which is looking for leftward motion and one which is looking for rightward motion—the first to reach threshold wins, and that’s the decision made.
Now that we’ve seen how this integration-to-threshold idea can work with two choices, it is straightforward to imagine how it would work with more choices.14 For example, I doubt that monkeys evolved to make a choice between whether dots were going left or right. More likely, these experiments are tapping into a system that evolved to detect the direction (any direction) that a camouflaged object was moving. Instead of two neurons, we have hundreds or thousands of neurons, representing a range of possibilities, each integrating the information, each racing to threshold.
This is something called a winner-take-all network and arises from a simple model combining excitatory and inhibitory cells (cells that increase the firing of the cells they send axons to and cells that decrease the firing of the cells they send axons to). The excitatory cells are assumed to be connected up such that cells that represent similar things (say similar directions) support each other, while cells that represent different things (say directions 180 degrees apart) don’t.15 The inhibitory cells work as simple negative feedback, so that the total activity in the excitatory cells must remain a constant. This network was first examined in the 1970s as a model of cortex, and it turns out to be a very reasonable model of many aspects of the cortex. Mathematical work in the 1980s showed that the stable final state of this network is an agreement between the excitatory cells, with a subset of cells that agree on a certain result all having high firing rates and cells that disagree with that result having low firing rates. This network was used in the 1990s as a model of the rat’s sense of direction and the rat’s sense of location (place cells in the hippocampus) and as a model of cortex. Functionally, these models are a special case of the content-addressable memories discussed in Appendix C.
A radar sweeping around the sky, looking for incoming airplanes, is a serial perception—it can only see one direction at a time; each direction is checked sequentially. An analog camera perceives light in parallel, with each light-detecting chemical on the photographic plate reacting at the same instant. (Digital cameras use a combination of parallel and serial processing. Each charge-coupled device on each pixel of the camera detects light at the same time [integrating the photons over the time the shutter is open], but then the pixels are usually read into the memory serially.) Our perceptual systems use a combination of parallel and serial processing, but the parallel step generally goes much farther than simple light detectors.16
It’s useful to examine this parallel and serial processing in vision. Light is detected by the retina, which works in a massively parallel manner, like the pixels on our digital camera, integrating the photons that reach our eyes. From there, signals are sent on to the thalamus, and then to the primary visual cortex, which contains feature detectors, particularly for dots, lines, and edges. Each of these feature detectors is repeated for each part of the visual field, as if for the pixels of our eyes. From there, signals are sent to many different visual systems, which attempt to pull information out of the signal in parallel. One system, for example, tries to identify objects, another tries to identify faces,J another recognizes objects moving through the visual field (MT).
The classic experiment examining the difference between parallel and serial perception is the pop-out experiment (Figure 11.2).20 Your goal in this task is to identify a certain object (the target) in a field of distractors. When the target is really different from the distractors (O in a field of Xs), the target seems to pop out, and the speed at which you recognize the target does not depend on the number of distractors (because you have different feature detectors for the target and the distractors and you can just have the feature detector tuned to the target shout out when it finds it). When the target is really similar to the distractors (Y in a field of Xs), you have to check each one individually. This means that the time it takes you to find the target depends on the number of distractors. For parallel recognition (pop-out), your accuracy is independent of the time it takes you to respond. However, for serial recognition (searching through candidates), the longer you take to respond, the more accurate you will be (up to some point when you have gathered all the information available). This means that there is a clear tradeoff between speed and accuracy for serial recognition.

Figure 11.2 POP-OUT IN VISION. Try to find the Y in the left panel and the O in the right panel. It is much easier to find the O because it “pops out” in our vision, whereas the Y requires a serial search through the display. Of course, once you know where to look, both the Y and the O are easy to find.
The race-to-threshold model provides a good explanation for the speed–accuracy tradeoff of serial search.21 If the agent using a race-to-threshold algorithm wants to respond faster, it just lowers the threshold. A lower threshold means that the race ends faster (so the agent responds more quickly) but with the lower threshold, the agent has had less time to analyze the information, and is thus going to be more susceptible to noise. Equivalently, the agent can increase the slope. In either case—lowering the threshold or increasing the slope—with each small piece of information you gather, you approach the threshold more quickly. Increasing slope and decreasing threshold are mathematically equivalent. On the other hand, moving your starting point closer to threshold is different—that’s moving your bias—guessing before the information arrives. If you move your bias above the threshold, you don’t even have to wait for information, you could just make the decision without information! (I suspect this is more common than it should be.)
Certainly, it is possible in some tasks that you have gathered all the information you can, that at some point there is no new information available, and you have reached what is mathematically called an asymptote. In those cases, waiting longer isn’t going to make your decision worse, it’s just not going to make your decision better either. At some point, you have to act. However, in psychology experiments with noisy and ambiguous data (such as the television snow experiment described above), waiting is always better and there is a tradeoff between speed and accuracy.
So why can experts act quickly? How did Ted Williams or Tony Gwynn hit close to 40% of the pitches thrown at them?K It takes a baseball about 400 milliseconds to get from the pitcher’s mound to home plate.L Given that human reaction time (even for the fastest athletes) is about 200 milliseconds,23 one has only a couple of hundred milliseconds (a couple of tenths of a second) to integrate the information about how the ball is spinning, where it’s going to cross the plate, and when it’s going to be there. Players with better reaction times have better batting averages.
Experts have two advantages over nonexperts—they have trained up their perceptual system to recognize better features about the task and they have trained up their habit system to cache the most reliable choices of what to do. Perceptual training is like the chunking that we saw in Chapter 10. Experts have learned how to represent the task in such a way that it is easier to determine the correct responses from the available inputs; they have identified good categories for the task. The classic examples of this are chess and videogames. We have already seen how a computationally expensive search algorithm can beat a grandmaster at chess (Deep Blue vs. Gary Kasparov), but that chess grandmasters don’t actually do that same computationally expensive search.24 Instead, chess grandmasters have learned to represent the board in ways that limit the search they have to do. The experiment that proved this was that chess masters are better at remembering the positions of pieces on boards when those positions can arise from legal moves than when they can’t. Just as an expert musician no longer thinks about the fingering for a chord on a guitar, a chess master no longer looks at each piece on the board as an individual thing. Playing videogames produces a similar specific expertise—faster recognition of the events in the game (training perceptual recognition systems, this chapter) and faster recognition of what to do in response to those events (training procedural systems, Chapter 10).25
It is important to recognize that this is not saying that “intuition” is better than “analysis,” even for experts. Real experts shift from intuitive decisions to analytical decisions (from procedural to deliberative) as necessary. Similarly, it is important to recognize that raw intuition is not reliable in these situations—experts have spent years (often decades!) training their perceptual and procedural systems. In a sense, what the procedural decision-making system we examined in Chapter 10 does is trade perceptual and deliberative time during the decision for time during training, so that, while it takes longer to learn to do the task, once trained, the task can be done more quickly, if less flexibly. Typical estimates of training time for most human expert-level tasks is about 10,000 hours.26 (That’s five years at 40 hours per week at 50 weeks per year, or four years at 50 hours per week for 50 weeks per year.) This is why most apprenticeships, such as graduate school, medical school, time in the minor leagues, etc., are about four to six years.M
It is important to recognize that the opposite of “analytical” is not “intuitive.” Both analytical (deliberative) decision-making and intuitive (procedural) decision-making arise from systems that have evolved to make accurate decisions in the face of integrating information. The opposite of “analytical” is “glib,” moving the threshold down so far that no information is gathered (or moving the bias above the threshold), both of which are disastrous. In fact, both analytical and intuitive responses show speed–accuracy tradeoffs. One key to Tony Gwynn’s success is that he used a very light bat and waited until the last moment to hit the ball.27 One of the big differences between Ted Williams, Tony Gwynn, and the rest of us is that Williams and Gwynn had much better eyesight. When Tony Gwynn retired, he commented to a reporter that his eyes were going and he couldn’t pick up the ball as early as he used to be able to. When the reporter asked what his eyesight was now, Gwynn responded that it was now about 20/15, but at one time had been 20/10. With better eyesight, he could pick up the rotation of the ball earlier, giving himself more time to react, more time to integrate information, and a better chance of hitting the ball.
• Jan Lauwereyns (2010). The Anatomy of Bias. Cambridge, MA: MIT Press.
• Joshua I. Gold and Michael N. Shadlen (2002). Banburismus and the brain: Decoding the relationship between sensory stimuli, decisions, and reward. Neuron, 36, 299–308.
• Joshua I. Gold and Michael N. Shadlen (2007). The neural basis of decision making. Annual Review of Neuroscience, 30, 535–574.