CHAPTER 2

Exponents, Roots, and Number Properties

Exponents

Exponents are a common shorthand used in mathematics. You have probably seen terms like 4² or 3⁴. Both of these are written with exponents. These are read as “four to the second power” and “three to the fourth power,” respectively. This is why you sometimes hear people call exponents “powers.”

In a term like the one shown, the exponent tells you how many times to multiply the base by itself. For example, 4² = 4 × 4 = 16 and 3⁴ = 3 × 3 × 3 × 3 = 81. The following are a few special rules and some terminology you should be familiar with in regard to exponents.

• Any number with an exponent of 0 is equal to 1.

This means that 4⁰ = 1, 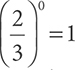, and 1215⁰ = 1. (The only exception is 0⁰, which is considered an indeterminate form. This will not be on the GED^® test, however!)

• Any number to the power of 1 is just that number.

For example, 8¹ = 8 and .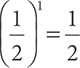

• Any number to the power of 2 is said to be “squared.” Any number to the power of 3 is said to be “cubed.”

For example, 5² can be read as “five squared” and 5³ can be read as “five cubed.”

Negative Exponents

Negative exponents have a special meaning. They can be thought of as a way to rewrite a fraction. As a general rule, for any number A that is not zero:

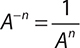
In other words, any number with a negative exponent can be rewritten as a fraction with 1 above the fraction bar and the same number with a positive exponent below the fraction bar. Here are some examples.

EXAMPLE 1

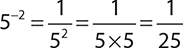
EXAMPLE 2

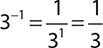
EXAMPLE 3

---

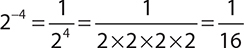
EXERCISE 1

Exponents

Directions: Evaluate each of the following expressions containing exponents.

1. 3²

2. 1⁵

3. 12¹

4. 7³

5. 2²

6. 18⁰

7. 8^–2

8. 6^–1

9. 4^–3

10. 1^–4

Answers are on pages 509–510.

---

The Rules of Exponents

Expressions with exponents have rules that allow you to simplify them. These are commonly called the rules or laws of exponents. These rules apply whether the exponents are negative or positive, or even if they are not whole numbers.

Rule 1: When Multiplying Two Terms with the Same Base, Add the Exponents

Aⁿ × A^m = A^n+m

Remember that this rule applies only if the base numbers are the same. For example, 2³ × 2^–1 can be simplified using rule 1 because in both terms the base is 2. 3² × 4¹⁰ cannot be simplified in that way because the base is 3 in one term but 4 in the other.

EXAMPLE 4

Using the laws of exponents, write a numerical expression that is equivalent to 4⁴ × 4².

Because the two terms with exponents have the same base, you can apply rule 1: 4⁴ × 4² = 4⁴⁺² = 4⁶.

EXAMPLE 5

Using the laws of exponents, write a numerical expression that is equivalent to .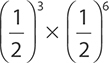

Again, the two terms have the same base, so .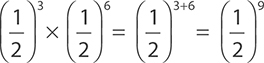

Rule 2: When Dividing Two Terms with the Same Base, Subtract the Exponents

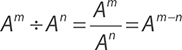
On the GED^® test, you may see division written with the usual division symbol, or you may see it written as a fraction. Both of these are shown in this rule, and both mean the same thing.

EXAMPLE 6

Using the laws of exponents, write a numerical expression that is equivalent to .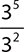

The two terms have the same base and are being divided, so apply rule 2: .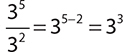

EXAMPLE 7

Using the laws of exponents, write a numerical expression that is equivalent to 4⁵ ÷ 4.

Both terms have the same base, but the second 4 does not appear to have an exponent. However, recall that any number to the power of 1 is that same number. Therefore, 4 can be thought of as 4¹. Thus, 4⁵ ÷ 4 = 4^5–1 = 4⁴

Rule 3: To Take a Term with an Exponent to a Power, Multiply the Powers

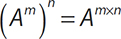
For this rule, you do not need to worry about the base. Just remember that when a power is taken to a power, the exponents are multiplied.

For example, .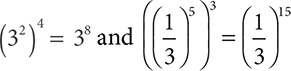

When simplifying some expressions, you may need to use more than one of the rules provided above. In these cases, the order in which you apply the rules does not matter so long as anything within parentheses is simplified first.

EXAMPLE 8

Simplify the expression 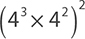using the laws of exponents.

Working inside the parentheses first, .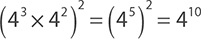

---

EXERCISE 2

Rules of Exponents

Directions: For each of the following, select the expression that is equivalent to the one given.

1. 2³ × 2⁵

A.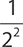

B. 2

C. 2²

D. 2⁸

2.

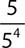
A.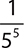

B.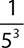

C. 5⁴

D. 5⁵

3.

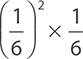
A.

B.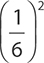

C.

D.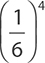

4. (8⁴)⁴

A.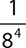

B. 1

C. 8⁸

D. 8¹⁶

5.

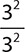
A. 1

B.

C. 0

D. 3⁴

6. (3² × 3)³

A. 3³

B. 3⁶

C. 3⁷

D. 3⁹

7.

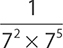
A.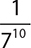

B. 7¹⁰

C.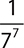

D. 7⁷

8.

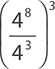
A. 4⁵

B. 4⁸

C. 4¹⁵

D. 4²¹

9. 18 × 18 × 18²

A. 1

B. 18

C. 18²

D. 18⁴

10. (9³)⁴ × 9

A. 9²

B. 9⁴

C. 9⁸

D. 9¹³

Answers are on page 510.

---

Square Roots and Cube Roots

Square roots and cube roots are two ways of “undoing” exponents. For example, because 6² = 36, the square root of 36 is 6. Also, because 2³ = 8, the cube root of 8 is 2. The symbol used for any type of root is called a radical.

For a square root, the symbol is 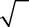. For the cube root, the symbol is . For the first two examples, you could have written 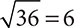and .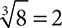

Numbers for which the square root or the cube root is a whole number are referred to as “perfect squares” or “perfect cubes.” It is a good idea to know some of the common perfect squares and perfect cubes. The most common of these are listed here:

Selected Perfect Squares

---

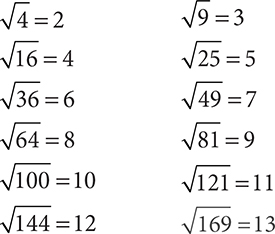
Selected Perfect Cubes

---

Expressions involving square roots and cube roots can be simplified by using your knowledge of the perfect squares and cubes. The next two examples show how this works.

EXAMPLE 9

Simplify: .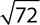

Anytime you need to simplify a square root term, try to rewrite the number under the radical as an expression containing a perfect square. For example, 72 = 2 × 36 and 36 is a perfect square. Therefore, .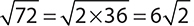

Because the square root of 36 is 6, the 36 under the radical can be rewritten as 6 in front of the radical. The final answer is read as “6 times the square root of 2.”

EXAMPLE 10

Simplify: .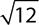

Because 12 can be rewritten as the product of 3 and 4, you can simplify this term as .

The same process can be applied to perfect cubes and cube roots. For example, .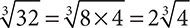

Note that not all expressions with square roots or cube roots can be simplified. If the number cannot be rewritten as an expression containing a perfect square or a perfect cube, then the radical cannot be simplified.

---

EXERCISE 3

Square Roots and Cube Roots

Directions: Simplify each of the following using your knowledge of perfect squares and perfect cubes.

1.

2.

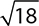
3.

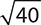
4.

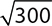
5.

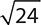
6.

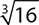
7.

8.

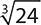
9.

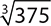
10.

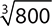
Answers are on page 510.

---

Exponents and Roots on the TI-30XS

Here are the basics of how to calculate exponents and roots on the TI-30XS calculator.

Exponents

To calculate the value of any exponent, type in the base first followed by the caret key located in the left-hand column of the calculator. For example, to find 3⁴:

This works for any power, but there is a shortcut key that can be used for squaring numbers.

Roots

The radical symbols on the calculator are both above the regular buttons in green writing. This means that you must utilize the 2nd key to access them. For cube roots, the calculator will give a decimal approximation, but for square roots, the calculator will give the simplified version by default. In order to get the decimal approximation, you will need to press (the toggle key).

(finds the simplified answer)

(converts to a decimal approximation)

Cube roots are found using a different key, as you can see in the following example. Notice that the 3 from the root symbol is typed in first.

Go back and try the practice problems with the calculator. For square roots, make sure to practice getting the decimal approximation as well as the simplified versions of the answers.

Order of Operations

Which of the following is equal to 3 + 4(1 + 2)? Is it 15, or 27, or is it 9? Which answer you get depends on the order in which you did the operations, but only one answer is correct. Getting the correct answer depends on following a set of rules called the “order of operations.” You may have heard this referred to as PEMDAS or even by a common saying used to remember it: “Please Excuse My Dear Aunt Sally.” The following is the process you should follow anytime you are simplifying a numerical expression.

• Parentheses. Complete any operations inside of parentheses first. If there is more than one set, start with the innermost parentheses.

• Exponents. Find the value of any exponents.

• Multiplication and division. Perform any multiplication or division from left to right.

• Addition and subtraction. Perform any addition or subtraction from left to right.

The example was the expression 3 + 4(1 + 2). Following the order of operations:

Multiplication is performed next because there are no terms with exponents. (Remember that multiplication can be written as 4(3) or 4 × 3.)

Let’s go through a couple more examples to make sure it all makes sense.

EXAMPLE 11

Find the value of .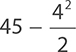

Just as there are different ways to write multiplication, there are

different ways to write division. The term 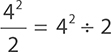. However, before the division can be completed, the term with the exponent must be calculated (this is the first step because there are no parentheses):

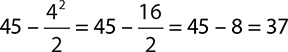
EXAMPLE 12

Find the value of 2(2 + 5)² – 6.

2(2 + 5)² – 6 = 2(7)² – 6 = 2(49) – 6 = 98 – 6 = 92

---

EXERCISE 4

Order of Operations

Directions: Find the value of each of the following numerical expressions.

1. 8 ÷ 2² + 1

2.

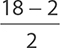
3. 4 + 2(8 + 6) – 1

4. 3(6 – 5)³

5. 4 × 3 – 2

6. 3 –1 + 2² × 5

7. (8 + 1 – 5)³

8. (2 + 4) ÷ 2 – 1

9.

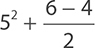
10. 16 + 4(3 + 2)

Answers are on page 510.

---

The Distributive Property

Using the order of operations, you know that 2(1 + 5) = 2(6) = 12, but a test question may ask you simply to rewrite this expression instead of calculate its final value. This can be done using the distributive property. If A, B, and C are any numbers, then:

A(B + C) = A(B) + A(C)

and

A(B − C) = A(B) − A(C).

This property says that with an expression such as 2(1 + 5), you can first add the terms inside the parentheses as previously shown, or you can multiply each term inside the parentheses by the 2 to get 2(1 + 5) = 2(1) + 2(5). If you calculate the value, you will see that the result is 12, just as before. The distributive property will be very useful later on when you work with algebraic expressions.

Some important things to note: The distributive property only works if the operation inside the parentheses is addition or subtraction. It will not work with any other operations.

However, the property will work no matter how many terms are added or subtracted within the parentheses. The expression 4(5 + 6 – 1 + 2) is equivalent to 4(5) + 4(6) – 4(1) + 4(2). Notice that the 4 is multiplied by (“distributed to”) each term inside the parentheses and that the terms keep the same operation (addition or subtraction).