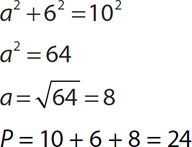ANSWERS AND EXPLANATIONS
Mathematical Reasoning
Chapter 1 Whole Numbers and Operations
Exercise 1: Operations with Whole Numbers
1. 1164
2. 284
3. 1009
4. 121.71
5. 3192
6. 4298
7. 13
8. 179,602
9. 10,501
10. 127.33
11. 786
12. 287
13. 2630
14. 405
15. 469
16. 1125
17. 4018
18. 3794
19. 738.17
20. 44,800
Exercise 2: Word Problems
Chapter 2 Exponents, Roots, and Number Properties
Exercise 1: Exponents
1. 9
2. 1
3. 12
4. 343
5. 4
6. 1
7. 
8. 
9. 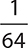
10. 1
Exercise 2: Rules of Exponents
1. D
2. B
3. C
4. D
5. A
6. D
7. C
8. C
9. D
10. D
Exercise 3: Square Roots and Cube Roots
1. 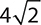
2. 
3. 
4. 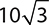
5. 
6. 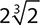
7. 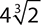
8. 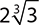
9. 
10. 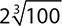
Exercise 4: Order of Operations
1. 3 8 ÷ 22 + 1 = 8 ÷ 4 + 1 = 2 + 1 = 3
2. 8 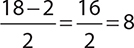
3. 31 4 + 2(8 + 6)–1 = 4 + 2(14) –1 = 4 + 28 –1 = 31
4. 3 3(6 – 5)3 = 3(1)3 = 3(1) = 3
5. 10 4 × 3 – 2 = 12 – 2 = 10
6. 22 3 –1 + 22 × 5 = 3 –1 + 4 × 5 = 3 –1 + 20 = 22
7. 64 (8 + 1 – 5)3 = (4)3 = 64
8. 2 (2 + 4) ÷ 2 –1 = 6 ÷ 2 –1 = 3 –1 = 2
9. 26 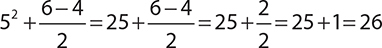
10. 36 16 + 4(3 + 2) = 16 + 4(5) = 16 + 20 = 36
Chapter 3 Decimal Numbers and Operations
Exercise 1: Comparing Decimals
1. 25.099 < 25.915
2. 0.108 > 0.0108
3. 0.00054 < 0.0019
4. 8.6 > 8.09
5. 0.40 = 0.4
6. 0.1053 > 0.0153
7. 2.00501 < 2.51
8. 0.133 < 1.33
9. 1.69401 > 1.694
10. 14.9 < 14.988
Exercise 2: Scientific Notation
1. 2.5 × 10–3
2. 7.836 × 109
3. 1.0 × 10–6
4. 6.05 × 10–1
5. 3.6 × 108
6. 0.0000000024
7. 130,000,000
8. 0.0408
9. 0.0009
10. 560,000
Exercise 3: Operations with Decimals
1. 30.13
2. 16.31
3. 3.03
4. 8.12
5. 223.40
6. 19.85
7. 1.02
8. 12.70
9. 80.70
10. 0.46
11. 37.50
12. 7.81
13. 31.45
14. 24.01
15. 130.00
16. 50.00
17. 42.80
18. 0.13
19. 1.80
20. 5.02
Chapter 4 Fractions and Operations
Exercise 1: Equivalent Fractions
1. 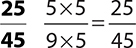
2. 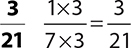
3. 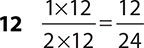
4. 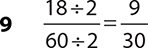
5. 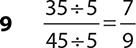
6. 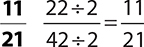
7. 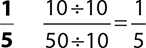
8. 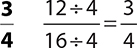
9. 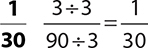
10. 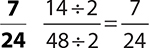
Exercise 2: Converting Between Fractions and Decimals
1. 0.75
2. 0.40
3. 0.25
4. 0.21
5. 0.47
6. 
7. 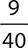
8. 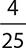
9. 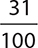
10. 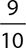
Exercise 3: Mixed Numbers
1. 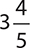
2. 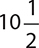
3. 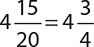
4. 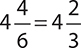
5. 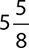
6. 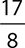
7. 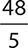
8. 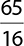
9. 
10. 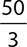
Exercise 4: Comparing Fractions
1. 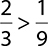
2. 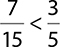
3. 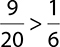
4. 
5. 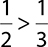
6. 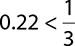
7. 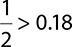
8. 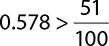
9. 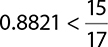
10. 
Exercise 5: Adding and Subtracting Fractions
1. 
2. 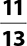
3. 
4. 
5. 
6. 
7. 
8. 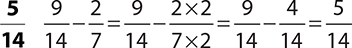
9. 
10. 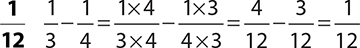
Exercise 6: Multiplying and Dividing Fractions
1. 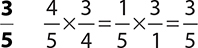
2. 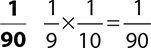
3. 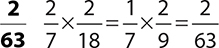
4. 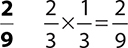
5. 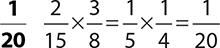
6. 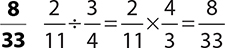
7. 
8. 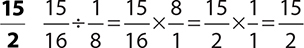
9. 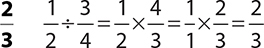
10. 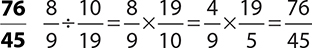
Exercise 7: Operations with Fractions, Whole Numbers, and Mixed Numbers
1. 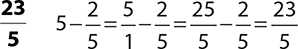
2. 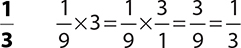
3. 
4. 
5. 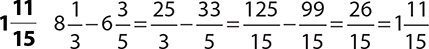
6. 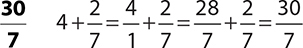
7. 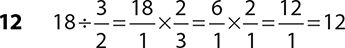
8. 
9. 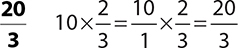
10. 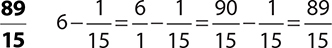
Chapter 5 Ratios, Rates, and Proportions
Exercise 1: Ratios and Rates
1. C
2. A
3. E
4. 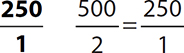
5. 
6. 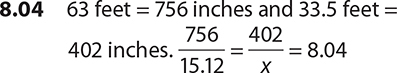
7. 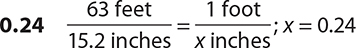
8. 5:6 10:12 = 5:6
9. 
10. 
Exercise 2: Proportions
1. 9 8n = 72 ⇒ n = 72 ÷ 8 = 9
2. 10 15a = 150 ⇒ a = 150 ÷ 15 = 10
3. 16 5x = 80 ⇒ x = 80 ÷ 5 = 16
4. 18 9m = 162 ⇒ m = 162 ÷ 9 = 18
5. 4 8x = 32 ⇒ x = 32 ÷ 8 = 4
Exercise 3: Word Problems with Proportions
1. 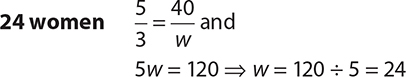
2. 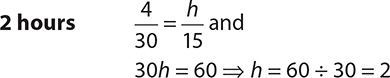
3. 
4. 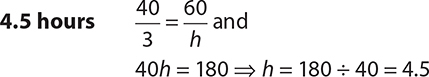
5. 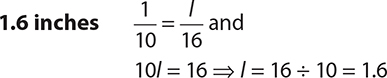
Chapter 6 Percents and Applications
Exercise 1: Converting Between Percents, Decimals, and Fractions
1. 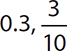
2. 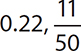
3. 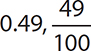
4. 
5. 
6. 4.4%
7. 90%
8. 0.1%
9. 37.5% 100 × (3 ÷ 8) = 37.5
10. 70% 100 × (7 ÷ 10) = 70
Exercise 2: Working with Percents
1. 
2. 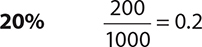
3. 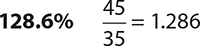
4. 150 0.6 × 250 = 150
5. 0.5 0.03 × 18 = 0.54
6. 0.5 0.005 × 90 = 0.45
7. 72 3.6 × 20 = 72
8. 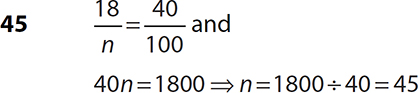
9. 
10. 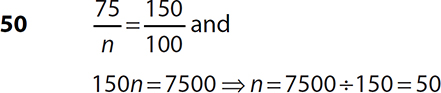
Exercise 3: Word Problems with Percents
1. $4.20 0.03 × 140
2. 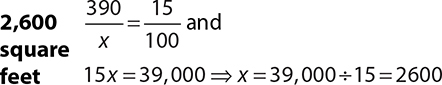
3. $5.82 (0.01 × 580.00) + 0.02 = 5.82
4. 
5. 12 minutos 0.4 × 30 = 12
Exercise 4: Simple Interest
1. 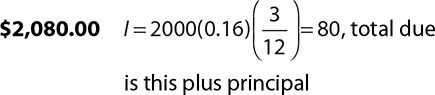
2. 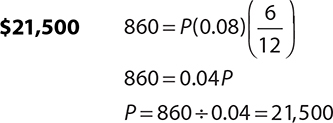
3. $72 I = 900(0.04)(2) = 72
4. 
5. 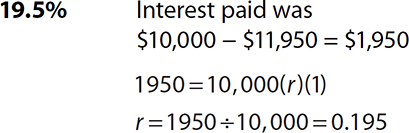
Chapter 7 The Number Line and Negative Numbers
Exercise 1: Adding and Subtracting Negative Numbers
1. 3
2. −6
3. −64
4. −23
5. −12
6. −4
7. 14
8. 5
9. 1
10. −22
Exercise 2: Multiplying and Dividing Negative Numbers
1. −24
2. 25
3. −10
4. −16
5. 18
6. −2
7. 3
8. −4
9. 2
10. −3
Chapter 8 Probability and Counting
Exercise 1: Basic Probability
1. 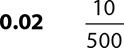
2. 
3. 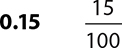
4. 
5. 
Exercise 2: Compound Probability
1. 
2. 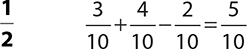
3. 
4. 
5. 
Exercise 3: Combinations
1. 18 3 × 2 × 3
2. 30 10 × 3
3. 
4. 48 8 × 6
5. 288 3 × 2 × 2 × 4 × 3 × 2 × 1
Chapter 9 Statistics and Data Analysis
Exercise 1: Analyzing Data Sets
1. 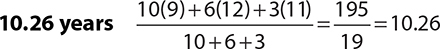
2. 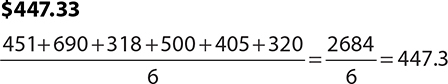
3. 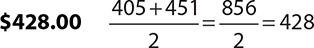
4. $372.00 690 − 318 = 372
5. 
Exercise 2: Bar Charts and Circle Graphs
1. March 80 + 90 = 170
2. 40
3. April
4. 135 70 + 65 = 135
5. February This month had the biggest height difference between the bars.
6. 324 0.18(1800) = 324
7. Senior Associate I
8. 900 0.5(1800) = 900
9. 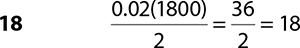 .
.
10. 
Exercise 3: Histograms and Dot Plots
1. 15 total number of dots
2. 3
3. 7
4. Group 1
5. 60
6. 25% Based on the plot, 60 is the third quartile.
7. 32 2 + 6 + 8 + 10 + 6
8. 26 2 + 6 + 8 + 10
9. 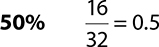
10. 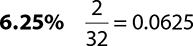
Exercise 4: Relationships Between Data Sets
1. 40 miles 50 – 10 = 40
2. 3, 4, 5, and 6
3. 4400 calories 40 miles × 110 calories per mile = 4400
4. 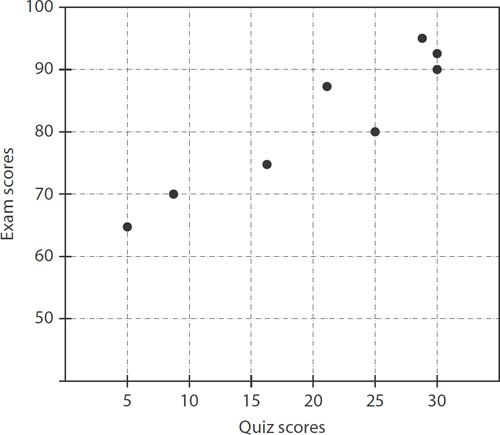
5. B The general trend is positive.
Chapter 10 Algebraic Expressions
Exercise 1: Evaluating Expressions
1. −40 5(−6) − 10 = −40
2. −20 16(−1) − 4 = −16 − 4 = −20
3. −9 9(0 − 1) = 9(−1) = −9
4. −29 −2(2)4 + 22 −1 = −2(16)+ 4 −1= −32 + 4 −1= −29
5. 12 32 + 5(3) − 12 = 9 + 15 − 12 = 12
6. 14 2(4 − 5)2 +3(4) = 2(−1)2 + 12 = 2 + 12 = 14
7. −28 −(3)3 − 1 = −(27)−1 = −27−1 = −28
8. −7 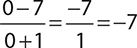
9. −5 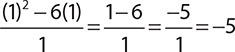
10. 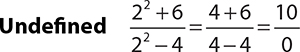
Exercise 2: Combining Like Terms
1. 6x + 10
2. 17y – 4
3. –16z2
4. –x + 4 −2(x −2) + x = −2x + 4 + x
5. 11y4 + 5 16y4 + 5(1 − y4)= 16y4 + 5 − 5y4
Exercise 3: Adding and Subtracting Polynomials
1. 2x2 − 3
2. x5 + 8
3. 2x2 − 7x + 6
4. x4 − x2 + x
5. 13x2 + 7x − 1
6. −14
7. x
8. −3x2 − 5x + 1
9. x2 −15x − 2
10. 4x3 −2x2 −3x
Exercise 4: Multiplying Polynomials (Single Terms)
1. 4x3
2. x6
3. 30x4
4. −3x2
5. 6xy2
Exercise 5: Multiplying Polynomials (Single Terms and Larger Terms)
1. −6x2 −54x
2. 
3. x5 − 5x4 − x6
4. −5x4 −50x2
5. 4x7 − 4x5 + 24x4 − 36x3
Exercise 6: Multiplying Two Binomials
1. x2 + x − 2
2. 5x2 + 23x − 10
3. −8x2 + 10x − 2
4. x4 − 1
5. 2x3 − 9x2 − 12x + 54
Exercise 7: Multiplying Polynomials with More than Two Terms
1. x3 + 2x2 – 14x – 3
x3 + 5x2 + x − 3x2 −15x − 3 = x3 + 2x2 −14x −3
2. –2x3 – 3x2 + 7x + 4
−2x3 −2x2 + 8x − x2 − x + 4 = −2x3 −3x2 + 7x + 4
3. 9x3 + 21x2 – 16x + 6
9x3 − 6x2 + 2x + 27x2 −18x + 6 = 9x3 + 21x2 − 16x + 6
4. x5 – x4 + x3 – x
x5 + x3 + x2 − x4 − x2 − x = x5 − x4 + x3 − x
5. x5 + 2x4 – x3 – 4x2 – 8x + 4
This is the result of distributing both terms. It can’t be simplified further.
Exercise 8: Factoring Using the Greatest Common Factor
1. 3(x2 + 3)
2. 4x2 (x − 4)
3. 9(2x +1)
4. x(x4 − x −2)
5. 2x2 (5x + 7)
Exercise 9: Factoring by Reversing FOIL
1. (x − 3)(x − 4)
2. (x −2)(x + 1)
3. (x − 6)(x + 3)
4. (x −10)(x + 4)
5. (x −2)(x −3)
Exercise 10: Difference of Squares
1. (x + 1)(x − 1)
2. (x + 2)(x − 2)
3. (x + 9)(x − 9)
4. (x + 6)(x − 6)
5. (x + 3)(x − 3)
Exercise 11: Simplifying Rational Expressions
1. 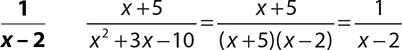
2. 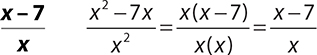
3. 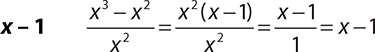
4. 
5. 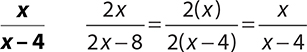
Exercise 12: Adding and Subtracting Rational Expressions
1. 
2. 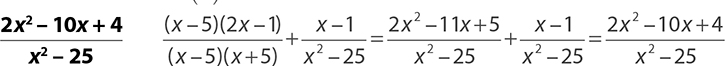
3. 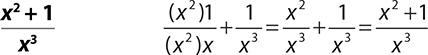
4. 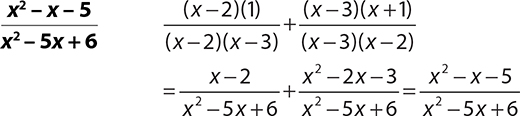
5. 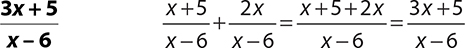
6. 
7. 
8. 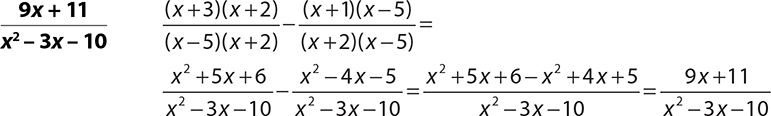
9. 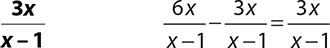
10. 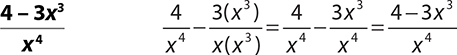
Exercise 13: Multiplying and Dividing Rational Expressions
1. 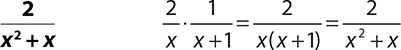
2. 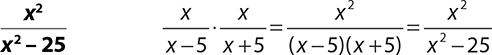
3. 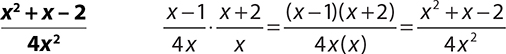
4. 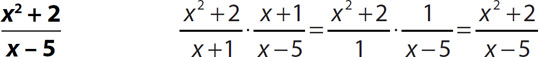
5. 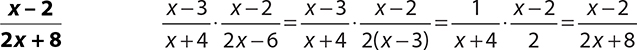
6. 
7. 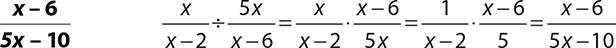
8. 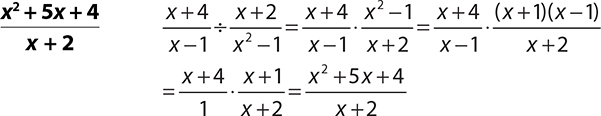
9. 
10. 
Exercise 14: Writing Expressions
1. 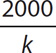
2. x + 505
3. y + 6
4. 0.15m + 30
5. 
Chapter 11 Solving Equations and Inequalities
Exercise 1: One-Step Equations
1. 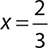
2. x = 5
3. x = 20
4. x = 17
5. x = −4
Exercise 2: Two-Step Equations
1. x = 8
2. x = 12
3. x = 4
4. x = −16
5. 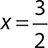
Exercise 3: Multiple-Step Equations
1. 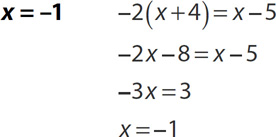
2. 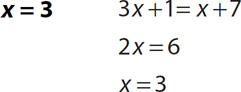
3. 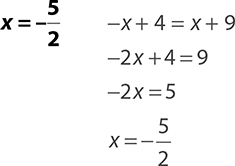
4. 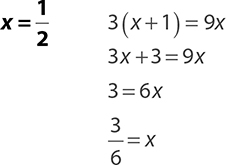
5. 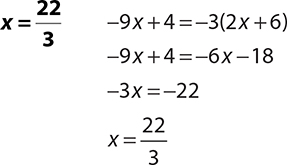
Exercise 4: Solving Inequalities
1. x > 5
2. x < 14
3. x < 6
4. x ≥ 1
5. x ≤ −24
Exercise 5: Writing Linear Equations and Inequalities
1. x = 2y − 3
2. G ≥ 90
3. x > 6 x >(2)(3)
4. m ≥ 305 m≥ 300 + 5
5. w = r − 34
Exercise 6: Word Problems with Equations and Inequalities
1. 120 125 + 0.14m = 141.80
2. −12 x − 10 = 2x + 2
3. 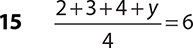
4. 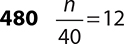
5. 11 6 + 2w = 28
Exercise 7: Solving Systems of Equations
1. x = −1, y = 1
2. x = 4, y = 4
3. x = 0, y = 2
4. x = 1, y = 6
5. x = 2, y = −2
Exercise 8: Word Problems and Systems of Equations
1. 40 n + d = 61
0.05n + 0.10d = 4.10
2. 8 10f + 15a = 260
f + a = 20
3. 20 m + b = 40
1.5m + 2b = 70
4. 5 c + 1.5t = 14
1.5c + 2t = 19.5
5. 10 95g + 12s = 1022
6g + 3s = 78
Exercise 9: Solving Quadratic Equations with the Square Root Rule
1. 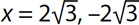
2. x = 9, –9
3. x = 4, –4
4. 
5. x = 0, –4
Exercise 10: Solving Quadratic Equations by Factoring
1. x = 4, –1 (x − 4)(x + 1) = 0
2. x = 2, 3 (x − 2)(x − 3)= 0
3. x = –2, –1 (x + 2)(x + 1) = 0
4. x = 3, 6 x2 − 9x + 18 = (x − 6)(x − 3) = 0
5. x = –4, 1 x2 + 3x − 4 = (x + 4)(x − 1) = 0
Exercise 11: Solving with the Quadratic Formula
1. 
2. 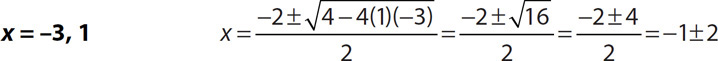
3. 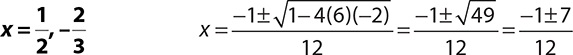
4. 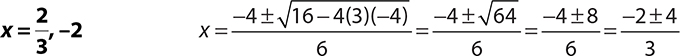
5. 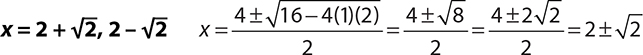
Chapter 12 Graphing Equations
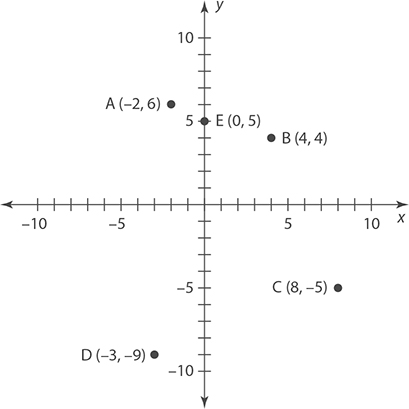
Exercise 1: Plotting Points
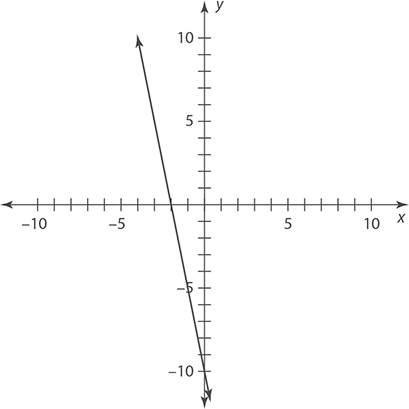
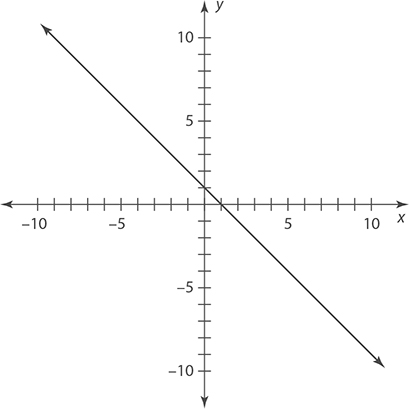
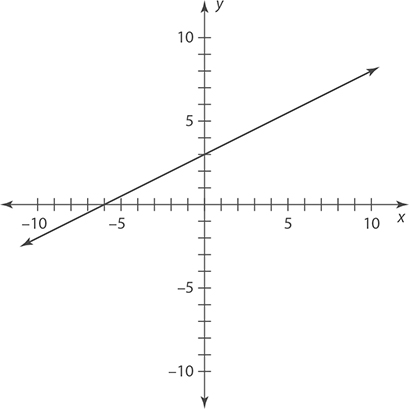
Exercise 2: Graphing Lines
1. 
2. 
3. 
4. 
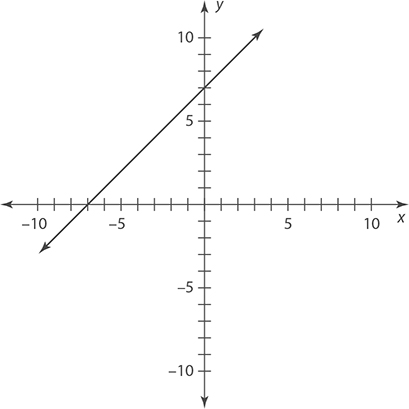
5. 
Exercise 3: Intercepts
1. x intercept  , y intercept −2
, y intercept −2
2. x intercept −5, y intercept 5
3. x intercept  , y intercept −10
, y intercept −10
4. x intercept 5, y intercept −15
5. x intercept 2, y intercept 2
Exercise 4: Slope
1. 
2. 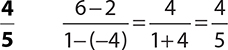
3. 
4. 
5. 
6. 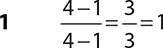
7. 2 y = 2x + 2 and any line parallel will have the same slope.
8. 
9. 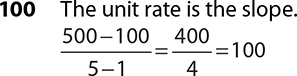
10. Jackson Manufacturing
Jackson Manufacturing is producing 150 per hour based on the slope.
Exercise 5: Finding the Equation of a Line
1. y = −5x + 8
2. 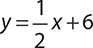
3. y = 2x − 6
4. y = 3x − 1
5. (a) y = 4x + 2
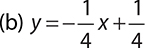
Chapter 13 Functions
Exercise 1: Evaluating Functions
1. 22 5(4) + 2 = 20 + 2 = 22
2. −28 5(−6) + 2 = −30 + 2 = −28
3. 3 2(0)2 − 0 + 3 = 2(0) + 3 = 3
4. 6 2(−1)2 − (−1) + 3 = 2(1) + 1 + 3 = 2 + 1 + 3 = 6
5. 9 2(2)2 − 2 + 3 = 2(4) − 2 + 3 = 8 − 2 + 3 = 9
Exercise 2: Recognizing Functions
1. function
2. not a function
3. function
4. function
5. not a function
Exercise 3: Intercepts
1. x intercept: 2, y intercept: 6
2. x intercept: −1, 5, 10; y intercept: 4
3. x intercept: 0; y intercept: 0
4. x intercept: −5, 1; y intercept: 3
5. x intercept: −2; y intercept: 8
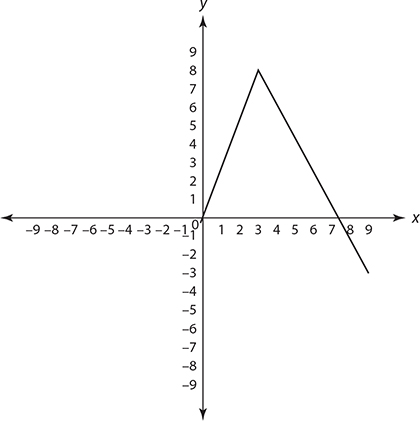
Exercise 4: Other Properties of Functions
1. x smaller than −4, x between −1 and 1, and x larger than 4
2. x between −4 and −1 and x between 1 and 4
3. relative minimums at x = −3 and x = 3
4. relative maximum when x = 0
5. The function is increasing when x is between −3 and 0 and when x is larger than 3.
6. The function is decreasing when x is smaller than −3 and when x is between 0 and 3.
7. As x gets very large, f (x) also gets large.
8. As x gets very negative, f (x) gets very large.
9. 4
10. 
Chapter 14 Geometry
Exercise 1: Area and Perimeter of Polygons
1. 36 feet 9 + 12 + 15
2. Area: 64 square inches 8 × 8
Perimeter: 32 inches 8 + 8 + 8 + 8
3. Area: 32 square meters 16 × 2
Perimeter: 36 meters 16 + 16 + 2 + 2
4. x = 5 8x = 40
5. 12 3x = 36
Exercise 2: Circles
1. 50.3 square feet π42 = 16π
2. 25.1 feet 2π(4) = 8π
3. 125.7 meters radius is 20 m; 2π(20) = 40π
4. 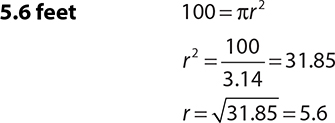
5. 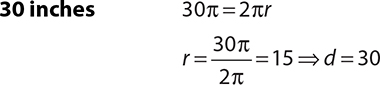
Exercise 3: Volume and Surface Area of 3-Dimensional Objects
1. 
2. 3 feet
SA = 2ab + 2bc + 2ac
216 = 2(6)x + 2x(10) + 2(6)(10)
216 = 12x + 20x + 120
216 = 32x + 120
96 = 32x
x = 3
3. 
4. 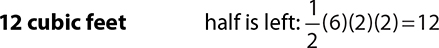
5. 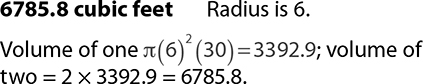
Exercise 4: Complex Figures
1. 1400 meters 300 + 300 + 200 + 100 + 100 + 400
2. 100,000 square meters (300 × 300) + (100 × 100)
3. 100 meters
4. 30 cubic mm (2 × 3 × 2) + (3 × 2 × 3)
5. 62 square mm
Surface Area of smaller rectangular prism: (2 × 3) + 2(2 × 2) + 2(2 × 3) = 26
Surface Area of larger rectangular prism: 2(3 × 2) + (1 × 3) + (3 × 3) + 2 (3 × 2) = 36
Total SA: 26 + 36 = 62
Exercise 5: The Pythagorean Theorem
1. 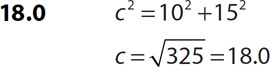
2. 
3. 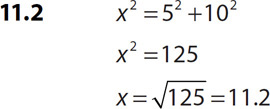
4. 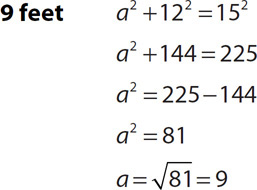
5. 24 To find the perimeter, you must first find the length of the remaining leg.