CHAPTER 3
Decimal Numbers and Operations
Decimals appear in a wide variety of questions on the GED® test either in basic calculations or in word problems, especially those that involve money. In this chapter, you will review how to work with decimals.
Decimals and Place Value
The following chart shows how to refer to each place value in a decimal. Using this table, a number such as 5.38 is read “5 and thirty-eight hundredths,” while 0.237 is read as “two hundred thirty-seven thousandths.” Notice that the place value of the last number determines how it is read.
Rounding Decimals
Often, you will need to be able to round a decimal to a specific place. For example, a GED® test question may say “to the nearest hundredth meter, what is the radius of the circle?” This indicates that the final answer must be rounded to the nearest hundredth.
When rounding decimals, look at the number immediately to the right of the place you are rounding to. If that number is 5 or larger, add 1 to the place you are rounding. If that number is smaller than 5, keep the place the same. Remove all numbers to the right of the place you are rounding to.
EXAMPLE 1
Round 1.09256 to the nearest thousandth.
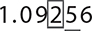
The number in the thousandths place is 2. The number immediately to the right of this number is 5. Therefore, the 2 is rounded up to 3 to get 1.093.
EXAMPLE 2
Round 8.63 to the nearest tenth.
Because the number to the right of the 6 is 3, the 6 stays the same and the final result is 8.6.
Comparing Decimals
Some questions on the GED® test will ask you to determine which decimal in a group or pair is largest or smallest. You may also have to order the decimals from largest to smallest or the other way around. A common mistake is to think that a decimal with more numbers is always the largest. For example, 0.12 is smaller than 0.3.
In order to compare two decimals, it is helpful to rewrite the decimals so that they have the same number of digits. Any zero written on the end of a decimal number does not change its value. 0.3 is the same as 0.30, and that is the same as 0.300.
By rewriting 0.3 as 0.30 and comparing it to 0.12, you can see that 0.12 is smaller because 12 is smaller than 30. This works anytime you are comparing two decimal numbers.
To indicate that one number is larger or smaller than another, mathematics uses the symbols > and <. In each case, the open part of the symbol always points to the larger number. Which one you use just depends on the order in which the numbers are written.
EXAMPLE 3
Use > or < to indicate which number is larger.
0.098 ______ 0.22
Rewriting the decimals so that they each have three digits, you are comparing 0.098 and 0.220. Because 220 is larger than 98, 0.22 must be larger. Using one of the symbols:
0.098 < 0.22.
This is read as “Ninety-eight thousandths is less than twenty-two hundredths.”
EXAMPLE 4
Use > or < to indicate which number is larger.
0.001 ______ 0.0009
Again rewriting, the decimals are 0.0010 and 0.0009, and because 10 is larger than 9:
0.001 > 0.0009
When the open part of the symbol faces left, it is read as “greater than.” Therefore, this statement is read as “one thousandth is greater than nine ten thousandths.”
EXERCISE 1
Comparing Decimals
Directions: Use >, <, or = to compare the given decimals.
1. 25.099 ______ 25.915
2. 0.108 ______ 0.0108
3. 0.00054 ______ 0.0019
4. 8.6 ______ 8.09
5. 0.40 ______ 0.4
6. 0.1053 ______ 0.0153
7. 2.00501 ______ 2.51
8. 0.133 ______ 1.33
9. 1.69401 ______ 1.694
10. 14.9 ______ 14.988
Answers are on page 510.
Scientific Notation
When working with decimals that have a lot of digits, you can write them in a kind of shorthand called scientific notation. Scientific notation is based on the idea that multiplying or dividing a decimal by 10 is the same as moving the decimal point one place.
For example, take the decimal 0.52. If this decimal is multiplied by 10, the result is 5.2. In other words, multiplying by 10 moves the decimal point one place to the right. If 0.52 is divided by 10, the result is 0.052. Here, dividing by 10 moved the decimal point one place to the left.
Dividing by 10 is the same as multiplying by the fraction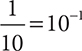 
. This concept is used anytime a decimal is rewritten using scientific notation. In general, numbers written with scientific notation are written as
___ . ___ × 10___,
where the numbers in the blank spaces depend on the original number. The first part of the notation is typically a number between 1 and 10, while the power on the 10 is either positive or negative. The sign indicates whether the decimal is moved left or moved right.
EXAMPLE 5
Write 0.000381 using scientific notation.
Start with the number 3.81 and count how many places you would have to move the decimal point to the left in order to get the original number back. If you count carefully, you will see that you would have to move the decimal point in 3.81 four decimal places to the left. Therefore:
0.000381 = 3.81 × 10–4
EXAMPLE 6
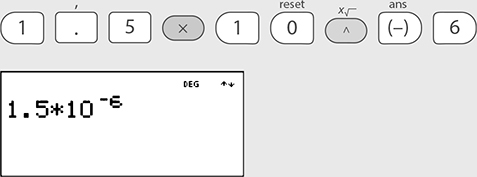
Write 1.9 × 10–6 as a decimal.
Starting with 1.9, move the decimal point 6 places to the left (because the power on 10 is negative 6). Remember to place zeros between the decimal point and the start of the number.
1.9 × 10–6 = 0.0000019
Scientific notation can also be used to represent very large numbers. In this case, the power on the 10 is positive, indicating the decimal is moved to the right. Look at the next two examples.
EXAMPLE 7
Write 19,750,000 using scientific notation.
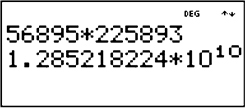
As before, start with a number smaller than 10. In this case, that would be 1.975. How many places to the right would you have to move the decimal point in order to get the original number? The answer is 7, so 19,750,000 = 1.975 × 107.
EXAMPLE 8
What number is represented by 9.6 × 104 ?
Because the power on the 10 is a positive 4, move the decimal point four places to the right.
9.6 × 104 = 96,000
Scientific Notation on the Calculator
When you are working with very large numbers or very small numbers, your calculator may give you the final answer in scientific notation. As an example, the following is the output when multiplying 56,895 by 225,893.
Now that you know how scientific notation works, you could easily convert this to a whole number if you needed to for a final answer.
There may be times where you want to enter a number in the calculator using scientific notation. Luckily, it can be entered just as it looks—like a multiplication problem. If you don’t remember how to enter exponents, you can find those instructions on page 333.
The following shows how 1.5 × 106 is entered.
Notice that the (−) key was pressed and not the subtraction key! Pressing the subtraction key will result in an error.
EXERCISE 2
Scientific Notation
Directions: Write each of the following numbers in scientific notation.
1. 0.0025
2. 7,836,000,000
3. 0.000001
4. 0.605
5. 360,000,000
Write the number represented by each of the following.
6. 2.4 × 10–9
7. 1.3 × 108
8. 4.08 × 10–2
9. 9.0 × 10–4
10. 5.6 × 105
Answers are on page 511.
Adding and Subtracting Decimals
Adding and subtracting decimals works the same way as adding and subtracting whole numbers. You still line up the numbers by place value (which here means making sure the decimal points line up), and when necessary, you carry numbers when adding and regroup numbers when subtracting. Just remember to add zeros to the end of any decimals that have fewer digits than the others.
EXAMPLE 9
Find the sum of 8.1, 0.026, 30, and 0.45.
EXAMPLE 10
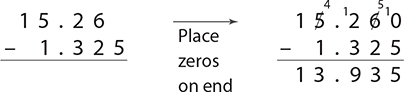
Subtract: 15.26 − 1.325.
Multiplying Decimals
When multiplying decimals, you do not need to line up the numbers by place value. Instead, you multiply as if the two numbers were whole numbers and then count the number of digits to the right of the decimal point (“decimal digits”) in both numbers to determine the number of decimal digits in the final answer.
EXAMPLE 11
Multiply 5.18 and 0.2.
EXAMPLE 12
Multiply 0.0062 and 0.099.
In example 12, notice that the final answer needs to have 7 decimal digits but there are only 4 digits left after multiplying. In situations like this, add zeros at the beginning of the number until there are enough decimal digits.
Dividing Decimals
When dividing decimals, there are three possibilities: you may be dividing a decimal by a whole number, a whole number by a decimal, or a decimal by a decimal. For each of these, the process is slightly different. While that may sound complicated, the steps are actually all very similar.
Dividing a Decimal by a Whole Number
When dividing a decimal by a whole number, the process is exactly the same as when you divide a whole number by another whole number. As you compute your answer, make sure that the decimal point in the answer is directly above the decimal point in the number you are dividing.
EXAMPLE 13
Divide: 12.56 ÷ 4.
Dividing a Whole Number by a Decimal
When dividing a whole number by a decimal, the process is a little different. First, rewrite the decimal as a whole number. Do this by moving the decimal point to the right. Then, in the whole number, move the decimal point (which is understood to be located after the last digit) the same number of places to the right. Fill up the empty places with zeros. Then divide. Again, make sure that the decimal point in the answer is directly above the decimal point in the number you are dividing.
EXAMPLE 14
Divide: 18 ÷ 1.4.
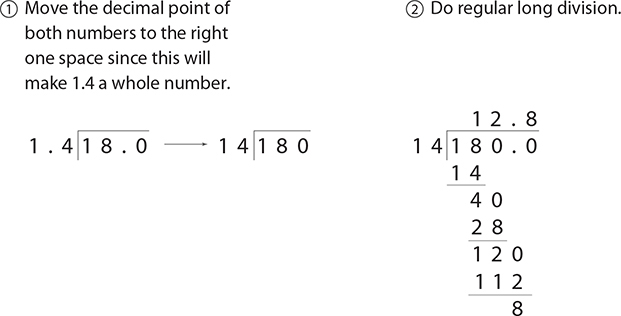
Notice in the division that a zero is added after the decimal point in 180. Adding a decimal point with zeros after it doesn’t change the number (180 is the same as 180.0), but it gives you “room” to finish the division, just as you did in Chapter 1. You can keep adding zeros after the decimal point to get a more and more accurate answer. For example, suppose for the problem in example 14 you are asked for an answer to the nearest thousandths place. You can do this by adding two more zeros on the end of 180.0 and continuing with the division.
Dividing a Decimal by a Decimal
To divide a decimal by a decimal, the process is nearly the same. In the decimal by which you are dividing, move the decimal point to the right until you have a whole number. Then, in the decimal that is being divided, move the decimal point the same number of places to the right. Then divide, remembering to place the decimal point in the answer directly above the decimal point in the decimal that is being divided.
EXAMPLE 15
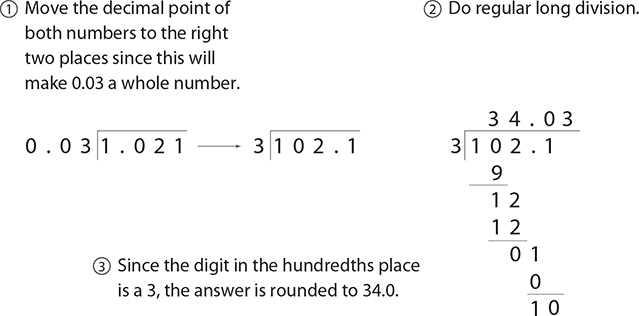
Divide: 1.021 ÷ 0.03. Round your answer to the nearest tenth.
Finally, you may need to deal with decimals even when you are dividing two whole numbers. Consider 4 divided by 5. Since 5 is larger than 4, the final answer will have to be smaller than 1, but how would you use division here?
The key is to add a decimal point and zeros to the end of the 4. Remember that adding zeros after a decimal point does not change the value of the number.
EXAMPLE 16
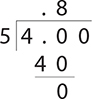
Divide: 4 ÷ 5.
Later, this method will be used to convert fractions to decimals.
EXERCISE 3
Operations with Decimals
Directions: Perform each of the following calculations by hand and then check your final answer using your calculator. Round your answer to the nearest hundredth.
1. 18.03 + 12.1 + 0.0036
2. 15.4295 + 0.8826
3. 0.029 + 0.0041 + 3
4. 8.11 + 0.011
5. 16.5 + 206.9
6. 20 − 0.15
7. 1.023 − 0.0014
8. 15.6 − 2.9
9. 230.8 − 150.1
10. 0.554 − 0.099
11. 25 × 1.5
12. 1.22 × 6.4
13. 18.5 × 1.7
14. 2.63 × 9.13
15. 5.0001 × 26
16. 15 ÷ 0.3
17. 2.14 ÷ 0.05
18. 2 ÷ 16
19. 7.016 ÷ 3.9
20. 50.22 ÷ 10
Answers are on page 511.