CHAPTER 7
The Number Line and Negative Numbers
So far, you have seen how to work with positive whole numbers, fractions, and decimals. In this chapter, you will see how to work with negative numbers. Any of the number types you have worked with so far can be negative as well as positive. Whether a fraction or a whole number is negative or positive, its basic properties stay the same.
The Number Line
One common way to picture the set of all possible numbers is the number line. The number line includes all negative and positive numbers in order from left to right. This means that every number on the line is greater than the number to its left but smaller than the number to its right. You can imagine that in between any two whole numbers are all the fractions and decimals that have values that are between those two numbers.
EXAMPLE 1
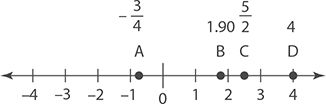
The following figure shows four numbers marked on the number line: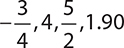 
. Determine which of these numbers is represented by the letter B.
Point B appears to be slightly to the left of the line marking 2. Therefore, it must be slightly smaller than 2. Therefore, point B must represent 1.90.
Just as an exercise in ordering numbers (which the GED® may ask you to do), let’s figure out the values of the other points. If you convert any fractions to decimals, then you can easily see which is larger and which is smaller.
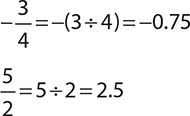
Looking at the number line, point A is slightly to the right of −1. This means that point A is slightly greater than −1. Another way to think about this is that point A is slightly less negative than −1. The only value you have that makes sense for this is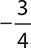 
.
Point C is halfway between 2 and 3, so it must be greater than 2 but smaller than 3. The only candidate is 2.5.
Finally, point D is right on the line for 4, so its value is 4. The figure below shows what you just found.
Absolute Value
The absolute value of a number represents its distance from 0 on the number line. Based on this definition, the points 3 and −3 are both 3 units away from 0, so each one has an absolute value of 3. In fact, for any number, positive or negative, the absolute value is the positive value of that number.
The symbol for absolute value is two bars. For example, the absolute value of −5 is written as |−5| while the absolute value of 10 is written as |10|.
EXAMPLE 2
Find the absolute value of the following numbers: −15, 12, −2, and 1.
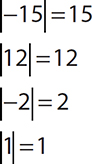
EXAMPLE 3
Which of the following points has the greatest absolute value?
The correct answer is point A. Remember that absolute value is the distance from 0, and point A is the farthest from 0. Therefore, it has the greatest absolute value.
Adding and Subtracting Negative Numbers
When adding and subtracting negative and positive numbers, different rules apply depending on whether or not the numbers share the same sign.
• To add a negative and a positive number, find their absolute values, and then subtract the smaller from the greater one. Your answer will have the same sign as the number with the greater absolute value.
(−8) + (+3) = −5
The absolute values are 8 and 3. Subtract 8 − 3. The answer is −5 because −8 has the greater absolute value.
• To add two negative numbers, add their absolute values, and then put a minus sign in front of the total.
(−3) + (−8) = −11
The absolute values are 3 and 8. Add: 3 + 8. The answer is −11 because both numbers added are negative.
• To subtract a negative number from a positive number, add their absolute values, and then put a positive sign in front of the total.
5 − (−3) = 5 + (+3) = 8
The absolute values are 5 and 3. Add: 5 + 3 = 8. The answer is +8 (positive).
• To subtract a positive number from a negative number, add their absolute values, and then put a minus sign in front of the total.
(−5) − (+3) = 5 + 3 = −8
The absolute values are 5 and 3. Add: 5 + 3 = 8. The answer is −8 (negative).
• To subtract one negative number from another, reverse the sign on the second number, and then add.
(−3) − (−8) = (−3) + (+8) = 5
EXERCISE 1
Adding and Subtracting Negative Numbers
Directions: Perform the indicated operation.
1. 5 + (−2)
2. 19 − 25
3. −44 + (−20)
4. −18 − 5
5. (−10) + (−2)
6. 4 − 8
7. −15 + 29
8. 6 + (−1)
9. −2 + 3
10. −8 − 14
Answers are on page 515.
Multiplying and Dividing Negative Numbers
When multiplying and dividing signed numbers, follow these rules:
• Opposite signs result in a negative answer.
• Same signs result in a positive answer.
In multiplication and division, the sizes of the numbers have nothing to do with the sign of the answer. The sign of the answer depends only on the signs of the numbers that are being multiplied or divided.
EXAMPLE 4
EXAMPLE 5
EXERCISE 2
Multiplying and Dividing Negative Numbers
Directions: Perform the indicated operation.
1. 6 × (−4)
2. (−5) × (−5)
3. (−1) × 10
4. 8 × (−2)
5. (−6) × (−3)
6. –6 ÷ 3
7. –3 ÷ (–1)
8. 16 ÷ (–4)
9. –14 ÷ (–7)
10. 9 ÷ (–3)
Negative Numbers on the Calculator
Any of the operations done in this chapter can also be done on the calculator. When entering negative numbers, make sure to use the (−) key instead of the subtraction key. For example, to find −5 + 26, you would type:
