CHAPTER 4
Fractions and Operations
Fractions are a way of representing a “part” of some larger “whole” when the whole has been divided into an equal number of parts.
• The top of a fraction (the number above the bar) is called the numerator. It represents the number of parts “taken out” of the whole.
• The bottom part of a fraction (the number below the bar) is called the denominator. It represents the number of equal parts in the whole.
For example, the fraction  represents 3 parts out of a whole that has been divided into 5 equal parts. The numerator is 3 and the denominator is 5.
represents 3 parts out of a whole that has been divided into 5 equal parts. The numerator is 3 and the denominator is 5.

Equivalent Fractions
Two different fractions can represent the same part of a whole. For example, in the following figures, you can see that  . These are called equivalent fractions.
. These are called equivalent fractions.
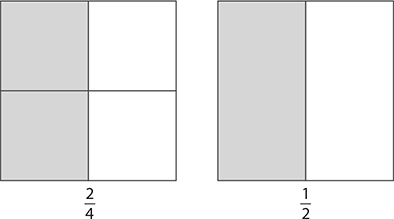
If the numerator and denominator of any fraction are multiplied or divided by the same number, the result will be an equivalent fraction. For example, if you divide the numerator and denominator of  each by 2, the result will be the equivalent fraction
each by 2, the result will be the equivalent fraction  .
.
EXAMPLE 1
Write a fraction that is equivalent to  but has a denominator of 12.
but has a denominator of 12.
The denominator of  is 4. Multiplying 4 by 3 will give a denominator of 12, but to produce an equivalent fraction, the numerator must be multiplied by the same number. Therefore,
is 4. Multiplying 4 by 3 will give a denominator of 12, but to produce an equivalent fraction, the numerator must be multiplied by the same number. Therefore,  .
.
EXAMPLE 2
What number should replace the question mark? 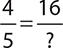
To get from 4 to 16, the numerator must have been multiplied by 4. Therefore to make an equivalent fraction, the denominator must be multiplied by 4 as well: 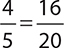 . These are equivalent fractions.
. These are equivalent fractions.
Reducing Fractions to Lowest Terms
Fractions are said to be reduced, or written in lowest terms, if there is no whole number that will evenly divide both the numerator and the denominator. Examples of fractions written in lowest terms are 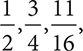 , and
, and  .
.
For most questions on the GED® test involving fractions, you will be expected to reduce fractions to lowest terms. To reduce fractions, see if there is any whole number that evenly divides both the numerator and the denominator, and then divide it out.
EXAMPLE 3
Write the fraction 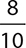 in lowest terms.
in lowest terms.
Because 8 and 10 are even numbers, both can be divided by 2.
Therefore, 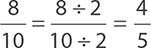 . You know the fraction
. You know the fraction  is in lowest terms because there is no whole number other than 1 that will divide both 4
is in lowest terms because there is no whole number other than 1 that will divide both 4
and 5 evenly.
EXAMPLE 4
Write the fraction  in lowest terms.
in lowest terms.
The numerator 27 is the same as 9 × 3 and the denominator is 9 × 9 = 81. This means that the numerator and the denominator can each be divided by 9.

In  , however, the numerator and the denominator can each be divided by 3. This means that the fraction is not yet reduced to lowest terms.
, however, the numerator and the denominator can each be divided by 3. This means that the fraction is not yet reduced to lowest terms.

 reduced to lowest terms is
reduced to lowest terms is  .
.
EXERCISE 1
Equivalent Fractions
Directions: For each of the following, write an equivalent fraction as indicated by either dividing or multiplying the numerator and the denominator by the same number.
1. Write a fraction that is equivalent to  but has a denominator of 45.
but has a denominator of 45.
2. Write a fraction that is equivalent to  but has a denominator of 21.
but has a denominator of 21.
3. What number should replace the question mark: 
4. What number should replace the question mark: 
5. What number should replace the question mark: 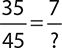
Write each of the following fractions in lowest terms. Check your answer using your calculator.
6. 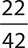
7. 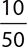
8. 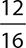
9. 
10. 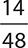
Answers are on page 511.
Fractions and Decimals
Fractions and decimals can represent the same number. By dividing the numerator by the denominator, you can see what number or decimal is equivalent to the fraction.
EXAMPLE 5
Find the decimal that represents  .
.
Because 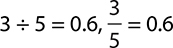 .
.
EXAMPLE 6
Find the decimal that represents 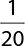 .
.
1 ÷ 20 = 0.05. Therefore, 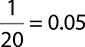 .
.
Decimals can be converted to fractions by using their place value and numbers like 10, 100, 1000, and 10,000. The place value tells you which number to use.
EXAMPLE 7
Write 0.05 as a fraction in lowest terms.
You read this decimal as “five hundredths” because the 5 is in the hundredths place. The equivalent fraction is  , which can be reduced to
, which can be reduced to  .
.
EXAMPLE 8
Write 0.480 as a fraction in lowest terms.
You read this decimal as “four hundred eighty thousandths.” As before, use the place value to write the equivalent fraction, and then reduce.
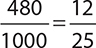
EXERCISE 2
Converting Between Fractions and Decimals
Directions: For each of the following fractions, find the equivalent decimal. Round your answer to the nearest hundredths place.
1. 
2. 
3. 
4. 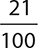
5. 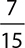
For each of the following decimal numbers, find an equivalent fraction and write it in lowest terms.
6. 0.028
7. 0.225
8. 0.16
9. 0.31
10. 0.90
Answers are on page 512.
Improper Fractions and Mixed Numbers
In the fraction  the numerator is greater than the denominator. A fraction of this kind is called an improper fraction. The decimal equivalent of
the numerator is greater than the denominator. A fraction of this kind is called an improper fraction. The decimal equivalent of  is 2.5, which is greater than 1. Improper fractions will always have decimal equivalents that are greater than 1.
is 2.5, which is greater than 1. Improper fractions will always have decimal equivalents that are greater than 1.
Another way to represent an improper fraction like  is as a mixed number. Mixed numbers show the whole number part of the fraction and the fractional part separately. For example,
is as a mixed number. Mixed numbers show the whole number part of the fraction and the fractional part separately. For example,  becomes
becomes 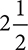 when written as a mixed number.
when written as a mixed number.
To write an improper fraction as a mixed number, determine how many times the denominator can divide the numerator evenly. Then, write any remaining part as a fraction with the original denominator.
EXAMPLE 9
Write 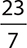 as a mixed number.
as a mixed number.
The denominator 7 can divide the numerator 3 times with 2 left over. Therefore, 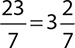 .
.
EXAMPLE 10
Write 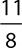 as a mixed number.
as a mixed number.
The denominator 8 can divide 11 once with 3 left over: 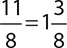 .
.
Converting from a mixed number back to an improper fraction is a quick process illustrated in the following examples.
EXAMPLE 11
Write 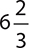 as an improper fraction.
as an improper fraction.
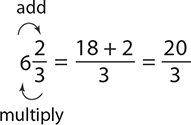
EXAMPLE 12
Write 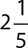 as an improper fraction.
as an improper fraction.
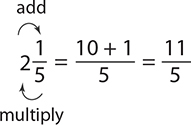
EXERCISE 3
Mixed Numbers
Directions: Rewrite each of the following improper fractions as mixed numbers and check your answer with your calculator.
1. 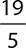
2. 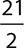
3. 
4. 
5. 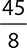
Rewrite each of the following mixed numbers as improper fractions and check your answers with your calculator.
6. 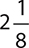
7. 
8. 
9. 
10. 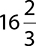
Answers are on page 512.
Comparing Fractions
Ordering fractions from greatest to smallest or smallest to greatest is a skill that is commonly tested on the GED® test. To order fractions correctly, you need to be able to compare fractions with each other.
Suppose you want to determine which is larger, 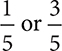 . Remember that fractions represent parts of a whole. In that case,
. Remember that fractions represent parts of a whole. In that case,  must be larger because 3 is more “parts” than 1 (
must be larger because 3 is more “parts” than 1 ( has a larger numerator than
has a larger numerator than  ). This works because both fractions have a denominator of 5.
). This works because both fractions have a denominator of 5.
To compare fractions with different denominators, such as  , you will need to find equivalent fractions with a common denominator. A common denominator is one number that can be used as a denominator for both equivalent fractions. The easiest to use is the least common multiple of both denominators (the smallest multiple they have in common).
, you will need to find equivalent fractions with a common denominator. A common denominator is one number that can be used as a denominator for both equivalent fractions. The easiest to use is the least common multiple of both denominators (the smallest multiple they have in common).
For example,  can each be written as equivalent fractions with a denominator of 14:
can each be written as equivalent fractions with a denominator of 14:  . Now you can compare the two fractions and see that
. Now you can compare the two fractions and see that  is the greater fraction.
is the greater fraction.
To find a common denominator for two different fractions, follow these steps:
• Determine if one of the denominators can be divided by the other. If so, this larger denominator is a common denominator.
• Otherwise, multiply the two denominators and use the result as a common denominator.
The following examples use the same symbols that were used when comparing decimals.
EXAMPLE 13
Use <, >, or = to compare the fractions:  .
.
Looking at the denominators, 8 can be divided by 4, so 8 is the common denominator. Rewrite  using this denominator.
using this denominator.

Because the numerator of  is greater than the numerator of
is greater than the numerator of  , it is the greater fraction. Therefore,
, it is the greater fraction. Therefore, 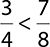 .
.
EXAMPLE 14
Use <, >, or = to compare the fractions:  .
.
Neither denominator can be divided by the other, so the common denominator is their product: 5 × 9 = 45. Both fractions have to be rewritten using this denominator.
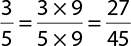

Because 27 is less than 40,  .
.
Comparing Fractions and Decimals
As shown in the preceding section, rewriting two fractions with a common denominator makes it easier to compare them. The same idea applies when comparing fractions and decimals. Because every fraction can be written as a decimal, converting the fraction to a decimal lets you compare the two numbers on the same footing.
EXAMPLE 15
Fill in the blank with <, >, or = to make a true statement:  _______ 0.455.
_______ 0.455.
Written as a decimal, 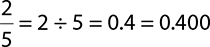 . This decimal is smaller than 0.455, so
. This decimal is smaller than 0.455, so 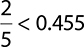 .
.
EXAMPLE 16
Fill in the blank with <, >, or = to make a true statement: 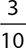 _______ 0.29.
_______ 0.29.
Because 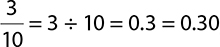 , and 0.30 is greater than 0.29:
, and 0.30 is greater than 0.29:  .
.
EXERCISE 4
Comparing Fractions
Directions: Use >, <, or = to compare the given fractions.
1. 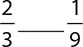
2. 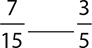
3. 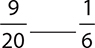
4. 
5. 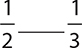
Use >, <, or = to compare the given fractions and decimals.
6. 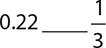
7. 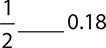
8. 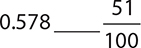
9. 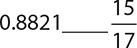
10. 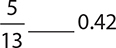
Answers are on page 512.
Adding and Subtracting Fractions
The rules for adding and subtracting fractions depend on whether or not the fractions share the same denominator. When the fractions share the same denominator, you will just add or subtract the numerators from left to right. When they do not, you must find a common denominator before doing anything else.
EXAMPLE 17
Find the sum:  . Write your answer in lowest terms.
. Write your answer in lowest terms.
The fractions have the same denominator, so the sum is found by just adding the numerators.
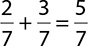
EXAMPLE 18
Find the difference: 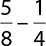 . Write your answer in lowest terms.
. Write your answer in lowest terms.
Because these fractions do not have the same denominator, use the techniques to find a common denominator. The denominator 8 can be divided by 4, so 8 is the common denominator. Once both fractions are rewritten with that denominator, you can subtract the numerators in the same way as you added in example 17. To rewrite  , the numerator and the denominator must be multiplied by 2.
, the numerator and the denominator must be multiplied by 2.

EXAMPLE 19
Find the sum:  . Write your answer in lowest terms.
. Write your answer in lowest terms.
Neither denominator will divide the other, but a common denominator is 6 × 10 = 60. Both fractions must be rewritten before they can be added.

The answer 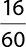 is not written in lowest terms, because 16 and 60
is not written in lowest terms, because 16 and 60
can each be divided evenly by 4. To reduce the fraction, divide the numerator and denominator each by 4 to reach your final answer.
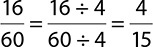
You could also use a common denominator of 30. In that case, you would have

Then reduce  .
.
EXERCISE 5
Adding and Subtracting Fractions
Directions: Calculate the indicated sums or differences and write your final answer in lowest terms.
1. 
2. 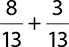
3. 
4. 
5. 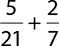
6. 
7. 
8. 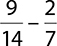
9. 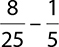
10. 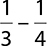
Multiplying Fractions
When multiplying two fractions, you do not need to worry about common denominators. Whether or not the two fractions have the same denominator, the process is always the same: multiply the numerators and multiply the denominators. In fact, by cross canceling, you can reduce the fraction before you even multiply!
EXAMPLE 20
Multiply:  .
.

EXAMPLE 21
Multiply:  .
.

Dividing Fractions
When dividing fractions, simply “flip and multiply.” This works because multiplication and division are closely related. Any division problem can be written as a multiplication problem. For example, multiplying by  is the same as dividing by 3. When a fraction is “flipped,” the resulting fraction is called its reciprocal. The numbers 3 and
is the same as dividing by 3. When a fraction is “flipped,” the resulting fraction is called its reciprocal. The numbers 3 and  are reciprocals, as are
are reciprocals, as are  . When you “flip and multiply,” you are actually just rewriting the division as multiplication by the reciprocal.
. When you “flip and multiply,” you are actually just rewriting the division as multiplication by the reciprocal.
EXAMPLE 22
Divide: 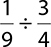 .
.
The first fraction stays the same, but the second fraction is flipped. Then you multiply instead of divide.

Note that you cannot cross cancel until you reach the multiplication step!
EXAMPLE 23
Divide:  .
.
Keep the first fraction the same and multiply by the reciprocal of the second.
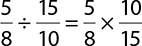
It is now possible to cross cancel before multiplying to find the final answer.
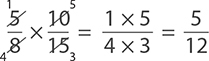
EXERCISE 6
Multiplying and Dividing Fractions
Directions: Multiply or divide the following fractions as indicated. Write your answer in lowest terms.
1. 
2. 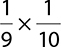
3. 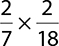
4. 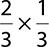
5. 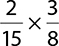
6. 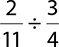
7. 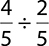
8. 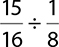
9. 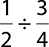
10. 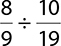
Answers are on page 513.
Operations with Fractions, Whole Numbers, and Mixed Numbers
Sometimes you may need to add or subtract two mixed numbers, divide a whole number by a fraction, or multiply a mixed number by a whole number. In these cases, the following facts can help you with your calculations:
• The reciprocal of any whole number is a fraction with 1 in the numerator and the whole number in the denominator. The following pairs are all reciprocals:  and 5, 9 and
and 5, 9 and  and 2.
and 2.
• Mixed numbers can always be converted to improper fractions. Once converted, the regular rules of operations with fractions apply.
• Any fraction with the same number in the numerator and the denominator equals 1. (This rule does not apply if the number is zero.) All of the following are equal to 1:  .
.
• Any whole number can be rewritten as a fraction with a denominator of 1. For example, 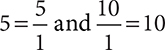 .
.
Let’s see how these facts can help with a few examples.
EXAMPLE 24
Divide: 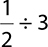 .
.
Use the “flip and multiply” technique. Remember that the reciprocal of 3 is  :
:

EXAMPLE 25
Multiply: 10 × 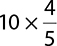 .
.
Rewrite 10 as a fraction with a denominator of 1. Then multiply as you would with any other fractions (including cross canceling).

EXAMPLE 26
Add: 2 .
.
First, convert  to an improper fraction. Then you can add fractions as usual. Remember that you need like denominators when adding and subtracting fractions.
to an improper fraction. Then you can add fractions as usual. Remember that you need like denominators when adding and subtracting fractions.
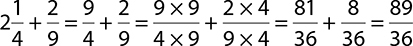
How you format your final answer depends on the question being asked. When working with mixed numbers, you usually will need to write your final answer as a mixed number. In this example, the final answer would be:
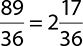
EXERCISE 7
Operations with Fractions, Whole Numbers, and Mixed Numbers
Directions: Find the sum, difference, product, or quotient as indicated. If the original problem contains a mixed number, write your final answer as a mixed number. Otherwise, write your final answer in lowest terms.
1. 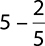
2. 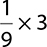
3. 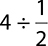
4. 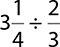
5. 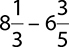
6. 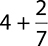
7. 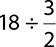
8. 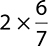
9. 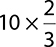
10. 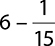
Answers are on page 513.
 key. Press this key before entering your fraction, and then press the ENTER key to reduce the fraction to lowest terms.
key. Press this key before entering your fraction, and then press the ENTER key to reduce the fraction to lowest terms.
 button, so the 2nd key must be pressed to access it. The following steps show how to use this with the previous example of 0.480.
button, so the 2nd key must be pressed to access it. The following steps show how to use this with the previous example of 0.480.
 key. Just above this key is the mixed numbers function. By pressing the 2nd key followed by the
key. Just above this key is the mixed numbers function. By pressing the 2nd key followed by the  to an improper fraction.
to an improper fraction.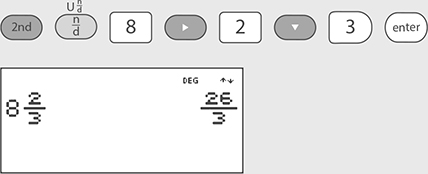
 function located above the
function located above the  key can be used to convert between improper fractions and whole numbers. Here is an example converting
key can be used to convert between improper fractions and whole numbers. Here is an example converting  to a mixed number.
to a mixed number.
 key and that mixed numbers can be entered using the
key and that mixed numbers can be entered using the 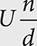 function (see the mixed numbers section for more details).
function (see the mixed numbers section for more details). .
.