CHAPTER 8
Probability and Counting
Finding probabilities is all about determining the likelihood or the chances of some event occurring. You are already familiar with some types of probability. For example, you know that a 10% chance of rain today means that it probably will not rain, while a 90% chance means that it probably will. In this chapter, you will learn how to calculate some simple probabilities.
Basic Probability
When working with probabilities, think in terms of experiments. A probability experiment is just a situation that has some type of result. When a 6-sided die is rolled, that is an experiment. If someone tries to guess a whole number between 1 and 10, that is also an experiment.
In probability, all of the possibilities of an experiment are called outcomes. In the experiment where someone guesses a whole number between 1 and 10, one possible outcome is 2. Because someone could guess any one of the whole numbers between 1 and 10, there are ten possible outcomes.
A question might ask for the probability that someone guesses a number “greater than 6.” In probability, this is called an event. An event is a grouping of one or more outcomes that you might be interested in. For example, the outcomes that make up the event “greater than 6” are 7, 8, 9, and 10.
The following formula is used to find the probability that an event will occur:
Using this formula, the probability that someone will guess a number greater than 6 is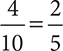 
. In the experiment, there are a total of 10 possible numbers to guess, and 4 of them are larger than 6.
Let’s review some important rules about probabilities:
• A probability can never be smaller than 0 or larger than 1 (smaller than 0% or larger than 100%).
• Probabilities can be represented as fractions, decimals, or percents.
EXAMPLE 1
The accounting department of a large firm has 45 male employees and 100 female employees. If one of the employees is randomly selected to be in charge of refilling the copier, what is the probability that the chosen person is male? Write your answer as a whole number percent.
The specified event is that a randomly selected person from this group will be a male. There are 45 male employees, so 45 possibilities that this could happen. There are a total of 45 + 100 = 145 employees in the department. Because each employee has an equal chance of being picked, this represents all of the possible outcomes. Therefore, the probability is:
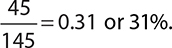
EXAMPLE 2
A single fair, six-sided die is rolled. What is the probability that it will land on a number smaller than 3? Write your answer as a reduced fraction.
There are a total of 6 possibilities when rolling the die and only 2 (the numbers 1 and 2) are smaller than 3, so the probability is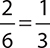 
.
EXERCISE 1
Basic Probability
Directions: Answer each of the following questions. Write your answer as a decimal rounded to the nearest hundredths place.
1. A shipment of 500 computer monitors is known to have 10 defective monitors. If one of the monitors is selected randomly, what is the probability that the selected monitor is defective?
2. A high school club has 10 members who are seniors and 8 members who are juniors. If a member is randomly selected to be the club president, what is the probability that the person will NOT be a senior?
3. A game is played in which a card is drawn from a special deck that contains red, green, and blue cards. If a blue card is drawn, the player can advance to the next level. The deck has 100 cards, of which 30 are red, 15 are blue, and 55 are green. If a player draws a card at random, what is the probability that the player will advance to the next level?
4. Beth is trying to guess the number that her friend Harry is thinking. All she knows is that the number is between 1 and 20 (including 1 and 20). If she guesses randomly, what is the probability that she will guess the right number?
5. A drawer contains 6 spoons and 3 forks. If someone picks one utensil out of the drawer without looking, what is the probability of picking a spoon?
Answers are on page 516.
Compound Probabilities
“And” Events
When two events occur at the same time or one after the other, this is called an “and” event or the intersection of two events. In some cases, the probability of an intersection occurring can be found just by multiplying the probability of the two events. When the first event affects the probability of the second event, a different method is needed. Let’s look at the simple case first.
EXAMPLE 3
In a survey of 1000 people, 450 are currently working full-time, 300 are taking college classes, and 120 are taking college classes and working full-time. If a person from this survey is selected at random, what is the probability that he or she is working full-time and taking college classes?
In this example, you are told that there are 120 people in the group who are taking college classes and working full-time. In other words, you are given the number of outcomes in the event. The same formula can still be used. The probability is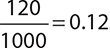 
.
EXAMPLE 4
Suppose that a bag contains 10 red and 12 green marbles. You will randomly select one marble from the bag and then put it back in the bag, and then randomly select a second marble from the bag. What is the probability that your first selection will be a red marble and your second selection will be a green marble?
First, identify the two events that make up the “and” event. The first event is selecting a red marble, and the second event is selecting a green marble. You want to find the probability of selecting a red marble, returning it to the bag, and then selecting a green marble. First identify the probability of the first event. Because there are 10 red marbles in the bag and a total of 22 marbles, the probability based on the probability formula would be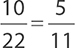 
. The probability of the second event follows the same rule and would be 
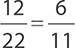. The probability of both events occurring is calculated using the formula:
probability of two independent events = probability of first event × probability of second event
Using this formula, the probability that the first marble selected is red and the second is green is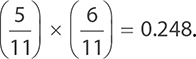 
The more difficult case is when the first event affects the probability of the second event. Suppose that the same bag contains 10 red and 12 green marbles. The experiment is to select two marbles, one at a time, without returning the first selected marble back to the bag. What is the probability that both selected marbles will be green?
Use this formula:
probability of first event × probability of second event after the first has occured
The probability that the first selected marble is green is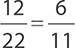
because there are 12 green marbles and 22 total marbles. What is the probability that the second selected marble is green? Because the first marble is no longer in the bag, there are now only 21 marbles in the bag. Also, there are only 11 green marbles in the bag because the first selected marble was a green one. The probability that the second selected marble is green is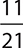 
. Now, using these fractions and the formula, the probability that both selected marbles are green is 
.
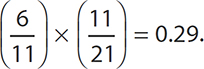EXAMPLE 5
Two employees at a small company are to be randomly selected for a team-building exercise. If there are 20 senior employees and 30 junior employees at the company, what is the probability that both of the selected employees will be senior employees?
Probability that the first employee will be senior is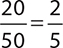 
.
Probability that the second employee will be senior is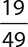 
.
(Remember, one employee has already been selected, and that employee was one of the senior ones.)
Probability that both will be senior is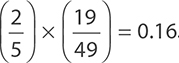 
.
“Or” Probabilities
Finding the probability of one event or the other occurring is not as complicated as the examples you just saw. The basic formula for this type of probability is:
probability of first event + probability of second event – probability of both events
EXAMPLE 6
If a fair, six-sided die is rolled, what is the probability that the number that comes up is greater than 2 or even?
probability of first event (greater than 2): 
(there are 4 numbers greater than 2)
probability of second event (even): 
(there are three even numbers: 2, 4, and 6)
probability of both events: 
(there are two numbers that are both even and greater than 2)
Therefore, the probability of one or the other event is: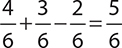 
.
EXERCISE 2
Compound Probability
Directions: Answer each of the following probability questions. Give your answers as fractions in their lowest terms.
1. In a group of 10 third and 8 fourth graders, two students must be randomly selected to be the leaders for the day. If the first student selected is a fourth grader, what is the probability that the second student selected is a third grader?
2. At a hospital, out of 10 doctors, 3 are on duty on Saturday, 4 on Sunday, and 2 on both days. If one of these doctors is randomly selected, what is the probability that she or he is on duty on Saturday or Sunday?
3. There are 4 chocolate chip cookies and 3 oatmeal cookies in a cookie jar. If a child randomly takes 2 cookies, what is the probability that both are chocolate chip?
4. In a raffle, two names of contestants are drawn one at a time. The first person drawn wins a prize of $500 and the second person drawn wins a prize of $100. Contestants can enter their names into the contest only once, and a total of 400 people have entered. After the winner of the first prize is chosen, what is the probability of winning the second prize?
5. The table below shows data from a survey of 46 students at a local high school. The numbers each represent the total number of students in the given category.
If one of the surveyed students is selected at random, what is the probability that she or he lives within 5 miles of the school and plans to attend college?
Answers are on page 516.
Counting
Counting and probability are closely related because you will almost always have to count something in order to find a probability. On the GED® test, some questions may ask you to just do some counting without finding a probability. In these questions, the focus is on the number of possibilities, given a particular situation. Finding this number can be done using the multiplication rule. By this rule, the numbers of possibilities at each step of a process are multiplied to find the number of possibilities overall.
EXAMPLE 7
A soup shop allows customers to design their own soup. Customers choose one base, one main vegetable, and one main meat. If there are 3 possible bases, 10 possible main vegetables, and 4 possible meats, how many different types of soups can be made?
To make any soup, there are three steps: choose a base, choose a vegetable, and choose a meat. Using the multiplication rule, there are 3 × 10 × 4 = 120 possible soups.
EXAMPLE 8
A group of 4 students must line up for a photo. If each possible lineup is a different photo, how many different photos are possible?
This one is trickier, but think of the photo as representing four spots that need to be filled. There are 4 students who could be in the first spot, 3 in the second, 2 in the third, and 1 in the fourth. This has to be true because a student cannot be in two spots in a single photo.
By the multiplication rule, the number of possible photos is: 4 × 3 × 2 × 1 = 24.
EXERCISE 3
Counting
1. Carlos has three dress shirts, two dress pants, and three pairs of dress socks. How many different outfits does he have for an occasion that requires formal dress?
2. A special at a pizza parlor lets customers pick one topping from a choice of 10 and one crust from a choice of 3. How many different kinds of pizza are possible with this special?
3. In a club of 20 members, a club president, vice president, and secretary must be chosen to form a club cabinet. If members can hold only one position, how many possibilities are there for the club cabinet?
4. Yin is designing a flyer and must choose among 8 fonts and 6 templates to determine the overall design. With these fonts and templates, how many different designs are possible?
5. A stage manager is trying to seat important guests in the front row of a theater. The row has seven seats, and she would like a diplomat in the first seat, a singer in the second seat, and a movie director in the third seat. After this, the remaining diplomats, singers, and movie directors will be seated in the last four seats, in no particular order. If there are 3 diplomats, 2 singers, and 2 directors attending the show, how many different front row plans are possible?
Answers are on page 516.