CHAPTER 10
Algebraic Expressions
Algebra involves working with unknown values called variables. These variables are the common x, y, z, or other letters that you think of when you think of algebra. (By contrast, a simple number with a known value is called a constant.) The power of using variables is that applications can be generalized. That is, instead of solving similar problems over and over again with different numbers, you can follow a set of general rules using variables in place of the numbers. Those rules are what you study when you study algebra.
Variables, Terms, and Expressions
In algebra, terms are numbers, variables, and combinations such as 7, 3x, y, and 2x2.
In a term such as 3x, the 3 and the x are actually being multiplied together. This term is read “3x,” but it really means “3 times x.” The 3 in this case is called the coefficient. Any term with a variable has a coefficient. In a term such as y, the coefficient is understood to be 1 because 1 times y is just y.
When terms are combined with operations or grouping symbols such as parentheses, the result is called an algebraic expression. As you work through different types of algebraic expressions, you may notice that sometimes multiplication is written differently. As explained previously, the term 3x is actually a multiplication of 3 and x. Multiplication in algebra is also commonly shown with parentheses. For example, the expression 4(x − 1) represents 4 times the expression (x − 1).
Some types of expressions occur often enough to be given special names. In the following table, each of these is shown so that you can be familiar with vocabulary you may see on the GED® test.
Evaluating Expressions
To evaluate an expression means to find its value if the variables were replaced with numbers. For linear and polynomial expressions, this means carefully applying the order of operations. With rational expressions, you follow the same order of operations, but there can be some extra considerations when giving a final answer.
EXAMPLE 1
Evaluate the expression 3x3 + 5x2 − 10 for x = 2.
To evaluate the expression, replace each x term with a 2 and then compute. Be sure to follow the order of operations!
3(2)3 + 5(2)2 − 10 = 3(8) + 5(4) − 10 = 24 + 20 − 10 = 34
EXAMPLE 2
Evaluate the expression 3(x2 + 2)2 for x = –1.
3((−1)2 + 2)2 = 3((1) + 2)2 = 3(3)2 = 3(9) = 27
When working with rational expressions, remember that in mathematics, division by zero is said to be “undefined.” Any number that makes the denominator of a rational expression zero makes the whole expression undefined.
For example, the expression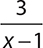 
is undefined when x = 1. Because the denominator is x − 1, evaluating this for x = 1 would give 1 − 1 = 0.
EXAMPLE 3
Evaluate the expression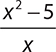 
for x = 4.
In algebra, the final answer is almost always left as a simplified fraction (even if it is an improper fraction).
EXAMPLE 4
Evaluate the expression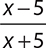 
for x = −5.
Replacing each x with −5 yields the numerical expression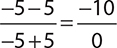 
, which is undefined. The final answer here would be “The expression is undefined when x = −5.”
EXERCISE 1
Evaluating Expressions
Directions: Evaluate each of the expressions for the given value of the variable. If a rational expression is undefined, write your final answer as “undefined.”
1. 5y − 10 for y = −6
2. 16x − 4, for x = −1
3. 9(x −1), for x = 0
4. −2x4 + x2 −1, for x = 2
5. x2 + 5x −12, for x = 3
6. 2 (x − 5)2 + 3x for x = 4
7. −x3 − 1 for x = 3
8. 
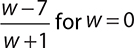
9. 
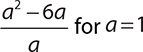
10. 
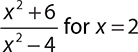
Combining Like Terms
In algebra, like terms are terms that have the same variable and the same exponent. Because plain numbers do not include any variable, they are always considered like terms. Following are some more examples.
Like terms can be combined by adding their coefficients. This process is often part of finding the final answer to a problem. Answers to many algebra problems must be simplified, and an algebraic expression is considered simplified when there are no remaining parentheses and all of the like terms have been combined.
EXAMPLE 5
Simplify the expression 3x2 − 4x + 2x2 − 1.
In this expression, the terms 3x2 and 2x2 are like terms, so they can be combined by adding the coefficients 3 and 2. There are no other like terms, so once these are combined the expression is completely simplified.
3x2 − 4x + 2x2 − 1 = 5x2 − 4x −1
EXAMPLE 6
Simplify the expression 2w − 6w + w.
There are three like terms in this expression. Remember that a variable without a coefficient has a default coefficient of 1. The coefficient of the final answer is found by adding the coefficients of the like terms: 2 − 6 + 1 = −3.
2w − 6w + w = −3w
In some cases, you will need to use the distributive property. Remember that with the distributive property, when terms inside parentheses are multiplied by a number outside the parentheses, each term inside the parentheses must be multiplied by the number outside the parentheses.
EXAMPLE 7
Simplify the expression 5x − 6(x + 2).
Distribute the −6: 5x − 6x + (−6)(2) = 5x − 6x − 12
Combine like terms: 5x − 6x − 12 = −x −12
When working with parentheses, the order of operations still applies. If there is an exponent on the parentheses, you need to calculate that value before applying the distributive property. The expression 2(x + 1)2 does not equal 2x2 + 4. Instead, you first need to multiply (x + 1) × (x + 1). (This is called “expanding” the term.) Expanding uses a method called FOIL, which will be discussed later in this chapter.
EXERCISE 2
Combining Like Terms
Directions: Simplify each of the expressions below.
1. 8 x − 2 x +10
2. 14 y + 1 + 3y − 5
3. −2 z2 − 15 z2 + z2
4. −2 (x − 2)+ x
5. 16 y 4 + 5(1- y4)
Answers are on page 518.
Adding and Subtracting Polynomials
Combining two polynomials by either adding them or subtracting them is actually just a form of combining like terms. However, when subtracting polynomials, just remember to distribute the negative!
EXAMPLE 8
Find the sum of x2 + 2 x − 5 and 9 x2 − 6x +1.
First, write both polynomials with a “+” symbol between them. Then combine like terms to find the answer.
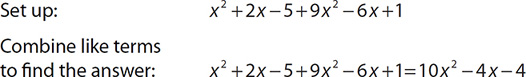
Notice that it doesn’t matter if the like terms are not next to each other. For example, x2and 9 x2 can be combined even though there are two terms between them.
EXAMPLE 9
Find the difference of x4 + x2 − 1 and 6 − x4 + 3 x2.
“Find the difference” always means subtract. To set up a subtraction problem with two polynomials, write the first polynomial as it is, then write the second polynomial in parentheses with a “−” in front. Next, distribute the negative to every term inside the parentheses. Finally, combine like terms. Remember the rules you learned in Chapter 7 for subtracting signed numbers.
When the negative is distributed to the terms inside the parentheses, the sign for every one of those terms changes. Let’s study another example to see how this works.
EXAMPLE 10
Find (16 y − 2)- (18 y +16 − y2).
In this subtraction problem, the parentheses around 16 y − 2 can be dropped because there is nothing in front of them. However, the parentheses around 18 y + 16 − y2 cannot be dropped until the negative in front of them is distributed.
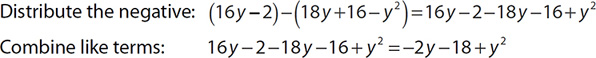
EXAMPLE 11
Find (3 x2 − x)+ (4 x + x2).
When two polynomials are added, both sets of parentheses can be dropped in the first step because distributing a “+” does not change any of the signs.
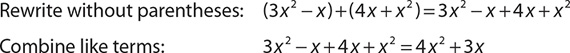
On the GED® test, problems asking you to add or subtract polynomials are sometimes written using words like sum or difference and other times are written using parentheses as in the last two examples. Either way, the solution steps are the same.
EXERCISE 3
Adding and Subtracting Polynomials
Directions: Find the sum or the difference as indicated.
1. (x2 − 2)+ (x2 −1)
2. (x5 − x + 2) + (x + 6)
3. (3 x2 − 2 x + 5) + (− x2 − 5 x +1)
4. (x4 − 2 x)+ (3 x − x2)
5. (12 x2 + 3 x)+ (4 x + x2 − 1)
6. (x3 − 4) − (x3 + 10)
7. (3 x + x2)- (x2 + 2 x)
8. (3 x2 −10x + 2)- (6 x2 − 5 x + 1)
9. (x2 − 9 x)- (6 x + 2)
10. (4 x3 + x)- (2 x2 + 4x)
Answers are on page 518.
Multiplying Polynomials
The method used to multiply polynomials depends on the number of terms that make up the polynomials. In all cases, you need to remember how to work with the laws of exponents (see Chapter 2), use the distributive property (see Chapter 2), and simplify by combining like terms. As you work through the examples in this section, remember that in algebra, multiplication can be indicated by parentheses, as in 2x(3x), or by a dot between the terms, as in 2 x · 3 x.
Multiplying Single Terms
Recall that according to the laws of exponents, when you multiply two exponents with the same base, the exponents are added. This still applies in multiplication involving variables. When multiplying single terms, you will multiply the coefficients and then add the exponents if the variables are the same.
EXAMPLE 12
Multiply 3 x2 · 2 x.
3x2 · 2x = 6x2+1 = 6x3
Remember that if there is no exponent written, the exponent is understood to be 1.
EXAMPLE 13
y2 · (−2y4)= −2y2+4 = −2y6
The rules of exponents cannot be used if the bases are different. Here the bases are the variables. If the variables are different, only the coefficients are multiplied.
EXAMPLE 14
Multiply 3x · 8y.
3x · 8y = 24 xy
EXERCISE 4
Multiplying Polynomials (Single Terms)
Directions: Multiply the given terms.
1. 4x2 · x
2. x2 · x4
3. 10x2 · 3x2
4. 
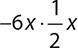
5. 2x · 3y2
Answers are on page 518.
Multiplying Single Terms and Larger Polynomials
Using the distributive property, you can multiply any polynomial by a single term by distributing the single term to every term in the polynomial. After that, it is just a matter of applying the rules of exponents and simplifying.
EXAMPLE 15
Multiply 3x (4x2 −1).
3 x (4 x2 −1)= 3 x · 4 x2 − 3 x · 1 = 12 x3 − 3 x
EXAMPLE 16
Multiply (−2 x3) · (x2 − x + 4).
(−2 x3) · (x2 − x + 4)= −2 x3 · x2 − (−2 x3) · x + (−2 x3) · 4 = −2 x5 + 2 x4- 8 x3
EXERCISE 5
Multiplying Polynomials (Single Terms and Larger Terms)
Directions: Multiply the given polynomials.
1. −6 x (x + 9)
2. 
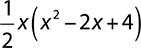
3. x4 (x − 5 − x2)
4. 5x2 (−x2 − 10)
5. 4x3 (x4 − x2 + 6x − 9)
Answers are on page 518.
Multiplying Two Binomials
A binomial is a polynomial with two terms. Some examples of binomials are x − 4, 2 x2 + 1, 3 x − 5, and x2 − x. There are certain steps to follow when multiplying two binomials. They are commonly referred to by the shorthand term FOIL.
Let’s use the example of multiplying 3x + 1 and x − 2 to understand the steps of FOIL.
Step 1: F—multiply the First two terms
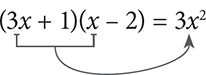
Step 2: O—multiply the Outer two terms
Step 3: I—multiply the Inner two terms
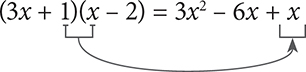
Step 4: L—multiply the Last two terms
Now you can just combine like terms to find the final answer.
(3x + 1)(x – 2) = 3x2 – 6x + x – 2 = 3x2 – 5x – 2
EXAMPLE 17
Multiply (x − 5)(2 x +1).
Apply FOIL and simplify.
(x − 5)(2x +1) = 2 x2 + x −10 x − 5 = 2 x2 − 9 x − 5
EXERCISE 6
Multiplying Two Binomials
Directions: Multiply the given binomials.
1. (x −1)(x + 2)
2. (5 x − 2)(x + 5)
3. (−2 x + 2)(4 x −1)
4. (x2 +1)(x2 −1)
5. (x2 − 6)(2 x − 9)
Answers are on page 518.
Multiplying Polynomials with More than Two Terms
Some questions on the GED® test may ask you to multiply two polynomials with many terms, such as x2 – 9x + 2 and 4x2 – 6x + 1. In questions like these, keep your work organized (there will be a lot of terms to keep track of), and remember to “distribute every term.”
EXAMPLE 18
Multiply (x + 5)(x2 − 2 x +1).
There are two terms in the first polynomial: x and 5. In order to multiply these two polynomials, each term in the second polynomial must be multiplied by x and then again by 5.
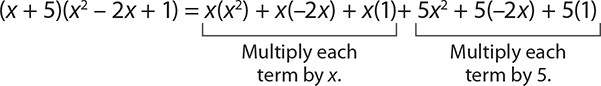
Now simplify the expression to get the final answer.
x3 − 2 x2 + x + 5 x2 −10 x + 5 = x3 + 3 x2 − 9 x + 5
EXAMPLE 19
Multiply (2 x −1)(4 x2 + 3 x + 2).
As in example 18, distribute the 2x and the −1 to each term in the second polynomial.
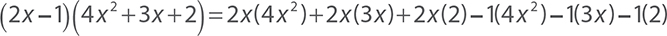
Again, simplify to find the final answer.
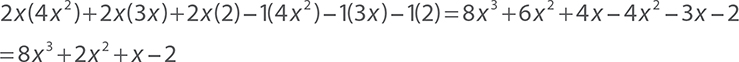
EXERCISE 7
Multiplying Polynomials with More than Two Terms
Directions: Multiply the given polynomials.
1. (x − 3)(x2 + 5 x +1)
2. (2 x +1)(− x2 − x + 4)
3. (x + 3)(9 x2 − 6 x + 2)
4. (x2 − x)(x3 + x +1)
5. (x3 − 4)(x2 + 2 x −1)
Answers are on page 518.
Factoring
Factors are terms or expressions that are multiplied together to produce a more complex expression. You can simplify many complex expressions by dividing them into their factors. This process is called factoring. Not every polynomial can be factored, but when it can, factoring can be used to simplify complex expressions and even solve some equations.
Factoring Using the Greatest Common Factor
The greatest common factor (GCF) between two terms is the largest factor that both terms share. To understand this better, consider the terms 4x2 and x3. You can rewrite these terms showing all of their factors.
As you look at these rewritten terms, you can see that they each share x as a factor. However, they also each share 2 x’s, or x · x = x2, as a factor. Because this is the largest term that both of them share, the GCF is x2. Using this knowledge, you can factor the expression x3 + 4x2 and rewrite it as x2 (4 + x). The factors of the expression are x2 and (4 + x). In a way, factoring using the GCF is like undoing a distributive property problem.
EXAMPLE 20
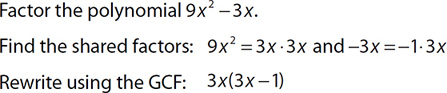
Once you have rewritten the polynomial with the GCF, you have completely factored the expression and this is your final answer.
EXAMPLE 21
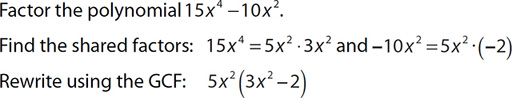
EXAMPLE 22
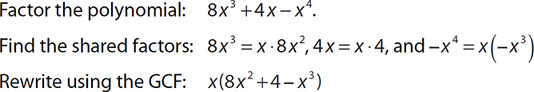
Note that you can always check your answer by distributing. If you did the problem correctly, distributing the GCF should give you the same polynomial you started with.
EXERCISE 8
Factoring Using the Greatest Common Factor
Directions: Factor the given polynomial expression using the GCF.
1. 3 x2 + 9
2. 4 x3 −16 x2
3. 18 x + 9
4. x5 − x2 − 2 x
5. 10 x3 +14 x2
Answers are on page 519.
Factoring by Reversing FOIL
Many (not all) polynomials that are made up of an x2 term, an x term, and a number term can be factored into two binomials by undoing the steps of FOIL. The steps in this type of factoring are best shown in an example. Let’s go through the steps and factor x2 + 2 x − 15.
Step 1: Find all the pairs of factors for the number term.
In this case, the number term is −15. There are many pairs of numbers that when multiplied together make 15. They are:
−1(15), 1(−15), −3(5), 3(−5)
Step 2: Pick the pair of factors that add up to the coefficient of the x term.
The coefficient of the x term is 2. Checking each pair of factors, the pair that adds to 2 is −3 and 5.
Step 3: Use these to factor the polynomial into two binomials.
These types of polynomials will always factor into (x + or − some number)(x + or − another number). The numbers used are those from step 2. For this polynomial, those numbers are −3 and 5. The factored form is (x – 3)(x + 5).
EXAMPLE 23
Factor x2 − 6 x −7.
Step 1: The pairs of factors for −7 are −7(1) and 7(−1).
Step 2: The pair of factors that add to −6 are −7 and 1.
Step 3: The factored form is therefore (x −7)(x +1).
EXAMPLE 24
Factor x2 + 9 x + 20.
Step 1: The pairs of factors for 20 are 20(1), 2(10), and 4(5).
Step 2: The pair of factors that add to 9 are 4 and 5.
Step 3: The factored form is therefore (x + 4)(x + 5).
If the x term in the polynomial is negative but the number term is positive, look for negative factors of the number. Remember that when you multiply two negatives, you get a positive.
EXAMPLE 25
Factor x2 − 6 x + 8.
Step 1: Because the x term is negative and the number term is positive, look for negative factors to make positive 8. These are −1(−8) and −2(−4).
Step 2: The pair of factors that add to −6 are −2 and −4.
Step 3: The factored form is therefore (x − 2)(x − 4).
You can always check your final answer by using FOIL on the factored form. If your answer is correct, you should get the same polynomial you started with.
EXERCISE 9
Factoring by Reversing FOIL
Directions: Factor the given polynomial.
1. x2 −7 x + 12
2. x2 − x − 2
3. x2 − 3 x − 18
4. x2 − 6 x − 40
5. x2 − 5 x + 6
Answers are on page 519.
Difference of Squares
Any polynomial that is the difference between x2 and a perfect square can be factored into two binomials. The two binomials are written in the same way as when you were reversing FOIL except this time, the numbers are the positive and negative square roots of the perfect square. A list of perfect squares can be found on page 331.
EXAMPLE 26
Factor x2 − 25.
This is a difference of squares because 25 = 52. Therefore, the polynomial can be factored into (x + 5)(x − 5).
EXAMPLE 27
Factor x2 − 16.
The number term is equal to 42, so x2 − 16 = (x + 4)(x − 4).
It is important to note that this technique will work with a difference of squares, but it will not work with a sum of squares. The expression x2 + 25, for instance, cannot be factored.
EXERCISE 10
Difference of Squares
Directions: Factor the given polynomial.
1. x2 − 1
2. x2 − 4
3. x2 − 81
4. x2 − 36
5. x2 − 9
Answers are on page 519.
Rational Expressions
Working with rational expressions is a lot like working with fractions. In both cases, you look for like denominators and simplify by eliminating factors. To find common denominators, you will need to know how to multiply polynomials. To simplify, you will need to know how to factor.
Simplifying Rational Expressions
When you studied fractions in Chapter 4, you saw that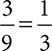 
because 
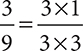. To simplify this fraction, you divided the numerator and the denominator each by 3. One way to think of this is that you “canceled out” the 3 because it was a factor of both the numerator and the denominator. Thinking this way, to simplify an algebraic expression, you can cancel out any factors shared by the numerator and the denominator.
EXAMPLE 28
Simplify the expression 
.
A 2x can be factored out of both the numerator and the denominator. Once it is factored out, canceling this term will give the simplified expression.
EXAMPLE 29
Simplify the expression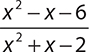 
.
The numerator and the denominator can both be factored by reversing FOIL.
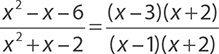
Now you can see that the numerator and the denominator share a factor of x + 2, so the simplified form is:
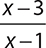
EXAMPLE 30
Simplify the expression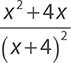 
.
It is hard to see what factors the numerator and denominator may share, but factoring the numerator may make it easier to see if there are any shared factors.
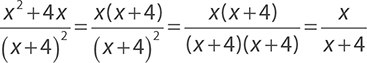
EXERCISE 11
Simplifying Rational Expressions
Directions: Simplify the given rational expression.
1. 
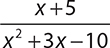
2. 
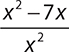
3. 
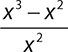
4. 
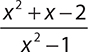
5. 
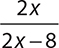
Answers are on page 519.
Adding and Subtracting Rational Expressions
When you were adding and subtracting fractions, you were able to add the numerators whenever the denominators were the same. The same holds true when adding and subtracting rational expressions. Just as with fractions, if the denominators are not the same, you must find a common denominator before completing the problem.
EXAMPLE 31
.
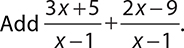The denominators are the same, so add numerators and simplify if needed.
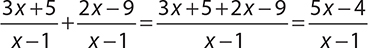
EXAMPLE 32
.
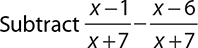Once again, the denominators are the same, so subtract numerators and simplify (if needed).
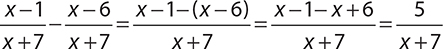
When two rational expressions do not share the same denominator, you will need to find a common denominator. One trick to do this is first to check if one of the denominators is a factor of the other. If so, the larger expression is the common denominator. If not, you can always multiply the two expressions to find a common denominator.
EXAMPLE 33
.
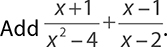The denominator of the first fraction, x2 − 4, can be factored into (x + 2) (x − 2). The denominator of the second fraction is a factor of x2 − 4. Thus x2 − 4 is the common denominator. You need to rewrite the second fraction with this denominator. Because the denominator of the second fraction is missing only an (x + 2), multiply both the numerator and the denominator of the second fraction by this value.
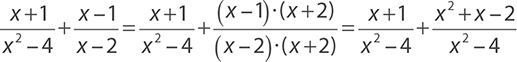
Now the numerators can be added across. Do not forget to simplify your final answer if it is possible.
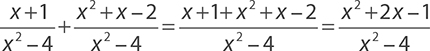
This final expression cannot be simplified any further, so it is the final answer.
EXAMPLE 34
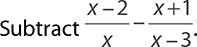
Neither denominator is a factor of the other, so a common denominator is x (x − 3) = x2 − 3x. Both fractions must be rewritten by multiplying both the numerator and the denominator by the “missing” piece.
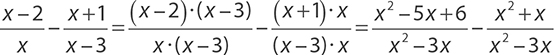
Now, subtract and simplify.
EXERCISE 12
Adding and Subtracting Rational Expressions
Directions: Add or subtract as indicated.
1. 
2. 
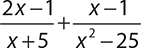
3. 
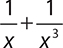
4. 
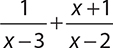
5. 
6. 
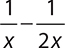
7. 
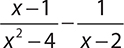
8. 
9. 
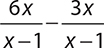
10. 
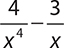
Multiplying Rational Expressions
When multiplying rational expressions, a common denominator is not necessary. Instead, the expressions are always multiplied straight across. Sometimes you will need to simplify the result before you have a final answer. As before, you will use cross canceling to simplify before multiplying to make things easier.
EXAMPLE 35
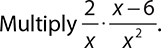
Multiply across:
.
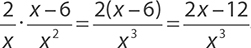EXAMPLE 36
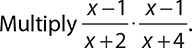
Multiply across:
In examples 35 and 36, the last expression could not be simplified, so it was the final answer. Sometimes you will need to simplify, but this will be before you use FOIL or distribute.
EXAMPLE 37
Before multiplying, notice that x2 − 4 = (x + 2) (x − 2). This means that there are terms that can be cross canceled. That should be your first step.
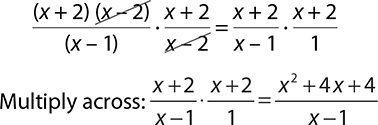
Dividing Rational Expressions
Rational expressions are divided with the same “flip and multiply” rule you used with fractions. Rewrite the division as a multiplication problem in which the first expression is multiplied by the reciprocal of the second.
EXAMPLE 38
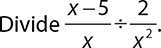
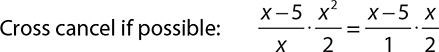
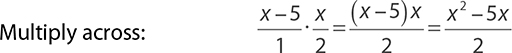
EXAMPLE 39
EXERCISE 13
Multiplying and Dividing Rational Expressions
Directions: Multiply or divide the expressions as indicated.
1. 
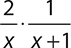
2. 
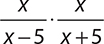
3. 
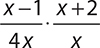
4. 
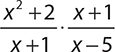
5. 
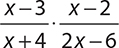
6. 
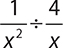
7. 
8. 
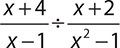
9. 
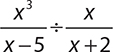
10. 
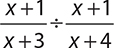
Answers are on page 520.
Writing Expressions
Writing algebraic expressions is a way to represent, or model, real-life situations using variables. As you learn to write expressions to represent a given situation, you need to watch for some key phrases. While there are many possible clues to indicate which operation makes sense, the following phrases will often appear.
• Addition: increased by, the sum, more than (as in “5 more than”), added to
• Subtraction: decreased by, the difference, less than (as in “6 less than”), subtracted from
• Multiplication: the product, double (times 2), triple (times 3), multiplied by
• Division: the quotient, divided by, halved (divided by 2)
• Exponents: squared or square refers to taking a variable to the second power; cubed or cube refers to the third power
EXAMPLE 40
A number is doubled and then decreased by 5. Write an algebraic expression to represent the value of the resulting number.
You are not given the variable in the question, so your first step is to choose a variable to represent the unknown value. Let’s use n.
If n is doubled, it is multiplied by 2, resulting in 2n. It was then decreased by 5, which means 5 is subtracted from it. Therefore the final expression is 2n − 5.
EXAMPLE 41
To find the volume of a square chest, the width is squared and then multiplied by the height. If the height is 3 feet and the width is w feet, write an expression that represents the volume of this chest in terms of w.
The width is squared, so you can represent it by w2. Multiplying this by 3 gives you the final expression 3w2.
EXAMPLE 42
Gary pays $3.50 in tolls and $0.53 per mile to drive to and from work each day. If m represents the number of miles he drives each day, write an expression to represent his cost in terms of m.
The word “per” is a clue that you should multiply; it indicates the cost for each mile driven. The tolls are paid only once, so you can add them on at the end.
The expression that represents his cost: 0.53m + 3.5.
EXAMPLE 43
Five friends go out to lunch and plan to split the bill evenly. If the final bill is $b, write an expression that represents the amount each friend will pay in terms of b.
If the bill is divided evenly, it will be divided by 5. Because the bill is $b, the cost to each friend will be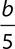 
dollars.
EXERCISE 14
Writing Expressions
Directions: Write an expression to represent the given situation.
1. A company has k employees where k is a whole number. A bonus of $2,000 is to be divided evenly among all the employees. Write an expression to represent the amount each employee will receive in terms of k.
2. In the past two weeks, the amount in a student’s checking account has increased by $505. If the amount two weeks ago was $x, write an expression to represent the current amount in terms of x.
3. Ryan collects action figures and adds two to his collection every month. If he starts with y action figures, then in terms of y, how many will he have in 3 months?
4. A cell phone plan charges $30.00 a month for service plus $0.15 a minute for any calls. If Janelle makes a total of m minutes of calls in a month, what expression will represent Janelle’s total bill in terms of m?
5. A staple gun is used to secure fabric by placing a staple every n feet. Write an expression that represents the number of staples used to secure 20 feet of fabric.
Answers are on page 520.