CHAPTER 6
Percents and Applications
Percents, fractions, and decimals are all ways to represent a part of a whole. With percents, that whole has been divided into 100 equal parts. Percents come up constantly in everyday life in situations involving, for example, sales taxes, bank interest, and tips on restaurant meals. On the GED® test, questions about percents tend to involve uses like these and require a firm understanding of how percents work.
Converting Between Fractions, Decimals, and Percents
The first thing it is important to know is how to convert between fractions, decimals, and percents.
Converting a Percent to a Fraction
Because a percent represents a portion taken from 100 equal parts, any percent can be written as a fraction by writing its value over 100 and simplifying.
EXAMPLE 1
Write 35% as a fraction.
Write 35 over 100 and simplify.
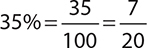
EXAMPLE 2
Write 2% as a fraction.
Write 2 over 100 and simplify.
Converting a Percent to a Decimal
Similarly, converting a percent to a decimal involves dividing by 100. If you imagine a decimal point on the end of a whole number such as 12, you can divide by 100 by moving that decimal point two places to the left.
EXAMPLE 3
Write 12% as a decimal.
Divide by 100 (or move the decimal point two places to the left): 12% = 0.12.
EXAMPLE 4
Write 4% as a decimal.
Divide by 100 (or move the decimal point two places to the left): 4% = 0.04.
These conversions even work when you are dealing with fractional or decimal percentages. For example:
0.5% = 0.005 (move the decimal point two places to the left)
% = 0.125% − 0.00125 (because 1 ÷ 8 = 0.125)
Converting a Decimal to a Percent
Going in the other direction, a decimal can be written as a percent by moving the decimal point two places to the right. This has the same effect as multiplying by 100. Since any fraction can also be quickly written as a decimal, this also allows you to convert fractions to percents as well.
EXAMPLE 5
Write 0.226 as a percent.
Multiply by 100 (or move the decimal two places to the right): 0.226 = 22.6%.
EXAMPLE 6
Write 
as a percent.
As a decimal, = 0.6 because 3 ÷ 5 = 0.6. Multiply by 100: 0.6 = 60%.
EXERCISE 1
Converting Between Percents, Decimals, and Fractions
Directions: Write the following percents as decimals and as fractions. Make sure the fraction you give is in its lowest terms.
1. 30%
2. 22%
3. 49%
4. 1%
5. 8%
Write each of the following as a percent. Round to the nearest tenth of a percent if necessary.
6. 0.044
7. 0.9
8. 0.001
9. 
10. 
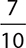
Answers are on page 514.
Working with Percents
Understanding the relationship between percents, decimals, and fractions can be very helpful in solving many types of problems. As you work through the following examples, pay close attention to the wording because it will be similar to the wording you will find in application problems later.
EXAMPLE 7
What percent of 50 is 4?
The question is asking “What is x if 50 × x = 4?” Solve for x.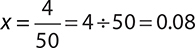 
and 0.08 = 8%
EXAMPLE 8
What is 16% of 34?
The word “of” in the question implies multiplication. In fact, to find any percent of any number, always multiply by the decimal form of the percent.
0.16 × 34 = 5.44
EXAMPLE 9
What is 150% of 20?
Multiplication will work here too. The decimal equivalent of 150% is 1.5 (imagine there is a decimal point on the end of 150 and move it two places to the left), so 150% of 20 is 1.5 × 20 = 30.
Examples 8 and 9 illustrate two important rules you should know:
• Less than 100% of a number will always be a smaller number.
• More than 100% of a number will always be a larger number.
You may be wondering what 100% of a number is. Because percent means “a part out of 100,” 100% means 100 out of 100 or, in other words, everything, so 100% of any number is the number itself.
For many types of percent problems you may encounter, the following proportion is very useful.
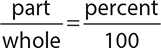
When working with these types of percent problems, the goal is to decide which parts of the ratio you have and which parts you need to find.
EXAMPLE 10
30 is 60% of what number?
Here you have the part and the percent and you are trying to find the whole. Set up a ratio and let n represent the unknown number,
Now cross multiply to find the value of n.
Cross multiply: 3000 = 60n.
Divide by 60: n = 50.
EXERCISE 2
Working with Percents
Directions: Solve each of the following problems. Round your answer to the nearest tenth or the nearest tenth of a percent, as necessary.
1. What percent of 60 is 15?
2. What percent of 1000 is 200?
3. What percent of 35 is 45?
4. What is 60% of 250?
5. What is 3% of 18?
6. What is 0.5% of 90?
7. What is 360% of 20?
8. 18 is 40% of what number?
9. 100 is 10% of what number?
10. 75 is 150% of what number?
Word Problems with Percents
When solving application problems on the GED® test, you will use the very same techniques you use when working with percents in general. The problems may require you to determine the total cost of an item after tax, calculate the commission a salesperson will earn, or determine a percent increase over time. The next two examples show you some of the types of percent application problems you can expect on the test.
EXAMPLE 11
Mary, Jackson, and Bob go out for lunch. Including tax, Mary’s bill was $12.99, Jackson’s bill was $11.20, and Bob’s bill was $18.50. If they plan to tip 20% of the total, how much will they tip?
This question has two parts—finding the total bill and then finding the amount of the tip. Recall that to find a total, you must add:
Total bill is $12.99 + $11.20 + $18.50 = $42.69.
The next step is to find the tip. The question states that they wish to “tip 20% of the total.” From working with percents before, you know that “of” implies multiplication:
Tip is 0.2 × $42.69 = $8.54.
EXAMPLE 12
When Geri started her running program, she ran 3 miles in the first week. Now she is able to run 4.5 miles in a week. What is the percent increase in the number of miles she is able to run?
Problems involving percent increase or percent decrease can always be solved using the formula
where the change is the new value minus the original value. In this example, the percent increase would be
EXERCISE 3
Word Problems with Percents
1. For each sale that she makes, a salesperson is paid a 3% commission. How much will her commission be on a sale of $140?
2. A home office takes up 15% of the square footage of a home. If the home office is 390 square feet, what is the square footage of the home?
3. A company that accepts credit cards is charged $0.02 a transaction in addition to a 1% fee on the value of the transaction. How much will the company be charged for a transaction of $580.00?
4. Eric has been working to conserve energy around his home. His electric bill last month was $125, while his bill this month was $98. What is the percent decrease in his electric bill over the past month?
5. An office manager estimates that she spends 40% of her 30-minute lunch break driving to and from a restaurant. If this is true, how many minutes of her lunch break are spent driving?
Answers are on page 515.
Simple Interest
Typically, interest is earned when money is loaned or invested. One kind of interest is called simple interest. Simple interest is earned only on the principal, or amount loaned or invested. Questions on the GED® test about interest will deal only with simple interest. (Another kind of interest, called compound interest, is earned on the principal and also on the interest that accumulates over time. Questions on the GED® test about interest will not deal with compound interest.)
All simple interest problems can be solved with the simple interest formula I = Prt. In this formula, I is the interest earned, P is the principal, r is the rate of interest expressed as a decimal, and t is the time in years.
EXAMPLE 13
A simple interest loan of $500 is made for 2 years at a rate of 5% per year. What is the total amount of interest that will be paid on this loan?
This is one of the more straightforward types of interest problems you may see. You are given the principal ($500), the time in years (2), and the rate (0.05). Therefore, to find the total amount of interest that will be paid, just plug these numbers into the formula.
I = 500 × 0.05 × 2 = 50
The interest to be paid will be $50.
Note that sometimes you may be asked to find the total payment due on a loan. The total payment includes the original amount borrowed as well as any interest. In example 13, the total payment due is $500 + $50 = $550.
EXAMPLE 14
Jason deposits $2,500 in a savings account that will pay 3% simple interest in one year. Interest is paid in monthly installments. What will be the total value of the account after 6 months?
There are two parts to this question. First, you must calculate the interest that will be paid during 6 months. Then you need to calculate the total value of the account, including the $2,500 initial deposit. You need to be careful because the time given is in months while the interest formula uses time in years.
In terms of years, 6 months represents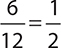 
year. Additionally, be sure to express the rate (3%) as a decimal (0.03). Using this to find the interest:
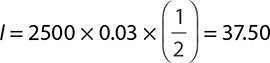
If the interest earned in 6 months is $37.50, then the total value of the account after 6 months will be $2,500 + $37.50 = $2,537.50.
EXAMPLE 15
Jennifer made purchases worth $3,000 using a store credit card. She paid off the charge after 4 months and paid $36 in simple interest. What was the yearly interest rate on the credit card?
In this question, you are given the principal ($3,000), the time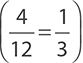 
, and the interest paid ($36). Plugging these into the interest formula, you have:
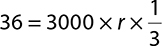
Multiplying the fraction and 3000, this simplifies to:
36 = 3000 × r
To find the rate, r, in this equation, divide both sides by 1000:
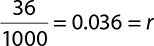
The yearly interest rate on the card was 3.6%. Not bad at all for a credit card!
In problems like these where you are missing one of the values from the formula, you will always follow the same steps. Simplify (as when you multiplied 
and 3000) and then divide.
EXERCISE 4
Simple Interest
1. A loan of $2,000 is made for 3 months at a yearly simple interest rate of 16%. What is the total amount due at the end of the 3 months?
2. A shop owner took out a 6-month loan at a yearly simple interest rate of 8% to purchase inventory. If the owner paid $860 in interest, what was the original amount of the loan?
3. Jamal invests $900 in a bond that pays 4% annual simple interest. How much interest will he earn on the investment after 2 years?
4. Which will earn more interest over 1 year: an investment of $5,000 at 3% simple interest or an investment of $6,000 at 2.6% simple interest?
5. A repair shop took a short-term 1-year loan to purchase new equipment. The original loan amount was $10,000, but at the end of the year the shop had to repay a total of $11,950. What was the simple interest rate on the loan?
Answers are on page 515.