AP* Statistics: 8th Edition

There are several primary principles dealing with the proper planning and conducting of experiments. First, possible confounding variables must be controlled for, usually through the use of comparison. Second, chance should be used in assigning which subjects are to be placed in which groups for which treatment. Third, natural variation in outcomes can be lessened by using more subjects.

In an experiment we impose some change or treatment and measure the result or response. In an observational study we simply observe and measure something that has taken place or is taking place, while trying not to cause any changes by our presence. A sample survey is an observational study in which we draw conclusions about an entire population by considering an appropriately chosen sample to look at. An experiment often suggests a causal relationship, while an observational study may show only the existence of associations.

A study is to be designed to determine whether daily calcium supplements benefit women by increasing bone mass. How can an observational study be performed? An experiment? Which is more appropriate here?

Answer: An observational study might interview and run tests on women seen purchasing calcium supplements in a pharmacy. Or perhaps all patients hospitalized during a particular time period could be interviewed with regard to taking calcium and then their bone mass measured. The bone mass measurements of those taking calcium supplements could then be compared to that of those not taking supplements.

An experiment could be performed by selecting some number of subjects, using chance to pick half to receive calcium supplements while the other half receives similar-looking placebos, and noting the difference in bone mass before and after treatment for each group.

The experimental approach is more appropriate here. With the observational study there could be many explanations for any bone mass difference noted between patients who take calcium and those who don’t. For example, women who have voluntarily been taking calcium supplements might be precisely those who take better care of themselves in general and thus have higher bone mass for other reasons. The experiment tries to control for lurking variables by randomly giving half the subjects calcium.

A study is to be designed to examine the life expectancies of tall people versus those of short people. Which is more appropriate, an observational study or an experiment?

Answer: An observational study, examining medical records of heights and ages at time of death, seems straightforward. An experiment where subjects are randomly chosen to be made short or tall, followed by recording age at death, would be groundbreaking (and, of course, nonsensical).

A study is to be designed to examine the GPAs of students who take marijuana regularly and those who don’t. Which is more appropriate, an observational study or an experiment?

Answer: As much as some researchers might want to randomly require half the subjects to take an illegal drug, this would be unethical. The proper procedure here is an observational study, having students anonymously fill out questionnaires asking about marijuana usage and GPA.

Experiments involve explanatory variables, called factors, that are believed to have an effect on response variables. A group is treated with some level of the explanatory variable, and the outcome on the response variable is measured.

To test the value of help sessions outside the classroom, students could be divided into three groups, with one group receiving 4 hours of help sessions per week outside the classroom, a second group receiving 2 hours of help sessions outside the classroom, and a third group receiving no help outside the classroom. What are the explanatory and response variables and what are the levels?

Answer: The explanatory variable, help sessions outside the classroom, is being given at three levels: 4 hours weekly, 2 hours weekly, and 0 hours weekly. The response variable is not specified but might be a final exam score or performance on a particular test.

The different factor-level combinations are called treatments. In Example 8.4, there are three treatments (corresponding to the three levels of the one factor). Suppose the students were further randomly divided into a morning class and an afternoon class. There would then be two factors, one with three levels and one with two levels, and a total of six treatments (AM class with 4 hours help, AM class with 2 hours help, AM class with 0 hours help, PM class with 4 hours help, PM class with 2 hours help, and PM class with 0 hours help).

When there is uncertainty with regard to which variable is causing an effect, we say the variables are confounded. For example, suppose two fertilizers require different amounts of watering. In an experiment it might be difficult to determine if the difference in fertilizers or the difference in watering is the real cause of observed differences in plant growth. Sometimes we can control for confounding. For example, we can have many test plots using one or the other of the fertilizers, with equal numbers of sunny and shady plots for each fertilizer, so that fertilizer and sun are not confounded.

Sometimes a variable drives two other variables, creating the mistaken impression that the two other variables are related by cause and effect. For example, elementary school students with larger shoe sizes appear to have higher reading levels. However, there is a variable, age, which drives both the other variables. That is, older students tend to wear larger shoes than younger students, and older students also tend to have higher reading levels. Wearing larger shoes will not improve reading skills! There is a common response; that is, changes in both shoe size and reading level are caused by changes in age.

In an experiment there is a group that receives the treatment, and there is a control group that doesn’t. The experiment compares the responses in the treatment group to the responses in the control group. Randomly putting subjects into treatment and control groups can help reduce the problems posed by confounding and lurking variables. Thus these problems are easier to control for when doing experiments than when doing observational studies.

It is a fact that many people respond to any kind of perceived treatment. This is called the placebo effect. For example, when given a sugar pill after surgery but told that it is a strong pain reliever, many patients feel immediate relief from their pain. In many studies, subjects appear to consciously or subconsciously want to help the researcher prove a point. Thus when responses are noticed in any experiment, there is concern whether real physical responses are being caused by the psychological placebo effect. Blinding occurs when the subjects or the response evaluators don’t know which subjects are receiving different treatments such as placebos.

Blinding and placebos in experiments are important but are not always feasible. You can still have “experiments” without these.

A study is intended to test the effects of vitamin E and beta carotene on heart attack rates. How should it be set up?

Answer: Using randomization, the subjects should be split into four groups: those who will be given just vitamin E, just beta carotene, both vitamin E and beta carotene, and neither vitamin E nor beta carotene. For example, as each subject joins the test, the next digit in a random number table can be read off, ignoring 0 and 5–9, and with 1, 2, 3, and 4 designating which group the subject is placed in. Or if the total number of subjects is known and available, for example, 800, then each can be assigned a number and three digits at a time be read off the random number table. With repeats and numbers over 800 thrown away, the first 200 numbers picked represent one group, the next 200 another, and so on. More meaningful results will be obtained if the study is double-blind, that is, if not only are the subjects unaware of what kind of tablets they are taking but so are the doctors evaluating whether or not they have heart problems. Many diagnoses are not clear-cut, and doctors can be influenced if they know exactly which potential preventive their patients are taking.

An experiment is performed on objects called experimental units, and if the units are people, they are called subjects. The experimental units or subjects are often divided into two groups. One group receives a treatment and is called the treatment group. A comparison is made between the response noted in the treatment group and the response noted in the control group, the group that receives no treatment.

To help minimize the effect of lurking variables, and of confounding, it is important to use randomization, that is, to use chance in deciding which subjects go into which group. It is not sufficient to try to systematically match characteristics between the two groups. It seems reasonable, for example, to hand-sort subjects so that both the treatment group and the control group have the same number of women, the same number of Catholics, the same number of Hispanics, the same number of short people, and so on, but this method does not work well. There are always other variables that one might not think of considering until after the results of the experiment start coming in. The best method to use is randomization employing a computer, a hat with names in it, or a random number table.

Note that randomization usually refers to how given subjects are assigned to treatments, not to how a group of subjects are chosen from an entire population. The object of an experiment is to see if different treatments lead to different responses, and so we randomly assign subjects to treatments to balance unknown sources of variability. Random assignment to treatments is critical, especially if the subjects are not randomly selected, as is the case in medical/drug experiments. Generalizing the findings of the study is a separate question, one that depends on how the initial group of subjects was assembled.

Comparing two treatments using randomization is often the design of choice. To help minimize hidden bias, it is best if subjects do not know which treatment they are receiving. This is called single-blinding. Another precaution is the use of double-blinding, in which neither the subjects nor those evaluating their responses know who is receiving which treatment.

There is a pressure point on the wrist that some doctors believe can be used to help control the nausea experienced following certain medical procedures. The idea is to place a band containing a small marble firmly on a patient’s wrist so that the marble is located directly over the pressure point. Describe how an experiment might be run on 50 postoperative patients.

Answer: Assign each patient a number from 01 to 50. From a random number table read off two digits at a time, throwing away repeats, 00, and numbers over 50, until 25 numbers have been selected. Put wristbands with marbles over the pressure point on the patients with these assigned numbers. Put wristbands with marbles on the remaining patients also, but not over the pressure point. Have a researcher check by telephone with all 50 patients at designated time intervals to determine the degree of nausea being experienced. Neither the patients nor the researcher on the telephone should know which patients have the marbles over the correct pressure point.

A chemical fertilizer company wishes to test whether using their product results in superior vegetables. After dividing a large field into small plots, how might the experiment proceed?

Answer: If the company has one recommended fertilizer application level, half the plots can be randomly selected (assigning the plots numbers and using a random number table) to receive the prescribed dosage of fertilizer. This random selection of plots is to ensure that neither fertilized plants nor unfertilized plants are inadvertently given land with better rainfall, sunshine, soil type, and so on. To avoid possible bias on the part of employees who will weed and water the plants, they should not know which plots have received the fertilizer. It might be necessary to have containers, one for each plot, of a similar-looking, similar-smelling substance, half of which contain the fertilizer while the rest contain a chemically inactive material. Finally, if the vegetables are to be judged by quantity and size, the measurements will be less subject to bias. However, if they are to be judged qualitatively, for example, by taste, the judges should not know which vegetables were treated with the fertilizer and which were not.

If the researchers also wish to consider level, that is, the amount of fertilizer, randomization should be used for more groupings. For example, if there are 60 plots on which to test four levels of fertilizer, the first 12 different two-digit numbers in the range 01–60 appearing on a random number table might receive one level, the next 12 new two-digit numbers a second level, and so on, with the last 12 plots receiving the “placebo” treatment.

Two treatments can be compared based on the responses of paired subjects, one of whom receives one treatment while the other receives the second treatment. Often the paired subjects are really single subjects who are given both treatments, one at a time.

The famous Pepsi-Coke tests had subjects compare the taste of samples of each drink. How could such a paired comparison test be set up?

Answer: It is crucial that such a test be blind, that is, that the subjects not know which cup contains which drink. Furthermore, to help avoid hidden bias, which drink the subjects taste first should be decided by chance. For example, as each subject arrives, the researcher could read off the next digit from a random number table, with the subject receiving Pepsi or Coke first depending on whether the digit is odd or even.

Note: Even though the subjects are being given a drink, and there is some randomization going on, some statisticians consider this to be a sample survey aimed at estimating a population proportion rather than a true experiment.

Does seeing pictures of accidents caused by drunk drivers influence one’s opinion on penalties for drunk drivers? How could a comparison test be designed?

Answer: The subjects could be asked questions about drunk driving penalties before and then again after seeing the pictures, and any change in answers noted. This would be a poor design because there is no control group, there is no use of randomization, and subjects might well change their answers because they realize that that is what is expected of them after seeing the pictures.

A better design is to use randomization to split the subjects into two groups, half of whom simply answer the questions while the other half first see the pictures and then answer the questions.

Another possibility is to use a group of twins as subjects. One of each set of twins is randomly picked (e.g., based on choosing an odd or even digit from a random number table) to answer the questions without seeing the pictures, while the other first sees the pictures and then answers the questions. The answers could be compared from each set of twins. This is a paired comparison test that might help minimize lurking variables due to family environment, heredity, and so on.

When differences are observed in a comparison test, the researcher must decide whether these differences are statistically significant or whether they can be explained by natural variation. One important consideration is the size of the sample—the larger the sample, the more significant the observation. This is the principle of replication; that is, the treatment should be repeated on a sufficient number of subjects so that real response differences are more apparent.

Just as stratification in sampling design first divides the population into representative groups called strata, blocking in experiment design first divides the subjects into representative groups called blocks. One can think of blocking as running a separate experiment on each block. This technique helps control certain lurking variables by bringing them directly into the picture and helps make conclusions more specific. The paired comparison design is a special case of blocking in which each pair (or each subject if the subjects serve as their own controls) can be considered a block.

Use proper terminology! The language of experiments is different from the language of observational studies—you shouldn’t mix up blocking and stratification.

There is a rising trend for star college athletes to turn professional without finishing their degrees. A study is performed to assess whether reading an article about professional salaries has an impact on such decisions. Randomization can be used to split the subjects into two groups, and those in one group given the article before answering questions. How can a block design be incorporated into the design of this experiment?

Answer: The subjects can be split into two blocks, underclass and upperclass, before using randomization to assign some to read the article before questioning. With this design, the impact of the salary article on freshmen and sophomores can be distinguished from the impact on juniors and seniors.

Similarly, blocking can be used to separately analyze men and women, those with high GPAs and those with low GPAs, those in different sports, those with different majors, and so on.

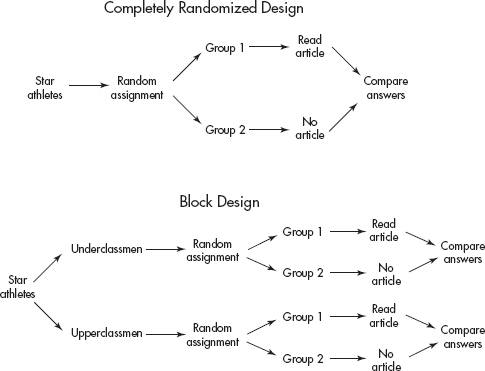
A major goal of experiments is to be able to generalize the results to broader populations. Often an experiment must be repeated in a variety of settings. For example, it is hard to generalize from the effect a television commercial has on students at a private midwestern high school to the effect the same commercial has on retired senior citizens in Florida. Generally, comparison and randomization are important, blinding is sometimes critical, and taking care to avoid hidden bias as much as possible is always indicative of a well-designed experiment. However, knowledge of the subject so that realistic situations can be created in testing should also be emphasized. Testing and experimenting on people does not put them in natural states, and this situation can lead to artificial responses.

Experiments involve applying a treatment to one or more groups and observing the responses.

Blocking is the process of dividing the subjects into representative groups to bring certain differences into the picture (for example, blocking by gender, age, or race).

Random assignment of subjects to treatment groups is extremely important in handling unknown and uncontrollable differences.

Random assignment refers to what is done with subjects after they’ve been picked for a study, whereas random sampling refers to how subjects are selected for a study.

Variables are said to be confounded when there is uncertainty as to which variable is causing an effect.

The placebo effect refers to the fact that many people respond to any kind of perceived treatment.

Double-blinding refers to subjects and those evaluating their responses not knowing who received which treatments.

Completely randomized designs refer to experiments in which everyone has an equal chance of receiving any treatment.

Randomized block designs refer to experiments in which the randomization occurs only within blocks.

Randomized paired comparison designs refer to experiments in which subjects are paired and randomization is used to decide who in each pair receives what treatment.

Directions: The questions or incomplete statements that follow are each followed by five suggested answers or completions. Choose the response that best answers the question or completes the statement.

1. A study is made to determine whether taking AP Statistics in high school helps students achieve higher GPAs when they go to college. In comparing records of 200 college students, half of whom took AP Statistics in high school, it is noted that the average college GPA is higher for those 100 students who took AP Statistics than for those who did not. Based on this study, guidance counselors begin recommending AP Statistics for college bound students. Which of the following is incorrect?

(B) There could well be a confounding variable responsible for the seeming relationship.

(D) A more meaningful study would be to compare an SRS from each of the two groups of 100 students.

2. In a 1927–32 Western Electric Company study on the effect of lighting on worker productivity, productivity increased with each increase in lighting but then also increased with every decrease in lighting. If it is assumed that the workers knew a study was in progress, this is an example of

3. When the estrogen-blocking drug tamoxifen was first introduced to treat breast cancer, there was concern that it would cause osteoporosis as a side effect. To test this concern, cancer subjects were randomly selected and given tamoxifen, and their bone density was measured before and after treatment. Which of the following is a true statement?

(B) By controlling certain variables, blocking can make conclusions more specific.

(D) Blocking results in increased accuracy because the blocks have smaller size than the original group.

6. Consider the following studies being run by three different nursing home establishments.

I. One nursing home has pets brought in for an hour every day to see if patient morale is improved.

II. One nursing home allows hourly visits every day by kindergarten children to see if patient morale is improved.

III. One nursing home administers antidepressants to all patients to see if patient morale is improved.

(D) Important information can be obtained from all these studies, but none will be able to establish causal relationships.

7. A consumer product agency tests miles per gallon for a sample of automobiles using each of four different octanes of gasoline. Which of the following is true?

(C) Miles per gallon is the only explanatory variable, but there are four response variables corresponding to the different octanes.

8. Is hot oatmeal with fruit or a Western omelet with home fries a more satisfying breakfast? Fifty volunteers are randomly split into two groups. One group is fed oatmeal with fruit, while the other is fed Western omelets with home fries. Each volunteer then rates his/her breakfast on a one to ten scale for satisfaction. If the Western omelet with home fries receives a substantially higher average score, what is a reasonable conclusion?

(A) In general, people find Western omelets with home fries more satisfying for breakfast than hot oatmeal with fruit.

(B) There is no reasonable conclusion because the subjects were volunteering rather than being randomly selected from the general population.

(E) There is no reasonable conclusion because there are too many possible confounding variables such as age, race, and ethnic background of the individual volunteers and season when the study was performed.

(A) In well-designed observational studies, responses are systematically influenced during the collection of data.

(B) In well-designed experiments, the treatments result in responses that are as similar as possible.

(E) In well-designed, well-conducted experiments, strong association implies cause and effect.

11. Which of the following is a true statement about the design of matched-pair experiments?

(B) Each pair of subjects receives the identical treatment, and differences in their responses are noted.

12. Do teenagers prefer sports drinks colored blue or green? Two different colorings, which have no effect on taste, are used on the identical drink to result in a blue and a green beverage; volunteer teenagers are randomly assigned to drink one or the other colored beverage; and the volunteers then rate the beverage on a one to ten scale. Because of concern that sports interest may affect the outcome, the volunteers are first blocked by whether or not they play on a high school team. Is blinding possible in this experiment?

(A) No, because the volunteers know whether they are drinking a blue or green drink.

(B) No, because the volunteers know whether or not they play on a high school team.

(C) Yes, by having the experimenter in a separate room randomly pick one of two containers and remotely have a drink poured from that container.

(D) Yes, by having the statistician analyzing the results not know which volunteer sampled which drink.

(E) Yes, by having the volunteers drink out of solid colored thermoses, so that they don’t know the color of the drink they are tasting.

13. Some researchers believe that too much iron in the blood can raise the level of cholesterol. The iron level in the blood can be lowered by making periodic blood donations. A study is performed by randomly selecting half of a group of volunteers to give periodic blood donations while the rest do not. Is this an experiment or an observational study?

Directions: You must show all work and indicate the methods you use. You will be graded on the correctness of your methods and on the accuracy of your final answers.

1. The belief that sugar causes hyperactivity is the most popular example of how people believe that food influences behavior.

(a) Many parents, witnessing the aftermath of cake and ice cream at birthday parties, attest to the relationship between sugar and hyperactivity. Are these observational studies or experiments? Explain.

(b) Name a confounding variable to the above and explain how it is confounded with sugar.

(c) Design a study to allow a parent to determine whether sugar causes hyperactivity in his/her child and explain why double blinding is so important here.

2. Suppose a new drug is developed that appears in laboratory settings to completely prevent people who test positive for human immunodeficiency virus (HIV) from ever developing full-blown acquired immunodeficiency syndrome (AIDS). Putting all ethical considerations aside, design an experiment to test the drug. What ethical considerations might arise during the testing that would force an early end to the experiment?

3. A new weight-loss supplement is to be tested at three different levels (once, twice, and three times a day). Design an experiment, including a control group and including blocking for gender, for 80 overweight volunteers, half of whom are men. Explain carefully how you will use randomization.

4. Two studies are run to measure the health benefits of long-time use of daily high doses of vitamin C. Researchers in the first study send a questionnaire to all 50,000 subscribers to a health magazine, asking whether they have taken large doses of vitamin C for at least a 2-year period and what they perceive to be the health benefits, if any. The response rate is 80%. The 10,000 people who did not respond to the first mailing receive follow-up telephone calls, and eventually responses are registered from 98% of the magazine subscribers. Researchers in a second study take a group of 200 volunteers and randomly select 100 to receive high doses of vitamin C while the others receive a similar-looking, similar-tasting placebo. The volunteers are not told whether they are receiving the vitamin, but their doctors know and are asked to note health changes during a 2-year period. Comment on the designs of the two studies, remarking on their good points and on possible sources of error.

5. Explain how you would design an experiment to evaluate whether subliminal advertising (flashing “BUY POPCORN” on the screen for a fraction of a second) results in more popcorn being sold in a movie theater. Show how you will incorporate comparison, randomization, and blinding.

6. Throughout history millions of people have used garlic to obtain a variety of perceived health benefits. A vitamin production company decides to run a scientific test to assess the value of garlic in promoting a general sense of well-being. They randomly pick 250 of their employees, and once a day for 2 months the employees fill out questionnaires about their sense of well-being that day. For the next 2 months the employees take garlic capsules daily and again fill out the same questionnaires. Finally, for 2 concluding months the employees stop taking the pills and continue to fill out the daily questionnaires. Comment on the design of this experiment.

7. A new pain control procedure has been developed in which the patient uses a small battery pack to vary the intensity and duration of electric signals to electrodes surgically embedded in the afflicted area. Putting all ethical considerations aside, design an experiment to test the procedure. What ethical considerations might arise during the testing that would force an early end to the experiment?

8. A new vegetable fertilizer is to be tested at two different levels (regular concentration and double concentration). Design an experiment, including a control, for 30 test plots, half of which are in shade. Explain carefully how you will use randomization.

9. Two studies are run to measure the extent to which taking zinc lozenges helps to shorten the duration of the common cold. Researchers in the first study send questionnaires to all 5000 employees of a major teaching hospital asking whether they have taken zinc lozenges to fight the common cold and what they perceive to be the benefits, if any. The response rate is 90%. The 500 people who did not respond to the first mailing receive follow-up telephone calls, and eventually responses are obtained from over 99% of the hospital employees. Researchers in the second study take a group of 100 volunteers and randomly select 50 to receive zinc lozenges while the others receive a similar-looking, similar-tasting placebo. The volunteers are not told whether they are taking the zinc lozenges, but their doctors know and are asked to accurately measure the duration of common cold symptoms experienced by the volunteers. Comment on the designs of the two studies, remarking on their good points and on possible sources of error.

10. Explain how you would design an experiment to evaluate whether praying for a hospitalized heart attack patient leads to a speedier recovery. Show how you would incorporate comparison, randomization, and blinding.

11. The computer science department plans to offer three introductory-level CS courses: one using Pascal, one using C++, and one using Java.

(a) The department chairperson plans to give all students the same general programming exam at the end of the year and to compare the relative effectiveness of using each of the programming languages by comparing the mean grades of the students from each course. What is wrong, if anything, with the chairperson’s plan?

(b) The chairperson also wishes to determine whether math majors or science majors do better in the courses. Suppose he calculates that the average grade of science majors was higher than the average grade of math majors in each of the courses. Does it follow that the average grade of all the science majors taking the three courses must be higher than the average grade of all the math majors? Explain.

(c) Suppose 300 students wish to take introductory programming. How would you randomly assign 100 students to each of the three courses?

(d) How would you randomly assign students to the three courses if you wanted the assignment to be independent from student to student with each student in turn having a one-third probability of taking each of the three classes.

A high school offers two precalculus courses, one that uses a traditional lecture and drill method, and a second that divides students into small groups to work on open-ended problems. To compare the effectiveness of the two methods, the administration proposes to compare average SAT math scores for the students in the two courses.

(b) Suppose a group of 50 students are willing to take either course. Explain how you would use a random number table to set up an experiment comparing the effectiveness of the two courses.

84177 06757 17613 15582 51506 81435 41050 92031 06449
05059 59884 31180 53115 84469 94868 57967 05811 84514
75011 13006 63395 55041 15866 06589 13119 71020 85940
91932 06488 74987 54355 52704 90359 02649 47496 71567
94268 08844 26294 64759 08989 57024 97284 00637 89283
03514 59195 07635 03309 72605 29357 23737 67881 03668
33876 35841 52869 23114 15864 38942