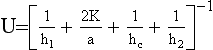Mathematical Modelling in Action
3.1 Introduction
This chapter contains reprints of a selection of articles on mathematical modelling which have been published in books or journals. Each article deals with a different situation and they all demonstrate mathematical modelling in action. The author of each article has developed one or more mathematical models to describe a particular situation and has used the models to answer questions about the situation.
There are several reasons why we should study published articles on modelling. First it gives us information about, and insights into the particular situation described, and we learn something about the world which we did not know before. Secondly it shows us how other people have used mathematics to model situations and to solve problems, and we learn something about the mathematical modelling process just by observing what others have done. Thirdly we may learn some new mathematics or see familiar mathematics being used in a new situation. Finally, and perhaps most importantly, we learn how to read mathematical modelling articles with a critical eye, we learn to ask pertinent questions about the author’s models - What has (s)he done? Why did (s)he do this? How did (s)he do it? Is it valid? -and we learn not to take everything on trust, that sometimes people make mistakes and get things wrong and that it could be important to us to find these mistakes and to correct them.
When confronted with a new problem, the first thing a professional mathematician does is to see if someone else has already solved the problem, or one like it. (S)he does this, in the first instance, by reading books and journals. So reading mathematics is part of the way of life of a mathematician. And this is more than just a “skim read”. It is a careful, critical read with the reader working through much of the mathematics for themselves. In this way (s)he comes to a fuller understanding of what has been written and how the author has solved the problem. It is also important, in the everyday world, that politicians and journalists should not be able to “blind us with science”. In these circumstances, having the ability to read with a critical eye and to ask pertinent questions will save us from being hoodwinked!
3.2 How to use the articles
In the first case study we shall give you an article to read and then we shall take you through it slowly, asking pertinent questions as we go along and pointing out important features of the article. Hopefully this will give you an idea of how we read the article and came to an understanding of it.
Each of the remaining case studies contain an article for you to read, together with a set of questions which we consider pertinent and which should tease out your understanding of the article. You should attempt to understand each article before looking at our questions, otherwise you will read the article only with a view to answering the questions and you may miss other things in the article. As you read it, you should jot down your own pertinent questions and your answers to these questions. In this way you will probably anticipate most of our questions and will probably ask many more besides. It would also be useful for a group of students to pool their ideas and questions and to discuss these with one another before looking at the set questions. You can usually learn quite a lot from the other people in your group. But do this yourselves; do not depend on your teacher for either the questions or the answers.
As you read the articles keep the following questions in mind:-
• What modelling assumptions has the author made?
• Has (s)he stated these explicitly or are they implied by something (s)he has written?
• Are they reasonable assumptions? Would you be happy to make these assumptions or would you make others?
• Does the author justify the assumptions? If not can you give a justification of them?
• Can you follow the mathematics through from line to line? Has (s)he made any mistakes?
• Are the numerical calculations correct?
• Can you explain all statements like “it can be shown that …” or “it follows from the above that …”?
• Has (s)he attempted to validate the model by comparing with observations? If not, can you suggest an experiment that could be carried out?
• Does (s)he draw valid inferences and conclusions from the work?
• Is sufficient background information to the problem given in the article or is it necessary to find out things from other sources?
There is quite a lot here to think about, but don’t worry, most of it is just natural curiosity and you will get better at asking the right questions after you have studied a few articles.
Now read through the article in Case Study 1 and study our commentary on it. The numbers in the left margin are line numbers which are referred to in the commentary.
The Percy Grainger Feat
Percy Grainger was born in 1882 and was one of Australia’s best known composers. His hobby was sport – he loved running – and he was widely known as the jogging pianist! The story goes that he was able to throw a cricket ball over the roof of his house and to run through the house and catch the ball on its way down. This article attempts to model this feat so that we can decide whether or not it really is feasible.
2. The Model and a Solution
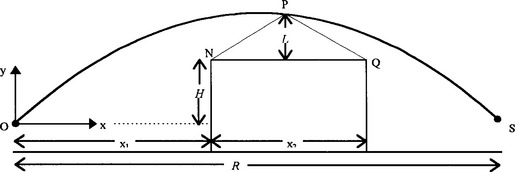
Fig 3.1 illustrates the situation.
10 The origin 0 of the co-ordinate system is at the point of projection of the ball. x1 is the distance of the thrower from the house and x2 is the distance through the house. H is the vertical distance from the x-axis to the top of the wall and L is the further distance to the apex of the house. R is the range of the ball assuming that it is caught at the same height from which it was thrown.
15 We assume that the ball is thrown with speed V0 at an angle of projection θ to the horizontal. Typical values for these constants are H = 5, L = 2, x1 = 10, x2 = 10 and V0 = 20 in appropriate units.
From standard projectile formulae, we known that, in the absence of air resistance, the time of flight is 2V0 sinθ/g and the horizontal range is 2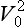 sin2θ/g. The equation of the flight path is
sin2θ/g. The equation of the flight path is
20 Assume that the thrower is stationary when the ball is released.
What angle should the ball be thrown at?
25 There are several things to bear in mind. If θ is too small, the ball will hit the side of the house or the near-side of the roof. If θ is too large, the ball may clear the apex of the roof but hit the far side of the roof on the way down. If the thrower runs too slowly, he may not arrive in time to catch the ball, although we are not too worried if he arrives too early and has to wait for the ball to come down.
Now, the horizontal speed of the ball is constant at V0cosθ so clearly this must be the minimum average speed of the thrower to allow him to arrive at the point S in time to catch the ball.
30 In addition there are other constraints to be met:
Imposing constraint (2) yields the quadratic inequality
where T = tanθ and the typical values of the parameters given above have been used.
The solution set of this inequality is
which means that
The reader can verify that constraint (1) is automatically satisfied when θ lies in the range.
Imposing constraint (3) implies that
Hence the set of possible angles of projection which satisfies the three constraints is
50 Now the thrower must run at an average speed greater than V0cosθ. Since cosθ is a decreasing function of θ in the range 0° < θ < 90°, then we should take θ as large as possible, i.e. θ = 73.68°. Then the speed required of the runner is 20cosθ or 5.62ms–1. When θ = 45°, the average running speed is 14.14ms–1, but speeds like this have not yet been achieved! So, while it is easier to throw the ball at 45° and still clear the roof, there is no possibility of catching it as it descends.
3. The Bounding Parabola
60 When a projectile is launched from an origin 0 with speed V0 there are certain regions in the xy plane which are within the range of the projectile and other regions which are out of range. In the absence of air resistance, the curve in the plane which separates these regions is known as the bounding parabola or the enveloping parabola or the parabola of safety. Let us try to find the equation of this curve.
The equation of the trajectory of a projectile is
which can be written in the form
65 A point (X,Y) is within range if a value of θ can be found such that X and Y satisfy this equation
This is a quadratic equation for tanθ and can be written in the form
70 75 A quadratic equation like this may have real roots, equal roots or complex roots. The significance of complex roots is that there is no angle θ which will give a trajectory which passes through (X,Y). If the roots are real and unequal, then there are two trajectories, with different angles θ which will pass through (X,Y). If the roots are equal then there is only one trajectory through (X,Y). This case separates the accessible region from the inaccessible region. Applying the condition for equal roots, we obtain
Where 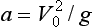 .
.
80 Simplifying we get a2 = X2 + 2aY and conclude that the equation of the bounding parabola is 2ay = a2 – x2.
Commentary: The first question that occurred to us was “Is this feat possible at all?” Is it possible to throw a cricket ball over a house and run through to catch it? Is it possible to throw a ball that high and that distance, and is it possible to run that distance in the time available?
What do we know about throwing a cricket ball, and what do we know about sprinting? Well, professional cricketers can readily throw a cricket ball from the boundary of a cricket pitch to the wicket at the centre, a distance of about 75 yards, or about 70m. From this we can estimate the speed at which it is possible to throw a cricket ball. Also top class sprinters can run 100m in about 10 seconds. Lesser mortals will take a few seconds longer. This should help us estimate the sprinting speed of Percy Grainer and we can work out whether it is fast enough or not.
But what about the modelling? Clearly the author is using a projectile model. Since “standard projectile formulae” is referred to in the line labelled [17]. You probably know them as
You can work out the time of flight by putting y = 0 in (2) and solving for t. Then R can be obtained by substituting the positive value for t into (1).
What are the modelling assumptions implicit in using a projectile model? It is important to consider these so that we can decide if they are reasonable assumptions to make in this situation.
The projectile formulae are obtained by solving the differential equations
subject to the initial conditions
Here we are using Newton’s 2nd law of motion
(i) that the projectile (the ball) is a particle and so does not have a moment of inertia and does not spin;
(ii) that the coordinate system we are working in is not accelerating and so we are ignoring the fact that the earth is spinning on its axis;
(iii) that Newton’s 2nd law is a valid law, that is, we can explain acceleration by considering the forces acting.
We are further assuming in equations (3)
(iv) that the only force acting is gravity, and so we are ignoring air resistance;
(v) that the force of gravity is constant both in magnitude and direction, and so we are taking an approximation to Newton’s universal law of gravity.
Assumption (v) is an interesting one. Newton’s universal law of gravity says that the force of gravity between two bodies is directed along the line between their centres of mass and is proportional to 1/r2 where r is the distance between the centres of mass. In assumption (v) we are effectively saying that for projectile motion the earth is flat since the direction of the force (which is perpendicular to the earth’s surface) changes by less than 50/r radians, which is very small since r = 6.4 × 106m. Also, the ratio of the magnitude of the force of gravity on the ball at the top of its flight to the magnitude at the bottom is approximately
which again is very small.
So clearly assumption (v) is a reasonable one. So also is assumption (iii) because we know that Newton’s 2nd law is very good for modelling the motion of small bodies. (In fact it wasn’t until astronomers in this century noticed small discrepancies in the predicted orbit of the planet Mercury that mathematicians found it necessary to develop a new model. This eventually appeared as Einstein’s General Theory of Relativity).
We can accept assumptions (i), (ii) and (iv) for now but these should be investigated later when you have studied moments of inertia, rotating co-ordinate systems and air resistance. These are all small effects as far as this problem is concerned and so it is reasonable to ignore them as our author has done.
Next, have you worked out the significance of the three inequality constraints (1), (2) and (3) given in the article at [3l]-[33]? These imply that the trajectory of the ball will clear points N, P and Q on the house respectively and so the ball will go over the house.
At [16] in the text the author refers to “appropriate units”. These are probably SI units involving metres and seconds, but don’t you think the author should have been more explicit?
How does the size of this house compare with yours? Did the author just pick these numbers for convenience or are they reasonable dimensions for a house of bungalow? The height of the house is 5 + 2 + 2 (the height of the thrower) which equals 9m or about 30 ft. This would be a two storey house with a roofspace. The house is also 10m or about 33ft from front to rear. A good sized room in a house is about 12ft x 12ft and so this house is of the right size.
The suggested throwing speed is V0 = 20ms–1. How does this compare with the speed of throw of our professional cricketer? Suppose 70m is the maximum throw of a cricketer. This implies a speed of projection given by
So 20ms–1 should be achievable by our hero. (His maximum range will then be R = V02/g = 40m.) The inequality at [35] can be derived fairly easily but some care must be exercised in solving it.
Start with the equation at [19], put g = 10, V0 = 20 and tan θ = T to get
The graph of the left hand side is a cup shaped parabola which is negative far values of T between the roots.
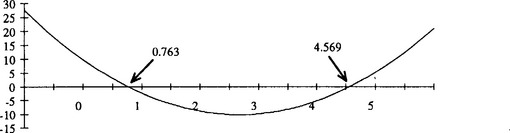
or 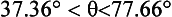
Inequality (3) at [33] leads to
or 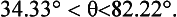
Since 34.33 < 37.36 and 77.66 < 82.22 then condition (3) is automatically satisfied when condition (1) is satisfied as the author claims.
and combining (1) and (2) give
So Perry must throw his cricket ball at 20ms–1 at some angle between 37.36° and 73.68°.
The time of flight of a projectile is 2V0 sin θ/g and this increases with θ. So it would give him more time to run through the house if he could achieve a large angle of projection. Have you tried this? It gets harder to give the ball the necessary initial speed as θ increases.
However assuming that V0 is always 20, the time of flight lies between 2.43 seconds (at θ = 37.36°) and 3.84 seconds (at θ = 73.68°).
The average sprinting speed of the thrower must be greater than the horizontal speed (V0 cosθ) of the ball. Since 37.36° < θ < 73.68° then the minimum sprinting speed lies in the range 5.62ms–1 to 15.90ms–1.
The distance to be covered lies between 21.6m (at θ = 73.67°) and 40m (at θ = 45°). (Did you spot this?)
If the ball is thrown at 73.67° then the thrower must cover 21.6m in at most 3.84 seconds i.e. he must run at average speed of at least 5.62ms–1.
From a standing start, the first part of a short sprint is run at an average speed slower than the average speed for the whole sprint. Thus if a sprinter can cover 100m in, say 12 seconds, (an average speed of 8.3ms–1) then he might only achieve an average speed of 7.0ms–1 over the first 25m. He would then be required to throw the ball at 20ms–1 at an angle of at least 70° in order to achieve the feat.
The Enveloping Parabola
3.1 Derivation Of The Enveloping Parabola
It is intuitively obvious that if a projectile is launched from an origin O with speed V0 there are certain regions of the xy plane within its range, and there are other regions which are not. In the absence of air resistance the dividing curve between these regions has become variously known as the Bounding Parabola, the Enveloping Parabola, or the Parabola of Safety. In this chapter we develop the theory of this special curve and show how it can be used to solve many maximum-range-type problems.
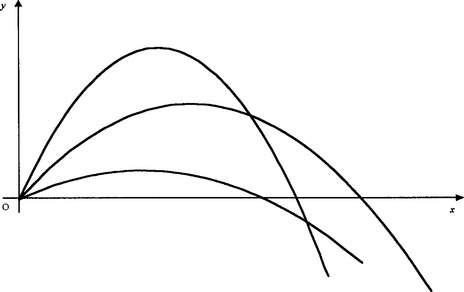
Consider the family of curves obtained when we plot the trajectories of a projectile, launched with a given, fixed speed V0 at various angles of projection θ. A number of such curves are shown in Fig 3.2.
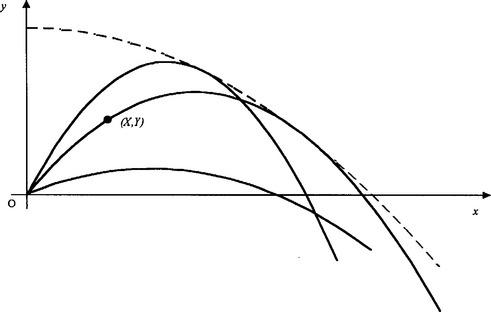
If we add more and more members of the family, it soon becomes apparent that there is a curve, which is not a trajectory, which touches all the trajectories. This is the dashed curve in Fig 3.3.
Since all the trajectories lie under this curve, it is the dividing curve between so-called ‘accessible’ regions and ‘inaccessible’ regions of the xy plane. We now develop its equation in two ways.
Recall that the equation of the trajectory is given by
which we can write in the form
A point (X,Y) is accessible if some trajectory passes through it as shown in Fig 3.3. In this case the corresponding angle of projection is found by solving
This is a quadratic equation for tanθ which can be written in the form
It is well known that a quadratic equation ax2 + bx + c = 0 possesses
and
In the last case there are clearly no real values of tanθ for which a trajectory passes through (X,Y), and thus (X,Y) is in the inaccessible region of the xy plane. On the other hand, if there are two real distinct roots then (X,Y) can be reached along two different trajectories. If only equal roots exist then (X,Y) is reached by only one trajectory. This case divides the inaccessible from the accessible regions, so it is precisely this case which represents the enveloping parabola. Applying the condition for equal roots we find
where 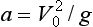 This is rearranged to
This is rearranged to
We conclude that the equation of the enveloping parabola is
Extract from: Modelling with Projectiles by Derek Hart and Tony CroftChapter 9. Ellis Horwood, 1988.
Safe Driving Speeds on Newly Surfaced Roads
Cheshire County Council in common with many local authorities recommends that drivers limit their speeds to 20 mph when travelling over roads which have been newly dressed with a bituminous binder and stone chippings. One unavoidable snag with this method of maintenance is that some surplus stones remain on the road until they are swept up some hours after laying. The advisory limit is intended to avoid the situation where stones are caused to fly into the path of other vehicles and so cause damage to paintwork and even breakage of windscreens. In this chapter we present various mathematical models which describe some aspects of this situation, and we argue that a ‘safe’ speed is not significantly lower than that recommended.
9.2 Assumptions
1. The wheel does not skid. Owing to a variety of factors such as the nature of the tyre, the tackiness of the binder, the weight and size of the vehicle, stones are thrown up at random speeds not greater than the speed of the vehicle. We therefore assume the simplest case in which stones are projected with the speed of the vehicle.
2. In practice it is observed that the direction of projection is random, but in the first simple model we assume that a stone remains in the vertical plane containing the direction of motion of the vehicle.
3. Vehicles travel at constant speed, their separation from the vehicle in front being not less than that recommended by the Highway Code.
4. Air resistance is negligible.
5. Drivers are not unduly worried by stones hitting the front bumper, grille, etc.
9.3 Solution
A stone is projected from the origin 0 at time t=0 and moves along a typical trajectory as shown in Fig 3.4. The front of the bonnet of the following car, FC, has coordinates (S,h). As a first attempt we will argue as follows.
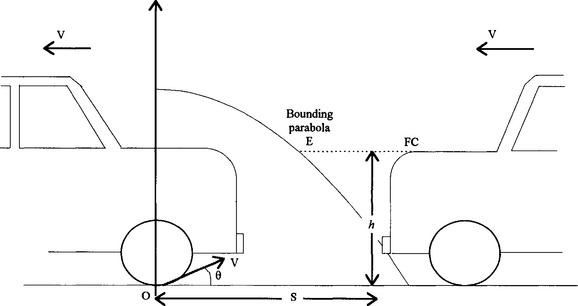
Fig 3.4
There is certainly a danger of the bonnet, windscreen or top of the car being hit by the stone if FC has crossed the bounding parabola, i.e. if FC is within the bounding parabola at time tE, the time of flight of the stone from O to E.
After time tE the position of FC is
and so the vehicle is in danger of being hit if
where XE is the x coordinate of E.
9.4 Separation Distances
An expression for S is now required and experience shows this to be related to the speed of travel V. We will assume that drivers adhere to the Highway Code recommended separation distances. This assumption enables us to determine S as a function of V in the following way.
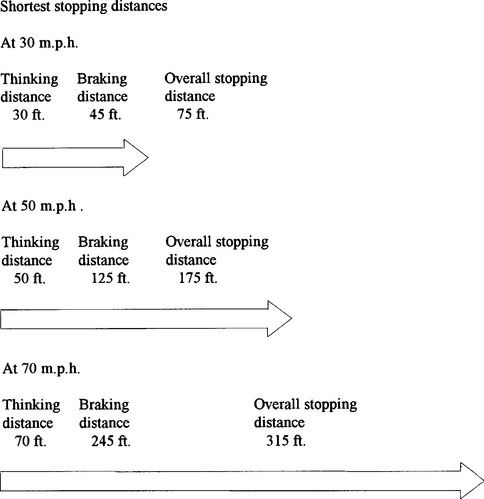
The Highway Code provides the information depicted in Fig 3.5. The data show that S can be divided into two parts, namely (a) the thinking distance ST (which is the distance travelled in the time it takes for the driver to react and depress the brake pedal), and (b) the braking distance SB (which is the distance travelled whilst braking from speed V to rest).
It is clear from the data that ST = V feet.
To obtain the formula between SB and V it is useful to assume a relationship of the form SB = kVα where k and α are constants. Then log SB = αlog V + log k.
Plotting log SB against log V should yield a straight-line graph if the assumed relationship is true. From such a graph the values of α and k can be determined. This graph is illustrated in Fig 3.6.
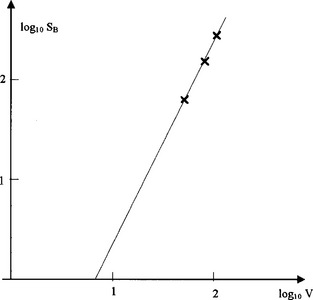
Fig 3.6
The graph is indeed a straight line of gradient 2, so that the assumed relationship between SB and V is true, and the value of α is 2. Furthermore the value of k can be shown to be 0.05. We conclude that S = V + 0.05 V2, where S is measured in feet and V in mph. However, our model requires the use of SI units. It is straightforward to show that the equivalent formula when S is measured in metres and V in metres per second is
9.5 Solution Continued
Since E lies on the bounding parabola its x coordinate is obtained from (3.5) as
where a = V2/g. Furthermore from (3.8)
whence 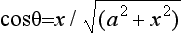 and since x = Vtcosθ we obtain
and since x = Vtcosθ we obtain
Combining (9.1), (9.3) and (9.5), we have the result that the following vehicle is in danger of being hit by the stone if
Therefore from (9.2), there is danger if
9.6 Interpretation of the Result
If the equality given by (9.7) is solved numerically for h = 0.75 m (typical of many popular makes of car) we find that if a driver exceeds 5.531 ms–1 (12.372 mph) he is in danger of being hit. It might be argued that even though the car remains outside the bounding parabola at time tE, at some later time when it is within the bounding parabola it could still be hit by a stone which has taken time th > tE to reach height h. It can easily be shown that the time taken for a stone to rise and then fall to height h is
from which we deduce that th is an increasing function of θ. Taking V = 5.531 ms–1 and h = 0.75 m, equations (9.3) and (9.4) imply that θE, the angle of projection which takes a stone to the point E on the bounding parabola, is about 54°. Consequently a greater time to reach a height h must arise from any angle of projection greater than this. However, observation shows that the wheel arches and rubber flaps of the vehicle constrain angles to be much less than 54°. We therefore conclude that if vehicles travel at 5.531 ms–1 with a separation of at least that recommended by the Highway Code, there is no danger of being hit. The value of 5.531 ms–1 obtained in this way is rather lower than the advisory limit recommended by local authorities, and in practice, drivers are reluctant to slow down even to 20 mph and would almost certainly ignore requests to slow down even further.
9.7 Model 2
Suppose, now, that we no longer assume a Highway Code separation. Consider a stone projected from O (Fig 3.4). The time it takes to reach height h as shown is given by (9.8). Its x coordinate is then
If the following car has separation S1 given by
then a stone projected at angle θ will reach the bonnet at time th. Our procedure is as follows: choose V and calculate the smallest angle θMIN that can cause a stone to reach height h at this speed, then gradually increase θ from this smallest value up to π/2, at each stage calculating S1 from (9.10). Simultaneously we calculate S = 0.682V + 0.076V2, the Highway Code separation. We then gradually increase V and repeat the whole procedure. It soon becomes apparent that at very low speeds, S1 < S for all angles of projection. This means that if a vehicle travels at the recommended separation it must be outside the range of the furthest stone to reach height h. Eventually, as V is increased there comes a point when S1 > S for some angles of projection, meaning that a vehicle travelling at the recommended separation can be hit on the front of the bonnet by a stone at some angle. This searching problem is easily handled on a microcomputer. For h = 0.75 m it reveals that if V is less than about 5.17 ms–1, a car travelling at the recommended separation is safe.
Above this speed there is the possibility of a stone hitting the car. Again a value of 5.17 ms–1 is unrealistic in practice, but we can argue that instead of allowing θ to vary from θMIN to π/2, we constrain it to lie between θMIN and 35°, say. The searching routine so modified yields a speed of approximately 8 ms–1 or 18 mph. Measurement of the overhang of the boot on many makes of car leads us to the conclusion that 35° is a maximum value, stones projected at a higher angle hitting the underside of the vehicle. Many saloon-type cars have a much smaller maximum. (We are of course neglecting tractors, etc.) This second model leads us to the conclusion that for most types of vehicle travelling at the Highway Code recommended separation, a safe driving speed is not significantly lower than that recommended by the local authority.
(i) By applying the condition for equation (3.4) to have equal roots, show that the equation a2 = X2 + 2Ya is correct.
(ii) Using the data in Fig 3.5, calculate log SB and log V, and plot the data on a graph, the first quadrant of which is sketched in Fig 3.6.
Use your graph to find α and k. Show your working clearly and verify that the results in the article are correct.
(iii) Find the printer’s mistake in equation (9.2).
(iv) Showing your working clearly, verify that the values 0.682 and 0.076 in equation (9.2) are correct.
Note: 1 mile = 1609 metres; 1 metre = 3.282 feet.
where SB is in metres and V is in metres per second implies that the car is undergoing a constant deceleration.
Calculate the value of this deceleration.
If the mass of the car is 100kg, calculate the braking force on the car.
(vi) Solve equation (3.4) for tan θ in the “equal roots” case and hence obtain equation (9.4).
(vii) Derive equation (9.8),
(viii) Find a formula for θMIN (which is referred to in the article 2 lines after equation (9.10)).
(ix) Why do drivers following a tractor need to be careful?
What advice would you give them?
(x) Show that a car following a tractor, both travelling at speed V, will certainly be safe from flying stones if the distance between them is 4V2/g.
(xi) Modify the model to meet the needs of a driver who is worried by stones hitting the front bumper or grill (Assumption 5).
Note: Questions (i) to (x) are taken from the NISEAC A level paper, Further Mathematics (Mode 2) Paper 3, 1990 and are reproduced with permission.
18 Drug Therapy
Patients with asthma have constriction of the airways in the lungs and consequent difficulty in breathing out. This ailment can be alleviated by introducing the drug theophylline into the bloodstream. This is done by injecting another drug, aminophylline, which the body quickly converts to theophylline. Once present in the blood, however, the drug is steadily excreted from the body via the kidneys. In other words, the system ‘leaks’, and unless there is replenishment the quantity of drug in the blood will fall.
10 It is known from experiments that theophylline has hardly any therapeutic effect if its concentration in the bloodstream is below 5 mg/1, and that concentrations of above 20 mg/1 are likely to be toxic. The problem is to administer the drug in such a way that the concentration remains within the therapeutic range between 5 mg/1 and 20 mg/1.
20 Experimental measurements can be obtained by injecting a known dose of theophylline into a patient, allowing time for it to diffuse throughout the bloodstream, and finding the drug concentration in blood samples taken at regular intervals. One then knows the initial quantity put into the bloodstream and the concentrations at various later times, but there is no time for which both the quantity and the concentration are known. The following data come from such an experiment.
| Concentration, mg/l | Time, hours |
| 10.0 | 1 |
| 7.0 | 3 |
| 5.0 | 5 |
| 3.5 | 7 |
| 2.5 | 9 |
| 2.0 | 11 |
| 1.5 | 13 |
| 1.0 | 15 |
| 0.7 | 17 |
| 0.5 | 19 |
Another experimental observation is that the apparent volume of distribution (V litres) and the patient’s weight (W kg) are connected by the simple relationship V = ½W. Thus the dose necessary to achieve a required initial theophylline concentration can be inferred from the patient’s weight alone: the dose D mg to obtain a 12 mg/1 concentration in a 50 kg patient is obtained from
so that D = 12 V= 6 W= 300 mg.
30 Assuming that the rate at which the drug is removed by the kidneys is proportional to the amount of drug in the body, obtain a differential equation which describes the concentration c(t) at any time t. Solve this equation, and apply the answer to the data given above to see how well the model agrees with reality.
It is clear that in order that the drug concentration remains inside the therapeutic range a series of injections must be given, and the desired concentration pattern may be as in Fig 3.7.
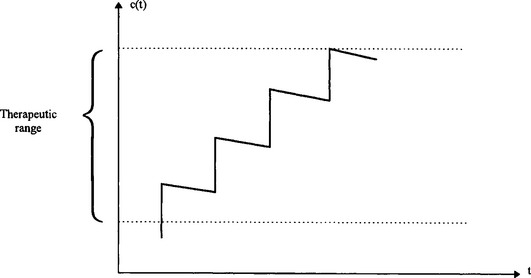
Fig 3.7
40 By considering a very simple case where equal sized doses D mg are administered at equal intervals of time T hours, confirm that it is possible to achieve a saturation as in the Fig 3.7. Is it possible to choose the dose D and the interval T to remain in the therapeutic range? What would you advise for the patient mentioned above? Is there any advantage in giving a larger dose initially and then a series of doses of size D as above?
18.2 Possible solution
When given a question involving data, it is always a good idea to plot them. Doing so in this case gives the graph shown in Fig 3.8. This reminds us of an exponential curve, and replotting as In c against t (Fig 3.9) confirms this guess.
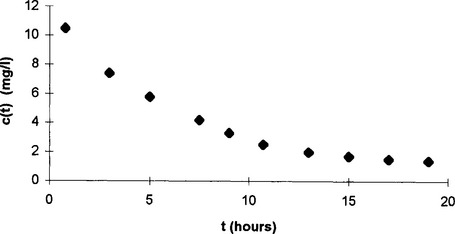
Fig 3.8
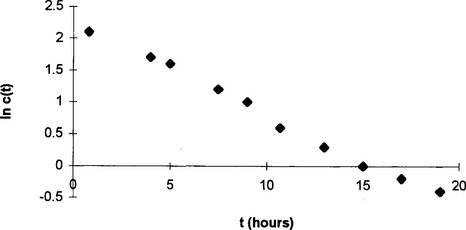
Fig 3.9
Thus we expect that our theory will yield something like 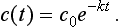 To confirm this result theoretically we note that the drug is removed by the kidneys at a rate proportional to the amount present. Thus if y(t) is the amount of drug present at time t, then
To confirm this result theoretically we note that the drug is removed by the kidneys at a rate proportional to the amount present. Thus if y(t) is the amount of drug present at time t, then
We also know, though, that the amount of drug and the concentration are connected via the apparent volume:
To complete this part of the analysis, we must evaluate the parameters c0 and k. The linear graph, Fig 3.9, is In c against t. However, we have
so the intercept on the graph is In c0 and the slope is −k. This gives
and agrees well with the data given for the 50 kg patient.
We now assume that another dose of D mg (where D/V = c0) is given at time T. This will yield the form of concentration with time shown in Fig 3.10,
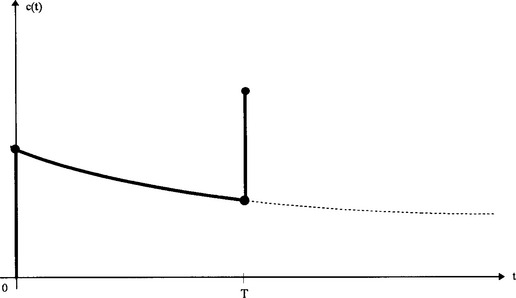
Fig 3.10
where we assume that the drug is instantaneously dispersed throughout the body. We know that c(t) = c0e−kt, so we have
This new amount of drug now decays exponentially as before, so that
and c(2T+) = c0(1+e−kT + e−2kT) after another dose. It is now clear that we can generalise this result to any number of doses. We obtain
which tends to the value c0/(1 − e−kT) for large n.
80 This has all become rather mathematical, so let’s bring it back to earth by trying to decide the dose D and interval T to keep the concentration in the therapeutic range 5 ≤ c(t) ≤ 20. For our 50 kg patient we already have k = 0.17/hour, and it seems fairly clear that we want the limit c0/(1 − e−kT) above to be 20 mg/1. Thus c0 = 20(1 − e−kT), and so we can choose convenient values for T and obtain the corresponding dose D = 25 c0. This gives the following table, where we have also included the concentration just before the second dose.
| T hours | D mg | c(T) mg/1 |
| 1 | 78 | 2.6 |
| 2 | 144 | 4.1 |
| 3 | 200 | 4.8 |
| 4 | 247 | 5.0 |
| 6 | 320 | 4.6 |
| 8 | 372 | 3.8 |
| 12 | 435 | 2.3 |
| 16 | 467 | 1.2 |
| 18 | 477 | 0.9 |
| 24 | 492 | 0.3 |
[Note that we could also have graphed D against T, but in some ways the table above is more useful. This is because the hospital administering the treatment will want a regular timetable for giving the injection, probably every 4, 6, or 8 hours, and so will not be interested in other values.]
90 We now see that if we choose T = 4 hours the concentration never leaves the therapeutic range. Thus, unless a concentration just less than 20 mg/1 is preferable to one just greater than 5 mg/1, there is no point at all in giving a large dose and smaller repeat doses. Our advice to the doctor must be
“Give a dose of 250 mg every 4 hours”.
(i) Use the method of separation of variables, or otherwise to solve the differential equation:
(ii) The authors claim in line [61] that the relationship
’agrees well with the data given for the 50kg patient”.
Verify this claim by copying and completing the following extended version of the table below line [20].
| Measured concentration mg/1 | Time (t) hours | 12e−0.17t (to 1 decimal place) |
| 10.0 | 1 | |
| 7.0 | 3 | |
| 5.0 | 5 | |
| 3.5 | 7 | |
| 2.5 | 9 | |
| 2.0 | 11 | |
| 1.5 | 13 | |
| 1.0 | 15 | |
| 0.7 | 17 | |
| 0.5 | 19 |
(iii) Given that c(nT+) denotes c(nT) + c0 for any positive integer n, state briefly how you would interpret c(nT+).
(iv) Given that 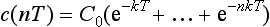 for all integers n ≥ 1, show that c(nT) < c((n + 1)T) for all integers n ≥ 1.
for all integers n ≥ 1, show that c(nT) < c((n + 1)T) for all integers n ≥ 1.
Hence or otherwise deduce that c(nT+) < c((n+1)T+) for all integers n ≥ 1.
(v) It follows from the formulae given in (iii) and (iv) that c(nT+) = c0(1 + e−kT + … + e−nkT) for all integers n ≥ 1.
(vi) Use the inequalities in (iv) and the result in (v)(a) to show that
c0e−kT ≤ c(t) < c0/(1 − e−kT) at any time T.
(vii) Suppose that the advice given in [92] is followed and the 50kg patient is given an initial dose of 250mg of theophylline and a similar dose every four hours.
(a) the initial concentration is 10 mg/l;
(b) the minimum concentration at any subsequent time is just over 5 mg/l;
(c) the concentration eventually settles down in the range from 10 mg/l to just over 20 mg/l.
(viii) Suppose that the doctor treating the 50kg patient tries out the following alternative strategy.
An initial dose of D mg of theophylline is to be administered in order to achieve an initial concentration of 18 mg/1. Every T hours after this (when the concentration level has fallen to 10 mg/1), a smaller dose of d mg will be injected to raise the concentration level back to 18 mg/1.
(ix) Discuss the advantages and disadvantages of each of the strategies outlined in (vii) and (viii).
These questions are taken from the NISEAC A-level paper, Further Mathematics (Mode 2), Paper 3, 1988 and are reproduced with permission.
19 Rats
5 In an experiment by the biologist B. F. Calhoun (reported in Scientific American, (1962), 206 139), a population of wild Norway rats was confined in a ¼-acre enclosure. There was an abundance of food and places to live, and predation and disease were almost eliminated. Thus only the animals’ behaviour with respect to one another remained as a factor that might affect the increase in their number.
10 It was noted that although the adult death rate remained constant at around 5% per month, the number of surviving infants fell as the population density increased. These data were presented as an effective change to the birth rate, so that instead of producing an average 0.4 infants/month each female rat only produced 0.4 K infants/month. The graph of this multiplicative factor K against population density is shown in Fig 3.11.
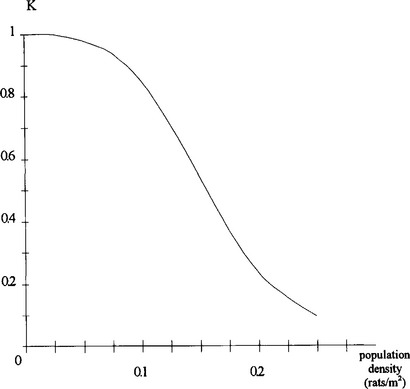
Fig 3.11
15 Draw a rough sketch of birth rate and death rate (rats/month) against population (rats), and use this to justify the existence of an equilibrium population of about 200 rats. Approximate the graph for K above in a suitable way, and hence derive a differential equation model. Confirm the size of the equilibrium population, and find out by how much the population has grown in one year.
19.2 Possible solution
20 In this question the information is presented in months, so we will take this as a natural timescale. We are told that the death rate is 5% per month, so we write
25 with P being the adult rat population. To write down an expression for the birth rate, we assume − in the absence of any other information − that half the adult population is female. Then the birth rate is given as
30 To be able to sketch BR and DR against the population P we must now look at the graph for K. This is given as K (non-dimensional) against population density (rats/m2). We also know, however, that the rats are in a 1/4-acre enclosure − about 1000 m2 − so we can change the axis
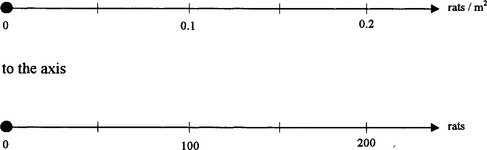
and leave the curve unchanged.
35 We are now in a position to sketch, very roughly, the birth and death rates against the population (Fig 3.12). [Here the birthrate curve was obtained by choosing a few values of P, reading off the related value of K, and working out BR = 0.2 KP.] We see at once that BR = DR (and hence the numbers joining and leaving the population balance, leaving the population in equilibrium) when P ≈ 200. To confirm this result using a differential equation model we can write
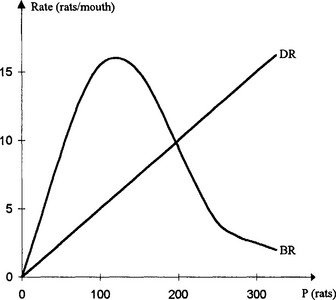
Fig 3.12
Thus the population will be in equilibrium (i.e. dP/dt = 0) when K = 0.25, which can be seen to correspond to a population of about 200 rats from the original data.
45 The advantage of this latter approach is that we now have an equation which we can solve for the population P at any time t. We must firstly, though, express K in terms of P. Since we are interested mainly in the region around P = 200, it seems sensible to approximate K by a linear function in this region (Fig 3.13). We then have something like
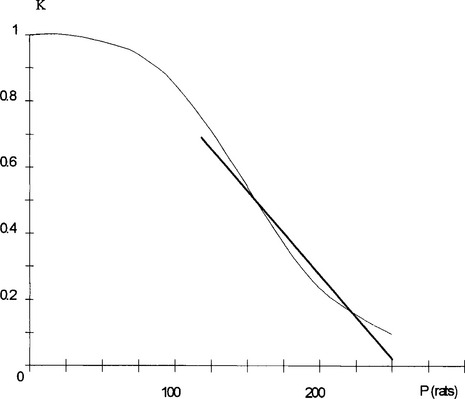
Fig 3.13
which can be put into our differential equation to give
We confirm, again, the equilibrium value of 200 rats.
55 To answer the last part of the question, and find out the rat population after one year, we need to solve this equation. This is simply enough done, using separation of variables and partial fractions, and we obtain
Thus 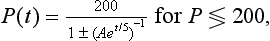 and
and
After one year (i.e. 12 months) the population will be
64 which is sketched as a multiple of the initial population P0 in Fig 3.14. The graph effectively answers the original question.
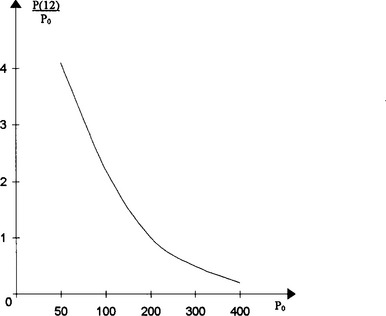
Fig 3.14
(i) Why did the number of surviving infants fall as the population density increased?
(ii) Given that 1 yard = 0.9144m and 1 acre = 4840 square yards, calculate the error involved in taking 1/4 acre = 1000m2.
(iii) Using the large scale version of Fig 3.13 provided below, cany out the calculations necessary to obtain the BR curve in Fig 3.12, as described in lines [34]-[36] of the article.
Hence draw your own version of Fig 3.12 and use it to find the equilibrium value of P.
(iv) How accurate is the statement in lines [43] and [44] which starts “which can be seen …”?
(v) How does the author obtain the equation in line [50]? Does it relate accurately to the data? Explain your answer.
(vi) Solve the equation in line [58] for P in each of the cases P < 200, P > 200.
(vii) Express P(12) in line [62] in terms of P0 and hence find an expression for P(12)/P0.
and sketch the graph of P(12)/P0 against P0.
Is the y-axis (P(12)/P0) an asymptote to the graph, as could be suggested by the authors in Fig 3.14?
(ix) In line [64] the authors claim that this graph “effectively answers the original question”, which was “find out by how much the population has grown in one year”.
Use your graph or the formula to answer this question when the initial population is
(x) The author obtains the equation in line [62] by solving the equation in line [53]. Bearing this in mind, are the one year growth figures you have just calculated valid? Explain your answer.
(xi) What would the graph in Fig 3.11 look like for logistic growth, modelled by the differential equation
(xii) Solve the differential equation in line [53] and rearrange your solution into the form of line [58]. Explain why the modulus function | | is introduced.
1 Handicapping Weightlifters
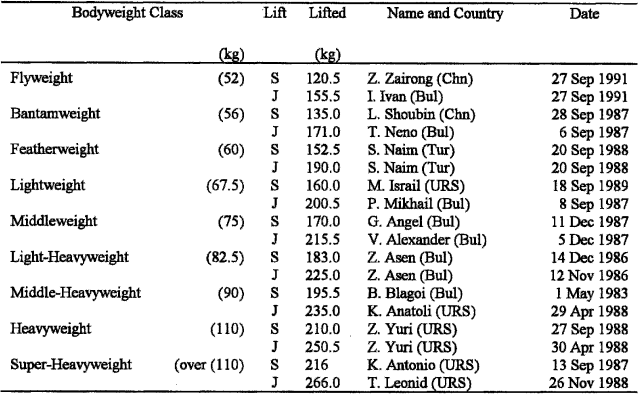
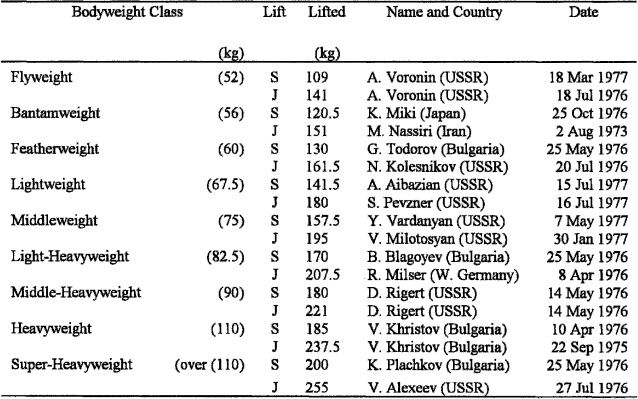
Weightlifting is a minority sport, but it is a sport which can be understood readily by the layman. There are nine official bodyweight classes (see Table 3.1) and there are two principal lifts, namely the snatch and the jerk. In the snatch, the weight is pulled from the floor to a locked arm overhead position in a single move, although the lifter is allowed to move or squat under the weight as it is being lifted, whereas for the jerk, two movements are allowed, the first to the chest and the second to the overhead position.
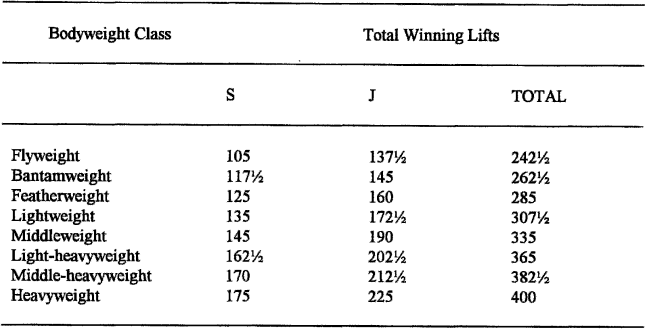
10 Table 3.1 lists the world weightlifting records, current on 31 July 1977. The maximum bodyweight for each class is also shown.
It is clear that as bodyweight increases so does the lift, but what is not clear is the functional form of this increase. The problem is not just a physics/mathematics problem, but is a real practical one, as for many competitions (e.g. school, college) there are just not sufficient numbers to warrant the utilization of the nine weight classes. It is also of some interest, even in serious competitions, to have an ‘overall’ winner. So the problem is to design some form of handicapping, which compensates for the various bodyweights.
20 Having formulated a method of handicapping weightlifters, use it to find an overall winner for the winning snatch lifts at the 1976 Montreal Olympic Games, which are detailed in Table 3.2.
Table 3.2
1.2 Mathematical models for weightlifting
There have been many models formulated which have been used for handicapping weightlifters. We will firstly describe several of these models, and then in section 1.3 use them to answer the question (and compare the results).
30 In Fig 3.15, we have illustrated the world record data points from Table 3.1 for both the snatch and the jerk, assuming that lifters are at their maximum allowed weight for their class. It is evident that a straight line is not a very accurate model, but nevertheless it does have some use. For example, the television programme “TV Superstars” uses the model
40 where L′ is the handicapped lift, L the lift, and B the lifter’s bodyweight. This model implies a linear relationship between L and B with a unit slope, and a check with the data points in Fig 3.15 indicates that this approximation is not very accurate. At the level of performance of superstars it turns out to be much worse, favouring the lighter competitors substantially. On the other hand, the model has as its virtue simplicity. It can be understood by the average television viewer, and for this purpose can be viewed as a ‘good’ model. Entertainment is the object of TV Superstars, and a more complicated form of handicapping might leave viewers in some doubt as to what was happening.
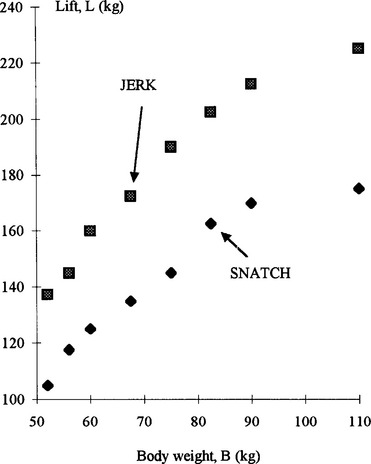
Fig 3.15
Looking at the data points in Fig 3.15 suggests that some power law model should be a more accurate description than a linear model. So if we assume that L = kBα where k and α are constants, then
50 this means that a log L − log B graph should be a straight line, with slope α. For the world record data given above we obtain the points illustrated in Fig 3.16. A straight line looks a reasonable approximation for all the data points except the heavyweight. Remembering, however, that the super-heavyweight data have not been included, a power law model does not seem entirely satisfactory, particularly for the upper weight classes. In fact, two power laws have been used extensively. These are as follows.
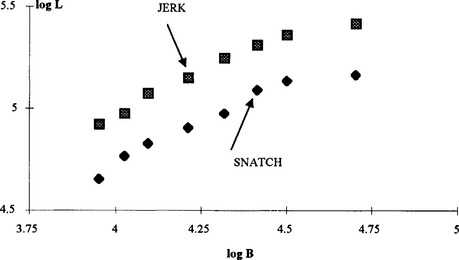
Fig 3.16
(a) Austin formula which is a 3/4 power law,
and was used some 20 years ago in the UK for odd lift comparison and championship best awards.
(b) Classical formula which is a 2/3 power law,
60 and has been used for some time. This model can in fact be deduced from physiological arguments in simple terms. Briefly we assume that the lift is proportional to the average cross-sectional area of the lifter’s muscle, say A,
We also assume that A is proportional to the square of a typical body length, say l,
and finally, the ‘typical’ body length is related to the bodyweight by
With these assumptions,
The arguments presented above for the classical 2/3 power law are not altogether convincing. In 1967, an improved formula, designed by O’Carroll (1967) was introduced, and it has since gained wide acceptance by the weightlifting authorities. It is based both on zoological arguments and statistical analysis of the top 50 worldwide lifters for each division, overall time up to 1964. This was the most ‘robust’ and broadest based sample available, and it was used with an automatic compensation for the differing populations of competitors in the various bodyweight classes.
80 The assumptions (1.4), (1.5), and (1.6) above are generalised to:
which allows for the loss of efficiency at large size;
which allows for variations in shape. Here l is now a muscular length scale and
This treats the total bodyweight B = B0 + B1 as the sum of B0, being non-muscular weight such as cerebral which is almost independent of size, and B1 = K3l3 denoting the varying muscular and related weights. Now from (1.8), (1.9), and (1.10) we deduce a formula of the form
where K and β are constants. From the statistical analysis in O’Carroll (1967), the values of the parameters are taken as
giving the model as
Using this model, the handicapped lift is
100 In Fig 3.17 we illustrate a plot of log L against log(B − 25) for the data given in the introduction. We also illustrate straight lines with slope 1/3, which indicate the accuracy of this model. The three best performing classes (middle, light-heavy, and mid-heavy) are relatively highly populated with competitors, whereas the extreme bodyweight classes have relatively few competitors. This is probably the major factor behind the differences between the population-compensated formula and the population-affected world record figures.
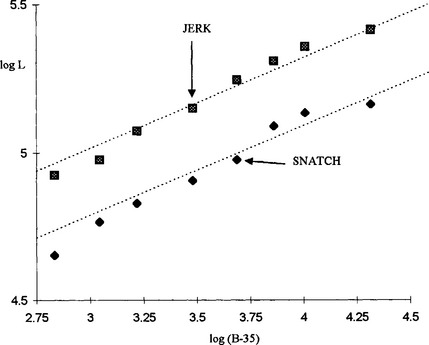
Fig 3.17
This is a Russian formula which is based on determining a ‘degree of merit’ index n, which is given by
110 Note that L + B is based on the idea that the lifter lifts himself along with the barbell, so that the factor (L + B)/B is the total lift as a multiple of bodyweight. The factor [0.45 − (B − 60)/900] represents the proportion of available usable weight, which decreases with body weight.
The degrees of merit values for the world record lifts are given in Table 3.3.
Table 3.3
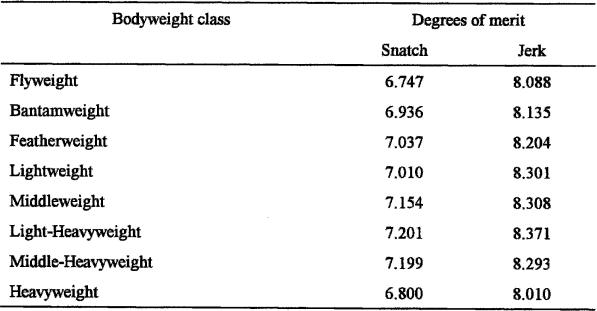
Using this handicapping model, the best snatch lifter is the light-heavyweight (Blagoyev of Bulgaria) and the best jerk lifter is the middleweight (Milotosyan of the USSR).
1.3 Solutions of problem
We now use the models to find the ‘overall’ winner for the snatch winning lifts in the 1976 Olympic Games.
120 To compare the various models of handicapping we must select a common base; we adapt the handicapped lifts so that L′ = L when B = 75, the middleweight lifter’s maximum bodyweight. That is to say, L′ is an equivalent lift made at middleweight. From equations (1.1), (1.2), (1.3), (1.12), and (1.13) we obtain the handicapped lifts
130 The handicapped lifts are given below for their snatch lift together with their numerical positions (assuming each lifter is at his maximum allowed bodyweight).

Perhaps what is most surprising about these handicapped lifts is their agreement. With the exception of the Superstars model, all the models give the same first three places. In fact the Austin and Vorobyev models have complete agreement in all the rankings, and for all but the heavyweight the actual values of L′ are very close. So, on the evidence here, we conclude that the best snatcher among the Montreal Olympics champions was the light-heavyweight, V. Shery (USA).
1.4 Reference
O’Carroll, M J., (1967), On the relation between strength and bodyweight,Researchin Physical Education, 1, 6.
(i) Which body weight class has been omitted from Fig 3.15? Explain why.
(ii) With reference to Table 3.1 and Fig 3.15, if only the first seven classes were included, would it still be true to say (line [29]) “It is evident that a straight line is not a very accurate model”?
For the “snatch” lift only, find the slopes of the best fit straight line for the cases.
(Hint: use a graphics calculator, a graph plotter or graph paper to plot the first seven points, draw the regression line and find its equation. Use the equation to calculate y for the seven values of x and compare with the observed values of y. Use this comparison to make a judgement about the accuracy of the model. Then add the eighth point and repeat the exercise.)
(iii) Is there a contradiction between the claim in line [37] that the “TV Superstars” linear model favours the “lighter competitors substantially” and the data in lines [134]-[137]?
(iv) Bearing in mind the results of part (ii) suggest a modified linear “TV Superstars” handicapping model which is fairer to all the competitors. Explain your answer.
(v) For the “snatch” lift only, reproduce Fig 3.16 using a graph plotter or graph paper and find the slope of the best fit line for
Do these values match more closely the Austin formula or the Classical formula?
(vi) Consider these two statements:-
line [49] - “A straight line looks a reasonable approximation for all the data points except the heavyweight”,
line [29] - “It is evident that the straight line is not a very accurate model”.
Is the author guilty of “selective reporting”? Explain your answer.
(vii) Explain how each of the formulae at lines [32], [55], [59], [97] are modified to give the formulae at lines [125]-[128].
[Were you able to obtain line [129] from the formulae at line [108]?]
(viii) Describe and comment on the modelling assumptions made in developing the Classical formula.
(ix) Explain why the author believes that the O’Carroll formula is an improvement on the Classical formula.
(x) Using the Austin formula, and the 1992 world record data given in the attached table, decide which body weight class has improved the most between 1977 and 1992 for the “Snatch”.
World Weightlifting Records, January 1992
(Taken from World Weightlifters Magazine)
7. Insulating a House
5 Heating a house, or a flat, is an expensive part of the weekly budget. In recent years the cost of heating fuels, that is, coal, gas, electricity, oil, has increased in price quite considerably.
It is important that as much of the heat as possible is retained within the dwelling. Heat energy can escape throughthe walls, windows, roofspace and floor, and there are several products on the market to try to reduce this heat loss e.g.
10 (i) the cavity between the walls can be filled with various materials; polystyrene balls and a chemical called urea formaldehyde are just two such materials; (ii) the windows can be double glazed forming a thin cavity of air between the two panes of glass.
15 Fig 3.18 shows the relative proportions of heat loss for an average sized detached house.
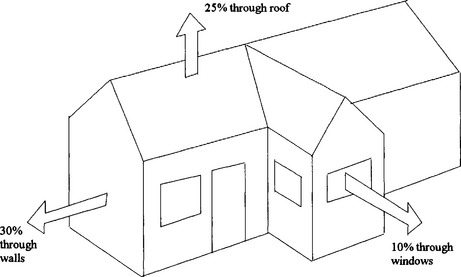
Fig 3.18 Heat losses from a house without roof or wall insulation or double glazing. The remaining 35% of heat loss goes through the floor, gaps round the windows and doors, etc.
20 Clearly if some of escaping heat can be retained within the house then less fuel is needed to heat the house to a certain level and hence fuel bills will be lower. The heat loss can be reduced by INSULATION.
25 New houses have a ten centimetre thickness of insulating material in the loft reducing the heat loss through the roofspace quite considerably. However the walls usually have an unfilled air cavity between them and the windows consist of a single pane of glass of about 4-6mm thickness.
A house owner wanting to reduce the fuel bills can invest in “cavity-wall insulation” and/or “double glazing”.
Figs 3.19 and 3.20 show portions of two advertisements for such forms of insulation.
30 Fig 3.19 suggests that cavity wall insulation could save nearly five times the amount than double glazing. But that soft of claim might be expected from a firm advertising the installation of cavity wall insulation. How good are these figures? This question is one that this modelling case study
35 sets out to answer. It is perhaps interesting to note that the double glazing advertisement only compares competing manufacturers and not other methods of insulation. Fig 3.20 introduces the term “U-value” which is one way in which heat losses through material can be defined.
40 45 Compare the relative cost effectiveness of installing cavity-wall insulation against double glazing. If you had to choose one form of insulation, by comparing the return on the capital investment, which would you choose? What factors that have not be included in your mathematical model, might affect your decision? Would this change your decision?
50 This case study is ideally suited to students who have studied some basic physics or applied mathematics that has included some models of heat transfer. It shows how a simple linear model representing heat flow through a material can be used to solve a problem of practical importance.
If students have not the background knowledge, then the relevant material is contained in this chapter.
7.2 Formulating a Model
55 It is very tempting for this problem, to rush in to the physics of heat transfer and to start data collecting on the average temperatures both inside and outside the house. However that approach would soon lead to too much data and progress would seem slow. At some stage the process of heatflow through the
60 walls and windows does need investigating but first it is a good idea to stand back from the problem and see where we are going.
65 The problem statement asks for a comparison of the costs of installing two forms of insulation – double glazing and cavity-wall insulation. So there are two aspects of the problem to consider:
70 Formulating a mathematical model for the first aspect does not require any specialist knowledge of economics. However the model for heat transfer may either be a familiar one to the students or may require some investigation. In the description of possible solution to this problem a standard model is used.
75 The first stage is to write down a list of those features which we may need to take into account in the mathematical modelling process.
Perhaps the construction of a feature list would be a good place for the students to begin in a class discussion.
80 The following lists of features are relevant to the two different aspects of the problem already identified.
(i) Features affecting the ‘economics’
It is perhaps apparent that there are other features that do not seem to fit in the two categories given above. Two features that seem difficult to quantify are
i.e. double glazed windows are more comfortable to sit by than single glazed windows;
110 i.e. “replacement windows” are possibly nicer to have in the living area than “secondary double glazing”.
115 The second one, (b), will affect the price of having the house double glazed; so that ifwe choose double glazing by installing replacement windows then, since this costs more than secondarydouble glazing, a decision to have cavity-wall insulation instead of double glazing may be because ofthe concern for what it looks like.
7.2.2 Choosing variables and finding relations
120 The class could now be set the task of formulating a model based on the feature lists given above. Each aspect, i.e. the economics and the physics, can initially be investigated separately although features 3 and 4 do provide a link.
125 With the list of 18 features given under headings (i) and (ii) above, a model, which is based on the most important of them, can now be formulated. Initially, for a simple model, we will assume that the important economic features are
Features 3 and 4 provide the link between the two aspects of ‘economies’ and ‘heat transfer’. In fact
135 At this stage we will not worry about the ‘type of double glazing’. This feature affects the cost of installation so that when a model to compare cost-effectiveness is formulated, then, for different types of installation, different strategies can be predicted.
Now consider the features that affect heat loss.
140 Fig 3.21 shows the physical processes involved with the heat transfer through walls and windows. The variable T represents the temperature (in °C) and Q is the heat loss per unit time (measured in watts).
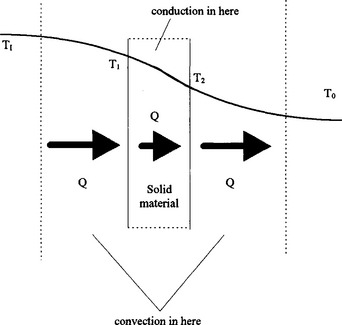
Fig 3.21
145,150,155 In Fig 3.21 the heat transfer due to radiation has not been considered. It is assumed inthis model that the heat loss due to radiation is negligible in comparison with the heat loss due to conduction and convection. Convection is due to the movement of the air on either side of the material causing temperature drops TI – T1 and T2 – T0. Conduction is due to contact between the particles making up the materialand there is a temperature drop of T1 – T2 across its faces. The thermal properties of materials are modelled by a simple expression called the U-value. This is a coefficient that relates the heat transfer per unit area to the total temperature difference (T1 – T0 in the variables of Fig 3.21). The U-value can be calculated experimentally for different substances so that it takes into account convection and conduction. Fig 3.22 shows the U-values for walls and windows.
The basic heat transfer model is
160 This formula can be deduced theoretically by combining simple models for convection and conduction, in the following way.
Consider again the slab of material of thickness a separating two regions of temperature T1 and T0 shown in Fig 3.21.
165 Heating is conducted through the material because there is a temperature difference T1 – T0 across its faces. The rate of heat loss per unit area, Q, is related to T1 – T2 by the simple linear model
where K is the thermal conductivity and a is the thickness of the material.
170 Convection occurs in thin boundary layers on each side of the material. Simple linear models of convection for the inner and outer boundary layers are given by
175 where h1 and h2 are constants called convective heat transfer coefficients. Their values depend on (a) the type of boundary; (b) air speeds near the boundary. In each of the models for conduction and convection we are assuming that the temperature is independent of time, i.e. steady state conditions prevail.
180 Now we have three equations relating the temperatures TI, T1, T2 and T0. They are
185 Eliminating T1 and T2 between these three equations we have
is the U-value introduced earlier.
190 Typical values for a single glazed window are
195 Most of the features in list (ii) have been considered in this simple model of heat transfer. Feature 18 can be written in terms of the difference between the heat losses for non-insulated and insulated boundaries.
In terms of variables, we define
Putting these variables into the three models I, II and III gives
II and III: HG = UN AG (TI – T0) – UI AG (TI – T0) (in Watts)
where UN and UI are the U values for single and double glazed windows respectively.
(in watts)
where 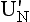 and
and 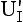 are the U values for unfilled and filled cavity walls respectively.
are the U values for unfilled and filled cavity walls respectively.
7.3 A Strategy for Cost-Effectiveness
220 Now we must make a decision as to the cost-effectiveness of installing double glazing orcavity wall insulation. Defining the “payback period” P, for each type of insulation to be the ratio of the cost of the insulation to the money saved due toinstalling the insulation, then for the windows
A model for cost-effectiveness can then be formulated in the following way;
7.4 Putting it all Together
235,240 If we use the U-values given in Fig 3.22, we have reached an equation that does not include the data on temperature differences and the fuel costs. Hence the increase of the price of fuel due to inflation and other factors do not affect the decision. Furthermore, the strategy that we adopt will hold for all types of heating fuel.
245 To proceed further, suppose the cost of installing double glazing and cavity wall insulation are calculated at a basic rate per square metre cG and cB respectively, then
where
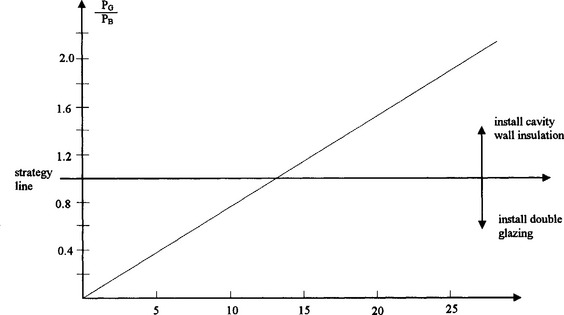
250 Fig 3.23 shows a graph of 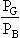 against x.
against x.
From this graph we can make a decision whether to install cavity wall insulation or double glazing. The value of X will depend on the type of double glazing and cavity wall insulation, and probably the manufacturer.
7.5 Making a Decision
255 Table 3.5 gives some examples of the cost per square metre of cavity wall insulation and double glazing for the author’s house.
Table 3.5
| Type of insulation | Average cost per square metre in pounds (Winter (1981) |
| Professionally fitted sealed double glazed units replacement windows | 181 |
| Professionally fitted secondary units | 28.9 |
| Do-it-yourself secondary double glazing (frame and single pane) | 16 |
| Do-it-yourself sealed units | 30 |
| Cavity wall insulation | 2 |
260 Using this data and the graph in Fig 3.22 we have the ratio 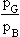 for the four double glazing systems given by 6.57, 1.05, 0.58, 1.09 so that only for do-it-yourself secondary double glazing does the payback period become less than for cavity wall insulation.
for the four double glazing systems given by 6.57, 1.05, 0.58, 1.09 so that only for do-it-yourself secondary double glazing does the payback period become less than for cavity wall insulation.
7.6 Towards a More Complicated Model?
265 There are several features that may change the decision made on purely economic grounds. For instance it is more comfortable sitting by a window that has been double glazed.
270 If comfort is considered as important as cost then perhaps we should consider a model based on double glazing the “living ” rooms only; or alternatively we could add a weighting so that for instance, we would install double glazing provided
275 We have not taken into account the heat saved by lining the curtains and drawing them more often. Curtains can save quite a lot of heat although there is still an uncomfortable draught under and around the edges of the curtains.
280 Installing cavity wall insulation and double glazing can increase the value of the house. An improved model could include an amount that takes this into account so that the true cost of the installation is reduced by a “recoverable amount”.
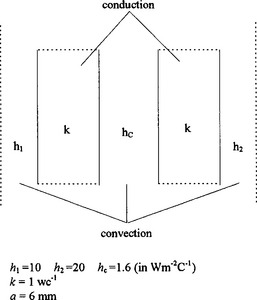
Diagram for Exercise 2
(i) In line [1] it is claimed that “heating a house or flat is an expensive part of the weekly budget”. State whether you agree or disagree with this statement, giving reasons for your answer. Include appropriate facts and figures.
(ii) Referring to line [8], are there any other routes for heat escape?
(iii) Referring to Fig 3.18, is the greatest heat loss per unit area through the walls, the roof or the windows? Estimate areas for these routes.
(iv) Referring to Fig 3.19 and your answer to question (i), estimate the cost of cavity wall insulation. Does this concur with your other enquiries/experiences or the data in Table 3.4? Explain your answer.
(v) Describe briefly the difference between “replacement windows” and “secondary double glazing”. (Refer to lines [108]-[110]).
(vi) Define “U-value”. (Refer to line [157]).
(vii) List the assumptions made in creating the heat transfer model. (Refer to lines [136] to [189]).
(viii) Comment on the statement in line [205].
(ix) In line [221] why does it make sense to call P the “payback period”? Explain how P could be defined differently to take account of the hidden economic costs (e.g. cost of borrowing the capital, or loss of interest that might otherwise have been earned).
(x) Indicate how the value 0.0726 is obtained in line [234],
(xi) Correct the misprints in lines [244], [245].
(xii) Why do you think h2 > h1?
Why do you think hc  h1 and h2?
h1 and h2?
(Refer to the diagram for Exercise 2)
(xiii) Do Exercise 2.
(xiv) Do Exercise 4.
(xv) Which feature of double glazing does most to reduce the U-value? (Refer to question (xiv).
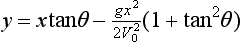
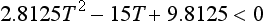
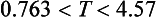
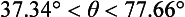
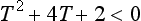
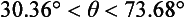
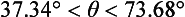
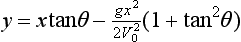
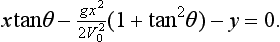
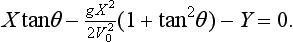
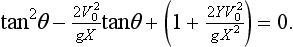
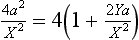
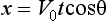
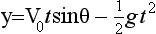

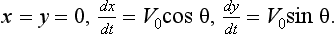
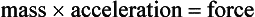
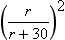
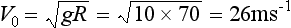
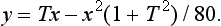
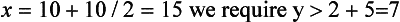
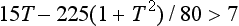
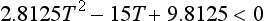
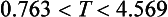
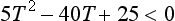
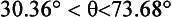
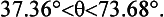
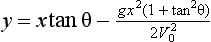
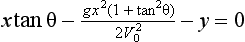
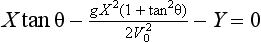
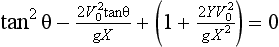
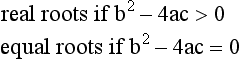
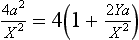
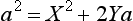
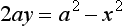
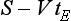
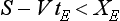
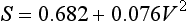
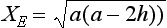
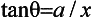
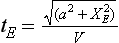
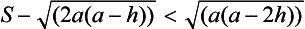
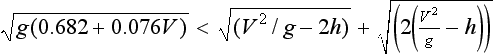
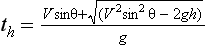
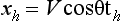
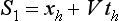
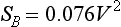
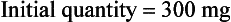
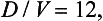
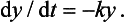
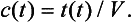
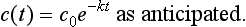
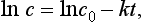
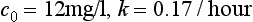
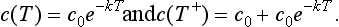
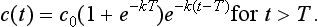
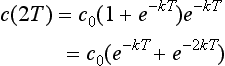
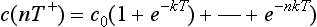
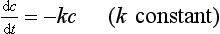
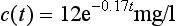
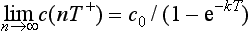
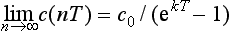
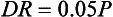
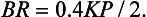
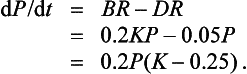
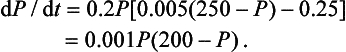
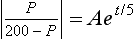
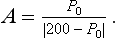
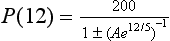
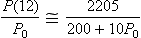

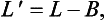
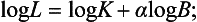
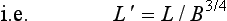
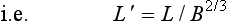
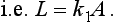
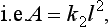
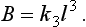
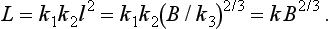
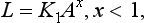
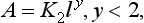
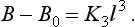
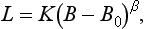
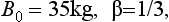
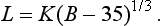
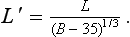
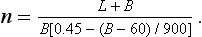
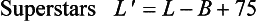
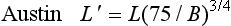

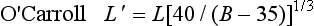
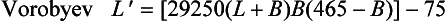

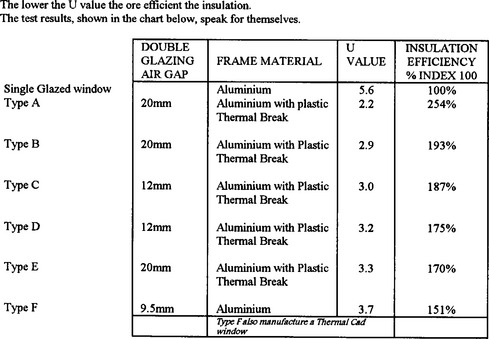
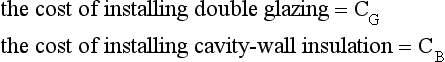
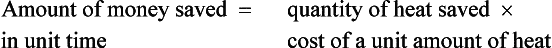
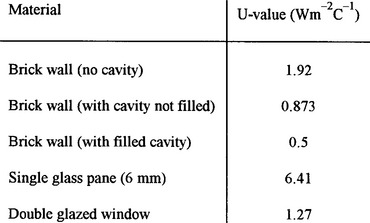
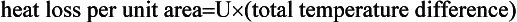
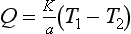
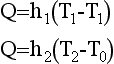
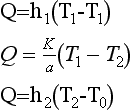
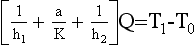
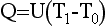
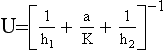
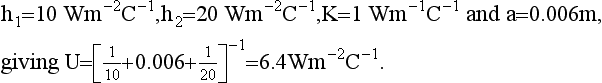
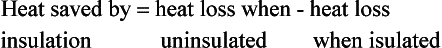

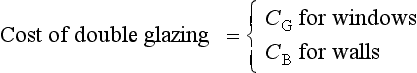
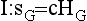
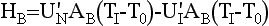
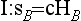
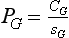
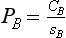

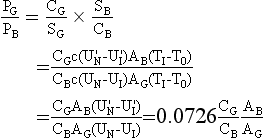

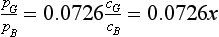
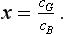
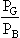 against x
against x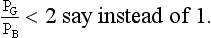
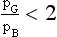
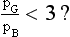
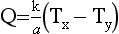 for conduction and
for conduction and 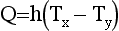 for convection show that the theoretical formula for the U value of a double glazed window is
for convection show that the theoretical formula for the U value of a double glazed window is