I
Quite independently of the definition of elementary structures as the ‘reverse’ of a negative rule, the question now is to find out what Lévi-Strauss means by the term and whether the book devoted to this concept actually constitutes ‘an introduction to a general theory of kinship systems’ (Lévi-Strauss 1949: x).
The consideration of Les Structures élémentaires de la parenté as a general theory does not come only from its author but from other social scientists as well. In a recent work on the definition of the word ‘structure’ as used in the social sciences, Boudon classifies Lévi-Strauss’s treatment of marriage rules as an ‘exact’, ‘falsifiable’, ‘general’ theory. This characterization places Lévi-Strauss’s work at the highest degree on Boudon’s scale of ‘levels of verifiability’ of theories. Boudon classifies theories according to two criteria: (1) whether the criterion of falsifiability is applicable or not, and (2) whether the theory is ‘general’ (a single theory explaining a great number of facts) or ‘partial’ (a number of theories each explaining a small number of facts) (Boudon 1968: 203).
Boudon does not, however, provide in his book any reason why Lévi-Strauss’s treatment of marriage rules should merit such rating. The question would be to point out which of Lévi-Strauss’s propositions are falsifiable and what are the ‘great number of facts’ that they explain. Boudon refers instead to Bush’s mathematical interpretation of Lévi-Strauss’s elementary structures, to a succinct ‘description’ of the Kariera rules of marriage and ‘marriage types’, and to the axioms by which Kemeny, Snell, and Thompson formulate the basic traits of elementary structures.1 After these references, one still does not know what are the facts that are meant to be explained and what the propositions to be falsified.
In any case, and as we state in detail in chapter 7 below, we do not think that either Bush’s formulations or Kemeny, Snell, and Thompson’s axioms translate Lévi-Strauss’s treatment of marriage rules or any other possible theory with an ethnographic reference. Because of this, Boudon’s statements on the scientific status of Lévi-Strauss’s proposals remain to be considered.
II
According to its author, Les Structures élémentaires de la parenté ‘constitutes . . . an introduction to a general theory of kinship systems’ (Lévi-Strauss 1949: x). He classifies these systems under two headings: elementary structures and complex structures. Elementary structures are defined as:
those systems in which the nomenclature permits the immediate determination of the circle of kin and that of affines, that is, those systems which prescribe marriage with a certain type of relative (1949: ix).
Complex structures on the other hand are:
systems which limit themselves to defining the circle of relatives and leave the determination of the spouse to other mechanisms, economic or psychological (1949: ix).
In the light of these definitions, the book seems to be concerned with a dichotomous classification of societies, the types in which are distinguished by the presence or absence of a prescriptive terminology, i.e. a terminology that establishes to which terminological category the possible spouse belongs.2
In this sense Lévi-Strauss proposes, at least by definition, a dichotomous nominal typology of kinship systems. He does not, then, propose a ‘continuum’, as he himself thinks he does and as Fox interprets the elementary–complex typology.3 When it comes to analysing the above definitions of ‘elementary’ and ‘complex’, the only criterion stipulated by Lévi-Strauss is whether or not a given society prescribes marriage with a certain type of relative. Thus, it is hard to see how Fox can assert that ‘all complex systems are complex, but some are more complex than others’ (Fox 1967: 222) if what matters is the presence or absence of a certain kind of prescription derived from the articulation of the relationship terminology. According to this typology, a system is to be classified either as ‘elementary’ or as ‘complex’, and the consideration of degrees is by definition excluded. Hence the characterization of Crow–Omaha systems as an ‘intermediary type’ (Lévi-Strauss 1967: xxxvi) is meaningless; for this necessarily implies that a possible third type can be defined in Lévi-Strauss’s typology, which is inconceivable by the very nature of the criterion employed. First of all, there is no continuum involved: according to Lévi-Strauss’s definition of the kinds of structure, Crow–Omaha systems are merely another case of ‘complex structures’ because they do not contain a prescriptive category of spouse (Lévi-Strauss 1949: ix). The fact that they imply a wide range of prohibitions and that therefore the ‘choices’ are fewer, does not make them any the less complex, since complex, as defined by Lévi-Strauss, means that they are non-prescriptive and not that they offer a greater or lesser choice.4 On the other hand, Lévi-Strauss himself says:
The Crow Indians are divided into thirteen exogamous clans. All we learn from this is that a man can regard twelve out of thirteen woman as a possible spouse. Apart from the scale, the marriage rule is as indeterminate as in our society (1949: 92).5
The degree of choice could constitute a secondary criterion distinguishing subtypes within complex structures, but it is not mentioned as such in Les Structures élémentaires de la parenté.
Quite apart from their classification in the elementary–complex typology, there is still a prior matter to be discussed when considering Crow–Omaha ‘systems’. Needham’s analysis of the Gurage terminology (1969) concludes that the so-called ‘Crow–Omaha’ terminological traits do not amount to a distinct class of terminologies. These traits do not characterize systems other than the Crow and the Omaha themselves.
III
Going back to Boudon’s views on the classification of theories, when he comes to consider the levels of verifiability of theories, the emphasis is on the object: ‘We should note . . . the close correlation between the level of verification reached and the characteristics of the object studied’ (Boudon 1968: 202). So what is the object of Lévi-Strauss’s theory? According to Boudon, it is the study of marriage rules, and this object has a fascinating characteristic, namely: ‘the rules of marriage can be analysed by reference to the rules of marriage alone’ (Boudon 1968: 202).
In fact, the object is not marriage rules but elementary structures, as the very title of Lévi-Strauss’s book states. There is a correlation between the two concepts, of course, but ‘marriage rules’ cover a wider field than ‘elementary structures’. For Lévi-Strauss, the rules are only one of the elements of the structure (cf. 1949: ix). Complex structures, on the other hand, were to form the subject of a separate work (cf. 1949: x).
For Lévi-Strauss, the ‘basic purpose’ of Les Structures élémentaires de la parenté is ‘to show that marriage rules, nomenclature, and the system of rights and prohibitions are indissociable aspects of one and the same reality, viz., the structure of the system under consideration’ (1949: ix). Thus, the ‘introduction to a general theory’ that the book is meant to contain refers to the interrelation of the composite elements of those systems that can be defined as elementary structures.
Unless the structure of a system is something different from the ensemble of marriage rules, nomenclature, and rights and prohibitions, the book is meant to be concerned with a description and definition of the different types of elementary structures. None of the component elements of the structure (marriage rules, nomenclature, and rights and prohibitions) is considered by Lévi-Strauss independently from the others. The description of their interrelation in each type of elementary structure would not in itself be explanatory, therefore, unless each particular interrelationship defining each particular type of elementary structure were related to something else, independent from the structure. Only this last kind of relationship between types of structure and an independent variable can be considered an explanatory proposition concerning the former. We shall consider the existence of this sort of proposition contained in Lévi-Strauss’s book in the following section.
With respect to the concept of ‘structure’ as used in Les Structures élémentaires de la parenté, there is no consistent meaning of the term throughout the book. ‘Structure’ is assimilated by Lévi-Strauss to ‘regulating principle’, or to the Gestalt concept of ‘whole’ (cf. 1949: 129), or alternatively to the division of societies into actual institutions such as moieties, sections, and subsections (cf. 1949: 274-5).
IV
In the book under consideration there is no explanatory proposition to account for the existence of elementary structures, except for the fallacious relation between a ‘basic principle of reciprocity’ and these structures, which we have already analysed in chapter 1 above. The general principle of exchange that, according to Lévi-Strauss, underlies any kinship system (cf. Lévi-Strauss 1949: 592-3), as it is common to all of them, does not ‘explain’ any particular type. The different types of exchange do not ‘explain’ any particular kind of elementary structure, because these structures are defined by means of the modes of exchange they imply.
But there is in Les Structures élémentaires de la parenté at least one explanatory proposition relating different types of exchange, i.e. different subtypes of elementary structures, and something else. This is the relationship postulated by Lévi-Strauss between types of exchange and ‘regimes’, as we shall see below.
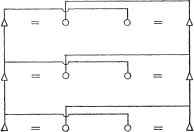
There are three possible elementary structures, says Lévi-Strauss, and they are constructed by means of two forms of exchange (1949: 611). These two forms of exchange are ‘restricted’ exchange and ‘generalized’ exchange. ‘Exchange’ refers to the ‘exchange of women’ among a number of units. Systems of restricted exchange are those ‘which effectively or functionally divide the group into a certain number of pairs of exchange units so that, for any pair X–Y there is a reciprocal exchange relationship. In other words, where an X man marries a Y woman, a Y man must always be able to marry an X woman’ (1949: 189). The ‘formula’ of a system of ‘restricted’ exchange is therefore the representation of a symmetric relationship: A  B. Cross-cousin marriage is the ‘privileged case’ (1949: 186), and Australia the ‘privileged area’ of this type of exchange (1949: 190). In Australia it is possible to find ‘the different systems of restricted exchange, viz., dual organization, the four-section system, and the eight-subsection system’ (1949: 190). The simplest form of a system of ‘restricted’ exchange is a ‘moiety’ system, the representation of which is as in Figure 1. This system merely requires the differentiation between parallel and cross-cousins, regardless of whether the latter are patrilateral or matrilateral. Cross-cousins of both sides are, in principle, included in the prescribed category.
B. Cross-cousin marriage is the ‘privileged case’ (1949: 186), and Australia the ‘privileged area’ of this type of exchange (1949: 190). In Australia it is possible to find ‘the different systems of restricted exchange, viz., dual organization, the four-section system, and the eight-subsection system’ (1949: 190). The simplest form of a system of ‘restricted’ exchange is a ‘moiety’ system, the representation of which is as in Figure 1. This system merely requires the differentiation between parallel and cross-cousins, regardless of whether the latter are patrilateral or matrilateral. Cross-cousins of both sides are, in principle, included in the prescribed category.
Figure 1 Restricted exchange: moiety system
The second type of exchange, generalized, differs from restricted exchange by the way in which ‘reciprocity’ takes place and by the number of units involved in a single transaction of exchange. In the ‘generalized’ or ‘indirect’ form, exchange takes place among more than two units. Women are transferred from one unit to another, i.e. A → B → C →(A). For this kind of exchange a further differentiation between patrilateral and matrilateral cross-cousins is required. If the system is based on MBD marriage, the ‘exchange’ is ‘continuous’ as is represented in Figure 2. If, instead, the system is based on FZD marriage, the ‘exchange’ is ‘discontinuous’, i.e. there are two different cycles (cf. Figure 3).
Figure 2 MBD marriage: continuous exchange
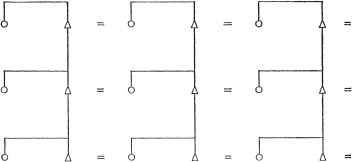
Figure 3 FZD marriage: discontinuous exchange

V
Thus Lévi-Strauss distinguishes three types of elementary structures that are defined by (i) the type of exchange, i.e. restricted or generalized; and by (ii) the ‘continuous’ or ‘discontinuous’ character of the exchange.
The systems categorized by the two kinds of exchange, i.e. restricted and generalized, are related by Lévi-Strauss to another variable, namely, the relationship between the rule of residence and the rule of descent, a relationship that he calls ‘regime’. In his own words, the relationship between ‘structures’ and ‘regimes’ is as follows:
The whole imposing apparatus of prescriptions and prohibitions could be reconstructed a priori from one question and one alone: in the society concerned, what is the relationship between the rule of residence and the rule of descent? Every disharmonic regime leads to restricted exchange, just as every harmonic regime announces generalized exchange (1949: 612).
His definitions of ‘harmonic’ and ‘disharmonic’ regimes are summarized in Table 1. Harmonic regimes are those in which
Table 1
Definition of harmonic and disharmonic regimes

locality and descent follow the same matrilineal or patrilineal principle. Disharmonic regimes are those in which locality and descent follow opposite principles.
The relationship that Lévi-Strauss establishes between type of structure (restricted or generalized exchange) and regime (harmonic or disharmonic) is as in Table 2. Hence the relationship between regime and structure is falsifiable, because it proposes an empirical relationship between two independently defined variables, namely type of structure and type of regime. Any empirical example of a system with a harmonic regime and a structure of restricted exchange, or of a system with a disharmonic regime and a structure of generalized exchange, would be a refutation of Lévi-Strauss’s proposition.
Table 2 Relationship between regime and structure

VI
The trouble is that Lévi-Strauss’s book itself provides the refutation. We shall examine here one of the typical examples of restricted exchange, i.e. the eight-subsection ‘structure’ of the Aranda system, as presented by Lévi-Strauss.
The Aranda are presented by Lévi-Strauss as one of the classical examples of ‘restricted exchange’ because they exchange sisters. They marry a person categorized by a term the genealogical description of which is ‘second cross-cousin’, that is, the people who intermarry are the children of cross-cousins. The case is important in Lévi-Strauss’s argument, because it represents ‘the second dichotomy of the disharmonic regime’, that is, there is a distinction between first cross-cousins and second cross-cousins (1949: 272), and it makes understandable how systems of harmonic regimes (and consequently, of generalized exchange) are intermediary in function between two disharmonic regimes, namely, the Kariera and the Aranda (1949: 217). This functional series permits Lévi-Strauss to construct his ‘general table’ of the relationship between harmonic and disharmonic regimes (1949: 273, Figure 44).
As seems to be the rule in Australia, the Aranda are patrilocal. In this, Lévi-Strauss follows Pink, who ‘was able to speak of the Northern Aranda as “landowners”, among whom the “ancestral clan state” and the patrilineal line by which it is transmitted together with the ritual, play a leading part in both collective and individual life’ (1949: 193).
On the question of which grouping is to be considered ‘owners’ of the land, Lévi-Strauss says that ‘the question is not so much whether it is the horde or the clan which should be considered the real landowning group, but which of these two patrilineal groups is at the basis of the social organization’ (1949: 193).
As for the rule by which an Aranda man belongs to one of the eight subsections, Lévi-Strauss says: ‘in the Aranda system a man falls into the same class as his grandfather (FF) and he always finds his grandson (SS) in the same class as himself’ (1949: 171).
He also says that ‘in the final analysis it is the relationship of consanguinity which plays the principal role, while class membership, at least in practice, is secondary’ (1949: 165). In this respect, the representation of the relationship terms in his diagram of the Aranda system (1949: 214, Figure 15) arranges them in the form of four patrilines.
So facdications would point to a ‘harmonic regime’ in Lévi-Strauss’s terms. The Aranda certainly seem to be patrilocal, and whatever Lévi-Strauss means by ‘descent’ he mentions patrilineal hordes, patrilineal clans, patrilineal determination of membership to a subsection, and represents the system formally by patrilines. Yet he also says that in the Aranda type ‘descent and residence are transmitted in separate lines’ (1949: 270). By this, he can only mean that ‘descent’ is transmitted separately from the patrilocal residence that he recognizes, i.e. matrilineally. As we have already seen, however, he gives no indication of any right or membership to a group that could be conceptualized as ‘descent’ and which is transmitted in this way. Even if we take into account Leach’s observation that ‘Lévi-Strauss . . . confuses the notion of descent, a legal principle governing the transmission of rights from generation to generation, with the notion of filiation, the kinship link between parent and child’ (Leach 1969a: 101), the representation of this latter link in Lévi-Strauss’s diagram is still patrilineal. The only instances in which he refers to some kind of matrilineal transmission among the Aranda are (1) his representation of an eight-subsection system by which the child of a couple takes the name of the mother and the residence of the father (1949: 212, Figure 14), and (2) a paragraph in which he refers to matrilineal moieties among the Aranda (1949: 272).
With regard to Lévi-Strauss’s representation of an eight-subsection system mentioned above, he does not refer to any trait of the Aranda system that could correspond to the matrilineal transmission of the ‘name’. On the other hand, no such trait is reported in the ethnographical accounts of the Aranda. With regard to the moieties, although these were referred to as ‘matrilineal’ by Durkheim (1902: 109) and by Radcliffe-Brown (1931: 27), among others, they are not in fact reported as such by the ethnographers.
VII
Spencer and Gillen, in their first account, say that among the Aranda ‘descent is counted in the male line’ (1899: 68). They reaffirm this view still in 1927, when they say: ‘the child passes into the father’s moiety, but not into a section (or subsection) to which he does not belong; that is, descent is counted in the indirect male line’ (1927: 43). According to Spencer and Gillen also, the totemic name of an individual among the Aranda is not related to the totem name of the father or to that of the mother, although it can coincide with them in some cases. This is possible because, among the Aranda, the totemic groups are not exogamous.
Spencer and Gillen compare the descent system of the Aranda with that of the Arabana and they say that the systems are ‘male in the Arunta, female in the Urabuna’ (1927: 43 n. 1). When they explain how the Arabana classify a Southern Aranda in terms of their own system, Spencer and Gillen make an equivalence between the matrilineal moieties of the Arabana and the four sections of the Southern Aranda (where ‘descent is counted in the indirect male line’). They do not refer to equivalences between the Arabana matrilineal moieties and the putative Aranda matrilineal moieties, because among the latter these matrilineal moieties do not exist.
Mathews, however, tried to prove in 1908 that descent among the Aranda was in fact matrilineal. By ‘descent’ he meant the principle by which an Aranda individual was ascribed to a section or subsection, because what he tries to demonstrate is that the interpretation of the tables presented by his informants, showing that an Aranda individual belongs to the section or subsection to which his or her father’s father belongs, is wrong. Using the same tables, he claims to have demonstrated that an Aranda individual belongs to the section to which his or her mother’s mother’s mother’s mother belonged (1908: 96). The fact that the Aranda also take the name of their father’s father does not constitute for Mathews a diagnostic feature in the consideration of ‘descent’, because he says that ‘in fact, in every tribe I know possessing female descent, all over Australia, the child takes the name of the father’s father’ (1908: 95). This last statement by Mathews is curious because, at the time he wrote it, the reports of Gason and Howitt about the Dieri were already known. Even though the Dieri did not have sections or subsections, they certainly were matrilineal, and the term by which they classified a person was the term by which they classified his or her mother’s mother’s brother, and not his or her father’s father.
In any case, Mathew’s conclusions about the Aranda were contested by the most authoritative and detailed ethnographic report on the Aranda, namely Strehlow’s Die Aranda- und Loritja-Stämme in Zentral-Australien (1907-20).
Referring to the article by Mathews mentioned above, Strehlow says that Mathews, in his attempts to show that the Aranda were matrilineal, used Strehlow’s own material without citing the source. With respect to Mathew’s conclusions, he says that ‘it cannot be too strongly stressed that R. H. Mathews groups the marriage classes of the Aranda in a quite arbitrary way in order to prove his theory’ (part IV, I, 1913: 71).
According to Strehlow, both the eight classes of the Northern Aranda and the four classes of the Southern Aranda are divided into two major groups. Although Spencer and Gillen say that these two groups or moieties are not named, Strehlow reports three different sets of names for them, as used by the Aranda. They call them Alurinja, the moiety that in the Southern Aranda is divided into the Purula and the Kamara sections, and Kwatjarinja, the moiety that in the same region is divided into the Panaka and the Paitara sections.
The Aranda also apply the terms Nákarakia and Etnákarakia to these divisions. Nákarakia derives from nuna, we, na, father, and inkaraka, all; thus the term is translated by Strehlow as ‘we the fathers and everybody’, i.e. ‘our whole kindred’ or ‘all of us’. Etnákarakia derives from etna, they, and inkaraka, all; the term is therefore translated as ‘their fathers and everybody’ or ‘their whole kindred’ or ‘all of them’ (Strehlow 1907-20; part IV, I: 62). On page 63, Strehlow further translates Etnákarakia as ‘those people’. These two terms, Nákarakia and Etnákarakia, are not absolute designations of groups, but are relative terms which designate reciprocally own moiety and the opposite moiety (p. 62).
The third set of names by which the Aranda designate their moieties are Lakakia, which corresponds to Nákarakia and means ‘our people’, and Maljanuka, which corresponds with Etnákarakia and means ‘my friends’ (Strehlow 1907-20; part IV, I: 63).
Children belong to the class of their father’s father, Strehlow says, and when a ‘wrong’ marriage takes place, that is, when a man marries a woman who is not his noa (‘wife’), the child born of such a marriage is also ‘ascribed to the class of his father’s father (paternal grandfather)’. He then adds that ‘these cases only confirm the rule that the class is transmitted in the paternal line, not in the maternal’ (1907-20; part IV, I: 71).
In accordance with this, Pink, who was also among the Aranda, says: ‘when “wrong” marriages do take place, the problem of descent is mechanically solved by the children invariably going into the other couple of subsections to their father, thus utterly ignoring their mother’s subsection’ (1936: 297).
The list of terms in Strehlow’s report is reproduced in Table 3.6
Table 3 |
||
| I. | aranga | FF, FFeB, FFyB, FFZ, WFM, SS, SD, BSS, BSD, WZSS, WZSD |
| 2. | palla | FM, FMZ, FMB, WFF, ZSS, ZSD, WBSS, WBSD, HBSS, HBSD |
| 3. | tjimia | MF, MFeB, MFyB, MFZ, WMM, HMM, DS, DD, BDS, BDD, WZDS, WZDD |
| 4. | ebmanna | MM, MMZ, MMB, WMF, ZDS, ZDD, WBDS, WBDD, FZSW, MBSW, DS (w.s.), DD (w.s.) |
| 5. | kata | F, FB |
| 6. | knaia | F (w.s.), FB (w.s.), SSS |
| 7. | maia | M, MZ, FBW |
| 8. | wonna | FZ, MBW |
| 9. | kamuna | MB, FZH, DH, BDH, WZDH |
| 10. | antara | WF, WFZ |
| 11. | marra | WM, DH (w.s.), DHB (w.s.), WBSW, WBDH, ZDH, ZSW |
| 12. | kalja | eB, FeBS, MeZS, MeZH |
| 13. | itia | yB, FyBS, MyZS, WyZH, HyZH, yZ, FyBD, MyZD, WyBW, HyBW |
| 14. | kwaia | eZ, FeBD, MeZD, WeBW, HeBW |
| 15. | ankalla | FeZS, MeBS, FyZS, MyBS, FeZD, MeBD, FyZD, MeBD |
| 16. | noa | W, WZ, FBSW, H, HB, FBDH (w.s.), MZDH (w.s.) |
| 17. | mbana | WB, ZH, FBDH, MZSW |
| 18. | intanga | HZ, eBW (w.s.), yBW (w.s.), FBSW (w.s.), MZSW (w.s.) |
| 19. | iliarra | FZDH, MBDH |
| 20. | alirra | S, D, BS, BD, HZS, HZD, [FFF] |
| 21. | Amba | ZS, ZD, WBD, HBS, HBD, HF, S (w.s.), D (w.s.), ZC (w.s.) |
| 22. | namara | SW, BSW, WZSW, HF |
| 23. | nêrra | SW (w.s.), ZSW (w.s.), HBSW, HM |
According to this table, a diagram can be drawn of the Aranda relationship terms as in Figure 4. In this diagram it is possible to see that the terms compose four patrilines, that they alternate by genealogical level in each line, and that they can also be arranged symmetrically.
T. G. H. Strehlow, who in 1947 talks about the ‘typically Aranda patrilineal order’ (1947: 71), reproduces in his book Fry’s table of the relationship between subsections (Fry 1931). This table is consistent with the data provided by Spencer and Gillen and by C. Strehlow, and we have arranged it as in Figure 5. From Figures 4 and 5 it can be seen that the arrangement of the relationship term is perfectly consistent with the arrangement of subsections. In both cases, the same principles are followed. In Figure 4 there are four patrilines arranged in two formal divisions, and in Figure 5 there are four lines of subsections that are also patrilineally transmitted and belong to two moieties. The moieties, as we have seen, were actually patrilineal, i.e. they each contained four subsections patrilineally transmitted, and were actually named. The terms alternate according to genealogical level within the patrilines (see Figure 4), and the subsections are also transmitted by alternate genealogical level within the same moiety and the same line. The terms are disposed symmetrically in Figure 4, and the relationship between subsections, as shown in Figure 5, is also symmetrical.
Figure 4 Aranda relationship terminology (cf. Table 3)
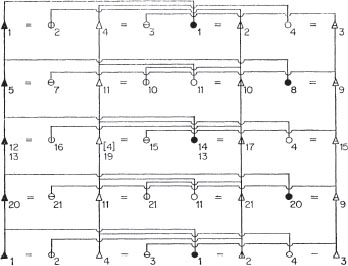
With regard to totemic groups, all the ethnographers concur in their findings that none of the totemic groups definable for the Aranda was exogamous.
Figure 5 Relationship between subsections among the Aranda (after Fry, in Strehlow 1947: 173-4)

Note: 1 = Panaka 2 = Banata 3 = Knurea 4 = Paltara
5 = Purula 6 = Kamara 7 = Nala 8 = Mbijana
C. Strehlow refers to two kinds of totem. Every individual belongs to one totem that is neither patrilineal nor matrilineal but which depends on the place where the mother first became aware of her pregnancy. Thus the children of one mother can belong to different conceptional totems (ratapa). At the same time, every individual also belongs to another totem (altjirà), which is inherited from the mother: ‘thus, each individual is connected with two totems; one totem to which he belongs by birth and the second which belongs to him and which is inherited by him through his mother’ (Strehlow 1907-20; part II, II: 58).
T. G. H. Strehlow does not, however, refer to totems inherited from the mother, but to the conception-site totem and to the local totemic clans that include the ‘own nearest male relatives’ (1947: 120). In his account, even the tjurunga objects and ceremonies that ‘belong’ to an individual, and depend on the conception-site totem, are passed, after the death of the owner, into the possession of his son or of some other male relative if the son is still too young (1947: 133).
VIII
Durkheim, basing his argument on the Spencer and Gillen report of 1899, infers the previous existence of matrilineal ‘phratries’ among the Aranda in order to explain the formation of the sections and subsections. His hypothesis is that they had matrilineal moieties and matrilineal exogamous totems, which, in combination with the patrilocal groups, produced the system of sections and subsections (1902: 109-11). Once the new divisions (all of them patrilineal) were established, the former matrilineal groups lost their function of regulating relationships and, as such, they disappeared.
Radcliffe-Brown in 1931 talks about matrilineal moieties among the Aranda, but in his case they seeem to be a formal inference from the composition of the relationship terminology. ‘The Aranda system of eight subsections, of course, involves the existence of a pair of matrilineal moieties though they are unnamed’ (Radcliffe-Brown 1931: 27).
For Lévi-Strauss, instead, the matrilineal moieties and matrilineal descent among the Aranda seem to be not an inference but a fact. The moieties are ‘elements’ of the system. In his own words:
The generalized system goes beyond the Kariera system since it employs the same number of elements as the Aranda system, if not of the same nature: two moieties (patrilineal in one case, matrilineal in the other), and a four-component complex (of lines in one and local groups in the other) (Lévi-Strauss 1949: 272).
The matrilineal moieties of the Aranda are thus for Durkheim a hypothetical condition for an evolutionary explanation, for Radcliffe-Brown an inferred entity, and for Lévi-Strauss objective institutions defining ‘descent’, even when their existence is not reported in the ethnography.
Lévi-Strauss represents the Aranda system by the names of two French families and four French towns, ‘following the double stipulation that the family name be transmitted in the maternal line, and the residential name in the paternal line’ (1949: 212). The system is then said to be homologous to the following combinations:
| If a man | marries a woman | the children will be |
| Durand of Caen | Dupont of Laon | Dupont of Caen |
| Durand of Laon | Dupont of Lille | Dupont of Laon |
| Durand of Lille | Dupont of Lyons | Dupont of Lille |
| Durand of Lyons | Dupont of Caen | Dupont of Lyons |
| Dupont of Caen | Durand of Lyons | Durand of Caen |
| Dupont of Laon | Durand of Caen | Durand of Laon |
| Dupont of Lille | Durand of Laon | Durand of Lille |
| Dupont of Lyons | Durand of Lille | Durand of Lyons |
No matrilineal descent groups are reported in the Aranda ethnography. The only hint of a matrilineal transmission of anything among the Aranda is the inheritance of the altjirà totem from the mother, reported by C. Strehlow. Lévi-Strauss, however, does not so much as mention this source of evidence.7 Yet even supposing that these hypothetical matrilineal moieties, either recognized by the Aranda or inferred by the analyst, could be established, this solitary matrilineal transmission could not be the fundamental characterization of ‘descent’ when all the other factors that define the status of an Aranda individual are transmitted patrilineally.
IX
Durkheim proposed the hypothesis of former matrilineal moieties in order to account for the existence of sections and subsections as far as they contained categories belonging to alternate genealogical levels. That is, he was explaining the alternation.
For Lévi-Strauss, instead, the main issue is the relationship between disharmonic regimes and ‘restricted exchange’. He employs Durkheim’s independent variables (patrilocality and matrilinearity), but as the cause of a different consequence.
Right or wrong, Durkheim’s hypothesis has a logical argument. Lévi-Strauss’s hypothesis, by contrast, establishes a link between two variables which are not logically related. Apart from the fact that the Aranda system seems to refute the hypothesis, there is no demonstrated logical connection between patrilocal residence, matrilineal descent, and a symmetric rule of marriage.
In Durkheim’s hypothesis symmetric exchange is a condition: the societies considered possessed, according to him, exogamous matrilineal ‘phratries’ and patrilocal groups. These two factors are together responsible for the separation of alternate generations into different sections or subsections. Adjacent generations within a single group belong to different matrilineal moieties, and this is the reason why they are separated into different sections. In other words, adjacent generations within a single patrilocal group belong to different moieties, but as they live together they are ‘too near’ to intermarry (Durkheim 1898: 19).
For Lévi-Strauss, symmetric exchange is not a condition but a result. ‘Every disharmonic regime leads to restricted exchange,’ he says; also, the form of exchange ‘depends’ on the harmonic or disharmonic character of the regime considered (1949: 612). But a disharmonic regime ‘leads’ (conduit) to restricted exchange when restricted exchange existed already, and what Lévi-Strauss is really trying to explain is the passage from one form of restricted exchange to another. This can be seen from the following quotation:
disharmonic systems have naturally developed towards organizations with marriage classes, because, in such systems, direct exchange is the simplest and most effective process for ensuring the integration of the group (Lévi-Strauss 1949: 550).
Thus ‘restricted’, ‘direct’, or ‘symmetric’ exchange8 already exists before disharmonic regimes can ‘lead’ to another form of restricted exchange. The kind of restricted exchange that is prior to the relationship between disharmonic regimes and another form of restricted exchange is a system with exogamous moieties. ‘The moiety system is based solely upon descent, and the harmonic or disharmonic features of the corresponding regime are confused’ (Lévi-Strauss 1949: 273). From here, the pronouncement that the form of exchange ‘depends’ on the harmonic or disharmonic character of the regime is difficult to follow. It is also difficult to understand how one can ‘reconstruct a priori’ the kind of exchange structure one is dealing with ‘from one question and one alone: in the society concerned, what is the relationship between the rule of residence and the rule of descent’ (1949: 612). How can one know beforehand when the harmonic or disharmonic features of the regime are going to be ‘confused’? Or is one to think that when ‘regime’ cannot be defined because ‘locality’ and ‘descent’ are ‘confused’, one is not dealing with an ‘elementary structure’? If this were so, a system with exogamous moieties and a corresponding two-line symmetric prescriptive terminology could not be classified as an elementary structure. This would certainly be an odd conclusion.
Either restricted exchange ‘depends’ on disharmonic regimes or it does not. If it does in some cases and does not in some others, one cannot ‘reconstruct a priori‘, from the indications of the rule of residence and the rule of descent, what the mode of exchange will be.
X
To return to Boudon’s characterization of Lévi-Strauss’s theory, the hypothesis considered above does not explain ‘a great number of facts’. What is more, it can be shown to be false. On the other hand, if by ‘les règles de mariage peuvent être analysées à partir des seules règles du mariage’ Boudon refers to Lévi-Strauss’s ‘deduction’ of the rule of marriage with the matrilateral cross-cousin and the rule of marriage with the second cross-cousin from the rule of marriage with the bilateral cross-cousin, this deduction is neither supported by the facts nor reduced to a relationship between rules of marriage. Lévi-Strauss’s logical derivation of the matrilateral or patrilateral cross-cousin marriage and of the second cross-cousin marriage from cross-cousin marriage, takes into account a factor other than the rules, namely harmonic and disharmonic regimes; and in any case neither the logical relation between the rules nor their relationship to another factor can be confirmed with the very facts he presents.
1 Bush’s work and Kemeny, Snell, and Thompson’s formulations are analysed in chapter 7 below.
2 For the sake of clarity we deliberately leave aside Lévi-Strauss’s use of the term ‘preference’ as synonymous with ‘prescription’ in the definitions already discussed. The problems raised by the synonymous use of the two concepts in the context of Lévi-Strauss’s definitions of ‘elementary’ and ‘complex’ are specifically analysed in chapter 3 below.
3 cf. Fox 1969.
4 We follow here Lévi-Strauss’s reasoning in the preface to the second French edition of Les Structures élémentaires de la parenté (pp. xxiv-xxx), which is different from the ideas expressed in 1949: 576, where Crow–Omaha systems are considered as sometimes having and sometimes not having a prescriptive rule (cf. Needham 1964b: 312-13).
5 As a matter of fact, with only these specifications to go on, we certainly cannot be sure that for a Crow man ‘twelve out of thirteen women’ are a ‘possible spouse’. The information that the Crow Indians have thirteen exogamous clans can tell us only that a Crow looking for a wife can choose from all the women of the Crow society minus the number of women belonging to his own particular clan. But any anthropologist dealing with the Crow society would correct this information, knowing – by the very definition of the type – that at least two clans in addition to Ego’s will be forbidden as sources of a wife.
6 Strehlow arranges the terms by ‘classes’, i.e. aranga, palla, etc., and gives a descriptive combination of terms for each genealogical specification within each class, e.g. aranga knara, FFeB, aranga larra, FFyB, etc.
7 In La Pensée sauvage (1962), Lévi-Strauss cites both the fourth volume of Strehlow’s Die Aranda- und Loritja-Stämme in Zentral-Australien and T. G. H. Strehlow’s Aranda Traditions (1947). He describes the Aranda as having ‘filiation patrilinéaire’, totemic affiliation not dependent on a rule of descent, non-exogamous totemic groups, and eight subsections (1962: 108). On the very next page, nevertheless, he again represents the Aranda system as composed of matrilineal moieties (1962: 109).
8 Lévi-Strauss employs these three adjectives to qualify the same kind of exchange.