Permutation Models and Prescriptive Systems
I
The Appendix to the first part of Les Structures élémentaires de la parenté written by André Weil on the ‘Algebraic Study of Certain Types of Marriage (Murngin System)’ (Lévi-Strauss 1949: 278-85), inaugurated a series of articles on the mathematical treatment of marriage rules.1
The goals of such an effort are not self-evident. According to Piaget, Lévi-Strauss ‘has succeeded in discerning, in various kinship organizations, algebraical network structures and transformation groups, etc., which he has been able to formalize with the aid of mathematicians such as A. Weil and G. Th. Guilbaud’ (1968: 92). Weil himself states that the purpose of his work is ‘to show how a certain type of marriage laws can be interpreted algebraically, and how algebra and the theory of groups of substitutions can facilitate its study and classification’ (Weil 1949: 278). In Kemeny, Snell, and Thompson (1957: 343-53) the emphasis is didactic, and concentrates on how permutation matrices serve also to represent marriage rules in primitive societies. For Bush, ‘when the rules of marriage and descent are sufficiently specific and unique we might expect to describe the system mathematically’ (Bush 1963: 159).
We intend to analyse here some of the works dealing with the mathematical expression of marriage rules (Weil 1949; Kemeny, Snell, and Thompson 1957; Bush 1963; White 1963; Courrège 1965) and to do so by considering them under several aspects: (1) the purposes of mathematical translation of this sort; (2) the premises on which the different works are based; (3) the relevance of the empirical examples adduced.
II
All the works mentioned above are concerned primarily with the mathematical expression of ‘marriage rules’. A mathematical expression of a social phenomenon of any sort constitutes, in the first place, a translation into a formal notation. The possible purposes of translating in general would seem to be: (i) to communicate with a public who do not understand the original; (ii) to record or transmit information in a more synthetic form of expression; and (iii) to express a certain content in a language permitting operations to be carried out that are not possible by means of the language in which that content was originally expressed.
The general content and presentation of the works under consideration are very similar and consist of a number of conditions and axioms describing the sort of system and units they are going to deal with, the mathematical devices they employ to represent rules of marriage and descent, and some examples of their application to the data on concrete societies.
Let us summarize the specific content of each of the works, and then try to assess which of the possible purposes of a translation they fit.
III
Weil (1949) deals with societies in which:
the individual men and women are divided into classes, each person’s class being determined, according to certain rules, by those of his parents. According to the respective classes of a man and of a woman, the marriage rules indicate whether they can marry or not (Weil 1949: 278).
He also postulates two conditions:
(A) For any individual, man or woman, there is one and only one type of marriage which he (or she) has the right to contract. (B) For any individual, the type of marriage which he (or she) may contract depends solely on sex and the type of marriage from which he (or she) is descended (Weil 1949: 279).
He proposes ‘f(Mi)’ as the notation for the type of marriage of a son descended from marriage Mi, and the notation ‘g(Mi)’ as that for the type of marriage of a daughter descended from the same type Mi. Knowledge of the two functions ƒ and g, he says ‘completely determines the marriage rules in the society studied’ (Weil 1949: 279).
Weil then presents three examples: (1) a society with four classes and generalized exchange (p. 279); (2) a society with four classes and restricted exchange (280-1); and (3) a society with eight classes and two ‘marriage formulas’ to be applied alternatively (281-5). He demonstrates in each case how f(Mi), i.e. son’s marriage type, and g(Mi), i.e. daughter’s marriage type, can be expressed as permutations of the set parent’s marriage types (Mi. . .Mn). He also demonstrates that in the third case marriage with father’s sister’s daughter, expressed by the formula

is not possible.
IV
Bush (1963)2 works with societies in which:
rather specific clans, moieties, generations, etc., are culturally defined for each man, his wife and his children. This permits us to distinguish a specified number of possible marriage types and to deduce from the ethnographic material the allowed marriage type of a man or woman when we know the marriage type of his or her parents (Bush 1963: 159).
He introduces the notions of matrix (p. 161), permutation operator (p. 161), vector (p. 161), cyclic group (p. 162), commutation of two operators (p. 162), and some others, which he applies to the Kariera, the Tarau, and the Aranda systems. In the first case, viz. Kariera, applying different operations to the matrices representing parents’ type of marriage and children’s type of marriage, he reaches the ‘interpretation’ that:
my daughter’s son and my son’s daughter may contract the same type of marriage and hence may marry one another (p. 166),
and, further, that
I belong to the same class as my daughter’s son’s daughter’s son if I am a man or to my son’s daughter’s son’s daughter if I am a woman (p. 166).
As for the Tarau, Bush gives the names of what he calls their ‘four classes’, and the rules of marriage and descent, and ‘deduces’ that
a child is always of the same class as his or her father (p. 167);
cross-cousin marriage is permissible (p. 167);
my daughter’s daughter’s daughter’s daughter must contract the same type of marriage as I have (p. 168).
In the case of the Aranda, he describes them as having eight classes and again ‘deduces’ that
my daughter’s son’s son may marry my son’s daughter, i.e. . . . a man may marry his father’s mother’s brother’s son’s daughter (p. 170);
my daughter’s son’s daughter may marry my son’s son’s son (p. 171);
a man can marry his mother’s father’s sister’s daughter’s daughter (p. 171).
V
Kemeny, Snell, and Thompson deal with ‘Marriage Rules in Primitive Societies’ in sections 7 and 8 of the seventh chapter of their book Finite Mathematics (1957). According to White, these brief sections ‘are a major advance over the previous work (viz. Weil 1949)’ (White 1963: 32), because the properties of the societies to be investigated are formulated as an integrated set of axioms.
In the first section devoted to marriage rules (section 7, pp. 343-8), their seven axioms postulate conditions that do not differ from those proposed by Weil. They indicate, as in Weil’s work, that ‘each member of the society is assigned a marriage type’ (Kemeny, Snell, and Thompson 1957: 343 [Axiom I]). They adopt the same mathematical device as Bush proposes, and they give a number of problems to be solved by the reader, again using as examples the Kariera and the Tarau systems. The problems posed are of this form: given the ‘marriage types’ of parents, sons, and daughters, find the ‘rules’ that allow cross-cousin marriage, for instance, or the matrices that represent rules of descent and ‘marriage type’ of sons and daughters.
In the second section devoted to the subject (section 8, pp. 348-53) they consider the axioms 5, 6, and 7 proposed in the previous section. They present for each of the axioms the expressions that represent them in terms of matrices representing son’s marriage type and daughter’s marriage type. Axiom 6, for example, which states that ‘in particular, no man is allowed to marry his sister’ (p. 343), requires, they say, that S-1D be a complete permutation, which is an immediate consequence of the fact that the matrix of the brother-sister relationship is S-1D (p. 350).3 They finally give an example (pp. 351-2) of how to calculate how many possible combinations of rules of descent and ‘marriage types’ (of parents, sons, and daughters) exist in societies with four ‘marriage types’: the possibilities, they conclude, are six, and two of these six are said to be exemplified in known societies, viz. the Kariera and the Tarau.
VI
White devotes the main part of his book, An Anatomy of Kinship (1963), to the ‘descriptions’ of ‘kinship structures that satisfy Kemeny-Snell-Thompson’s axioms’ (p. 32). He proposes only one conceptual modification: namely, to change the expression ‘marriage type’ in axiom 1 to that of ‘clan’, because ‘marriage type’ is ‘not a concept to be found in the field notes of anthropologists or the thinking of members of the societies’ (p. 32). ‘Clan’, instead, is defined as ‘the largest group of persons in a tribe who follow the same preferential marriage rule with respect to other clans’ (p. 33).4
The book is concerned with ‘models of kinship systems with prescribed marriage’ (as the title of the second chapter states). It presents an analysis of the mathematical definitions of a ‘typology of societies’, and an application of these models to ‘known tribes,’ viz. Kariera, Arunta, Murngin, Purum.
The typology presented in chapter 11 (p. 42) consists of:
I Bilateral marriage, in which W2 = I and WC = CW;
II Matrilateral marriage, in which WC = CW, but W2 ≠ 1;
III Patrilateral marriage, where WC = CW-1, but W2 ≠ 1;
IV Paired clans, where W2 = ƒ, and WC ≠ CW;
V Residual.
In these definitions, W is the permutation matrix of side n (n = number of clans) and where ‘each row of the matrix corresponds to a husband’s clan, the wife’s clan being identified with the column in which the number 1 appears in that row’ (p. 35); and C is the permutation matrix in which ‘Cij = I if fathers of clan i have children of clan j’ (p. 35).
A major reformulation over the previous works consists in White’s proposal of the matrices W and C instead of (as in the case of Kemeny, Snell, and Thompson) the matrices representing the transformation of parent’s marriage type into son’s and daughter’s marriage type. This reformulation derives from the change of the concept of ‘marriage type’ for that of ‘clan’.
A fundamental question for White is to answer ‘what kind of relations can marry in a society specified by given C and W matrices’ (p. 39). But prescriptive marriage types are for White only ideal types, limiting cases [in his book he succeeded in deriving ideal types only (pp. 148-9)], and the problem is not ‘whether a tribe has a prescriptive as opposed to a preferential marriage system, but rather to what extent the tribe conforms to one or to some mixture of ideal types of prescribed marriage systems’ (p. 148).
VII
In Courrège’s ‘Un modéle mathématique des structures élémentaires de parenté’ (1965), the intention is:
to present, using the axiomatic method, a simple mathematical model that enables the study, for societies where the population is divided in discrete matrimonial classes, of the functioning K of the kinship system, i.e. the rules of marriage and descent expressed uniquely as a function of these classes (p. 248).
The mathematical model presented was built, Courrège says, to represent some of the kinship structures studied by Lévi-Strauss in Les Structures élémentaires, and specifically the Kariera, the Aranda, and the Murngin systems (p. 248), but it is also intended as a basis for classifying any kinship system with n matrimonial classes.
An elementary structure of kinship on a finite set S, says Courrège, is any triad (ω, μ, π) of permutations of S satisfying the following axiom:
(D) π = μω (p. 253).
The ethnological meaning of S, ω, μ, π, is: the set S represents the set of classes of the society considered (and not, as White proposes, the set of individuals); the conjugal function ω represents a positive rule which ‘prescribes’ that a man of class  shall choose his spouse in class ω (x); the maternal function μ represents a positive rule which ‘prescribes’ that all the children of a woman of class
shall choose his spouse in class ω (x); the maternal function μ represents a positive rule which ‘prescribes’ that all the children of a woman of class  belong to class μ,(x); and the paternal function π represents the same positive rule which ‘prescribes’ that all the children of a man of class
belong to class μ,(x); and the paternal function π represents the same positive rule which ‘prescribes’ that all the children of a man of class  belong to class π (x).
belong to class π (x).
Courrège goes on consistently giving mathematical expression to every possible analytical element in Lévi-Strauss’s definition of elementary structures. An example of this is the ‘condition for marriage between cross-cousins’ (p. 261), where one learns that
if a structure allows marriage with the matrilateral cross-cousin, in order for it to permit marriage with the patrilateral cross-cousin as well it is necessary and sufficient that it be a structure of restricted exchange.
This condition is expressed in Courrège’s terminology by the following implication:
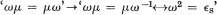
the verification of which is, he adds, ‘immediate’.
One learns also that:
for a set S of four elements, any regular structure allows marriage with the matrilateral cross-cousin (p. 26I), and that in such a structure patrilateral cross-cousin marriage is also allowed, so that for the ‘structure’ (ω1, μ1 π1) and a set of four elements, S = {p, q, r, s},

from which it may be ‘verified’ that

This structure (ω1, μ1 π1) is to be called a ‘Kariera structure’ (p. 262).
He also gives formulations of this kind for a ‘theoretical Murngin structure’, ‘structures of generalized exchange’, and an ‘Aranda structure’.
VIII
A common feature of all the articles examined is that none of their ‘deductions’ or ‘interpretations’ adds anything to the ethnographical facts known for any of the social structures analysed. Moreover, the ‘deductions’ or ‘rules’ that one is supposed to derive from Kemeny, Snell, and Thompson’s exercises are facts readily available in the ethnographic accounts of any of the systems considered, and to know them is the first task of any anthropologist working on these topics. They are simply the basic data to consider when analysing a system anthropologically.
Thus one could hardly say that purpose (iii) of a translation, i.e. to be able to effect new developments by means of the translation applies to this case, at least from an anthropological point of view. Needless to say, purpose (i), viz. to communicate with a wider public, is out of the question, for what Leach says of White’s book applies to all the works considered:
The book is, in part, explicitly addressed to anthropologists (Preface), 99.9 per cent of whom could not read it even if they wanted to (Man 1964: 156).
Finally, what we have called purpose (ii) of a translation (to record and transmit information in a more synthetic form of expression) does not seem to be the case here either, for not only is it not the intention of the authors but one cannot see the point in transmitting the information in that way.
One consideration about this sort of formalization remains: sometimes, just by the effort of expressing a certain body of theory in a more formal language, the assumptions and premises involved become clearer or are made more explicit. With this possibility in mind, we shall analyse in the next section the axioms on which the works considered above are based.
IX
We need not take into account all seven of Kemeny, Snell, and Thompson’s axioms, but just the first one and the variations on it in the rest of the articles on the subject.
The development of that axiom can be approached by way of Weil’s statement that ‘the individual men and women are divided into classes’ (p. 278), and one of the conditions he posits: ‘for any individual, man or woman, there is one and only one type of marriage he (or she) has the right to contract’ (p. 279).
As we have seen above, Bush expresses this idea as follows:
rather specific clans, moieties, generations, etc., are culturally defined for each man, his wife and his children. This permits us to distinguish a specific number of possible marriage types (p. 159).
Kemeny, Snell, and Thompson adopt this notion in their first axiom: ‘each member of the society is assigned a marriage type’ (p. 343).5 White proposes instead to change the expression ‘marriage type’ to ‘clan’, because the former is not an anthropological concept. Therefore, he translates the first axiom into the following propositions:
(1) the entire population of the society is divided into mutually exclusive groups, which we call clans;
(2) there is a permanent rule fixing the single clan among whose women the men of a given clan must find their wives (p. 34).
Finally, Courrège deals with societies in which the population is divided into discrete matrimonial classes and where the rules of marriage and descent are expressed uniquely as a function of these classes (p. 248).
We can summarize the different definitions of the types of society with which these authors are dealing as in Table 11. They are all supposed to be dealing with the mathematical interpretation of Lévi-Strauss’s ‘structures élémentaires’, or at least, let us say, with societies in which the regulation of marriage is expressed as a positive rule. In other words, they are all trying to classify prescriptive systems, i.e. to classify societies that possess closed systems of classification.
Table 11
Operational Concepts in Permutation Models
| author | society divided into | units to be analysed |
| Weil (1949) | classes | marriage types |
| Bush [195?] | 'rather specific’ clans, moieties, generations | marriage types |
| Kemeny, Snell, & | [unstated] | marriage types |
| Thompson (1957) | ||
| White (1963) | clans | clans |
| Courrège (1965) | classes | rules of marriage |
X
In the light of the examples we have considered in this monograph, it is clear that what is meant by a ‘prescriptive system’ is a system in which the terminology constitutes a closed classification that implies a prescribed category of spouse.6 The defining features of prescriptive systems are then:
1 a lineal classification;
2 a closed classification; and as an aspect of this,
3 a necessary affinal relationship between categories that can be genealogically specified.
The defining features of these systems are not, therefore, a particular kind of ‘mutually exclusive groupings’, ‘rather specific clans’, or ‘marriage classes’, but specific modes of social classification that define one category as the prescribed spouse, or what Fison called in 1895 an ascriptive ‘marital right’ regarding certain categories of persons.7 From the point of view of an individual in a society that possesses a prescriptive terminology, what counts in the selection of the spouse is primarily the people classified in terms of the prescribed category. Thus the Dieri marry a nadada, and this prescription is related to their special kind of classification and not to actual discrete groups.
The fact that there exist in the societies considered actual institutions or groups related to their social classification is independent of the prescriptive character of their terminologies, since these groupings or institutions vary from one society to another. The ‘sections’ and ‘subsections’ of the Aranda have a local reference and differ in any institutional respect from the matrilineal totemic clans of the Dieri. The ‘sections’ or ‘semi-moieties’ of the Mara, in turn, do not define their system of classification and are not comparable with either the subsections of the Aranda or the clans of the Dieri. The ngaiva of the Iatmül do not in themselves define the Iatmül social classification, and are not similar to the subsections of the Aranda, the clans of the Dieri, or the ‘semi-moieties’ of the Mara.
XI
What then is a ‘marriage type’ and what is a ‘clan’, in the sense White gives to the latter term? How to classify by means of permutation models systems that possess a prescriptive terminology and no ‘classes’?
Concerning ‘marriage types’, there is no possible way to find an empirical referent for such a conceptualization. Even in the case of a two-line symmetric prescriptive terminology, concomitant with four sections, as in the Kariera case, there exists only one prescribed category, and the fact that the people denoted by that category belong to different sections in consecutive genealogical levels does not alter the definition of the terminology or the prescription of a single category.
If we were to classify such a system by its terminology, it would belong to the class of two-line symmetric prescriptive terminologies, which could in turn be subdivided into systems that possessed a concomitant set of sections8 and systems that did not. But this subdivision would be composed of subclasses defined by a criterion different from the kind of terminology.
If, instead, we considered the existence of sections as the basic feature, we would create a classification from which systems with prescriptive terminologies of the same sort but without ‘classes’ would be excluded. In this latter case, the systems to classify would be fewer than in the first case.
While the terminological criterion cuts quite neatly between systems with or without prescriptive terminologies, the ‘section’ criterion has to deal with a heterogeneous set of systems, some of them with a set of sections concomitant with their relationship terminologies, some of them possessing sections not related to marriage alliances at all.
Still, our point here is that any prescriptive system possesses only one prescribed category, so that the concept of ‘marriage types’ is hard to visualize.
Regarding ‘marriage classes’, next, let us start by considering the definition of them in the second edition of Lévi-Strauss’s Les Structures élémentaires de la parenté:
I adopt a much broader definition of marriage class; i.e. class is defined unequivocally, such that the members of the class have certain marriage constraints which are different from those imposed on the members of another class (1967: 310).
If we adopt this definition, the term becomes confused with that of ‘marriage type’ as used by Weil, Bush, and Kemeny, Snell, and Thompson, and with that of ‘clan’ as used by White.
In this case one cannot do less than point out that Weil’s use of both terms, viz. ‘class’ and ‘marriage type’, becomes redundant. But that could be just Weil’s problem and we could still consider the relevance of the concept. In connection with this point, let us consider first a modification Sperber suggests for the formalization of the ‘Kariera structure’ (Sperber 1968: 225-6). He considers an example in which there are two hypothetical systems, E and F, the models of which are:

E is a system of two exogamous patrilineal classes (moieties).
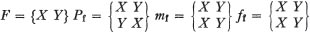
F is a system of exogamous matrilineal moieties.
One is able to construct a system G, which is the product of E and F:
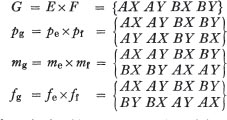
The model thus obtained is a representation of the Kariera system, Sperber says, but he adds that the Kariera do not possess actual matrilineal moieties, so the system could be derived from E and, instead of F (exogamous matrilineal moieties), a rule of alternation of generations, which he calls H and represents as follows:

But if one rejects the first formulation he gives, because it is not convenient to introduce in the models ‘potential matrilineal moieties’, what is the ground for Lévi-Strauss’s ‘marriage classes’, which also are a ‘conceptual tool’ and do not always have an actual empirical referent?
Another problem in the reformulation presented by Sperber is that ‘alternation of generations’ is not a ‘rule’, but a distinctive feature (itself the resultant of certain principles, cf. chapter 6) of a type of terminology, in the case of a four-line symmetric prescriptive terminology, or a rule superimposed on a two-line symmetric prescriptive terminology. It does not seem convenient, therefore, to introduce it into the models.
XII
There is a further consideration on the validity of permutation models that derives from our definition of prescriptive terminologies. The question is whether the models would apply if the symbols A, B, . . . N, in the models were redefined as the component lines of prescriptive terminologies; i.e. in which the lines corresponded to the arrangements of the terms as they were put into practical effect by the people who actually employed these terminologies.
Let us consider the case of symmetric prescriptive terminologies. In the case of one of these terminologies composed of two lines, we could consider these two lines as A and B. A would be the set of terms that form a line; B the set of terms that form the opposite line.
The functions m, ƒ, and w employed in the permutation models would represent the relationship between categories in the terminology according to (i) line, and (ii) prescribed category.
Thus m would represent the relationship between categories specified as M (mother) and C (children); ƒ, the relationship between categories specified as F (father) and C (children), and w, the relationship between categories specified as H (husband) and W (wife).
A system E, defined by a two-matriline prescriptive terminology, would be represented as follows:9
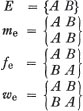
This system does not seem to present any inconvenience and the logic seems to be the same as when considering the symbols A, B . . . N, representing actual groupings in a ‘two-section system’.
Let us consider now the case of a four-line prescriptive terminology. We will take the Dieri as our example. A system S, thus, will be composed of A, B, C, D, each of the symbols representing a matriline. Lines A and B correspond to one division of the terminology and have their prescribed categories in C and D, which compose the opposite division. The prescribed categories for C and D, then, belong to A and B.
The system S can be represented as follows:
S = {A B C D}
Function m is represented as:

That is to say, the categories specified as C (children) belong to the same line as the categories specified as M (mother).
Function ƒ is represented as:

in which the subindices 1 and 2 stand for different genealogical levels: 1 for levels I, III, and V, and 2 for levels II and IV.
But, even without going any further, it can be seen that m and ƒ do not represent permutations; and there is no way to transform a permutation composed of A, B, C, and D into fs by means of a rule of alternation of genealogical levels such as the rule H proposed by Sperber for the Kariera.
Still, one could consider the four lines (A, B, C, D) and the alternating levels 1 and 2 and represent the Dieri terminology as:

In this representation of a four-matriline symmetric prescriptive terminology:
(i) there is no way of composing this system deductively from any previous system (cf. Sperber 1967: 224-6), not even by applying a rule H; and
(ii) setting aside the deductibility of the model, as a representation of the Dieri terminology, it does not express anything more clearly or more revealingly than a diagram such as in Figure 12 (p. 65). Moreover, in order to state ms, fs, and ws one has to construct the diagram first.
From this last point, one wonders, therefore, whether it would not be better to represent the terminologies in the usual and considerably simpler form of a diagram. In this connection, Lévi-Strauss states:
I fail to see why an algebraic treatment of, let us say, symbols for marriage rules, could not teach us, when aptly manipulated, something about the way a given marriage system actually works, and bring out properties not immediately apparent at the empirical level (1960b: 53).
After considering the works devoted to the algebraical treatment of prescriptive systems, we fail to see, instead, what are the advantages of such a treatment and what ‘properties not immediately apparent at the empirical level’ they bring out.
1 This chapter constitutes my contribution to Korn and Needham 1970.
2 The date of composition of Bush’s work is unknown. White, who describes it as a ‘pioneer’ piece on the mathematics of kinship (1963: viii), published it for the first time as an appendix to his own book (159-72). He supplies no information on its previous circulation. It was certainly written after 1949, since it refers to Les Structures élémentaires de la parenté, and evidently before 1957, when Kemeny, Snell, and Thompson acknowledge their obligation to ‘the work of . . . Robert Bush’ (1957: 343).
3 S = permutation matrix representing the marriage type of sons; D = permutation matrix representing the marriage type of daughters (Kemeny, Snell, and Thompson 1957: 346).
4 It is not claimed, though, that this definition of the term is any more likely to be found in the field notes of anthropologists or in indigenous conceptions.
5 They do not, however, provide any gloss on the operational interpretation of the qualifier that the clans are ‘rather specific’.
6 The technical distinction of a mode of alliance defined by the term ‘prescription’ seems to have been established by Hodson (1925).
7 cf. Lévi-Strauss 1949: 9; 1967:10; 1969: 8.
8 Including exogamous moieties in correspondence with a two-line terminology.
9 We are considering a terminology composed of matrilines for the sake of continuity with our next example.