4
From Logic to Graphs for Semantic Representation

In this chapter, we shall show how graph structure can be used to represent sentence semantics.

Truth-conditional semantics [TAR 35] aims to determine the conditions under which a sentence is true. According to the compositionality principle put forward by Frege [FRE 26], these conditions are defined based on the meanings of the words and the way in which they are put together. The meaning of a sentence is thus represented by a logical formula. Historically, first order logic (FOL) [HEI 98] has been most widely used as a formal framework for sentence semantics.

In practice, this approach is not satisfactory: it is not able to handle ambiguity in sentences, quantifications or intentionality. A variety of formalisms have emerged, based on logic, which take account of one or more of the aspects of semantics not covered by FOL.

In this chapter, we shall present two formalisms that have been used to annotate large corpora:

• – abstract meaning representation (AMR), which focuses on a precise representation of predicate–argument relations using a lexicon. AMR has been used to annotate the English edition of Saint-Exupéry’s The Little Prince¹;
• – minimal recursion semantics (MRS), which takes an innovative approach in creating underspecified representations of scope relations between quantifiers and certain adverbs. MRS is notably used alongside the HPSG format in developing large-scale grammars in different languages, combining syntax and semantics [COP 00].

Discourse representation theory (DRT) [KAM 93] is another formalism of this type, but it is more usually applied to discourse than to sentences; furthermore, we do not wish to present an exhaustive list of semantic representation formalisms here. Without wishing to promote a specific formalism, we have selected two examples to highlight the way in which graphs may be used to model sentence semantics.

This chapter is organized as follows:

• – we shall begin by presenting FOL, the framework which underpins both AMR and MRS;
• – next, we shall present AMR. This formalism works using oriented acyclic graphs with a single root;
• – the final section is devoted to two versions of MRS: Robust Minimal Recursion Semantics (RMRS) and Dependency Minimal Recursion Semantics (DMRS). We shall show how the objects handled by these formalisms may be represented in graph form. The second variant is a compact version of the first in which variables have been eliminated. The graphs used in both cases are acyclic and oriented, but unlike AMR, they can have multiple roots.

4.1. First order logic

FOL, or predicate logic, is an extension of propositional logic designed to express quantification.

4.1.1. Propositional logic

Propositions express facts that may be true or false. They are constructed, using logical connectors, from elementary propositions.

DEFINITION 4.1.– Let A be a set of elementary propositions. The set P(A) of propositions constructed over A is defined by induction in the following manner:

• – every element in A is a proposition in P(A);
• – if P is a proposition in P(A), then ¬P (negation) is a proposition in P(A);
• – if P and Q are propositions in P(A), then P ∧ Q (conjunction), P ∨ Q (disjunction), P ⇒ Q (implication) and P ⇔ Q (logical equivalence) are propositions in P(A).

Assigning arbitrary truth values to the elementary propositions in A, i.e. giving them one of two values, true or false, we can compute the truth value of every proposition in P(A).

DEFINITION 4.2.– Let us assume that a truth value has been assigned to every proposition in A. Hence, in P(A), we establish by induction that:

• – P is true if and only if ¬P is false;
• – P ∧ Q is true if and only if P and Q are both true;
• – P ∨ Q is false if and only if P and Q are both false;
• – P ⇒ Q is false if and only if P is false and Q is true;
• – P ⇔ Q is true if and only if P and Q are both true or both false.

For example, consider the sentence If it rains or if it snows, the road is dangerous and visibility is reduced. Taking it rains, it snows, the road is dangerous and visibility is reduced as expressions of elementary propositions noted P, N, R and V respectively, the whole sentence can be represented by the proposition:

Prop = (P ∨ N) ⇒ (R ∧ V).

The truth value of Prop depends on the truth values of P, N, R and V. Suppose that P, N and R are true and V is false. It is thus easy to see that Prop must be false.

4.1.2. Formula syntax in FOL

FOL is an extension of propositional logic. The elementary propositions are replaced by predicates, i.e. propositions that depend on arguments. For example, love(x, y) is a predicate that depends on two arguments: x, the individual who loves, and y, which is loved. The number of arguments in a predicate is its arity. Arguments are terms that designate individuals. For simplicity’s sake, we shall consider terms to be either constants or variables. Quantification is possible over variables. There are two quantifiers: the universal quantifier ∀ and the existential quantifier ∃. For example, ∀x ∃y love(x, y) expresses the idea that every individual loves somebody.

In what follows, we shall take P to be a fixed set of predicates, C a set of constants and V a set of variables.

DEFINITION 4.3.– The set F(P, C, V) of FOL formulas constructed over P, C and V is defined as follows:

• – for any predicate P of arity n and any sequence of terms t₁, … , t_n in C ∪ V, P(t₁, … , t_n) is a formula in F(P, C, V);
• – if F is a formula in F(P, C, V), then ¬F is a formula in F(P, C, V);
• – if F and G are formulas in F(P, C, V), then F ∧ G, F ∨ G, F ⇒ G and F ⇔ G are formulas in F(P, C, V);
• – if F is a formula in F(P, C, V) and x is a variable of V, ∀xF and ∃xF are formulas in F(P, C, V).

Consider the following sentence:

(4.1) Tous les enfants portent un bonnet rouge.

All children wear a red hat.

“All children wear a red hat.”

To represent the semantics of this sentence in FOL, let us consider the set of formulas F(P, C, V) such that P = {enfant₁, porter₂, bonnet₁, rouge₁} (the arity of each predicate is indicated by the index), C = ∅ and V = {x, y}. The semantics of the sentence is thus given by the following formula in F(P, C, V):

(4.2) ∀x (enfant(x) ⇒ ∃y (bonnet(y) ∧ rouge(y) ∧ porter(x, y))).

4.1.3. Formula semantics in FOL

Formula semantics for FOL are obtained by interpreting them within a specific domain through a model; this interpretation links back to a truth value. Thus, a formula may be true in one model but false in another.

DEFINITION 4.4 (Model).– Let U be a set, considered as the interpretation domain. A model M of F(P, C, V) is the result of an interpretation of each predicate P with arity n of P by an n-ary relation M(P) in U and an interpretation of each constant c in C by an element M(c) in U.

This definition can be illustrated using formula [4.2]. Let the following set be the domain of interpretation: U = {e₁, e₂, e₃, e₄, e₅}. Let e₁ and e₂ be “enfants” and e₃, e₄ and e₅ “bonnets”, of which e₄ and e₅ are red. The “enfants” e₁ and e₂ are wearing the “bonnets” e₃ and e₄, respectively. In formal terms, this gives us:

M(enfant) = {e₁, e₂}

M(bonnet) = {e₃, e₄, e₅}

M(rouge) = {e₄, e₅}

M(porter) = {(e₁, e₃), (e₂, e₄)}

Once the notion of the model has been established, we need to define what we mean by the interpretation of a FOL formula in a model. As the model does not tell us how to interpret variables, we need to add something called a valuation, which assigns a value from the domain of interpretation to each variable.

DEFINITION 4.5 (Interpretation of a formula in a model).– Let M be a model over a domain U of formulas in F(P, C, V). Let v be a valuation of V in U. The interpretation of any formula in F(P, C, V) in the model M is defined by induction, as follows:

• – if F is a predicate p(t₁, … , t_n), then the interpretation I_M,v(F) is true if and only if the relation M(p)(I_M,v(t₁), … , I_M,v(t_n)) is true, given that I_M,v(t_i) = v(t_i) if t_i is a variable and I_M,v(t_i) = M(t_i) if t_i is a constant;
• – I_M,v(¬F) is true if and only if I_M,v(F) is false;
• – I_M,v(F ∧ G) is true if and only if I_M,v(F) and I_M,v(G) are true;
• – I_M,v(F ∨ G) is false if and only if I_M,v(F) and I_M,v(G) are false;
• – I_M,v(F ⇒ G) is false if and only if I_M,v(F) is false and I_M,v(G) is true;
• – I_M,v(F ⇔ G) is true if and only if I_M,v(F) and I_M,v(G) are both true or both false;
• – I_M,v(∀xF) is true if and only if I_w(F) is true for any valuation w that coincides fully with v except, potentially, for x;
• – I_M,v(∃xF) is true if and only if I_w(F) is true for at least one valuation w that coincides with v except, potentially, for x.

To illustrate this definition, let us interpret formula (4.2) in model M as defined above. Intuitively, considering the sentence (4.1), we see that the formula is false, as the chosen model features an “enfant”, e₁, without a “bonnet rouge”. Now, let us demonstrate this formally. Take a valuation v such that v(x) = e₁. Whatever the value of v(y), the interpretation I_M,v(bonnet(y) ∧ rouge(y) ∧ porter(x, y)) is always false. The interpretation of I_M,v(∃y (bonnet(y) ∧ rouge(y) ∧ porter(x, y))) is therefore false. Now, as I_M,v(enfant(x)) is true, according to the truth table for the implication, the interpretation I_M,v(enfant(x) ⇒ ∃y (bonnet(y) ∧ rouge(y) ∧ porter(x, y)) is false. In conclusion, for any valuation v′, the interpretation I_M,v′∀x (enfant(x) ⇒ ∃y (bonnet(y) ∧ rouge(y) ∧ porter(x, y))) will always be false.

4.2. Abstract meaning representation (AMR)

Designed to facilitate semantic annotation for large corpora [BAN 12], the AMR semantic formalism essentially aims to represent all predicate–argument relations in a sentence under the abstract form of concept relationships. The designers applied this formalism to English, and in this section, we shall use examples taken from their annotation of the English translation of The Little Prince. Nevertheless, use of the AMR formalism is not limited to any specific language, and we shall demonstrate its application to French in Chapter 5.

Generally speaking, the semantic representation of a sentence is based on the meanings of the words it contains, meanings which are generally linked to a lexicon. AMR, however, operates at a higher level of abstraction, connecting several meanings to a single concept. This is notably true of derived verbs. Thus, the verb destroy and the noun destruction are represented by the same concept. The noun investor is represented using the same concept as for the verb invest, based on the fact that the investor is the person who invests. The definition of the semantics of English verbs is based on the PropBank annotation scheme [PAL 05], which lists the semantic roles of verbs in the Wall Street Journal corpus, taken from the Penn Treebank².

4.2.1. General overview of AMR

AMR associates each sentence with a structure representing its semantics, also known as an AMR. An AMR is a directed acyclic graph with a single root. Its nodes represent events, states, entities or properties. In general terms, a node is an instance of a concept, shown by its label. When a concept is drawn from the Propbank lexicon, its name is followed by a number (solve−01, oblige−02, …). Certain leaves are constants, representing a number, string, etc.

The edges represent predicate–argument relations between the instances of different concepts. They are labeled with a role name. AMR uses around 100 roles³:

• – core roles that are governed by the predicate; these are denoted as ARG₀, ARG₁, ARG₂, etc. For example, the predicate solve−01 governs two central roles, ARG₀ for the solver and ARG₁ for that which is solved;
• – non-core roles that express general relations, such as purpose, cause, location, manner or polarity;
• – specific roles for date entities (day, weekday, month, etc.);
• – roles used to denote different elements in a list or a logical operation: these are denoted as op₁, op₂, etc.

Figure 4.1 shows an example of AMR taken from the Little Prince corpus annotated using this scheme⁴. The annotated sentence is:

(4.3) [lpp_1943.227] And I was obliged to make a great mental effort to solve this problem, without any assistance.

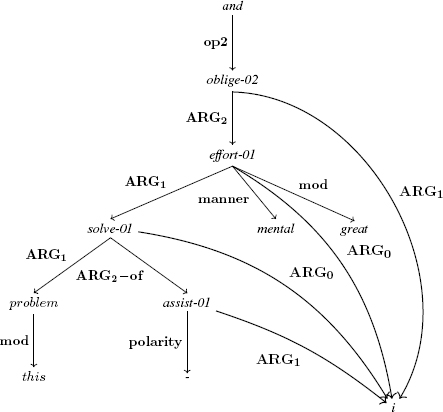
Figure 4.1. An example of AMR represented as a graph

With the exception of reflexive pronouns, pronouns are generally represented at semantic level by a concept of the same name. Thus, i denotes the concept associated with the personal pronoun I. Most determiners are not represented in AMR; the exceptions are demonstratives, possessives and cardinals. This is why only one determiner is represented at semantic level in the example above: this.

The edges of the graph feature different types of roles, as shown above: core roles, ARG₀, ARG₁, ARG₂; and non-core roles, mod and manner. The polarity role attached to “-” indicates that the scope of the negation contained in the preposition without is limited to the concept assist-01. The concept and represents a logical operator that usually has two operands. In this case, the unusual construction of the sentence means that only the second operand is present, linked to and by the role op2; the first part of the conjunction is “missing”.

The single root and in AMR represents the semantic head of the sentence. In order to retain a single root and preserve the acyclic character of the graph, roles may be replaced by their inverse where necessary, with the addition of an −of suffix to the label. Thus, in our example, the role ARG₂ from assist-01 to solve-01 has been replaced by ARG₂−of from solve-01 to assist-01 in order to prevent assist-01 from becoming a second root of the AMR.

Why, then, insist on an acyclic, rooted graph? The reason, not specified by the authors of the AMR formalism [BAN 12], is that in this way we can also represent the rhetorical structure of a sentence. For example, the two sentences Jean, que je connais, vient d’arriver (Jean, whom I know, just arrived) and je connais Jean, qui vient d’arriver (I know Jean, who just arrived) do not have the same semantic representation in AMR: the root of the first is the concept associated with arrive, while that of the second is know. This difference is shown through the choice of roots and inverted roles. However, there are limits to this means of representing the rhetorical structure of a sentence. Consider the sentence Je connais Jean que je souhaite rencontrer et embaucher (I know Jean whom I want to meet and hire). The semantics can be represented in AMR, but only if we invert six roles, which makes the structure hard to read.

EXERCISE 4.1.– Construct an AMR to represent the semantics of each of the following sentences: Jean, que je connais, vient d’arriver (Jean, whom I know, just arrived) and je connais Jean, qui vient d’arriver (I know Jean, who just arrived).

Let us suppose that connaître (to know) is linked to a concept connaître-01 with two roles, ARG₀ for the individual who knows and ARG₁ for the object of this knowledge. The verb arriver is associated with the concept arriver-01, with a single role, ARG₀, for the individual who arrives. The verb venir in this example is an aspect auxiliary, with the semantic concept venir-01. It does not have an ARG₀ role, only an ARG₁ role played by the phenomenon that has just occurred (in this case, Jean’s arrival).

In the introduction of [BAN 12], AMRs are presented in text form. Their syntax may be formalized using the following grammar:

      AMR::= (ID / CONCEPT LISTE_ARG)
LISTE_ARG::= | : ROLE ARG LISTE_ARG
      ARG::= AMR | ID | CONST

In other words, an AMR is a triplet (ID / CONCEPT LISTE_ARG) in which the identifier ID is the reference for an instance of concept CONCEPT, and LISTE_ARG represents the list of arguments of ID. Each role takes the form of a couple (ROLE, ARG) in which ROLE denotes the name of the role and ARG the argument that fulfills the role, which is either a new AMR, an instance introduced previously, or a constant. The AMR from 4.1 is shown below in the textual form.

(a / and
    :op1 (o / oblige-02
         :ARG1 (i / i)
         :ARG2 (e / effort-01
               :ARG0 i
               :ARG1 (s / solve-01
                     :ARG0 i
                     :ARG1 (p / problem
                           :mod (t / this))
                     :ARG2-of (a2 / assist-01: polarity -
                           :ARG1 i))
               :manner (m2 / mental)
               :mod (g / great))))

Note that the grammar defined above offers no guarantee that all of the AMR it generates will be correctly defined. Any references to other identifiers must not produce cycles.

Here, a link back to logic can be made by translating an AMR into a neo-Davidsonian style conjunctive formula. Each identifier ID in an AMR defined as (ID/CONCEPT(ROLE₁ARG₁) … (ROLE_nARG_n)) is associated with a characteristic variable x, and the AMR itself is associated with the conjunctive logical formula CONCEPT(x) ∧ ROLE₁(x, x₁) … ROLE_n(x, x_n), where x_i is the variable associated with ARG_i in the case of an AMR and where x_i identifies to ARG_i if it is a constant. Thus, the translation of the AMR in Figure 4.1 is the following conjunction:

and(x₁) ∧ oblige-02 (x₂) ∧ effort-01 (x₃) ∧ solve-01 (x₄) ∧ mental(x₅) ∧ great(x₆) ∧ problem(x₇) ∧ assist-01 (x₈) ∧ this(x₉) ∧ i (x₁₀) ∧ op1(x₁, x₂) ∧ ARG₂(x₂, x₃) ∧ ARG₁(x₃, x₄) ∧ manner(x₃, x₅) ∧ mod(x₃, x₆) ∧ ARG₁(x₄, x₇) ∧ ARG₂(x₈, x₄) ∧ mod(x₇, x₉) ∧ polarity(x₈, -) ∧ ARG₁(x₂, x₁₀) ∧ ARG₀(x₃, x₁₀) ∧ ARG₀(x₄, x₁₀)

The formulas are in the conjunctive fragment of FOL, without negations or disjunctions. This fragment offers a low level of expression. As the logical connectors have been externalized, reasoning is no longer possible. For example, we cannot show that sentences such as il mange des pommes et des poires (he eats apples and pears) and il mange des poires et des pommes (he eats pears and apples) are equivalent using their logical translations.

4.2.2. Examples of phenomena modeled using AMR

In this section, we shall demonstrate the variety of phenomena that can be represented with the AMR formalism using a number of examples.

4.2.2.1. Modality

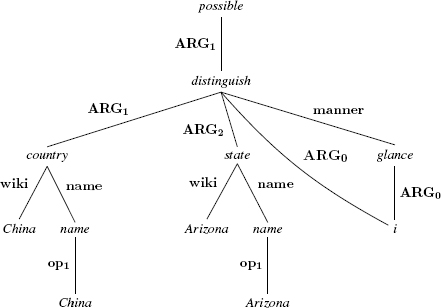
First, let us consider the way in which modality is expressed. We do this using the predicates possible, obligate-01, permit-01, recommend-01, likely-01, prefer-01, use, etc. Our example is an extract from The Little Prince, sentence (4.4), of which the AMR annotation is shown below. In this AMR, the non-core roles wiki and name represent, respectively, a Wikipedia entry and a name.

Sentences (4.5) and (4.6) are represented, at semantic level, by the same AMR. They are therefore paraphrases. In AMR, modality is expressed using the possible predicate, and it takes a single argument, the predicate distinguish, corresponding to the verb concerned by the modality.

(4.4) [lpp_1943.23]: At a glance I can distinguish China from Arizona

(4.5) At a glance I am able to distinguish China from Arizona

(4.6) At a glance, it is possible for me to distinguish China from Arizona

4.2.2.2. Negation

The negation phenomenon is interesting in that its range may stretch beyond its host constituent. AMR expresses this by marking the concept corresponding to this range using the polarity role, played by the constant "-". The sentence below is ambiguous, as the negation may apply to the whole sentence or only to the adverb really. In the annotation of The Little Prince, the first option was selected, corresponding to the first AMR below.

(4.7) [lpp_1943.148]: But that did not really surprise me much.

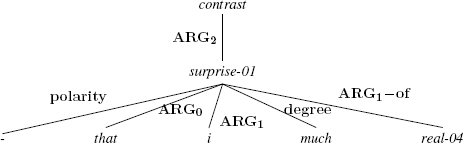
The interpretation in which the negation only applies to really is shown in the AMR below:

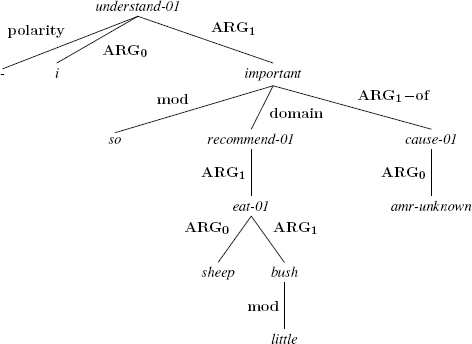
4.2.2.3. Wh-questions

Wh-questions are treated differently from yes/no questions. AMR uses the amr-unknown concept to represent the element concerned by the question. The figure below shows an AMR for a “why” question. The predicate cause-01 has two arguments: that which is the cause, represented here by the concept amr-unknown as it is unknown, and that which is affected by the fact, represented by the conceptimportant.

(4.8) [lpp_1943.217]: I did not understand why it was so important that sheep should eat little bushes.

4.2.2.4. Derived words

AMR uses a high level of abstraction, representing words derived from other words using the same concept. This is the case for deverbal nouns and the verbs from which they are derived. The example below shows an AMR in which the concept succeed-01 represents the semantics of both the noun success and the verb succeed.

(4.9) [lpp_1943.196]: But I am not at all sure of success.

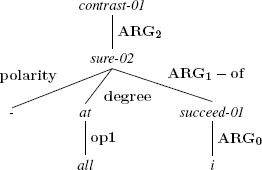
This approach applies to different forms of derivation, such as names of professions derived from verbs. Thus, the word teacher is represented, semantically, as the person who teaches. It also applies to -able adjectives; thus, the adjective breakable is represented as which may be broken.

4.2.2.5. Role reification

In some cases, a role needs to be considered as a concept; to do this, we create a concept associated with the role. This situation is similar to the neo-Davidsonian notion of reification of predicates [PAR 90]. In FOL, a predicate cannot be the argument of another predicate. This difficulty can be overcome by associating a characteristic variable to each instance of the predicate, which can then be used as an argument for other predicates. Within the context of AMR, a similar approach is taken in cases where a predicate–argument relation is, itself, the argument of a concept.

An example of reification is shown in the figure below. Under normal circumstances, the AMR should include a location role between i and relative-position, but as this role needs to be used as the argument concept for and, it is reified as the concept be-located-at-91, which takes three arguments: the person who places, that which is placed, and the placement location. In our example, the first argument is missing.

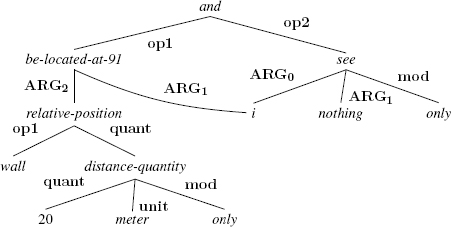
(4.10) [lpp_1943.1373]: I was only twenty meters from the wall, and I still saw nothing.

This figure also illustrates the semantics of coordination. The predicate associated with the coordination conjunction, and in this case, is the root of the subgraph representing the semantics of the coordinated expression. The AMR of each conjunct is then linked to this predicate by a role op_k, in which the integer k gives the rank of the conjunct in the coordination.

EXERCISE 4.2.– Construct an AMR to represent the semantics of each sentence below.

(4.11) La construction de la maison a nécessité deux mois.

The building of the house required two months.

“The building of the house required two months”

(4.12) Peter bought and resold his computer in the year.

(4.13) Every day it rains John reads a book.

(4.14) Marie n’a pas pu s’acheter un ordinateur avec ses

Marie could not buy a computer with her

économies.

savings.

“Marie could not buy a computer with her savings.”

(4.15) Il est venu sans la solution du problème.

He came without the solution of the problem.

‘He came without the solution of the problem’

4.3. Minimal recursion semantics, MRS

AMR is designed to produce an abstract representation of predicate–argument relations with the highest possible level of precision, but does not attempt to represent the full semantics of a sentence. MRS takes the opposite approach [COP 05], featuring a minimal representation of predicate–argument relations alongside a full representation of sentence semantics. The authors of MRS selected a minimal representation of predicate–argument relations in the hope of avoiding favoring any one linguistic theory with regard to this question, which is treated in a variety of ways. They aimed to use the lowest common denominator found in these theories [COP 09]. MRS offers an original logical representation of sentences that sub-specifies relations between the scope of quantifiers and certain adverbs.

4.3.1. Relations between quantifier scopes

Two quantifiers are used in FOL: the universal quantifier (∀) and the existential quantifier (∃). However, these are not sufficient to represent all of the possibilities for quantification found in the determiners of a language (such as certain, some, several or many, among others). These quantifiers have thus been generalized to extend their power of expression [BAR 81, WES 16]. A generalized quantifier is associated with three elements:

• – a variable, which represents a generic individual, to which the quantification applies,
• – the restriction, which represents the domain to which the individual is limited,
• – the body, which represents an affirmation made about the individual.

This terminology was not used in Barwise and Cooper’s article [BAR 81]. One early example is found in a book by Alshawi [ALS 92], and this is the version used by the authors of MRS, which we refer to as the body, is also known as the scope. However, we use the term scope to mean something different: the scope of the restriction (or the body) is the realization of the restriction (or the body) in the sentence in the form of an expression. The scope of a quantifier is the combination of the scope of its restriction and the scope of its body.

The semantics of each quantifier corresponds to a specific relation between the restriction and the body. Barwise and Cooper [BAR 81] demonstrated that the logical framework offered by FOL is too restrictive to represent this. A number of projects [WES 16] have contributed to defining a richer logical framework for expressing the semantics of generalized quantifiers, but these will not be presented here. Instead, we shall focus on the way in which the restrictions and bodies of different quantifiers interact. FOL quantifiers may be seen as generalized quantifiers with a restriction and a body, and we shall use these quantifiers to illustrate the way in which different restrictions and bodies can interact. The semantics of FOL quantifiers is easy to express in FOL, a fact which contributed to our choice.

Consider the following simple examples:

(4.16) tous les enfants adorent Pierre

all children love Pierre

“all children love Pierre”

(4.17) il adore un livre

he loves a book

“he loves a book”

(4.18) tous les enfants adorent un livre

all children love a book

“all children love a book”

In example (4.16), the determiner tous les is represented at semantic level by the universal quantifier ∀. Taking x to represent the quantified variable, the restriction is represented by the predicate enfant(x) and the body by adorer(x, Pierre). The relation between the restriction and the body depends on the semantics of tous les. In FOL, this is expressed in a general manner by the formula ∀x (restriction(x) ⇒ body(x)). In our example, it is instantiated as ∀x (enfant(x) ⇒ adorer(x, Pierre)).

In example (4.17), the determiner un is represented at semantic level by the existential quantifier ∃. Taking y to represent the quantified variable, the restriction is represented by the predicate livre(y) and the body by the predicate adorer(il, y). The relation between the restriction and the body depends on the semantics of un. In FOL, this is expressed in a general manner by the formula ∃x (restriction(x) ∧ body(x)). In our example, it is instantiated as ∃y (livre(y) ∧ adorer(il, y)).

Example (4.18) features both of the quantifiers from the previous examples. Their scopes are not independent, creating ambiguity in the reading of the sentence. If we consider that all of the children love the same book, then the scope of un encompasses that of tous les. The semantics of this sentence in FOL is thus: ∃y (livre(y) ∧ (∀x (enfant(x) ⇒ adorer(x, y)))). The restriction of the quantifier relating to un is the same as in example (4.17); however, its body is now ∀x (enfant(x) ⇒ adorer(x, y)).

If we consider that each child loves a different book, then the scope of tous les encompasses that of un. The semantics of the sentence in FOL is thus: ∀x (enfant(x) ⇒ (∃y (livre(y) ∧ adorer(x, y)))). The restriction of the quantifier relating to tous les is the same as in example (4.16); however, its body is now ∃y (livre(y) ∧ adorer(x, y)).

4.3.2. Why use an underspecified semantic representation?

One of the main obstacles to the classical expression of the meaning of sentences as logical formulas is the ambiguity of language, notably that which arises from the scope relations between quantifiers and certain adverbs, as discussed above. This type of ambiguity is present in real corpora. The examples below are taken from UD-FRENCH.

(4.19) [fr-ud-train_08143]:

Dusted est un guide non-officiel comprenant des

Dusted is a guide non-official including some

commentaires sur tous les épisodes de Buffy contre les

comments on all episodes of Buffy against the

vampires …

vampires …

“Dusted is an unofficial guide with comments on all episodes of Buffy the Vampire Slayer…”

(4.20) [fr-ud-train_01795]:

La pose d’un défibrillateur automatique implantable est

The putting up of a defibrillator automatic implantable is

souvent discutée.

often discussed.

“The installation of an automatic implantable defibrillator is often discussed.”

Example (4.19) includes four determiners: un, des, tous les and les (before vampires), of which the semantics can be represented using four generalized quantifiers. There is a scope ambiguity between des and tous les. If the scope of des encompasses that of tous les, this implies that each comment concerns all episodes; if the scope of tous les encompasses that of des, this implies that there is at least one comment for each episode. We generally choose the second reading in these cases on the basis of existing knowledge.

Example (4.20) features the adverb souvent (often), which expresses repetition over time, and which can be associated with a scope corresponding to the expression describing the repeated event. This scope may interact with the scope of quantifiers present in the sentence. In this example, there is an interaction with the quantifier un, creating an ambiguity in terms of meaning. If the scope of souvent encompasses that of un, this implies that each discussion concerns a different defibrillator; otherwise, each discussion must concern the same defibrillator. Here, we would select the first reading based on existing knowledge.

The multiplication of ambiguity issues within relatively long sentences can produce extensive lists of possible readings, and thus of semantic representations, of the same sentence. Poesio [POE 94] presents the example (4.21) below, which includes eight quantifiers. Broadly speaking, if we consider that the scopes interfere with each other on a two-by-two basis, then each reading of the sentence corresponds to a specific order of all eight quantifiers. Theoretically, this gives us 8! readings, i.e. 40320 possible readings of the same sentence5. Evidently, most of these readings are unacceptable.

(4.21) A politician can fool most voters on most issues most of the time, but no politician can fool all voters on every single issue all of the time.

Furthermore, for a number of applications, including translation, as highlighted by the results of the Vermobil project [BOS 96], it may be useless to resolve ambiguities between scope relations. For example, the meaning of the French sentence tous les enfants adorent un livre does not need to be clarified for it to be translated into English.

These two reasons were what motivated Copestake, Flickinger, Pollard and Sag to develop the MRS formalism [COP 05], which is innovative in that it allows the use of underspecified scopal representations⁶.

4.3.3. The RMRS formalism

Instead of presenting MRS in its initial form, we have chosen to present the robust version, RMRS [COP 09]. The main difference between the two lies in the neo-Davidsonian style of predicate presentation [PAR 90], described earlier. In this case, a predicate that would usually be represented in the form p(x₁, … , x_n) takes the form p(x₀), arg₁(x₀, x₁), … , arg_n(x₀, x_n) in RMRS, where x₀ is a new variable representing a reification of the predicate and the different arguments x₁, … , x_n are no longer linked to predicate p en masse; instead, they are linked separately to the characteristic variable x₀ by relations arg₁, … , arg_n.

In this way, we can say that a given entity e is the argument with rank i of predicate p, writing arg_i(x₀, e), without needing to refer to other arguments. This is useful in formulations, where certain arguments are often left out.

Semantic representations in RMRS, also referred to as RMRS, are underspecified logical formulas. In other terms, an RMRS is a compact description of a set of logical formulas.

Informally, an RMRS may be described as a set of occurrences of reified predicates, presented in neo-Davidsonian style. The occurrences of predicates are identified by anchors, used to connect their arguments. An occurrence of a predicate may thus be an argument of another occurrence of a predicate via its characteristic variable.

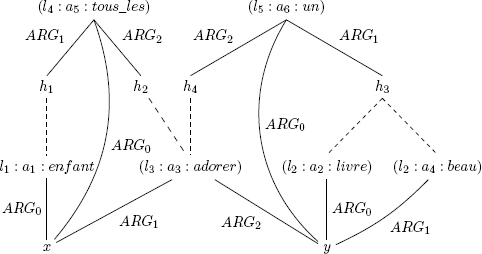
Figure 4.2. A first graphical representation of RMRS modeling the semantics of the sentence “tous les enfants adorent un beau livre”

For example, if a₁, a₂ and a₃ are occurrences of the predicates enfant, livre and adorer, respectively, and if x and y are the characteristic variables of a₁ and a₂, then the relations ARG₁(a₃, x) and ARG₂(a₃, y) signify that an “enfant” (child) x “adore” (loves) a “livre” (book) y.

Predicate occurrences are all grouped into conjunctions using handles. Staying with the same example, using three handles l₁, l₂ and l₃, we may write: (l₁: a₁: enfant), (l₂: a₂: livre), (l₃: a₃: adorer), (l₂: a₄: beau), ARG₀(a₁, x), ARG₀(a₂, y), ARG₁(a₃, x), ARG₂(a₃, y), ARG₁(a₄, y) to say that a child x loves a beautiful book y. Handle l₂ is shared by the anchors a₂ and a₄ expresses the fact the occurrences of livre and beau should be considered together as a conjunction.

Underspecification is guaranteed through the use of holes. A hole represents an argumentation position that is not filled, but which may be completed by an occurrence of a predicate. Constraints may be applied to the occurrences of predicates, filling these holes. In our example, we may add items to those shown above, completing the semantic representation of the sentence tous les enfants adorent un beau livre.

A first group of items may be added to represent the semantics of the determiner tous les as that of a generalized quantifier: (l₄, a₅, tous_les), ARG₀(a₅, x), ARG₁(a₅, h₁), ARG₂(a₅, h₂). All three elements of a generalized quantifier, as presented in section 4.3.1, are present here: the characteristic variable x is that to which quantification is applied, and is also the characteristic variable of the predicate enfant; the restriction and the body are the arguments ARG₁ and ARG₂, filled by the holes h₁ and h₂. The constraints h₁ =_q l₁ and h₂ =_q l₃, shown as dotted lines in the figure, mean that the scope of the restriction covers occurrence a₁ of the predicate enfant, and the scope of the body covers occurrence a₃ of the predicate adorer.

Similarly, another group of items is used to represent the semantics of the determiner un in the form of a generalized quantifier: (l₅, a₆, un), ARG₀(a₆, y), ARG₁(a₆, h₃), ARG₂(a₆, h₄), with constraints h₃ =_q l₂ and h₄ =_q l₃.

The RMRS obtained in this way is shown graphically in Figure 4.2 for ease of reading. This illustration clearly shows the scope constraints in the form of dotted lines. Ways of simplifying graphics of this kind will be discussed below. We shall also consider the way in which these constraints may be resolved to give two different readings of the sentence.

Now, let us consider the formal definition of an RMRS. Take a signature made up of several components: a set of handles L = {l₁, l₂, … }, a set of anchors A = {a₁, a₂, … }, a set of variables X = {x₁, x₂, … }, a set of constants C = {c₁, c₂, … }, a set of holes H = {h₁, h₂, … } and a set of predicate symbols P = {p₁, p₂, … }, some of which are identified as representations of generalized quantifiers.

DEFINITION 4.6.– An RMRS is a finite set of items It of the following form:

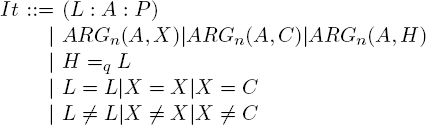
where L is a handle, A an anchor, P a predicate symbol, X a variable, C a constant, H a hole and n an integer representing the rank of an argument.

In this definition, the first type of item (L : A : P) represents an occurrence of predicate P, which is identified by its anchor A, used to attach the arguments to the predicate. Handle L is used to group predicate occurrences into conjunctions7. Two predicate occurrences (L : A₁ : P₁) and (L : A₂ : P₂) that share a handle L are grouped into the same conjunction; these occurrences are said to be conjuncts.

The second type of item connects a predicate anchored to A to an argument which is a variable X (item ARG_n(A, X)), a constant C (item ARG_n(A, C)) or a hole H (item ARG_n(A, H)). The arguments are numbered, with n expressing the rank of the argument. In this way, the arguments of a predicate may be declared separately from each other, creating flexibility in terms of representation. Furthermore, the decision to use a rank rather than a semantic role to represent an argument is a deliberate one, reflecting the MRS designers’ desire to avoid favoring any given theory of semantic roles. Unlike AMR, they do not consider semantic alternances of the type il a cassé la branche (he broke the branch) and la branche a cassé (the branch broke). Different predicates are used to represent the semantics of the two uses of casser in these examples.

The third type of item H =_q L is a scope constraint expressing the fact that only a series (potentially empty) of generalized quantifiers is permitted between hole H and the conjunction of predicates connected to handle L. This explains the notation =_q, denoting a “quasi-equality” between H and L.

The other types of items are equality and inequality constraints between handles, variables and constants. These items are useful when assembling RMRS attached to components of an expression in order to generate an RMRS for the expression as a whole.

When formed correctly, an RMRS should verify the following criteria:

1. 1) An anchor only appears once in items of the form (L : A : P), meaning that a predicate occurrence is attached to a single handle and a single predicate.
2. 2) any item of the form ARG_n(A, _) is reliant on the existence of an item of the form (L : A : P), and there cannot be any other items of the form ARG_n(A, _). This means that a predicate occurrence cannot have multiple arguments of the same type, and is necessarily attached to both a predicate and a handle.
3. 3) ARG₀ always links a predicate occurrence to its characteristic variable, which cannot be common to multiple predicate occurrences. The only exception is in the case of a generalized quantifier, which may share its characteristic variable with a maximum of one predicate which is not, itself, a generalized quantifier.
4. 4) any declaration (L : A : P) of a predicate representing a generalized quantifier is always associated with the declaration of three arguments: ARG₀(A, X) for the quantified variable X, ARG₁(A, H₁) for the hole H₁ to be filled by the quantifier restriction, and ARG₂(A, H₂) for the hole H₂ to be filled by the quantifier body.
5. 5) equality or difference relations express constraints over variables, constants or holes that must already have been declared in other items.

An RMRS may represent the semantics of an incomplete expression, in which the predicates do not have all of their obligatory arguments. To represent the semantics of a sentence, an RMRS needs to verify three further completeness conditions:

1. 1) every variable is the characteristic variable of exactly one predicate which is not a generalized quantifier;
2. 2) the characteristic variable of every generalized quantifier is the characteristic variable of a predicate which is within the scope of its restriction;
3. 3) every hole H is present in exactly one constraint of the form H =_q L.

Condition 1 is verified for every grammatical sentence. A variable represents an argument of a predicate. This argument is realized as a common noun, adverb, adjective or verb, all of which have a characteristic variable. Arguments that take the form of a pronoun or proper noun are represented by constants.

Condition 2 is also verified in all cases. Generalized quantifiers generally take the form of a determiner applied to a common noun, and the quantified variable is the characteristic variable of the predicate representing the semantics of the common noun. Pronouns that express a quantification (tous, certains, chacun, etc.) are not problematic, as they always have an implicit restriction.

There is no real linguistic justification for condition 3; it was introduced by Ann Copestake with the aim of facilitating conversion from RMRS to DMRS format [COP 09], and it is rarely un-verified. As we shall see later, it is also useful in defining a model of an RMRS.

The semantics of the sentence tous les enfants adorent un beau livre, discussed previously, constitute an example of a correctly formed, complete RMRS. A summary is given in the following:

(l₁: a₁: enfant), (l₂: a₂: livre), (l₃: a₃: adorer), (l₂: a₄: beau), ARG₀(a₁, x), ARG₀(a₂, y), ARG₁(a₃, x), ARG₂(a₃, y), ARG₁(a₄, y), (l₄, a₅, tous_les), ARG₀(a₅, x), ARG₁(a₅, h₁), ARG₂(a₅, h₂), h₁ =_q l₁, h₂ =_q l₃ (l₅, a₆, un), ARG₀(a₆, y), ARG₁(a₆, h₃), ARG₂(a₆, h₄), h₃ =_q l₂, h₄ =_q l₃

Presentations of RMRS in the form of a series of items are hard to read; a first type of graphical representation is shown in Figure 4.2. We shall now simplify this graph.

The simplification shown in Figure 4.3 consists of deleting the names of anchors and handles, and of specifying the conjunction relations between predicate occurrences using specific conjunction edges. These are shown as double lines, as in the case of the livre and beau predicates in Figure⁸. Every constraint H =_q L is represented only once by a scope edge from H to one of the elements of the conjunction class represented by L⁹. The labels of the argumental edges have also been simplified, replacing ARG_i with i.

Figure 4.3. RMRS for the sentence “tous les enfants adorent un beau livre” in graph form

The construction of the graph associated with an RMRS is formalized below.

DEFINITION 4.7.– An RMRS δ is represented by an oriented, acyclic, labeled graph G(δ), defined as follows:

• – each variable, constant and hole is represented by a labeled node with the same name. Equality constraints between variables and constants are shown as merged nodes (showing the names of all equal variables or constants). Inequality between constraints is shown by the fact that the corresponding nodes are distinct;
• – each item of the form (L : A : P) results in the creation of a node labeled P associated with anchor A;
• – each handle L associated with a set of several occurrences results in the creation of conjunction edges between all of the nodes which correspond to items of the form (L : A : P);
• – each item of the form ARG_n(A, X) is represented by an edge, labeled with the integer n, from the node associated with A to the node associated with X. The same is true for items of the form ARG_n(A, C) and ARG_n(A, H);
• – each constraint of scope H =_q L is represented by a scope edge from the node associated with H to a node representing an item (L : A : P).

There is a one-to-one correspondence between the representation of an RMRS as a list of items and as a graph. Henceforth, each RMRS will be identified with its graph.

When associated with a sentence, an RMRS constitutes a compact representation of the different possible readings. Each reading is represented by a logical formula, which is a model of this RMRS. A formalization of the notion of the model of an RMRS is given by Koller and Lascarides [KOL 09]. According to these authors, a model is a tree representing a logical formula. We shall use this notion here, with one minor modification: instead of permitting copies of variables or constants in the leaves of the tree, we have chosen to permit the sharing of variables or constants, meaning that our models no longer adhere strictly to the tree format. These structures, in which leaves (and only leaves) may have multiple parents, are known as quasi-trees.

DEFINITION 4.8.– A quasi-tree is an acyclic graph with a single root, in which the only nodes with multiple parents are leaves.

Using quasi-trees instead of trees means that variable names can be left off. There are now two ways of defining a model of an RMRS. This may be done externally, taking a quasi-tree form and interpreting the RMRS in this quasi-tree via an interpretation function, which projects each node of the RMRS onto a node in the quasi-tree. The other option is to operate internally, transforming the RMRS into a quasi-tree. We have chosen to use this second method as it is easier to understand.

To define a model in this way, we simply complete the holes in an RMRS with some of its predicate occurrences. This is done using the notion of an RMRS specification.

DEFINITION 4.9.– The specification of an RMRS is an injective application, from all holes to conjunction classes of predicate occurrences (in other words, handles), in which the image of a hole H is either a generalized quantifier or a conjunction class L such that H =_q L.

The specification of an RMRS allows us to define a structure which is a realization of the RMRS in graph form from which all of the holes have disappeared. However, this graph is not necessarily a quasi-tree.

DEFINITION 4.10.– The realization of an RMRS induced by a specification is a graph obtained from the RMRS using two operations:

• – first, all conjunction links between predicate occurrences belonging to the same conjunction class are replaced by a node ∧, with all elements of the conjunction class as children. If an edge in the RMRS terminates at one of the elements in the class, its target is transferred to node ∧;
• – second, we delete all scope edges and merge each hole with its image via specification, only retaining the label of the specification.

Given a realization of an RMRS, the notion of realization of its nodes relates to their status in the realization of the RMRS. If a node is a predicate occurrence, it and its realization are one and the same. If a node is a hole, its realization is its specification. Realizations of conjunction classes are the nodes ∧ that replace the classes.

We also need to define the notion of a model.

DEFINITION 4.11.– A model of an RMRS is a realization that is a quasi-tree satisfying the scope constraints found in the RMRS, i.e. if H is any given hole in the RMRS such that H =_q L, the path from the realization of H to the realization of L only passes through generalized quantifiers, with the exception of the terminal point.

To illustrate these definitions, we shall use the same RMRS found elsewhere in this presentation. Our RMRS features four holes. We apply the following specification: h₁ ↦ {enfant}, h₂ ↦ {un}, h₃ ↦ {livre, beau}, h₄ ↦ {adorer} This specification gives us the realization in the following:

This realization is a quasi-tree that verifies four scope constraints found in the RMRS. Verification is simple in three of these cases, as the path realizing the scope constraint is empty. Only the constraint between h₂ and adorer needs to be verified. This constraint is realized by the path from un to adorer. Since un is a generalized quantifier, the constraint is verified. We can conclude that the realization is a model of the RMRS.

The realizations of the RMRS are easy to enumerate: there are 24, only two of which are models. The first is presented above, and the second results from the following specification: h₁ ↦ {enfant}, h₂ ↦ {adorer}, h₃ ↦ {livre, beau}, h₄ ↦ {tous_les}. This gives us the model below.

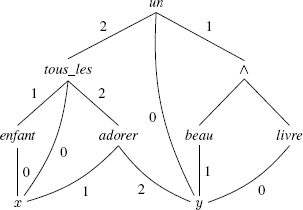
Readers may wish to verify the scope constraints in this model. The two models represent two logical formulas corresponding to the two readings of the sentence tous les enfants adorent un beau livre mentioned earlier. Expressed in the linear form, the two formulas are written:

F₁ = tous_les(x, enfants(x), un(y, beau(_, y) ∧ livre(y), adorer(_, x, y)))

F₂ = un(y, beau(_, y) ∧ livre(y), tous_les(x, enfants(x), adorer(_, x, y)))

Note that the predicates are reified, and that the first argument of rank 0 is the characteristic variable of the predicate. When an argument is noted _, this indicates that it is not expressed in the sentence.

Formulas F₁ and F₂, as written above, are not FOL formulas, but they may be transformed by interpreting the generalized quantifiers tous_les and un to create a FOL form, as indicated in section 4.3.1.

The formal definition of MRS [COP 05] includes an additional constraint not found in RMRS models: any path realizing a scope constraint, passing through a node representing a generalized quantification, must use the argument corresponding to the body of the quantifier. We have not applied this specific restriction to our models.

EXERCISE 4.3.– Consider the following sentence, which is taken from [fr-ud-train_08143].

(4.22) Dusted comprend de longs commentaires sur tous les

Dusted includes some long comments on all

épisodes

episodes

“Dusted includes long comments on all episodes”

The semantics of this sentence may be represented by the following RMRS:

{(l₂: a₂: des), ARG₀(a₂, x), ARG₁ (a₂, h₁), ARG₂(a₂, h₂), (l₅: a₅: tous), ARG₀ (a₅, y), ARG₁ (a₅, h₃), ARG₂(a₅, h₄), (l₁: a₁: comprendre), ARG₁(a₁, Dusted), ARG₂ (a₁, x), (l₄: a₃: long), ARG₁(a₃, x), (l₄: a₄: commenter), ARG₀(a₄, x), ARG₂ (a₄, y), (l₆: a₆: episode), ARG₀ (a₆, y), h₁ =_q l₄, h₂ =_q l₁, h₃ =_q l₆, h₄ =_q l₄}

Construct the graph of this RMRS and show all of its models.

EXERCISE 4.4.– Define an RMRS to represent the semantics of the sentence below and show all of its models. Introduce a date predicate taking two arguments: the characteristic variable of an event and a date.

(4.23) Every day it rains John reads a book.

4.3.4. Examples of phenomenon modeling in MRS

The examples presented below have been selected to highlight the expressive capacities of MRS. Let us consider the RMRS in the figure below.

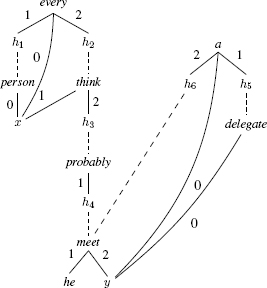
(4.24) Everyone thought he probably met a delegate.

Chacun a pensé qu’il probablement a rencontré un délégué.

“Chacun a pensé qu’il a probablement rencontré un délégué.”

The semantics of the pronoun everyone is that of every person. Next, the predicate think has two arguments. The second, which corresponds to the object subordinate, is represented by a hole to permit the insertion of quantifiers between think and the semantic head of the subordinate, which is the predicate probably. This predicate is a fixed scopal predicate, according to the classification established by [COP 09], as quantifiers may be inserted between it and its argument, meet. It differs from floating scopal predicates in that its scope cannot extend beyond the subordinate, something which is expressed by the scope relation from think to probably.

There are four models of the RMRS which can be represented in linear form as follows10:

a(y, delegate(y), every(x, person(x), think(x, probably(meet(he, y)))))

every(x, person(x), a(y, delegate(y), think(x, probably(meet(he, y)))))

every(x, person(x), think(x, a(y, delegate(y), probably(meet(he, y)))))

every(x, person(x), think(x, probably(a(y, delegate(y), meet(he, y)))))

Now, based on our existing knowledge, not all of these models have the same likelihood of being selected; the second option seems most plausible. In this version, the delegate has a real-world existence, rather than existing only in thought, but the “thinkers” are not necessarily all thinking of the same delegate.

Now, consider the example below.

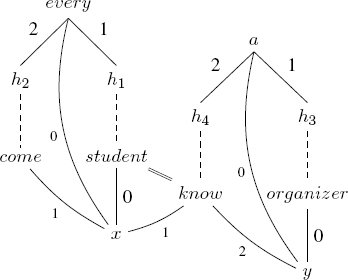
(4.25) Every student who knows an organizer came.

This example includes a relative proposition, interpreted in a restrictive and non-appositive manner. In the RMRS, this is demonstrated by the fact that the semantic head of the relative, the predicate know, is conjoined to the predicate student, which represents the antecedent. The scope relation originating in h₁ indicates that student and know are both within the scope of the restriction of the quantifier every.

The RMRS includes two models, which may be represented in the linear form as follows:

every(x, a(y, organizer(y), student(x) ∧ knows(x, y)), come(x))

a(y, organizer, every(x, student(x) ∧ knows(x, y), come(x)))

The first model corresponds to the most likely reading, in which each student knows a specific organizer.

Now, let us consider a more complex example, including a coordination. This example is represented in the figure below.

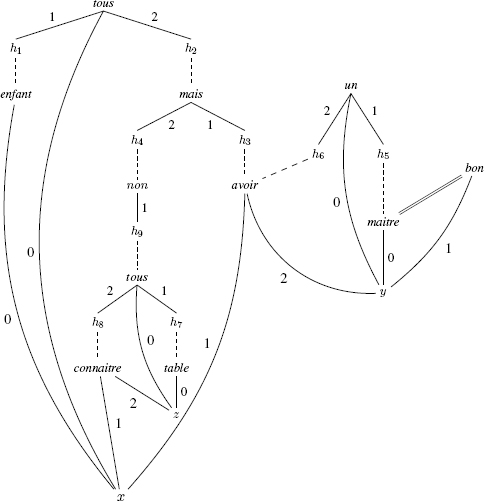
(4.26) Tous les enfants ont eu un bon maître mais ne

All children had a good teacher but do not

connaissent pas toutes les tables.

know all tables.

“All children had a good teacher but do not know all tables.”

In the RMRS shown above, non and mais are fixed scopal predicates, in that their scope cannot go beyond the host proposition. There are three quantifiers: two occurrences of tous and one of un. These are floating scopal predicates, but the positional freedom of the predicate tous corresponding to toutes les tables is limited by the fact that the predicate must remain within the scope of non as a result of syntax.

In these conditions, we obtain three models of the RMRS, which may be represented in linear form by the following three formulas¹¹:

tous(x, enf(x), un(y, bon(y) ∧ ma(y), mais(non(tous(z, table(z), co(x, z))), avoir(x, y))))

tous(x, enf(x), mais(non(tous(z, table(z), co(x, z))), un(y, bon(y) ∧ ma(y), avoir(x, y))))

un(y, bon(y) ∧ ma(y), tous(x, enf(x), mais(non(tous(z, table(z), co(x, z))), avoir(x, y))))

The first two formulas are logically equivalent, so we only have two possible readings of sentence (4.26), depending on whether or not all of the children have the same teacher.

These examples give us an idea of the expressive capacity of MRS but further work is needed before we can precisely express the semantics of corpus sentences on a large scale. This would involve studying a whole series of linguistic questions, which have yet to be addressed. One important issue concerns the semantics of determiners, as not all determiners can be represented as generalized quantifiers. Even for generalized quantifiers, if the relations between the restrictions and bodies of different quantifiers become overly complex, MRS is no longer able to model them.

EXERCISE 4.5.– Determine an RMRS to represent the semantics of each of the sentences below.

(4.27) Tous les voisins ont souvent entendu un bruit

All neighbors often heard a sound

étrange.

strange.

“All neighbors often heard a strange sound.”

(4.28) I suppose that a tutor helps all students.

(4.29) I cannot find a piece of paper.

(4.30) Dusted comprend de longs commentaires sur tous les

Dusted includes some long comments on all

épisodes

episodes

“Dusted includes long comments on all episodes”

(4.31) Tous les enfants dont les notes sont excellentes ont eu

All children whose marks are excellent had

un bon maître.

a good teacher.

“All children whose marks are excellent had a good teacher.”

EXERCISE 4.6.– Determine an RMRS to represent the semantics of each of the sentences below, taking into account your own existing knowledge in addition to linguistic information.

(4.32) Un drapeau flotte à chaque fenêtre.

A flag is flown at every window.

“A flag is flown at every window.”

(4.33) Chaque professeur a proposé deux tuteurs à chaque

Every professor has proposed two tutors to every

étudiant.

student.

“Every professor suggested two tutors for every student.”’

(4.34) Somewhere in Britain, some woman has a child every thirty seconds.

4.3.5. From RMRS to DMRS

Ann Copestake introduced DMRS with the aim of removing the redundancies found in RMRS and thus creating representations which are as compact as possible [COP 08, COP 09]. A semantic representation in DMRS is obtained from an RMRS by deleting variables and holes, following a method presented below. As we shall see, no information is lost in this process, and a reverse method can be applied to recreate the original RMRS. Both methods are taken from [COP 08].

First, let us consider the structures of DMRS, also known as DMRS, separately from the RMRS from which they may originate. Once again, we shall use the sentence “tous les enfants adorent un beau livre”. Its semantics are shown in the DMRS in Figure 4.4.

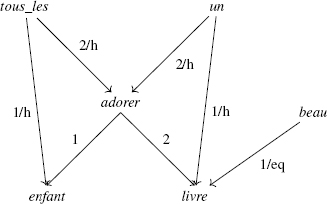
Figure 4.4. DMRSS of the sentence “tous les enfants adorent un beau livre”

A DMRS takes the form of an oriented acyclic graph, in which the nodes represent predicate occurrences (or constants) and the edges represent arguments with a number indicating their rank. This rank is sometimes followed by the indication eq, as in the case for the edge leading from the node beau to the node enfant, which is labeled 1/eq. This represents the rank 1 argument of the predicate beau, while indicating, through eq, that the occurrences of the predicates beau and livre are conjoined. The rank of an argument may also be followed by the indication h, as in the case of the edge from node tous_les to node enfant, labeled 1/h, representing the rank 1 argument of the predicate tous_les. As the predicate is a generalized quantifier, this is its restriction, but the indication h shows that enfant is within the scope of the restriction; the two do not necessarily merge.

There are no explicit variables, as the nodes are double-sided objects: they may be seen as predicate occurrences in relation to certain incoming edges, and as the characteristic variables of these predicates in relation to others. For instance, consider the node enfant. In relation of the edge originating from adorer, labeled 1, it represents the characteristic variable of the predicate occurrence enfant, previously denoted as x. From the perspective of the edge originating from tous_les and labeled 1/h, it represents the predicate occurrence enfant.

The DMRS shows all of the information found in an RMRS, but in compact form. In formal terms, a DMRS is defined as follows.

DEFINITION 4.12.– A DMRS is an acyclic oriented graph in which the nodes are labeled by predicates or constants, and where the edges are labeled n, n/eq, n/h or /eq (where n is a strictly positive integer). Certain predicates are identified as generalized quantifiers.

A DMRS must verify the following form conditions:

1. 1) nodes labeled with constants cannot have daughters, and the edges arriving at these nodes can only be labeled with integers;
2. 2) nodes labeled with generalized quantifiers have exactly two daughters, connected to them by edges labeled 1/h (for the restriction) and 2/h (for the body).

The labels n/eq and n/h are used as a means of simplifying notation: an edge labeled n/eq (n/h) is equivalent to two edges labeled n (n) and eq (h), respectively.

Henceforth, it is easy to define the transformation of an RMRS representing the semantics of a sentence, into an DMRS.

DEFINITION 4.13.– Consider a graph γ representing an RMRS. The transformation of γ into DMRS, denoted as DMRS(γ) is defined as follows:

CHOICE OF NODES: the nodes in DMRS(γ) are the nodes in γ representing predicates and constants with the same labels;

CONSERVATION OF CONSTANTS: any edge in γ pointing toward a constant is retained in DMRS(γ) with the same label;

HOLE DELETION: for any edge in γ labeled n from a predicate occurrence p to a hole h, there are two options:

• – if p does not represent a generalized quantifier or n is not equal to 1, then h is the source of a scope edge leading to a predicate q; in this case, an edge labeled n/h is created from p to q in DMRS(γ),
• – if p represents a generalized quantifier and n is equal to 1, then the predicates which are conjoined to the child of h include a predicate q with the same characteristic variable as p. In these conditions, an edge labeled n/h is created from p to q in DMRS(γ);

VARIABLE DELETION: for every edge in γ labeled 0 from a predicate occurrence p, which is not a generalized quantifier toward its variable characteristic x such that there is another edge labeled n from a predicate occurrence q to x, an edge is created from q to p in DMRS(γ). This edge is then labeled n/eq if p and q are part of the same conjunction or n otherwise;

CONSERVATION OF CONJUNCTION RELATIONS: when two predicate occurrences p and q are conjoined in γ without the characteristic variable of one being the argument of the other, an edge labeled /eq is created between the two in DMRS(γ).

This transformation is only possible for RMRS representing the semantics of sentences, since completeness conditions must be respected in addition to the conditions for correct formation of an RMRS. Readers may wish to apply this definition to the RMRS in Figure 4.3 in order to obtain the DMRS shown in Figure 4.4.

Now, let us consider the reverse transformation from a DMRS to an RMRS to show that enough information has been retained to regenerate the original RMRS.

DEFINITION 4.14.– Take a DMRS γ. The RMRS associated with γ and noted RMRS(γ) is defined in the following manner:

CONSERVATION OF PREDICATES AND CONSTANTS: nodes labeled with predicates and constants in γ are retained in RMRS(γ) with the same labels;

CREATION OF VARIABLES: for each predicate occurrence p in γ which is not a generalized quantifier and which is the target of an edge labeled n, n/eq or n/h, we create a node car(p) in RMRS(γ) to represent the characteristic variable of p and an edge ARG₀ from p to car(p);

CREATION OF EDGES AND HOLES: for each edge in γ leading from a predicate p to a predicate or constant q, there are five possibilities:

• – if the edge is labeled n and if q is a constant, we create an edge from p to q, labeled n, in RMRS(γ);
• – if the edge is labeled n and if q is a predicate occurrence, we create an edge from p to car(q), labeled n, in RMRS(γ);
• – if the edge is labeled n/eq, we create an edge from p to car(q), labeled n, and a conjunction edge between p and q in RMRS(γ);
• – if the edge is labeled n/h, a hole h is created in RMRS(γ), along with an edge from p to h, labeled n, and a scope edge from h to q;
• – if the edge is labeled /eq, we create a conjunction edge between p and q;

CREATION OF LINKS WITH QUANTIFIED VARIABLES: for any edge in γ leading from a generalized quantifier p to its restriction q, we create an edge from p to car(q), labeled 0, in RMRS(γ).

Readers may wish to apply this transformation to the DMRS in Figure 4.4 to recreate the RMRS shown in Figure 4.3.

EXERCISE 4.7.– Transform each RMRS from the examples in section 4.3.4 and exercises 4.5 and 4.6 into a DMRS.

1 http://amr.isi.edu/download/amr-bank-v1.6.txt

2 https://www.cis.upenn.edu/~treebank/.

3 A detailed list of these roles can be found on the AMR website, on the format description page (https://github.com/amrisi/amr-guidelines/blob/master/amr.md#amr-slogans).

4 http://amr.isi.edu/download/amr-bank-v1.6.txt.

5 This sentence is a reformulation of a citation by Abraham Lincoln.

6 The idea of using underspecifications of scopal representations in a semantic formalism had already been put forward by Uwe Reyle [REY 93] and Johan Bos [BOS 95], but MRS was developed independently.

7 The creators of MRS initially used the word handle [COP 05] then label [COP 09]; we have chosen not to use the term “label” here to avoid confusion with the labels attached to nodes or edges in graphs.

8 Strictly speaking, as the graph is oriented, each non-oriented edge should be replaced by two edges oriented in opposite directions. Furthermore, as the conjunction relation is an equivalency, we may simply represent a minimum number of edges on the basis that the others can be obtained by transitivity.

9 In cases where several items are associated with L, we select one; this choice is not important, since as long as the scope relation is established with one element in the conjunction, it is established with the conjunction as a whole.

10 The presence of think in the sentence introduces a world outside of reality, that of the actor’s thoughts. FOL is not sufficient to interpret our four models, as the truth value of the logical formulas is relative to one of these worlds. A more expressive logic, for example a modal logic, is therefore required.

11 To save space, certain predicate names have been abbreviated.