TURTLE GEOMETRY IS A DIFFERENT STYLE OF DOING GEOMETRY, JUST as Euclid’s axiomatic style and Descartes’s analytic style are different from one another. Euclid’s is a logical style. Descartes’s is an algebraic style. Turtle geometry is a computational style of geometry.

Euclid built his geometry from a set of fundamental concepts, one of which is the point. A point can be defined as an entity that has a position but no other properties—it has no color, no size, no shape. People who have not yet been initiated into formal mathematics, who have not yet been “mathematized,” often find this notion difficult to grasp, and even bizarre. It is hard for them to relate it to anything else they know. Turtle geometry, too, has a fundamental entity similar to Euclid’s point. But this entity, which I call a “Turtle,” can be related to things people know because unlike Euclid’s point, it is not stripped so totally of all properties, and instead of being static it is dynamic. Besides position the Turtle has one other important property: It has “heading.” A Euclidean point is at some place—it has a position, and that is all you can say about it. A Turtle is at some place—it, too, has a position—but it also faces some direction—its heading. In this, the Turtle is like a person—I am here and I am facing north—or an animal or a boat. And from these similarities comes the Turtle’s special ability to serve as a first representative of formal mathematics for a child. Children can identify with the Turtle and are thus able to bring their knowledge about their bodies and how they move into the work of learning formal geometry.

To see how this happens we need to know one more thing about Turtles: They are able to accept commands expressed in a language called TURTLE TALK. The command FORWARD causes the Turtle to move in a straight line in the direction it is facing (see Figure 3). To tell it how far to go, FORWARD must be followed by a number: FORWARD 1 will cause a very small movement, FORWARD 100 a larger one. In LOGO environments many children have been started on the road to Turtle geometry by introducing them to a mechanical turtle, a cybernetic robot, that will carry out these commands when they are typed on a typewriter keyboard. This “floor Turtle” has wheels, a dome shape, and a pen so that it can draw a line as it moves. But its essential properties—position, heading, and ability to obey TURTLE TALK commands—are the ones that matter for doing geometry. The child may later meet these same three properties in another embodiment of the Turtle: a “Light Turtle.” This is a triangular-shaped object on a television screen. It too has a position and a heading. And it too moves in response to the same TURTLE TALK commands. Each kind of Turtle has its strong points: The floor Turtle can be used as a bulldozer as well as a drawing instrument; the Light Turtle draws bright-colored lines faster than the eye can follow. Neither is better, but the fact that there are two carries a powerful idea: Two physically different entities can be mathematically the same (or “isomorphic”).¹

The commands FORWARD and BACK cause a Turtle to move in a straight line in the direction of its heading: Its position changes, but its heading remains the same. Two other commands change the heading without affecting the position: RIGHT and LEFT cause a Turtle to “pivot,” to change heading while remaining in the same place. Like FORWARD, a turning command also needs to be given a number—an input message—to say how much the Turtle should turn. An adult will quickly recognize these numbers as the measure of the turning angle in degrees. For most children these numbers have to be explored, and doing so is an exciting and playful process.

A square can be produced by the commands

FORWARD 100

RIGHT 90

FORWARD 100

RIGHT 90

FORWARD 100

RIGHT 90

FORWARD 100

RIGHT 90

FD 100 (note the abbreviations to reduce typing)

RT 100

FD 100

ERASE 1 (this undoes the effect of the previous command)

RT10 (fiddling the turtle in search of the right angle)

LT 10

FD 100

RT 100 (gets there faster this time)

LT 10

RT 100

LT 10

FD 100

RT 40

FD 100

RT 90

FD 100

Figure 3. An Actual Transcript of a Child’s Early Attempt at a Square

Since learning to control the Turtle is like learning to speak a language, it mobilizes the child’s expertise and pleasure in speaking. Since it is like being in command, it mobilizes the child’s expertise and pleasure in commanding. To make the Turtle trace a square, you walk in a square yourself and describe what you are doing in TURTLE TALK. And so, working with the Turtle mobilizes the child’s expertise and pleasure in motion. It draws on the child’s well-established knowledge of “body-geometry” as a starting point for the development of bridges into formal geometry.

The goal of children’s first experiences in the Turtle learning environment is not to learn formal rules but to develop insights into the way they move about in space. These insights are described in TURTLE TALK and thereby become “programs” or “procedures” or “differential equations” for the Turtle. Let’s look closely at how a child, who has already learned to move the Turtle in straight lines to draw squares, triangles, and rectangles, might learn how to program it to draw a circle.

Let us imagine, then, as I have seen a hundred times, a child who demands: How can I make the Turtle draw a circle? The instructor in a LOGO environment does not provide answers to such questions but rather introduces the child to a method for solving not only this problem but a large class of others as well. This method is summed up in the phrase “play Turtle.” The child is encouraged to move his or her body as the Turtle on the screen must move in order to make the desired pattern. For the child who wanted to make a circle, moving in a circle might lead to a description such as: “When you walk in a circle you take a little step forward and you turn a little. And you keep doing it.” From this description it is only a small step to a formal Turtle program.

TO CIRCLE REPEAT [FORWARD 1 RIGHT 1]

Another child, perhaps less experienced in simple programming and in the heuristics of “playing Turtle,” might need help. But the help would not consist primarily of teaching the child how to program the Turtle circle, but rather of teaching the child a method, a heuristic procedure. This method (which includes the advice summed up as “play Turtle”) tries to establish a firm connection between personal activity and the creation of formal knowledge.

In the Turtle Mathland, anthropomorphic images facilitate the transfer of knowledge from familiar settings to new contexts. For example, the metaphor for what is usually called “programming computers” is teaching the Turtle a new word. A child who wishes to draw many squares can teach the Turtle a new command that will make it carry out in sequence the seven commands used to draw a square as is shown in Figure 3. This can be given to the computer in several different forms, among which are:

TO SQUARE

FORWARD 100

RIGHT 90

FORWARD 100

RIGHT 90

FORWARD 100

RIGHT 90

FORWARD 100

END

TO SQUARE

REPEAT 4

FORWARD 100

RIGHT 90

END

TO SQUARE:SIZE

REPEAT 4

FORWARD:SIZE

RIGHT 90

END

Similarly we can program an equilateral triangle by:

TO TRIANGLE

FORWARD 100

RIGHT 120

FORWARD 100

RIGHT 120

FORWARD 100

END

TO TRIANGLE:SIDE

REPEAT 3

FORWARD:SIDE

RIGHT 1200

END

These alternative programs achieve almost the same effects, but informed readers will notice some differences. The most obvious difference is in the fact that some of them allow figures to be drawn with different sizes: In these cases the command to draw the figure would have to be SQUARE 50 or SQUARE 100 rather than simply SQUARE. A more subtle difference is in the fact that some of them leave the Turtle in its original state. Programs written in this clean style are much easier to understand and use in a variety of contexts. And in noticing this difference, children learn two kinds of lessons. They learn a general “mathetic principle,” making components to favor modularity. And they learn to use the very powerful idea of “state.”

The same strategy of moving from the familiar to the unknown brings the learner into touch with some powerful general ideas: for example, the idea of hierarchical organization (of knowledge, of organizations, and of organisms), the idea of planning in carrying through a project, and the idea of debugging.

One does not need a computer to draw a triangle or a square. Pencil and paper would do. But once these programs have been constructed they become building blocks that enable a child to create hierarchies of knowledge. Powerful intellectual skills are developed in the process—a point that is most clearly made by looking at some projects children have set for themselves after a few sessions with the Turtle. Many children have spontaneously followed the same path as Pamela. She began by teaching the computer SQUARE and TRIANGLE as described previously. Now she saw that she can build a house by putting the triangle on top of the square. So she tries:

TO HOUSE

SQUARE

TRIANGLE

END

But when she gives the command HOUSE, the Turtle draws (Figure 4):

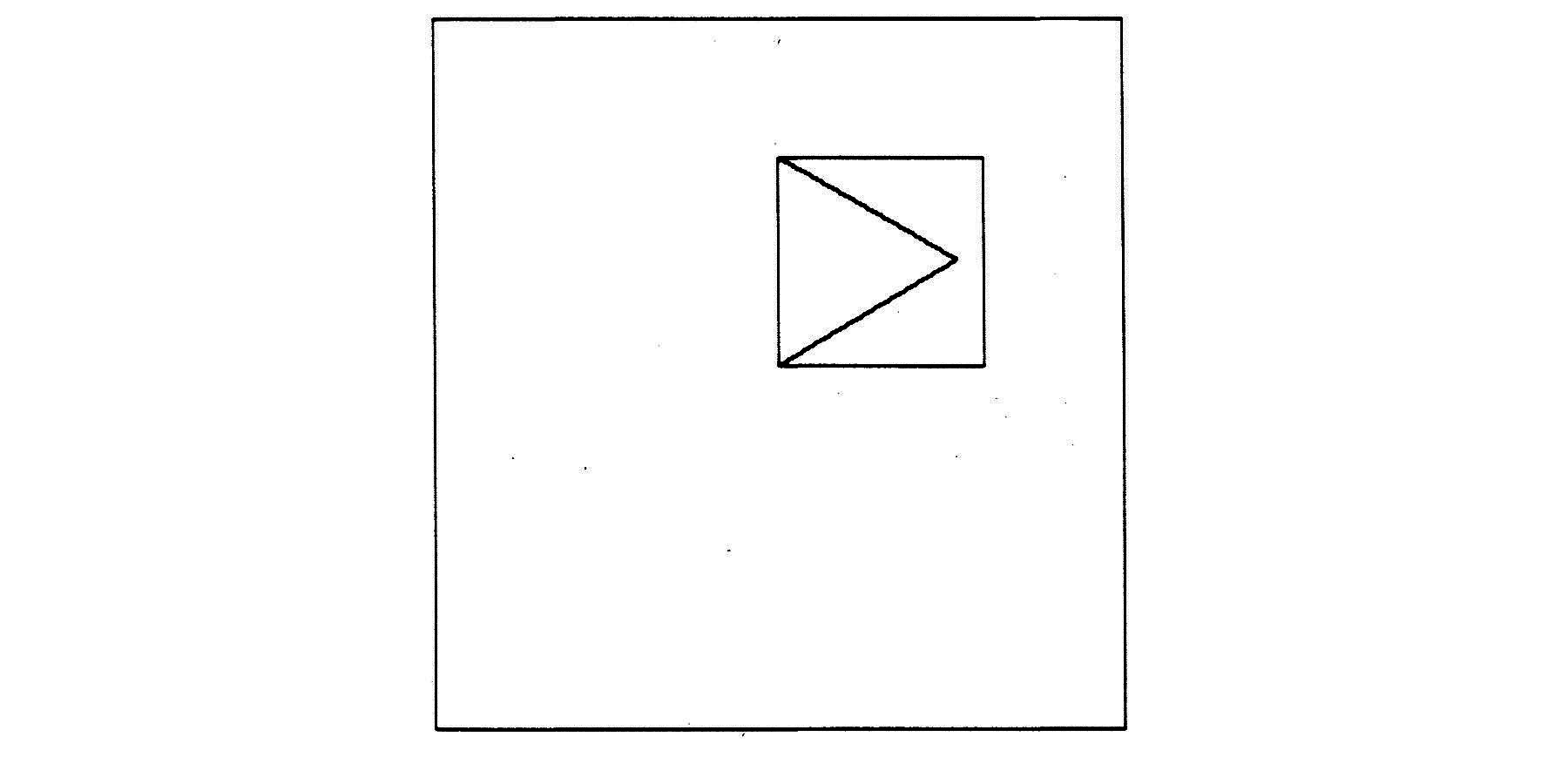
Figure 4

The triangle came out inside the square instead of on top of it!

Typically in math class, a child’s reaction to a wrong answer is to try to forget it as fast as possible. But in the LOGO environment, the child is not criticized for an error in drawing. The process of debugging is a normal part of the process of understanding a program. The programmer is encouraged to study the bug rather than forget the error. And in the Turtle context there is a good reason to study the bug. It will pay off.

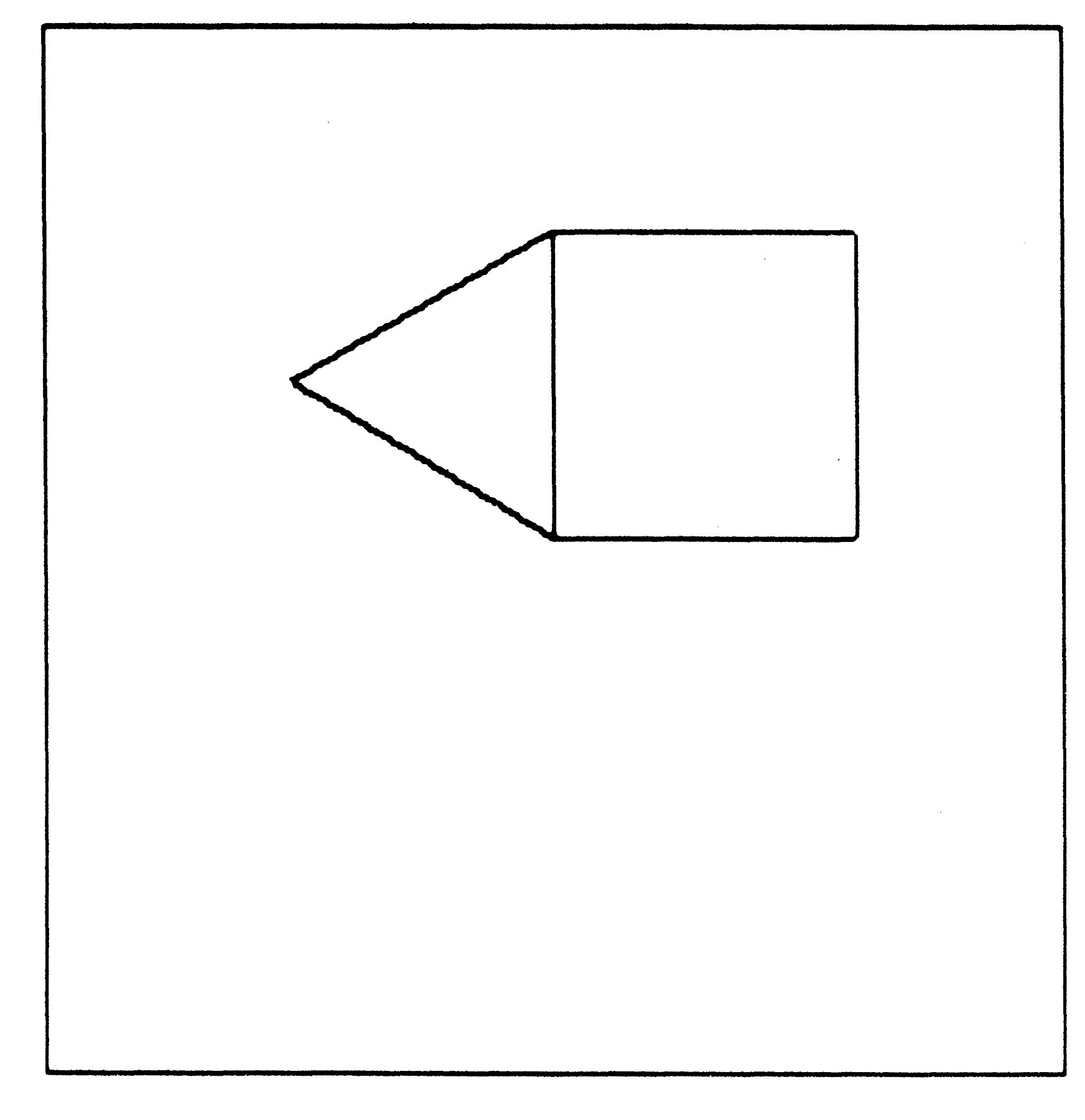
Figure 5

There are many ways this bug can be fixed. Pamela found one of them by playing Turtle. By walking along the Turtle’s track she saw that the triangle got inside the square because its first turning move in starting the triangle was a right turn. So she could fix the bug by making a left-turning triangle program. Another common way to fix this bug is by inserting a RIGHT 30 between SQUARE and TRIANGLE. In either case the amended procedure makes the following picture (Figure 5).

The learner sees progress, and also sees that things are not often either completely right or completely wrong but, rather, are on a continuum. The house is better but still has a bug. With a little more playing Turtle this final bug is pinned down and fixed by doing a RIGHT 90 as the first step in the program.

Some children use program building blocks to make concrete drawings such as HOUSE. Others prefer more abstract effects. For example, if you give the command SQUARE, pivot the Turtle with a RIGHT 120, do SQUARE again, pivot the TURTLE with RT 120 or with RT 10, do SQUARE once more and keep repeating, you get the picture in Figure 6a. A smaller rotation gives the picture in Figure 6b.

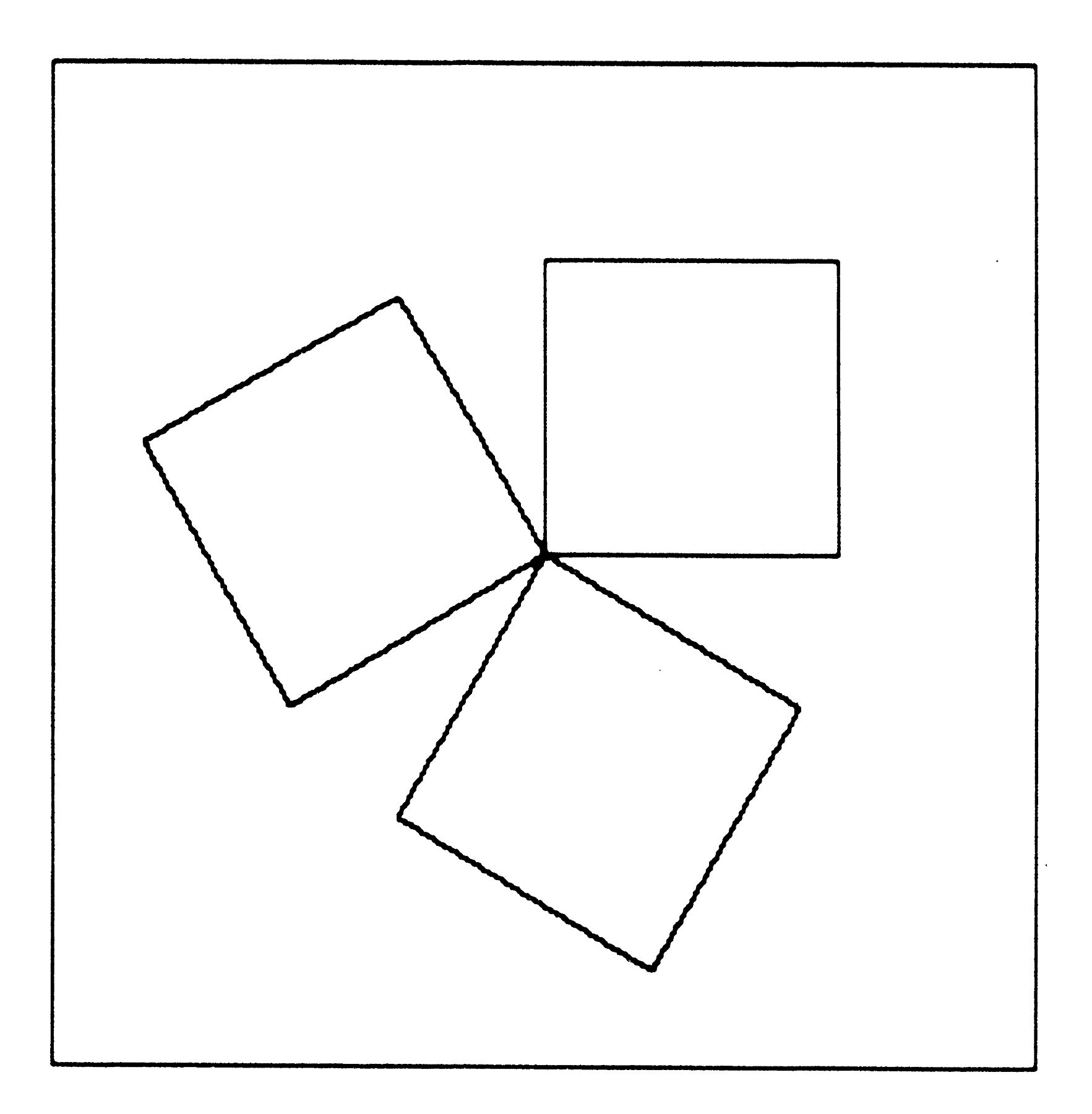
Figure 6a

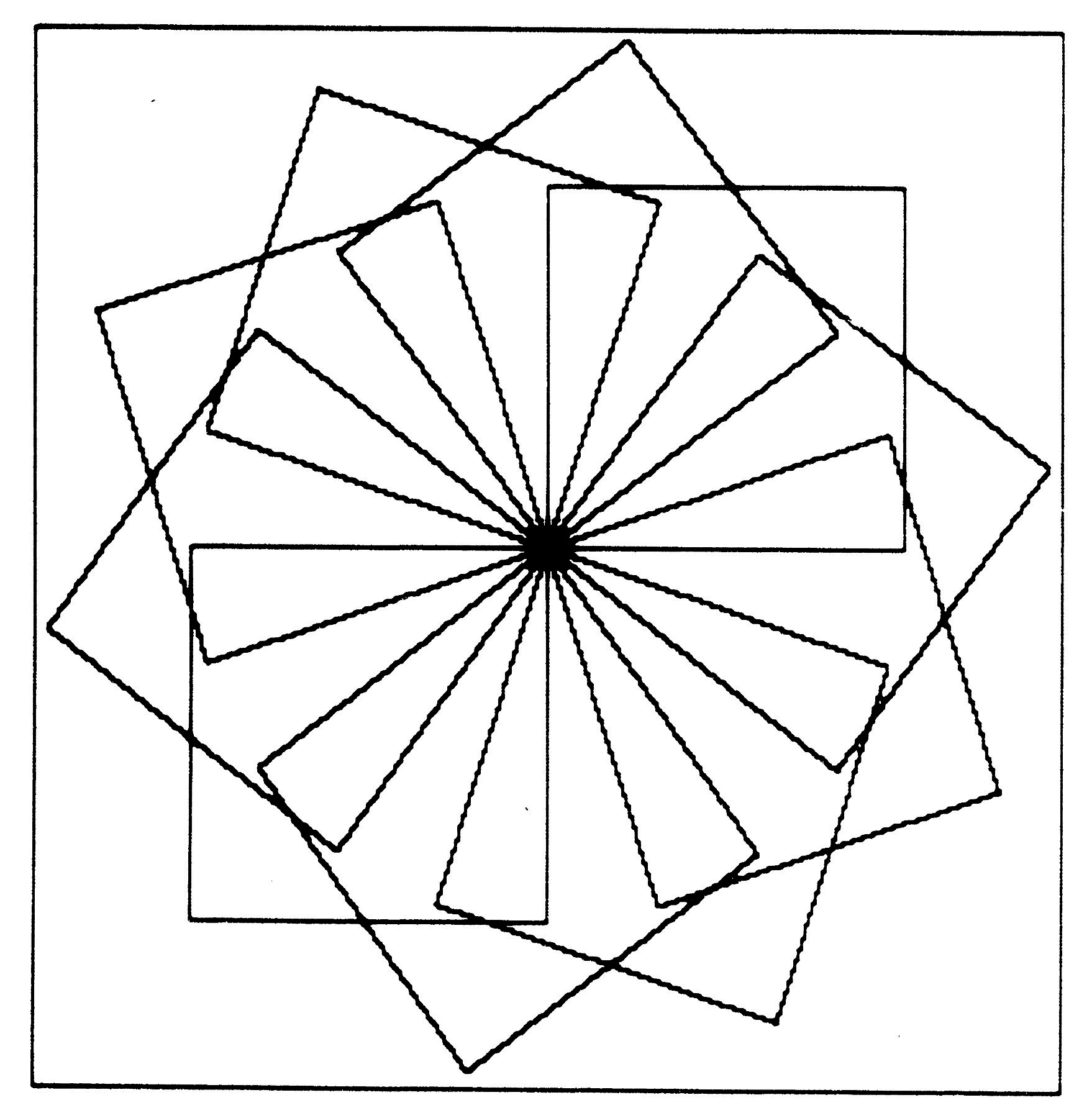
Figure 6b

These examples show how the continuity and the power principles make Turtle geometry learnable. But we wanted it to do something else as well, to open intellectual doors, preferably to be a carrier of important, powerful ideas. Even in drawing these simple squares and stars the Turtle carried some important ideas: angle, controlled repetition, state-change operator. To give ourselves a more systematic overview of what children learn from working with the Turtle we begin by distinguishing between two kinds of knowledge. One kind is mathematical. The Turtles are only a small corner of a large mathematical subject, Turtle geometry, a kind of geometry that is easily learnable and an effective carrier of very general mathematical ideas. The other kind of knowledge is mathetic: knowledge about learning. First we shall look more closely at the mathetic aspects of the Turtle experience and then turn to its more technically mathematical side. Of course, the two overlap.

We introduced Turtle geometry by relating it to a fundamental mathetic principle: Make sense of what you want to learn. Recall the case of Jenny, who possessed the conceptual prerequisites for defining nouns or verbs but who could not learn grammar because she could not identify with this enterprise. In this very fundamental way, grammar did not make sense to her. Turtle geometry was specifically designed to be something children could make sense of, to be something that would resonate with their sense of what is important. And it was designed to help children develop the mathetic strategy: In order to learn something, first make sense of it.

The Turtle circle incident illustrates syntonic learning.² This term is borrowed from clinical psychology and can be contrasted to the dissociated learning already discussed. Sometimes the term is used with qualifiers that refer to kinds of syntonicity. For example, the Turtle circle is body syntonic in that the circle is firmly related to children’s sense and knowledge about their own bodies. Or it is ego syntonic in that it is coherent with children’s sense of themselves as people with intentions, goals, desires, likes, and dislikes. A child who draws a Turtle circle wants to draw the circle; doing it produces pride and excitement.

Turtle geometry is learnable because it is syntonic. And it is an aid to learning other things because it encourages the conscious, deliberate use of problem-solving and mathetic strategies. Mathematician George Polya³ has argued that general methods for solving problems should be taught. Some of the strategies used in Turtle geometry are special cases of Polya’s suggestions. For example, Polya recommends that whenever we approach a problem we should run through a mental checklist of heuristic questions such as: Can this problem be subdivided into simpler problems? Can this problem be related to a problem I already know how to solve? Turtle geometry lends itself to this exercise. The key to finding out how to make a Turtle draw a circle is to refer to a problem whose solution is known very well indeed—the problem of walking in a circle. Turtle geometry provides excellent opportunities to practice the art of splitting difficulties. For example, HOUSE was made by first making SQUARE and TRIANGLE. In short, I believe that Turtle geometry lends itself so well to Polya’s principles that the best way to explain Polya to students is to let them learn Turtle geometry. Thus, Turtle geometry serves as a carrier for the general ideas of a heuristic strategy.

Because of Polya’s influence, it has often been suggested that mathematics teachers pay explicit attention to heuristics or “process” as well as to content. The failure of this idea to take root in the educational system can be explained partially by the paucity of good situations in which simple and compelling models of heuristic knowledge can be encountered and internalized by children. Turtle geometry is not only particularly rich in such situations, it also adds a new element to Polya’s advice: To solve a problem, look for something like it that you already understand. The advice is abstract; Turtle geometry turns it into a concrete, procedural principle: Play Turtle. Do it yourself. In Turtle work an almost inexhaustible source of “similar situations” is available because we draw on our own behavior, our own bodies. So, when in trouble, we can play Turtle. This brings Polya’s advice down to earth. Turtle geometry becomes a bridge to Polya. The child who has worked extensively with Turtles becomes deeply convinced of the value of “looking for something like it” because the advice has often paid off. From these successes comes the confidence and skill needed to learn how to apply the principle in situations, such as most of those encountered in school math, where similarities are less evident. School math, though elementary in terms of its arithmetic content, is a relatively advanced subject for the exercise of Polya’s principles.

Arithmetic is a bad introductory domain for learning heuristic thinking. Turtle geometry is an excellent one. By its qualities of ego and body syntonicity, the act of learning to make the Turtle draw gives the child a model of learning that is very much different from the dissociated one a fifth-grade boy, Bill, described as the way to learn multiplication tables in school: “You learn stuff like that by making your mind a blank and saying it over and over until you know it.” Bill spent a considerable amount of time on “learning” his tables. The results were poor, and in fact, the poor results themselves speak for the accuracy of Bill’s reporting of his own mental processes in learning. He failed to learn because he forced himself out of any relationship to the material—or rather, he adopted the worst relationship, dissociation, as a strategy for learning. His teachers thought that he “had a poor memory” and had even discussed the possibility of brain damage. But Bill had extensive knowledge of popular and folk songs, which he had no difficulty remembering, perhaps because he was too busy to think about making his mind a blank.

Current theories about the separation of brain functions might suggest that Bill’s “poor memory” was specific to numbers. But the boy could easily recount reference numbers, prices, and dates for thousands of records. The difference between what he “could” and “could not” learn did not depend on the content of the knowledge but on his relationship to it. Turtle geometry, by virtue of its connection with rhythm and movement and the navigational knowledge needed in everyday life, allowed Billy to relate to it more as he did to songs than to multiplication tables. His progress was spectacular. Through Turtle geometry, mathematical knowledge Billy had previously rejected could enter his intellectual world.

Now we turn from mathetic to mathematical considerations. What mathematics does one learn when one learns Turtle geometry? For the purposes of this discussion we distinguish three classes of mathematical knowledge, each of which benefits from work with Turtles. First, there is the body of knowledge “school math” that has been explicitly selected (in my opinion largely by historical accident) as the core of basic mathematics that all citizens should possess. Second, there is a body of knowledge (let me call it “protomath”) that is presupposed by school math even though it is not explicitly mentioned in traditional curricula. Some of this knowledge is of a general “social” nature: for example, knowledge that bears on why we do mathematics at all and how we can make sense of math. Other knowledge in this category is the kind of underlying structure to which genetic epistemology has drawn the attention of educators: deductive principles such as transitivity, the conservations, the intuitive logic of classifications, and so on. Finally, there is a third category: knowledge that is neither included in nor presupposed by the school math but that ought to be considered for inclusion in the intellectual equipment of the educated citizen of the future.

I think that understanding the relations among the Euclidean, the Cartesian, and the differential systems of geometry belongs to this third category. For a student, drawing a Turtle circle is more than a “common sense” way of drawing circles. It places the child in contact with a cluster of ideas that lie at the heart of the calculus. This fact may be invisible to many readers whose only encounter with calculus was a high school or college course where “calculus” was equated with certain formal manipulations of symbols. The child in the Turtle circle incident was not learning about the formalism of calculus, for example that the derivative of xⁿ is nx^n_1, but about its use and its meaning. In fact the Turtle circle program leads to an alternative formalism for what is traditionally called a “differential equation” and is a powerful carrier of the ideas behind the differential. This is why it is possible to understand so many topics through the Turtle; the Turtle program is an intuitive analog of the differential equation, a concept one finds in almost every example of traditional applied mathematics.

Differential calculus derives much of its power from an ability to describe growth by what is happening at the growing tip. This is what made it such a good instrument for Newton’s attempts to understand the motion of the planets. As the orbit is traced out, it is the local conditions at the place where the planet now finds itself that determine where it will go next. In our instructions to the Turtle, FORWARD 1, RIGHT TURN 1, we referred only to the difference between where the Turtle is now and where it shall momentarily be. This is what makes the instructions differential. There is no reference in this to any distant part of space outside of the path itself. The Turtle sees the circle as it goes along, from within, as it were, and is blind to anything far away from it. This property is so important that mathematicians have a special name for it: Turtle geometry is “intrinsic.” The spirit of intrinsic differential geometry is seen by looking at several ways to think about a curve, say, the circle. For Euclid, the defining characteristic of a circle is the constant distance between points on the circle and a point, the center, that is not itself part of the circle. In Descartes’s geometry, in this respect more like Euclid’s than that of the Turtle, points are situated by their distance from something outside of them, that is to say the perpendicular coordinate axes. Lines and curves are defined by equations connecting these coordinates. So, for example, a circle is described as:

(x_a)² +(y_b)² = R²

In Turtle geometry a circle is defined by the fact that the Turtle keeps repeating the act: FORWARD a little, TURN a little. This repetition means that the curve it draws will have “constant curvature,” where curvature means how much you turn for a given forward motion.⁴

Turtle geometry belongs to a family of geometries with properties not found in the Euclidean or Cartesian system. These are the differential geometries that have developed since Newton and have made possible much of modern physics. We have noted that the differential equation is the formalism through which physics has been able to describe the motion of a particle or a planet. In chapter 5, where we discuss this in more detail, we shall also see that it is the appropriate formalism to describe the motion of an animal or the evolution of an economy. And we shall come to understand more clearly that it is not by coincidence that Turtle geometry has links both to the experience of a child and to the most powerful achievements in physics. For the laws of motion of the child, though less precise in form, share the mathematical structure of the differential equation with the laws of motion of planets turning about the sun and with those of moths turning about a candle flame. And the Turtle is nothing more or less than a reconstruction in intuitive computational form of the qualitative core of this mathematical structure. When we return to these ideas in chapter 5, we shall see how Turtle geometry opens the door to an intuitive grasp of calculus, physics, and mathematical modeling as it is used in the biological and social sciences.

The effect of work with Turtle geometry on some components of school math is primarily relational or affective: Many children have come to the LOGO lab hating numbers as alien objects and have left loving them. In other cases work with the Turtle provides specific intuitive models for complex mathematical concepts most children find difficult. The use of numbers to measure angles is a simple example. In the Turtle context children pick this ability up almost unconsciously. Everyone—including the few first graders and many third graders we have worked with—emerges from the experience with a much better sense of what is meant by 45 degrees or 10 degrees or 360 degrees than the majority of high school students ever acquire. Thus, they are prepared for all the many formal topics—geometry, trigonometry, drafting, and so on—in which the concept of angle plays a central part. But they are prepared for something else as well, an aspect of the use of angular measure in our society to which the school math is systematically blind.

One of the most widespread representations of the idea of angle in the lives of contemporary Americans is in navigation. Many millions navigate boats or airplanes or read maps. For most there is a total dissociation between these live activities and the dead school math. We have stressed the fact that using the Turtle as metaphorical carrier for the idea of angle connects it firmly to body geometry. We have called this body syntonicity. Here we see a cultural syntonicity: The Turtle connects the idea of angle to navigation, activity firmly and positively rooted in the extraschool culture of many children. And as computers continue to spread into the world, the cultural syntonicity of Turtle geometry will become more and more powerful.

A second key mathematical concept whose understanding is facilitated by the Turtle is the idea of a variable: the idea of using a symbol to name an unknown entity. To see how Turtles contribute to this, we extend the program for Turtle circles into a program for Turtle spirals (Figure 7).

Look, for example, at the coil spiral. Like the circle, it too can be made according to the prescription: Go forward a little, turn a little. The difference between the two is that the circle is “the same all the way” while the spiral gets flatter, “less curvy,” as you move out from the middle. The circle is a curve of constant curvature. The curvature of the spiral decreases as it moves outward. To walk in a spiral, one could take a step, then turn, take a step, then turn, each time turning a little less (or stepping a little more). To translate this into instructions for the Turtle, you need some way to express the fact that you are dealing with a variable quantity. In principle you could describe this by a very long program (see Figure 8) that would specify precisely how much the Turtle should turn on each step. This is tedious. A better method uses the concept of symbolic naming through a variable, one of the most powerful mathematical ideas ever invented.

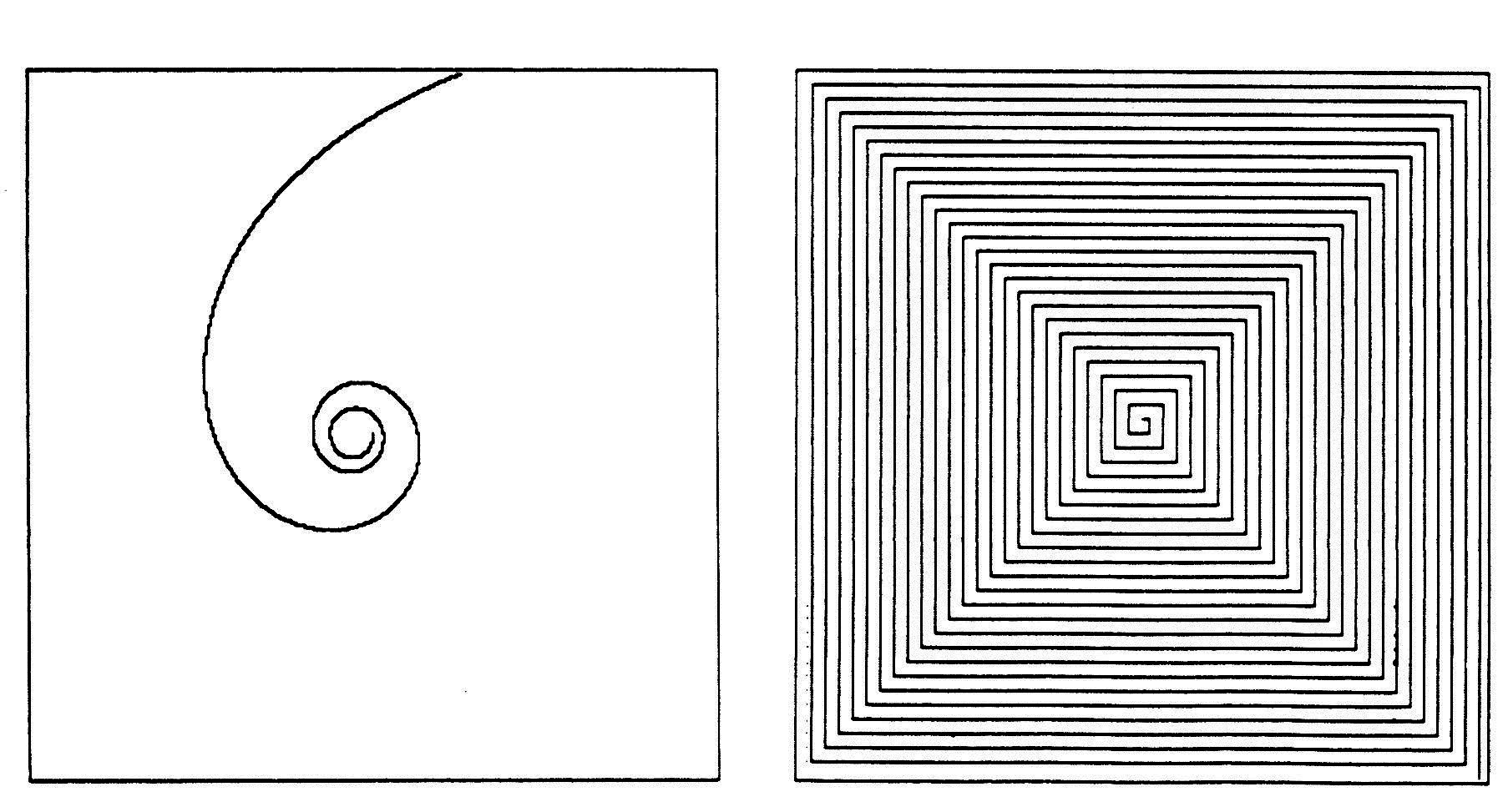
Figure 7

Figure 8. How NOT to Draw Spirals

In TURTLETALK, variables are presented as a means of communication. What we want to say to the Turtle is “go forward a little step, then turn a certain amount, but I can’t tell you now how much to turn because it will be different each time.” To draw the “squiral” we want to say “go forward a certain distance, which will be different each time, and then turn 90.” In mathematical language the trick for saying something like this is to invent a name for the “amount I can’t tell you.” The name could be a letter, such as X, or it could be a whole word, such as ANGLE OR DISTANCE. (One of the minor contributions of the computer culture to mathematics is its habit of using mnemonic words instead of single letters as names for variables.) To put the idea of variable to work, TURTLE TALK allows one to create a “procedure with an input.” This can be done by typing:

TO STEP DISTANCE

FORWARD DISTANCE

RIGHT 90

END

The command STEP 100 will make the Turtle go forward 100 units and then turn right 90 degrees. Similarly STEP 110 will make it go forward 110 units and then turn 90 degrees. In LOGO environments we encourage children to use an anthropomorphic metaphor: The command STEP invokes an agent (a “STEP man”) whose job is to issue two commands, a FORWARD command and a RIGHT command, to the Turtle. But this agent cannot perform this job without being given a message—a number that will be passed on to the “FORWARD man” who will pass it on to the Turtle.

The procedure STEP is not really very exciting, but a small change will make it so. Compare it with the procedure SPI, which is exactly the same except for having one extra line:

TO SPI DISTANCE

FORWARD DISTANCE

RIGHT 90

SPI DISTANCE + 5

END

The command SPI 100 invokes a SPI agent and gives it the input message 100. The SPI agent then issues three commands. The first is just like the first command of the STEP agent: Tell the Turtle to go forward 100 units. The second tells the Turtle to turn right. Again there is nothing new. But the third does something extraordinary. This command is SPI 105. What is its effect? It tells the Turtle to go forward 105 units, tells the Turtle to turn right 90, and then issues the command SPI 110. Thus we have a trick called “recursion” for setting up a never-ending process whose initial steps are shown in Figures 9a and 9b on the following pages.

Of all the ideas I have introduced to children, recursion stands out as the one idea that is particularly able to evoke an excited response. I think this is partly because the idea of going on forever touches on every child’s fantasies and partly because recursion itself has roots in popular culture. For example, there is the recursion riddle: If you have two wishes what is the second? (Two more wishes.) And there is the evocative picture of a label with a picture of itself. By opening the rich opportunities of playing with infinity the cluster of ideas represented by the SPI procedure puts a child in touch with something of what it is like to be a mathematician. Another aspect of living a mathematical experience is illustrated by Figure 9b where we see how a curious mathematical phenomenon can be explored by varying the angle in the SPI procedure. Angles close to 90 produce a surprising emergent phenomenon: The arms of the galaxy like twisted squirals were not actually programmed into the procedure. They come as a shock and often motivate long explorations in which numerical and geometric thinking intertwines with aesthetics.

Figure 9a

Figure 9b

In the LOGO environment new ideas are often acquired as a means of satisfying a personal need to do something one could not do before. In a traditional school setting, the beginning student encounters the notion of variable in little problems such as:

5 + X = 8. What is X?

Few children see this as a personally relevant problem, and even fewer experience the method of solution as a source of power. They are right. In the context of their lives, they can’t do much with it. In the LOGO encounter, the situation is very much different. Here the child has a personal need: to make a spiral. In this context the idea of a variable is a source of personal power, power to do something desired but inaccessible without this idea. Of course, many children who encounter the notion of variable in a traditional setting do learn to use it effectively. But it seldom conveys a sense of “mathpower,” not even to the mathematically best and brightest. And this is the point of greatest contrast between an encounter with the idea of variables in the traditional school and in the LOGO environment. In LOGO, the concept empowers the child, and the child experiences what it is like for mathematics to enable whole cultures to do what no one could do before.

If the use of a variable to make a spiral were introduced as an isolated example to “illustrate” the “concept of mathpower,” it would have only a haphazard chance of connecting with a few children (as gears connected with me). But in Turtle geometry it is not an isolated example. It is typical of how all mathematical knowledge is encountered. Mathpower, one might say, becomes a way of life. The sense of power is associated not only with immediately applicable methods such as the use of angular measure of variables but also with such concepts as “theorem” or “proof” or “heuristic” or “problem-solving method.” In using these concepts, the child is developing ways to talk about mathematics. And it is to this development of mathematical articulateness we now turn.

Consider a child who has already made the Turtle draw a square and a circle and would now like to draw a triangle with all three sides equal to 100 Turtle steps. The form of the program might be:

TO TRIANGLE

REPEAT 3

FORWARD 100

RIGHT SOMETHING

END

But for the Turtle to draw the figure, the child needs to tell it more. What is the quantity we called SOMETHING? For the square we instructed the Turtle to turn 90 degrees at each vertex, so that the square program was:

TO SQUARE

REPEAT 4

FORWARD 100

RIGHT 90

END

Now we can see how Polya’s precept, “find similarities,” and Turtle geometry’s procedural principle, “play Turtle,” can work together. What is the same in the square and the triangle? If we play Turtle and “pace out” the trip that we want the Turtle to take, we notice that in both cases we start and end at the same point and facing the same direction. That is, we end in the state in which we started. And in between we did one complete turn. What is different in the two cases is whether our turning was done “in three goes” or “in four goes.” The mathematical content of this idea is as powerful as it is simple. Priority goes to the notion of the total trip—how much do you turn all the way around?

The amazing fact is that all total trips turn the same amount, 360 degrees. The four 90 degrees of the square make 360 degrees, and since all the turning happens at the corner, the three turns in a triangle must each be 360 degrees divided by three. So the quantity we called SOMETHING is actually 120 degrees. This is the proposition of “The Total Turtle Trip Theorem.”

If a Turtle takes a trip around the boundary of any area and ends up in the state in which it started, then the sum of all turns will be 360 degrees.⁵

Part and parcel of understanding this is learning a method of using it to solve a well-defined class of problems. Thus the child’s encounter with this theorem is different in several ways from memorizing its Euclidean counterpart: “The sum of the internal angles of a triangle is 180 degrees.”

First (at least in the context of LOGO computers), the Total Turtle Trip Theorem is more powerful: The child can actually use it. Second, it is more general: It applies to squares and curves as well as to triangles. Third, it is more intelligible: Its proof is easy to grasp. And it is more personal: You can “walk it through,” and it is a model for the general habit of relating mathematics to personal knowledge.

We have seen children use the Total Turtle Trip Theorem to draw an equilateral triangle. But what is exciting is to watch how the theorem can accompany them from such simple projects to far more advanced ones—the flowers in the boxes that are reproduced in the center of the book show a project a little way along this path. For what is important when we give children a theorem to use is not that they should memorize it. What matters most is that by growing up with a few very powerful theorems, one comes to appreciate how certain ideas can be used as tools to think with over a lifetime. One learns to enjoy and to respect the power of powerful ideas. One learns that the most powerful idea of all is the idea of powerful ideas.

CHAPTER 3

Turtle Geometry

A Mathematics Made for Learning