CHAPTER 4
Languages for Computers and for People
The Centipede was happy quite
Until the toad in fun
Said, Pray which leg comes after which?
This wrought her mind to such a pitch
She lay distracted in a ditch
Considering how to run
—ANONYMOUS
THE CENTIPEDE STORY IS DISTURBING. WE USUALLY LIKE TO THINK that thinking and understanding are, by definition, good things to do, and that, in particular, they are useful in learning. But the centipede came to grief by thinking about her own actions. Would the same thing happen to us? Does this mean we should give up thinking about ourselves? In fact, in our “rational” culture, the notion that thinking impedes action, even that thinking impedes learning, is quite prevalent. It is our usual way of talking about learning to ride a bicycle: “Keep trying—one day you’ll just ‘get it’” is standard parental advice to children struggling with the two-wheeler.
Many philosophers have developed the idea that some knowledge cannot be described in words or grasped by conscious thought. The idea was brought into recent curriculum reforms by advocates of active learning and given theoretical support by J. S. Bruner’s1 influential classification of ways of knowing: Some knowledge is represented as action, some as image, and only the third category as symbols. Bruner has asserted that “words and diagrams” are “impotent” to represent certain kinds of knowledge which are only representable as action. In this chapter I try to develop a more flexible perspective on these problems.
My perspective is more flexible because it rejects the idea of the dichotomy verbalizable versus nonverbalizable. No knowledge is entirely reducible to words, and no knowledge is entirely ineffable. My perspective is more flexible also in recognizing a historical dimension: An important component in the history of knowledge is the development of techniques that increase the potency of “words and diagrams.” What is true historically is also true for the individual: An important part of becoming a good learner is learning how to push out the frontier of what we can express with words. From this point of view the question about the bicycle is not whether or not one can “tell” someone “in full” how to ride but rather what can be done to improve our ability to communicate with others (and with ourselves in internal dialogues) just enough to make a difference to learning to ride. The central theme of this chapter is the development of descriptive languages for talking about learning. We shall focus particular attention on one of the kinds of learning that many people believe to be best done by “just doing it”—the learning of physical skills. Our approach to this is the exact opposite of the way schools treat “physical education”—as a nonintellectual subject. Our strategy is to make visible even to children the fact that learning a physical skill has much in common with building a scientific theory.
With this realization comes many benefits. First, I know from work in the LOGO laboratory that it means more effective learning of physical skills.2 Without this direct benefit, seeking to “motivate” a scientific idea by drawing an analogy with a physical activity could easily degenerate into another example of “teacher’s double talk.” But if we can find an honest place for scientific thinking in activities that the child feels are important and personal, we shall open the doors to a more coherent, syntonic pattern of learning.
In this chapter I show that this can be done and suggest that relating science to physical skills can do much more for learning science than providing what educators like to call a “motivation.” It can potentially place children in a position of feeling some identification with scientists through knowing that scientists use formal descriptive languages and knowing that they too can use such languages as tools for learning physical skills—juggling for example. The idea is to give children a way of thinking of themselves as “doing science” when they are doing something pleasurable with their bodies. If children could see Descartes’s invention of coordinate geometry as something not totally alien to their own experiences of daily life, this could not only make Descartes more meaningful but, at the same time, help the children come to see themselves as more meaningful.
Let us look a bit more closely at what our culture thinks about learning physical skills. It is no more consistent regarding this than it is regarding the mathematics of more “abstract” subjects we discussed earlier. Although the popular wisdom and much of educational psychology may agree that learning physical skills is a domain where “conscious” thinking doesn’t help, people who make sports their livelihood don’t always agree. Some of the most successful coaches put great effort into analyzing and verbalizing the movements that must be learned and perfected. One sportswriter, Timothy Gallwey, has turned popular sensitivity to this contradiction into publishing success. In his book Inner Tennis he offers some suggestions for a way out of the dilemma. Gallwey encourages the learner to think of himself as made up of two selves: an analytic, verbal self and a more holistic, intuitive one. It is appropriate, he argues, that now one and now the other of these two selves should be in control; in fact, an important part of the learning process is teaching each “self” to know when to take over and when to leave it to the other.
Gallwey’s description of the negotiation and transactions that go with successful learning is unusual in educational circles. In the choice between analytic and holistic modes of thinking, he gives control to the learner. This is very different from what usually happens in curriculum design for schools. Curriculum reformers are often concerned about the choice between verbal and nonverbal experimental learning. But their strategy is usually to make the choice from above and build it into the curriculum. Gallwey’s strategy is to help learners learn how to make the choice for themselves, a perspective that is in line with the vision already suggested of the child as epistemologist, where the child is encouraged to become expert in recognizing and choosing among varying styles of thought.
Taking Timothy Gallwey as an example is not an endorsement of everything he says. Most of his ideas strike me as problematic. But I think he is quite right in recognizing that people need more structured ways to talk and think about the learning of skills. Contemporary language is not sufficiently rich in this domain.
In a computer-rich world, computer languages that simultaneously provide a means of control over the computer and offer new and powerful descriptive languages for thinking will undoubtedly be carried into the general culture. They will have a particular effect on our language for describing ourselves and our learning. To some extent this has already occurred. It is not uncommon for people with no knowledge of computers to use such concepts as “input,” “output,” and “feedback” to describe their own mental processes. We shall give an example of this process by showing how programming concepts can be used as a conceptual framework for learning a particular physical skill, namely, juggling. Thus we look at programming as a source of descriptive devices, that is to say as a means of strengthening language.
Many scientific and mathematical advances have served a similar linguistic function by giving us words and concepts to describe what had previously seemed too amorphous for systematic thought. One of the most striking examples of the power of descriptive language is the genesis of analytic geometry, which played so decisive a role in the development of modern science.
Legend has it that Descartes invented analytic geometry while lying in bed late one morning observing a fly on the ceiling. We can imagine what his thinking might have been. The fly moving hither and thither traced a path as real as the circles and ellipses of Euclidean mathematics, but one that defied description in Euclidean language. Descartes then saw a way to grasp it: At each moment the fly’s position could be described by saying how far it was from the walls. Points in space could be described by pairs of numbers; a path could be described by an equation or relationship that holds true for those number pairs whose points lie on the path. The potency of symbols took a leap forward when Descartes realized how to use an algebraic language to talk about space, and a spatial language to talk about algebraic phenomena. Descartes’s method of coordinate geometry born from this insight provided tools that science has since used to describe the paths of flies and planets and the “paths” of the more abstract objects, the stuff of pure mathematics.
Descartes’s breakthrough has much in common with the experience of the child in the Turtle circle episode. The child, we recall, was explicitly looking for a way to describe the process of walking in a circle. In LOGO this description takes a very simple form, and the child has to invent only the description. Descartes had to do more. But in both cases the reward is the ability to describe analytically something that until then was known in a global, perceptual-kinesthetic way. Neither the child nor Descartes suffered the fate of the centipede: Both could walk in circles as well after knowing how to describe their movements analytically as before.
But Descartes’s formalism, powerful as it is for describing processes in the world of physics, is not what is needed for describing processes in the world of physical skills.
Using calculus to describe juggling or how a centipede walks would indeed be confusing. Attempts to use such descriptions in learning physical skills very likely would leave the learner lying with feverish mind in the nearest ditch. This mode of formal description is not matched to this task. But other formalisms are.
The field of education research has not worked in the direction of developing such formalisms. But another research community, that of computer scientists, has had (for its own reasons) to work on the problem of descriptive languages and has thereby become an unexpected resource for educational innovation. Computers are called upon to do many things, and getting a computer to do something requires that the underlying process be described, on some level, with enough precision to be carried out by the machine. Thus computer scientists have devoted much of their talent and energy to developing powerful descriptive formalisms. One might even say that computer science is wrongly so called: Most of it is not the science of computers, but the science of descriptions and descriptive languages. Some of the descriptive formalisms produced by computer science are exactly what are needed to get a handle on the process of learning a physical skill. Here we demonstrate the point by choosing one important set of ideas from programming: the concept of structured programming, which we shall illustrate by the learning experience of a fifth grader in a LOGO environment.
Keith had set himself the goal of making the computer draw a stick figure as in the box GOAL (see Figure 10a).
His plan was to start with one foot and draw the Turtle strokes illustrated in the box SEQUENCE. In doing so he is using an image familiar in his precomputational culture, where he has learned to do connect-the-dots drawing and to describe his activities in a step-by-step way. So it is perfectly natural for him to adopt this method here. The task seemed simple if somewhat tedious. He wrote (Figure 10b):
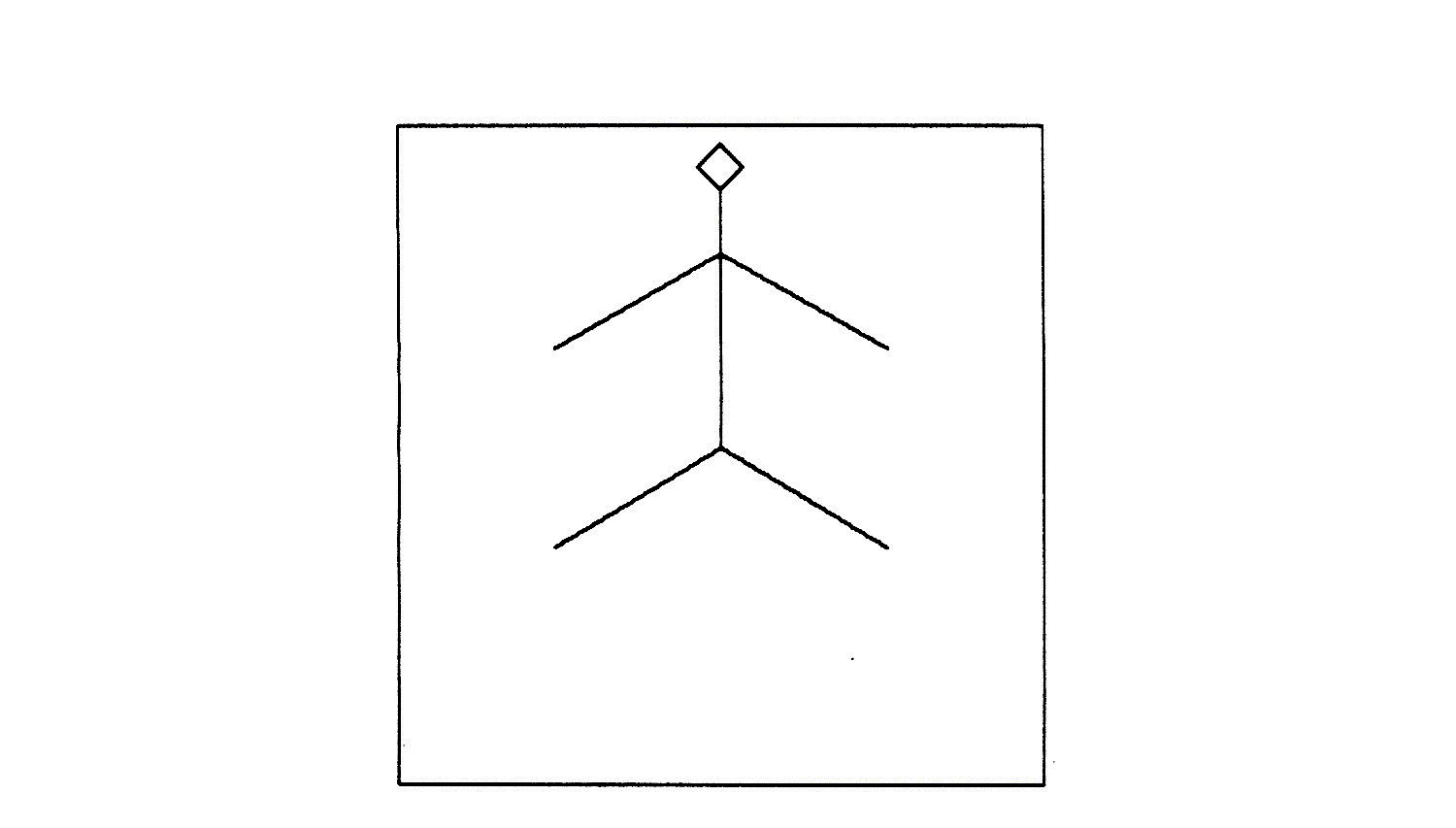
Figure 10a. Goal

Figure 10b
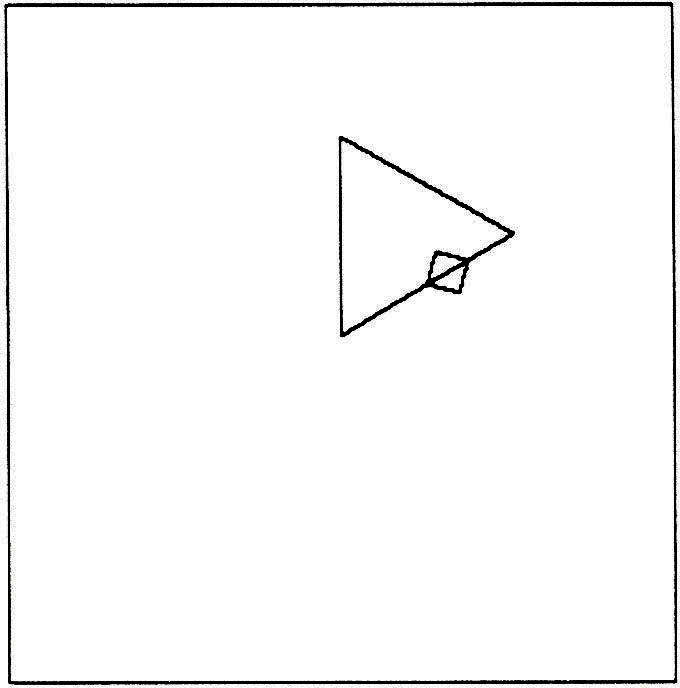
Figure 10c. Bugged Man
What appeared on the screen was the totally unexpected drawing of the BUGGED MAN (see Figure 10c). What went wrong?
Keith was prepared for surprises of this sort. As mentioned earlier, one of the mainstays of the LOGO environment is the cluster of concepts related to “bugs” and “debugging.” One does not expect anything to work at the first try. One does not judge by standards like “right—you get a good grade” and “wrong—you get a bad grade.” Rather one asks the question: “How can I fix it?” and to fix it one has first to understand what happened in its own terms. Only then can we make it happen on our terms. But in this situation Keith was unable to figure out what had happened. He had written his program in such a way that it was extremely difficult to pinpoint his error. Where was the bug in his program? What error could cause such a wild transformation of what he had intended?
In order to understand his predicament we contrast his program with a different strategy of programming known as “structured programming.” Our aim is to subdivide the program into natural parts so that we can debug programs for each part separately. In Keith’s long, featureless set of instructions it is hard to see and trap a bug. By working with small parts, however, bugs can be confined and more easily trapped, figured out. In this case a natural subdivision is to make a program to draw a V-shaped entity to use for arms and legs and another to draw a square for the head. Once these “subprocedures” have been written and tested, it is extremely easy to write the “superprocedure” to draw the stick figure itself. We can write an extremely simple program to draw the stick figure:
TO MAN
VEE
FORWARD 50
VEE
FORWARD 25
HEAD
END
This procedure is simple enough to grasp as a whole. But of course it achieves its simplicity only by making the assumption that the commands VEE and HEAD are understood by the computer. If they are not, the next step must be to define VEE and HEAD. We can do this in the same style of always working with a procedure we can understand as a whole. For example:
TO VEE
RIGHT 120
LINE 50
RIGHT 120
LINE 50
RIGHT 120
END
(In this program we assume we have defined the command LINE, which causes the Turtle to go forward and come back.)
To make this work we next define LINE:
TO LINE:DISTANCE
FORWARD:DISTANCE
BACK:DISTANCE
END
Since the last procedure uses only innate LOGO commands, it will work without further definitions. To complete MAN we define HEAD by:
TO HEAD
RIGHT 45
SQUARE 20
END
Robert, a seventh grader, expressed his conversion to this style of programming by exclaiming: “See, all my procedures are mind-sized bites.” Robert amplified the metaphor by comments such as: “I used to get mixed up by my programs. Now I don’t bite off more than I can chew.” He had met a powerful idea: It is possible to build a large intellectual system without ever making a step that cannot be comprehended. And building with a hierarchical structure makes it possible to grasp the system as a whole, that is to say, to see the system as “viewed from the top.”
Keith, the author of the nonstructured MAN program, had been exposed to the idea of using subprocedures but had previously resisted it. The “straight-line” form of program corresponded more closely to his familiar ways of doing things. He had experienced no compelling need for structured programming until the day he could not debug his MAN program. In LOGO environments we have seen this happen time and again. When a child in this predicament asks what to do, it is usually sufficient to say: “You know what to do!” And often the child will say, sometimes triumphantly, sometimes sheepishly: “I guess I should turn it into subprocedures?” The “right way” was not imposed on Keith; the computer gave him enough flexibility and power so that his exploration could be genuine and his own.
These two styles of approaching the planning and working out of a project are pervasive. They can be seen by observing styles of learning “physical” as well as “intellectual” skills. Consider, for example, the case of two fifth graders who learned both programming and physical skills in our children’s learning laboratory.
Michael is strong, athletic, a “tough kid” in his own eyes. Paul is more introverted, studious, slightly built. Michael does poorly at school and Paul does well, so when Paul got on faster in work with the computer, moving quickly into quite complex structured programming procedures, neither one was surprised. After several weeks Michael was still able to write programs only in the straight-line style. There was no doubt that he possessed all the necessary concepts to write more elaborate programs, but he was held back by a classical and powerful resistance to using subprocedures.
At this time both began to work on stilt walking. Michael’s strategy was to fix in his mind a model of stilt walking in sequential form: “Foot on the bar, raise yourself up, foot on the other bar, first foot forward…” When attempting to do it led to a rapid crash, he would bravely start again and again and again, confident that he would eventually succeed, which in fact he did. But, to the surprise of both of them, Paul got there first.
Paul’s strategy was different. He began in the same way but when he found that he was not making progress he tried to isolate and correct part of the process that was causing trouble: “the bug.” When you step forward you tend to leave the stilt behind. This bug, once identified, is not hard to eradicate. One trick for doing so is to think of taking the step with the stilt rather than with the foot and let the stilt “carry” the foot. This is done by lifting the stilt with the arm against the foot. The analogy with his approach to programming was so apparent to Paul that this might have been a case of “transfer” from the programming work to learning this physical skill.
Actually, it is more likely that both situations drew on long-standing features of his general cognitive style. But the experience with LOGO did enable Paul to articulate these aspects of his style. The relation between programming and stilt walking was even clearer in Michael’s case. It was only through this analogy that he came to recognize explicitly the difference between his and Paul’s style of going about the stilt walking! In other words the experience of programming helped both boys obtain a better grasp of their own actions, a more articulated sense of themselves.
The generality of the idea of structured programming as a mathetic principle, that is to say an aid to learning, will become more apparent through the next example, which describes the process involved in learning another physical skill—juggling. We do not choose it at random. The Turtle circle was a good carrier for learning mathematics “with one’s body.” Juggling turns out to be an equally good carrier for learning a body skill “with mathematics.” Of course, the picture is more complicated and also more interesting because in both cases the process works in both directions, from computational metaphor to body language and back again. In passing through an experience of Turtle geometry, children sharpen their sense of their bodies and their physical movements as well as their understanding of formal geometry. And theoretical ideas about structured programs, when couched in juggling terms—real body terms—take on new concreteness and power. In both cases, knowledge takes on the quality we have characterized as syntonic.
There are many different kinds of juggling. When most people think of juggling, they are thinking about a procedure that is called “showers juggling.” In showers juggling, balls move one behind the other in a “circle” passing from left to right at the top and from right to left at the bottom (or vice versa). This takes two kinds of throws: a short, low throw to get the balls from one hand to the other at the bottom of the “circle” (near the hands), and a long, high throw to get the balls to go around the top of the circle. (See Figure 11.)
Cascade juggling has a simpler structure. There is no bottom of the circle; balls travel in both directions over the upper arc. There is only one kind of toss: a long and high one. (See Figure 11.) Its simplicity makes it a better route into juggling as well as a better example for our argument. Our guiding question is this: Will someone who wishes to learn cascade juggling be helped or hindered by a verbal, analytic description of how to do it? The answer is: It all depends. It depends on what materials the learner has for making analytic descriptions. We use cascade juggling to show how good computational models can help construct “people procedures” that improve performance of skills and how reflection on those people procedures can help us learn to program and to do mathematics. But, of course, some verbal descriptions will confuse more than they will help. Consider, for example, the description:
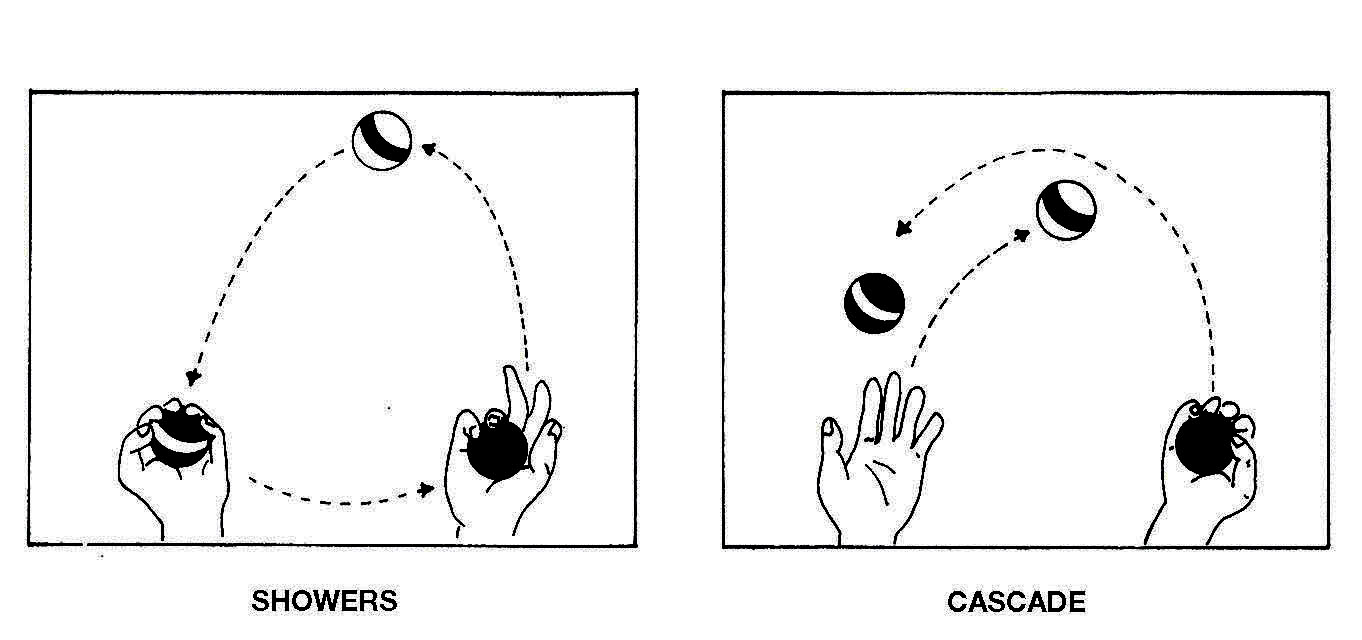
Figure 11. Two Forms of Juggling
1. Start with balls 1 and 2 in the left hand and ball 3 in the right.
2. Throw ball 1 in a high parabola to the right hand.
3. When ball 1 is at the vertex throw ball 3 over to the left hand in a similar high parabola, but take care to toss ball 3 under the trajectory of ball 1.
4. When ball 1 arrives at the right hand and ball 3 is at the vertex, catch ball 1 and throw ball 2 in a trajectory under that of ball 3, and so on.
This description is basically a brute-force straight-line program. It is not a useful description for the purpose of learning. People outside the computer culture might say it is too much like a computer program, “just one instruction after another.” It is like certain programs, for example Keith’s first MAN program. But we have seen that stringing instructions together without good internal structure is not a good model for computer programming either, and we shall see that the techniques of structured programming that are good for writing programs are also good as mathetic descriptions of juggling.
Our goal is to create a people procedure: TO JUGGLE. As a first step toward defining this procedure, we identify and name subprocedures analogous in their role to the subprocedures Keith used in drawing his stick figure (TO VEE, TO HEAD, TO LINE). In the case of juggling, a natural pair of subprocedures is what we call TOSSRIGHT and TOSSLEFT. Just as the command VEE was defined functionally by the fact that it causes the computer to place a certain V-shaped figure on the screen, the command TOSSRIGHT given to our apprentice juggler should “cause” him to throw a ball, which we assume he is holding in his left hand, over to the right hand.
But there is an important difference between programming TO MAN and programming TO JUGGLE. The programmer of TO MAN need not worry about timing, but in setting up the procedure for juggling we must worry about it. The juggler must perform the actions TOSSRIGHT and TOSSLEFT at appropriate moments in a cycle, and the two actions will have to overlap in time. Since we have chosen to include the catching phase in the same subprocedure as the throwing phase, the procedure TOSSRIGHT is meant to include catching the ball when it comes over to the right hand. Similarly, TOSSLEFT is a command to throw a ball from the right hand over to the left and catch it when it arrives.3
Since most people can perform these actions, we shall take TOSSLEFT and TOSSRIGHT as given and concentrate on how they can be combined to form a new procedure we shall call TO JUGGLE. Putting them together is different in one essential way from the combination of subprocedures TO VEE and TO HEAD to make the procedure TO MAN. TOSSLEFT might have to be initiated before the action initiated by the previous TOSSRIGHT is completed. In the language of computer science, this is expressed by saying that we are dealing with parallel processes as opposed to the strictly serial processes used in drawing the stick figure.
To describe the combination of the subprocedures we introduce a new element of programming: the concept of a “WHEN DEMON.” This is illustrated by the instruction: WHEN HUNGRY EAT. In one version of LOGO this would mean: Whenever the condition called HUNGRY happens, carry out the action called EAT. The metaphor of a “demon” expresses the idea that the command creates an autonomous entity within the computer system, one that remains dormant until a certain kind of event happens, and then, like a demon, it pounces out to perform its action. The juggling act will use two such WHEN DEMONS.
Their definitions will be something like:
WHEN something TOSSLEFT
WHEN something TOSSRIGHT
To fill the blanks, the “somethings,” we describe two conditions, or recognizable states of the system, that will trigger the tossing action.
At a key moment in the cycle the balls are disposed about like this (Figure 12):
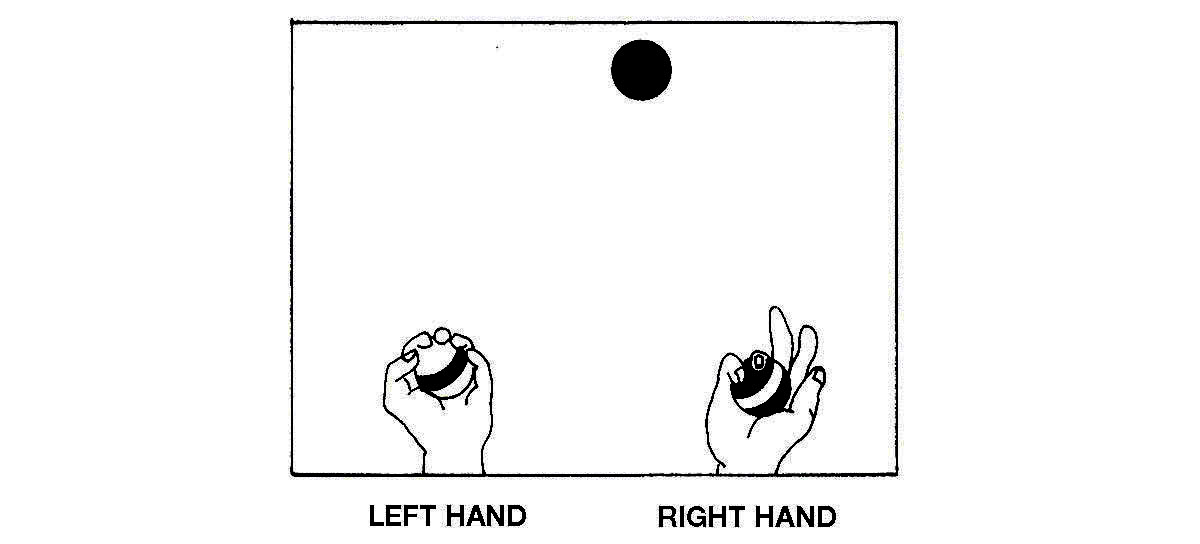
Figure 12
But this diagram of the state of the system is incomplete since it fails to show in which direction the top ball is flying. To complete it we add arrows to indicate a direction (Figure 13a) and obtain two state descriptions (Figures 13b and 13c).
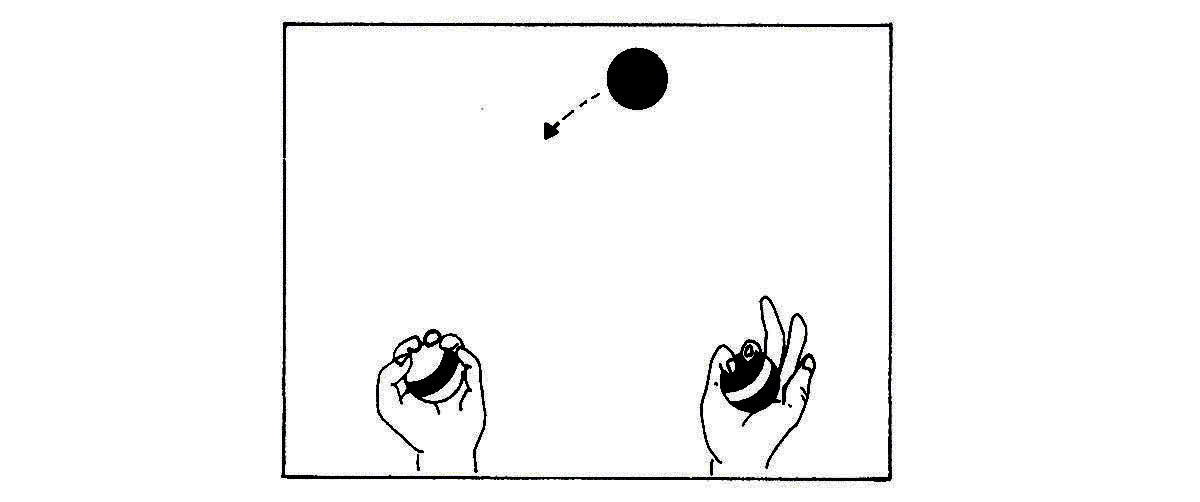
Figure 13a
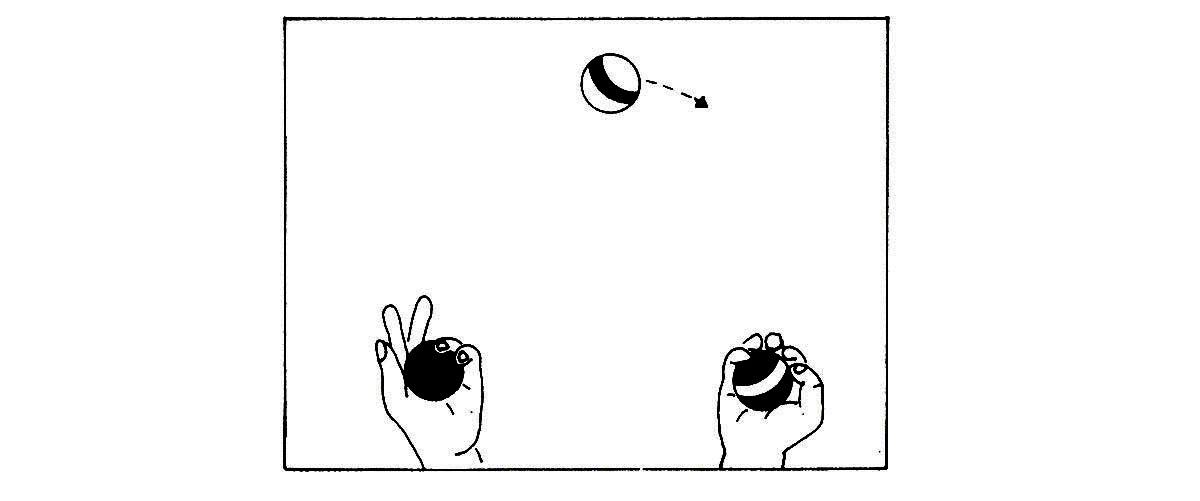
Figure 13b. TOPRIGHT: The ball is at the top and is moving to the right
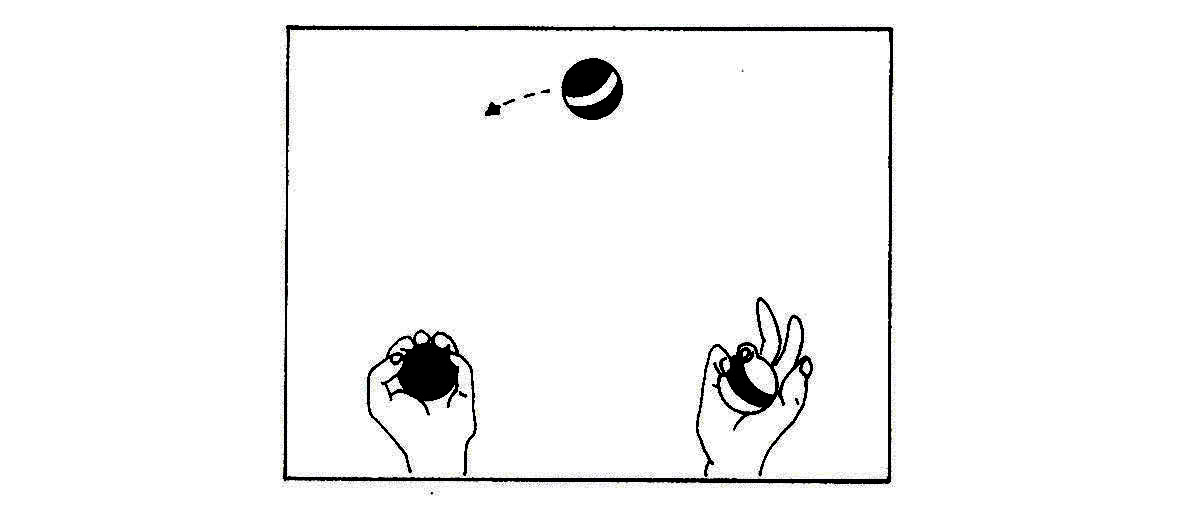
Figure 13c. TOPLEFT: The ball is at the top and is moving to the left
If we assume, reasonably, that the juggler can recognize these two situations, the following formalism should be self-explanatory:
TO KEEP JUGGLING
WHEN TOPRIGHT TOSSRIGHT
WHEN TOPLEFT TOSSLEFT
or even more simply:
TO KEEP JUGGLING
WHEN TOPX TOSSX
which declares that when the state TOPRIGHT occurs, the right hand should initiate a toss and when TOPLEFT occurs, the left hand should initiate a toss. A little thought will show that this is a complete description: The juggling process will continue in a self-perpetuating way since each toss creates a state of the system that triggers the next toss.
How can this model that turned juggling into a people procedure be applied as a teaching strategy? First, note that the model of juggling made several assumptions:
1. that the learner can perform TOSSRIGHT and TOSSLEFT
2. that she can recognize the trigger states TOPLEFT and TOPRIGHT
3. that she can combine these performance abilities according to the definitions of the procedure TO KEEP JUGGLING
Now, we translate our assumptions and our people procedure into a teaching strategy.
STEP 1. Verify that the learner can toss. Give her one ball, ask her to toss it over into the other hand. This usually happens smoothly, but we will see later that a minor refinement is often needed. The spontaneous procedure has a bug.
STEP 2. Verify that the learner can combine tosses. Try with two balls with instructions:
TO CROSS
TOPRIGHT
WHEN TOPRIGHT TOSSLEFT
END
This is intended to exchange the balls between left and right hands. Although it appears to be a simple combination of TOSSLEFT and TOSSRIGHT, it usually does not work immediately.
STEP 3. Look for bugs in the toss procedures. Why doesn’t TO CROSS work? Typically we find that the learner’s ability to toss is not really as good as it seemed in step 1. The most common deviation or “bug” in the toss procedure is following the ball with the eyes in doing a toss. Since a person has only one pair of eyes, their engagement in the first toss makes the second toss nearly impossible and thus usually ends in disaster with the balls on the floor.
STEP 4. Debugging. Assuming that the bug was following the first ball with the eyes, we debug by returning our learner to tossing with one ball without following it with her eyes. Most learners find (to their amazement) that very little practice is needed to be able to perform a toss while fixing the eyes around the expected apex of the parabola made by the flying ball. When the single toss is debugged, the learner again tries to combine two tosses. Most often this now works, although there may still be another bug to eliminate.
STEP 5. Extension to three balls. Once the learner can smoothly execute the procedure we called CROSS, we go on to three balls. To do this, begin with two balls in one hand and one in the other (Figure 14).
Ball 2 is tossed as if executing CROSS, ignoring ball 1. The TOSSRIGHT in CROSS brings the three balls into a state that is ready for KEEP JUGGLING. The transition from CROSS to KEEP JUGGLING presents a little difficulty for some learners, but this is easily overcome. Most people can learn to juggle in less than half an hour by using this strategy.
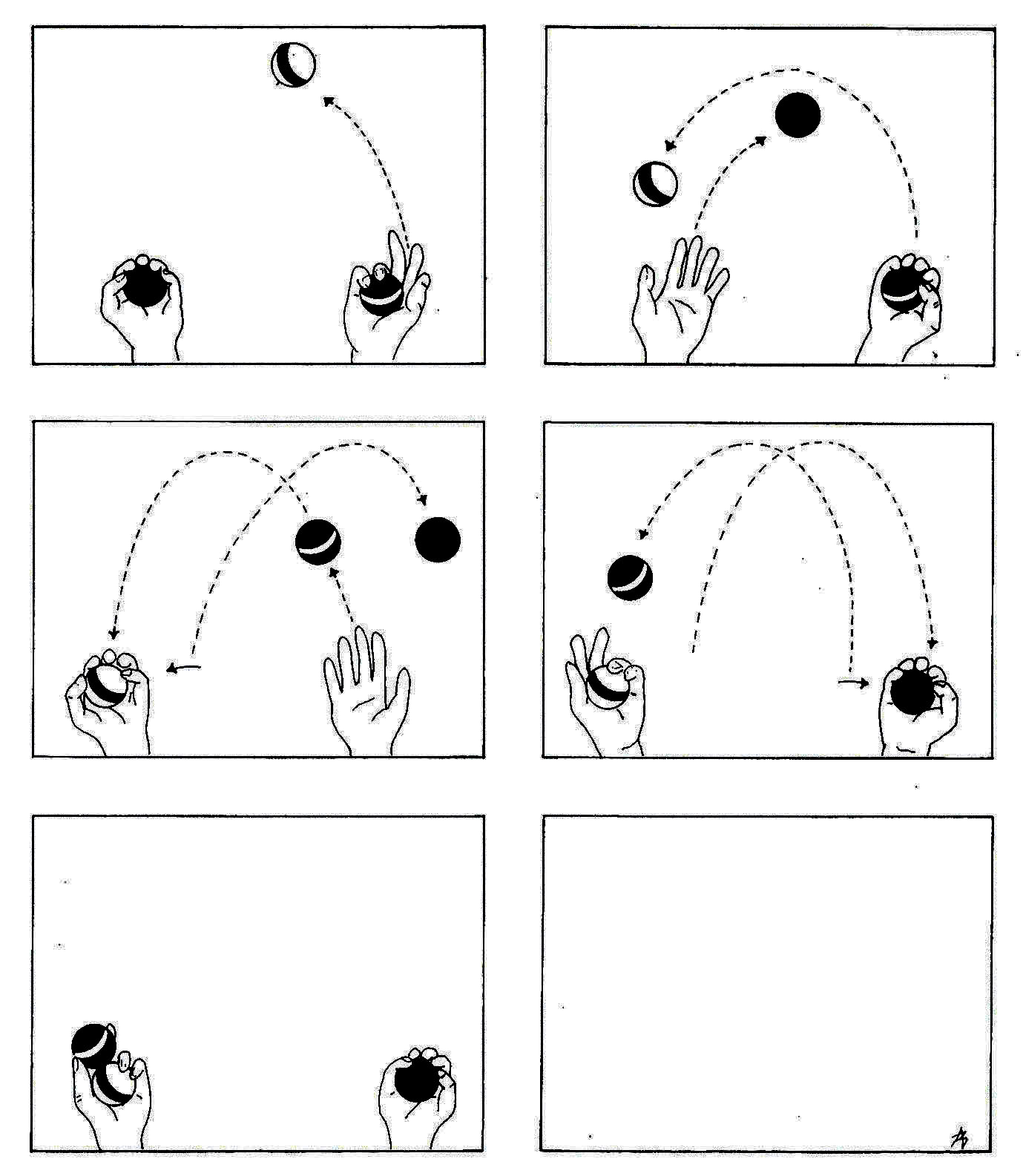
Figure 14. Cascade Juggling
Variants of this teaching strategy have been used by many LOGO teachers and studied in detail by one of them, Howard Austin, who took the analysis of juggling as the topic of his Ph.D. thesis. There is no doubt that the strategy is very effective and little doubt as to the cause: The use of programming concepts as a descriptive language facilitates debugging.
In our description of drawing a stick figure and of learning to juggle, a central theme was how debugging is facilitated by the use of an appropriate description of a complex process. In both cases the description reflected a representation of the process in modular form, that is to say broken up into natural, functional units, and catching the bug was helped by containing it within as narrow a set of boundaries as possible. The worst conditions for debugging are created when several bugs are present simultaneously. The debugging process is especially effective if the modules are small enough for it to be unlikely that any one contains more than one bug.
The difficulties produced by multiple bugs are well illustrated by what happens when beginners try to learn juggling by the brute-force approach. In fact (just as Michael learned to walk on stilts) they often succeed, usually after hours of frustrating attempts to keep three balls in the air without yet being able to cross two. But it takes them a long time to learn. When Howard Austin looked closely at the actions of the learner, he saw the same bugs that we described in our rational strategy approach, for example, the eye-following bug. In the course of very many repetitions, so-called “trial and error learning” will shape a behavior that works. By sheer chance, the eyes will happen to move a little less on one toss. Like other animals, human beings have learning mechanisms that are capable of picking up on such events and increasing the probability that they will happen again. Eventually, the bugs are ironed out and the subject learns to juggle. People are capable of learning like rats in mazes. But the process is slow and primitive. We can learn more, and more quickly, by taking conscious control of the learning process, articulating and analyzing our behavior.
The fact that computational procedures enhance learning does not mean that all repetitive processes can be magically removed from learning or that the time needed to learn juggling can be reduced to almost nothing. It always takes time to trap and eliminate bugs. It always takes time to learn necessary component skills. What can be eliminated are wasteful and inefficient methods. Learning enough juggling skill to keep three balls going takes many hours when the learner follows a poor learning strategy. When a good one is adopted the time is greatly reduced, often to as little as twenty or thirty minutes.
Children often develop a “resistance” to debugging analogous to the resistance we have seen to subprocedurizing. I have seen this in many children’s first sessions in a LOGO environment. The child plans to make the Turtle draw a certain figure, such as a house or stick man. A program is quickly written and tried. It doesn’t work. Instead of being debugged, it is erased. Sometimes the whole project is abandoned. Sometimes the child tries again and again and again with admirable persistence but always starting from scratch in an apparent attempt to do the thing “correctly” in one shot. The child might fail or might succeed in making the computer draw the picture. But this child has not yet succeeded in acquiring the strategy of debugging.
It is easy to empathize. The ethic of school has rubbed off too well. What we see as a good program with a small bug, the child sees as “wrong,” “bad,” “a mistake.” School teaches that errors are bad; the last thing one wants to do is to pore over them, dwell on them, or think about them. The child is glad to take advantage of the computer’s ability to erase it all without any trace for anyone to see. The debugging philosophy suggests an opposite attitude. Errors benefit us because they lead us to study what happened, to understand what went wrong, and, through understanding, to fix it. Experience with computer programming leads children more effectively than any other activity to “believe in” debugging.
Contact with the LOGO environment gradually undermines long-standing resistances to debugging and subprocedurizing. Some people who observe the children’s growing tolerance for their “errors” attribute the change of attitude to the LOGO teachers who are matter-of-fact and uncritical in the presence of programs the child sees as “wrong.” I think that there is something more fundamental going on. In the LOGO environment, children learn that the teacher too is a learner, and that everyone learns from mistakes.
A group of twelve fifth graders had had several hours a week of LOGO experience since the beginning of the term in September. Early in December the group decided on a collective project. A mechanical Turtle would be programmed to write “Merry Christmas” on huge paper banners that would be strung in the school corridors. An ideal project. The letters of the alphabet were divided up among members of the group. Each would write programs for two or three letters, for decorative drawings, and for whole messages, using the letter programs as subprocedures.
But snowstorms and other disruptions delayed the work, and when the last week of school arrived the banners had not yet been made. The instructor in charge of the group decided to break a general rule and to do some of the programming herself. She worked at home without a Turtle so when she came in the next morning she had a collection of un-debugged programs. She and the children would debug them together. The instructor and a child were on the floor watching a Turtle drawing what was meant to be a letter R, but the sloping stroke was misplaced. Where was the bug? As they puzzled together the child had a revelation: “Do you mean,” he said, “that you really don’t know how to fix it?” The child did not yet know how to say it, but what had been revealed to him was that he and the teacher had been engaged together in a research project. The incident is poignant. It speaks of all the times this child entered into teachers’ games of “let’s do that together” all the while knowing that the collaboration was a fiction. Discovery cannot be a setup; invention cannot be scheduled.
In traditional schoolrooms, teachers do try to work collaboratively with children, but usually the material itself does not spontaneously generate research problems. Can an adult and a child genuinely collaborate on elementary school arithmetic? A very important feature of work with computers is that the teacher and the learner can be engaged in a real intellectual collaboration; together they can try to get the computer to do this or that and understand what it actually does. New situations that neither teacher nor learner has seen before come up frequently and so the teacher does not have to pretend not to know. Sharing the problem and the experience of solving it allows a child to learn from an adult not “by doing what teacher says” but “by doing what teacher does.” And one of the things that the teacher does is pursue a problem until it is completely understood. The LOGO environment is special because it provides numerous problems that elementary schoolchildren can understand with a kind of completeness that is rare in ordinary life. To appreciate the point more fully, it may be useful to rethink the simple examples of debugging discussed earlier.
We have discussed the program:
TO HOUSE
SQUARE
TRIANGLE
END
TO SQUARE
REPEAT 4
FORWARD 100
RIGHT 90
END
TO TRIANGLE
REPEAT 3
FORWARD 100
RIGHT 120
END
But this program contains a bug and draws the triangle inside the square instead of on it. Why? It might seem mysterious at first to a child. But you can figure out “why the Turtle did that dumb thing” by following through on a already well-known piece of heuristic advice: Play Turtle. Do it yourself but pretend to be as dumb as the Turtle. Finding out why the Turtle did it almost immediately suggests a way to fix it. For example, some say: “The Turtle turned into the square because TRIANGLE says RIGHT TURN.” A cure (one of several equally simple ones) is inherent in this diagnosis: Make a triangle procedure with left turns.
Similarly an adult who thought he could make the Turtle draw a triangle by REPEAT [FORWARD 100 RIGHT TURN 60] would be astonished to see a hexagon appear. But it is possible to “get into” the program and see why this happens. Moreover, it is possible to introspect and see how the bug came from a very superficial understanding of the most common statement of Euclid’s triangle theorem: “The sum of the angles of a triangle is 180 degrees.”
A child (and, indeed, perhaps most adults) lives in a world in which everything is only partially understood: well enough perhaps, but never completely. For many, understanding the Turtle’s action so completely that there is nothing more to say about it is a rare, possibly unique, experience. For some it is an exhilarating one: We can see this by the children’s eagerness to explain what they have understood. For all it is a better model of the crispness of analytic knowledge than most people ever encounter.
The reader might object that far from understanding the Turtle “fully” a child programmer hardly understands at all the complex mechanisms at work behind the scenes whenever a Turtle carries out a LOGO command. Are we in fact in danger of mystifying children by placing them in an environment of sophisticated technology whose complexities are only partially understood by advanced computer scientists?
These concerns bring us back full circle to the issues with which this chapter began. For example, I proposed a description of juggling in the form of a simple program. But the same concern arises: Does the description in procedural language grasp the essence of the process of juggling, or does it mystify by covering over the complexities of the juggling?
These questions are very general and touch on fundamental issues of scientific method. Newton “understood” the universe by reducing whole planets to points that move according to a fixed set of laws of motion. Is this grasping the essence of the real world or hiding its complexities? Part of what it means to be able to think like a scientist is to have an intuitive understanding of these epistemological issues, and I believe that working with Turtles can give children an opportunity to get to know them.
It is in fact easy for children to understand how the Turtle defines a self-contained world in which certain questions are relevant and others are not. The next chapter discusses how this idea can be developed by constructing many such “microworlds,” each with its own set of assumptions and constraints. Children get to know what it is like to explore the properties of a chosen microworld undisturbed by extraneous questions. In doing so they learn to transfer habits of exploration from their personal lives to the formal domain of scientific theory construction.
The internal intelligibility of computer worlds offers children the opportunity to carry out projects of greater complexity than is usually possible in the physical world. Many children imagine complex structures they might build with an erector set or fantasize about organizing their friends into complex enterprises. But when they try to realize such projects, they too soon run into the unintelligible limitations of matter and people. Because computer programs can in principle be made to behave exactly as they are intended to, they can be combined more safely into complex systems. Thus, children are able to acquire a feel for complexity.
Modern science and engineering have created the opportunity for achieving projects of a degree of complexity scarcely imaginable until recently. But science teaches us the power of simplicity as well and I end the chapter with what I find to be a moving story of a child who learned something of this in a particularly simple but personally important experience.
Deborah, a sixth grader who had problems with school learning, was introduced to the world of screen Turtles by being shown how they could obey the commands FORWARD, LEFT, and RIGHT. Many children find the fact that these commands can be assigned any number an exhilarating source of power and an exciting area of exploration. Deborah found it frightening, the reaction she had to most of what she did at school. In her first few hours of Turtle work she developed a disturbing degree of dependence on the instructor, constantly asking for reassurance before taking the smallest exploratory step. A turning point came when Deborah decided to restrict her Turtle commands, creating a microworld within the microworld of Turtle commands. She allowed herself only one turning command: RIGHT 30. To turn the Turtle through 90 degrees, she would repeat RIGHT 30 three times and would obtain the effect of LEFT 30 by repeating it eleven times. To an onlooker it might seem tedious to obtain simple effects in such complicated ways. But for Deborah it was exciting to be able to construct her own microworld and to discover how much she could do within its rigid constraints. She no longer asked permission to explore. And one day, when the teacher offered to show her a “simpler way” to achieve an effect, she listened patiently and said, “I don’t think I’ll do it that way.” She emerged when she was ready, several weeks later, with a new sense of confidence that showed itself not only in more ambitious Turtle projects but in her relationship to everything else she did in school. I like to see in Deborah’s experience a small recapitulation of how the success of such thinkers as Copernicus and Galileo allowed people to break away from superstitious dependencies that had nothing in themselves to do with physics. In both cases—in Deborah’s personal history and in the history of Western thought—the success of a mathematical theory served more than an instrumental role: It served as an affirmation of the power of ideas and the power of the mind.