6. How Loud Is Loud?
Ten times one equals about two…
We can all tell when music is getting quieter or louder but it is extremely difficult to say exactly how much louder one sound is compared to another. Trying to decide whether one sound is exactly twice as loud as another is just as difficult as trying to decide whether or not you find one joke exactly twice as funny as another.
One of the main oddities about loudness has to do with the addition of sounds. Normally when you add things together the result makes sense—if I give Fred one orange and you give him one, then lucky Fred has two oranges; if I give him three and you give him two then he has five. The addition of sounds doesn’t work like this. When you listen to a solo violinist playing a concerto with an orchestra, the number of people playing can vary from 1 to 100 in just a second or so, but we don’t clamp our hands over our ears and think “Cripes! The music just got a hundred times louder.” (The coarser individuals among you may substitute “Cripes” for even stronger language—up to, and including, “Jeepers.”) It is difficult to generalize about how much louder the music gets on these occasions: it depends on which instruments are involved and whether or not the composer has asked everyone to play loudly or quietly. It is, for example, possible for the whole orchestra (playing quietly) to make less noise than a single instrument playing loudly.
If you add the noise of ten violins (or any other instrument) together, you don’t hear ten times the loudness of one instrument on its own. In fact, it’s very difficult to estimate exactly how many times louder the sound is, but most people would agree that ten violins (playing the same note with the same amount of effort) sound approximately twice as loud as one. Similarly, for 100 instruments the answer would be, “One hundred times one?… That’ll be about four… Obviously.”
So, ten instruments sound only twice as loud as one, and 100 instruments sound only four times as loud as one. These “strange but true” statements need some explanation. Fortunately I have one ready….
Before we start our discussion, let’s simplify matters by talking about only one kind of instrument at a time. We’ll concentrate on flutes for the next bit, but the following points are also true of any mixed group of instruments.
So, let’s imagine we’ve gathered together an orchestra of 100 flute players. First of all there is silence. Then one of the flutes starts to play a note. The difference between silence and one flute is very impressive—it’s rather like sitting in darkness and then lighting a candle. Then another flute starts playing the same note. This makes a difference—but it’s not as big as the difference between the silence and the first flute. When the third flute joins in (playing the same note) it only makes a small difference to the volume of the sound and the fourth makes even less difference. If they all play the same note, and the flautists keep on joining in one at a time, you will soon find it impossible to tell when a new one joins the group because the difference between, say, sixty-two flutes and sixty-three is so tiny.
This is all very odd because you could have asked that sixty-third flautist to be the first in the group—and in that case he or she would have been the one who made the biggest difference. In fact, you could ask every one of the flute players to play a solo note as loud as they can after a silence and they would all sound equally loud.
There are two reasons why our 100 flute players sound less loud than you would expect. One of them has to do with how sound waves add together, and the other is related to how our hearing system works. Let’s look at these things one at a time.
How sound waves join together
By now, we are all clued up about the fact that a musical note is a regular pattern of changes in air pressure which makes our eardrums flex in and out. The number of times the eardrum flexes every second tells the brain the pitch of the note—and louder notes involve bigger pressure changes, so the eardrum flexes more. (If you overdo it by listening to a very loud noise like an explosion, the high pressure will flex your eardrum too far and tear it, giving you what’s called a perforated eardrum.)
The illustration below gives you a picture of what’s going on. Both of these ripple patterns have the same frequency—but one of them involves much bigger pressure changes, so it pushes and pulls at the eardrum more and sounds louder.
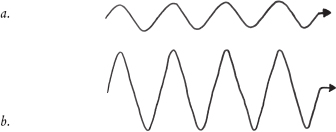
The pressure ripple patterns of the same note: played quietly (top) and loudly (bottom). The frequency of the note has not changed but the variation in pressure is greater for the louder note.
Let’s go shopping. You go to the music shop and buy a pair of identical glockenspiels and I’ll go off and buy a sound pressure monitor. This equipment contains a microphone which works just like an ear—sound pressure waves push a part of it in and out like an eardrum—and it has a computer which measures how powerful the waves are. I’m using a sound pressure monitor because it responds in a very straightforward way to changes in sound pressure—if you double the sound pressure you get double the reading from the computer.
Now all we need is a big hotel and a pair of identical twins (trust me, this is eventually going to be interesting). We start in one room and get the first twin to hit any note on the glockenspiel while we measure the power of the pressure waves it produces. Let’s say the computer tells us that the loudness of the note just after hitting the glockenspiel is ten pressure units.
Now we take the second twin to any other room in the hotel and get him to hit the same note on the other glockenspiel with the same force as his brother. (We picked identical twins because we want them to hit with the same force as each other.) As you would expect, when we measure the pressure ripples the computer says that the loudness is, once again, ten.
Now we get them both together in the same room. First of all they take turns hitting their notes—and, not surprisingly, there is no difference in the reading we get; as long as they hit the same note with the same force, we always get a reading of ten.
Finally we get them both to hit the note at the same time. We might now expect the computer to say that ten plus ten is twenty. But it doesn’t. We can do this a few times and the average sound pressure measured for the combination of the two notes will be about fourteen…. Some of our sound has gone missing.
And if we went out and bought more glockenspiels and hired more twins, we would find that, for forty instruments, instead of getting a pressure reading of 400, the result would only be sixty-three!
Widespread disappointment—we have a roomful of expensive twins and glockenspiels but a lot of the sound is simply disappearing. Let’s send them all down to the hotel lobby for afternoon tea while I explain what is happening.
When we hit only one instrument we get the best value for our efforts: we hit the bar, it wiggles up and down, and passes on these wiggles to the air as ripples in air pressure. So we get our money’s worth from the hit.
If we have two instruments, we only get double the effect if the up–down–up–down pressure ripples from them are perfectly in step with each other—so they can act together to give an UP–DOWN–UP–DOWN pressure ripple.
But, when we hit both instruments, you can bet your life that we don’t hit them exactly at the same time, so the pressure ripples from the two instruments won’t be in step when they reach the microphone. This means that sometimes the “pressure up” part of one ripple will be trying to raise the air pressure as the “pressure down” part of the other is trying to lower it. If the wave patterns were perfectly out of step, the up–down–up–down of one of them would be canceled out by the down–up–down–up of the other—and we wouldn’t hear a note at all.
This is weird but true—it’s how some farmers protect their hearing when they are driving noisy tractors all day. They buy “active ear defenders” which look like headphones. Inside each of the earpieces is a microphone and a speaker connected to some electronics. The microphone listens to the sound which is about to reach your eardrum and makes the speaker produce the same pressure wave—but out of step with the original one. The idea is that when the two pressure waves meet, one of them tries to raise the pressure at the same time as the other tries to lower it—so nothing much happens and the eardrum is left in peace. In practice the sound waves are too complicated for this to work exactly, but it does reduce most of the noise.
Going back to our glockenspiels, the canceling out is nowhere near perfect because it would be too difficult to organize—the sound waves are coming from different places in the room and also bouncing off the walls, and it’s incredibly unlikely that you would hit the instruments at precisely the right times to get the ripple patterns exactly out of step just at the point where they meet the microphone. What actually happens is that we do get more sound pressure from two instruments than we would from one—but there is some interference from the low-pressure bits of one wave pattern with the high-pressure bits of the other, so there is some canceling out.
If more instruments are involved, the amount of canceling out gets more serious. The pressure of the air next to the microphone can only be higher than normal (pushing the microphone inward) or lower than normal (pulling it outward): it can’t be both at once. Each of our forty glockenspiels has an “up pressure” or “down pressure” vote at any point in time—but a lot of these votes cancel each other out. If a forty-first glockenspielist joins our little party, then his note will be mostly canceled—though a little bit will get through to contribute to the overall loudness.
This effect is not the only one involved in our appreciation of loudness. If it was, 100 instruments would sound ten times as loud as one. But, as I said earlier, we perceive 100 instruments as being only four times as loud as one. This extra diminution in perceived loudness is the result of the way we humans are designed—so let’s have a look at that.
Why our brains don’t add up sounds properly
Why don’t our brains add up sounds normally? The surprising answer is that our brains and ears add up sounds in an unusual way in order to help us stay alive. From the times of the earliest cavemen to the present day, we have used our ears to help us avoid danger. This is one of the main reasons we have ears in the first place (although they are also useful for supporting your sunglasses). To be effective, your ears have to be able to hear very quiet noises (like the sound of someone creeping up on you), but also they must not get damaged by loud noises (such as thunder). It wouldn’t be any good if you had excellent hearing for quiet noises but your ears stopped working after the first loud noise you heard.
Our ears are organized in such a way that quiet noises can be heard clearly but any increase in the volume of the noise has progressively less and less impact. This effect is also true of our other four senses: smell, taste, sight and touch. Six smelly socks aren’t six times as smelly as one on its own (even though each of the socks is releasing the same amount of smell) and ten salted peanuts in your mouth aren’t five times as salty as two of them (even though you now have five times as much salt on your tongue). If you light 100 candles one at a time in a dark room you get the same effect as you got with the flutes—the first one makes the biggest difference and the eighty-seventh makes hardly any difference. If you are daft enough to stick a pin in your fingertip then it will hurt, but if you stick a second one in (next to the first one) the pain will not be doubled.
Why, you may ask yourself, did I carefully point out in that last sentence that the pins should be next to each other? Well, there is a reason, and it is surprisingly relevant to our discussion about the loudness of sound. Imagine that I have accidentally trodden on a thumbtack with my big toe. Obviously I would feel quite a lot of pain and would probably do a fair bit of swearing about it. If I trod on two thumbtacks with my big toe, the overall sensation would only be a little worse than a single tack—nothing like twice as bad. If, on the other hand, I trod on one thumbtack with my left big toe and another with my right big toe, then the pain would feel much worse than two tacks in one toe (don’t try this at home—just take my word for it). The reason for the increase in pain is the fact that my brain would receive two distinct pain signals (one from each foot) rather than a “two-tack” pain signal from one toe.
What has all this got to do with music? Well… earlier on I said that the ear/brain would calculate ten flutes as being only about twice as loud as one flute. This is only true if the ten flutes are playing the same note. If you divide the flutes into two groups and ask group 1 to play a note with a much higher (or lower) pitch than group 2, then the two notes played together sound louder than when everyone is playing the same note. The difference in pitch between the two notes needs to be bigger than the difference between “Baa” and “Black” for this effect to work. One reason for this apparent increase in volume is the fact that the brain is now receiving two distinct sound signals (like the two pain signals). The other reason is that the notes from the two smaller groups experience less of the “canceling out” effect I mentioned earlier.
Loudness and pitch
The sensitivity of our hearing system is not the same at all frequencies. The most extreme demonstration of this is the fact that there are some sounds that we can’t hear at all because they have a pitch which is too high (e.g., the note from a dog whistle) or too low (e.g., the subsonics you sometimes experience if a large truck engine vibrates the windows of the building you are in). Both the dog whistle and the trembling windows produce a note or noise—it’s just that our ears are not designed to hear them. Even within the range which can be heard by the human ear there are differences in sensitivity. We are most sensitive at the rather high, squeaky frequency range covered by the top few notes on a piccolo—which is why you can hear a piccolo clearly above the other instruments of an orchestra or marching band. In fact, music textbooks advise composers that the piccolo should be used only sparingly because it is difficult to blend it in with the other instruments.
At frequencies higher or lower than this high, squeaky range, our ears are progressively less sensitive. Most musical notes are below this range. This means that if you want to get a balanced sound between a bass instrument like a bassoon and a higher pitched instrument such as a clarinet, the bassoonist might have to play as loud as he can while the clarinetist takes it easy. Similarly, if two identical instruments are playing together but one is playing high notes and the other is playing low notes, then the one playing the low notes must play harder in order to sound as loud as the one playing the high notes.
Loudness and note duration
Yet another peculiarity of loudness is that of note duration. The normal loudness of the note can be heard if it is played for a second or so, but if the note is played for half a second or less, it will sound quieter. (It should be borne in mind that lots of music involves notes which are shorter than half a second; for example, when we sing “have you any wool?” only the word “wool” is longer than half a second.)
On the other hand, if a note is played for several tens of seconds then its loudness will appear to decrease as the brain begins to stop noticing it so much. This effect, of diminishing intensity for a continuous stimulus, also happens with our other senses, particularly our sense of smell (which is something we can be quite glad of at times). The reason why the sound appears to diminish after a while is that your brain is constantly monitoring your senses for danger signals. If a sound is continuous, and nothing bad is happening, your brain loses interest because the noise is obviously not important to your well-being. Your brain is primarily interested in any sudden changes in the sounds you are hearing, which is why you sit up and take notice if a long-lasting sound suddenly stops—the “deafening silence” effect.
Measuring loudness
Human beings like measuring things—we measure our height, weight, the speed of our cars and the size of our bathrooms. Measurements help us to discuss things more accurately and clearly. There are, of course, a lot of things we can’t apply accurate measurement systems to, such as kissing ability, or the social skills of hamsters, but whenever we can we invent and use a measurement system. As we shall see, the invention of a measurement system for loudness was nearly as tricky as getting one to work for kissing (and probably a lot less fun). Before we start this section I would like to go over a couple of points about measurement systems in general.
There are two basic types of measurement systems: the absolute type and the comparative (or relative) type. If we are using the absolute type, we would say “Farmer Smith has eight cows and Farmer Jones has four cows.” If we use a comparative system, we would say “Farmer Smith has twice as many cows as Farmer Jones.” As you can see, both systems give us some useful information, but the absolute system is more precise, which is why we normally use it. In some cases, however, we can’t use the absolute system and we need to use the comparative one. Yes… you guessed it… loudness is one of these awkward cases.
Because our ears respond to pressure changes, any system for measuring loudness should be based on the measurement of pressure. Unfortunately, however, the earliest system of loudness measurement was adapted from a method for measuring the decrease in strength of electrical signals after they had traveled down a mile of phone cable, so we ended up with a system based on intensity rather than pressure. This is rather like measuring distances in gallons of gas (if New York to Boston uses fourteen gallons of gas, then the distance from here to Poughkeepsie is six gallons). The numbers are useful and accurate in their way, but it’s all a bit clunky. This energy-intensity system of measuring the loudness of sounds has advantages and disadvantages, as we shall see.
Measuring the intensity of sounds
Remember our twins with their trusty glockenspiels? They would get just as tired hitting the instruments in individual rooms as they would if they were standing next to each other. In each case they are using the same amount of energy and it’s not their fault if the pressure waves refuse to cooperate fully. The intensity system looks at how much energy they both put into their bonging, rather than at how much sound they make. This system says to itself: “The bonging energy involved doesn’t change just because they both now share a room—one bong plus one bong equals two bongs’ worth of energy intensity.” This convenient ability to use simple addition is the main advantage of the intensity system of loudness measurement.
If we take a microphone, attach it to a computer and ask it to convert the pressure readings it hears into energy-intensity measurements, we can add sounds together by the normal rules of addition. A computer can be programed to recognize that the ten flute players are working equally hard to produce ten times as much sound intensity as a single flute. So, for example, we could now say: ten violins produce ten times the sound intensity and twice the loudness of one violin.
Let’s say we are going to use a computer and microphone to measure sound intensity from total silence to painfully ear-damaging. After some careful experiments we could find the quietest noise that a human can hear. We could then set the computer so that it gave this sound intensity a value of “1” and call it the threshold of hearing. This noise would be, perhaps, equivalent to someone ten yards away sighing. If ten people were sighing ten yards away (let’s not go into why they are all so unhappy), then the computer would give this new sound an intensity level of 10 (but, of course, we would hear it as only twice as loud).
Moving up in loudness, we can abandon all those miserable sods and start measuring the sound intensities of motorbikes or brass bands. You might imagine that, by the time we get to the noise levels which cause pain (e.g., putting your ear a few centimeters from a road drill), we would be measuring sound intensities a few hundred times greater than our original sigh. Well, stand by to be flabbergasted—the sound intensity which causes pain is 1,000,000,000,000 times greater than that of the quietest noise you can hear—yes, the sound intensity generated by a road drill is a trillion times greater than that of a sigh. So if you’re unhappy with your job as a road drill operator, and you want your sighs to be noticed, remember to turn the drill off first.
We need a quick reality check here. As I said earlier, our ears do not directly measure intensity—they monitor pressure differences. Pressure differences are related to intensities, but to convert the intensity to pressure we need to do a calculation. In this case the calculation tells us that the range of sound pressure difference between near silence and pain is not 1,000,000,000,000—it’s just 1,000,000, a million. It’s still an enormous number but it’s not a ridiculously enormous number.
Let’s re-enter the world of intensity measurement… We know that every time we multiply the sound intensity by ten (by having ten violinists play rather than one), then the loudness of the sound doubles. So—let’s put together a list of sounds starting from the quietest to the loudest we can hear. Every sound in this list is twice as loud as the one above it.
| A list of sounds from the threshold of hearing to the threshold of pain | ||
|---|---|---|
| Example | Relative loudness | Relative sound intensity |
| Almost silence (a sigh 10 yards away) | 1 | 1 |
| A small fly in the room | 2 | 10 |
| A large bee in the room | 4 | 100 |
| Someone nearby humming a tune | 8 | 1,000 |
| A fairly quiet conversation | 16 | 10,000 |
| Solo violin, moderate volume | 32 | 100,000 |
| A busy restaurant (or ten violins) | 64 | 1,000,000 |
| City traffic, rush hour | 128 | 10,000,000 |
| An orchestra playing loudly | 256 | 100,000,000 |
| Very noisy nightclub | 512 | 1,000,000,000 |
| Close to the speakers at a rock concert | 1024 | 10,000,000,000 |
| Big fireworks explosion | 2048 | 100,000,000,000 |
| Pain—a few inches from a road drill | 4096 | 1,000,000,000,000 |
(All my examples are, of course, just guidelines—perhaps you have raucous, noisy bees where you live—or maybe your sister is a spectacularly loud hummer.)
This table illustrates some of the main points about loudness and gives us two methods for comparing loud and quiet noises. However, neither system provides us with a useful numerical scale of loudness because the numbers are so large. The relative sound-intensity numbers on the right say that a fly has a value of 10 and the violin has one of 100,000, which means that you would need 10,000 small flies in the room to produce the same sound intensity as a violin. This is useful stuff if you are a violin-playing maggot farmer, but we still need a noise level measurement system which uses a smaller range of numbers.
Decibel madness
The search for a system with a small range of numbers gave someone, sometime in the first half of the twentieth century, the clever idea of a loudness measurement scale based on how many zeros there were after the “1” in the “relative sound intensity” column in the table above. This is the “Bel” scale and in it a sound intensity of 1,000 would have a loudness of 3 Bels and 1,000,000 would be 6 Bels, etc. (just count the zeros in each case). This was thought to be a brilliant idea for about seven and a half minutes until someone even cleverer pointed out that this would only give us twelve numbers of loudness measurement from extremely quiet to painfully loud and that this wasn’t going to be a very useful system—because now we didn’t have enough numbers.
Finally it was decided that 120 measures of loudness would be more useful and that could be achieved by multiplying all the numbers in the Bel system by ten and thus measuring loudness in “tenths of a Bel” or “deci-Bels” (decibels). So now we have a system where a sound intensity of 1,000 is equal to 30 decibels and 1,000,000 is 60 decibels, etc. (count the number of zeros and multiply by ten). A rough sketch of what the decibel system means to our ears is presented in the table below (“decibel” is usually abbreviated to “dB”).
| Intensity, decibels and loudness | ||
|---|---|---|
| Relative sound intensity | Decibels (dB) | Relative loudness |
| 1 | 0 | 1 (almost silence—sigh) |
| 10 | 10 | 2 (small fly) |
| 100 | 20 | 4 (large bee) |
| 1,000 | 30 | 8 (humming) |
| 10,000 | 40 | 16 (quiet conversation) |
| 100,000 | 50 | 32 (solo violin) |
| 1,000,000 | 60 | 64 (busy restaurant) |
| 10,000,000 | 70 | 128 (rush hour) |
| 100,000,000 | 80 | 256 (loud orchestra) |
| 1,000,000,000 | 90 | 512 (nightclub) |
| 10,000,000,000 | 100 | 1024 (rock concert speakers) |
| 100,000,000,000 | 110 | 2048 (big fireworks) |
| 1,000,000,000,000 | 120 | 4096 (pain—road drill) |
Now we have a system that can be used to measure loudness from the quietest noise to the loudest which only goes from zero to 120. But I’m afraid that even though the numbers are now simple, the use of this scale is complicated. The table shows that each time the loudness of the noise doubles, you add 10 decibels. This sounds simple enough until you realize that this means that not only is 20dB twice as loud as 10dB (which seems obvious) but also that 90dB is twice as loud as 80dB (which seems crazy, but it’s true—just look at the table).
At this point I must come clean and admit that I don’t like the decibel system of loudness measurement at all. It isn’t easy to use even if you have studied math or physics up to college level. Even a professional scientist would need a calculator and a few minutes to be able to tell you the difference in loudness between 53 decibels and 87 decibels. I have no proof of this, but I think the decibel was invented in a bar, late one night, by a committee of drunken electrical engineers who wanted to take revenge on the world for their total lack of dancing partners. Apart from the calculation problems, the use of intensity for measuring sounds is indirect and overly complicated.
I started this book with the promise that there would be no mathematical formulas and I intend to keep that promise. However, I can’t explain how to calculate the difference between 53 and 87 decibels without using formulas. Anyone who would like a bit more information on using the decibel system will find some in part B of the Fiddly Details section at the end of this book. Frankly, though, I think we should leave the horrid decibels behind us, and move on to discuss the much more user-friendly systems developed in the 1930s by a bunch of American researchers, led by an experimental psychologist called Stanley Smith Stevens.
Better loudness measuring systems: the phon and the sone
While the electrical engineers were giggling to themselves about lumbering us all with the decibel system, the sound engineers, concert hall designers and psychologists specializing in hearing decided to strike back. Because they were dealing with loudness measurements all day, these people knew that the decibel system had two big flaws:
Big flaw 1. As I said earlier, the human hearing system is more sensitive at some frequencies than others. This means that a 32dB high note from a flute will sound (to a human) a lot louder than a 32dB low note from a bass guitar—so the decibel system is an unreliable measure of loudness for human beings.
Big flaw 2. Before the advent of pocket calculators, you had to sit up all night with six pencils and three erasers working out stuff like, “How much louder than 49dB is 83dB?” Even after calculators came along you had to buy one with a farcical number of buttons on it and an instruction book as big as Webster’s Dictionary.
“Aha!” said the experimental psychologists, “we can eschew the decibel system and develop one which gives a more accurate picture of the response of the human ear.” (Experimental psychologists talk in this superior, pedantic way whenever they get the chance.)
The only way to develop a system based on the subjective response of the human ear is to carry out tests on lots of people. This is why the work was carried out by psychologists: they were measuring people’s opinions, rather than things which can be measured by scientific equipment.
The first set of tests was designed to overcome big flaw 1 and involved a large number of people who were asked to compare notes of different frequencies and say when they thought they were equally loud. These tests were carried out over a wide range of loudnesses and frequencies and led to the development of a unit of loudness called the phon.
To explain the difference between phons and decibels, let’s imagine that we have enlisted a robot to play the piano for us. First of all, we ask the robot to produce a loudness of 50 decibels for each note and play all the notes, one at a time, starting from the top one.
Because our ears are progressively less sensitive as we move from the high notes on a piano to the lower ones, we would hear the notes getting gradually quieter as the robot moved down the keyboard. On the other hand, a computer attached to a microphone, “listening” to the same notes, would “hear” each one as having the same energy intensity.
Now we ask the robot to do the same thing again, but this time producing a loudness of 50 phons from each note. This time our mechanical pal would hit the notes more and more forcefully as it moved down the keyboard. You would hear all the notes as being equally loud because the robot would be compensating for the fact that you can’t hear the low notes on a piano as easily as the high notes (your computer would “hear” exactly what the robot is doing and would be able to tell that it was playing the low notes louder).
The phon system is just the decibel system after we have compensated for the fact that human ears are less sensitive to low notes.
Having conquered Big flaw 1 the psychologists moved on to Big flaw 2. As the phon system is basically a version of the decibel system, we still have exactly the same problem working out what the numbers mean. What’s the loudness difference between 55 and 19 phons? Pass me a calculator and some chocolate chip cookies…
So the psychologists decided to drop the decibel system entirely and find a way of using a scale based on relative loudness, much to the annoyance of the electrical engineers who developed the decibel system. No party invitations have passed between the two groups since 1936.
If you look back at the table here, then you will see that the relative loudness scale goes from “1” (a sigh) to “4096” (a road drill) and, as we saw, this involves too many big numbers to be a useful scale. But hang on a minute, the numbers for loud noises are only this big because we started with 1 as the quietest noise we can hear. This is the same as measuring the price of everything in pennies—we don’t say “my car cost 1,500,000 pennies.” We don’t need to use the smallest possible coin as the basis for our measurement system. The psychologists gave this some thought and decided to move the “1” from an extremely quiet sound to somewhere nearer the middle of our hearing range. They moved it to the level of a fairly quiet conversation—so now we have a new measurement range with “1” where “16” used to be. This means we have to divide all the numbers in our “relative loudness” column by 16 and the numbers now only go up to 256, as you can see in the next table. Although we have to use fractions of 1 for quiet noises, this is not much of a problem because we don’t need to discuss quiet noises very often.
So now we have a system which really works for humans—it’s called the sone system, and there is no need to worry about big numbers or complicated math. Eight sones sounds twice as loud as 4 sones and 5 sones sounds half as loud as 10 sones.
Modern loudness meters should measure different loudness levels in sones because it’s the most sensible system for monitoring and discussing loudness levels as far as humans are concerned. For example, if an acoustic guitar player has a loudness level of 4 sones and a rock band’s level is 40 sones, it means that the rock band is ten times louder for any human listener. Because the sone system is based on human hearing, sone-based loudness meters automatically make the necessary compensations related to the frequencies of the sounds they are monitoring. Meters like this are used to help the relevant engineers to develop better loudspeakers and sound insulation materials.
However, you may have noticed my use of the word “should” at the beginning of the last paragraph. In fact, most of today’s loudness measurements are carried out using the decibel system, although there is usually an adjustment for the human sensitivity to different frequencies. This is simply because the decibel system was the first to become established and is the one referred to in the government documents and legislation dealing with noise levels and soundproofing. So we’re stuck with it.
| The sone system of loudness measurement | ||
|---|---|---|
| Example | Relative loudness (after compensating for frequency) | Sones |
| Almost silence (a sigh) | 1 | 0.06 |
| A small fly in the room | 2 | 0.12 |
| A large bee in the room | 4 | 0.25 |
| Someone nearby humming a tune | 8 | 0.5 |
| A fairly quiet conversation | 16 | 1.0 |
| Solo violin, moderate volume | 32 | 2.0 |
| A busy restaurant (or ten violins) | 64 | 4.0 |
| City traffic, rush hour | 128 | 8.0 |
| An orchestra playing loudly | 256 | 16.0 |
| Very noisy nightclub | 512 | 32.0 |
| Close to the speakers at a rock concert | 1024 | 64.0 |
| Big fireworks explosion | 2048 | 128.0 |
| Pain—a road drill | 4096 | 256.0 |
But one day we will all rise up and, impaling our scientific calculators on especially pointy road drills, we will free ourselves from the evil, oppressive shackles of the ridiculous, loathso—
But perhaps my cold, authorial objectivity is slipping a little here…. Let’s move on to a subject less troubled by controversy: the art and science of harmony.