Appendix A. AI and Machine Learning Algorithms
Even though human-like deductive reasoning, inference, and decision making by a computer is still a long way away, there have been remarkable gains in the development and application of AI techniques and algorithms. We can use these techniques to create incredibly powerful and exciting AI-based solutions to real-world problems.
The algorithms that power AI and machine learning, along with properly selected and prepared training data, are able to create these solutions in ways that are not possible for humans to create any other way. There are many different goals of AI, as discussed in this book, with different techniques used for each.
This appendix is written for anyone interested in learning more about the technical nuts and bolts of AI and machine learning at a high level, including biological neural models that have inspired and helped form the field of AI. Although perhaps more technical than other content in this book, my goal is to present the information in a way that nontechnical folks can understand.
The primary topics of this chapter are how machines learn, biological neurons and neural networks, artificial neural networks, and deep learning. Deep learning is one of the most exciting and promising algorithmic techniques used to build AI solutions; it represents a special type of neural network architecture, which we discuss further in this chapter. First, let’s begin by learning more about how machines learn.
Parametric versus Nonparametric Machine Learning
A more technical way to describe machine learning is that it represents algorithm-based learning techniques that learn a target (or mapping) function that maps input variables (feature data) to one or more output variables (targets).
Learned functions can be either parametric or nonparametric. Parametric functions are characterized by a model that has an assumed form upfront, where the form includes the number and types of terms, functions, and parameters.
Here is the equation of the straight line that some of us learned when we were young:
y = mx + b
The model is parametric because it has a predetermined form that includes two parameters (m and b), where one of the parameters m is given in a single linear function of x in the term mx. In this case, y is modeled as a linear function of x, where m represents the slope of the line (change of y for a corresponding change of x), and b, the y-intercept (value of y when x equals zero).
Figure A-1 shows the straight-line equation again in a form more common to statistics and machine learning, usually referred to by the name simple linear regression.
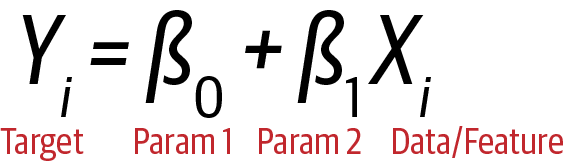
Figure A-1. Straight-line equation
The equation represents a target function where Yi is the target, and Xi is the feature data. The value of Y is therefore dependent and modeled as a function of X.
Two parameters (β0, β1) are needed to properly model the exact relationship between X and Y. This is the equivalent to m and b in the earlier straight-line equation. Note that we can create other predefined parametric functions that include x raised to different exponents (e.g., x2) and/or where each term is either added, subtracted, multiplied, or divided, for example. Here is an example of a parametric model of increased complexity:
y = θ0x - θ1x2 + θ2x3
Nonparametric models have no assumed form upfront and therefore no predefined parameters, functions, or operations. Figure A-2 summarizes the difference between parametric and nonparametric machine learning models.

Figure A-2. Parametric versus nonparametric models
Let’s discuss how the learning mechanism works at a high level for different types of machine learning techniques.
How Machine Learning Models Are Learned
In the case of supervised machine learning applied to parametric functions, the machine learning algorithm has the goal of finding the optimal parameter values—for example, β0 and β1 in the simple linear regression example—that create the best performing model; that is, the model that best describes the true relationship between the target variable and feature variables. Finding the optimal parameter values is the “learning” part of machine learning, and the learning is possible given the machine learning technique (algorithm) used and the data provided.
Nonparametric supervised machine learning functions are characterized by having no assumed form. The machine learning algorithm actually generates the model form during the learning process in some cases (e.g., decision trees), whereas in other cases the machine learning model is based on data similarity; for instance, determining the output based on similarity to existing data examples. K-nearest neighbors is a common and specific algorithm used for similarity-based, nonparametric machine learning applications.
Unsupervised learning is carried out by a variety of algorithmic approaches that depend on the type of application. Clustering applications are based on advanced data grouping algorithms, whereas anomaly detection are based on algorithms that specialize in finding abnormal data outliers.
All of the examples discussed so far fall into two additional categories: either error-based or similarity-based learning. Error-based learning works by choosing a performance metric that indicates how well a machine learning model is performing; that is, how often it predicts correctly in the case of predictive analytics (e.g., accuracy). The algorithm works by trying to minimize (via a loss function) the errors produced by the model, which is done by finding the optimal parameters in the case of parametric learning, or by finding the optimal model and parameters in the case of nonparametric learning. Similarity-based learning works by determining the greatest similarity between data points as opposed to using an error-based model.
It’s worth noting that statistical learning is a term sometimes used synonymously with machine learning, and other times to differentiate statistical and probability-based learning techniques such as linear regression. We use the term machine learning here as a catch-all for any applications involving machine-based learning from data without requiring explicit programming.
Biological Neural Networks Overview
The human brain is exceptionally complex and quite literally the most powerful computing machine known.
The inner workings of the human brain are often modeled around the concept of neurons and the networks of neurons known as biological neural networks. It’s estimated that the human brain contains roughly 100 billion neurons, which are connected along pathways throughout these networks.1 Figure A-3 shows a complete biological neuron cell diagram.
At a very high level, neurons interact and communicate with one another through an interface consisting of axon terminals that are connected to dendrites across a gap (synapse), as shown in the figure. Some estimates indicate that the human brain has between 100 and 500 trillion synapses, which is enough to store all information learned and memories developed in an entire human lifetime.

Figure A-3. Complete neuron cell diagram (LadyofHats, http://bit.ly/2RwrAW3, accessed February 25, 2019)
In plain English, a single neuron passes a message to another neuron across the synapse if the sum of weighted input signals from one or more neurons (summation) into it is great enough (exceeds a threshold) to cause the transmission. This is called activation when the threshold is exceeded and the message is passed along to the next neuron.
The summation process can be mathematically complex. Each neuron’s input signal is actually a weighted combination of potentially many input signals, and the weighting of each input means that that input can have a different influence on any subsequent calculations, and ultimately on the final output of the entire network. Each neuron also applies a linear or nonlinear transformation to the weighted inputs.
These input signals can originate in many ways, with our five senses being some of the most important, as well as ingestion of gases (breathing), liquids (drinking), and solids (eating), for example. A single neuron might receive hundreds of thousands of input signals at once that undergo the summation process to determine whether the message is passed along and thus ultimately cause the brain to generate actions and cognitive functions.
The “thinking” or processing that our brain carries out and the subsequent instructions given to our muscles and organs are the result of these neural networks in action. In addition, the brain’s neural networks continuously change and update themselves, which includes modifications to the amount of weighting applied between neurons. This happens as a direct result of learning and experience.
Given this, it’s a natural assumption that for a computing machine to replicate the brain’s functionality and capabilities, including being “intelligent,” it must successfully implement a computer-based or artificial version of this network of neurons. This is the genesis of the advanced statistical technique and term known as artificial neural networks (ANNs).
Before moving on to ANNs, it’s worth revisiting how humans learn. It turns out that the brain, particularly the neocortex, starts at birth as an initialized massive biological neural network, but one that has not yet learned and subsequently developed any significant understanding and memories.
As children begin observing their environment and processing stimuli by sensing the world around them, the billions of neurons and trillions of synapses work together to learn and store information. This results in our ability to understand and comprehend information, recognize spatial and temporal patterns, have thoughts and make mental predictions, recall information and memories, drive motor actions based on recall and prediction, and continue to learn throughout our lifetime. This is what makes humans intelligent.2
Let’s now discuss how humans have tried to mimic this natural phenomena with machines.
An Introduction to ANNs
ANNs are one of the primary tools used to build AI applications, and they are being used in many powerful and exciting ways, many covered throughout this book.
ANNs are statistical models directly inspired by and partially modeled on biological neural networks. They are capable of modeling and processing nonlinear relationships between inputs and outputs in parallel. The related algorithms are part of the broader field of machine learning, and we can use them in many applications such as prediction, natural language processing, and pattern recognition.
ANNs are characterized by parameters that can be tuned by a learning algorithm (parametric learning) that learns from observed data in order to build an optimized model. Some of these parameters include weights along paths between neurons and also values referred to as bias. Hyperparameters (tunable model configuration values) such as the algorithm’s learning rate can also be tuned for optimal performance. When using an ANN, the practitioner must choose an appropriate learning algorithm and what is known as a loss (or cost) function.
The loss function is what’s used to learn the optimal parameter values for the problem being solved. Learning the optimal parameter values is usually done through optimization techniques such as gradient descent. These optimization techniques basically try to make the ANN solution get as close as possible to the optimal solution, which when successful means that the ANN is able to solve the intended problem with high performance; or, put another way, predictive accuracy.
At a very high level, gradient descent works by trying different combinations of parameter values in an algorithmic, strategic way in order to iterate to the optimal overall parameter combination, and thus model. Although a bit oversimplified, the algorithm is able to determine when it has approached the best possible parameter combination and will stop the iteration process as a result.
Architecturally, an ANN is modeled using layers of artificial neurons, or computational units able to receive input and apply an activation function along with a threshold to determine whether messages are passed along, similarly to biological neurons and neural network information-propagating mechanisms.
In a shallow ANN, the first layer is the input layer, followed by one hidden layer, and finally by an output layer. Each layer can contain one or more neurons. The term “hidden” is used to indicate that the layer is between the input and output layers, and that the layer transforms its own input values into input values for the next layer. The term also refers to the fact that hidden layer output values are neither easily interpreted nor explainable relative to the human understandable input and output values of the network.
Figure A-4 shows an example of a simple ANN.
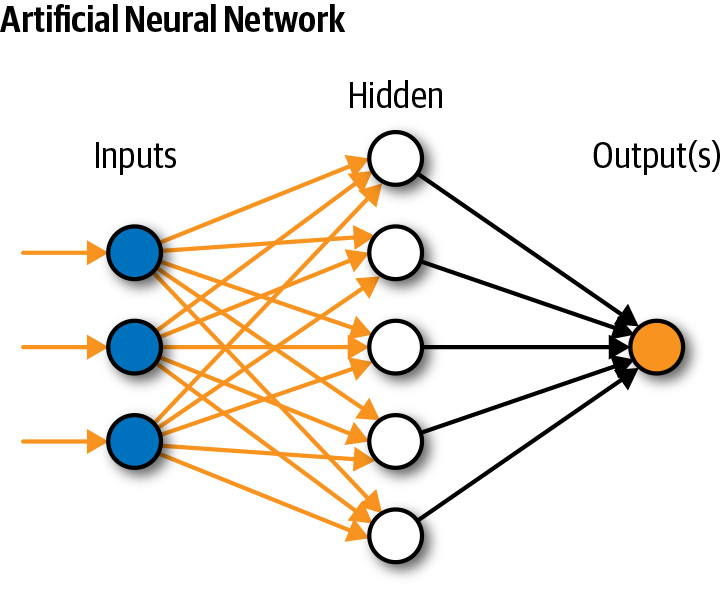
Figure A-4. An artificial neural network
ANN model architectures can be modified to solve a wider and more complex set of problems by adding hidden layers and/or neurons in any given layer, for example. Note that an increased chance of overfitting can also occur with increased model complexity, which means that the model performs well on training data, but not on new and unseen data (e.g., test data and/or real-world data).
The chain of transformations that occur from input to output is known as the credit assignment path, or CAP. The CAP value is a proxy for the measurement or concept of “depth” in a deep learning model architecture, and is the number of hidden layers plus the output layer. Deep learning generally refers to a neural network architecture that has a CAP greater than two; that is, more than two nonlinear transformation (hidden) layers.
Model architecture and tuning are therefore major components of ANN techniques, in addition to the actual learning algorithms themselves. All of these characteristics of an ANN can have significant impact on the performance of the model.
Additionally, ANNs are characterized and tunable by the activation function used to convert a neuron’s weighted input to its output activation. There are many different types of transformations that can be used as the activation function.
One thing worth noting is that although ANNs are extremely powerful, they can also be very complex and are considered black-box algorithms, which means that their inner workings are very difficult to interpret, understand, and explain. Choosing whether to employ ANNs and deep learning to solve problems should therefore be considered with that in mind.
An Introduction to Deep Learning
Deep learning, although sounding flashy, is really just a term to describe neural networks with two or more hidden layers. Deep learning is further characterized by the consumption of raw input data and by different types of architectures and associated algorithms. These deep networks process data through many layers of nonlinear transformations in order to calculate a target output in the supervised case. Deep learning is able to do things with data that humans are unable to do using other techniques, and, as of this writing, is a very hot area of AI research and development.
More generally, deep learning represents a group of techniques known as feature learning or representation learning. Feature learning algorithms are able to learn features from raw data, or, stated another way, are algorithms that learn how to learn! This characteristic of deep learning is incredibly useful when it is extremely difficult or impossible for humans to select or engineer the appropriate features for a given application. The benefits of feature learning algorithms are realized most when learning from unstructured data such as images, video, audio, and language in the form of digital text. In these cases, deep learning algorithms automatically learn features and use them for a specific task such as image classification.
For deep learning neural networks, the number of layers are greater than in learning algorithms referred to as shallow. Shallow algorithms tend to be less complex and require more upfront knowledge of optimal features to use, which typically involves feature selection and engineering. In contrast, deep learning algorithms rely more on optimal model selection and optimization through model tuning. They are better suited to solve problems where prior knowledge of features is less desired or less necessary, and where labeled data is unavailable or not required for the primary use case.
Image recognition is a good example. It would be very difficult, if not impossible, for someone to write an explicitly programmed algorithm that tests all pixels, pixel groupings of varying sizes (areas) and locations, and color variations of an image to recognize and detect a cat. The reason is that the algorithm would need to know how to look for many different features of a cat in the image; for example, whiskers, pointy ears, and cat-like eyes. These features differ in many ways such as size and shape depending on the type and age of the cat.
In reality, the algorithm would need to detect even smaller and more simple features first, such as lines (vertical, horizontal, diagonal), curves, geometric shapes, and much more. When combined, these simple features could represent the cat’s face and head features, as described, and when those features are combined, can represent an image of a cat. Unlike explicitly programmed code that depends heavily on feature selection and feature engineering, deep learning is able to automatically learn and create representations and combinations of these smaller features just from being given an adequate training dataset. The end result is an ANN that is able to recognize a cat in an image, which is truly remarkable.
More specifically, you can think of each layer of the network as being able to learn features and components that contribute to the overall goal of the given neural network. For example, suppose that you are training a neural network to be able to recognize whether an image is of a cat. One layer might simply learn different low-level patterns such as straight lines and curves, whereas the next layer might learn to find different features such as eyes and a nose, the next layer groups of features such as a face or torso, and then finally put it all together to determine whether the image is a cat. The network is therefore able to learn features from simple to complex in a hierarchy and then combine them into an overall solution.
Another important benefit of deep learning algorithms is that they are great at modeling nonlinear and potentially very complex relationships between inputs and target outputs. Many phenomena observed in the physical universe are actually best modeled with nonlinear transformations. A couple of very well-known examples include Newton’s law of universal gravitation and Albert Einstein’s famous mass–energy equivalence formula (i.e., e = mc2).
It’s worth mentioning that deep learning has some potential disadvantages, as well. Most prominently, deep learning can require very large amounts of training data, computing resources (cost), and training time. Also, deep learning algorithms are considered some of the blackest of black-box algorithms in use, which makes interpretability, explainability, diagnostics, and verifiability basically impossible in most cases.
Also worth noting is that single hidden-layer neural networks, the shallow networks we referred to earlier, can carry out many of the same learning tasks as their deep counterparts. That said, to be able to perform the same tasks as deep networks, shallow networks might need an extremely wide single hidden layer with an inordinate amount of neurons, which will likely be nowhere near as computationally efficient as the deep alternative.
Another important type of learning associated with neural networks and deep learning is called transfer learning. Transfer learning is a very useful technique, and particularly effective when the labeled data needed for a given application is in short supply.
We discussed the concept of feature space earlier in the book, which refers to the number of possible feature–value combinations across all features included in a dataset being used for a specific problem. Not only do the values of each feature span a certain range of values (or space), each feature’s values can also be characterized by some type of distribution.
Typically in machine learning applications, the training data should be representative of the data likely to be seen by the model in the real world, in terms of the feature space and each feature’s distribution. Sometimes, it is very difficult to procure domain-specific data that meets these requirements, whereas data from another related domain is abundantly available and similar enough in the context of deep learning applications.
In this case, deep learning models can be trained on the widely available data, and then the knowledge learned can be transfered to a new model that fine-tunes the knowledge learned based on the less available, domain-specific data. Additionally, transfer learning is great for reusing knowledge learned for quicker training times.
Deep Learning Applications
There are many different general applications now possible with deep-learning model architectures and algorithms. Although a detailed discussion is beyond the scope of this book, following is a list of some of the more interesting ones; many more applications are discussed in Deep Learning: A Practitioner’s Approach:3
-
Audio-to-text transcription
-
Speech recognition
-
Audio and text analysis
-
Sentiment analysis
-
Natural language translation
-
Generating sentences
-
Handwriting recognition
-
Image modeling and recognition
-
Synthesis of artificial images, video, and audio
-
Visual question answering
Deep learning has also been used successfully in many specific applications, including:
Summary
Machine learning in general is truly powerful and amazing, particularly given the ability to learn from data and carry out tasks without requiring explicit programming. That said, the ability of deep neural networks to model very complex, nonlinear relationships and also automatically extract features from raw data to effectively “learn how to learn” is what sets deep learning models apart from the rest and is also why AI is most associated today with deep learning.
Despite the dominance of neural networks and deep learning specifically as a premier AI algorithmic technique, they are not the only advanced techniques in the AI toolbox. Nonneural network–based examples include algorithms associated with reinforcement learning and natural language, for example.
1 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2776484/
2 Hawkins, Jeff, and Sandra Blakeslee. On Intelligence. New York: Times Books/Henry Holt. 2008.
3 Patterson, Josh and Adam Gibson. Deep Learning: A Practitioner’s Approach. O’Reilly Media, 2017.