Chapter 5
Forces and Mechanics
GOALS
By the end of this chapter, you will be able to:
• Describe what a force is
• Understand Newton’s three force laws and how to apply them
• Solve Newton’s Second Law for the acceleration of objects
• Solve Newton’s Second Law for rotational systems
• Apply your knowledge of rotating and non-rotating systems to understand equilibrium
Lesson 5.1
Forces
Now that we have sufficiently discussed motion, we can come to what is really the heart of classical physics: the force. What is a force? A force is a physical quantity that produces a change in motion, i.e., it produces an acceleration. As we know, acceleration is what drives motion, and forces are what produce accelerations. Since acceleration is a vector, a force is also a vector (the direction of the force is what determines the direction of the acceleration).
Forces should be thought of as the central quantity of physics. They are what produce everything. We already discussed how acceleration produces motion, and forces produce acceleration. But there are so many more things that we have yet to discuss. Forces produce changes in an object’s energy, giving or removing energy from it. Forces produce pressure on submerged vehicles, and changes in atmospheric forces produce changes in barometric pressure. Forces during collisions produce changes in the momentum of the objects partaking in the collisions. These are all topics that we will discuss in later chapters, so it is important to learn everything we can about forces now.
Lesson 5.2
Newton’s Laws
A force can more properly be defined as the physical quantity that obeys Newton’s three laws. These laws were first published in his Principia in 1687, mentioned in the introduction.
1. Law of Inertia: An object will maintain its current state of motion unless acted upon by a force.
Equation 5.1
2. Mathematical Law: 
3. Interaction Law: For any force an object could exert on a second object, the second object must exert an equal and opposite force on the first object.
The unit for force is a Newton, N.
The first and third laws are qualitative, which describe the essence of what it means to be a force. The first law states that only forces are responsible for motion. An object that’s still won’t move until a force acts on it. An object that’s moving moves in the same state of motion (i.e., with the same velocity) unless acted on by a force.
The third law states that all forces come in pairs. There is no force in nature that one object can put on another without the other reciprocating. These force pairs are often referred to as action-reaction pairs. Action-reaction pairs have specific properties, and it is easy to confuse two forces of equal magnitude and opposite direction as an action-reaction pair. Action-reaction pairs:
• Act on two separate objects: An action-reaction pair of forces cannot be two forces that act on the same object. Recall that Newton’s Third Law discusses the force that one object puts on another.
• Must be the same type of force: If one object puts a contact force (a force that requires contact between two objects, such as a push), then the second object puts a contact force back on the first.
• Must be equal in magnitude and opposite in direction: This is stated clearly in the law and is a hallmark quality of action-reaction pairs. If an object puts a force of magnitude F on a second object in some direction, then the second object puts a force of magnitude F back on the first in the opposite direction.
The second law is the quantitative description of a force. It defines the relationship between a force and the acceleration it produces. Since an object can feel multiple forces at once (a simple example is the rope in a game of tug of war; it feels a force from each team pulling on it), the resulting acceleration is produced by the sum of all the forces acting on the object, referred to as the net force.
The variable m in Equation 5.1 is the mass of the object. In the context of Newton’s Second Law, the mass is referred to as the inertial mass. The inertial mass is an object’s inherent resistance to acceleration. The units of mass are kilograms, kg. Notice that the units of force are equal to the units of mass times acceleration, so
N = 
EXAMPLE 
Consider a falling object of mass m. Ignoring air resistance, what is the magnitude of the force acting on it as it falls through the air?
You know from Newton’s Second Law that the net force acting on this object is just
where g is the vector acceleration due to gravity. In the case of an object in free fall, the only force acting on it is gravity, so the gravitational force on the object is m
. This is known as the weight:
Equation 5.2
EXAMPLE 
A book rests on a flat surface. It feels the force due to its weight, as well as the supporting force from the surface known as the normal force. The normal force acts to oppose the weight of the book, so it is of the same magnitude and opposite direction as the weight. Do these forces count as an action-reaction pair, as defined by Newton’s Third Law?
No, they do not. Look back to the three properties of action-reaction pairs. The only property satisfied is the third. Both forces act on the same object, the book, so this pair violates property 1. They are also different types of forces. Weight is caused by gravity, which is a force that acts over vast distances. The book does not need to touch the Earth to have a gravitational force on it. However, the book needs to contact the table to feel the supportive force, so this pair violates property 2.
In order for something to be a force, it has to satisfy all three of Newton’s laws. It isn’t enough for it to produce motion, as explained in the introduction to this chapter. Quantities that produce motion but do not satisfy all of Newton’s laws are known as fictitious forces. The two common fictitious forces are the Coriolis force, (named after the French mathematician Gaspard-Gustave de Coriolis) and the centrifugal force. Neither of these is a true force because neither is produced by one object acting on another; therefore, both violate Newton’s Third Law. They actually exist only if an object is under rotational motion.
The Coriolis force is important for large-scale objects in the Earth, like clouds in a hurricane. The rotation of the Earth causes a lateral force to be placed on the clouds, rotating them within the hurricane. Furthermore, the centrifugal force is responsible for objects being pushed outward in a rotational motion. However, since neither of these “forces” satisfies Newton’s Third Law, both are referred to as fictitious.
Lesson 5.3
Newtonian Mechanics
The field of mechanics, as explained in Chapter 1, is the field in physics that concerns itself with answering the following question:
If an object is at a certain position at a certain time, where will it be at a future time if we know all the forces acting on it?
The first method for answering this question is referred to as Newtonian mechanics. In Newtonian mechanics, the question is answered by solving Newton’s Second Law. Recall that the second law relates the net force acting on an object to its acceleration. So, if you can find the net force acting on an object, you can find its acceleration, and then you can figure out its motion (as we discussed in the previous two chapters). This is the essential idea to Newtonian mechanics.
Now, the question is, how do we use Newton’s Second Law? Well, it involves finding the net force acting on an object, and the net force is just the vector sum of all the forces acting on the object. To aid this summation, we will be using a tool referred to as a free body diagram. A free body diagram is simply a diagram that illustrates all of the forces acting on a single object, placed within a chosen coordinate system. Free body diagrams are very convenient tools to aid in solving Newton’s Second Law because they diagram all forces in a coordinate system, which allows for easy conversion between the magnitude-direction form of a vector and the component form of a vector. Forces will often be given in magnitude-direction form, and once they are converted into their components, they are easily summed.
Take a look at an example that illustrates this point.
EXAMPLE 
An object feels a horizontal force of 10 N forward (a push, for instance) and feels a second horizontal force of 5 N backward (a pull, for instance). This object has a weight of 98 N and so also feels the supportive normal force of equal magnitude.
What is the acceleration of this object?
You can diagram these four forces as in the following figure.
In this case, all of the forces were given in magnitude-direction form, but since each of them lies on an axis, you already know all of their components. This is actually the goal when you are choosing your coordinate system for a free body diagram: to get as many forces to lie on an axis as possible. That way their components are obvious, and no trigonometry is needed. Every time a force lies off axis, you must break it into its two components.
Now you can perform the vector addition of these forces. Instead of generating a single vector to represent the net force, it is more convenient to consider the two components of the net forces separately. That way, all you have to do is sum the components of each force. In this case, you have a net horizontal force of
ΣFx = 10N − 5N = 5N
and a net vertical force of
ΣFy = 98N − 98N = 0
So, the net force lies along only the horizontal axis. Since the object weighs 98 N, its mass is just 10 kg (since mass is weight divided by gravitational acceleration). Now that you know the net force (which is 5 N in the positive x-direction), you can find the acceleration:
a =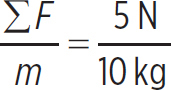 
= 0.5 m/s2
This is the general idea with applying free body diagrams to solving Newton’s Second Law.
Something to notice is that the vertical forces cancelled each other out. This is no coincidence. The normal force must cancel the gravitational force. If we view Newton’s Second Law from the other direction, this becomes apparent. Instead of looking at the net force, let’s look at the acceleration. The acceleration in the vertical direction is clearly zero (the object has no vertical motion, so it cannot have a vertical acceleration). This means that, by default, the net vertical force has to be zero. In order to accomplish this, the surface that the object is resting on puts a normal force on the object, canceling its gravitational force.
Forces such as the normal force will appear often in this book, as they are important to physics. These forces are referred to as adaptive forces: They can change their magnitude to satisfy Newton’s Second Law. The motion of the object demands that there be no vertical acceleration, so the normal adapts to make this so. We will revisit this concept again in the future as we come across more adaptive forces.
EXAMPLE 
Two forces act on an object of mass 5 kg: one in the x-direction, of magnitude 10 N, and one that makes an angle above the x-axis of 35°, with a magnitude of 6 N. We will call these forces 
1 and 2, respectively. What is the net force on the object? What is the magnitude of the net force? In what direction is the net force? And what is the magnitude of the acceleration of the object?
Well, first you need to find the components of each force. You already know the components of 
1, because it lies entirely on the x-axis. The components of 2 are
F2x = F2 cos θ = (6 N) cos(35°) = 4.9 N
F2y = F2 sin θ = (6 N) sin(35°) = 3.4 N
So, the components of the net force are
∑Fx = F1x + F2x = 10 N + 4.9 N = 14.9 N
∑Fy = F1y + F2y = 0 N + 3.4 N = 3.4 N
So, the net force is simply
∑ = (14.9 N)î + (3.4 N)ĵ
with a magnitude of
∑F = 
= 15.3 N
The tangent of the angle it makes to the x-axis is
tan θ = 
= 0.228
Using the inverse tangent function, this leads to an angle of θ = 12.9° above the x-axis. Finally, the magnitude of the acceleration of the object is given by Newton’s Second Law:
a = 
= 3.1m/s2
You already know the direction of this acceleration: It’s in the same direction as the net force.
EXAMPLE 
A book of mass 4 kg lies at rest on a table. If you were to push down on top of the book with a force of 21 N, what would be the normal force the table exerted on the book?
First, draw a free body diagram of the forces acting on the book:
Since the book remains at rest on the tabletop, you know that the net force has to be zero, so the vertical forces must cancel. Thus,
N = 39 N + 21 N = 60 N
EXAMPLE 
The following forces act on an object:
1 = (4 N)î − (2 N)ĵ
2 = (2 N)î − (1 N)ĵ
If the object were to remain at rest, what would be the third force that would have to be applied to the object?
First, you have to find the sum of the two forces 1 and 2. The third force must balance out this sum:
1 + 2 = (4 N + 2 N)î + (−2 N + 1 N)ĵ = (6 N)î − (1 N)ĵ
So, the force that needs to be applied, 3, is just this force, pointing in the opposite direction, or
3 = −(1 + 2) = −(6 N)î + (1 N)ĵ
Now that we’re starting to get the hang of solving Newton’s Second Law, we need to cover some specific forces that you might come across in an introductory physics course. First, let’s discuss friction. Friction comes in two types, each of which does something different. Kinetic friction is the friction that opposes motion, and this is what most people think of when they think of friction. If there were no kinetic friction, then if you slid something across the floor, it would slide for forever. The reason it slows to a stop is because of kinetic friction. Kinetic friction is a constant force that points directly opposite the direction of motion. The magnitude of kinetic friction is equal to
Equation 5.3
fk = μk N
where μk is the coefficient of kinetic friction, and N is just the normal force. The coefficient of kinetic friction is a number smaller than 1 and describes how large the frictional force on an object is going to be. The coefficient depends upon the surface. Smooth surfaces (like Teflon) have a small coefficient; rough surfaces (like sandpaper) have large coefficients. Notice that friction depends upon the normal force on an object, and not the weight of an object. This is because friction is an interaction between the molecules that make up the two interacting surfaces (these interactions are known as van der Waals interactions). The more these two surfaces are interacting, the larger the friction. The normal force describes how “hard” an object is pressed against the surface. The harder it is, the more interaction there is, and so the more friction.
Static friction is the friction that opposes the relative motion between two surfaces. This is a tricky definition, so we’ll explain it thoroughly. Static friction does not imply that an object does not move. Imagine resting your cell phone flat on your hand, and then slowly moving your hand through the air. Your phone moves along with your hand. The force that moves your phone through the air is actually the static friction between your hand and your cell phone. In this case, static friction is producing motion. It’s very important to realize that static friction opposes relative motion between two surfaces, or the sliding of two surfaces along one another. When there is no sliding, the friction is static. When there is sliding, the friction is kinetic.
Let’s talk about the magnitude of static friction. Imagine a large box at rest on the floor. You approach it and start to push it. You know you’re going to have to apply some minimum amount of force on the box to get it to start moving; for a light box, this force is small, but for a heavy box, this force could be quite large. Let’s say you apply 5 N of force on the box, and it doesn’t move. What is the force of static friction?
Well, since there are no other horizontal forces, static friction has to oppose your push, which means its magnitude has to be 5 N. Now you push with 10 N and the box still doesn’t move. In this case, static friction is 10 N. As you can see, static friction is changing so that whatever force you apply on the box, it cancels to keep Newton’s Second Law satisfied (i.e., the box remains at rest). So, static friction is what we called an adaptive force.
However, static friction can adapt to a force only so large. No matter how heavy the box, eventually if you push it hard enough, it will start moving, even if it were on a surface like sandpaper. This means that there is always a maximum static friction, which is equal to
Equation 5.4
fs,max = μsN
where μs is the coefficient of static friction. Something that is important to realize here is that the above equation is equal to the maximum magnitude that static friction can achieve; at any arbitrary time, static friction is trying to adapt to keep the box from moving. If the forces pushing an object are greater than the maximum static friction, the object starts moving.
It is also important to note that the coefficient of static friction is typically larger than the coefficient of kinetic friction. This is why it is easier to push a moving object than it is to get an object going. Once you break through the static friction, the force required to keep it moving and overcome kinetic friction is less.
EXAMPLE 
You want to push a 30 kg box, with the following coefficients of friction, across a floor:
μs = 0.7
μk = 0.5
How much force do you need to get the box moving? How much force is required to keep the box moving?
In order to get the box moving, you need to overcome the maximum static friction:
fs,max = μsN = (0.7)(30 kg × 9.8 m/s2) = 206 N
So you need to apply a force greater than 206 N to break static friction and get the box moving. Notice that we used the weight of the object as the normal force. This is because the only vertical forces acting on the box are the weight and the normal force (your push is assumed to be horizontal unless it’s specifically mentioned that it’s not).
Now, how much force is required to keep the box moving? Well, you just have to overcome kinetic friction:
fk = μkN = (0.5)(294 N) = 147 N
So, you need to apply 147 N to keep the box moving. What happens if you apply less than that? Well, then your forward push force is less than the backward force of kinetic friction, so the box will decelerate to a stop. If you push with more than 147 N? Well, then your forward push force will be greater than the backward kinetic friction force, and the box will accelerate forward.
The next force we need to discuss is tension. Tension is the force that prevents ropes from stretching (and also, technically, rigid objects like rods from breaking). We will be dealing only with ropes that are referred to as inelastic, meaning they do not stretch. If you pull on a rope anchored to some point, what force prevents it from stretching? The tension.
Let’s say you pull on an inelastic rope with a force of 5 N. Since it cannot stretch, the end of the rope you’re holding onto cannot move; thus the net force on it has to be zero. So, the tension has to balance your pulling force, or equal 5 N. What if you pulled the rope with 10 N of force? Well, in order to prevent the rope from stretching, the tension would have to be 10 N as well. Tension is another example of an adaptive force.
So far we’ve seen three adaptive forces: the normal force, static friction, and tension. We mentioned it specifically for static friction, but in reality, all adaptive forces have a maximum limit. If you keep piling items on a table, the table will increase the normal force to support all the items, but eventually the weight will get so large that the table breaks. The maxiumum limit would be the largest normal force the table could produce. The same thing applies to tension. Eventually, you’ll pull on the rope so hard that the rope snaps. At this point, you’ve passed the maximum tension supported by the rope.
Tension is important when we discuss pulleys. Pulleys are an excellent topic of discussion in physics because they often provide the first look at how physics can make one’s life easier. Pulleys provide mechanical advantage, which has a proper definition, but think of it as how it sounds: Pulleys provide an advantage by making a task easier. In the case of pulleys, the task that they make easier is lifting objects. A pulley system is diagrammed in the following figure, with the appropriate forces shown.
Figure 5.1: A Two-Pulley System
The reason the tension is the same everywhere in the rope is because tension is conserved in a massless pulley. So, if we focus on the lower pulley, we can see that the two tension forces upward must balance the weight pulling it downward, or
2T = W → T =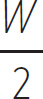 
So, this two-pulley system reduced the force needed to lift the weight by 2. In fact, it is easy to show that for the n pulleys, the tension in the rope is
Equation 5.5
T =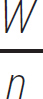 
Pulleys can be extremely useful in everyday applications, if you need to lift something.
Now that we have explored some important forces, let’s return to free body diagrams for a moment. When you construct a free body diagram, it can be overwhelming to keep track of all these kinds of forces that could appear in your diagram. There is a way to simplify your approach to free body diagrams. There are three types of forces that appear in free body diagrams:
• Forces that are explicitly stated: You could be told that a box is being pushed with 10 N, or pulled with 5 N. These explicit forces should be the first ones on your free body diagram.
• Forces due to known interactions: Next, list all forces that you know exist no matter what. All objects with mass have a weight, so you know the weight belongs in your free body diagram. If you know the surface an object is moving along has friction, then friction belongs in your free body diagram.
• Adaptive forces to satisfy Newton’s Second Law: Finally, look at what you know about the motion of the object in question. If you know it’s sliding along a horizontal surface, you know that its vertical acceleration is zero, so the net vertical force must be zero as well. A normal force is usually necessary to support an object on a horizontal surface, and the magnitude of the normal force is set by Newton’s Second Law—it must be such that the object has no vertical acceleration.
Looking at how objects move along inclined planes gives us an opportunity to combine everything we have discussed so far.
EXAMPLE 
Find the acceleration of the two masses in the following figure, assuming there is no friction along the surface of the inclined plane. Assume M is much larger than m.
In this case, you want to consider that mass M is much larger than mass m. Then, you can expect M to slide down the incline, and m to be pulled upward by the rope. In order to find the acceleration, you need to construct free body diagrams and solve Newton’s Second Law. Since this is the first example with multiple objects, it is important to remember that a free body diagram is particular for a single object; only the forces acting on that object appear on that free body diagram. The two free body diagrams are
Now, there are a few things to discuss about these free body diagrams. The most apparent thing is that we did not use the standard x-y coordinate system for the free body diagram of M. The reason is because of something we said awhile back: Always choose your coordinate system so that the largest number of forces falls on it. In the case of mass M, because it is moving on an incline, many of the forces are slanted.
The normal force is always perpendicular to the surface an object lies on (this is the definition of normal), and the tension is along the axis parallel to the surface. If there were friction, it would also be parallel to the inclined surface. Therefore, we have chosen to use a coordinate system in which one axis is parallel to the surface and one axis is perpendicular.
Next, the tension pulling m up is the same as the tension on M. This is because tension is conserved in a massless pulley, and you should always consider pulleys to be massless unless otherwise indicated.
Lastly, the acceleration for both objects is the same. This is due to the fact that the rope connecting them is assumed to be inelastic. Since the rope cannot stretch, M, the rope, and m have to move as one. So their displacements, velocities, and accelerations will all be the same. Now that we have discussed these free body diagrams, you can move on to finding the net forces and solving Newton’s Second Law. First note that there are two unknowns in this problem: the tension and the acceleration. Therefore, you will need two equations to solve for the two unknowns.
Look at the forces on m first. There are no horizontal forces, so you can ignore that direction. Choose upward to be the positive direction (making T positive and mg negative), so that Newton’s Second Law for this object states
T − mg = ma → T = ma + mg
The reason we wrote the above equation in terms of T will become apparent momentarily. Now, look at the forces acting on M. Since there is no acceleration in the perpendicular direction, you know the net force along that axis must be zero. Using Newton’s Second Law in this direction will tell you the magnitude of the normal force. If there were friction in the problem, this would be important (remember kinetic friction is µkN), but since you are not dealing with friction, you can ignore this direction. Along the parallel axis, you have T pointing up the slope and you also have a component of Mg pointing down the slope. As should be apparent from the free body diagram, this is the opposite edge from the angle θ, so this component is
Mg sin θ
So, if you choose down the slope as the positive direction, Newton’s Second Law states
Mg sin θ − T = Ma → T = Mg sin θ − Ma
Look, now you have two equations for T. You can set these equal to one another, and you have eliminated T from the system of equations, resulting in one equation for a:
Mg sin θ − Ma = ma + mg
→ Ma + ma = Mg sin θ − mg
→ (M + m)a = (Mg sin θ − m)g
→ a =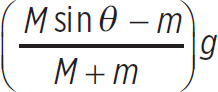 
Lesson 5.4
Rotational Mechanics
We’ve discussed rotational motion already, so now it is time to discuss how to apply mechanics to a rotational system. Well, it turns out to be very similar to the manner in which we applied mechanics to solve a linear system. We will be doing a lot of this by analogy, much like we did with rotational motion.
The first analogy we have to make is the rotational analogy of a force. In a linear system, a force is something that produces a linear acceleration. In a rotational system, a torque is what produces an angular acceleration. A torque is not its own unique quantity; it takes a force to produce a torque. Consider the following figure:
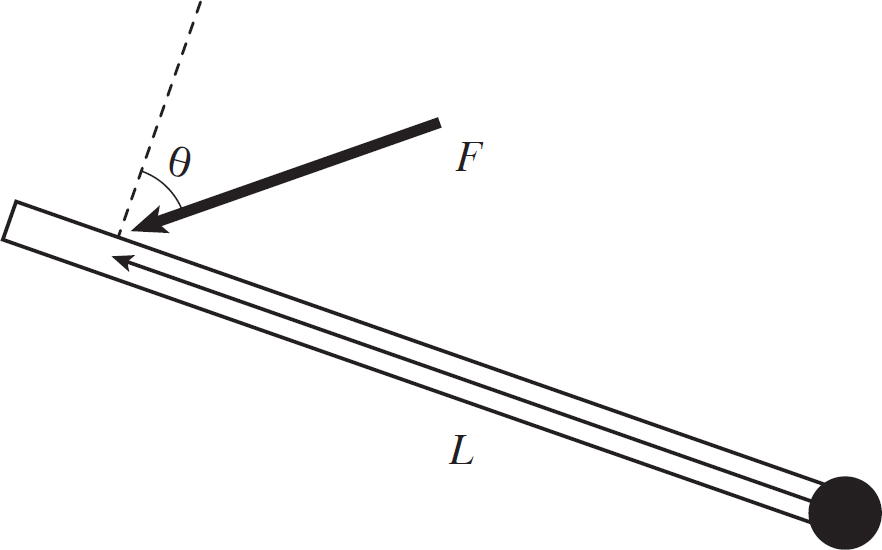
Figure 5.2: A Force Applied Against a Lever
This force has two components: one along the lever and one perpendicular to the lever. The force along the lever will not do anything to the lever, because the lever is a solid object and therefore resists the force. However, the force perpendicular to the lever will produce a tangential acceleration on the lever, increasing its tangential speed. It is clear that in this scenario, the only motion possible is rotational—the lever spins around its fixed point. Since this force is causing a tangential acceleration, it also has to be causing an angular acceleration. Therefore, this force puts a torque on the lever.
Torque is defined as
Equation 5.6
where 
is called the lever arm, and is the force applied against the lever arm. The lever arm is just the straight distance from the point of rotation to the point of application of the force. As we can see from the above equation, the units of torque are N•m.
Since the torque is the result of a cross product, it is also a vector. However, a much more useful thing to know is the magnitude of the torque, which is given by
Equation 5.7
τ = rF sin θ
where θ is the angle between the force and the lever arm. The reason that the magnitude is more important to know than the torque in general is because an object can rotate in only two directions: clockwise or counterclockwise. So we can say positive torques produce an acceleration in one direction, and negative torques produce an acceleration in the opposite direction. As always, the choice of coordinate system is up to you.
EXAMPLE 
What is the torque produced by the following force acting on the following lever arm?
= (4 N) 
−(2 N) 
= (2 m) + (3 m)
To find the torque, simply perform the cross product between the lever arm and the force applied:
= [(4 N)(3 m) − (−2 N)(2 m)] 
= (16 Nm)
As expected, the torque would be along the z-axis. This is because both the force applied and the lever arm were in the x-y plane, and since the torque is the cross product between them, it has to be perpendicular to the x-y plane.
Now that you are familiar with what a torque is, it is time to talk about how it relates to angular motion. Analogous to a force, a torque produces an angular acceleration. There is an angular form of Newton’s Second Law:
Equation 5.8
where I is known as the moment of inertia, and 
is the angular acceleration. It’s more practical to deal with the magnitude of torque, so one would also just use the magnitude of the angular acceleration as well.
Something that is important to discuss is the moment of inertia. Analogous to inertial mass, the moment of inertia defines an object’s inherent resistance to angular acceleration. However, relating the moment of inertia to an object’s mass is not trivial. For a single object of mass m rotating about a central point at a radius r, it has a moment of inertia of
Equation 5.9
I = mr2
However, for rigid bodies spinning about their own axes, the moment of inertia is not what is given above. A rigid body is any object that resists being deformed. Most objects you encounter on a day-to-day basis are rigid: a desk, a pen, a car, etc. The moment of inertia of a rigid body is determined by two things: the geometry of the object and where the rotating axis is on the body. Common moments of inertia are presented in the following figure.
Figure 5.3: Common Moments of Inertia
You can see from all the equations for moment of inertia that the units are kg•m2.
EXAMPLE 
A force of 10 N is applied perpendicularly to the end of a lever of length 1 m and mass 5 kg. What is the torque produced on this rod? What is the rod’s angular acceleration? If the force remains constant in magnitude and perpendicular to the lever, how fast will the lever be rotating after 5 s, assuming it started at rest?
First, find out the torque. Since the force is applied perpendicular to the lever, the angle between them is 90°. So the torque is
τ = rF sin θ = (1 m)(10 N) sin(90°) = 10 N•m
Now, to find the angular acceleration, you have to apply the rotational form of Newton’s Second Law, Equation 5.8. This requires knowing the moment of inertia of our rigid body. Since it is a rod with the axis of rotation at the end, the moment of inertia is
l = 
ML2 = (5 kg)(1 m)2 = 1.67 kg·m2
Now, the angular acceleration is just
α = 
= 6 rad/s2
Finally, you can solve for the angular speed of the lever:
ω = αt = (6 rad/s2)(5 s) = 30 rad/s
You can use this kinematic equation because the angular acceleration is constant. This is because the force maintains its magnitude and its direction to the rod, so the torque remains constant. A constant torque will produce a constant angular acceleration.
So, much like linear mechanics involves finding the net force on an object to figure out the object’s acceleration, rotational mechanics involves finding the net torque on an object to figure out its angular acceleration. This will allow you to solve for its angular motion.
Lesson 5.5
Equilibrium
The last topic of this chapter is equilibrium. Knowledge of equilibrium is incredibly important in engineering, so much so that engineering students take an entire class devoted to it (typically called statics). There are three forms of equilibrium: translational equilibrium, rotational equilibrium, and static equilibrium. Translational equilibrium is the specific case when the net force equals zero. In this case, the object is either not translating (moving linearly) or is translating at a constant rate. An example of translation equilibrium is a box sliding across a frictionless floor with some velocity. If there is no force pushing it forward, and there is no frictional force slowing it down, then it has an acceleration of 0, and is in translational equilibrium. Rotational equilibrium is the case when the net torque is zero. In this case, the object is either not rotating or is rotating at a constant rate. A disc that’s rotating on a frictionless axis is in rotational equilibrium if there is no torque acting on it to accelerate it. Static equilibrium is the case when an object is in both translational and rotational equilibrium, typically at rest. For example, a building has no linear or angular acceleration, so it is in static equilibrium. Static equilibrium is a useful tool to determine structural stability, which is why engineers care so much about it.
EXAMPLE 
A rod of mass M and length L is supported at its far end by a rope and at its near end by friction against a wall. At the center of the rod, a mass m hangs. This scenario is described in the following figure.
What is the static friction required to hold up the rod?
First, let’s take the above figure and draw all the relevant forces:
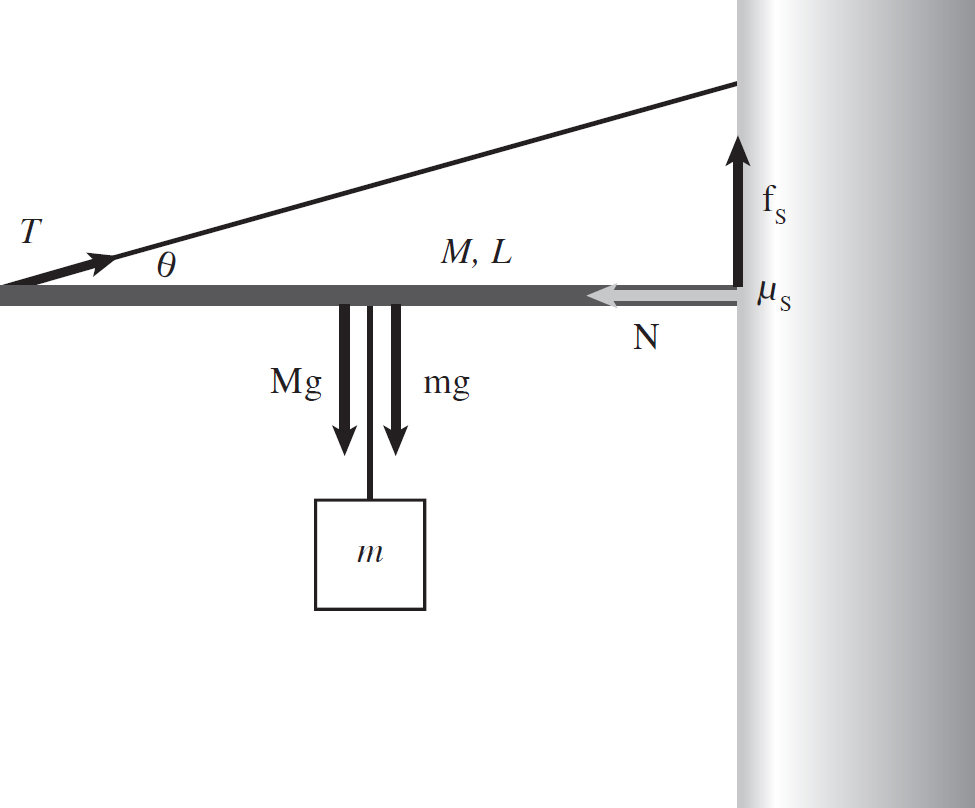
There is a tension force T in the rope supporting the far end of the rod, at some angle theta. This rope is pulling the rod towards the wall, so the wall pushes the rod away from it, producing a normal force N on the near end of the rod. Once the near end of the rod is in contact with the wall, it wants to slide down the face of the wall (due to the gravity acting on it), but the wall has a supportive frictional force on the near end of the rod. This frictional force is static, since the rod is not slipping, and it points upward, to oppose gravity.
Now, this system is in static equilibrium, which means the net force is zero and the net torque is zero about all points. It is important to note that torque has to be measured with respect to a rotational axis; in rotational equilibrium, the net torque is zero about all possible rotational axes. Something else to note is the position of the weight on the rod: the center. This is because objects with uniformly distributed mass (a mass that is evenly spread throughout the object, i.e., homogeneous) always have gravity act at their geometric centers. Unless specifically mentioned, always assume an object has uniformly distributed mass.
So, the rod has the vertical forces Tsin θ, fs, Mg, and mg, and the horizontal forces Tcos θ and N. Newton’s Second Law for the horizontal direction is straightforward:
N = T cos θ
The problem is that this tells you nothing. Both N and T are adaptive forces, so you can’t possibly know either. Newton’s Second Law in the vertical direction gives us
T sin θ + fs = Mg + mg
The problem with this equation is that there are two unknowns: T and fs. So, you cannot solve the problem yet. Luckily, you still have rotational equilibrium to apply. Consider the rotational point at the far end of the rod, where the rope attaches, and find the torques due to all of the forces. The tension doesn’t produce torque in this case because it is acting at the rotation point (r = 0). The normal force also does not produce a torque because it acts against the lever arm (θ = 0). The forces that do produce torques are fs, Mg, and mg, which are
τ1 = fsL
τ2 = 
τ3 =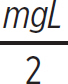 
Now, the torque from fs is in the opposite direction of the torques due to Mg and mg, so if the net torque is zero, then
fsL = 
gL
→ fs = 
g
Perfect. You now know the static friction force required to hold up the rod.
DRILL
CHAPTER 5 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 5 Practice Questions.
Directions: Complete the following problems as specified by each question, and then check your work using the solutions that follow. For extended, step-by-step solutions, access your Student Tools online.
1. A box of mass 5 kg is pushed along a horizontal, smooth (i.e, frictionless) surface with a horizontal force of 15 N. What is the acceleration of this box (both magnitude and direction)?
2. A 1000 kg elevator descends with an acceleration of 2 m/s2. What is the tension in the cables supporting the elevator?
3. A 10 kg box on a flat surface has three forces applied to it, as shown in the figure below. What is the net force on this box? What is the normal force on this box?
4. Two forces act on an object of mass 8 kg on a flat surface: 1 acts along the positive x-axis with a magnitude of 8 N, and 2 acts at an angle of 37° above the negative x-axis with a magnitude of 10 N. What is the net force on the object?
5. A box of mass 5 kg slides down an incline of 40°. If the coefficient of kinetic friction is 0.4, what is the box’s acceleration down the ramp?
6. In the previous question, if the ramp’s height is 1 m and the box starts from the top at rest, how long will it take to reach the bottom?
7. If the coefficient of static friction between a box and an incline is µs, what is the maximum angle that the incline could be without the box sliding down?
8. Two boxes, A and B, are stacked with box B atop box A. Assume that there is friction between all surfaces. If a person pulls on box A, the system moves as a whole.
(a) When the acceleration is nonzero, is there friction on the lower surface of box A? If so, what kind?
(b) When the acceleration is nonzero, is there friction on the lower surface of box B? If so, what kind?
9. You put a force of 10 N perpendicular to the end of a wrench of length 0.5 m, what is the torque you are putting on the wrench?
10. Imagine a basketball player spinning a ball on his finger. If he slaps the ball with a force of 10 N tangential to its surface, and the ball has a mass of 0.6 kg and a radius of 24 cm, what is the angular acceleration of the ball?
11. In the previous example, imagine the friction between his finger and the ball produces a uniform angular acceleration of −10 rad/s2. How long would it take the ball to stop spinning if the ball were originally spinning at 50 rad/s?
12. A telephone pole is embedded in the ground and has two telephone lines putting tensions on it as shown in the following figure.
If the upper wire has a tension of 10 N on the pole, and the lower wire has a tension of 8 N, what is the net torque on the pole? Consider the pole to have a height above the ground of 8 m and the lower wire is 7 m above the ground.
SOLUTIONS TO CHAPTER 5 PRACTICE QUESTIONS
1. Since this object has no motion along the vertical direction, you know those forces cancel out. So the net force is just going to be the horizontal force, the push, and the acceleration is going to point in the same direction. The magnitude of this acceleration is going to be
a = 
= 3 m /s 2
2. If the elevator descends with an acceleration of 2 m/s2, then the net force in the vertical direction is not zero in this case. Applying Newton’s Second Law, with the positive direction as down, we get
mg − T = ma
→ T = mg − ma = m(g − a) = (1000 kg)(9.8 m/s2 − 2 m/s2) = 7800 N
3. Since the object is on a flat surface, and the vertical force on it is not enough to lift it (the box’s weight is 9.8 N and the vertical force is only 4 N), then you know there will be no vertical motion, and so the net force in the vertical direction is zero. So, the net force is going to be horizontal, and it is simply 8 N − 5 N = 3 N. The normal force on the box is given by Newton’s Second Law in the vertical direction:
N + 4 N = 9.8 N → N = 5.8 N
4. Since the object is on a flat surface, and the vertical component of F2 is not enough to lift it off the surface, then the net force in the vertical direction has to be zero. This means that the net force is going to be in the horizontal direction. This is
∑F = 8 N − (10 N) cos(37°) = 8 N − 8 N = 0
5. The box feels a component of the weight pulling it down the ramp (wsin θ) and the kinetic friction up the ramp opposing its motion. In order to know the kinetic friction, you first need to figure out the normal force. In this case, the normal force simply balances with the component of the weight that is perpendicular to the surface:
N = mg cos θ = (5 kg)(9.8 m/s2) cos(40°) = 37.5 N
So, if the coefficient of kinetic friction is 0.4, then the kinetic friction is
fk = μkN = (0.4)(37.5 N) = 15 N
So, the net force is
∑F = wsin θ − fk = (49 N) sin(40°) − 15 N = 31.5 N − 15 N = 16.5 N
Since this answer is positive, the net force points in the direction of wsin θ, or down the ramp. The magnitude of this acceleration is
a = 
= 3.3 m / s2
6. This is just a kinematics problem. You know the acceleration, the initial speed, and the distance down the ramp (you don’t technically know that yet, but you will), so you can use the first kinematic equation to solve for the time. You can use basic trigonometry to find the distance down the ramp:
d = 
= 1.6 m
So, using the first kinematic equation:
x = 
at2
→ t2 =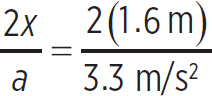 
= 1 s2
So, the time it takes to reach the bottom is 1 s.
7. At the maximum possible angle, θmax, static friction will be a maximum, or µsN. At this angle, the normal force is equal to mgcos θmax. The frictional force needs to balance out the component of the weight down the ramp, mgsin θmax, and so
mg sin θmax = μs mg cos θmax
μ5 = 
= tan θmax
So, the angle is the inverse tangent of the coefficient of static friction:
θmax = tan−1(μs)
8. (a) If the acceleration is nonzero, there is a frictional force on the bottom of box A. Because the acceleration is nonzero, the box will start sliding across the surface it is on, and so the friction will be kinetic.
(b) If the acceleration is nonzero, then there has to be a frictional force on the bottom of box B. Recall Newton’s First Law: That box wants to remain at rest. Why does it start moving along with box A? Because a force compelled it to. And what force is that? Static friction. This is because in order for box B to remain at rest, box A would have to slide out from under it. Static friction opposes this sliding.
9. The torque is simply
τ = rF sin θ = (0.5 m)(10 N) sin(90°) = 5 N·m
10. The slap puts a torque on the basketball of
τ = rF sin θ = (0.24 m)(10 N) sin(90°) = 2.4 N·m
This basketball is a hollow sphere rotating on an axis through its center (you can ignore the mass of the air inside the basketball). Therefore, its moment of inertia is
l = 
MR2 = (0.6 kg)(0.24 m)2 = 0.023 kg·m2
So, the angular acceleration of the basketball is
α =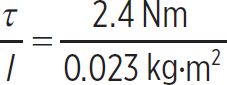 
= 104 rad/s2
12. In this case, the telephone pole is in static equilibrium, so the net torque on it is zero. This is a trick question. Enough information was given for you to calculate the torque due to both wires. However, since the pole is buried underground, the buried part of the pole does enough torque to oppose the torque due to the wires and prevent the pole from moving. No calculations are necessary in this problem.
REFLECT
Congratulations on completing Chapter 5!
Here’s what we just covered.
Rate your confidence in your ability to:
• Describe what a force is
1 2 3 4 5
• Understand Newton’s three force laws and how to apply them
1 2 3 4 5
• Solve Newton’s Second Law for the acceleration of objects
1 2 3 4 5
• Solve Newton’s Second Law for rotational systems
1 2 3 4 5
• Apply your knowledge of rotating and non-rotating systems to understand equilibrium
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.