Extending Plane Geometry into Solid Geometry

17.1   Solids

---

A solid is an enclosed portion of space bounded by plane and curved surfaces.

Thus, the pyramid , the cube , the cone , the cylinder , and the sphere are solids.

A solid has three dimensions: length, width, and thickness.

Practical illustrations of solids include a box, a brick, a block, and a ball. These are not, however, the pure or ideal solids that are the concern of solid geometry. In solid geometry we study the geometric properties of “perfect” solids, such as their shape, their size, the relationships of their parts, and the relationships along solids; physical properties such as their color, weight, or smoothness are disregarded.

17.1A   Kinds of Solids

Polyhedra

A polyhedron is a solid bounded by plane (flat) surfaces only. Thus, the pyramid and cube are polyhedrons. The cone, cylinder, and sphere are not polyhedra, since each has a curved surface.

The bounding surfaces of the polyhedron are its faces; the lines of intersection of the faces are its edges, and the points of intersection of its edges are its vertices. A diagonal of a polyhedron joins two vertices not in the same face.

Thus, the polyhedron shown in Fig. 17-1 has six faces. Two of them are triangles (ABC and CFG), and the other four are quadrilaterals. Note is a diagonal of the polyhedron. The shaded polygon HJKL is a section of the polyhedron formed by the intersection of the solid and a plane passing through it.

Fig. 17-1

The angle between any two intersecting faces is a dihedral angle. The angle between the covers of an open book is a dihedral angle. As the book is opened wider, the dihedral angle grows from one that is acute to one that is right, obtuse, and then straight. The dihedral angle can be measured by measuring the plane angle between two lines, one in each face, and in a plane perpendicular to the intersection between the faces.

Prisms

A prism (Fig. 17-2) is a polyhedron two of whose faces are parallel polygons, and whose remaining faces are parallelograms. The bases of a prism are its parallel polygons. These may have any number of sides. The lateral (sides) faces are the parallelograms. The distance between the two bases is h; it is measured along a line at right angles to both bases.

A right prism is a prism whose lateral faces are rectangles. The distance h is the height of any of the lateral faces.

Fig. 17-2

Fig. 17-3

A rectangular solid (box) is a prism bounded by six rectangles. The solid can be formed from a pattern of six rectangles, as shown in Fig. 17-3, folded along the dashed lines. The length l, width w, and height h are its dimensions.

A cube is a rectangular solid bounded by six squares. The cube can be formed from a pattern of six squares, as shown in Fig. 17-4, folded along the dashed lines. Each equal dimension is represented by e in the diagram.

Fig. 17-4

Fig. 17-5

A cubic unit is a cube whose edge measures 1 unit. Thus, a cubic inch is a cube whose edge is 1 in long.

A parallelepiped is a prism bounded by six parallelograms (Fig. 17-5). Hence, the rectangular solid and cube are special parallelepipeds.

The table that follows shows some relationships among polygons in plane geometry and the corresponding relationships among polyhedra in solid geometry.

Pyramids

A pyramid is a polyhedron whose base is a polygon and whose other faces meet at a point, its vertex. The base (B in Fig. 17-6) may have any number of sides. However, the other faces must be triangles. The distance from the vertex to the base is equal to the measure of the altitude or height h, a line from the vertex at a right angle to the base.

Fig. 17-6

A regular pyramid is a pyramid whose base is a regular polygon and whose altitude joins the vertex and the center of the base.

A frustum of a pyramid is the part of a pyramid that remains if the top of the pyramid is cut off by a plane parallel to the base. Note in Fig. 17-6 that its lateral faces are trapezoids.

Cones

A circular cone (Fig. 17-7) is a solid whose base is a circle and whose lateral surface comes to a point. (A circular cone is usually referred to simply as a cone.)

Fig. 17-7

A right circular cone is formed by revolving a right triangle about one of its legs. This leg becomes the altitude h of the cone, and the other becomes the radius r of the base.

A frustum of a cone is the part of a cone that remains if the top of the cone is cut off by a plane parallel to the base.

Cylinders

A circular cylinder (Fig. 17-8) is a solid whose bases are parallel circles and whose cross-sections parallel to the bases are also circles. (A circular cylinder is usually referred to simply as a cylinder.)

A right circular cylinder is a circular cylinder such that the line joining the centers of the two bases is perpendicular to the radii of these bases. The line joining the centers is the height h of the cylinder, and the radius of the bases is the radius r of the cylinder.

Fig. 17-8

Spheres

A sphere is a solid such that every point on its surface is at an equal distance from the same point, its center.

A sphere is formed by revolving a semicircle about its diameter as an axis. The outer end of the radius perpendicular to the axis generates a great circle, while the outer ends of other chords perpendicular to the diameter generate small circles.

Thus, sphere O in Fig. 17-9 is formed by the rotation of semicircle about as an axis. In the process, point C generates a great circle while points E and G generate small circles.

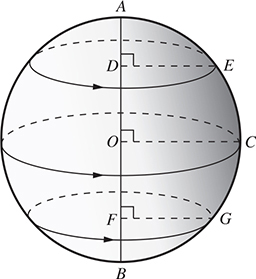
Fig. 17-9

Fig. 17-10

The way in which points on the earth’s surface are located is better understood if we think of the earth as a sphere formed by rotating semicircle NQS in Fig. 17-10, which runs through Greenwich, England (near London), about NS as an axis. Point O, halfway between N and S, generates the equator, EQ. Points A and B generate parallels of latitude, which are small circles on the earth’s surface parallel to the equator. Each position of the rotating semicircle is a semi-meridian, or longitude. (A meridian is a great circle passing through the North and South Poles.) The meridian through Greenwich is called the Prime Meridian.

Using the intersection of the equator and the Prime Meridian as the origin, we would locate New York City at North Latitude and West Longitude. The heavy arc shown on the globe is an arc of a great circle through New York City and London. Such an arc is the shortest distance between two points on the earth’s surface. We could find this line by stretching a rubber band tightly between New York City and London on a globe.

17.1B   Regular Polyhedra

Regular polyhedra are solids having faces that are regular polygons, with the same number of faces meeting at each vertex. There are only five such solids, shown in Fig. 17-11. Note that their faces are equilateral triangles, squares, or regular pentagons.

Fig. 17-11

Regular hexagons cannot be faces of a regular polyhedron. If three regular hexagons had a common vertex (Fig. 17-12), the sum of the measures of the three interior angles at that vertex would be 3(120°) or 360°. As a result, the three regular hexagons would lie in the same plane, so they could not form a solid.

Fig. 17-12

17.2   Extensions to Solid Geometry

---

17.2A   Extension of Plane Geometry Principles to Space Geometry Principles

“Sphere” in space geometry corresponds to “circle” in plane geometry. Similarly, “plane” corresponds to “straight line.” By interchanging “circle” and “sphere,” or “straight line” and “plane,” each of the following dual statements can be interchanged. When you do so, many plane geometry principles with which you are acquainted become space geometry principles.

Be sure, in obtaining dual statements, that there is a complete interchange of terms. If the interchange is incomplete, as in the following pair of statements, there is no duality.

Unlike a cylinder, a cylindrical surface is not limited in extent; nor does it have bases. Similarly, a conical surface is unlimited in the extent and has no base.

Extension of Distance Principles

Here are some dual statements involving distance—in a plane and in space.

Extension of Locus Principles

The following dual statements involve the locus of points—in a plane and in space.

17.2B   Extension of Analytic Geometry to Three-Dimensional Space

The analytic (or coordinate) geometry of two dimensions can easily be extended to three dimensions. Figure 17-13 shows the two- and three-dimensional axes; the z-axis is perpendicular to both the x- and y-axes. In the figure, arrows indicate the positive directions, and dashed lines indicate the negative axes.

Four specific extensions from geometry in a plane to geometry in space follow.

Fig. 17-13

17.3 Areas of Solids: Square Measure

---

The area of each face of the cube in Fig. 17-14 is A 5 e². The total surface area S of the cube is then

S = 6e²

The areas of the six rectangles that make up the rectangular solid in Fig 17-15 are

The total surface area S of the rectangular solid is then

S = 2lw + 2lh + 2wh

The total surface area S of the sphere in Fig. 17-16 is

S = 4 πr²

The total surface area S of the right circular cylinder in Fig. 17-17 is

S = 2πr² + 2πrh = 2πr(r + h)

Fig. 17-14

Fig. 17-15

Fig. 17-16

Fig. 17-17

SOLVED PROBLEM

  17.1 Finding total surface areas of solids

Find, to the nearest integer, the total surface area of

(a)  A cube with an edge of 5 m (Fig. 17-18)

(b)  A rectangular solid with dimensions of 10 ft, 7 ft, and [&4*cf*{1}{2}~rom~ft~normal~&] (Fig. 17-19)

(c)  A sphere with a radius of 1.1 cm (Fig. 17-20)

Fig. 17-18

Fig. 17-19

Fig. 17-20

Solutions

(a)  s = 6e² = 6(5²) = 150 m²

(b)  

(c)  s = 4πr² = 4(3.14)(1.1²) = 15.1976 cm²

17.4 Volumes of Solids: Cubic Measure

---

A cubic unit is a cube whose edge is 1 unit long. Thus, a cubic inch is a cube whose side is 1 in long (Fig. 17-21).

Fig. 17-21

Fig. 17-22

The volume of a solid is the number of cubic units that it contains. Thus, a box 5 units long, 3 units wide, and 4 units high has a volume of 60 cubic units; that is, it has a capacity or space large enough to contain 60 cubes, 1 unit on a side. (See Fig. 17-22.)

Here are some formulas for the volumes of solids. In these formulas, V is the volume of the solid, B is the area of a base, and h is the distance between the bases or between the vertex and a base. In volume formulas, the volume is in cubic units, the unit being the same as that used for the dimensions. Thus, if the edge of a cube measures 3 meters, its volume is 27 cubic meters.

1.  Rectangular solid (Fig. 17-23): V = lwh

2.  Cylinder (Fig. 17-24): V = Bh or V = πr²h

Fig. 17-23

Fig. 17-24

3.  Prism (Fig. 17-25): V = Bh

4.  Cube (Fig. 17-26): V = e³

Fig. 17-25

Fig. 17-26

5.  Pyramid (Fig. 17-27):

6.  Cone (Fig. 17-28):

7.  Sphere (Fig. 17-29):

Fig. 17-27

Fig. 17-28

Fig. 17-29

SOLVED PROBLEMS

  17.2 Relations among cubic units

Find the volume V of

(a)  A cubic foot in cubic inches

(b)  A cubic yard in cubic feet

(c)  A liter (cubic decimeter) in cubic centimeters

Solutions

(a)  V = e³ for a cube. Since 1 ft = 12 in, V = 12³ = 1728

So 1 ft³ = 1728 in³.

(b)  V = e³ for a cube. Since 1 yd = 3 ft, V = 3³ = 27

So 1 yd³ = 27ft³.

(c)  V = e³ again. Since 1 dm³ = 10 cm³, V = 10³ = 1000

So 1 liter = 1000 cm³.

  17.3 Finding volumes or cubes

Find the volume V of a cube, in cubic feet, if one edge is (a) 4 in, (b) 4 ft, (c) 4 yd.

Solutions

To find the volume in cubic feet, we must express the side in feet.

(a)  

(b)  V = e³ = 4³ = 64 ft³

(c)  V = e³, and since 4 yd = 12 ft, V = 12³ = 1728 ft³

  17.4 Finding the volumes of a rectangular solid, prism, and pyramid

Find the volume of

(a)  A rectangular solid having a length of 6 in, a width of 4 in, and a height of 1 ft

(b)  A prism having a height of 15 yd and a triangular base of 120 ft²

(c)  A pyramid having a height of 8 cm and a square base whose side is cm

Solutions

(a)  V = lwh = 6(4)(12) = 288 in³

(b)  V = Bh = 120(45) = 5400 ft³ = 200 yd³

(c)  

  17.5 Finding the volumes of a sphere, cylinder, and cone

Find the volume of

(a)  A sphere with a radius of 10 in

(b)  A cylinder with a height of 4 yd and a base whose radius is 2 ft

(c)  A cone with a height of 2 ft and a base whose radius is 2 yd

Solutions

In these calculations, we shall let p 5 3.14

(a)  

(b)  

(c)  

17.6 Deriving formulas from V = Bh

From V = Bh, the volume formula for a prism or cylinder, derive the volume formulas for the solids in Fig. 17-30.

Fig. 17-30

Solutions

(a)  Since B = lw, V = Bh 5 lwh

(b)  Since B = e² and h = e, V = Bh = (e²) e = e³

(c)  Since B = πr², V = Bh = πr²h

(d)  Since

Fig. 17-30

  17.7 Formulas for command volumes

State the formula for the volume of each solid in Fig. 17-31.

Fig. 17-31

Solutions

(a)  V = lwh for this solid. Now l = 4e, w = 3e, and h = 2e. Hence, V = (4e)(3e)(2e) = 24e³

(b)  V = lwh again. Here l = 2a, w = c, and h = 3b. Hence, V = (2a)(c)(3b) = 6abc

(c)  Here V = Vcyl. I + Vcyl. II = πR²h + πr²h. But R = 3r, so V = π(3r)²h + πr²h = 10πr²h

SUPPLEMENTARY PROBLEMS

17.1.   Find, to the nearest integer (using p 5 3.14), the total area of

(17.1)

(a)  A cube with an edge of 7 yd

(b)  A rectangular solid with dimensions of 8 ft, , and 14 ft

(c)  A sphere with radius of 30 m

(d)  A cylinder of revolution with a radius of 10 yd and a height of yd. [Hint: Use T = 2πr(r + h).]

17.2.   Find the volume of

(17.2)

(a)  A cubic yard in cubic inches

(b)  A cubic meter in cubic centimeters (1 m 5 100 cm)

17.3.   Find, to the nearest cubic inch, the volume of a cube whose edge is (a) 3 in; (b) in; (c) 7.5 in; (d) 0.3 ft; (e) 1 ft 2 in.

(17.3)

17.4.   Find, to the nearest integer, the volume of

(17.4)

(a)  A rectangular solid of length 3 in, width in, and height 8 in

(b)  A prism having a height of 2 ft and a square base whose side is 3 yd

(c)  A pyramid having a height of 2 yd and a base whose area is 6.4 ft²

17.5.   Find, to the nearest integer, the volume of

(17.5)

(a)  A sphere with radius of 6 m

(b)  A cylinder having a height of 10 ft and a base whose radius is 2 yd

(c)  A cone having a height of 3 yd and a base whose radius is 1.4 ft

17.6.   From the volume formula for a pyramid or cone, derive volume formulas for each of the solids in Fig. 17-32.

(17.6)

Fig. 17-32

17.7.   Find a formula for the volume of each solid in Fig. 17-33.

(17.7)

Fig. 17-33