6
Induction and Inductivism

Let us consider…what sort of subject is inductive or human logic— the logic of truth. Its business is to consider methods of thought, and discover what degree of confidence should be placed in them, i.e. in what proportion of cases they lead to truth. In this investigation it can only be distinguished from the natural sciences by the greater generality of its problems…. The proper plan of such a subject is to be found in Mill; I do not mean the details of his Methods or even his use of the Law of Causality. But his way of treating the subject as a body of inductions about inductions, the Law of Causality governing lesser laws and being itself proved by induction by simple enumeration. (Frank Ramsey)¹

1  Inductive logic

Books i and ii of the System of Logic have shown that no real inference or proposition is a priori, and that logic and mathematics themselves contain real propositions and inferences. The question must now be, what are the a posteriori grounds for belief ? How can belief be grounded on evidence? That is the question of inductive logic.

Terms like ‘inductive logic’, or ‘inductive reasoning’, can however be used in a broad or a narrow sense.

In the broad sense, induction is inference from singular to general propositions. That is how Mill defines it: ‘Induction may be defined, the operation of discovering and proving general propositions’ (VII 284). (Note that he sees it here both as a logic of discovery and as a logic of proof.) There is no incompatibility between this definition and the thesis that all inference is from particulars to particulars, as Mill goes on to note. Any inference from particulars to particulars can be represented as involving an inductive step from particulars to generals. The point made by the thesis that inference is from particulars to particulars, on our interpretation of it, was that general propositions express habits of inference. Induction therefore becomes the operation by which we accumulate habits of inference, and inductive logic becomes the ‘theory of evidence’, of how to extract sound habits of inference from one’s data.

Mistakenly, Mill asserts that all real inference is inductive: ‘all Inference…consists of inductions, and the interpretation of inductions’ (VII 283). That view derives, as we have seen, from his tendency to treat universal instantiation as the paradigm of all deductive reasoning—deduction becomes a case of ‘interpreting’ a general rule, or ‘decyphering’ a ‘memorandum’, which by previous processes of induction has been placed in one’s mental archives (4.8). But this ignores the point that inferences which rest on the laws of contradiction, excluded middle and transitivity of implication are not verbal inferences and neither are they ‘interpretations’ of a rule. They are real inferences, justified, on Mill’s empiricist principles. only by induction. But their use in reasoning is not itself a case of induction.

The same point in fact applies to Mill’s canons of eliminative induction, or ‘Methods of Experimental Inquiry’—which he himself sees as the centre-piece of his inductive logic. They are, as we shall see, demonstrative methods, in which a general proposition is deductively inferred from singular observations together with certain appropriate general propositions as background assumptions. They are inductive therefore only in the somewhat loose sense that the main work involved in applying them consists in observation and ‘operations subsidiary to induction’ such as the classification of possible causes. If induction is taken in the sense of inference from singular premises alone to general conclusions, they should not strictly speaking be included. We shall however follow Mill in referring to them as inductive methods of reasoning.

There is a narrower, and more common, sense of the word ‘induction’. In the narrower sense ‘induction’ is understood as enumerative induction: it is the generalisation to ‘All As are Bs’ from an enumerated sample of As which are all observed to be Bs.² Mill assumes that all inductive canons either are, or are justified by, enumerative induction. In particular, he rejects the hypothetico-deductive method as an independent method of arriving at the knowledge of new truths. He therefore makes no distinction between the narrow and the broad sense of ‘induction’, and defines induction in another place as

that operation of the mind, by which we infer that what we know to be true in a particular case or cases, will be true in all cases which resemble the former in certain assignable respects. In other words, Induction is the process by which we conclude that what is true of certain individuals of a class is true of the whole class, or that what is true at certain times will be true in similar circumstances at all times. (VII 288)

We, however, must be careful not to beg questions about the status of hypothetico-deductive inference or—as it is often illuminatingly called— ‘inference to the best explanation’. So we shall understand the word ‘induction’ exclusively in the broader sense, as covering every method of reasoning by which general beliefs may be grounded on singular data. Induction in the narrow sense we shall always specifically refer to as enumerative induction (EI for short).

This brings us to the term ‘inductivism’. Here two positions must be distinguished, corresponding to the broad and the narrow sense of ‘induction’:

(1) The view that there is such a thing as inductive logic in the broad sense explained above: a ‘logic of truth’.

(2) The view that inductive logic consists exclusively of enumerative induction, and such other methods as may be grounded in one way or another on enumerative induction.

Mill was committed to both (1) and (2); we shall accept (1) and reject (2). William Whewell, Mill’s great antagonist in the analysis of scientific method, would have fully agreed with Mill that there is such a thing as inductive logic in the broad sense of the word ‘inductive’. His argument with Mill was not about the existence of inductive reasoning in this sense, or about the possibility of codifying its methods. It was a disagreement about what the methods were, and about their metaphysical presuppositions. The issues involved in this debate between Mill and Whewell were, and remain, fundamental in philosophy. We shall consider them in section 6.8, and in 7.1–4.

It might be thought that acceptance of (1) is a formality. To reject it is to deny that there are wholly general, topic-neutral rules of inductive reasoning. What reason, short of a thoroughgoing scepticism about induction as such, could there be for doing so?

We shall encounter reasons later on for doubting whether it is useful to talk of a logic of induction, reasons which have nothing to do with thoroughgoing inductive scepticism. But we must also briefly take account of the position of Popper. He rejects the very possibility of proving, confirming or probabilising beliefs by evidence. The hypothetical method, according to Popper, can no more do that than enumerative induction can. We can falsify hypotheses, but we cannot confirm them. A scientific hypothesis, it is true, may be ‘corroborated’; but this only means subjected to severe tests and not falsified.

There is a very obvious difficulty in this view. Since there is no ground for thinking that a corroborated hypothesis is true, or probably true, there is no more ground for believing it than for believing a falsified hypothesis. Popper’s position, so far from offering an alternative to Hume’s scepticism about induction, is indistinguishable from it.³ In contrast, Mill and Whewell would both accept that inductive reasoning can give rational grounds for accepting a general conclusion. That is not to say that either of them had an answer to, or had even deeply considered, Hume’s inductive scepticism. Hume’s problem, which has quite rightly figured so largely in more recent philosophical discussion, hardly figured at all in nineteenth-century British philosophy before T.H. Green’s revival of Hume. This point should be stressed from the outset. In his analysis of induction Mill is not proposing a solution to the sceptical problem of induction posed by Hume.⁴ He takes it for granted that our ‘spontaneous’ —unreflective, habitual—inductions are reliable to some degree. Inductive logic is concerned only to refine and codify the methods of inductive reasoning. Mill’s philosophical discussion of inductive logic is not intended to give them a metaphysical justification, but simply to clarify the way in which, by applying inductive principles to their own results, we may be able to raise the degree of rational confidence we place in those principles. Anyone who reads Mill as searching for an answer to the epistemological sceptic, is bound to be baffled by what he says.

But what then are Mill’s questions? His discussion of induction, as of so many other topics, is much more intricate and subtle than at first appears. It also contains the usual measure of confusions and misstatements. Nevertheless, the questions are penetrating ones, and the answers are well worth getting clear.

2 ‘The question of Inductive Logic stated’

Chapter iii.iii (‘On the Ground of Induction’) is the natural starting point. Mill’s topic is ‘the propensity to generalize from unvarying experience’ (VII 312)—‘Inductio per enumerationem simplicem, ubi non reperitur instantia contradictoria’, to give it its full Baconian title; and ‘the question of Inductive Logic’, as Mill understands it, is stated in its last section (iii.iii.3).

Section 1 of the chapter deals with the ‘Axiom of the uniformity of the course of nature’. Sadly, it contains a traditional and important confusion, which throws the reader off the scent and makes Mill’s position look much weaker than it really is. Consider the following passage:

what happens once, will, under a sufficient degree of similarity of circumstances, happen again, and not only again, but as often as the same circumstances recur. This, I say, is an assumption involved in every case of induction. And if we consult the actual course of nature, we find that the assumption is warranted. The universe, so far as known to us, is so constituted, that whatever is true in any one case, is true in all cases of a certain description; the only difficulty is, to find what description. (VII 306)

Mill calls this assumption the ‘principle, or axiom, of the uniformity of nature’. But he also says that it is established by induction. And thus he gives every appearance of making two points which entail an immediate vicious circle: (a) that general uniformity is assumed in every induction, and (b) that the existence of general uniformity is known only on the basis of induction.

But both in fact, and considered in terms of his overall position, (a) is false.

Enumerative inductions presuppose no unvarying uniformity through-out nature. They assume only the legitimacy, in the particular case in question, of inferring from a sample of observed As found without exception to be B, to the unrestricted generalisation that all As are Bs. Now the noteworthy fact, of which Mill is fully aware, is that it may be more or less legitimate to do so, depending on the subject matter in question. The degree of trust one can place in an EI depends on one’s background knowledge of the kind and degree of uniformity, or lack of it, in the empirical domain within which one is making one’s induction. And it is this fact, that the reliability of EI is not invariant across subject matter, which interests Mill and gives rise to his question.

Why, in that case, does he appear to concede that general uniformity is ‘assumed’ in all inductions? He ought at most to have allowed that it is assumed in eliminative inductions (we shall come to these). In Mill’s overall picture, which comes into focus only in iii.iv and iii.xxi, mankind begins with ‘spontaneous’ and ‘unscientific’ inductions about particular unconnected natural phenomena or aspects of experience. Generalisations accumulate, interweave and are found to stand the test of time: they are not disconfirmed by further experience. As they accumulate and interweave, they justify the second-order inductive conclusion that all phenomena are subject to uniformity, and more specifically, that all have discoverable sufficient conditions. In this less vague form, the principle of general uniformity becomes, given Mill’s analysis of causation, the Law of Universal Causation. This conclusion in turn serves (Mill believes) as the grounding assumption for a new style of reasoning about nature, eliminative induction. The improved effectiveness of the ‘inductive process’ which results from this new style of reasoning spills back onto the principle of Universal Causation on which it rests, and raises its certainty to a new level. That in turn raises our confidence in the totality of particular enumerative inductions from which the principle is derived. In short, the amount of confidence with which one can rely on the ‘inductive process’ as a whole depends on the point which has been reached in its natural history. But within that overall level of confidence, the confidence that can be attached to particular EIs will continue to be variable; nor does any principle of universal uniformity feature as a premise in enumerative inductions.

As so often, confusion is caused by Mill’s over-concessive attitude towards an inherited tradition. In this case, it is the notion that enumerative inductions can somehow be made into deductive arguments by conjoining an ‘axiom’ of the uniformity of nature to their premises. Having got off on the wrong foot by seeming to accept this idea he is led by his own analysis to see its inadequacies; but instead of jettisoning it he insists on reinterpreting it unconvincingly.

Following Whately, Mill grants that ‘every induction may be thrown into the form of a syllogism by supplying a major premise’ (VII 308). If this is done, the principle of the ‘uniformity of the course of nature’ appears as ‘the ultimate major premise of all inductions’. But as he straightaway points out, ‘the immediate major premise in every inductive argument it certainly is not’ (VII 309, my emphasis). For example, ‘John, Peter &c. are mortal, therefore all mankind are mortal’, is not turned into a deductive argument by adding some such premise as ‘Nature is uniform’. It needs a specific assumption about ‘John, Peter &c’: a major premise of the form ‘what is true of John, Peter &c. is true of all mankind’. There is nothing about the general uniformity of nature here.

What, however, is the ‘proof’ of this major premise? In ‘the long run’, according to Mill, it ‘can only be, that a different supposition would be inconsistent with the uniformity which we know to exist in the course of nature’ (VII 310). Mill’s reason for saying this, it seems, is that he thinks that the major premise is only proved when, in ‘the long run’, it is deduced from the principle of uniformity. That is to say, in the initial stage the assumption is made, and with justice: but it can be made only as a working assumption. Gradually however the general principle of uniformity gathers inductive support from the success of vast numbers of particular generalisations, to the point of becoming certain. Its inductive certainty then flows back onto the generalisations from which it derived support, raising their level of certainty, by collecting and transmitting the confidence generated by the whole body of generalisations to each individual one.

The broad picture is sound, but in no way justifies the traditional claim that ‘uniformity of the course of nature’ is ‘the ultimate major premise of all inductions’. For first, given this picture, it must be possible for particular EIs to be legitimate even when the reasoner is in no position to assert any such overarching principle. He can have some degree of confidence in the particular uniformity he has inferred even though he has no equal confidence in the general uniformity of nature.⁵ And second, even when his confidence in the general uniformity of nature has mounted to the point where it spills back and raises his confidence in the reliability of particular inductions, it does not do so by converting those particular inductions into deductive arguments in which either it, or some proposition deductively derived from it, features as a premise, All this is particularly obvious in the case of ‘What is true of John, Peter &c. is true of all mankind’. It could not possibly be deduced from any principle of general uniformity, nor does it in any way feature as a premise in the enumerative induction to ‘All men are mortal’.

Mill errs in trying to fill an old bottle with this new wine: he should have dismissed the traditional idea, which converts inductions into syllogistic reasoning from singular observations and the ‘axiom’ of the uniformity of nature, out of hand. The error obscures his other important point, which is the one that iii.iii should have been exclusively devoted to making, and which gives rise to his fundamental question of inductive logic. The point is this.

We are much more confident of some particular EIs than we are of others. We are willing to infer a general conclusion from an observed correlation only inasmuch as we take the correlation to be significant, and not accidental; but we are more willing to take some observed correlations to be significant, than others which are formally matched in respect of the number of observed instances. In one case, having observed n As which are Bs and no As which are not B, we are confident in inferring that all As are Bs; in another case we are not. But if formally matched enumerative inductions can rightly inspire unequal confidence, then there can be no ‘axiom’ of uniformity—i.e. no proposition which, added to the premises, would have the effect of making them all equally sound.

After only a few cases in which a particular make and type of tyre wears prematurely, I infer with some confidence that all tyres of that type and make will wear earlier than they should. But if I have visited a Saharan oasis the same number of times, and there has always been a cloudburst, I do not infer that whenever I visit the oasis there will always be a cloudburst. ‘To look for constancy where constancy is not to be expected…is justly accounted superstition’ (VII 311).⁶

I am willing to make the induction about the tyres because I take the observed correlation to be significant. I do not make the parallel induction about my presence in the oasis, because in that case I take it to be accidental. The difference in my attitude turns on my background causal knowledge. To take a correlation to be significant is to treat it as resulting from some underlying causal connection. Because so many background assumptions would be thrown into disarray by the conclusion that my presence in the oasis is somehow causally connected with rain, it would take a very stringent EI before we even begin to take the possibility seriously.

To this point Mill turns his attention in iii.iii.2 and 3:

The course of nature, in truth, is not only uniform, it is also infinitely various. Some phenomena are always seen to recur in the very same combinations in which we met with them at first; others seem altogether capricious; while some, which we had been accustomed to regard as bound down exclusively to a particular set of combinations, we unexpectedly find detached from some of the elements with which we had hitherto found them conjoined, and united to others of a quite contrary description. To an inhabitant of Central Africa, fifty years ago, no fact possibly appeared to rest on more uniform experience than this, that all human beings are black. To Europeans, not many years ago, the proposition, All swans are white, appeared an equally unequivocal instance of uniformity in the course of nature. Further experience has proved to both that they were mistaken; but they had to wait fifty centuries for this experience. During that long time, mankind believed in an uniformity of the course of nature where no such uniformity really existed. (VII 311–12)

There are, then, three kinds of phenomena: (1) there are the ‘capricious’ ones, about which no general propositions can be established by direct enumerative induction; (2) there are those which are stably uniform, in that enumerative reasoning establishes general propositions which stand the test of time, and (3) there are those in which enumeratively detected uniformities regularly break down and trap the spontaneous reasoner. It is because of these variations that our confidence in EI varies with the subject matter. But our knowledge that there are such variations derives from past experience of uniformity. Only as a result of that experience does our confidence in EI begin to vary systematically across subjects.

Enumerative induction, in Mill’s view, is the only ultimate type of inductive reasoning. But it is more reliable in some cases than in others. Can we find a type of inductive reasoning which will be more penetrating and more widely effective than direct enumerative reasoning while nevertheless being ultimately based on it? That, for Mill, is the ‘question of Inductive Logic’, to which Book iii is addressed:

As there were black swans, though civilized people had existed for three thousand years on the earth without meeting them, may there not also be ‘men whose heads do grow beneath their shoulders,’ notwithstanding a rather less perfect unanimity of negative testimony from observers? Most persons would answer No; it was more credible that a bird should vary in its colour, than that men should vary in the relative position of their principal organs. And there is no doubt that in so saying they would be right: but to say why they are right, would be impossible, without entering more deeply than is usually done, into the true theory of Induction….

Why is a single instance, in some cases, sufficient for a complete induction, while in others, myriads of concurring instances, without a single exception known or presumed, go such a very little way towards establishing a universal proposition? Whoever can answer this question knows more of the philosophy of logic than the wisest of the ancients, and has solved the problem of induction. (VII 314)⁷

That problem is not Hume’s sceptical problem. But it would be too simple to say that answering it is quite irrelevant to the sceptic’s question. The answer, in so far as it spells out the way in which induction can be self-vindicating as well as self-undermining, and has in fact turned out to be the former, provides what may be called an internal justification of induction. It leaves the sceptic in possession of his territory but it marginalises it.

We shall return to scepticism, and reconsider its significance and its relation to the internal justification of induction, in 6.7. But first we must examine Mill’s account of what he calls the ‘Methods of Experimental Inquiry’, and the analysis of causation on which he bases it. Mill himself considered this codification of eliminative inductive reasoning to be his main contribution to the ‘true theory of Induction’. His conception of inductive logic, of ‘the proper plan of such a subject’, in Ramsey’s phrase, is thoroughly bound up with it. We shall consider his account of causation and of the experimental methods (EMs) in the following three sections.

3  The Law of Universal Causation

‘The truth that every fact which has a beginning has a cause, is coextensive with human experience’ (VII 325). What then is a cause? Mill is concerned only with what he calls ‘physical causes’; that is to say, he regards causation exclusively as a relation between ‘phenomena'.⁸ Uniformities in the spatio-temporal relations among phenomena are all we can know. If there are ‘metaphysical’ causes—causes lying ‘behind’ natural phenomena, and which are not themselves natural phenomena— we can know nothing of them; nor need they be taken into account in the analysis of inductive reasoning: ‘The only notion of a cause, which the theory of induction requires, Is such a notion as can be gained from experience’ (VII 326).

Comte was wrong, Mill thinks, to take the notion of cause in an exclusively metaphysical sense, and then to draw the unnecessarily paradoxical doctrine that we can know nothing of the causes of things. We do have an ordinary notion of causation, which takes the causes of phenomena to be other phenomena, and we make an indispensable distinction by means of it:

M. Comte leaves himself without any term for marking a distinction which, however incorrectly expressed, is not only real, but is one of the fundamental distinctions in science; indeed it is on this alone… that the possibility rests of framing a rigorous Canon of Induction. (VII 342)

The distinction is between a uniformity which is ‘unconditional’, and one which results from a merely fortuitous combination of circumstances; or in the terms of more recent debate, between ‘law-like’ and ‘accidental generalisations.

Mill’s lengthy discussion of causation contains a number of worthwhile advances in the analysis of the concept.⁹ We shall not pursue it in detail, but confine ourselves to those aspects of it which are needed to complete his general picture of induction.

The formula Mill comes up with to summarise his own notion of cause is, that the cause of a phenomenon is its unconditional, invariable antecedent. ‘Invariable’ can easily mislead the casual reader. The ‘invariable antecedent’ of a phenomenon is not its necessary condition. It need not be an antecedent which invariably precedes the-phenomenon. It is, rather, the antecedent which the phenomenon invariably follows; that is to say, its sufficient condition. So a cause is an unconditionally sufficient condition.

One and the same phenomenon can have more than one distinct sufficient condition; there can therefore be a plurality of causes, as Mill notes. He also notes that, as the term is ordinarily used, it does not denote the ‘assemblage of conditions’ which together constitute a sufficient antecedent of the phenomenon; rather it is used to pick out some indispensable, though on Its own insufficient, part of this assemblage. We pick out the triggering event as the cause, taking for granted the background state of affairs without which that event could not have caused that effect. We say that a man died because he ate of a particular poisoned dish (VII 327–8), omitting to mention the conditions of bodily constitution and health, state of the atmosphere and so forth, without which the eating would not have caused the death.

There is however, Mill thinks, no ‘philosophical’ reason to distinguish what is ordinarily picked out as the cause of a phenomenon from among the total assemblage of antecedents which are jointly sufficient for it. And—as one might expect, given that his objective is to analyse eliminative methods for detecting causal uniformities—he decides to use the term to denote the assemblage of conditions which jointly constitute a sufficient condition of the phenomenon, taken as a whole. (It will have to be, as Mackie (1974:62) points out, a ‘minimal sufficient condition’; no proper subset of conditions in the assemblage should be sufficient for the phenomenon.)

In this philosophical definition, the causal relation is taken to hold between types of phenomena. We do use the term in that way (‘Smoking causes cancer’), but we also often use it in a different way, to predicate a relation between events or states of affairs taken as particulars— ‘phenomenon-tokens’ rather than ‘phenomenon-types’; for example when I say that the tyre punctured because I drove over a broken bottle, or that the prime minister’s resignation caused the government’s collapse. There is no ‘phenomenon’ which is ‘invariably’ followed by that puncture: since no other puncture is that puncture.

That is no objection to Mill’s definition so long as a particular a causes a particular b if and only if there is some regularity of which that sequence is an instance; so long, one might say, as singular causal statements are always in principle ‘universalisable’. Mill thinks they are, and indeed, given his general empiricist position, he has to think so. Causal statements must be ‘universalisble’ if Causal powers are supervenient: that is to say, if an object or event has its causal powers only in virtue of properties which could always also be instantiated by other particulars. For any particular which instantiated those properties would then, in virtue of having them, also have those same causal powers. But an empiricist must hold that causal powers are supervenient. There can be no more, for him, to saying that a particular is a cause than that some inherently general description of it could in principle be found which would warrant a real inference to the existence of another particular.

Suppose then that a is a particular instance of a type of phenomenon A, and b is a particular instance of a type of phenomenon B, such that in every case in which certain other conditions, C, D and E, are instantiated, an instance of A is succeeded by an instance of B. Suppose also that there are instances of every proper subset of A, C, D and E which are not succeeded by an instance of B. If we believe that, then we have unimprovable grounds for saying that a causes b. And if we believe that a causes b, then we are committed to believing that. The ‘assemblage of conditions’ ACDE is the Millian cause of the phenomenon B.

Mill says that the cause of a phenomenon is not just the ‘invariable antecedent’, but the ‘unconditional invariable antecedent’ (iii.v.6, VII 338). He means that the assemblage of anrecedent conditions must be exhaustive. That, he thinks, is all that can properly be meant by the doctrine that causes necessitate their effects. That which is necessary, that which must be, means that which will be, whatever supposition we make in regard to all other things’ (VII 339). Hence it is strictly speaking redundant to insist that a cause is an unconditional invariable antecedent. We are justified in holding that B will succeed ACDE whatever supposition is made in regard to all other things if we are justified in supposing that the assemblage is genuinely sufficient: that there is no case in which it is instantiated and the phenomenon does not occur:

Let me add, that the antecedent which is only conditionally invariable, is not the invariable antecedent. Though a fact may, in experience, have always been followed by another fact, yet if the remainder of our experience teaches us that it might not always be so followed, or if the experience itself is such as leaves room for the possibility that the known cases may not correctly represent all possible cases, the hitherto invariable antecedent is not accounted the cause; but why? Because we are not sure that it is the invariable antecedent. (VII 340)

What we are not sure of is that the observed uniformity justifies an unconditional inference.¹⁰

The Law of Universal Causation is that ‘every event has a cause’. If causal powers are supervenient, causal statements are universalisable, and that ensures that Mill’s other version of it is also true: it is the law ‘that every event depends on some law’, or ‘that there is a law for everything’ (VII 325).

This is the basic principle which Mill needs—or rather thinks he needs —for his ‘Methods of Experimental Inquiry’.

4  The eliminative methods of induction (i)

Mill presents these ‘methods’ in iii.viii. He took considerable pride in this chapter.¹¹ Not surprisingly: the message of the System of Logic, after all, is that there is no grounding a belief except on immediate observation and inductive evidence, and the codification of the methods —was Mill’s main substantive contribution to the ‘theory of evidence’.

The methods are ‘modes of singling out from among the circum-stances which precede or follow a phenomenon, those with which it is really connected by an invariable law’ (VII 388). They are ‘methods of elimination (VII 342) because they eliminate from among possible causes all except the real one. A phenomenon is to be understood, as we have seen, not as a particular but as a type; the eliminative canons identify causal connections among types of events or states.

Two basic ingredients are involved in any eliminative reasoning. The first is a pair of assumptions:

(a) that the phenomenon under investigation (P) has a cause (or an effect),

(b) that some list of the possible causes or effects (A, B, C, D, E.) can be taken as exhaustive. (This, as we shall see, need enter in only as a working, or revisable, assumption.)

The second is a set of observations, which, within the framework provided by assumptions (a) and (b), entail that some particular one of the possible causes or effects is the actual cause or effect. We shall call (a) the causation assumption and (b) the exbaustiveness assumption.

A fully general theory of the eliminative methods needs to take systematic account of two dimensions of freedom in this framework. The first concerns the causation assumption. It will vary depending on whether one takes a ‘cause’ to be a necessary, a sufficient, or a necessary and sufficient condition. The second concerns the notion of ‘possible causes’ (or ‘possible effects’). Should we assume that the possibly causally relevant factors A, B, C, D, E, constitute possible causes (or effects) of the phenomenon only as taken positively and singly? Or may the absence of a factor also be a cause or effect of the phenomenon P? May conjunctions, or disjunctions, of possible causes (or effects) also be possible causes (or effects)? There is a definite number of ways of answering this question: in fact eight, as Mackie shows (Mackie 1974: 301–2). There are therefore three possible options in the first dimension, and eight possible options in the second; and a general theory would study ways of formulating eliminative methods in all these cases, and the relationships between them.

But Mill’s methods are formulated with a particular case in mind. This only becomes clear in a later chapter, iii.x (‘Of Plurality of Causes; and of the Intermixture of Effects’); and that fact has caused considerable confusion.

Mill allows that the absence of a condition (call this a ‘negative condition’) may be the cause or effect of a phenomenon, and he allows that the cause or effect may be neither any single one of the conditions which are possibly relevant, nor the absence of any single condition, but an ‘assemblage’ (a conjunction) of conditions, positive and negative. In this he is faithful to his view that The cause…philosophically speaking, is the sum total of the conditions, positive and negative taken together; the whole of the contingencies of every description, which being realized, the consequent invariably follows’ (VII 332).¹²

Now this definition of ‘cause’ also allows for a plurality of causes: there can be more than one sufficient condition for a given type of phenomenon. But when he states the methods in the form of ‘canons’ in iii.viii, Mill silently ignores the point. The methods, as canonically stated there, are drawn up without regard to the possibility of a plurality of causes; that is to say, on the assumption that causes are necessary and sufficient conditions. Only in iii. x does he draw explicit attention to this: ‘we have supposed that there was only one possible assemblage of conditions, from which the given effect could result’ (VII 434) and he tries to deal (less than satisfactorily) with the complications introduced by the possibility of a plurality of causes. This procedure does, as he says, have the advantage of simplifying the initial presentation of the methods. But it is patently unsatisfactory to have left the canonical formulation of the methods in its original form—which is correct only on the assumption that causes are necessary as well as sufficent conditions—if the final view is that causes need not after all be necessary.

Mill states the Method of Agreement (MA) as follows:

FIRST CANON

If two or more instances of the phenomenon under investigation have only one circumstance in common, the circumstance in which alone all the instances agree is the cause (or effect) of the given phenomenon. (VII 390)

A good way of illustrating it diagrammatically is provided by Mackie (1974) and shown in Figure 6.1.

Figure 6.1 Method of Agreement

A, B, C represent the possible causes or effects of phenomenon P. The list is assumed to be exhaustive. I1 and I₂ are two observed instances of P. In I1, A and C were instantiated (‘p’=present), and B was not (‘a’ = absent). In I₂, A and B were present, C was absent. So long as a cause is taken to be a necessary and sufficient condition, Figure 6.1 identifies A as the cause. B, C, the absence of B, of C, and of A—and all combinations involving any one of these—are all eliminated. The argument proceeds in the same way whether the investigation is into the cause or the effect of P.

The Method of Difference (MD) is stated as follows:

SECOND CANON

If an instance in which the phenomenon under investigation occurs, and an instance in which it does not occur, have every circumstance in common save one, that one occurring only in the former; the circumstance in which alone the two instances differ is the effect or the cause, or an independent part of the cause, of the phenomenon. (VII 391)

This is illustrated by Figure 6.2, where I1 indicates a positive instance of the phenomenon, that is, one in which it is observed to be present, and N indicates a negative instance, one in which it is observed to be absent. Then B, C, the absence of A, of B, of C, and any combination made up exclusively of these is eliminated. Figure 6.2 proves that A is a cause or effect of P—or an ‘independent part of the cause’. For granting that the cause of P may be an assemblage of conditions, it remains perfectly possible that the cause of P is the joint presence of A and B, or the joint presence of A and absence of C.

Figure 6.2 Method of Difference

Next comes what Mill calls the Joint Method of Agreement and Difference. He states it thus:

THIRD CANON

If two or more instances in which the phenomenon occurs have only one circumstance in common, while two or more instances in which it does not occur have nothing in common save the absence of that circumstance; the circumstance in which alone the two sets of instances differ, is the effect, or the cause, or an indispensable part of the cause, of the phenomenon. (VII 396)

Here ‘the circumstance in which alone the two sets of instances differ’ is clearly to be understood as the circumstance which alone is present in all the positive instances, and absent in all the negative instances. Thus understood the method is illustrated in Figure 6.3.

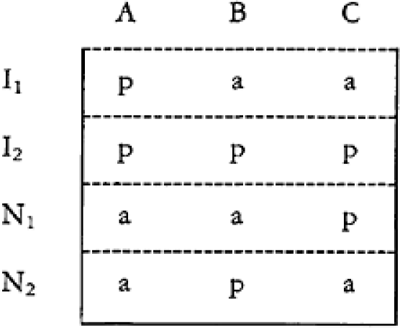
Figure 6.3 Joint Method of Agreement and Difference

But as Figure 6.3 shows, the method, so understood, is redundant. Given Mill’s formulation of the Third Canon, the positive instances alone must always suffice to show that one circumstance—in this case A —is the cause, by MA alone. Notice also that if the negative instances ‘have nothing in common save the absence of that circumstance’ then they alone eliminate every other circumstance—in this case, B, C, and the absence of A, of B, and of C—though they do not on their own exclude assemblages of these circumstances, such as BC. They do this by a form of agreement reasoning in which negative instances are compared in order to isolate the circumstance which is absent—Mackie (ibid., p. 303) calls it the ‘negative method of agreement’. That may be why Mill also describes this method as a ‘double employment of the Method of Agreement’ (VII 395).

But if no difference reasoning is involved at all, why does Mill call it the Joint Method of Agreement and Difference; and why does he also say that it can be called the ‘Indirect Method of Difference’? And why does he feel the need to introduce the qualification ‘…or an indispensable part of the cause’ in his statement of the canon?

The Third Canon, we have assumed, requires that only one circumstance is present in all the positive instances, and absent in all the negative instances. Now this may not identify that circumstance even as an indispensable part of the cause by the Method of Difference, since there may be no pair of positive and negative instances which have every other circumstance in common—there is not in Figure 6.3. It may not identify it as an indispensable part of the cause at all, because the cause may be an assemblage of circumstances in which it is not included. But if we rule out this last possibility, then the circumstance will have been identified as an essential part of the cause, and by what is essentially difference reasoning. Consider Figure 6.4.

Figure 6.4 Indirect Method of Difference

Here we can isolate A as the cause, or an indispensable part of the cause, by what is essentially difference reasoning: but no single pair of positive and negative instances drawn from the table suffices for that conclusion, nor does any application of the positive or negative method of agreement. This fits Mill’s description of what his Joint Method is intended to do: namely, to describe a way of applying difference reasoning where no direct use of the Method of Difference is possible, because the necessary pairs of positive and negative observations, matched in all but one factor, cannot be isolated. And it explains the presence of the restrictive clause (‘an indispensable part of the cause’).

Thus instead of Mill’s redundant ‘double employment of the Method of Agreement’ we might formulate the true Indirect Method of Difference as follows:

AMENDED THIRD CANON

If two or more instances in which a phenomenon occurs have a circumstance in common, while in two or more instances in which the phenomenon does not occur that circumstance is absent, and if there is no other circumstance or combination of circumstances which is present in all the instances in which the phenomenon occurs, and absent in all the instances in which it does not occur, then the given circumstance is the effect, or the cause, or an indispensable part of the cause, of the phenomenon.

(Notice that a combination of circumstances may be absent in more than one way: for example in the case AB, A might be absent in one case and B in another. Therefore AB might be present in all cases in which P is, and absent in all cases in which P is, even though the same does not hold individually of A or of B.)

I shall now state Mill’s two remaining ‘methods’, the Method of Residues, and the Method of Concomitant Variations, and make some main points about them, without discussing them in detail. Neither of them is on all fours with the basic methods of agreement and difference reasoning covered so far.

The Method of Residues:

FOURTH CANON

Subduct from any phenomenon such part as is known by previous inductions to be the effect of certain antecedents, and the residue of the phenomenon is the effect of the remaining antecedents. (VII 398)

And the Method of Concomitant Variations:

FIFTH CANON

Whatever phenomenon varies in any manner whenever another phenomenon varies in some particular manner, is either a cause or an effect of that phenomenon, or is connected with it through some fact of causation. (VII 401)

Mill says that the ‘Method of Residues is in truth a peculiar modification of the Method of Difference’ (VII 397). He explains the idea as follows. Suppose it is independently known that the phenomenon P! is the only effect of factor A taken on its own, and the phenomenon P₂ is the only effect of factor B taken on its own. And suppose that an instance of the complex phenomenon P1P2P3 is observed to occur when ABC occurs—these being the only possibly relevant causal factors of the complex phenomenon. We can then infer that P3 is caused by C, even if we are unable to observe the appropriate negative instance: that is to say, an instance in which P3 and C do not occur and A and B do occur. Strictly speaking, however, we need also to be able to rule out the possibility that C results from the combination of A and B. And even if that is discounted, we can infer only that C is an indispensable part of the cause of P₂, since we are proceeding by what is, in effect, difference reasoning on a postulated negative instance.

The fifth canon is very loosely stated. (Mill should at least have added: ‘all other circumstances remaining constant’.) It does no more than gesture at a whole new field of analysis brought in when we take into account the notion of functional causal dependence.¹³ ‘Functional’ variants can be stated for all three basic forms of agreement and difference reasoning. (Thus: joint non-variation of cause and effect against a varying background, joint variation of cause and effect against a constant background, joint variation and joint non-variation of cause and effect against suitably staged backgrounds of variation or non-variation among independent possible causes.) Given appropriate assumptions such methods can eliminatively identify variables on which a phenomenon functionally depends, or which functionally depend on it, and they can suggest the form of the function by identifying points onto which one can fit a curve.

5  The eliminative methods of induction (ii)

Before turning to consider how the eliminative canons fit into Mill’s general picture of induction, we must note some important weaknesses in his discussion.

There are two basic forms of eliminative reasoning: agreement and difference reasoning. Agreement reasoning isolates the single common factor present in two or more instances in which the phenomenon occurs. Or it could isolate the single common factor absent in two or more cases in which the phenomenon does not occur. Difference reasoning isolates the single common factor which is present whenever the phenomenon is present, and absent whenever the phenomenon is absent. On these basic elements more complicated variations, combining the two methods, can be built. Some of the instances may be ‘constructed’ from what is known by previous observations, and the instances may be instances of a joint variation.

For Mill a cause is an unconditionally sufficient condition. That means that a phenomenon can have a plurality of causes; but we have seen that Mill’s statement of the canons in iii.viii assumes that there is no such plurality.

When that assumption is relaxed the Method of Agreement turns out, he says in iii.x.2, to have a ‘characteristic imperfection’. That, to say the least, is an understatement. For when the restriction is lifted, the Method of Agreement simply ceases to be a method of identifying causes by elimination at all. Figure 6.1 does not then show that A is a cause of P. True, if one can assume that one of the circumstances A, B, C is a necessary condition of P, then it does indeed eliminatively demonstrate A to be that necessary condition. And given that causes are sufficient conditions of effects, effects must be necessary conditions of causes. Thus if A, B, C are taken to be possible effects of P, then Figure 6.1 does serve to identify A as the effect. But there is nothing in Mill’s analysis of causation to show that a phenomenon must have a causally necessary antecedent.

So Mill was wrong to leave the First Canon as it stood, once he had allowed for plurality of causes. He should at least have explicitly restricted its formulation to the detection of effects—even better, he should have thoroughly reviewed the use of eliminative agreement reasoning under conditions in which plurality of causes is allowed.

Why did he not do so? Because in his comments on MA (not in the statement of the canon itself) he systematically mixes up the eliminative Method of Agreement with a quite different principle of reasoning— that of enumerative induction from instances observed under widely differing conditions. In the latter case, we observe a number of instances of A, all followed by instances of P, and no instances which are not so followed. We infer by EI that all As are followed by Ps. The observed cases otherwise differ among each other in all prima facie relevant circumstances, and so we take it that A causes P. And as is characteristic of enumerative inductions, this conclusion becomes more plausible, the greater the number and variety of cases considered.

The confusion is evident in iii.viii.3 and iii.x.2 (especially at VII 436–7). Mill says he is comparing the Methods of Agreement and Difference, but what he in fact compares is enumerative induction under varying conditions with the Method of Difference.¹⁴ Once one has noticed that a good deal of what he says makes sense; in particular his favourable estimate of the greater power of MD over what he refers to as the Method of Agreement but is in fact EI under varied conditions. It is for example quite natural to suggest as Mill does that the ‘Method of Agreement’, considered as an enumerative induction, is best suited for suggesting possible causes of a phenomenon—these suggestions being more rigorously tested by MD.

Mill is perfectly aware that any listing of possible causes for purposes of eliminative reasoning is always provisional. Now in principle the implications for MA and MD are completely symmetrical: the conclusion of MA may fail because common circumstances which were unnoticed or considered irrelevant were not in fact so; the conclusion of MD may fail because relevantly differing circumstances were unnoticed or considered irrelevant. But Mill does not apply the point symmetrically: he applies it to enumerative induction, and eliminative difference reasoning. The implication for the first is that the putatively sufficient condition may not be unconditionally significant: the observed uniformity may be an accidental rather than a causal one, because some other unremarked circumstance common to all occurrences of P is the real cause. The implication for MD is that the elimination may fail: but as Mill says, the possibility of an unnoticed variation can be very greatly reduced in an experimental as against a purely observational situation. When, in a laboratory experiment, a possible cause is introduced by the experimenter into an environment which is carefully controlled to be otherwise invariant, the grounds for thinking that no other relevant circumstance is involved may be very good, There is then no need for a listing of possible causes, and an assumption that the list is exhaustive, The only assumption is that the phenomenon has a cause. MD is therefore particularly suited, as Mill suggests, to inquiries where experiment is possible.

We will now consider how Mill sees the role of the eliminative canons in inductive reasoning; this will lead us back to wider philosophical questions.

6  The place of the eliminative methods in M.ill’s inductive logic

The Methods of Experimental Inquiry are eliminative in that they demonstratively narrow down the possible causes (or effects) of a phenomenon to one—given the presence of appropriate causation and exhaustiveness assumptions.

But on this point Mill is too often over-ambitious and over-simple. He likes to present the following scenario. The causation assumption involved in every piece of eliminative reasoning—that the phenomenon under investigation has a cause—is deduced from the Law of Universal Causation (UC) (for example VII 562), and therefore has whatever certainty that law has. UC is established by enumerative induction. Now in Mill’s opinion certain very wide-ranging kinds of enumerative induction can approach certainty, or be practically certain, just because they span every domain; and the induction by which UC is established is an induction of this kind. UC is therefore practically certain. This certainty is transmitted to the causation assumption involved in every eliminative induction, and thence to conclusions derived by eliminative induction (cf. for example System VII 322; Comte X 293).

But the certainty of UC (and of the observations on which an eliminative induction is based) is transmitted to its conclusion only if the relevant exhaustiveness assumption is certain. In practice, Mill is well aware that such an assumption is always needed; he is conscious of the difficulties which are often involved in analysing the antecedents of a phenomenon into ‘possible causes’; he realises that such an analysis, together with the assumption that all relevant factors have been taken into account, is, in its early stages at least, inevitably provisional. But in programmatic utterances he ignores all this. And in a treatise which proposes to give a systematic epistemological survey of the nature and standing of inductive reasoning that is a serious fault.

A related point is raised by Whewell in his criticism of the methods:

Upon these methods, the obvious thing to remark is, that they take for granted the very thing which is most difficult to discover, the reduction of the phenomena to formulae such as are here presented to us. (Quoted by Mill, VII 429, from Whewell 1860:263)

Mill replies by comparing the Methods of Experimental Inquiry to the syllogistic forms. In both cases, finding a proof is one thing, ‘reducing it to a form which tests its conclusiveness’ is another. ‘But if we try to reduce it without knowing what it is to be reduced to, we are not likely to make much progress’ (VII 430). The business of Inductive Logic is to provide rules and models…to which if inductive arguments conform, those arguments are conclusive, and not otherwise’ (VII 430). The canons, Mill reasonably thinks, do codify ‘methods of discovery’ which are constantly used, and an inquirer is helped to the discovery of truths if he is consciously aware of them. But however that may be, they are in any case ‘methods of proof; they provide rules by which the value of the evidence provided for a conclusion can be tested, however that conclusion was arrived at.

This is sound doctrine. It remains the case, however, that a piece of eliminative reasoning, considered as an inductive proof, is only as strong as its exhaustiveness assumption can make it. What kind of evidence for the exhaustiveness assumption in an eliminative induction can be had, and how strong can it be? Mill’s relevant thoughts on this are contained in iii.vii (‘Of Observation and Experiment’) and in Book iv (‘Of Operations Subsidiary to Induction’).

Chapter iii.vii is a preliminary to iii.viii in which the eliminative canons are expounded; in it Mill notes the difficulties of performing the ‘mental analysis of complex phenomena’ which is presupposed in any application of the EMs:

the extent and minuteness of observation which may be requisite, and the degree of decomposition to which it may be necessary to carry the mental analysis, depends on the particular purpose in view. To ascertain the state of the whole universe at any particular moment is impossible, but would also be useless. In making chemical experiments, we do not think it necessary to note the position of the planets; because experience has shown, as a very superficial experience is sufficient to show, that in such cases that circumstance is not material to the result: and accordingly, in the ages when men believed in the occult influence of the heavenly bodies, it might have been unphilosophical to omit ascertaining the precise condition of those bodies at the moment of the experiment…. We have done enough when we have carried the subdivision as far as the point at which we are able to see what observations or experiments we require. It is only essential, at whatever point our mental decomposition of facts may for the present have stopped, that we should hold ourselves ready and able to carry it further as occasion requires, and should not allow the freedom of our discriminating faculty to be imprisoned by the swathes and bands of ordinary classification. (VII 380–1)

Our analysis always starts from received classifications and assumptions. It is these which initially determine how the ‘causal field’—the network of phenomena to be considered as forming a system of possible causes and effects for the purpose of eliminative inquiry—is separated from a background of phenomena which are deemed irrelevant. (Notice that once the causal field has been isolated, agreement reasoning need assume only that instances have just one ‘circumstance’ in common within that field, and difference reasoning need only assume that no feature within the causal field other than the singled out circumstance is present in the positive instance and absent in the negative one.) The classifications and assumptions which enter into a piece of eliminative reasoning are themselves products of experience; and though the analysis starts from them, it must be prepared where necessary to reject them or go beyond them.

So ‘mental analysis’ of phenomena, and hence the exhaustiveness assumption involved in eliminative reasoning, is neither presuppositionless nor final. It is based on an existing state of belief and remains provisional.

But what makes us decide that the provisional analysis has to be revised? Only the failure of eliminative inquiry to advance, on the basis of that provisional analysis, to a stable system of unrefuted causal laws. By the same token, if an eliminative inquiry, conducted on that basis, does succeed in establishing causal laws which remain unrefuted, and are incorporated into the fabric of belief, then confidence in the adequacy of the analysis is retroactively strengthened.

The other assumption involved in any piece of eliminative reasoning is the causation assumption. Obviously the Law of Universal Causation is not strictly required for eliminative reasoning to be possible within a restricted field; even if not all departments or regions of nature are deterministic, or if nature is not deterministic ‘all the way down’, there might still be levels or aspects of the phenomena which were so.

Again Mill was aware of the point. But he believed the Law of Universal Causation to be true—he wrote with a Laplacian confidence in the classical Newtonian synthesis. And he believed that it had a special degree of certainty deriving from its grounding in an enumerative induction spanning an unrestricted domain.

The theme is developed in iii.xxi.3–4. As the subject matter of the observations on which EI is based becomes less and less ‘special and limited in extent’, so

this unscientific method becomes less and less liable to mislead; and the most universal class of truths, the law of causation for instance, and the principles of number and geometry, are duly and satisfactorily proved by that method alone, nor are they susceptible of any other proof….

EI is fallible because a uniformity suggested by it may

be a consequence of collocations, which cannot be concluded to exist in one place because they exist in another; or may be dependent on the accidental absence of counteracting agencies, which any variation of time, or the smallest change of circumstances, may possibly bring into play. (VII 569)

But these possibilities are increasingly ruled out as the observations on which EIs are based are varied in time, place and circumstance, as in the case of the laws of number and geometry.

These points are worth making, and they help to make it clear that an enumerative induction to the Law of Universal Causation can have considerable force. But they certainly do not show that the law could, purely on that basis, be regarded as certain or conclusive; nor are Mill’s reasons for holding it to be so, ‘within the possible range of our experience’, convincing, though they are ingeniously stated (iii.xii.4).

His eagerness, as champion of ‘the inductive philosophy’, to stress the certainty and conclusiveness of ‘scientific’ —that is, eliminative— methods of induction betrays him. He treats the flow of justification from UC to the causation assumption involved in any eliminative reasoning as though it was exclusively one-directional. But just as the exhaustiveness assumption gains support retroactively from the success of the eliminative inductions based on it, so does the causation assumption, and thus in turn, the Law of Universal Causation.

In practice Mill appreciates the point; but he needed to step back and state it with full emphasis and generality. That there is give and take between particular inductions, enumerative and eliminative, and the law of causality he explicitly sees:

if we consider, not what mankind would have been justified in believing in the infancy of their knowledge, but what may rationally be believed in its present more advanced state, we shall find ourselves warranted in considering this fundamental law, though itself obtained by induction from particular laws of causation, as not less certain, but on the contrary, more so, than any of those from which it was drawn. It adds to them as much proof as it received from them. For there is probably no one even of the best established laws of causation which is not sometimes counteracted, and to which, therefore, apparent exceptions do not present themselves, which would have necessarily and justly shaken the confidence of mankind in the universality of those laws, if inductive processes founded on the universal law had not enabled us to refer those exceptions to the agency of counteracting causes, and thereby reconcile them with the law with which they apparently conflict. (VII 570)

Causal correlations are obtained in rough-hewn form by processes of enumerative induction; a further second-order enumerative induction suggests the universality of causation; the eliminative methods of induction based on this assumption are then successfully applied to the job of refining and delimiting the original rough-hewn generalisations. By showing how exceptions to these rough generalisations fall into place within an underlying and more exact system of uniformities, they strengthen our confidence in the law of causality on which they depend. At that stage,

The law of cause and effect…is capable of imparting its certainty to all other inductive propositions which can be deduced from it; and the narrower inductions may be regarded as receiving their ultimate sanction from that law, since there is no one of them which is not rendered more certain than it was before, when we are able to connect it with that larger induction, and to show that it cannot be denied, consistently with the law that everything which begins to exist has a cause. And hence we are justified in the seeming inconsistency, of holding induction by simple enumeration to be good for proving this general truth, the foundation of scientific induction, and yet refusing to rely on it for any of the narrower inductions. (VII 571)

It must be accepted, then, that Mill’s programmatic utterances about induction present an over-simple picture. It takes the flow of justification from EI via UC to the EMs as being one-directional, and it seems to assume that the classification of possible causes is somehow given in the phenomena. This ‘epistemological atomism’ is most in evidence where Mill is over-anxious to defend the value of his ‘inductive logic’ against aprioristic critics.

But this is merely programmatic. Underlying it is a coherentism which emerges clearly, for example, in the following passage from the Examination.

We are constantly told that the uniformity of the course of nature cannot itself be an induction, since every inductive reasoning assumes it, and the premise must have been known before the conclusion. Those who argue in this manner can never have directed their attention to the continual process of giving and taking, in respect of certainty, which reciprocally goes on between this great premise and the narrower truths of experience; the effect of which is, that, though originally a generalization from the more obvious of the narrower truths, it ends by having a fulness of certainty which overflows upon these, and raises the proof of them to a higher level…. (IX 482, note)

The passage occurs in the Examination in a context in which Mill is stressing the epistemological importance of the highly deductive and mathematical structure of scientific knowledge; a point he also makes in the System:

It may be affirmed as a general principle, that all inductions, whether strong or weak, which can be connected by ratiocination, are confirmatory of one another; while any which lead deductively to consequences that are incompatible, become mutually each other’s test, showing that one or other must be given up, or at least more guardedly expressed. In the case of inductions which confirm each other, the one which becomes a conclusion from ratiocination rises to at least the level of certainty of the weakest of those from which it was deduced; while in general all are more or less increased in certainty. (VII 321–2)

When Mill writes in this vein his conception of the ‘inductive process’ can be seen to stand in a line of development of which the naturalistic pragmatism of Quine is a further stage. Inductive inquiry modifies, revises and extends a given fabric of belief. It involves a virtuous circle, in which provisional assumptions are repeatedly revised, more fully confirmed, and thus continually rise in their degree of ‘certainty’.

Between Mill and the pragmatist naturalism which has increasingly dominated philosophy in this century, stand two important differences. One of them is to a considerable extent a matter of emphasis and tone, but none the less important: it is the contrast between Mill’s nineteenth-century rhetoric of inductive certainty and the twentieth-century rhetoric of fallibilism. Behind that rhetoric, as we have seen, the substantive differences are smaller than they at first appear. But there is, nevertheless, a vital substantive difference between Mill on the one hand and Peirce or Quine on the other: it turns on whether the ‘Hypothetical Method’ can be accepted as a part of the logic of truth. We come to this in 6.8. But we must first consider at greater length something which Mill and this twentieth-century naturalistic standpoint have in common: their attitude to philosphical scepticism.

7  Inductive scepticism and the internal validation of induction

The inductive process is cumulative, provisional and self-correcting. The gradually emerging organisation of detailed inductions into an ordered scientific scheme justifiably raises our confidence in the generalisations arrived at by these detailed inductions—and in inductive methods of reasoning as such. This is an a posteriori vindication of induction: it is because the world is as it is that induction cumulates into a system of generalisations. Precisely because inductive methods might have turned out to be self-undermining, it makes a genuine epistemological difference that they have in fact turned out to be self-supporting.

This naturalistic validation of inductive reasoning is ‘internal’: it provides no reply to pure scepticism about induction, nor is it intended to do so. The point has not always been clear, but it was clear enough to Mill. All the characteristic features of ‘naturalised epistemology’ are forcefully presented in the pages of the System of Logic. This point is, I think, worth documenting in some detail.

Consider the following passage (iii.iv.2, ‘Scientific inductions must be grounded on previous spontaneous inductions’):

the most scientific proceeding can be no more than an improved form of that which was primitively pursued by the human understanding, while undirected by science. When mankind first formed the idea of studying phenomena according to a stricter and surer method than that which they had in the first instance adopted, they did not, conformably to the well-meant but impracticable precept of Descartes, set out from the supposition that nothing had been already ascertained. Many of the uniformities existing among phenomena are so constant, and so open to observation, as to force themselves upon involuntary recognition…. No science was needed to teach that food nourishes, that water drowns, or quenches thirst, that the sun gives light and heat, that bodies fall to the ground. The first scientific inquirers assumed these and the like as known truths, and set out from them to discover others which were unknown: nor were they wrong in so doing, subject, however, as they afterwards began to see, to an ulterior revision of these spontaneous generalizations themselves, when the progress of knowledge pointed out limits to them, or showed their truth to be contingent on some circumstance not originally attended to. It will appear, I think, from the subsequent part of our inquiry, that there is no logical fallacy in this mode of proceeding; but we may see already that any other mode is rigorously impracticable: since it is impossible to frame any scientific mode of induction, or test of the correctness of inductions, unless on the hypothesis that some inductions deserving of reliance have been already made.

Let us revert, for instance, to one of our former illustrations, and consider why it is that, with exactly the same amount of evidence, both negative and positive, we did not reject the assertion that there are black swans, while we should refuse credence to any testimony which asserted that there were men wearing their heads underneath their shoulders. The first assertion was more credible than the latter. But why more credible? So long as neither phenomenon had been actually witnessed, what reason was there for finding the one harder to be believed than the other? Apparently because there is less constancy in the colours of animals, than in the general structure of their anatomy. But how do we know this? Doubtless, from experience. It appears, then, that we need experience to inform us, in what degree, and in what cases, or sorts of cases, experience is to be relied on. Experience must be consulted in order to learn from it under what circumstances arguments from it will be valid. We have no ulterior test to which we subject experience in general; but we make experience its own test. Experience testifies, that among the uniformities which it exhibits or seems to exhibit, some are more to be relied on than others; and uniformity, therefore, may be presumed, from any given number of instances, with a greater degree of assurance, in proportion as the case belongs to a class in which the uniformities have hitherto been found more uniform.

This mode of correcting one generalization by means of another, a narrow generalization by a wider, which common sense suggests and adopts in practice, is the real type of scientific Induction. All that art can do is but to give accuracy and precision to this process, and adapt it to all varieties of cases, without any essential alteration to its principle. (VII 318–19)

The contrast between Cartesian, pure epistemology, which sets out from the supposition that nothing has been already ascertained, and the naturalistic project, which takes ‘spontaneous’ processes of reasoning for granted, and aspires only to sharpen them against their own results, could not be more clearly drawn. For the pure inquirer, the world given in experience is a ‘spectacle’; his problem is to find some point of entry into it. Naturalised epistemology takes for granted our position within the world, and the reliability of our basic perceptual and inferential reactions to it. Scientific, ‘artificial’ methods of reasoning—the eliminative canons —are grounded on spontaneous, ‘inartificial’ enumerative inductions: in terms of Mill’s psychological framework, these are reasonings which directly manifest the basic associative processes of cognition.¹⁵ The inquirer is faced not with a spectacle but with a ‘predicament’; that of improving, revising and enlarging existing methods and beliefs.

An internal validation of the inductive process by the fact of its success in producing a comprehensive and coherent system of generalisations presupposes, however, that enumerative induction is accepted, ab initio, as sound:

Assuredly, if induction by simple enumeration were an invalid process, no process grounded on it would be valid; just as no reliance could be placed on telescopes, if we could not trust our eyes. But though a valid process, it is a fallible one, and fallible in very different degrees: if therefore we can substitute for the more fallible forms of the process, an operation grounded on the same process in a less fallible form, we shall have effected a very material improvement. And this is what scientific induction does.

A mode of concluding from experience must be pronounced untrustworthy, when subsequent experience refuses to confirm it. According to this criterion, induction by simple enumeration… affords in general a precarious and unsafe ground of assurance…. Still, however, it affords some assurance, sufficient, in many cases, for the ordinary guidance of conduct. (VII 567–8)

These passages exhibit all the three ingredients of naturalised epistemology which we highlighted in 1.2. There is the appeal to natural or ‘spontaneous’ reasoning processes, which are simply accepted as sound. There is the codification and internal validation of these reasoning processes: Mill’s analysis of induction seeks only to show how (if nature obliges) the fallible process of enumerative reasoning can give rise to methods which are less fallible and more searching.

And finally there is the avoidance of pure sceptical arguments. But it is time to consider this last ingredient more closely. What is it that Mill ignores?

Consider first the following point. I judge how much confidence to place in the conclusion of an enumerative induction according to its subject matter. Thus formally equivalent enumerative inductions may support their conclusions to different degrees. But my assessment of the reliability of an induction itself rests on a background of generalisations derived from experience—generalisations about the degree of uniformity to be expected in the domain with which the induction is concerned. We have seen Mill making the point (‘It appears, then, that we need experience to inform us, in what degree, and in what cases, or sorts of cases, experience is to be relied on. Experience must be consulted in order to learn from it under what circumstances arguments from it will be valid. We have no ulterior test to which we subject experience in general; but we make experience its own test’). But if those background generalisations themselves rest on enumerative inductions, as in Mill’s picture they ultimately must, we seem to have a vicious circle. We cannot judge the reliability of any induction without a background of knowledge derived from experience, but we cannot attain any such background of knowledge without being able to rely on induction.

This argument, however, rests on a subtle mistake. It is true that our confidence in an enumerative induction must respond to our background knowledge of the degree of general regularity in the domain with which that induction is concerned. But it does not follow that, if we have no such background knowledge at all, our confidence in the induction must equal zero.

For an empiricist, the judgement that an observed regularity is significant—that it warrants generalisation into a habit of inference— cannot be about some independent fact over and above facts about uniformities. We base habits of inference on observed correlations, with a confidence proportionate to the number of observed confirming instances—subject, however, to diminution or augmentation of that confidence by collateral information. Collateral information can raise our confidence, but it can also diminish it towards zero. But in the absence of any collateral information, all EIs are of equal, and positive, worth: any observed correlation, irrespective of subject matter, generates a habit of inference to a degree proportionate to the number of confirming instances and the variety of circumstances in which they are observed.¹⁶

It generates it—and it justifies it. In this specific sense, Mill takes it for granted that induction is—‘at square one’—a rational process. A philosophical sceptic will question precisely that. What, he will ask, is the status of this proposition—that induction is rational? Is it verbal, or is it real? Is it a priori or a posteriori? How is the fact that people do reason in this way supposed to justify the claim that it is reasonable to do so? The question is legitimate, and it requires an answer.

It should not be confused with the illegitimate notion that induction can be justified only by turning it into deduction On the contrary, Mill Epistemologically, the basic process is induction. But then the simple sees that there is a question about the epistemological basis of deduction. and fundamental question still remains—the question of the status of the proposition, ‘induction is rational’. Only one answer, it seems, is possible. It must be a real but a priori proposition. So in that narrowed-down sense Kant is right. But can we return Kant’s answer without resorting to his transcendental idealism? Can we square it with the naturalistic perspective, given the ‘master-inference’ (1.2) from naturalism to strict empiricism, that is, to the conclusion that all real propositions are a posteriori?

The key lies in recognising that a proposition may be a priori and yet in principle revisable. It may be reasonable to accept it prior to experience but no longer reasonable to do so after certain experiences. Yet such a conception of the a priori is not immediately intelligible. In fact it can only make sense against the background of a distinctive and unobvious account of understanding and meaning—the ‘epistemic conception’ which will be described in 7.4. We are then led to ask whether the epistemic conception is coherent—and if it is coherent, whether it can be squared with naturalism, or is itself a new form of transcendental idealism.

I believe that the epistemic conception is not only consistent with naturalism but is the inevitable upshot of a rigorously naturalistic analysis of reasoning. Now we cannot follow through these issues, concerning the contrast between the epistemic and the classical conception of meaning, in a study of Mill’s philosophy—they lie well outside the terms of philosophical debate that were available to him, and it would be anachronistic to give the impression that he himself could or should have raised them. On the other hand, we shall at least have to outline them, and relate them to the Kantian question of how real a priori propositions are possible, if we wish to make any estimate of what the present prospects of Millian naturalism are—or even if we wish to gain some sense of the questions which would have to be considered in making such an estimate. We do so in 7.4. For the moment we must leave the question and turn to the subject of hypotheses. As we study the sources of Mill’s inductivism we shall find ourselves being led back to it.

8  Hypotheses¹⁷

Eliminative reasoning is a ubiquitous feature of the inquiry into causes. In cases as utterly different as the search for the causes of a child’s allergy, and of the emergence of philosophy in archaic Greece (using the Phoenician city states as a contrast case) the very same methods of agreement and difference come into play.

Mill’s detailed exposition of the canons is garbled and inaccurate, but that is less important than what he did do. He showed how elegant and effective eliminative reasoning can be when conducted deliberately. His picture of the interplay between enumerative and eliminative reasoning, and of the way in which the overall success of the inductive process entrenches our rational confidence in its methods, is original and philosophically penetrating.

There is however one essential element missing from this picture, which diminishes its philosophical force: a proper recognition of what Mill calls the ‘Hypothetical Method’—or the ‘inference to the best explanation’, as it is often called. The form of this method of inductive reasoning can be characterised thus:

Phenomena P_1, …, P_n are observed.

P1, …, P_n would be explicable if H were true.

________________________________

There is reason to think that H is true.

Scientific practice attests its pervasiveness. Having read Whewell’s History of the Inductive Sciences, Mill could hardly fail to be aware of that. What he fails to recognise is not the fact of hypothetical reasoning but its epistemological significance. He was unable to accept that the Hypothetical Method is an autonomous method of induction—that it is an independent and primitive principle of the ‘Logic of Truth’.

This was the crucial issue at stake in the debate between Mill and Whewell. Mill was happy to recognise the heuristic value of hypotheses in suggesting ideas—which could then be inductively confirmed by methods which were genuinely fundamental principles of inductive logic. But he denied that the Hypochetical Method constituted, in its own right, a method of arriving at new truths from experience. He could not have accepted the premises in the above schema as constituting in themselves a reason for accepting the conclusion that H is true.

Whewell argued that hypothetical reasoning was the basic method of induction, and he did so by appealing to the actual practice of scientific reasoning, as observed in the history of science.¹⁸ Now an appeal of that kind was precisely what Mill, on his own principles, could not ignore. It was, after all, his own conviction that ‘Principles of Evidence and Theories of Method are not to be constructed a priori. The laws of our rational faculty, like those of every other natural agency, are only learnt by seeing the agent at work’ (VII 833).

Yet Mill resolutely refuses to shift from recognising that hypotheses are in fact a normal part of scientific inquiry to the epistemological conclusion which one might expect, given this methodological stance: the conclusion that hypothetical inference—inference to the best explanation—is an autonomous principle of reasoning in the logic of truth. The refusal has far-reaching consequences for his philosophy. Its immediate consequence is the positivist doctrine of the ‘phenomenal relativity of knowledge’. Through that it becomes the crucial stumbling block for his naturalism.

We shall examine in the next chapter the tensions involved in combining positivism with a naturalistic view of mind. But Mill’s inductivism is far from being an arbitrary stance., Naturalised epistemology, it is true, appeals to methods we naturally agree on: but it appeals to them as purified and systematised by critical reflection. It Is perfectly legitimate for Mill to reject some of the principles of reasoning which we naturally and spontaneously accept by appealing to arguments based on other principles which are equally natural.

There are weaknesses in Mill’s polemic against Whewell. Yet the essential point underlying his refusal to accredit hypothetical reasoning as part of the logic of truth is a powerful one. It is the familiar posslbility that a body of data may be explained equally well by a plurality of hypotheses. What justifies us in concluding, from the fact that a particular story would, if true, explain the data, that it is a true story? Other stories may equally explain the data.

Before we assess this challenge we must consider Mill’s analysis of hypothetical reasoning in more detail. He explains what he means by a hypothesis at VII 490:

An hypothesis is any supposition which we make (either without actual evidence, or on evidence avowedly insufficient) in order to endeavour to deduce from it conclusions in accordance with facts which are known to be real; under the idea that if the conclusions to which the hypothesis leads are known truths, the hypothesis itself either must be, or at least is likely to be, true…. Since explaining, in the scientific sense, means resolving an uniformity which is not a law of causation, into the laws of causation from which it results, or a complex law of causation into simpler and more general ones from which it is capable of being deductively inferred; if there do not exist any known laws which fulfil this requirement, we may feign or imagine some which would fulfil it; and this is making an hypothesis.

We have seen that Mill is no ‘naïve’ inductivist. He is far from conceiving of science as a series of mechanical and disconnected generalisations from experience. He places great emphasis on the increasingly deductive and mathematical organisation of science, and on the epistemological importance of that fact:

A revolution is peaceably and progressively effecting itself in philosophy, the reverse of that to which Bacon has attached his name…. That great man changed the method of the sciences from deductive to experimental, and it is now rapidly reverting from experimental to deductive. But the deductions which Bacon abolished were from premises hastily snatched up, or arbitrarily assumed. The principles were neither established by legitimate canons of experimental inquiry, nor the results tested by that indispensable element of a rational Deductive Method, verification by specific experience. (VII 482)

This may overestimate Bacon’s influence on seventeenth-century science and underestimate the degree to which modern science was mathematical and deductive from its Galilean beginnings; however that may be, one cannot accuse Mill of underestimating the importance of the ‘Deductive Method’. But he takes it to involve three steps: ‘induction’, ‘ratiocination’ and ‘verification’. A paradigm, in his view, is Newton’s explanation of Kepler’s laws of planetary motion. Induction establishes causal laws of motion and attraction, ratiocination deduces lower-level regularities from them in. conjunction with observed conditions, and verification tests these deduced propositions against observation. (Mill gives a detailed analysis of Newton’s reasoning in these terms at iii.xiv.4.) The logical order may well not coincide with the actual sequence of inquiry—it did not in this case—but ‘Not one of these three parts of the process can be dispensed with’ (VII 491).

Now ‘the Hypothetical Method suppresses the first of the three steps, the induction to ascertain the law; and contents itself with the other two operations, ratiocination and verification; the law which is reasoned from being assumed, instead of proved’ (VII 492). Mill accepts that there are cases in which it is legitimate to suppress induction as a step separate from verification—those in which the hypothesis in question can be shown to be the only one consistent with the facts. For then, he thinks, the induction is in effect present after all: it is a form of difference reasoning involving the method of residues. (The idea is that the actual deduction and verification provide the positive instance, and the argument, whatever it may be, for holding that no other hypothesis is consistent with the facts, must be sufficient to supply a constructed version of the negative instance.)

But when can alternative hypotheses be eliminated? Mill appeals to an interesting distinction between two kinds of hypothesis. Hypotheses of the first kind seek to explain a phenomenon by reference to causes whose existence is known or ascertainable; what is hypothesised is the law by which these are related to their effect (for example the law of planetary central force). Hypotheses of the second kind, in contrast, explain a phenomenon by postulating causes for it which are not directly knowable, but which are assumed to act by analogy with observable processes whose form is already known. Mill cites Descartes’ vortices, and the hypothesis that light is propagated through a luminiferous ether.

‘An hypothesis being a mere supposition’ there is no reason why we should not postulate both unknown causes and unknown laws; but since such a hypothesis

would not supply the want which arbitrary hypotheses are generally invented to satisfy, by enabling the imagination to represent to itself an obscure phenomenon in a familiar light; there is probably no hypothesis in the history of science in which both the agent itself and the law of its operation were fictitious. (VII 490)

Mill has no quarrel with hypotheses of the first kind. They fit the conditions of a genuine inductive proof. In one type of case, a specific functional relationship between measurable variables is postulated and then verified in more detail. Mill cites Kepler’s hypotheses about the relationship between the line of incidence and line of refraction of light passing through a medium. Another type of case is what might be called hypothetical description of a spatio-temporal structure: for example of the figures described in space by the heavenly bodies. Kepler’s various hypotheses about the shape of the planetary orbits are a case in point. The elliptical shape of the orbits cannot be directly observed; all that we can do is make a hypothesis and verify it in more detail.¹⁹

‘In all these cases, verification is proof’ (VII 495); only the two steps of deducing predictions from the hypothesis and verifying them are required. The case is otherwise when it comes to hypotheses of the second kind.

It is legitimate to postulate a cause for a phenomenon when the existence of that cause can subsequently be confirmed independently of the occurrence of the phenomenon—‘if the cause suggested by the hypothesis should be in its own nature susceptible of being proved by other evidence’ (VII 459).

It is certainly not necessary that the cause assigned should be a cause already known; otherwise we should sacrifice our best opportunities of being acquainted with new causes. But what is true…is that the cause, though not known previously, should be capable of being known thereafter; that its existence should be capable of being detached, and its connexion with the effect ascribed to it should be susceptible of being proved, by independent evidence. (VII 496)

The role of the hypothesis is to ‘put us on the road to that independent evidence if it is really attainable’ (VII 496). In this function, the method of hypothesis is indispensable in science, and illustrates once more the provisional, self-correcting nature of inductive inquiry:

The process of tracing regularity in any complicated, and at first sight confused set of appearances, is necessarily tentative; the simplest supposition which accords with the more obvious facts, is the best to begin with; because its consequences are the most easily traced. This rude hypothesis is then rudely corrected, and the operation repeated; and the comparison of the consequences deducible from the corrected hypothesis, with the observed facts, suggests still further correction, until the deductive results are at last made to tally with the phenomena. (VII 496–7)

Finally (iii.xiv.7), Mill makes allowance for a case which involves postulation of unobservable causes but is nevertheless in his view properly ‘inductive’ rather than merely ‘hypothetical’. He has in mind the geological and cosmological theories which formed such an important part of the nineteenth-century’s intellectual climate. But his point applies generally to any historical inquiry which postulates causes in the distant and unremembered past. Such explanations, he thinks, involve only

the legitimate operation of inferring from an observed effect, the existence, in time past, of a cause similar to that by which we know it to be produced in all cases in which we have actual experience of its origin. (VII 506)

They are simply a special case of inductive generalisation.

When all these legitimate cases have been taken into account, we are left with pure cases of the Hypothetical Method, in which the causes postulated are not directly observable, and not simply because they are assumed to operate—in accordance with known laws, inductively established—in regions of time or space too distant to observe. What are we to say of such hypotheses? For example of the ‘emission’ theory, or the ‘undulatory’ theory of light? They cannot be accepted as inductively established truths, not even as probable ones:

an hypothesis of this kind is not to be received as probably true because it accounts for all the known phenomena; since this is a condition sometimes fulfilled tolerably well by two conflicting hypotheses; while there are probably many others which are equally possible, but which from want of anything analogous in our experience, our minds are unfitted to conceive. (VII 500)

The Hypothetical Method cannot be regarded as leading us, in its own right, to new truths: because the fact that data are deducible from one hypothesis is consistent with their deducibility from an indefinite number of other, and incompatible hypotheses. This underdetermination of hypotheses by data is Mill’s basic objection to the Hypothetical Method, considered as an independent method of discovering truth. Even then it does not prevent him from acknowledging the usefulness of hypotheses in suggesting potentially fruitful analogies:

I am yet unable to agree with those who consider such hypotheses to be worthy of entire disregard…. If an hypothesis both explains known facts, and has led to the prediction of others previously unknown, and since verified by experience, the laws of the phenomenon which is the subject of inquiry must bear at least a great similarity to those of the class of phenomena to which the hypothesis assimilates it; and since the analogy which extends so far may probably extend further, nothing is more likely to suggest experiments tending to throw light upon the real properties of the phenomenon, than the following out such an hypothesis. But to this end it is by no means necessary that the hypothesis be mistaken for a scientific truth. (VII 560)

This passage reflects the influence of Whewell’s notion of consilience of inductions; but it gives it an all-important instrumentalist twist.

Mill’s treatment of hypothetical reasoning, then, is detailed and sympathetic; but it falls resolutely short of accepting hypothetical inference as an autonomous principle in the logic of truth. But we cannot take full stock of this position without following Mill into metaphysical questions. A certain metaphysical picture underlies Mill’s analysis, determining the lines along which he demarcates legitimate forms of induction. The issues are best dealt with in a separate chapter.