• II •
6. Logical constants; the old logic and the new logic
The constants with which we have to deal in every scientific theory may be divided into two large groups. The first group consists of terms which are specific for a given theory. In the case of arithmetic, for instance, they are terms denoting either individual numbers or whole classes of numbers, relations between numbers, operations on numbers, etc.; the constants which we used in Section 1 as examples belong here among others. On the other hand, there are terms of a much more general character occurring in most of the statements of arithmetic, terms which are met constantly both in considerations of everyday life and in every possible field of science, and which represent an indispensable means for conveying human thoughts and for carrying out inferences in any field whatsoever; such words as “not”, “and”, “or”, “is”, “every”, “some” and many others belong here. There is a special discipline, namely LOGIC, considered the basis for all the other sciences, whose concern it is to establish the precise meaning of such terms and to lay down the most general laws in which these terms are involved.
Logic developed into an independent science long ago, earlier even than arithmetic and geometry. And yet it has only been recently—after a long period of almost complete stagnation—that this discipline has begun an intensive development, in the course of which it has undergone a complete transformation with the effect of assuming a character similar to that of the mathematical disciplines; in this new form it is known as MATHEMATICAL or DEDUCTIVE or SYMBOLIC LOGIC, and sometimes it is also called LOGISTIC. The new logic surpasses the old in many respects,—not only because of the solidity of its foundations and the perfection of the methods employed in its development, but mainly on account of the wealth of concepts and theorems that have been established. Fundamentally, the old traditional logic forms only a fragment of the new, a fragment moreover which, from the point of view of the requirements of other sciences, and of mathematics in particular, is entirely insignificant. Thus, in regard to the aim which we here have, there will in this whole book be but very little opportunity to draw the material for our considerations from traditional logic.1
7. Sentential calculus; negation of a sentence, conjunction and disjunction of sentences
Among the terms of a logical character there is a small distinguished group, consisting of such words as “not”, “and”, “or”, “if …, then …”. All these words are well-known to us from everyday language, and serve to build up compound sentences from simpler ones. In grammar, they are counted among the so-called sentential conjunctions. If only for this reason, the presence of these terms does not represent a specific property of any particular science. To establish the meaning and usage of these terms is the task of the most elementary and fundamental part of logic, which is called SENTENTIAL CALCULUS, or sometimes PROPOSITIONAL CALCULUS or (less happily) THEORY OF DEDUCTION.2
We will now discuss the meaning of the most important terms of sentential calculus.
With the help of the word “not” one forms the NEGATION of any sentence; two sentences, of which the first is a negation of the second, are called CONTRADICTORY SENTENCES. In senténtial calculus, the word “not” is put in front of the whole sentence, whereas in everyday language it is customary to place it with the verb; or should it be desirable to have it at the beginning of the sentence, it must be replaced by the phrase “it is not the case that”. Thus, for example, the negation of the sentence:
1 is a positive integer
reads as follows:
1 is not a positive integer,
or else:
it is not the case that 1 is a positive integer.
Whenever we utter the negation of a sentence, we intend to express the idea that the sentence is false; if the sentence is actually false, its negation is true, while otherwise its negation is false.
The joining of two sentences (or more) by the word “and” results in their so-called CONJUNCTION or LOGICAL PRODUCT; the sentences joined in this manner are called the MEMBERS OF THE CONJUNCTION or the FACTORS OF THE LOGICAL PRODUCT. If, for instance, the sentences:
2 is a positive integer
and
2 < 3
are joined in this way, we obtain the conjunction:
2 is a positive integer and 2 < 3.
The stating of the conjunction of two sentences is tantamount to stating that both sentences of which the conjunction is formed are true. If this is actually the case, then the conjunction is true, but if at least one of its members is false, then the whole conjunction is false.
By joining sentences by means of the word “or” one obtains the DISJUNCTION of those sentences, which is also called the LOGICAL SUM; the sentences forming the disjunction are called the MEMBERS OF THE DISJUNCTION or the SUMMANDS OF THE LOGICAL SUM. The word “or”, in everyday language, possesses at least two different meanings. Taken in the so-called NON-EXCLUSIVE meaning, the disjunction of two sentences merely expresses that at least one of these sentences is true, without saying anything as to whether or not both sentences may be true; taken in another meaning, the so-called EXCLUSIVE one, the disjunction of two sentences asserts that one of the sentences is true but that the other is false. Suppose we see the following notice put up in a bookstore:
Customers who are teachers or college students are entitled
to a special reduction.
Here the word “or” is undoubtedly used in the first sense, since it is not intended to refuse the reduction to a teacher who is at the same time a college student. If, on the other hand, a child has asked to be taken on a hike in the morning and to a theater in the afternoon, and we reply:
no, we are going on a hike or we are going to the theater,
then our usage of the word “or” is obviously of the second kind since we intend to comply with only one of the two requests. In logic and mathematics, the word “or” is always used in the first, non-exclusive meaning; the disjunction of two sentences is considered true if both or at least one of its members are true, and otherwise false. Thus, for instance, it may be asserted:
every number is positive or less than 3,
although it is known that there are numbers which are both positive and less than 3. In order to avoid misunderstandings, it would be expedient, in everyday as well as in scientific language, to use the word “or” by itself only in the first meaning, and to replace it by the compound expression “either … or …” whenever the second meaning is intended.
* Even if we confine ourselves to those cases in which the word “or” occurs in its first meaning, we find quite noticeable differences between the usages of it in everyday language and in logic, In common language, two sentences are joined by the word “or” only when they are in some way connected in form and content. (The same applies, though perhaps to a lesser degree, to the usage of the word “and”.) The nature of this connection is not quite clear, and a detailed analysis and description of it would meet with considerable difficulties. At any rate, anybody unfamiliar with the language of contemporary logic would presumably be little inclined to consider such a phrase as:
2.2 = 5 or New York is a large city
as a meaningful expression, and even less so to accept it as a true sentence. Moreover, the usage of the word “or” in everyday English is influenced by certain factors of a psychological character. Usually we affirm a disjunction of two sentences only if we believe that one of them is true but wonder which one. If, for example, we look upon a lawn in normal light, it will not enter our mind to say that the lawn is green or blue, since we are able to affirm something simpler and, at the same time, stronger, namely that the lawn is green. Sometimes even, we take the utterance of a disjunction as an admission by the speaker that he does not know which of the members of the disjunction is true. And if we later arrive at the conviction that he knew at the time that one—and, specifically, which—of the members was false, we are inclined to look upon the whole disjunction as a false sentence, even should the other member be undoubtedly true. Let us imagine, for instance, that a friend of ours, upon being asked when he is leaving town, answers that he is going to do so today, tomorrow or the day after. Should we then later ascertain that, at that time, he had already decided to leave the same day, we shall probably get the impression that we were deliberately misled and that he told us a lie.
The creators of contemporary logic, when introducing the word “or” into their considerations, desired, perhaps unconsciously, to simplify its meaning and to render the latter clearer and independent of all psychological factors, especially of the presence or absence of knowledge. Consequently, they extended the usage of the word “or”, and decided to consider the disjunction of any two sentences as a meaningful whole, even should no connection between their contents or forms exist; and they also decided to make the truth of a disjunction—like that of a negation or conjunction—dependent only and exclusively upon the truth of its members. Therefore, a man using the word “or” in the meaning of contemporary logic will consider the expression given above:
2.2 = 5 or New York is a large city
as a meaningful and even a true sentence, since its second part is surely true. Similarly, if we assume that our friend, who was asked about the date of his departure, used the word “or” in its strict logical meaning, we shall be compelled to consider his answer as true, independent of our opinion as to his intentions.*
8. Implication or conditional sentence; implication in material meaning
If we combine two sentences by the words “if … , then …”, we obtain a compound sentence which is denoted as an IMPLICATION or a CONDITIONAL SENTENCE. The subordinate clause to which the word “if” is prefixed is called ANTECEDENT, and the principal clause introduced by the word “then” is called CONSEQUENT. By asserting an implication one asserts that it does not occur that the antecedent is true and the consequent is false. An implication is thus true in any one of the following three cases: (i) both antecedent and consequent are true, (ii) the antecedent is false and the consequent is true, (iii) both antecedent and consequent are false; and only in the fourth possible case, when the antecedent is true and the consequent is false, the whole implication is false. It follows that, whoever accepts an implication as true, and at the same time accepts its antecedent as true, cannot but accept its consequent; and whoever accepts an implication as true and rejects its consequent as false, must also reject its antecedent.
* As in the case of disjunction, considerable differences between the usages of implication in logic and everyday language manifest themselves. Again, in ordinary language, we tend to join two sentences by the words “if …, then …” only when there is some connection between their forms and contents. This connection is hard to characterize in a general way, and only sometimes is its nature relatively clear. We often associate with this connection the conviction that the consequent follows necessarily from the antecedent, that is to say, that if we assume the antecedent to be true we are compelled to assume the consequent, too, to be true (and that possibly we can even deduce the consequent from the antecedent on the basis of some general laws which we might not always be able to quote explicitly). Here again, an additional psychological factor manifests itself; usually we formulate and assert an implication only if we have no exact knowledge as to whether or not the antecedent and consequent are true. Otherwise the use of an implication seems unnatural and its sense and truth may raise some doubt.
The following example may serve as an illustration. Let us consider the law of physics:
every metal is malleable,
and let us put it in the form of an implication containing variables:
if x is a metal, then x is malleable.
If we believe in the truth of this universal law, we believe also in the truth of all its particular cases, that is, of all implications obtainable by replacing “x” by names of arbitrary materials such as iron, clay or wood. And, indeed, it turns out that all sentences obtained in this way satisfy the conditions given above for a true implication; it never happens that the antecedent is true while the consequent is false. We notice, further, that in any of these implications there exists a close connection between the antecedent and the consequent, which finds its formal expression in the coincidence of their subjects. We are also convinced that, assuming the antecedent of any of these implications, for instance, “iron is a metal”, as true, we can deduce from it its consequent “iron is malleable”, for we can refer to the general law that every metal is malleable.
Nevertheless, some of the sentences discussed just now seem artificial and doubtful from the point of view of common language. No doubt is raised by the universal implication given above, or by any of its particular cases obtained by replacing “x” by the name of a material of which we do not know whether it is a metal or whether it is malleable. But if we replace “x” by “iron”, we are confronted with a case in which the antecedent and consequent are undoubtedly true; and we shall then prefer to use, instead of an implication, an expression such as:
since iron is a metal, it is malleable.
Similarly, if for “x” we substitute “clay”, we obtain an implication with a false antecedent and a true consequent, and we shall be inclined to replace it by the expression:
although clay is not a metal, it is malleable.
And finally, the replacement of “x” by “wood” results in an implication with a false antecedent and a false consequent; if, in this case, we want to retain the form of an implication, we should have to alter the grammatical form of the verbs:
if wood were a metal, then it would be malleable.
The logicians, with due regard for the needs of scientific languages, adopted the same procedure with respect to the phrase “if …, then …” as they had done in the case of the word “or”. They decided to simplify and clarify the meaning of this phrase, and to free it from psychological factors. For this purpose they extended the usage of this phrase, considering an implication as a meaningful sentence even if no connection whatsoever exists between its two members, and they made the truth or falsity of an implication dependent exclusively upon the truth or falsity of the antecedent and consequent. To characterize this situation briefly, we say that contemporary logic uses IMPLICATIONS IN MATERIAL MEANING, or simply, MATERIAL IMPLICATIONS; this is opposed to the usage of IMPLICATION IN FORMAL MEANING or FORMAL IMPLICATION, in which case the presence of a certain formal connection between antecedent and consequent is an indispensable condition of the meaningfulness and truth of the implication. The concept of formal implication is not, perhaps, quite clear, but, at any rate, it is narrower than that of material implication; every meaningful and true formal implication is at the same time a meaningful and true material implication, but not vice versa.
In order to illustrate the foregoing remarks, let us consider the following four sentences:
if 2.2 = 4, then New York is a large city;
if 2.2 = 5, then New York is a large city;
if 2.2 = 4, then New York is a small city;
if 2.2 = 5, then New York is a small city.
In everyday language, these sentences would hardly be considered as meaningful, and even less as true. From the point of view of mathematical logic, on the other hand, they are all meaningful, the third sentence being false, while the remaining three are true. Thereby it is, of course, not asserted that sentences like these are particularly relevant from any viewpoint whatever, or that we apply them as premisses in our arguments.
It would be a mistake to think that the difference between everyday language and the language of logic, which has been brought to light here, is of an absolute character, and that the rules, outlined above, of the usage of the words “if …, then …” in common language admit of no exceptions. Actually, the usage of these words fluctuates more or less, and if we look around, we can find cases in which this usage does not comply with our rules. Let us imagine that a friend of ours is confronted with a very difficult problem and that we do not believe that he will ever solve it. We can then express our disbelief in a jocular form by saying:
if you solve this problem, I shall eat my hat.
The tendency of this utterance is quite clear. We affirm here an implication whose consequent is undoubtedly false; therefore, since we affirm the truth of the whole implication, we thereby, at the same time, affirm the falsity of the antecedent; that is to say, we express our conviction that our friend will fail to solve the problem in which he is interested. But it is also quite clear that the antecedent and the consequent of our implication are in no way connected, so that we have a typical case of a material and not of a formal implication.
The divergency in the usage of the phrase “if …, then …” in ordinary language and mathematical logic has been at the root of lengthy and even passionate discussions,—in which, by the way, professional logicians took only a minor part.3 (Curiously enough, considerably less attention was paid to the analogous divergency in the case of the word “or”.) It has been objected that the logicians, on account of their employment of the material implication, arrived at paradoxes and even plain nonsense. This has resulted in an outcry for a reform of logic to the effect of bringing about a far-reaching rapprochement between logic and ordinary language regarding the use of implication.
It would be hard to grant that these criticisms are well-founded. There is no phrase in ordinary language that has a precisely determined sense. It would scarcely be possible to find two people who would use every word with exactly the same meaning, and even in the language of a single person the meaning of the same word varies from one period of his life to another. Moreover, the meaning of words of everyday language is usually very complicated; it depends not only on the external form of the word but also on the circumstances in which it is uttered and sometimes even on subjective psychological factors. If a scientist wants to introduce a concept from everyday life into a science and to establish general laws concerning this concept, he must always make its content clearer, more precise and simpler, and free it from inessential attributes; it does not matter here whether he is a logician concerned with the phrase “if …, then …” or, for instance, a physicist establishing the exact meaning of the word “metal”. In whatever way the scientist realizes his task, the usage of the term as it is established by him will deviate more or less from the practice of everyday language. If, however, he states explicitly in what meaning he decides to use the term, and if he consistently acts in conformity to this decision, nobody will be in a position to object that his procedure leads to nonsensical results.
Nevertheless, in connection with the discussions that have taken place, some logicians have undertaken attempts to reform the theory of implication. They do not, generally, deny material implication a place in logic, but they are anxious to find also a place for another concept of implication, for instance, of such a kind that the possibility of deducing the consequent from the antecedent constitutes a necessary condition for the truth of an implication; they even desire, so it seems, to place the new concept in the foreground. These attempts are of a relatively recent date, and it is too early to pass a final judgment as to their value.4 But it appears today almost certain that the theory of material implication will surpass all other theories in simplicity, and, in any case, it must not be forgotten that logic, founded upon this simple concept, turned out to be a satisfactory basis for the most complicated and subtle mathematical reasonings.*
9. The use of implication in mathematics
The phrase “if …, then …” belongs to those expressions of logic which are used most frequently in other sciences and, especially, in mathematics. Mathematical theorems, particularly those of a universal character, tend to have the form of implications; the antecedent is called in mathematics the HYPOTHESIS, and the consequent is called the CONCLUSION.
As a simple example of a theorem of arithmetic, having the form of an implication, we may quote the following sentence:
if x is a positive number, then 2x is a positive number
in which “x is a positive number” is the hypothesis, while “2x is a positive number” is the conclusion.
Apart from this, so to speak, classical form of mathematical theorems, there are, occasionally, different formulations, in which hypothesis and conclusion are connected in some other way than by the phrase “if …, then …”. The theorem just mentioned, for instance, can be paraphrased in any of the following forms:
from: x is a positive number, it follows: 2x is a positive number;
the hypothesis: x is a positive number, implies (or has as a consequence) the conclusion: 2x is a positive number;
the condition: x is a positive number, is sufficient for 2x to be a positive number;
for 2x to be a positive number it is sufficient that x be a positive number;
the condition: 2x is a positive number, is necessary for x to be a positive number;
for x to be a positive number it is necessary that 2x be a positive number.
Therefore, instead of asserting a conditional sentence, one might usually just as well say that the hypothesis IMPLIES the conclusion or HAS it AS A CONSEQUENCE, or that it is a SUFFICIENT CONDITION for the conclusion; or one can express it by saying that the conclusion FOLLOWS from the hypothesis, or that it is a NECESSARY CONDITION for the latter. A logician may raise various objections against some of the formulations given above, but they are in general use in mathematics.
* The objections which might be raised here concern those of the above formulations in which any of the words “hypothesis”, “conclusion”, “consequence”, “follows”, “implies” occur.
In order to understand the essential points in these objections, we observe first that those formulations differ in content from the ones originally given. While in the original formulation we talk only about numbers, properties of numbers, operations upon numbers and so on—hence, about things with which mathematics is concerned—, in the formulations now under discussion we talk about hypotheses, conclusions, conditions, that is about sentences or sentential functions occurring in mathematics. It might be noted on this occasion that, in general, people do not distinguish clearly enough the terms which denote things dealt with in a given science from those which denote various kinds of expressions occurring within it. This can be observed, in particular, in the domain of mathematics, especially on the elementary level. Presumably only few are aware of the fact that such terms as “equation”, “inequality”, “polynomial” or “algebraic fraction”, which are met at every turn in textbooks of elementary algebra, do not, strictly speaking, belong to the domain of mathematics or logic, since they do not denote things considered in this domain; equations and inequalities are certain special sentential functions, while polynomials and algebraic fractions—especially as they are treated in elementary textbooks—are particular instances of designatory functions (cf. Section 2). The confusion on this point is brought about by the fact that terms of this kind are frequently used in the formulation of mathematical theorems. This has become a very common usage, and perhaps it is not worth our while to put up a stand against it, since it does not present any particular danger; but it might be worth our while to get to recognize that, for every theorem formulated with the help of such terms, there is another formulation, logically more correct, in which those terms do not occur at all. For instance, the theorem:
the equation: x2 + ax + b = 0 has at most two roots
can be expressed in a more correct manner as follows:
there are at most two numbers x such that x2 + ax + b = 0.
Returning to the questionable formulations of an implication, we must emphasize one still more important point. In these formulations we assert that one sentence, namely the antecedent of the implication, has another—the consequent of the implication—as a consequence, or that the second follows from the first. But ordinarily when we express ourselves in this way, we have in mind that the assumption that the first sentence is true leads us, so to speak, necessarily to the same assumption concerning the second sentence (and that possibly we are even able to derive the second sentence from the first). As we already know from Section 8, however, the meaning of an implication, as it was established in contemporary logic, does not depend on whether its consequent has any such connection with its antecedent. Anyone shocked by the fact that the expression:
if 2.2 = 4, then New York is a large city
is considered in logic as a meaningful and even true sentence will find it still harder to reconcile himself with such a transformation of this phrase as:
the hypothesis that 2.2 = 4 has as a consequence that
New York is a large city.
We see, thus, that the manners discussed here of formulating or transforming a conditional sentence lead to paradoxical sounding utterances and make yet more profound the discrepancies between common language and mathematical logic. It is for this reason that they repeatedly brought about various misunderstandings and have been one of the causes of those passionate and frequently sterile discussions which we mentioned above.
From the purely logical point of view we can obviously avoid all objections raised here by stating explicitly once and for all that, in using the formulations in question, we shall disregard their usual meaning and attribute to them exactly the same content as to the ordinary conditional sentence. But this would be inconvenient in another respect; for there are situations—though not in logic itself, but in a field closely related to it, namely, the methodology of deductive sciences (cf. Chapter VI)—in which we talk about sentences and the relation of consequence between them, and in which we use such terms as “implies” and “follows” in a different meaning more closely akin to the ordinary one. It would, therefore, be better to avoid those formulations altogether, all the more since we have several formulations at our disposal which are not open to any of these objections.*
10. Equivalence of sentences
We shall consider one more expression from the field of sentential calculus. It is one which is comparatively rarely met in everyday language, namely, the phrase “if, and only if”. If any two sentences are joined up by this phrase, the result is a compound sentence called an EQUIVALENCE. The two sentences connected in this way are referred to as the LEFT and RIGHT SIDE OF THE EQUIVALENCE. By asserting the equivalence of two sentences, it is intended to exclude the possibility that one is true and the other false; an equivalence, therefore, is true if its left and right sides are either both true or both false, and otherwise the equivalence is false.
The sense of an equivalence can also be characterized in still another way. If, in a conditional sentence, we interchange antecedent and consequent, we obtain a new sentence which, in its relation to the original sentence, is called the CONVERSE SENTENCE (or the CONVERSE OF THE GIVEN SENTENCE). Let us take, for instance, as the original sentence the implication:
(I) if x is a positive number, then 2x is a positive number;
the converse of this sentence will then be:
(II) if 2x is a positive number, then x is a positive number.
As is shown by this example, it occurs that the converse of a true sentence is true. In order to see, on the other hand, that this is not a general rule, it is sufficient to replace “2x” by “x2” in (I) and (II); the sentence (I) will remain true, while the sentence (II) becomes false. If, now, it happens that two conditional sentences, of which one is the converse of the other, are both true, then the fact of their simultaneous truth can also be expressed by joining the antecedent and consequent of any one of the two sentences by the words “if, and only if”. Thus, the above two implications—the original sentence (I) and the converse sentence (II)—may be replaced by a single sentence:
x is a positive number if, and only if, 2x is a positive number
(in which the two sides of the equivalence may yet be interchanged).
There are, incidentally, still a few more possible formulations which may serve to express the same idea, e.g.:
from: x is a positive number, it follows: 2x is a positive number, and conversely;
the conditions that x is a positive number and that 2x is a positive number are equivalent with each other;
the condition that x is a positive number is both necessary and sufficient for 2x to be a positive number;
for x to be a positive number it is necessary and sufficient that 2x be a positive number.
Instead of joining two sentences by the phrase “if, and only if”, it is therefore, in general, also possible to say that the RELATION OF CONSEQUENCE holds between these two sentences IN BOTH DIRECTIONS, or that the two sentences are EQUIVALENT, or, finally, that each of the two sentences represents a NECESSARY AND SUFFICIENT CONDITION for the other.
11. The formulation of definitions and its rules
The phrase “if, and only if” is very frequently used in laying down DEFINITIONS, that is, conventions stipulating what meaning is to be attributed to an expression which thus far has not occurred in a certain discipline, and which may not be immediately comprehensible. Imagine, for instance, that in arithmetic the symbol “![]() ” has not as yet been employed but that one wants to introduce it now into the considerations (looking upon it, as usual, as an abbreviation of the expression “is less than or equal to”). For this purpose it is necessary to define this symbol first, that is, to explain exactly its meaning in terms of expressions which are already known and whose meanings are beyond doubt. To achieve this, we lay down the following definition,—assuming that “>” belongs to the symbols already known:
” has not as yet been employed but that one wants to introduce it now into the considerations (looking upon it, as usual, as an abbreviation of the expression “is less than or equal to”). For this purpose it is necessary to define this symbol first, that is, to explain exactly its meaning in terms of expressions which are already known and whose meanings are beyond doubt. To achieve this, we lay down the following definition,—assuming that “>” belongs to the symbols already known:
we say that x ![]() y if, and only if, it is not the case that x > y.
y if, and only if, it is not the case that x > y.
The definition just formulated states the equivalence of the two sentential functions:
![]()
and
it is not the case that x > y;
it may be said, therefore, that it permits the transformation of the formula “![]() ” into an equivalent expression which no longer contains the symbol “
” into an equivalent expression which no longer contains the symbol “![]() ” but is formulated entirely in terms already comprehensible to us. The same holds for any formula obtained from “
” but is formulated entirely in terms already comprehensible to us. The same holds for any formula obtained from “![]() ” by replacing “x” and “y” by arbitrary symbols or expressions designating numbers. The formula:
” by replacing “x” and “y” by arbitrary symbols or expressions designating numbers. The formula:
![]()
for instance, is equivalent with the sentence:
it is not the case that 3 + 2 > 5;
since the latter is a true assertion, so is the former. Similarly, the formula:
![]()
is equivalent with the sentence:
it is not the case that 4 > 2 + 1,
both being false assertions. This remark applies also to more complicated sentences and sentential functions; by transforming, for instance, the sentence:
![]()
we obtain:
if it is not the case that x > y and if it is not the case that
y > z, then it is not the case that x > z.
In short, by virtue of the definition given above, we are in a position to transform any simple or compound sentence containing the symbol “![]() ” into an equivalent one no longer containing it; in other words, so to speak, to translate it into a language in which the symbol “
” into an equivalent one no longer containing it; in other words, so to speak, to translate it into a language in which the symbol “![]() ” does not occur. And it is this very fact which constitutes the role which definitions play within the mathematical disciplines.
” does not occur. And it is this very fact which constitutes the role which definitions play within the mathematical disciplines.
If a definition is to fulfil its proper task well, certain precautionary measures have to be observed in its formulation. To this effect special rules are laid down, the so-called RULES OF DEFINITION, which specify how definitions should be constructed correctly. Since we shall not here go into an exact formulation of these rules, it may merely be remarked that, on their basis, every definition may assume the form of an equivalence; the first member of that equivalence, the DEFINIENDUM, should be a short, grammatically simple sentential function containing the constant to be defined; the second member, the DEFINIENS, may be a sentential function of an arbitrary structure, containing, however, only constants whose meaning either is immediately obvious or has been explained previously. In particular, the constant to be defined, or any expression previously defined with its help, must not occur in the definiens; otherwise the definition is incorrect, it contains an error known as a VICIOUS CIRCLE IN THE DEFINITION (just as one speaks of a VICIOUS CIRCLE IN THE PROOF, if the argument meant to establish a certain theorem is based upon that theorem itself, or upon some other theorem previously proved with its help). In order to emphasize the conventional character of a definition and to distinguish it from other statements which have the form of an equivalence, it is expedient to prefix it by words such as “we say that”. It is easy to verify that the above definition of the symbol “![]() ” satisfies all these conditions; it has the definiendum:
” satisfies all these conditions; it has the definiendum:
![]()
whereas the definiens reads:
it is not the case that x > y.
It is worth noticing that mathematicians, in laying down definitions, prefer the words “if” or “in case that” to the phrase “if, and only if”. If, for example, they had to formulate the definition of the symbol “![]() ”, they would, presumably, give it the following form:
”, they would, presumably, give it the following form:
we say that x ![]() y, if it is not the case that x > y.
y, if it is not the case that x > y.
It looks as if such a definition merely states that the definiendum follows from the definiens, without emphasizing that the relation of consequence also holds in the opposite direction, and thus fails to express the equivalence of definiendum and definiens. But what we actually have here is a tacit convention to the effect that “if” or “in case that”, if used to join definiendum and definiens, are to mean the same as the phrase “if, and only if” ordinarily does.—It may be added that the form of an equivalence is not the only form in which definitions may be laid down.
12. Laws of sentential calculus
After having come to the end of our discussion of the most important expressions of sentential calculus, we shall now try to clarify the character of the laws of this calculus.
Let us consider the following sentence:
if 1 is a positive number and 1 < 2, then 1 is a positive
number.
This sentence is obviously true, it contains exclusively constants belonging to the field of logic and arithmetic, and yet the idea of listing this sentence as a special theorem in a textbook of mathematics would not occur to anybody. If one reflects why this is so, one comes to the conclusion that this sentence is completely uninteresting from the standpoint of arithmetic; it fails to enrich in any way our knowledge about numbers, its truth does not at all depend upon the content of the arithmetical terms occurring in it, but merely upon the sense of the words “and”, “if”, “then”. In order to make sure that this is so, let us replace in the sentence under consideration the components:
1 is a positive number
1 < 2
by any other sentences from an arbitrary field; the result is a series of sentences, each of which, like the original sentence, is true; for example:
if the given figure is a rhombus and if the same figure is a rectangle, then the given figure is a rhombus;
if today is Sunday and the sun is shining, then today is Sunday.
In order to express this fact in a more general form, we shall introduce the variables “p” and “q”, stipulating that these symbols are not designations of numbers or any other things, but that they stand for whole sentences; variables of this kind are denoted as SENTENTIAL VARIABLES. Further, we shall replace in the sentence under consideration the phrase:
1 is a positive number
by “p” and the formula:
1 < 2
by “q”; in this manner we arrive at the sentential function:
if p and q, then p.
This sentential function has the property that only true sentences are obtained if arbitrary sentences are substituted for “p” and “q”. This observation may be given the form of a universal statement:
For any p and q, if p and q, then p.
We have here obtained a first example of a law of sentential calculus, which will be referred to as the LAW OF SIMPLIFICATION for logical multiplication. The sentence considered above was merely a special instance of this universal law—just as, for instance, the formula:
2 · 3 = 3 · 2
is merely a special instance of the universal arithmetical theorem:
for arbitrary numbers x and y, x · y = y · x.
In a similar way, other laws of sentential calculus can be obtained. We give here a few examples of such laws; in their formulation we omit the universal quantifier “for any p, q, …”—in accordance with the usage mentioned in Section 3, which becomes almost a rule throughout sentential calculus.
If p, then p.
If p, then q or p.
If p implies q and q implies p, then p if, and only if, q.
If p implies q and q implies r, then p implies r.
The first of these four statements is known as the LAW OF IDENTITY, the second as the LAW OF SIMPLIFICATION for logical addition, and the fourth as the LAW OF THE HYPOTHETICAL SYLLOGISM.
Just as the arithmetical theorems of a universal character state something about the properties of arbitrary numbers, the laws of sentential calculus assert something, so one may say, about the properties of arbitrary sentences. The fact that in these laws only such variables occur as stand for quite arbitrary sentences is characteristic of sentential calculus and decisive for its great generality and the scope of its applicability.
13. Symbolism of sentential calculus; truth functions and truth tables
There exists a certain simple and general method, called METHOD OF TRUTH TABLES or MATRICES, which enables us, in any particular case, to recognize whether a given sentence from the domain of the sentential calculus is true, and whether, therefore, it can be counted among the laws of this calculus.5
In describing this method it is convenient to apply a special symbolism. We shall replace the expressions:
not; and; or; if …, then …; if, and only if
by the symbols:
~; ^; ∨; → ; ↔
respectively. The first of these symbols is to be placed in front of the expression whose negation one wants to obtain; the remaining symbols are always placed between two expressions (“→” stands therefore in the place of the word “then”, while the word “if” is simply omitted). From one or two simpler expressions we are, in this way, led to a more complicated expression; and if we want to use the latter for the construction of further still more complicated expressions, we enclose it in parentheses.
With the help of variables, parentheses and the constant symbols listed above (and sometimes also additional constants of a similar character which will not be discussed here), we are able to write down all sentences and sentential functions belonging to the domain of sentential calculus. Apart from the individual sentential variables the simplest sentential functions are the expressions:
~p, p ∧ q, p ∨ q, p → q, p ↔ q
(and other similar expressions which differ from these merely in the shape of the variables used). As an example of a compound sentential function let us consider the expression:
(p ∨ q) → (p ∧ r),
which we read, translating symbols into common language:
if p or q, then p and r.
A still more complicated expression is the law of the hypothetical syllogism given above, which now assumes the form:
[(p → q) ∧ (q → r)] → (p → r).
We can easily make sure that every sentential function occurring in our calculus is a so-called TRUTH FUNCTION. This means to say that the truth or falsehood of any sentence obtained from that function by substituting whole sentences for variables depends exclusively upon the truth or falsehood of the sentences which have been substituted. As for the simplest sentential functions “~p”, “p ∧ q”, and so on, this follows immediately from the remarks made in Sections 7, 8 and 10 concerning the meaning attributed in logic to the words “not”, “and”, and so on. But the same applies, likewise, to compound functions. Let us consider, for instance, the function “(p ∨ q) → (p ∧ r)”. A sentence obtained from it by substitution is an implication, and, therefore, its truth depends on the truth of its antecedent and consequent only; the truth of the antecedent, which is a disjunction obtained from “p ∨ q”, depends only on the truth of the sentences substituted for “p” and “q”, and similarly the truth of the consequent depends only on the truth of the sentences substituted for “p” and “r”. Thus, finally, the truth of the whole sentence obtained from the sentential function under consideration depends exclusively on the truth of the sentences substituted for “p”, “q” and “r”.
In order to see quite exactly how the truth or falsity of a sentence obtained by substitution from a given sentential function depends upon the truth or falsity of the sentences substituted for variables, we construct what is called the TRUTH TABLE or MATRIX for this function. We shall begin by giving such a table for the function “~p”:

And here is the joint truth table for the other elementary functions “p ∧ q”, “p ∨ q”, and so on:
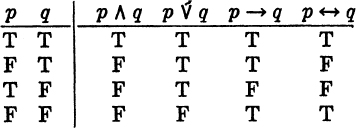
The meaning of these tables becomes at once comprehensible if we take the letters “T” and “F” to be abbreviations of “true sentence” and “false sentence”, respectively. In the second table, for instance, we find, in the second line below the headings “p”, “q” and “p → q”, the letters “F”, “T” and “T”, respectively. We gather from that that a sentence obtained from the implication “p → q” is true if we substitute any false sentence for “p” and any true sentence for “q”; this, obviously, is entirely consistent with the remarks made in Section 8.—The variables “p” and “q” occurring in the tables can, of course, be replaced by any other variables.
With the help of the two above tables, called FUNDAMENTAL TRUTH TABLES, we can construct DERIVATIVE TRUTH TABLES for any compound sentential function. The table for the function “(p ∨ q) → (p ∧ r)”, for instance, looks as follows:

In order to explain the construction of this table, let us concentrate, say, on its fifth horizontal line (below the headings). We substitute true sentences for “p” and “q” and a false sentence for “r”. According to the second fundamental table, we then obtain from “p ∨ q” a true sentence and from “p ∧ r” a false sentence. From the whole function “(p ∨ q) → (p ∧ r)” we obtain then an implication with a true antecedent and a false consequent; hence, again with the help of the second fundamental table (in which we think of “p” and “q” being for the moment replaced by “p ∨ q” and “p ∧ r”), we conclude that this implication is a false sentence.
The horizontal lines of a table that consist of symbols “T” and “F” are called ROWS of the table, and the vertical lines are called COLUMNS. Each row or, rather, that part of each row which is on the left of the vertical bar represents a certain substitution of true or false sentences for the variables. When constructing the matrix of a given function, we take care to exhaust all possible ways in which a combination of symbols “T” and “F” could be correlated to the variables; and, of course, we never write in a table two rows which do not differ either in the number or in the order of the symbols “T” and “F”. It can then be seen very easily that the number of rows in a table depends in a simple way on the number of different variables occurring in the function; if a function contains 1, 2, 3, … variables of different shape, its matrix consists of 21 = 2, 22 = 4, 28 = 8, … rows. As for the number of columns, it is equal to the number of partial sentential functions of different form contained in the given function (where the whole function is also counted among its partial functions).
We are now in a position to say how it may be decided whether or not a sentence of sentential calculus is true. As we know, in sentential calculus, there is no external difference between sentences and sentential functions; the only difference consisting in the fact that the expressions considered to be sentences are always completed mentally by the universal quantifier. In order to recognize whether the given sentence is true, we treat it, for the time being, as a sentential function, and construct the truth table for it. If, in the last column of this table, no symbol “F” occurs, then every sentence obtainable from the function in question by substitution will be true, and therefore our original universal sentence (obtained from the sentential function by mentally prefixing the universal quantifier) is also true. If, however, the last column contains at least one symbol “F”, our sentence is false.
Thus, for instance, we have seen that in the matrix constructed for the function “(p ∨ q) → (p ∧ r)” the symbol “F” occurs four times in the last column. If, therefore, we considered this expression as a sentence (that is, if we prefixed to it the words “for any p, q and r”), we would have a false sentence. On the other hand, it can be easily verified with the help of the method of truth tables that all the laws of sentential calculus stated in Section 12, that is, the laws of simplification, identity, and so on, are true sentences. The table for the law of simplification:
(p ∧ q) → p,

We give here a number of other important laws of sentential calculus whose truth can be ascertained in a similar way:
| ~[p ∧ (~p)], | p ∨ (~p), |
| (p ∧ p) ↔ p, | (p ∨ p) ↔ p, |
| (p ∧ q) ↔ (q ∧ p), | (p ∨ q) ↔ (q ∨ p), |
| [p ∧ (q ∧ r)] ↔ [(p ∧ q) ∧ r], | [p ∨ (q ∨ r)] ↔ [(p ∨ q) ∨ r]. |
The two laws in the first line are called the LAW OF CONTRADICTION and the LAW OF EXCLUDED MIDDLE; we next have the two LAWS OF TAUTOLOGY (for logical multiplication and addition); we then have the two COMMUTATIVE LAWS, and finally the two ASSOCIATIVE LAWS. It can easily be seen how obscure the meaning of these last two laws becomes if we try to express them in ordinary language. This exhibits very clearly the value of logical symbolism as a precise instrument for expressing more complicated thoughts.
*It occurs that the method of matrices leads us to accept sentences as true whose truth seemed to be far from obvious before the application of this method. Here are some examples of sentences of this kind:
p → (q → p),
(~p) → (p → q),
(p → q) ∨ (q → p).
That these sentences are not immediately obvious is due mainly to the fact that they are a manifestation of the specific usage of implication characteristic of modern logic, namely, the usage of implication in material meaning.
These sentences assume an especially paradoxical character if, when reading them in words of common language, the implications are replaced by phrases containing “implies” or “follows”, that is, if we give them, for instance, the following form:
if p is true, then p follows from any q (in other words: a true sentence follows from every sentence);
if p is false, then p implies any q (in other words: a false sentence implies every sentence);
for any p and q, either p implies q or q implies p (in other words: at least one of any two sentences implies the other).
In this formulation, these statements have frequently been the cause of misunderstandings and superfluous discussions. This confirms entirely the remarks made at the end of Section 9.*
14. Application of laws of sentential calculus in inference
Almost all reasonings in any scientific domain are based explicitly or implicitly upon laws of sentential calculus; we shall try to explain by means of an example in what way this happens.
Given a sentence having the form of an implication, we can, apart from its converse of which we had already spoken in Section 10, form two further sentences: the INVERSE SENTENCE (or the INVERSE OF THE GIVEN SENTENCE) and the CONTRAPOSITIVE SENTENCE. The inverse sentence is obtained by replacing both the antecedent and the consequent of the given sentence by their negations. The contrapositive is the result of interchanging the antecedent and the consequent in the inverse sentence; the contra-positive sentence is, therefore, the converse of the inverse sentence and also the inverse of the converse sentence. The converse, the inverse and the contrapositive sentences, together with the original sentence, are referred to as CONJUGATE SENTENCES. As an illustration we may consider the following conditional sentence:
(I) if x is a positive number, then 2x is a positive number,
and form its three conjugate sentences:
if 2x is a positive number, then x is a positive number;
if x is not a positive number, then 2x is not a positive number;
if 2x is not a positive number, then x is not a positive number.
In this particular example, all the conjugate sentences obtained from a true sentence turn out to be likewise true. But this is not at all so in general; in order to see that it is quite possible that not only the converse sentence (as has already been mentioned in Section 10) but also the inverse sentence may be false, although the original sentence is true, it is sufficient to replace “2x” by “x2” in the above sentences.
Thus it is seen that from the validity of an implication nothing definite can be inferred about the validity of the converse or the inverse sentence. The situation is quite different in the case of the fourth conjugate sentence; whenever an implication is true, the same applies to the corresponding contrapositive sentence. This fact may be confirmed by numerous examples, and it finds its expression in a general law of sentential calculus, namely the so-called LAW OF TRANSPOSITION or OF CONTRAPOSITION.
In order to be able to formulate this law with precision, we observe that every implication may be given the schematic form:
if p, then q;
the converse, the inverse and the contrapositive sentences will then assume the forms:
if q, then p; if not p, then not q; if not q, then not p.
The law of contraposition, according to which any conditional sentence implies the corresponding contrapositive sentence, may hence be formulated as follows:
if: if p, then q, then: if not q, then not p.
In order to avoid the accumulation of the words “if” it is expedient to make a slight change in the formulation:
(II) from: if p, then q, it follows that: if not q, then not p.
We now want to show how, with the help of this law, we can, from a statement having the form of an implication—for instance, from statement (I)—derive its contrapositive statement.
(II) applies to arbitrary sentences “p” and “q”, and hence remains valid if for “p” and “q” the expressions:
x is a positive number
and
2x is a positive number
are substituted. Changing, for stylistic reasons, the position of the word “not”, we obtain:
(III) from: if x is a positive number, then 2x is a positive number, it follows that: if 2x is not a positive number, then x is not a positive number.
Now compare (I) and (III): (III) has the form of an implication, (I) being its hypothesis. Since the whole implication as well as its hypothesis have been acknowledged as true, the conclusion of the implication must likewise be acknowledged as true; but that is just the contrapositive statement in question:
(IV) if 2x is not a positive number, then x is not a positive number.
Anyone knowing the law of contraposition can, in this way, recognize the contrapositive sentence as true, provided he has previously proved the original sentence. Further, as one can easily verify, the inverse sentence is contrapositive with respect to the converse of the original sentence (that is to say, the inverse sentence can be obtained from the converse sentence by replacing antecedent and consequent by their negations and then interchanging them); for this reason, if the converse of the given sentence has been proved, the inverse sentence may likewise be considered valid. If, therefore, one has succeeded in proving two sentences—the original and its converse—a special proof for the two remaining conjugate sentences is superfluous.
It may be mentioned that several variants of the law of contraposition are known; one of them is the converse of (II):
from: if not q, then not p, it follows that: if p, then q.
This law makes it possible to derive the original sentence from the contrapositive, and the inverse from the converse sentence.
15. Rules of inference, complete proofs
We shall now consider in a little more detail the mechanism itself of the proof by means of which the sentence (IV) had been demonstrated in the preceding section. Besides the rules of definition, of which we have already spoken, we have other rules of a somewhat similar character, namely, the RULES OF INFERENCE or RULES OF PROOF. These rules, which must not be mistaken for logical laws, amount to directions as to how sentences already known as true may be transformed so as to yield new true sentences. In the proof carried out above, two rules of demonstration have been made use of: the RULE OF SUBSTITUTION and the RULE OF DETACHMENT (also known as the MODUS PONENS RULE).
The content of the rule of substitution is as follows. If a sentence of a universal character, that has already been accepted as true, contains sentential variables, and if these variables are replaced by other sentential variables or by sentential functions or by sentences—always substituting equal expressions for equal variables throughout—, then the sentence obtained in this way may also be recognized as true. It was by applying this very rule that we obtained the sentence (III) from sentence (II). It should be emphasized that the rule of substitution may also be applied to other kinds of variables, for example, to the variables “x”, “y”, … designating numbers: in place of these variables, any symbols or expressions denoting numbers may be substituted.
*The formulation of the rule of substitution as given here is not quite precise. This rule refers to such sentences as are composed of a universal quantifier and a sentential function, the latter containing variables bound by the universal quantifier. When one wants to apply the rule of substitution, one omits the quantifier and substitutes for the variables previously bound by this quantifier either other variables or whole expressions (e.g., sentential functions or sentences for the variables “p”, “q”, “r”, …, and expressions denoting numbers for the variables “x”, “y”, “z”, …); any other bound variables which may occur in the sentential function remain unaltered, and one sees to it that no variables of the same form as these occur in the substituted expressions; if necessary a universal quantifier is set in front of the expression obtained in this way in order to turn it into a sentence. For instance, by applying the rule of substitution to the sentence:
for any number x there is a number y such that x + y = 5,
the following sentence can be obtained:
there is a number y such that 3 + y = 5,
but also the sentence:
for any number z there is a number y such that z2 + y = 5;
thus, in this case, one substitutes only for “x” and leaves “y” unaltered. We must not, however, substitute for “x” any expression containing “y”; for, although our original sentence was true, we might in this way arrive at a false sentence. For instance, by substituting “3 − y”, we should obtain:
there is a number y such that (3 − y) + y = 5.*
The rule of detachment states that, if two sentences are accepted as true, of which one has the form of an implication while the other is the antecedent of this implication, then that sentence may also be recognized as true which forms the consequent of the implication. (We “detach” thus, so to speak, the antecedent from the whole implication.) By means of this rule, the sentence (IV) had been derived from the sentences (III) and (I).
It can be seen that from this that, in the proof of the sentence (IV) as carried out above, each step consisted in applying a rule of inference to sentences which were previously accepted or recognized as true. A proof of this kind will be called COMPLETE. A little more precisely a complete proof may also be characterized as follows. It consists in the construction of a chain of sentences with these properties: the initial members are sentences which were already previously accepted as true; every subsequent member is obtainable from preceding ones by applying a rule of inference; and finally the last member is the sentence to be proved.
It should be observed what an extremely elementary form—from the psychological point of view—all mathematical reasonings assume, due to the knowledge and application of the laws of logic and the rules of inference; complicated mental processes are entirely reducible to such simple activities as the attentive observation of statements previously accepted as true, the perception of structural, purely external, connections among these statements, and the execution of mechanical transformations as prescribed by the rules of inference. It is obvious that, in view of such a procedure, the possibility of committing mistakes in a proof is reduced to a minimum.
Exercises
1. Give examples of specifically mathematical expressions from the fields of arithmetic and geometry.
2. Differentiate in the following two sentences between the specifically mathematical expressions and those belonging to the domain of logic:
(a) for any numbers x and y, if x > 0 and y < 0, then there is a number z such that z < 0 and x = y · z;
(b) for any points A and B there is a point C which lies between A and B and is the same distance from A as from B.
3. Form the conjunction of the negations of the following sentential functions:
x < 3
and
x > 3.
What number satisfies this conjunction?
4. In which of its two meanings does the word “or” occur in the following sentences:
(a) two ways were open to him: to betray his country or to die;
(b) if I earn a lot of money or win the sweepstake, I shall go on a long journey.
Give further examples in which the word “or” is used in its first or in its second meaning.
*5. Consider the following conditional sentences:
(a) if today is Monday, then tomorrow is Tuesday;
(b) if today is Monday, then tomorrow is Saturday;
(c) if today is Monday, then the 25th of December is Christmas day;
(d) if wishes were horses, beggars could ride;
(e) if a number x is divisible by 2 and by 6, then it is divisible by 12;
(f) if 18 is divisible by 3 and by 4, then 18 is divisible by 6.
Which of the above implications are true and which are false from the point of view of mathematical logic? In which cases does the question of meaningfulness and of truth or falsity raise any doubts from the standpoint of ordinary language? Direct special attention to the sentence (b) and examine the question of its truth as dependent on the day of the week on which it was uttered.
6. Put the following theorems into the form of ordinary conditional sentences:
(a) for a triangle to be equilateral, it is sufficient that the angles of the triangle be congruent;
(b) the condition: x is divisible by 3, is necessary for x to be divisible by 6.
Give further paraphrases of these two sentences.
7. Is the condition:
x · y > 4
necessary or sufficient for the validity of:
x > 2 and y > 2 ?
8. Give alternative formulations for the following sentences:
(a) x is divisible by 10 if, and only if, x is divisible both by 2 and by 5;
(b) for a quadrangle to be a parallelogram it is necessary and sufficient that the point of intersection of its diagonals be at the same time the midpoint of each diagonal.
Give further examples of theorems from the fields of arithmetic and geometry that have the form of equivalences.
9. Which of the following sentences are true:
(a) a triangle is isosceles if, and only if, all the altitudes of the triangle are congruent;
(b) the fact that x ≠ 0 is necessary and sufficient for x2 to be a positive number;
(c) the fact that a quadrangle is a square implies that all its angles are right angles, and conversely;
(d) for x to be divisible by 8 it is necessary and sufficient that x be divisible both by 4 and by 2 ?
10. Assuming the terms “natural number” and “product” (or “quotient”, respectively) to be known already, construct the definition of the term “divisible”, giving it the form of an equivalence:
we say that x is divisible by y if, and only if, …
Likewise formulate the definition of the term “parallel”; what terms (from the domain of geometry) have to be presupposed for this purpose?
11. Translate the following symbolic expressions into ordinary language:
(a) [(~p) → p] → p,
(b) [(~p) ∨ q] ↔ (p → q),
(c) [~(p ∨ q)] ↔ (p → q),
(d) (~p) ∨ [q ↔ (p → q)].
Direct special attention to the difficulty in distinguishing in ordinary language the three last expressions.
12. Formulate the following expressions in logical symbolism:
(a) if not p or not q, then it is not the case that p or q;
(b) if p implies that q implies r, then p and q together imply r;
(c) if r follows from p and if r follows from q, then r follows from p or q.
13. Construct truth tables for all sentential functions given in Exercises 11 and 12. Assume that we interpret these functions as sentences (what does this mean?), and determine which of these sentences are true and which are false.
14. Verify by the method of truth tables that, the following sentences are true:
(a) [~(~p)] ↔ p,
(b) [~(p ∧ q)] ↔ [(~p) ∨ (~q)],
[~(p ∨ q)] ↔ [(~p) ∧ (~q)],
(c) [p ∧ (q ∨ r)] ↔ [(p ∧ q) ∨ (p ∧ r)],
[p ∨ (q ∧ r)] ↔ [(p ∨ q) ∧ (p ∨ r)].
Sentence (a) is the LAW OF DOUBLE NEGATION, sentences (b) are called DE MORGAN’S LAWS6>, and sentences (c) are the DISTRIBUTIVE LAWS (for logical multiplication with respect to addition and for logical addition with respect to multiplication).
15. For each of the following sentences, state the three corresponding conjugate sentences (the converse, the inverse, and the contrapositive sentence):
(a) the fact that x is a positive number implies that – x is a negative number;
(b) if a quadrangle is a rectangle, then a circle can be circumscribed about it.
Which of the conjugate sentences are true?
Give an example of four conjugate sentences which are all false.
16. Explain the following fact on the basis of the truth table for the function “p ↔ q”: if in any sentence some of its parts which are themselves sentences (or sentential functions) are replaced by equivalent sentences, then the whole new sentence obtained in this way is equivalent to the original sentence. Some of our statements and remarks in Section 10 were dependent on this fact; indicate where this was the case.
17. Consider the following two sentences:
(a) from: if p, then q, it follows that: if q, then p;
(b) from: if p, then q, it follows that: if not p, then not q.
Suppose these sentences were logical laws, would it be possible to apply them in mathematical proofs in an analogous way to the law of contraposition (cf. Section 14)? What conjugate sentences would it be possible to derive from a given asserted implication? Consequently, can our supposition be maintained that the sentences (a) and (b) are true?
18. Confirm the conclusion which has been reached in Exercise 17 by applying the method of truth tables to the sentences (a) and (b).
19. Consider the following two statements:
the fact that yesterday was Monday implies that today is Tuesday;
the fact that today is Tuesday implies that tomorrow will be Wednesday.
What statement may be deduced from them in accordance with the law of the hypothetical syllogism (cf. Section 12)?
*20. Carry out the complete proof of the statement obtained in the preceding exercise; use the statements and law of the hypothetical syllogism mentioned there, and apply—in addition to the rule of substitution and the rule of detachment—the following rule of inference: if any two sentences are accepted as true, then their conjunction may be recognized as true.
1 Logic was created by ARISTOTLE, the great Greek thinker of the 4th century B.C. (384–322); his logical writings are collected in the work Organon. As the creator of mathematical logic we have to look upon the great German philosopher and mathematician of the 17th century G. W. LEIBNIZ (1646–1716). However, the logical works of LEIBNIZ failed to have a great influence upon the further development of logical investigations; there was even a period in which they sank into oblivion. A continuous development of mathematical logic began only towards the middle of the 19th century, namely at the time when the logical system of the English mathematician G. BOOLE was published (1815–1864; principal work: An Investigation of the Laws of Thought, London 1854). So far the new logic has found its most perfect expression in the epochal work of the great contemporary English logicians A. N. WHITEHEAD and B. RUSSELL: Principia Mathematica (Cambridge, 1910–1913).
2 The historically first system of sentential calculus is contained in the work Begriffsschrift (Halle 1879) of the German logician G. FREGE (1848–1925) who, without doubt, was the greatest logician of the 19th century. The eminent contemporary Polish logician and historian of logic J. LUKASIEWICZ succeeded in giving sentential calculus a particularly simple and precise form and caused extensive investigations concerning this calculus.
3 It is interesting to notice that the beginning of this discussion dates back to antiquity. It was the Greek philosopher PHILO OF MEGARA (in the 4th century B.C.) who presumably was the first in the history of logic to propagate the usage of material implication; this was in opposition to the views of his master, DIODORUS CRONUS, who proposed to use implication in a narrower sense, rather related to what is called here the formal meaning. Somewhat later (in the 3d century B.C.)—and probably under the influence of PHILO—various possible conceptions of implication were discussed by the Greek philosophers and logicians of the Stoic School (in whose writings the first beginnings of sentential calculus are to be found).
4 The first attempt of this kind was made by the contemporary American philosopher and logician C. I. LEWIS.
5 This method originates with PEIRCE (who has already been cited at an earlier occasion; cf. footnote 2 on p. 14).
6 These laws were given by A. DE MORGAN (1806–1878), an eminent English logician.