Nuclear Engineering and Technology for the 21st Century

7. Risk importance of component represented by multiple different FT modules or basic events in different accident scenarios, none involved in a CCF Group

7.1 Introduction

In this section we continue consideration of component-level importance measures for a component which is not involved in any CCF group. In Section 6 the component of concern was, wherever it appears in the PRA fault tree structure, always presented by the same FT module (sub-tree). For this reason, the logic expression for the top event could have been, with respect to the considered component, written as:

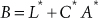
(7.1)

(This is the expression (5-3) rewritten for a FT module, instead of a single basic event.) However, many times a particular component in a PRA model may be represented by different FT modules (sub-trees) or different single basic events for the same failure mode under different conditions imposed by different accident sequences. The examples may include:

Higher likelihood of particular failure mode due to harsh ambient conditions created by particular initiators (e.g. high energy line break [HELB]) as compared to, e.g., general transient;
Different mission times applicable to different accident sequences (e.g. mission time for emergency feedwater turbine driven pump [EFW TDP] in the station blackout (SBO) sequence may be limited by the capacity of batteries (availability of instrumentation and control power), while in the general transient there may be no such limit);
Modeling of seismically induced failures of SSCs in a seismic PRA. (Different seismically induced failure probabilities apply when quantifying risk from different intervals of seismic intensity.)

In the case that different component-level FT modules apply in different event sequences the above expression (7-1) is to be rewritten as:

(7.2)

where Ai* refers to a specific FT module (or basic event) and Ci* to its corresponding C term as defined in Sections 6 and 5. It should be noted that for every pair i and j (i ≠ j) both apply: Ai* ≠ Aj* and Ci* ≠ Cj*. It is important to stress that none of the FT modules Ai* involves a basic event which would represent a CCF shared by other components, as we are still considering a component which is not involved in any CCF group.

In order to be able to obtain the component-level expressions for the importance measures for this case, we will introduce additional term:

Xi = Challenge to the considered component comes from the failure mode(s) represented by the FT module (or basic event) Ai*, given the component has been challenged, i = 1,...,n.

In order to simplify the evaluation it will be assumed that any Xi and Xj, i ≠ j, are mutually exclusive (i.e. 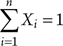cover , where sum refers to the union and “1” refers to the complete set of hypotheses). This assumption is a simplification. However, it can be supported by the point that different FT modules (or basic events representing failure modes under different conditions) of the considered component usually appear under different initiators (ETs) or different sequences under the same ET. Initiator categories in the PRA are usually defined in a way to be mutually exclusive (e.g. if LOCA event is “large”, then it is not “medium”; if reactor trip is due to loss of connection to grid then it is “loss of offsite power” initiator, otherwise it is one of “transients”, etc.). Different sequences within the same ET are mutually exclusive by definition (because each pair of sequences involves at least one function or system with opposite status). (It is noted here that minimal cutsets may not explicitly show the “success events” and for this reason some cases of mutual exclusivity may not be explicit. However, this is one of the PRA issues with broader implications and their evaluation is far beyond the scope of this discussion.)

The above assumption implies that challenges Ci* (i = 1,...,n) are mutually exclusive, which is explained by the same rationale (i.e. mutual exclusivity of event sequences in PRA). It enables introducing general term C* which represents occurrence of any scenario or combination of events (initiator followed by failures or errors) which requires successful operation of considered component in order to prevent the top event (e.g. reactor core damage) from occurring, and which is defined as:

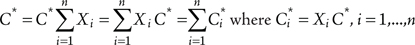
(7.3)

It is now, also, possible to introduce effective general failure of considered component upon challenge. The sum in (7-2) can now be rewritten as:

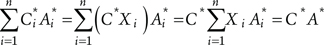
(7.4)

where

(7.5)

represents the mentioned effective failure of considered component. At the same time, this brings (7-2) back to the general form expressed by (7-1), meaning that the problem of calculating component-level importance measures is reduced to the one already discussed in Section 6. The same equations can be used for FC, RAW, RRW and reliability importance. However, to calculate the “effective” total failure probability P(A*), the terms P(Xi) (conditional probabilities) will have to be known for all particular FT-modules Ai* (i = 1,...,n). This is further discussed in the sections which follow. Sections 7.2 through 7.4 establish the expressions for all four importance measures for this case. Section 7.5 provides an example based on the simplified PRA model described in B.1, Appendix B.

7.2 FC

With above introduced terms considered, deriving the expression for FC measure for a component represented by a group of FT modules Ai*, i = 1,...,n, is straightforward.

Starting from the most general expressions for absolute contribution, (5-10) and (6-2), and considering mutual exclusivity of terms (Ci*Ai*), discussed above:

(7.6)

where the term IFC,i* (i = 1,...,n) represents the absolute contribution of the FT module Ai*.

Therefore, the absolute and fractional contributions of a component represented by n different FT modules (basic events) Ai* in the different sequences in PRA model can be written as:

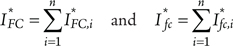
(7.7)

With component-level FC known, it will be possible to calculate other importance measures, as it was in the previous cases.

7.3 RAW

The formula (6-4), which is generalized form of (5-17), can be used to calculate the RAW for a component represented by multiple FT modules. However, the total effective failure probability P(A*) needs to be known. From (7-5) and the assumption that the terms Xi(i = 1,...,n) are mutually exclusive:

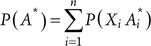
(7.8)

Any term X* is related to challenges to the component (specific challenge Ci* and general challenge C*) and not to the performance of the component. Therefore, it can be claimed independent from Ai* (on the same basis on which Ci* was earlier claimed independent from Ai*).

Therefore:

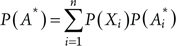
(7.9)

Thus, set of the conditional probabilities P(Xi) (i = 1,...,n) needs to be known in order to be able to calculate P(A*). Particular term P(Xi) can, according to the definition of Xi, be written as:

(7.10)

In the above derivation, it is considered that Ci* implies C* and that terms Ci* (i = 1,...,n) are assumed to be mutually exclusive. Considering that P(Ci*Ai*)=IFC,i (absolute contribution of FT-module Ai*, (7-6)) and that Ci* and Ai* are claimed independent (P(Ci*Ai*)=P(Ci*)P(Ai*), (6-2)):

(7.11)

With this, the conditional probability P(Xi) (i = 1,...,n) can, finally, be expressed as:

(7.12)

and total effective failure probability P(A*) becomes:

(7.13)

Thus, RAW for a component with multiple FT modules can be expanded into:

or:

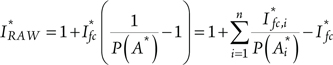
(7.14)

It is noted that, because P(Ai*) <1 (i = 1,...,n), it will always be 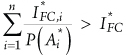(and, consequentially, IRAW > 1).

7.4 RRW and reliability importance

The RRW and reliability importance for a component with multiple FT modules can be directly calculated by (6-5) and (6-6), respectively, by using the component-level FC and above derived total effective failure probability P(A*).

7.5 Example: standby pump with two different operating failure rates

It is very important to be able to properly define different FT-modules Ai* and accompanying challenges Ci*, because the results of component-level importance calculations depend on this. Proper identification of FT-modules may call for “detailed” knowledge of the PRA model. We try to illustrate these points on the following example.

The example continues with CVCS Positive Displacement Pump from 6.3. For the sake of illustration, it will be assumed that pump has considerably higher operating failure rate under the conditions created by the initiators “Total Loss of Component Cooling Water (CCW)” and “Total Loss of Essential Service Water (ESW)” than its nominal failure rate. (For example, this may be due to loss of air conditioning unit in the pump’s room, which is cooled by the CCW.) For this reason, pump’s failure to run for the mission time needs for these two initiators to be modeled by a basic event different from the one which represents the nominal failure rate (Figure 6-1). Therefore, in this case we have the CVCS represented by two different FT modules which apply in different event sequences:

(7.15)

In (7-15) the term AFR represents “failure to run” basic event with nominal failure rate (same as in 6.3) while the term AFR,L represents “failure to run” basic event with higher failure rate which applies under the initiators “Total Loss of CCW” and “Total Loss of “ESW”. The applicability of basic events and the two FT modules is presented by Figure 7-1, which, also, shows the applicable module-level “C terms”.

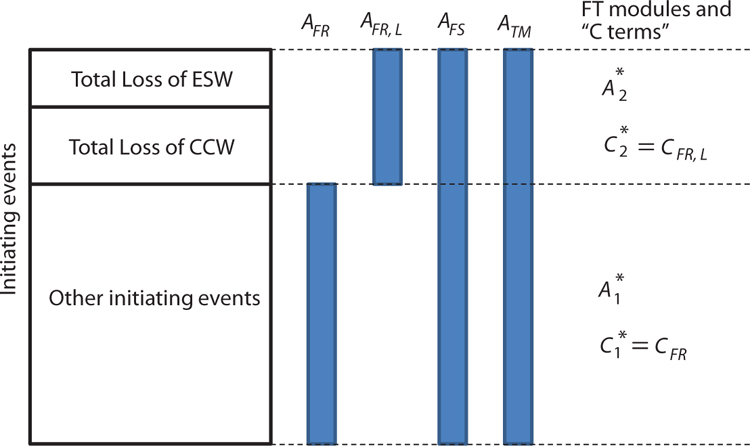
Figure 7-1 Applicability of basic events and the two FT modules (CVCS PDP example).

It is noted here that in the above discussions under Section 7 no statement was made regarding the dependency or mutual exclusivity of the component-level failure modes represented by the FT modules Ai*,i = 1,...,n. The only assumption which was made was regarding the mutual exclusivity of the challenges, i.e. terms Xi (and, hence, Ci*). Thus, in this example we have two component-level failure modes A1* and A2* which are obviously not mutually exclusive. However, they are assumed to be challenged in a mutually exclusive way (Figure 7-1), which comes from the PRA assumption on exclusivity of initiator categories.

First, module-level failure probabilities are calculated for the two modules from (7-15) above, in the same manner as in (6-9):

(7.16)

As before, the calculation of component-level importance measures starts with FC, which is then used to obtain other measures.

7.5.1 FC

With module-level probabilities P(A1*) and P(A2*) known, the component-level absolute contribution can be calculated by (7-6) if module-level challenges Ci*, i = 1,2, are known:

(7.17)

From Figure 7-1 it can be seen that C1* = CFR (i.e. the “C-term” which corresponds to the basic event AFR) and C2* = CFR,L (i.e. the “C-term” which corresponds to the basic event AFR,L). Therefore:

The terms C and A in the above expression are assumed to be independent based on the definitions of basic events in PRA as independent events. Expression (7-11) (which applies to FT module or to a single basic event) can now be used to calculate the terms P(CFR) and P(CFR,L):

(7.18)

Therefore:

(7.19)

In the above equations the terms Ifc,FR and Ifc,FR,L represent FCs of basic events AFR and AFR,L which can be directly obtained from the PRA results. Calculation of component-level FC is, for this case, demonstrated in Example B6 (Appendix B).

7.5.2 RAW

Starting from (7-14):

(7.20)

All terms can be directly “read” from (7-19). Thus:

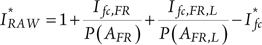
(7.21)

Calculation of component-level RAW for this case is demonstrated in Example B6 in Appendix B.

7.5.3 RRW and reliability importance

The component-level RRW and reliability importance are calculated from I*fc according to (6-5) and (6-6), respectively. This is also demonstrated in Example B6.