Fig. 16.1
Inventors put paradoxes into practice. Horseless carriage and wireless telephone were oxymorons before they became terms for commonplace artifacts. These wonders subtract some essential feature. At nineteen, Blaise Pascal (1623-1662) subtracted thought from subtraction.
In 1651 Pascal built an arithmetic machine to ease his father’s work as tax commissioner. This was a historic feat of engineering. For years, Pascal labored closely with carpenters and experts at gear assembly.
An arithmetic machine seemed especially absurd in the aftermath of René Descartes. He refined the common-sense distinction between mind and matter into a formidable metaphysical dualism.
Your body takes up space, has weight and other properties studied by physicists. Descartes recommended that bodies be studied as machines.
Your mind has no size or weight or other physical properties. Little wonder that your mind is private; only you have direct access to your thoughts. We outsiders only have indirect access to your mind—principally through what you say. Your words betoken thoughts and your thoughts manifest your essential nature as a thinking being. You can conceive of yourself existing without a body but it is self-defeating to conceive of yourself as a nonconceiver. Therefore, you are identical to your mind and only contingently occupy your body.
Descartes went to the morgue to find the point at which mind interacts with the body. He found that brains were symmetrical except for the pineal gland. Descartes deduced that this is the point of interaction. He hoped his discovery would help solve a paradox raised by Johannes Kepler’s advances in optics. Kepler had shown that the retinal image must be inverted relative to the physical world. Descartes directly confirmed Kepler’s discovery by looking through the eyeball of a dead ox. Why does the world look right side up when the retinal image is upside down? Descartes answered that the representation of the optical image is reinverted before it reaches the pineal gland. But dissections never revealed a reinversion mechanism.
George Berkeley eventually persuaded everybody that there was no need for reinversion. Descartes had mistakenly pictured himself as observing the world through his own eyes (in the way he looked through the ox’s eye). There is no internal observer inspecting the optical image. (If there were a little man inside your head, then how would he see?) Once we refrain from relativizing up/down to this homunculus,the paradox fails to get off the ground. The riddle of the inverted image is an example of a paradox that was raised by experiments and resolved by conceptual analysis.
According to Descartes, your body is determined by the laws of nature. But your mind is free. Indeed, Descartes blamed all errors on human willfulness. We jump to conclusions out of laziness and desire. We should be ashamed because God’s goodness ensures that he has given us enough resources to ascertain the true nature of reality. If God had rigged up the world in the way feared by the skeptics, then God would be a deceiver—which is incompatible with God’s beneficence and power. God must have given us a fair opportunity to learn about the nature of the external world beyond our minds. Descartes’s Discourse on Method shows philosophers and scientists how to exploit this opportunity.
In the Meditations Descartes endeavors to prove all this from an indubitable basis. The possibility of dreams and illusions drives him to a purely internal perspective. If he can prove that God exists, Descartes will prove that we can know the external world. But until God is proved, Descartes can only use the data available to his immediate consciousness. Thus Descartes is confined to a priori proofs of God’s existence. Descartes’s first proof portrays his idea of God as an infallible trace of God himself. All other sources for the idea are methodically excluded: Descartes could not have obtained that idea from himself because he is finite. Nor can an idea of God result from adding two finite ideas (in the way Descartes gets the idea of a unicorn by combining the idea of a horn and the idea of a horse). Adding finite things together only produces finite things. Nor can the idea of God come from subtracting one idea from another. Infinity is not a subtraction from finitude. So the idea of God must have come from God himself. Descartes also uses Saint Anselm’s ontological proof: God is the greatest conceivable being. It is better to exist than not exist. Therefore, we must conceive of God as existing.
We may think that Descartes’s philosophy overworks God. But after Descartes visited Pascal in 1647, Pascal complained to his sister Gilberte, “I cannot forgive Descartes: in his entire philosophy he would like to do without God; but he could not help allowing him a flick of the fingers to set the world in motion; after that Descartes had no more use for God.” (Coleman 1985, 19)
Descartes is impressed that we have access to abstract truths such as 10,000 - 2,000 = 8,000. This truth is not a summary of past experiences in which you have removed 2,000 objects from 10,000 objects and found the remainder to be 8,000 objects. You have never actually counted so many objects. And if you did, you would not accept any “counterexample” to 10,000 - 2,000 = 8,000. The equation transcends experience. From this lofty perspective, it is hard to see how gears could perform the fundamental operations of arithmetic. Yet, there sat Pascal’s calculator grinding out differences on the tax commissioner’s desk.
When descendants of Pascal’s adding machine acquired the versatility of the 1950s “electronic brains,” these mechanical marvels were increasingly regarded as near counterexamples to Descartes’s dualism. We now feel an awkward kinship with computers—especially the robots in science fiction.
Disciples of Alan Turing (1912-1954) welcome our inclination to attribute minds to machines. They see automata as an opportunity to demystify consciousness. What matters to functionalists is what the thing does, not what it is made of. This is the thrust of Turing’s test for thought: if a computer can converse in a way that is indistinguishable from a human being, then that computer is a thinking machine. If you are a silicon robot that is doing exactly what my carbon-based readers are doing, then you are reading my book and having thoughts about Pascal’s arithmetic machine (one of your earliest ancestors).
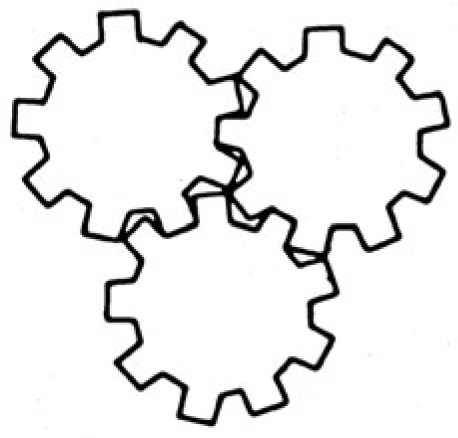
Those with lingering sympathy to Descartes believe that Turing’s emphasis on behavior is refuted by the possibility of zombies: mindless creatures who are functionally indistinguishable from people with minds. Since a zombie is not conscious but can do anything its minded counterpart can do, consciousness does not depend solely on input-output relations. Although the zombie thought experiment is intuitively persuasive, functionalists reply that our imaginations are faulty guides to what is possible. Suppose Pascal’s mechanical calculator had three gears aligned as in figure 16.1. It is easy to imagine the gears all spinning. But they are actually gridlocked.

Fig. 16.1
Perhaps you have now rerun the gear thought experiment and have spotted the subtle jam. Now focus your mind’s eye on a scenario involving four interlocked gears (fig. 16.2). Still jammed?

Fig. 16.2
The right answer is that the four-gear assembly can turn. In general, an even number of interlocked gears can turn but an odd number cannot. This principle dictates gridlock for the nineteen-gear circuit that is depicted on the silver-gold, two pounds coin introduced by the Royal Mint on June 15, 1998. Brute inspection cannot overturn the impression that this large assembly of gears can all spin. The gridlock is too sensitive to the small difference of whether the large number of gears are odd or even. We need theory to overrule imagination’s verdict. Similarly, the functionalist can insist that theory is needed to correct the impression that a functional equivalent of you can be free of consciousness.
During Descartes’s visit, Pascal tried to convince him that vacuums exist. Descartes believed that reality had to be a plenum. He wrote Christian Huygens that Pascal “had too much vacuum in his head.”
Pascal began thinking about vacuums in 1646 when he learned of Evangelista Torricelli’s experiment with a barometer. This involved placing a tube of mercury upside down in a bowl of mercury. Everybody wondered what kept the mercury suspended in the tube. The received view was that the “empty space” in the tube was filled with rarefied and invisible matter. Following Aristotle, they believed that nature abhors a vacuum. Pascal regarded the issue as empirical rather than conceptual. He conducted a series of experiments that dramatically supported the vacuum hypothesis. His conclusion was that there really was nothing holding up the mercury. Nor is there anything pulling liquid through a siphon. Instead the ocean of air that surrounds the earth presses down on the liquid except where there is a vacuum. In his 1653 “Treatise on the Equilibrium of Liquids,” Pascal states his law of pressure: “Pressure applied to a confined liquid is transmitted undiminished through the liquid in all directions.” When you suck on a straw, you decrease the pressure in the tube leading to your mouth. The liquid on the other end of the straw is no longer being so strongly pushed down and so rises to your lips.
In the age of rocket travel, we know empty space is a killer. But only in virtue of what it fails to do. If you were to step into the void without protection, your blood would boil. But not because empty space is hot. You would die because the void fails to exert pressure on your body. But what caused the death? Nothingness? Sheer space? Or must we suspend the requirement that effects have causes?
Physicists have not answered these questions with much more success than philosophers. However, physicists are at home with vacuums. They regard voids as part of the basic furniture of the universe.
Voids bubble more uncomfortably through common sense. The central stanza of Bette Midler’s “Wind Beneath My Wings” gratefully praises a selfless friend who quietly assists the outgoing singer in her ascent to fame: “Did you ever know that you’re my hero? You’re everything I would like to be. I can fly higher than an eagle, for you are the wind beneath my wings.” In light of Pascal, aerodynamicists now know that flight is made possible by the vacuum formed above moving wings. Thus, the refrain should be “I can fly higher than an eagle, for you are the void above my wings.”
Laws governing a vacuum seem impossible because there is nothing for the law to be about. Chance also seems law-resistant. Randomness is absence of order. Pascal was stimulated by the conceptual tension. In his 1654 “Address to the Academie Parisienne de Mathematiques,” Pascal concludes: “Thus, joining the rigor of demonstrations in mathematics with the uncertainty of chance, and conciliating these apparently contradictory matters, it can, taking its name from both of them, with justice arrogate the stupefying name: The Mathematics of Chance.”
Pausanias mentions a picture painted by Polygnotos in the fifth century which shows Palamedeo and Thresites playing dice. According to Greek tradition, Palamedo invented dice to entertain bored Greek soldiers waiting for the battle of Troy. But dice go back to the first dynasty in Egypt. Randomizing devices, fashioned from symmetrical animal bones, date back to the Paleolithic era.
Despite this long history, the first book on dice is Gerolama Cardano’s De Ludo Aleae, which was published in 1663, one hundred years after it was written. Cardano systematically addresses conflicts between theoretical predictions about how dice should behave and observations about how they actually behave. For instance, gamblers knew that with two dice, 9 and 10 can be made up in two different ways from 1, 2, 3, 4, 5, 6 namely, 9 = 3 + 6 = 4 + 5 and 10 = 4 + 6 = 5 + 5. They inferred that 9 and 10 should result with equal frequency. Yet experience indicates that 9 is more frequent.
Cardano accepts the observational evidence and amends the theory. He notes that the order of the cast is relevant. 9 can be made up by four permutations: 9 = 3 + 6 = 6 + 3 = 4+ 5 = 5 + 4. But 10 can only be made in three permutations: 10 = 4 + 6 = 6 + 4 = 5 + 5.
To a modern reader, this problem seems too easy to qualify as a paradox. But “paradox” should be relativized to the thinker in question. The earliest recorded use of “paradox” in 1616 states: “Paradox, an opinion maintained contrary to the commonly allowed opinion, as if one affirms that the earth doth move round and the heavens stand still.” (Bullokar’s Chapbook) What had been hailed as the “Copernican paradox” is no longer a paradox because Copernicus’s arguments in favor of the earth orbiting the sun are no longer held in check by Aristotle’s objections (that dropped objects would fall far from point of release, that wind would blow trees down, that we would see stars whoosh by). Just as news stops being news and becomes history, some solved paradoxes stop being paradoxes and become orthodoxies. “This was sometime a paradox, but now the time gives it proof.” (Shakespeare, Hamlet III.i.114–15)
People who have yet to distinguish between combinations (groupings in which order is irrelevant) and permutations (groupings in which order is relevant) will be baffled by the apparent misbehavior of dice. It will take a Cardano to fight his way up to the vantage point that makes the paradox seem like a trivial mistake.
Cardano was serious about making observation fit with theory. Cardano cast a horoscope predicting the hour of his own death. When that day dawned and he found himself healthy and safe, Cardano killed himself rather than falsify the prediction.
Recall the television game show “Let’s Make a Deal” hosted by Monty Hall. A contestant selects one of three doors and wins whatever prize is behind the door. Behind one door is a valuable prize while the other two contain prank prizes, such as a goat. Suppose that you are a contestant and have picked door number 1. To increase the suspense, Monty shows you what is behind door 2. You expect to see no prize behind the door Monty shows because you know that he always reveals a losing door. He then offers you the chance to trade your claim on what is behind door 1 for what is behind door number 3. Should you switch?
In the September 1991 issue of the Parade magazine column “Ask Marilyn,” Marilyn vos Savant advised switching. Many mathematicians scolded Marilyn for committing a fallacy.
But Marilyn was right. Most people infer that switching is pointless because you already know that Monty will reveal a losing door. And indeed, the two remaining doors would have an equal chance of being winners if Monty Hall had randomly revealed a door. However, Monty only reveals losing doors. Monty’s revelation that door 2 has a goat cannot raise the probability that door 1 has the prize because you already knew that Monty was going to either reveal 2 as a loser or reveal 3 as a loser. However, Monty’s revelation that door 2 is a loser does increase the probability that 3 is the winner. Prior to this news, door 3 only had a 1/3 chance of holding the prize. After learning that door 2 is a loser, the probability that the prize is behind door 3 rises to 2/3 because the probability of door 1 winning is not affected.
Nearly everybody gets the Monty Hall problem wrong. Many resist the correct answer even when it is explained to them. Despite Monty’s extensive roster of victims, I am reluctant to describe “Should you switch doors?” as a paradox. True, there are conflicting good answers if brute persuasiveness is the standard. But might does not make right. The goodness of answers must be ranked by an objective standard (consistency with observation, common sense, scientific principles, etc.). After all, the point of grading answers is to figure out what we should believe. The Monty Hall problem was never a theoretical anomaly. The only professional controversy has been between rival psychological theories as to why this fallacy is so powerful. At the level of refereed journal articles, there has always been total consensus on the correct answer to Should you switch doors?—including among philosophers (who supposedly disagree about everything).
There is looseness in what counts as the best available perspective. Consequently, there will be looseness in what counts as a paradox. If we relativize the phrase to ideal thinkers, few surprises will count as a paradox. If we relativize to an amateur’s perspective, then too many surprises will count as paradoxes. To keep paradox a discriminative term, we relativize to the perspectives of contemporary, well-functioning experts. For questions that lack experts, we relativize to the perspective of reasonable, intelligent people.
As illustrated by the circumnavigator’s paradox, systems of intellectual division of labor can change. In a society that did not defer to statistics professors, the Monty Hall problem would qualify as a paradox—as would the dice puzzles resolved by Cardano.
The French gambler Chevalier de la Méré introduced Blaise Pascal to the division paradox. Suppose two gamblers have agreed that whoever wins six rounds gets the whole prize. Each round is determined by chance, say, in accordance with the flip of a coin. The game is cut short after the first player has won five rounds and the second player has won three rounds. How can the prize be divided fairly?
The question was inconclusively discussed in the later middle ages as a problem of proportions. Pascal and his correspondent Pierre Fermat approached it as a problem of probabilities: from their fresh perspective, the players should divide the prize in accordance with the likelihood they would have won it had the game continued. The second player would win if and only if he won all of the next three rounds. The chance of that happening is ½ × ½ × ½ = 1/8. Therefore, the second player should receive 1/8 of the prize and the first player should receive 7/8. Pascal and Fermat generalized this solution, independently of each other, in 1654. The origin of probability theory is frequently traced to this date.
Probability theory was suddenly thriving in the 1660s. The revolutionary prospect of putting gambling and insurance on a mathematical basis intrigued entrepreneurs. By 1688 London business circles knew of the existence of an insurance company that was run within Edward Lloyd’s Thames-side coffeehouse on Tower Street. Hazardous maritime ventures could be undertaken without fear of utter ruin because one could hedge the risk by, in effect, betting that the cargo would be lost. The underwriters needed evidence about the probability of setbacks. However, the early underwriters made little meaningful use of probability theory. In practice, they fell back on ancient techniques for decreasing risk such as distributing cargo among several ships. Mainly, they used just the sort of heuristics that contemporary psychologists urbanely ridicule. These traditional businessmen were more prosperous than those who prematurely applied probability theory. After all, there was a critical lack of organized data and statistical techniques.
Anyone who could build the infrastructure needed for sound statistical inferences still stood to make a fortune in the insurance industry. To meet the demand for information about human life spans, mortality tables were compiled. These tables generated paradoxes similar to the dice enigmas discussed by Cardano. Edmond Halley showed that the average life span is 26 years and yet the chance of surviving beyond age 8 is ½. He was puzzled why the average age of the population is not 8.
Practical Englishmen were discouraged by the ease with which conflicting probabilities could be calculated. The statisticians often resembled those who prophesied by anagrams. The religious fanatic Lady Eleanor Davies (died 1652) discovered that the letters of her name, with an L substituted for the final S, could be rearranged as “Reveal, O Daniel.” When brought before the Court of High Commission, she cited this anagram as evidence that she was possessed by the spirit of the prophet Daniel. The bishops thought she was mad but she had replies to all their objections. Finally, one bishop, who had been writing furiously during the proceedings, announced that he had irrefutable proof that Lady Eleanor was insane. He read out the anagram “Dame Eleanor Davies—never so mad a ladie!”
“From around 10:30 until about 12:30 in the morning” on November 24, 1654, Pascal had a mystical experience. Eight years later, an inscription was discovered sewn into the jacket that clothed his corpse: “FIRE. God of Abraham, God of Isaac, God of Jacob, not of the philosophers or of the learned. Certainty. Certainty. Feeling, Joy, Peace. . . . Total Submission to Jesus Christ and to my director. Eternally in joy for one day of exercise on earth. . . . ” Following that November morning, Pascal withdrew from scientific research and devoted himself to religious activities.
Blaise Pascal retained an interest in converting his libertine acquaintances to Christianity. In his Pensées, Pascal argues that, from a nonbeliever’s perspective, it is prudent to acquire a belief in God: There is at least an outside chance that God exists. The implications are tremendous because God rewards believers with heaven and punishes unbelievers with hell. Since any fraction of the infinite is itself infinite, the expected value of theism is infinite. However much finite good accrues from secular living, the religious life is infinitely more prudent.
If belief were voluntary, as Descartes assumed, then the issue is simply a matter of deciding what to believe. But incentives for a belief do not directly cause beliefs in the way that evidence does. I hereby offer you a hundred dollars to believe that this book will ignite in ten seconds. Now you have a reason to believe this book will ignite. However, this incentive is not the sort of reason that makes you believe that this book will ignite. To believe, you need a reason that bears on the truth of the proposition that this book will ignite. So even if Pascal has given you a reason that you should believe that God exists (by pointing out the incentive of heaven), he has not given you the sort of reason (evidence) that produces belief that God exists.
Pascal’s Pensées contains remarks that show the wager is not derailed by the distinction between incentives and evidence. He advises the libertine to indirectly acquire a belief in God. Since belief is contagious, an unbeliever can gradually become a Christian by socializing with Christians and participating in rituals. At first, the libertine will be just going through the motions. Eventually, beliefs catch up with behavior. Once a Christian, the former libertine will disapprove of his original profit motive for becoming a Christian. But the selfish motive that precipitated his Christianity is not needed to continue his faith. Once the wager argument has done its work, the new Christian can jettison the crass calculations.
Pascal cannot get his foot in the door if the atheist believes he knows that God does not exist. To pry open the minds of dogmatic atheists, Pascal adapts Sextus Empiricus’s techniques. Pascal’s goal is to demonstrate that reason is a culde-sac. He humbles the reader’s intellect with a steady plipplop of antinomies. The paradoxes descend from man’s unique recognition of his finitude. All animals are finite but only man appreciates the contrast with infinity. Life is short for all animals. But man alone dreads death and perceives the menace it poses to the significance of his life. All creatures are specks in a vast cosmos but only man can recognize himself as a speck.
What sort of freak then is man! How novel, how monstrous, how chaotic, how paradoxical, how prodigious! Judge of all things, feeble earthworm, repository of truth, sink of doubt and error, glory and refuse of the universe!
Who will unravel such a tangle? This is certainly beyond dogmatism and scepticism, beyond all human philosophy. Man transcends man. . . .
Know then, proud man, what a paradox you are to yourself. Be humble, impotent reason! Be silent, feeble nature! Learn that man infinitely transcends man, hear from your master your true condition, which is unknown to you.
(1966, No. 131)
Pascal feels it is dangerous to explain how much man is an animal without also pointing out his greatness. Pascal wields an emotional analogue of Sextus Empiricus’s method of equipollence:
If he exalts himself, I humble him.
If he humbles himself, I exalt him.
And I go on contradicting him
Until he understands
That he is a monster that passes all understanding.
(1966, No. 130)
Voltaire and Fermat were disturbed by Pascal’s new polemics. They interpreted the wager as an effect of declining health. Pascal’s “Prayer to Ask God for the Good Use of Illnesses” suggests that Pascal might have agreed! As Pascal suffered through the final stages of stomach cancer, he expressed fear of recovery rather than of further illness or death: “Don’t pity me! Illness is the Christian’s natural state. We all ought always to be like the sick man, suffering from the privation of every good and of all sensual pleasures, exempt from every passion . . . , without ambition or greed, constantly awaiting death.” (Cole 1995, 249) The sick Christian, Pascal continues, should be thankful when forced to be just as he ought to be.
The main objections to Pascal’s wager focus on the argument rather than the man who devised it. In 1746, Denis Diderot declined the wager with the observation that “An Imam could reason just as well this way.” Pascal has left out the possibility that there is a Baal or a Moloch or a Zeus or some other claimant of faith. In the absence of doctrinal constraints, we must also include inversions such as the possibility that God rewards the doubters and punishes believers. To narrow the field of contenders, Pascal must revert to the theologizing that initially seemed bypassed by the wager.
Pascal’s wager is also challenged by economists who reject the possibility of infinite utility. Their finitism emerged in discussions of a problem that was first stated in a letter written by Nicholas Bernoulli and published in 1713. A fair coin will be tossed until a head results. You will then be paid $2n-1 where n equals the number of tosses. So the expected return is: (½ × $1) + (¼ × $2) + (1/8 × $4) + . . . :+ (½n × $2n-1 +. . . . Since each addend equals a half dollar, and there are infinitely many of them, the sum is infinite. Thus, someone who maximized expected money should be willing to pay any amount of money for this bet. Yet few people would pay $100 for the deal.
Jean d’Alembert named this puzzle the St. Petersburg paradox because the first article on the paradox was published by the Imperial Academy of Sciences at St. Petersburg. The author was Nicholas Bernoulli’s cousin Daniel Bernoulli. He pointed out that doubling one’s cash holdings from a million to two million does not really double its value to you. Each new dollar tends to have less influence on your welfare than the preceding dollar. Daniel Bernoulli’s insight is enshrined in contemporary economics as the law of the diminishing marginal utility of money. The rate of diminution resists precise calculation, but Daniel Bernoulli inferred that it is a logarithmic function. This would preclude infinite sums.
In economics, the most popular solution to both the wager and the St. Petersburg paradox is evaluative finitism. Following Daniel Bernoulli, economists formulate the axioms of decision theory in a way that ensures value is necessarily finite. This limit on desire grates against several economic themes. Economists tell us that desire is insatiable, that ends cannot be irrational, and that what counts are people’s beliefs about what they can acquire rather than what actually exists. Right or wrong, Pascal seeks the infinite reward of heaven and flees from the infinite punishment of hell. Indeed, most people have religious hopes and fears of infinite proportion. Whether or not infinite value can be actually secured, the economist seems obliged to model the choices of those who believe in infinite value.
Economists try to enforce their finitism by peppering doubters with the puzzles that accrue from allowing nearly any infinite aspect into decision theory. Take the possibility of infinite time. In Foundations of Statistics, Leonard Savage notes that the longer you save, the more you have. So it seems an immortal should save forever! Savage sidelines the enigma by stipulating that his theory only applies to finite quantities. But the puzzle does not require infinite value. Suppose a bottle of Everbetter wine improves endlessly but only to the limit set by the quality of a moderately nice wine. (Pollock 1983) This finitely good wine gets better only in the way 1/n gets closer to 0. When should an immortal connoisseur drink the wine? Not now because it will be better later. Not at any particular time later because the wine would be even better if the connoisseur waited. Yet it now seems that he never drinks the wine!
Alternatively, we can imagine the probability undergoing an infinite improvement. Suppose a bookkeeper is eternally lodged in limbo. Limbo is a neutral state, neither good nor bad. The bookkeeper has a single opportunity for a vacation to another state somewhat better than limbo, say, two weeks in Florida. Since the bookkeeper’s odds of failing to get the vacation equal 1/n for each year spent in limbo, the bookkeeper should definitely wait more than one year. But the numbers seem to doom him to an unbroken stay in limbo.
Economists also use their finitism to solve paradoxes that initially do not appear to involve infinity. Consider the two envelope paradox: You are offered a choice between two envelopes, A and B. You are informed one envelope contains twice as much as the other. You pick A. The organizer of the event then asks you whether you want to switch envelopes. Should you switch?
Go ahead, peek inside your envelope. You find $10. Now you know envelope B either contains $5 or $20. Since each alternative is equiprobable, the expected value of switching to B is (½ × $5) + (½ × $20) = $12.50. Since that is a gain of $2.50, you should switch. The same argument works regardless of how much money you find in the envelope. Therefore, you are justified in switching even if you do not bother to look inside envelope A.
The argument against switching is that envelope A is just as likely to contain twice as much as B as B is as likely to contain twice as much as A. So A and B are of equal value. Anti-switchers also note that the argument for switching has a weird implication. Suppose envelope B was given to another contestant. The switching argument would apply equally to him and so would advise him to trade his envelope for yours!
Commentators on the two envelope paradox agree that the question of whether to switch is resolvable if you know there is a limited supply of cash. For instance, if you know that the game organizers have at most $1,500 to distribute, then you would not want to switch if you found $1,000 in your envelope. Nor would you want to switch if the amount were close to $1,000. If you find $1, then you should definitely switch. Ditto for amounts close to $1. When you know how much money is available, the amount of money in your envelope becomes a clue as to how much money is in the other envelope.
But what should you do if the money supply is infinite? Now the problem resembles the St. Petersburg paradox. Economists who follow Nicholas Bernoulli complain that the two envelope paradox overlooks the diminishing marginal utility of money. They will toss the two envelope paradox in the same wastebasket that contains the Saint Petersburg paradox and Pascal’s wager.
I personally think that a complete economic theory (or ethical theory) must allow for some decision problems that involve infinite value, infinite time, and infinite populations. Possibly, physics or metaphysics will one day exclude these infinities as objectively impossible. But this only seems relevant when we overlook the subjective nature of decision theory. What counts for the decision theorist are people’s perceptions of their situation, not the situation itself. Therefore, a decision theory that does not take Pascal seriously cannot itself be taken seriously.
The strangeness of Pascal’s opinions has been surpassed by other gifted mathematicians—sometimes to the ruin of other mathematicians. In the course of researching the two envelope paradox (which has recently become a hot topic in economics and philosophy), I discovered that the prolific Edmund Landau introduced it in 1912 (Kraitchik 1930, 253). This is the same Edmund Landau who was fired by the University of Göttingen in 1934 for a Jewish definition of π. Landau’s textbook characterized π/2 as the value of x between 1 and 2 for which cosine x vanishes. Nazi students were incensed by such abstraction. The prominent number theorist Ludwig Bieberbach published a defense of the dismissal on the grounds that Landau was imposing his racial style on sensitive young Germans.