Fig. 17.1
According to Pascal, we are wise enough to appreciate our contradictions but not wise enough to resolve them. He winds up using probability calculations as a ladder to heaven—a ladder that is kicked away after religious conversion.
The philosophers in these next three chapters are more optimistic about our ability to solve the paradoxes. Their basic strategy is conservative. Each identifies some successful area of human thought and holds it up as a model of how we ought to think. Paradoxes are diagnosed as failures to absorb the lessons the model tacitly demonstrates. For rationalists, the model is mathematics and logic. The traditional problem with this model is application. How can lofty a priori reasoning instruct us about the nitty-gritty empirical world? This gap was widened by increasing reluctance to view the world of the senses as having a lesser degree of reality than the world of triangles and frictionless planes.
Gottfried Leibniz (1646-1716) interpreted probability theory as a new way to link pure deduction to the empirical realm. For him, probability theory is a branch of logic. Whereas deductive logic handles arguments that aim to make the conclusion certain given the premises, inductive logic deals with arguments that aim to make the conclusion probable given the premises. As a diplomat, Leibniz hoped that the mathematics of chance would become a tool of conflict resolution. The contending parties would pool their evidence and then calculate the probabilities of rival hypotheses. Although calculation need not yield the truth of the matter, it would produce agreement.
There has been some progress toward this ideal. In a well structured experiment, the scientists turn over their data to statisticians. Some parts of the job of assigning probabilities are so mechanical that they can be delegated to computers. Computer simulations have been used to demonstrate the correct solution to the Monty Hall problem. Perhaps computers will one day solve some deep paradoxes.
In 1678 Leibniz was the first to define probability as the ratio of favorable cases to the total number of equally possible cases. If equal possibility is understood as equiprobability, then Leibniz’s definition is circular. Pierre-Simon de Laplace (1749-1827), who is often mistakenly credited with inventing the definition, occasionally lapsed into this circularity.
But Laplace normally wielded an epistemic criterion: outcomes are equiprobable if there is no more reason to expect one event rather than another. Laplace’s criterion is satisfied by a coin that is biased in an unknown direction. Since you have no more reason to expect H(eads) than T(ails), H and T are equipossible. Although you know the coin does not have an equal propensity to come up heads or tails, you must assign the same probability. Probability is a measure of our ignorance. Laplace next invites us to consider the case in which the biased coin is to be tossed twice. There are four possible outcomes: HH, HT, TH, TT. Is the event of getting two homogeneous tosses (HH or TT) equipossible with the mixed outcomes (HT or TH)? No, because the bias makes a homogeneous outcome easier to produce than a mixed result. Laplace emphasizes that here the criterion of equipossibility is violated: when the coin is biased, the uniform possibility (HH or TT) is easier to bring about than the mixed result (HT or TH).
Many people think that Laplace’s biased coin illustrates the ambiguity of “probable.” In the objective sense, H and T are not equally probable outcomes for the biased coin. The equiprobability is only subjective: each outcome receives the same degree of credence. This subjective sense invites a further division between the probability we actually assign and the probability we ought to assign. A man who is less astute than Laplace might wrongly assign the same probability we ought to (HH or TT) as to the (HT or TH) outcome. The probability we ought to assign can be fleshed out by intellectual norms. Surprisingly, the requirement of consistency is enough to ensure conformity with the probability calculus. Your probability assignments are consistent just in case there is no way for anyone to make a “Dutchbook” against you. (A Dutchbook is a collection of individually fair bets that guarantees a net gain for the bookie.)
Leibniz had metaphysical views about equipossiblity that mix objective probability with subjective probability. He has the objective sense of “probable” in mind when explaining which possibilities succeed at becoming actual. Many possibilities are not co-possible. The possibility that conflicts with the fewest other possibilities becomes actual. Thus, simplicity and harmony are guides to empirical truth.
This objective picture of possibilities requires a limbo where nonexistent entities battle to enter the realm of existence. How can nonexistent things do anything? Perhaps this difficulty motivated Leibniz’s subjective account of equipossiblity: possibilities start out as God’s thoughts. These thoughts are complete plans for a universe. Each of these possible worlds is a consistent and complete way that things could be. Since there are many ways things could have been, the actual world is just one of many possible worlds. Those backed by better reasons have a stronger tendency to become actualized by God.
The subjective side of Leibniz’s philosophy assigns God a large role. When one concentrates on the objective side, God looks like a hanger-on, perhaps even an ornament to put Leibniz’s royal patrons at ease.
Leibniz’s system is founded on two principles. The principle of contradiction says that anything that involves a contradiction is false and whatever is opposed to a contradiction is true. At first blush this principle seems to exclude only trivial falsehoods such as “Leibniz was a secretary of the Rosicrucian Society and was not a secretary of the Rosicrucian Society.” But Leibniz believes that it excludes all falsehoods. According to Leibniz, statements always have a subject-predicate form. A statement is true if the predicate is contained in the subject. For instance, “Each man is male” is true because the subject, man, is defined as “male adult human being”; the subject term contains the predicate “male.” For individuals, the subject term consists of a complete description of the individual. Thus, if one could exhaustively analyze the subject term “Gottfried Leibniz,” one would find born in Leipzig on the infinite list of predicates. To an infinite mind, “Gottfried Leibniz was born in Leipzig” is therefore an a priori truth. Since Leipzig is part of the meaning of “Gottfried Leibniz,” a full understanding of Leibniz implies a full understanding of Leipzig. The subject term ‘Leipzig’ in turn involves the residents of Leipzig, relations with other cities, and so on. To fully know anything is to know everything. Each individual mirrors all the other individuals in the universe.
Despite this holism, each individual is “windowless” in that the truths about the individual do not depend on anything else. The internal nature of a thing completely determines its history. The apparent influence of shears upon a shrub is not really an intrusion on the shrub. There is a preestablished harmony between the blades and the twigs. Our actions are an unfolding of our inner natures, so we are free.
Finite minds cannot perform an infinite analysis. Often we limited thinkers can only know the truth by using empirical means—just as accountants must resort to calculators to confirm that 111, 111, 111 × 111, 111, 111 = 12, 345, 678, 987, 654, 321. But this does mean that this equation is made true by the gears of the calculator or any other contingent thing.
Leibniz’s principle of sufficient reason says that everything must have a reason. Leibniz says that we use this principle constantly in our inferences. He cites Archimedes’ reasoning: a scale with equal weights must be balanced because there is no more reason for one side to go up rather than the other.
Leibniz uses the principle of sufficient reason to prove that God exists. A possible world is a complete, alternative way things might be. There are many possible worlds. Why is our world the actual world? There can be a reason only if God exists.
Leibniz believes God chose our world because it is the best of all possible worlds. In Candide Voltaire lampooned Leibniz’s optimism as wishful thinking. But try to sketch out a complete alternative that is better. In Harry McClintock’s “The Big Rock Candy Mountain,” a hobo wistfully sings,
In the Big Rock Candy Mountain, You never change your socks, And little streams of alkyhol, Come trickling down the rocks, O the shacks all have to tip their hats, And the railway bulls are blind, There’s a lake of stew, And gingerale too, And you can paddle all around it in a big canoe, In the Big Rock Candy Mountain
The hobo’s paradise is not idyllic for the blind police with wooden legs, nor for the hens that lay soft-boiled eggs (not to mention the jerk who got hanged for inventing work). The hobo’s improvements over the actual world are relative to his limited perspective.
Don’t expect a perfect world to be perfect for you. The world is perfect in the objective sense of being better over all (as a world). Since variety is good, Leibniz predicted that there are animals of every size, including ones that are too small for us to detect with unaided vision. He also predicted, contrary to Aristotle, that there are intermediate species, including organisms that are borderline cases between animal and plant. Darwin was to later echo Leibniz with his favorite motto “Nature does not make jumps.”
Leibniz also inferred from the principle of sufficient reason that nature cannot make perfect duplicates. For God would have no more reason to put one duplicate here and the other duplicate there. If x is indiscernible from y, then x is identical to y. Leibniz deployed this principle of the identity of indiscernibles against atoms. Since atoms are simple things, they cannot differ qualitatively. There is at most one atom. Yet atomists say that there are many atoms. Therefore, the atomists are refuted by the principle that indiscernible things are identical.
A pair of vacuums would also be excluded by the identity of indiscernibles. One empty space is indiscernible from any other. Even a single vacuum constitutes a gap in nature. That is ruled out by the principle of continuity. God would not wish to forego the opportunity to fill every part of space with something good.
Leibniz put his metaphysics into empirical practice. One of his favorite anecdotes concerns the principle that
There is no such thing as two individuals indiscernible from each other. An ingenious gentleman of my acquaintance, discoursing with me in the presence of Her Electoral Highness, the Princess Sophia, in the garden of Herrenhausen, thought he could find two leaves perfectly alike. The princess defied him to do it, and he ran all over the garden a long time to look for some; but it was to no purpose. Two drops of water or milk, viewed with a microscope, will appear distinguishable from each other. This is an argument against atoms, which are confuted, as well as the void, by the principles of true metaphysics.
(1989, 333)
Leibniz uses the principle of the identity of indiscernibles to rescue the principle of sufficient reason. At first glance, Buridan’s ass is a counterexample to the principle of sufficient reason. Consider someone who attempts to starve an ass by presenting it with two equally appealing bales of hay. This is an unpromising method for killing asses. Wouldn’t the ass just arbitrarily choose one bale over the other? Leibniz responds by insisting that there will inevitably be a small difference between the two bales of hay.
This solution is incomplete because the identity of indiscernibles does not guarantee that the difference is a relevant difference. Leibniz concedes that two eggs can be completely similar in shape. He just denies that the two eggs can be completely similar in all respects. So what prevents the bales from being completely similar in desirability? And since we are really talking about perceived similarity, why can’t the ass just have equal desires for the distinct bales? Empirically, perceived similarity is easier to achieve than actual similarity.
One may also accuse Leibniz of exaggerating the precision of his predictions. Although the principle of the identity of indiscernibles implies that no two leaves are exactly alike, it does not predict that human beings can always detect those differences. If the gentleman had found two leaves that looked exactly alike, Leibniz would have retreated with the clarification that “indiscernible” must be relativized to God. For only God perceives all properties.
Scientists share Leibniz’s tendency to overestimate the precision of their theory’s predictions. When a prediction is confirmed, they do not draw attention to the role of background assumptions and the many inductive leaps needed to connect a theory with a prediction.
Games are usually organized into artificially discrete elements: the equal sides of a die, the uniformly shaped cards in a deck, etc. This encouraged the belief that probability always reduces to questions about combinations and permutations. The theory of combinations was first presented in Leibniz’s Ars Combinatoria.
In 1777, the French naturalist Georges Louis Leclerc, Comte de Buffon, showed that combinations cannot be a complete foundation for probability. His incompleteness argument was inspired by a popular game that involved continuous outcomes. Gamblers throw a coin at random on a floor tiled with congruent squares. They bet on whether the coin would land entirely within the boundaries of a single square tile. Buffon realized that the coin would land within the tile exactly if the center of the coin lands within a smaller square, whose side was equal to the side of the tile minus the diameter of the coin. The probability of winning is simply the ratio of the area of the small square to the area of the tile.
This was the beginning of the study of “geometric probability,” where probabilities are determined by comparing measurements, rather than by identifying and counting alternative, equally probable discrete events. Buffon went on to consider cases involving more complex shapes. In his famous Needle Problem, a needle is thrown at random on a floor marked with equidistant parallel lines. When the spacing of the lines equals the length of the needle, the probability of striking a line equals 2/π.
This unexpected appearance of π as a measure of probability illustrates the interrelatedness of mathematics. People were impressed by how π, an irrational number, could reliably percolate up through a random process. In 1901, M Lazzerini reported making 3,408 tosses and getting a value of π equal to 3.1415929, a figure which is only off by 0.0000003 from the true value of π. (Although a famous result, it is too good to be true. The few mathematicians who bother to probe the details conclude that there was either a methodological error or fakery).
Lazzerini was following the tradition of stochastic simulation inaugurated by Buffon. Buffon encouraged his readers to verify his calculations by repeatedly dropping a needle on a chessboard. In the same article, he reports a simulation used to establish the value of n in the St. Petersburg game. He had a child toss a coin until it appeared heads. The child did this 2,048 times. The results suggested that the value of the game is 5 despite the infinite expected value.
Laplace and Buffon solved the needle problem by extending the principle of indifference to cases involving an infinite number of events (corresponding to a point on a line and lines on a plane). The basic idea is to find a fair way of comparing the favorable region to the total area of possibilities. As a rationalist, Leibniz would have been very pleased to see the principle of indifference generate such an interesting, experimentally testable, precise result.
In 1889 Joseph Louis Bertrand published a collection of probability paradoxes that challenged the principle of indifference. His best known is like Buffon’s except that the needle is tossed on a small circle. Here is Bertrand’s mathematically pristine formulation: “A chord is drawn randomly in a circle. What is the probability that it is longer than the side of the inscribed equilateral triangle?” (1889, 4-5) Bertrand gives three conflicting but apparently cogent answers to this question.
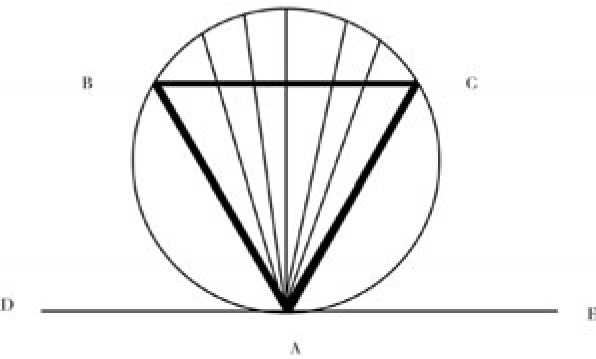
First solution: A chord of a circle is any straight line touching two points of its boundary. For convenience, consider all the chords emanating from point A at a vertex of the equilateral triangle, as in figure 17.1. (The argument can be adapted to points other than at this vertex.) There are chords emanating in every direction 180 degrees from A. Any chord lying within the angle BAC, the “shaded” region, is longer than the sides of the triangle. All the others that start from A must be shorter. Since the inscribed triangle is equiangular, angle BAC is 60 degrees. Therefore, 60/180 = 1/3 of the chords are longer than the sides of the inscribed triangle. Therefore, the answer is 1/3.

Fig. 17.1
Second solution: A chord is uniquely identified by its midpoint. Now consider the chords that have their midpoints within the small circle. This shaded circle (fig. 17.2) has a radius half of the big circle. Exactly those chords with midpoints within the shaded circle are longer than the side of an equilateral triangle. The small circle has an area ¼ of the big circle. Therefore, the answer is ¼.

Fig. 17.2
Third solution: Consider a line bisecting the triangle and circle, as in figure 17.3. The chords longer than the sides of triangles have their midpoints closer to the center than half the radius, i.e., below H and above I. If the midpoints are distributed uniformly over the radius (instead of over the area, as was the case in the second solution), the probability becomes ½.

Fig. 17.3
Bertrand has presented us with an embarrassment of riches. Each answer is acceptable on its own, both in its reasoning process and its conclusion. The paradox lies in the incompatibility between the deductions rather than within the deductions themselves. The deductions are individually plausible but jointly inconsistent.
The paradoxes of geometrical probability are trouble for theorists who classify each paradox in terms of an argument with an unacceptable conclusion. Bertrand’s three-armed antinomy has three individually acceptable conclusions.
Those who identify paradoxes with surprising conclusions might reply as follows: Bertrand’s paradox uses the separate calculations as the basis for separate subconclusions, which are then recruited into a superargument with three premises: “The probability is 1/3. The probability is ½. The probability is ¼. Therefore, the probability is 1/3 and ½ and ¼.” Under this analysis, the paradox is the superconclusion “The probability is 1/3 and ½ and ¼.”
This superargument approach cannot be generalized to a case in which there are infinitely many rival calculations. On mathematical grounds, Bertrand believes that there are infinitely many calculations of the above sort. An argument can only have finitely many premises. Therefore, an antinomy with infinitely many arms cannot be compressed into a single argument.
An antinomy is a collection of arguments rather than an argument. Collections can be infinitely large and therefore may contain infinitely many premises and conclusions. There can also be collections of antinomies. As we shall see in chapter 20, Immanuel Kant believed that the Antinomy of Pure Reason was a collection of antinomies that lurk beneath an epochal debate between Leibniz and Samuel Clarke. In principle, antinomies can be ordered in an infinite ascending hierarchy.
In addition to this formal problem, the superargument strategy is strained because simple inspection of the premises is enough to show that the superargument is unsound. We do not need to peek at the contradictory conclusion. Superarguments are not paradoxes for the same reason that jumble arguments (discussed in chapter 8) are not paradoxes.
Bertrand’s resolution of his paradox is skepticism: “Among these three answers, which one is proper? None of the three is incorrect, none is correct, the question is ill-posed.” (1889, 5) Bertrand belonged to a finitist school of mathematicians who questioned the meaningfulness of questions about infinite choices.
But is the matter so hopeless? E. T. Jaynes acknowledges that Bertrand’s paradox “has been cited to generations of students to demonstrate that Laplace’s ‘principle of indifference’ contains logical inconsistencies.” (1973, 478) But why not let Mother Nature dictate the right solution to the paradox? Accordingly, Jaynes and a colleague conducted an experiment. One of them tossed broom straws onto a five-inch-diameter circle drawn on the floor. His results suggest that the correct answer is ½.
Bas van Fraassen (1989, chap. 12) is willing to accept Jaynes’s experiment as providing the right answer but regards it as a Pyrrhic victory for the principle of indifference. According to van Fraassen, the principle of indifference is supposed to provide initial probabilities without evidence. The idea is that we can always avoid a probability gap (not having any probability to attach to a proposition) by using our very lack of evidence as the basis for assigning probabilities. Jaynes’s experiment only solves the problem by accumulating data.
Van Fraassen believes that the principle of indifference manifests the rationalist’s dream of getting something from nothing. He thinks Leibniz’s correct predictions about the empirical world are like the predictions of self-professed clairvoyants. Some of the accuracy of their predictions is an illusion; clairvoyants make many vague predictions and forget about most of the predictions that are so badly wrong that they cannot be reinterpreted as correct. If the clairvoyant’s prediction embodies any genuine knowledge, that is knowledge acquired through surreptitious reliance on observation and experiment. The rationalist may not realize that good old-fashioned perception is the real source of his grand insights into the nature of our world. But if he wants to really understand how he understands the world, he should confine himself to observation and experiment. Or so say van Fraassen’s empiricist forefathers. In the next chapter, we will see how well they manage to steer clear of the paradoxes that bedeviled rationalism.