Fig. 22.1
When the mathematics student Bertrand Russell (1872–1970) entered Cambridge University, he subscribed to the empiricism of his godfather, John Stuart Mill. However, the younger generation of philosophers believed that Mill had been superseded by Hegel. A recent graduate of Cambridge, John McTaggart, told the young Russell that although he did not believe in God, he did believe in immortality and a harmony between human beings and the universe. McTaggart claimed that the unreality of space and time could be proved with mathematical rigor. This colorful mixture of logic and spirituality contrasted with the black-and-white calculating of mathematicians.
Russell’s conception of philosophy was inspired by McTaggart’s Studies in the Hegelian Dialectic. After his graduation, Russell expressed an ambition to write “a dialectic logic of all the sciences and an ethic that should apply to politics.” He hoped that something like Spinoza’s religion could be rigorously demonstrated.
Part of Russell’s project was to show how contradictions led from mathematics to physics and from physics to metaphysics, and then onto the Absolute. Russell thought the contradictions would be most easily revealed in geometry, especially with respect to continua. Mathematicians were in danger of forgetting “that philosophical antinomies, in this sphere, find their counterpart in mathematical fallacies. These fallacies seem, to me at least, to pervade the Calculus, and even the more elaborate machinery of Cantor’s collections.” (1990, 52)
In An Essay on the Foundations of Geometry, Russell claimed to find contradictions related to the “relativity, infinite divisibility, and unbounded extension of space.” (1897, 177) For instance, a point must be spatial and yet must not contain any space. After all, any finite extension is capable of further analysis. Russell thought geometry’s contradictions are inherited from the nature of space. As such they are innate and inescapable. To solve the paradoxes endemic to “empty space” and “point,” one must introduce the concept of “matter.” That is, one must transcend geometry with kinematics.
Russell’s book on geometry was well received. He planned to next write a book on the foundations of physics. However, dynamics proved recalcitrantly empirical.
Russell shifted to the more familiar terrain of arithmetic. He was interested in Georg Cantor’s attempt to treat number as a continuous quantity. As a Hegelian, Russell rejected Cantor’s transfinite numbers on the grounds that infinity would have to be “a quantity larger than any assignable quantity.” If 1, 2, 3, . . . , n, . . . is unlimited, how could Cantor find a place for a number that would follow all these numbers?
Eventually Russell concluded that his criticism rested on two mistakes: treating infinity as an infinite number and treating all infinities as being equal. This retraction was partly precipitated by Alfred North Whitehead’s suggestion that Russell actually read Hegel’s books on logic. Russell had been reading mathematically literate interpretations of Hegel. Once he read Hegel in the original, Russell was shaken. The master was committing “ignorant and stupid” mistakes.
This was probably just the reaction Whitehead was hoping for. As Russell’s opinion about Hegel sank, his opinion of mathematicians rose. At Cambridge, the vast majority of mathematicians seemed narrow and uncultured. Students crammed to pass the Tripos examination, a marathon of tricky mathematics. To make a respectable showing, you had to train intensively. So teachers and students focused on competitive, time-sensitive problem-solving. This shallow regime did not encourage ruminations on the philosophical difficulties posed by infinitesimals, continua, and infinity.
But when Russell encountered mathematicians in France, Germany, and Italy, he no longer pictured the whole profession as hurriedly sweeping its contradictions under a rug. True, the usual reaction to George Berkeley’s criticisms of infinitesimals was some foot shuffling and a reminder that infinitesimals led to the right answers. But Karl Weierstrass showed how the right answers could be obtained through an alternative, epsilon-delta notation (which follows the linguistic strategy we saw pioneered by Peter of Spain). Since this avoided infinitesimals, mathematicians were now free to concede to Berkeley that infinitesimals were incoherent. Georg Cantor was persuading more and more mathematicians that his transfinite arithmetic solved Zeno’s paradoxes. Giuseppe Peano had axiomitized arithmetic. All of this showed that an effective cadre of mathematicians did take contradictions seriously. There were far fewer unsolvable contradictions than implied by Hegel. By 1899, Russell felt the number of contradictions had dwindled to one: “The number of finite numbers is infinite. Every number is finite. These two statements seem indubitable, though the first contradicts the second, and the second contradicts Cantor.” (Russell 1994, 123) But even this paradox seemed to disappear when Russell became persuaded that mathematics was not really the science of quantity. Once mathematics was pictured more abstractly, as a study of symbol manipulation, all contradictions appeared to evaporate. Mathematics looked increasingly like a body of secure tautologies.
Russell’s empty catch made him ripe for defection. His colleague at Cambridge University, G. E. Moore, was developing an analytic alternative to Hegelianism. Moore attacked idealism with a combination of conceptual analysis and appeals to common sense. Nowadays, many philosophy students regard Moore’s writings as a pedantic defender of the status quo. But at the beginning of the twentieth century, Moore’s writings were electrically dissident. Idealism was in magisterial hegemony in Europe and the Untied States. Moore countered with a charismatic naiveté.
Moore admitted that he could not pinpoint the missteps of many idealist arguments. He just knew that they were wrong because their conclusions contradicted everyday certitudes. One job for philosophers is to find the fallacy in such paradoxical arguments. In contrast with Russell, Moore did not think the philosopher was in the business of correcting or refining common sense. Like Reid, he thought philosophical challenges to common sense were insincere and self-defeating. Philosophers should instead analyze what common-sense statements mean. Unlike Reid, Moore accepted the Way of Ideas. He thought that statements such as “I see a hand” should be analyzed in terms of sense data. Analyses of common sense are not themselves common sense.
Russell felt Moore liberated him. As a realist, Russell could now see the grass as really green. He could construe science as having an ever-tightening grip on an objective world. Russell summarized his defection in “Why I took to Philosophy”:
Hegel thought of the universe as a closely knit unity. His universe was like a jelly in the fact that, if you touched any one part of it, the whole quivered; but it was unlike a jelly in the fact that it could not really be cut up into parts. The appearance of consisting of parts, according to him was a delusion. The only reality was the Absolute, which was his name for God. In this philosophy I found comfort for a time. As presented to me by its adherent, especially McTaggart, who was then an intimate friend of mine. Hegel’s philosophy had seemed both charming and demonstrable. . . . In a rash moment, however, I turned from the disciples to the Master and found in Hegel himself a farrago of confusions and what seemed to me little better than puns. I therefore abandoned his philosophy.
(1956, 21)
Russell now pictured the universe as a pile of buckshot. Like Hume’s ideas, Russell’s “atomic facts” were independent units that could be logically compounded into molecular facts. The role of the philosopher was to show how complex statements could be analyzed into simpler statements and how atomic statements manage to be true or false. Like Leibniz, Russell assigned a central role to logic in his metaphysics.
Ordinary language was unsuited for this project because it is larded with ambiguity, vagueness, and redundancy. What Russell needed was a logically perfect language; a language in which each object has a single name and each name has a single object; a language in which each concept is expressed by one and only one predicate; a language in which every sentence has clear rules for its construction. Paradoxes cannot arise in this language. Equivocation is impossible because all ambiguity has been removed. The sorites paradox cannot be expressed because there is no vagueness. Puzzles about nonexistence disappear because there are no empty names. Puzzles about identity are forestalled because no object goes around under different names. Finally, meaninglessness is prevented because each atomic sentence is meaningful and all other sentences are molecules that are meaningfully assembled from meaningful atoms.
In addition to rendering the negative service of preventing spurious issues from arising, the logically perfect language positively informs the metaphysician about the nature of reality. The language shows that the world is a collection of facts rather than a heap of objects. “Bertrand Russell was descended from Prime Minister John Russell” and “Prime Minister John Russell was descended from Bertrand Russell” are about the same individuals and employ the same concept. But only one of them is made true by the fact that the Prime Minister John Russell was Bertrand Russell’s grandfather.
This logically perfect language would have the same structure as reality itself. It would reflect all and only genuine possibilities. The role of science is to figure out which possibilities are actual. The role of the philosopher is to construct the framework. In this way, the scientist is spared the trouble of eliminating hypotheses that could not possibly be correct. The scientist would also benefit from this clear picture of what implies what. Although a philosopher lacks any special expertise as to which possibilities are actual, he would be able to say, “If this possibility is actual, then that possibility must also hold.”
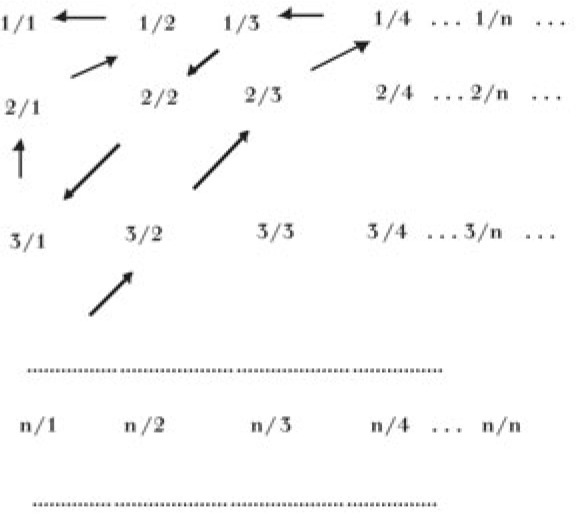
One important part of an ideal language would be mathematics. Rationalism is supported by our knowledge that 1 + 1 = 2. There is no causal link between us and numbers, so we appear to have nonempirical access to the truths of arithmetic. Empiricists suggested that our knowledge of arithmetic is like our knowledge of tautologies. This is logicism, the view that mathematics reduces to logic. Russell believed that Cantor’s conception of a set presented an opportunity to work out this reduction of mathematics to logic in rigorous detail. The size of a collection, its cardinality, is what is left after we abstract away the nature of its members and their order. One is the cardinality of a unit set composed of a single individual, say, the planet Mercury. The union of Mercury with the set of that set yields a set with two members. Adding the set of that set with the two previous members gives us three. All the natural numbers can be represented by continuing this progression.
Rational numbers are just those numbers that can be represented as a ratio of integers. These “fractions” can be put into a one-to-one correspondence with the natural numbers (fig. 22.1). Cantor was interested in proving that not all cardinalities are equal. After failing to prove that the set of all real numbers is greater than the set of real numbers between 0 and 1, Cantor surprised himself by demonstrating that all the real numbers could be put into a one-to-one correspondence with the real numbers in the interval between 0 and 1 (fig. 22.2). More importantly, Cantor devised the diagonal argument to show that there is no one-to-one correspondence between the real numbers and the natural numbers. Suppose there were a one-to-one correspondence. We would then be able to list all the real numbers in an infinite square. Each real number between 0 and 1 corresponds to an infinite decimal expansion. For instance, 1/3 = .333333. . . . So the list would look like something like figure 22.3. Now consider the sequence corresponding to the diagonal of the list: 3061. We can construct a new decimal expansion by letting the nth digit equal 1 if the diagonal digit is 0 and 0 for any other digit: That antidiagonal, .0100 . . . , cannot be on the list, for it differs from any number on the list by at least one digit.

Fig. 22.1
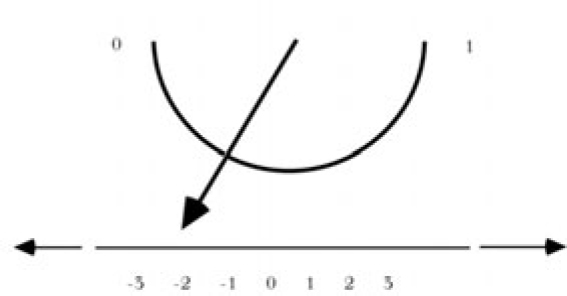
Fig. 22.2

Fig. 22.3
The diagonal argument can be used to show that the power set of the natural numbers (the set of all its subsets) is bigger than the set of natural numbers. We can describe any set of natural numbers by just writing true or false depending on whether the nth natural number is a member of the set. For instance, the set of even numbers is <False, True, False, True, . . . >. A one-to-one correspondence between the set of natural numbers and its power set would look like figure 22.4. The diagonal sequence is <False, False, True, True, . . . >. Now consider the sequence that results by reversing all those truth values: <True, True, False, False, . . . >. The sequence defined by this antidiagonal cannot be on the list. It diverges at least once with each sequence on the list.

Fig. 22.4
Cantor went on to prove that the power set of any set (the set of all subsets of that set) always has a higher cardinality than the set. It follows that there is an infinite hierarchy of transfinite numbers.
Cantor’s proof that there is no highest transfinite number was controversial. Henri Poincaré thought there was a set of real numbers only if its elements could be paired off with the natural numbers. Since the diagonal argument proved there was no pairing, Poincaré inferred that there is no set of real numbers. Luitzen Brouwer construed the diagonal argument as a recipe for constructing new real numbers. C. S. Peirce argued similarly that there is no completed whole of real numbers. For any real number, there is a higher real number. But the infinity is potential, not actual.
When Russell was calculating how many things are in the universe, he was led to a set that included everything. The number of things in this set must be the largest number because there is nothing further to add! Russell therefore suspected that the diagonal argument committed some subtle fallacy.
Cantor’s correspondence with Richard Dedekind suggests that Cantor was aware of how the universal set was an anomaly for the conclusion of the diagonal argument. If the power set of a set is always bigger than the set, then the universal set would be bigger than itself. Cantor was only mildly concerned. He was a religious man who believed that God had granted him a special gift to work out the nature of infinity. He had seen anomalies come and go in his development of transfinite arithmetic. From the history of number theory, he knew irrational numbers, negative numbers, and imaginary numbers had each faced trials. Why should transfinite numbers be different? Cantor flirted with the idea that some infinities are immeasurable: “manies too big to be regarded as one.” These “inconsistent multiplicities” inspired Cantor’s mystical awe: “The Absolute can only be acknowledged and admitted, never known, not even approximately.” (Hallet 1984, 13)
Russell was in no position to partake in Cantor’s ad hoc equanimity. Why didn’t the set of real numbers count as an immeasurable infinity? The diagonal argument for higher order infinities would be reduced to the status of revealed theology.
Like the editors who turned down the diagonal argument for publication, Russell noticed that the antidiagonal resembled the liar paradox. When evaluating “This statement is false,” you are forced to endlessly change true to false and false to true. The construction of the antidiagonal takes the same oscillating path.
This objection to the diagonal argument boomerangs. In May of 1901, while finishing Principles of Mathematics, Russell realized that the liar paradox bears a more damning resemblance to a slight variant of this universal set. A set that contains everything must contain itself. Now consider a set that includes all and only those sets that do not include themselves as members. If this set contains itself as a member, then it does not contain itself as a member. But if it does not contain itself as a member, then it does include itself as a member.
Russell at first thought this derivation of a contradiction was sophistical. He was not the first to have run across this type of argument. In 1889 an assistant to Peano, Cesare Burali-Forti, was working on the theory of ordinal numbers. Ordinals measure size like the ticket counters at butcher shops measure the length of the queue. Ordinals do not convey information about the distance that lies between the members of the sequence. When three customers are ranked by first, second, third, the sequence is well ordered because there is a first member and a unique next position in line. To extend the concept of well-ordering to infinite counters, we are careful not to require that there be a last member of the sequence. For instance, <0, 1, 2, 3, ...> is well ordered. But there must be a first member: <. . . , -2, -1, 0, 1, 2, ...> is not well ordered. The sequence of non-negative rational numbers <0, . . . , ¼, . . . , ½, . . . , 1, . . . , 2, ...> singles out a first number but fails to single out the second. The nonstandard ordering of the integers <0, 1, 2, . . . , . . . , -3, -2, -1> is not well ordered because it does not single out which whole succeeds all the natural numbers. However, a sequence that stacks all the evens before the odds, <0, 2, 4, . . . , 1, 3, 5, . . . >, is well ordered. The accelerated sequence so popular in Zeno’s paradoxes <½, ¾, 7/8, . . . , 1> is well ordered. Burali-Forti notes that the sequences constituting ordinals can be ranked in size. First comes <1>, second comes <1, 2>, then <1, 2, 3> and so on. That is to say, the set of ordinals is well ordered. Any set that is well ordered has an ordinal number. Therefore, it must have an ordinal. However, this ordinal must be greater than every element in the set and so cannot be in the set!
Nowadays, this is called the Burali-Forti paradox. But Burali-Forti regarded his reasoning as a reductio ad absurdum of the trichotomy law. This law says that given any pair of ordinal numbers A and B, either A; = B, A < B or A > B. Burali-Forti was shocked when Cantor later offered a proof of the trichotomy law. It turns out that Burali-Forti had misread Cantor’s definition of well ordering. After Burali-Forti renamed his concept “perfect ordering,” he concluded that both proofs were correct.
For Burali-Forti and most others, Cantor’s theory was too fluid to serve as the backdrop for paradoxes. Those sympathetic with Cantor construed surprising deductions from Cantor’s theory as intriguing conjectures. Those hostile to Cantor viewed such results as disconfirming implausibilities. Only after Cantor’s work hardened into mainstream mathematics did the surprises become commonly described as paradoxes.
Russell stands apart from the other set theorists in his refusal to put these anomalous sets on the back burner. At first he invested time in the puzzles just because they looked like resolvable sophistries. Time lost on “the contradiction” made the deadline for his book Principles of Mathematics more pressing. The systematic nature of the book made it difficult to dodge the question whether his set contained itself.
Russell became more and more fretful. He sought advice from fellow logicians. Once he telegraphed Alfred North Whitehead reporting that he had found a solution. After Whitehead congratulated him, Russell’s “indescribable relief” collapsed under the weight of a minor variation of the original paradox.
Still unsure whether “the contradiction” was an important discovery or a failure of ingenuity, Russell wrote Peano. Peano did not reply.
On June 16, 1902, Russell decided to turn to a logician he had read about in a review by Peano: Gottlob Frege. Russell had recently discovered that Frege was also working on the logicist program and had made much progress. Perhaps Frege could solve the paradox. Russell’s letter arrived just as the second volume of Frege’s Basic Laws of Arithmetic was in press. Whereas Russell had suffered pinprick by pinprick, Frege absorbed the lesson in a single stab. He quickly realized that his fifth law must be a contradiction. (This axiom permits the construction of Russell’s set by claiming that two sets are equal if and only if their corresponding functions coincide in values for all possible arguments. An expression such as f(x) must then be considered both a function of the argument f and a function of the argument x.) In a rapidly drafted appendix, Frege starts to ask the right questions: “Is it always permissible to speak of the extension of a concept, of a class? And if not, how do we recognize the exceptional cases? Can we always infer from the extension of one concept’s coinciding with that of a second, that every object which falls under the first concept also falls under the second?”
On June 22, Frege candidly replied to Russell:
Your discovery of the contradiction has surprised me beyond words and, I should like to say, left me thunderstruck, because it has rocked the ground on which I meant to build arithmetic. . . . I must give some further thought to the matter. It is all the more serious as the collapse of my law V seems to undermine not only the foundations of my arithmetic but the possible foundations of arithmetic as such. . . . Your discovery is at any rate a very remarkable one, and it may perhaps lead to a great advance in logic, undesirable as it may seem at first sight.
(Frege 1980, 132)
Russell was much impressed with Frege’s dedication to truth: “upon finding that his fundamental assumption was in error, he responded with intellectual pleasure clearly submerging any feelings of personal disappointment.”
Actually, Frege never again published anything significant. Depressed by the paradox, Frege feared that his whole life’s work had been shown to be nearly worthless.
Frege had thought that we have infallible access to logical truths by intuition. The abstraction axiom says that any coherent condition may be used to determine a set. What could be clearer? Yet, Russell’s paradox shows that this intuition is a contradiction.
Analogues of the abstraction axiom are common in semantics. We seem to define certain things into existence. During the heyday of American unionism, L. S. Johnston (1940) had a secretary who was annoyed by organizations that excluded their secretaries. The secretary wished there was a union for secretaries who could not be members of the organization they worked for. Since Johnston was a mathematician familiar with Russell’s set paradox, he was primed to notice that the secretary was asking for the impossible. Suppose there was a union that could be joined just by secretaries who were excluded from membership in an organization that employed them. The union grows so big that it hires a secretary. She is not excluded by any other organization. Is this secretary eligible to join the union for excluded secretaries? If she is eligible to join the union, then no organization excludes her. This makes her ineligible to join the union. But if she is ineligible, then she is excluded by the union and is therefore eligible!
We have fallen into a contradiction because we assumed that it is possible for such a secretary to exist. This result is paradoxical because we think that groups are defined into existence. If we want to form a chess club, we can do it by declaring ourselves to be members of the club. Gottlob Frege had the same intuition about sets: any condition that can be described is sufficient for defining a set.
Russell’s first effort to restrict the abstraction principle occurs at the end of Principles of Mathematics. In “Appendix B: The Doctrine of Types,” he suggests that we ban references to the paradoxical set. The sentences used to define sets need to be assembled into a hierarchy. At the lowest level are sentences about individuals. At the second level are sentences about sets of individuals. Third comes sentences about sets of sets of individuals, and so on. A predicate holds of “all objects” only when they are at the same level. According to Russell’s “vicious circle principle,” the meaning of a term cannot be specified until one specifies the exact range of objects that are candidates for satisfying it. Self-reference is meaningless.
But what about the previous sentence? Is that meaningless? Attempts to state the theory of types violate the theory. Russell struggles with this problem of self-defeat in the more mature version of the theory in his 1908 article “Mathematical Logic as Based on the Theory of Types” and in his monumental Principia Mathematica, co-authored with Whitehead.
After the gravity of Russell’s paradox was appreciated, there was a spate of paradoxes by Jules Richard, Kurt Grelling, Julius Konig, and Ernst Zermello. G. G. Berry was one of the first individuals to produce new semantic paradoxes. Berry’s paradox was presented by Russell in the following sentence: “‘The least integer not namable in fewer than nineteen syllables’ is itself a name consisting of eighteen syllables; hence the least integer not namable in fewer than nineteen syllables can be named in eighteen syllables, which is a contradiction.” (Russell 1908, 223)
Berry is a curious figure. He had a humble job as a librarian in the Bodleian library at Oxford. To introduce himself, Berry presented Russell with a visiting card. On one side was written, “The statement on the other side of this card is true.” On the other side was written, “The statement on the other side of this card is false.” (There is a myth that this looped liar was the invention of Philip Jourdain.)
Berry’s correspondence with Russell reveals that Berry was gifted at mathematical logic. But he never published theorems. As Leibniz wrote of Berkeley, Berry may have been “one of that class of men who wish to be known by their paradoxes.” (Russell 1900, 72)