Notational Index
Symbols
 (wedge product)
(wedge product)
 (Kulkarni–Nomizu product)
(Kulkarni–Nomizu product)
 (disjoint union)
(disjoint union)
 (interior multiplication)
(interior multiplication)
 (sharp)
(sharp)
 (Hodge star operator)
(Hodge star operator)
 (length of a vector)
(length of a vector)
 (length of a vector)
(length of a vector)
![$$[\mathbin {bad hbox} ] $$](../images/56724_2_En_BookBackmatter_OnlinePDF_TeX_IEq1504.png) (path class)
(path class)
![$$[\centerdot ,\centerdot ] $$](../images/56724_2_En_BookBackmatter_OnlinePDF_TeX_IEq1505.png) (commutator bracket)
(commutator bracket)
![$$[\mathbin {bad hbox} ,\mathbin {bad hbox} ] $$](../images/56724_2_En_BookBackmatter_OnlinePDF_TeX_IEq1506.png) (Lie bracket)
(Lie bracket)
 (global inner product on forms)
(global inner product on forms)
 (inner product)
(inner product)
 (pairing between vector and covector)
(pairing between vector and covector)
 (scalar product)
(scalar product)
 (inner product)
(inner product)
A
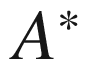 (adjoint of a matrix)
(adjoint of a matrix)
 (transpose of a matrix)
(transpose of a matrix)
 (set of connections on
(set of connections on
 )
)
 (adjoint representation of a Lie algebra)
(adjoint representation of a Lie algebra)
 (adjoint representation of a Lie group)
(adjoint representation of a Lie group)
 (alternating projection)
(alternating projection)
 (covering automorphism group)
(covering automorphism group)
B
 (flat)
(flat)
 (geodesic ball)
(geodesic ball)
 (closed geodesic ball)
(closed geodesic ball)
 (Poincaré ball)
(Poincaré ball)
C
 (Cotton tensor)
(Cotton tensor)
 (infinitely differentiable)
(infinitely differentiable)
 (smooth real-valued functions)
(smooth real-valued functions)
 (smooth maps)
(smooth maps)
 (complex projective space)
(complex projective space)
 (convexity radius at
(convexity radius at
 )
)
 (cut locus of
(cut locus of
 )
)
D
 (Kronecker delta)
(Kronecker delta)
 (Laplacian)
(Laplacian)
 (coordinate vector field)
(coordinate vector field)
 (coordinate vector)
(coordinate vector)
 (coordinate vector field)
(coordinate vector field)
 (coordinate vector)
(coordinate vector)
 (radial vector field)
(radial vector field)
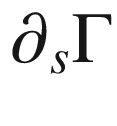 (velocity of a transverse curve)
(velocity of a transverse curve)
 (velocity of a main curve)
(velocity of a main curve)
 (covariant derivative)
(covariant derivative)
 (normal connection)
(normal connection)
 (tangential connection)
(tangential connection)
 (covariant Hessian)
(covariant Hessian)
 (second total covariant derivative)
(second total covariant derivative)
 (total covariant derivative)
(total covariant derivative)
 (covariant derivative)
(covariant derivative)
 (exterior derivative)
(exterior derivative)
 (exterior covariant derivative)
(exterior covariant derivative)
 (adjoint of
(adjoint of
 )
)
 (differential of a map)
(differential of a map)
 (Riemannian distance)
(Riemannian distance)
 (distance to a subset)
(distance to a subset)
 (density bundle)
(density bundle)
 (domain of
(domain of
 )
)
 (covariant derivative along transverse curves)
(covariant derivative along transverse curves)
 (covariant derivative along a curve)
(covariant derivative along a curve)
 (Riemannian density)
(Riemannian density)
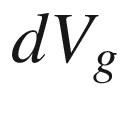 (Riemannian volume form)
(Riemannian volume form)
div
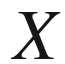 (divergence of
(divergence of
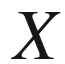 )
)
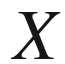 (divergence of
(divergence of
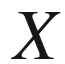 )
)
E
 (identity of a Lie group)
(identity of a Lie group)
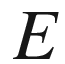 (normal exponential map)
(normal exponential map)
 (domain of the exponential map)
(domain of the exponential map)
 (restriction of a bundle)
(restriction of a bundle)
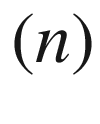 (Euclidean group)
(Euclidean group)
 (domain of the normal exponential map)
(domain of the normal exponential map)
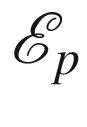 (domain of the restricted exponential map)
(domain of the restricted exponential map)
 (space of endomorphisms)
(space of endomorphisms)
 (exponential map)
(exponential map)
 (exponential map of a Lie group)
(exponential map of a Lie group)
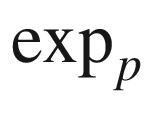 (restricted exponential map)
(restricted exponential map)
F
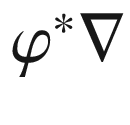 (pullback of a connection)
(pullback of a connection)
 (level set)
(level set)
 (level set)
(level set)
 (induced fundamental group homomorphism)
(induced fundamental group homomorphism)
 (induced Lie algebra homomorphism)
(induced Lie algebra homomorphism)
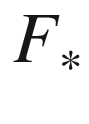 (pushforward of vector fields)
(pushforward of vector fields)
 (pullback of a density)
(pullback of a density)
 (pullback of a tensor field)
(pullback of a tensor field)
 (symmetric product of
(symmetric product of
 and
and
 )
)
G
 (velocity vector)
(velocity vector)
 (one-sided velocity vectors)
(one-sided velocity vectors)
 (geodesic with initial velocity
(geodesic with initial velocity
 )
)
 (smooth sections of
(smooth sections of
 )
)
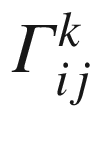 (connection coefficients)
(connection coefficients)
 (family of curves)
(family of curves)
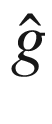 (pullback of the round metric)
(pullback of the round metric)
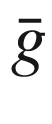 (Euclidean metric)
(Euclidean metric)
 (round metric)
(round metric)
 (round metric of radius R)
(round metric of radius R)
 (hyperbolic metric)
(hyperbolic metric)
 (hyperbolic metric of radius
(hyperbolic metric of radius
 )
)
 (metric coefficients)
(metric coefficients)
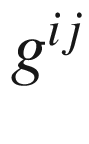 (inverse of
(inverse of
 )
)
GL
 (complex general linear group)
(complex general linear group)
 (complex general linear group)
(complex general linear group)
GL
 (general linear group)
(general linear group)
 (general linear group)
(general linear group)
 (matrix Lie algebra)
(matrix Lie algebra)
 (Lie algebra of linear maps)
(Lie algebra of linear maps)
![$$[G_1,G_2] $$](../images/56724_2_En_BookBackmatter_OnlinePDF_TeX_IEq1609.png) (group generated by commutators)
(group generated by commutators)
 (warped product metric)
(warped product metric)
 (product metric)
(product metric)
GL
 (group of invertible linear maps)
(group of invertible linear maps)
 (group of invertible linear maps)
(group of invertible linear maps)
 (gradient of
(gradient of
 )
)
H
 (scalar second fundamental form)
(scalar second fundamental form)
 (mean curvature)
(mean curvature)
 (hyperbolic space)
(hyperbolic space)
 (hyperbolic space of radius
(hyperbolic space of radius
 )
)
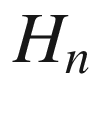 (Heisenberg group)
(Heisenberg group)
 (traceless Hessian operator)
(traceless Hessian operator)
 (Hessian operator)
(Hessian operator)
 (pseudohyperbolic space)
(pseudohyperbolic space)
Hol
 (holonomy group)
(holonomy group)
 (holonomy group)
(holonomy group)
Hol
 (restricted holonomy group)
(restricted holonomy group)
 (restricted holonomy group)
(restricted holonomy group)
I
 (interior multiplication)
(interior multiplication)
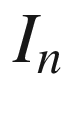 (identity matrix)
(identity matrix)
 (index form)
(index form)
 (injectivity domain)
(injectivity domain)
 (second fundamental form)
(second fundamental form)
 (second fundamental form in direction
(second fundamental form in direction
 )
)
 (injectivity radius of
(injectivity radius of
 )
)
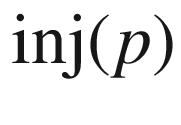 (injectivity radius at
(injectivity radius at
 )
)
 (isometry group)
(isometry group)
 (isotropy group of a point)
(isotropy group of a point)
J
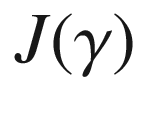 (space of Jacobi fields)
(space of Jacobi fields)
 (normal Jacobi fields)
(normal Jacobi fields)
 (tangential Jacobi fields)
(tangential Jacobi fields)
K
 (Cayley transform)
(Cayley transform)
 (geodesic curvature)
(geodesic curvature)
 (principal curvatures)
(principal curvatures)
 (signed curvature)
(signed curvature)
 (Gaussian curvature)
(Gaussian curvature)
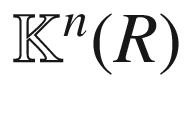 (Beltrami–Klein model)
(Beltrami–Klein model)
L
 (bundle of alternating tensors)
(bundle of alternating tensors)
 (space of alternating tensors)
(space of alternating tensors)
 (length of curve)
(length of curve)
 (Lie algebra of left-invariant vector fields on
(Lie algebra of left-invariant vector fields on
 )
)
M
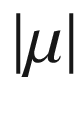 (density associated with an
(density associated with an
 -form)
-form)
 (
(
 with opposite orientation)
with opposite orientation)
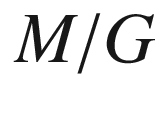 (orbit space)
(orbit space)
 (space of matrices)
(space of matrices)
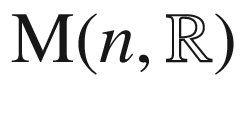 (space of
(space of
 matrices)
matrices)
N
 (normal space)
(normal space)
 (normal bundle)
(normal bundle)
O
 (connection
(connection
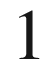 -forms)
-forms)
 (space of
(space of
 -forms)
-forms)
 (orthonormal bases on
(orthonormal bases on
 )
)
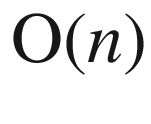 (orthogonal group)
(orthogonal group)
 (Lorentz group)
(Lorentz group)
 (orthochronous Lorentz group)
(orthochronous Lorentz group)
 (orthogonal group)
(orthogonal group)
P
 (fundamental group)
(fundamental group)
 (normal projection)
(normal projection)
 (tangential projection)
(tangential projection)
 (Schouten tensor)
(Schouten tensor)
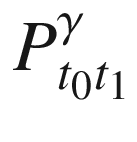 (parallel transport operator)
(parallel transport operator)
Q
 (pseudo-Euclidean metric)
(pseudo-Euclidean metric)
 (pseudohyperbolic metric)
(pseudohyperbolic metric)
 (pseudospherical metric)
(pseudospherical metric)
R
 (rotation index)
(rotation index)
 (radial distance function)
(radial distance function)
 (curvature endomorphism)
(curvature endomorphism)
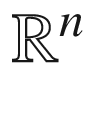 (Euclidean space)
(Euclidean space)
 (pseudo-Euclidean space)
(pseudo-Euclidean space)
 (real projective space)
(real projective space)
 (space of algebraic curvature tensors)
(space of algebraic curvature tensors)
 (curvature endomorphism)
(curvature endomorphism)
 (curvature endomorphism)
(curvature endomorphism)
 (Ricci tensor)
(Ricci tensor)
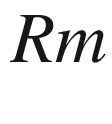 (curvature tensor)
(curvature tensor)
S
 (bundle of symmetric tensors)
(bundle of symmetric tensors)
 (space of symmetric tensors)
(space of symmetric tensors)
 (shape operator)
(shape operator)
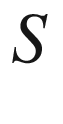 (scalar curvature)
(scalar curvature)
 (surface of revolution)
(surface of revolution)
 (geodesic sphere)
(geodesic sphere)
 (unit
(unit
 -sphere)
-sphere)
 (
(
 -sphere of radius
-sphere of radius
 )
)
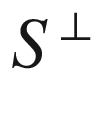 (orthogonal complement)
(orthogonal complement)
§
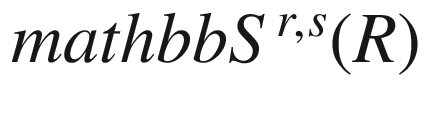 (pseudosphere)
(pseudosphere)
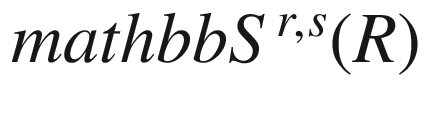 (pseudosphere)
(pseudosphere)
 (complex special linear group)
(complex special linear group)
 (special linear group)
(special linear group)
 (special orthogonal group)
(special orthogonal group)
 (special unitary group)
(special unitary group)
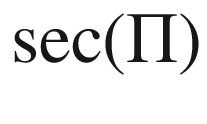 (sectional curvature)
(sectional curvature)
 (sectional curvature)
(sectional curvature)
 (sign of a permutation)
(sign of a permutation)
 (
(
 -dimensional solvable Lie group)
-dimensional solvable Lie group)
 (support of
(support of
 )
)
 (symmetrization)
(symmetrization)
T
 (torsion tensor)
(torsion tensor)
 (
(
 -torus)
-torus)
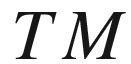 (tangent bundle)
(tangent bundle)
 (ambient tangent bundle)
(ambient tangent bundle)
 (tangent space)
(tangent space)
 (space of vectors tangent to a curve)
(space of vectors tangent to a curve)
 (space of vectors normal to a curve)
(space of vectors normal to a curve)
 (space of tensor fields)
(space of tensor fields)
 (bundle of contravariant
(bundle of contravariant
 -tensors)
-tensors)
 (bundle of covariant
(bundle of covariant
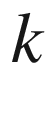 -tensors)
-tensors)
 (space of contravariant
(space of contravariant
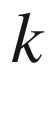 -tensors)
-tensors)
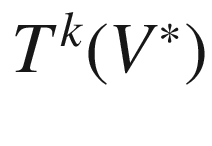 (space of covariant
(space of covariant
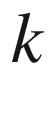 -tensors)
-tensors)
 (bundle of mixed tensors)
(bundle of mixed tensors)
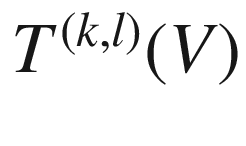 (space of mixed tensors)
(space of mixed tensors)
 (tangent cut locus)
(tangent cut locus)
 (trace of a tensor)
(trace of a tensor)
 (trace with respect to
(trace with respect to
 )
)
U
 (unitary group)
(unitary group)
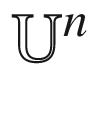 (Poincaré half-space)
(Poincaré half-space)
V
 (dual space of
(dual space of
 )
)
 (norm of an alternating
(norm of an alternating
 -tensor)
-tensor)
 (Stiefel manifold)
(Stiefel manifold)
 (volume of a Riemannian manifold)
(volume of a Riemannian manifold)
W
 (Weyl tensor)
(Weyl tensor)
 (Weingarten map in direction
(Weingarten map in direction
 )
)
X
 (semidirect product)
(semidirect product)
 (Euler characteristic)
(Euler characteristic)
 (space of vector fields)
(space of vector fields)
 (normal projection of
(normal projection of
 )
)
 (normal vector fields along a curve)
(normal vector fields along a curve)
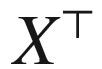 (tangential projection of
(tangential projection of
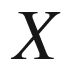 )
)
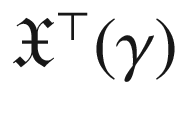 (tangential vector fields along a curve)
(tangential vector fields along a curve)
 (space of vector fields along a curve)
(space of vector fields along a curve)
Subject Index
Symbols
 -Hessian
-Hessian
 -center
-center
 -point homogeneous
-point homogeneous
 -point homogeneous
-point homogeneous
A
abelian Lie algebra
absolute derivative
acceleration
in
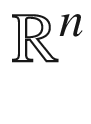
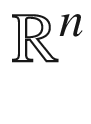
of a curve in a manifold
of a plane curve
tangential
action,
see
group action
adapted frame
adjoint matrix
adjoint representation
of a Lie algebra
of a Lie group
admissible curve
admissible family
admissible loop
admissible partition
for a curve
for a family of curves
for a vector field along a curve
affine connection
aims at a point
algebraic Bianchi identity
algebraic curvature tensor
Alt convention for wedge product
alternating tensor
alternation
ambient manifold
ambient tangent bundle
Ambrose, Warren
analytic continuation of a local isometry
angle
between vectors
of a geodesic triangle
tangent
angle excess
angle-sum theorem
anti-de Sitter space
universal
anti-self-dual
anticommutative
antipodal points
arc length, parametrization by
arc-length function
area-minimizing hypersurface
area of a hypersurface
aspherical
asymptotically parallel
atlas
automorphism of a Lie group
inner
Avez, André
axial isometry
axis for an isometry
B
Böhm, Christoph
Böhm–Wilking theorem
backward reparametrization
ball
geodesic
metric
Poincaré
regular coordinate
smooth coordinate
volume of
base of a vector bundle
basis isomorphism
Beltrami–Klein model
Berger sphere
Berger, Marcel
bi-invariant metric
curvature of
existence of
exponential map of
Bianchi identity
algebraic
contracted
differential
first
second
Bieberbach, Ludwig
bilinear form
Bishop, Richard L.
Bishop–Gromov theorem
Bochner's formula
Bonnet, Ossian
boundary chart
boundary normal coordinates
boundary of a manifold with boundary
boundary problem, two-point
boundary slice coordinates
bounded subset
bracket
commutator
in a Lie algebra
Brendle, Simon
bump function
bundle
normal
of tensors
vector
C
CR manifold
Calabi–Yau manifold
calculus of variations
canonical form
for a nonvanishing vector field
for commuting vector fields
Carathéodory metric
Carnot–Carathéodory metric
Cartan's first structure equation
Cartan's fixed-point theorem
Cartan's second structure equation
Cartan's torsion theorem
Cartan, Élie
Cartan–Ambrose–Hicks theorem
Cartan–Hadamard manifold
Cartan–Hadamard theorem
catenoid
Cauchy–Riemann manifold
Cayley transform
central projection
chart
containing a point
smooth
Cheeger, Jeff
Cheng's maximal diameter theorem
Cheng, Shiu-Yuen
Chern, Shiing-Shen
Chern–Gauss–Bonnet theorem
Choquet-Bruhat, Yvonne
Christoffel symbols
circle classification theorem
circle group
circumference theorem
Clarke, Chris J. S.
classification theorem
circle
compact surfaces
constant-curvature metrics
plane curve
closed form
closed geodesic
closed geodesic ball
closed map
closed subgroup theorem
Codazzi equation
for a hypersurface
Codazzi tensor
codimension
coframe
commutator bracket
commuting vector fields
canonical form
comparison theorem
Bishop–Gromov
conjugate point
diameter
Günther
Hessian
injectivity radius
Jacobi field
Laplacian
metric
principal curvature
Riccati
volume
compatibility with a metric
complete Riemannian manifold
geodesically
metrically
complex projective space
component functions
composable paths
conformal diffeomorphism
conformal invariance
of the Cotton tensor
of the Weyl tensor
conformal Laplacian
conformal metrics
conformal transformation
of the curvature
of the Levi-Civita connection
conformally equivalent metrics
conformally flat, locally
hyperbolic space
spheres
conformally related metrics
congruent
conjugate point
critical point of
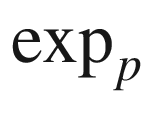
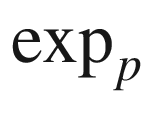
geodesic not minimizing past
conjugate point comparison theorem
connection
Euclidean
existence of
flat
in a vector bundle
in components
in the tangent bundle
Koszul
naturality of
normal
on a manifold
on tensor bundles
Riemannian
tangential
connection
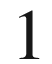 -forms
-forms
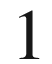 -forms
-forms
connection coefficients
transformation law for
constant Gaussian curvature
constant mean curvature
constant rank
constant sectional curvature
characterization of
classification
formula for curvature tensor
formula for metric
local uniqueness
model spaces
uniqueness
constant-speed curve
constraint equations, Einstein
contracted Bianchi identity
contraction
contravariant tensor
control theory
convex hypersurface
convex subset
convex, geodesically
convexity radius
coordinate representation
coordinate ball
regular
smooth
coordinate chart
smooth
coordinate domain
coordinate frame
coordinate vector
coordinate vector field
coordinates
boundary slice
Fermi
graph
have upper indices
local
natural, on tangent bundle
normal
polar Fermi
polar normal
semigeodesic
slice
standard, on


cosmological constant
cotangent bundle
cotangent space
Cotton tensor
conformal invariance of
covariant derivative
along a curve
exterior
of tensor field
second
total
covariant Hessian
covariant tensor
covector
covector field
covering automorphism
covering automorphism group
covering map
homeomorphism criterion
normal
Riemannian
smooth
universal
critical point
of the exponential map
critical value
crystallographic groups
curl
curvature
conformal transformation of
constant sectional
Gaussian
geodesic
mean
of a curve in a manifold
of a plane curve
principal
Ricci
Riemann
scalar
sectional
signed
curvature
 -forms
-forms
 -forms
-forms
curvature endomorphism
curvature operator
curvature tensor
determined by sectional curvatures
is isometry invariant
symmetries of
curve
admissible
in a manifold
piecewise regular
plane
smooth
curve segment
curved polygon
curved triangle
cusp vertex
cut locus
and injectivity radius
tangent
cut point
cut time
is continuous
cylinder, principal curvatures
D
 -pinched
-pinched
pointwise
strictly
Darboux theorem
de Sitter space
defining function
local
del
delta, Kronecker
density
on a manifold
on a vector space
pullback of
Riemannian
density bundle
derivation
of


determinant convention for wedge product
diameter
diameter comparison theorem
diffeomorphism
in


local
difference tensor
differentiable sphere theorem
differential
global
of a function
of a map
differential Bianchi identity
differential form
closed
exact
dihedral groups
direct product of Lie groups
directional derivative of a vector field on


Dirichlet eigenvalue
Dirichlet's principle
discrete Lie group
discrete subgroup
disjoint union
distance function
has geodesic integral curves
has unit gradient
local
distance, Riemannian
on a disconnected manifold
diverge to infinity
divergence
in coordinates
in terms of covariant derivatives
of a tensor field
divergence theorem
domain of the exponential map
dot product
double elliptic geometry
double of a manifold
dual basis
dual coframe
dual space
E
 -tubular neighborhood
-tubular neighborhood
edge of a curved polygon
effective group action
eigenfunction of the Laplacian
eigenvalue of the Laplacian
Dirichlet
Neumann
Einstein constraint equations
Einstein equation
Einstein field equation
Einstein metric
 -dimensional
-dimensional
Einstein summation convention
Einstein, Albert
Einstein–Hilbert action
embedded submanifold
embedding
isometric
endomorphism
curvature
equivalent to a
 tensor
tensor
 tensor
tensor
of a vector space
energy functional
equivariant map
equivariant rank theorem
escape lemma
Euclidean connection
Euclidean geodesics
Euclidean group
Euclidean metric
Euclidean space
sectional curvature of
Euclidean space form
Euclidean triangle
Euclidean, locally
Euler characteristic
Euler–Lagrange equation
evenly covered neighborhood
exact form
existence and uniqueness
for linear ODEs
of geodesics
of Jacobi fields
exponential map
differential of
domain of
naturality of
normal
of a bi-invariant metric
of a Lie group
of a Riemannian manifold
extendible Riemannian manifold
extendible vector fields
extension
of functions
of sections of vector bundles
exterior angle
exterior covariant derivative
exterior derivative
naturality of
extrinsic curvature of a curve
F
 -related
-related
faithful representation
family of curves
admissible
Fermi coordinates
polar
Fermi, Enrico
fiber
of a map
of a vector bundle
fiber metric
on a tensor bundle
on differential forms
figure eight
Finsler metric
first Bianchi identity
first fundamental form
first structure equation
first variation
flat (
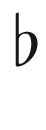 )
)
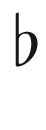 )
)
flat connection
flat metric
flat vertex
flatness criterion
flow
fundamental theorem on
flow domain
focal point
form
bilinear
closed
exact
forward reparametrization
frame
coordinate
global
local
frame-homogeneous
locally
Frankel, Theodore
free group action
free homotopy class
trivial
freely homotopic
Fubini–Study metric
curvature of
functional
length
linear
fundamental form
first
second
fundamental group
homotopy invariance
fundamental theorem
of hypersurface theory
of Riemannian geometry
on flows
G
Gauss equation
for a hypersurface
Gauss formula
along a curve
for a curve in a hypersurface
for a hypersurface
Gauss lemma
for submanifolds
Gauss map
Gauss's
Theorema Egregium
Gauss, Carl Friedrich
Gauss–Bonnet formula
Gauss–Bonnet theorem
Gaussian curvature
constant
is isometry invariant
of an abstract
 -manifold
-manifold
 -manifold
-manifold
general linear group
general relativity
generating curve
genus
geodesic
closed
existence and uniqueness of
is locally minimizing
maximal
naturality of
on Euclidean space
on hyperbolic spaces
on spheres
pseudo-Riemannian
radial
Riemannian
with a conjugate point
with respect to a connection
geodesic ball
closed
geodesic curvature
geodesic equation
geodesic loop
geodesic polygon
geodesic segment
in path-homotopy class
geodesic sphere
geodesic triangle
geodesic vector field
geodesically complete
equivalent to metrically complete
geodesically convex
geometrization conjecture
global differential
global frame
gradient
Gram–Schmidt algorithm
graph coordinates
graph of a smooth function
graph parametrization
Grassmann manifold
Grassmannian
Gray, Alfred
great circle
great hyperbola
Green's identities
Greene, Robert
Gromoll, Detlef
Gromov, Misha
group action
by diffeomorphisms
by isometries
effective
free
isometric
left
proper
right
smooth
transitive
Günther, Paul
Günther's volume comparison theorem
H
Hadamard, Jacques
half-cylinder, principal curvatures
half-space, Poincaré
Hamilton's
 -manifold theorem
-manifold theorem
 -manifold theorem
-manifold theorem
Hamilton's
 -manifold theorem
-manifold theorem
 -manifold theorem
-manifold theorem
Hamilton, Richard
harmonic function
Heisenberg group
Hermann, Robert
Hessian
covariant
of length functional
Hessian comparison theorem
Hessian operator
Hicks, Noel
Hilbert, David
Hodge star operator
holonomy
restricted
homogeneous
 -point
-point
 -point
-point
 -point
-point
locally
homogeneous Riemannian manifold
homogeneous space
homomorphism
Lie algebra
Lie group
homotopic maps
homotopic, freely
homotopy
homotopy equivalence
Hopf, Heinz
Hopf–Rinow theorem
horizontal index position
horizontal lift
horizontal tangent space
horizontal vector field
hyperbolic metric
hyperbolic plane
hyperbolic space
distance function of
locally conformally flat
sectional curvature of
hyperbolic space form
hyperbolic stereographic projection
hyperboloid model
hypersurface
I
ideal triangle
immersed submanifold
with boundary
immersion
isometric
index
of a geodesic segment
of a scalar product
upper and lower
index form
index positions
induced homomorphism
of fundamental groups
of Lie algebras
induced metric
on a submanifold
induced orientation
infinitesimal generator
injectivity domain
injectivity radius
and cut locus
continuity of
injectivity radius comparison theorem
injectivity theorem for covering maps
inner automorphism
inner product
of tensors
inner product space
integral
of a function
with respect to arc length
integral curve
integral of an
 -form
-form
 -form
-form
integration by parts
interior angle
interior chart
interior multiplication
interior of a curved polygon
interior of a manifold with boundary
interpretation of an axiomatic system
intrinsic curvature of a curve
intrinsic property
invariant inner product
invariant metric
invariant under a flow
invariant, local
inverse function theorem
inward-pointing normal
irreducible symmetric space
isometric embedding
isometric group action
isometric immersion
isometric manifolds
isometries
of Euclidean space
of hyperbolic spaces
of spheres
isometry
axial
linear
local
metric
of a Riemannian manifold
Riemannian
isometry group
of Euclidean space
of hyperbolic spaces
of spheres
isomorphism of Lie groups
isothermal coordinates
isotropic
at a point
isotropy representation
isotropy subgroup
J
Jacobi equation
Jacobi field
existence and uniqueness
normal
on constant-curvature manifolds
tangential
transverse
Jacobi field comparison theorem
Jacobi identity
Jacobian matrix
jumps in tangent angle
K
 -point homogeneous
-point homogeneous
Kazdan, Jerry
Killing vector field
Killing–Hopf theorem
Klein bottle
Klingenberg, Wilhelm
Kobayashi metric
Koszul connection
Koszul's formula
Kronecker delta
Kulkarni–Nomizu product
L
Lagrange multiplier
Laplace–Beltrami operator
Laplacian
conformal
Dirichlet eigenvalue of
eigenfunction of
eigenvalue of
in coordinates
Neumann eigenvalue of
Laplacian comparison theorem
latitude circle
lattice
law of inertia, Sylvester's
left action
left-invariant metric
left-invariant vector field
left translation
length
additivity of
isometry invariance of
of a curve
of a group element
of a vector
parameter independence of
length functional
lens space
level set
Levi-Civita connection
naturality of
Levi-Civita, Tullio
Lichnerowicz's theorem
Lie algebra
abelian
of a Lie group
Lie algebra automorphism
Lie algebra homomorphism
induced
Lie algebra isomorphism
Lie bracket
naturality of
of vectors tangent to a submanifold
Lie derivative
and Lie bracket
of a tensor field
of a vector field
Lie group
direct product of
discrete
semidirect product of
Lie group homomorphism
Lie group isomorphism
Lie subalgebra
Lie subgroup
lift of a map
from simply connected spaces
lifting criterion for covering maps
lifting property
path
unique
line in a Riemannian manifold
linear connection
linear functional
linear isometry
linear ODEs
local coordinates
local defining function
local diffeomorphism
local distance function
local frame
local invariant
local isometry
local parametrization
local section
of a submersion
local-to-global theorem
local trivialization
local uniqueness of constant-curvature metrics
locally conformally flat
 -manifolds
-manifolds
hyperbolic space
spheres
locally Euclidean
locally finite
locally frame-homogeneous
locally homogeneous
locally minimizing curve
locally symmetric space
and parallel curvature
loop
geodesic
Lorentz group
Lorentz metric
existence of
lowering an index
M
main curve
manifold
smooth
topological
with boundary
without boundary
matrix Lie algebra
matrix Riccati comparison theorem
maximal diameter theorem
maximal geodesic
mean curvature
meridian
metric
bi-invariant
Carathéodory
Carnot–Carathéodory
Euclidean
fiber
Finsler
Fubini–Study
hyperbolic
induced by an immersion
Kobayashi
Lorentz
on a tensor bundle
on differential forms
product
pseudo-Riemannian
Riemannian
round
semi-Riemannian
singular Riemannian
sub-Riemannian
metric ball
metric comparison theorem
metric connection
metric isometry
metric space
metrically complete
equivalent to geodesically complete
Milnor's theorem on growth of the fundamental group
Milnor, John
minimal hypersurface
minimal surface
minimizing curve
is a geodesic
locally
Minkowski metric
Minkowski space
mixed tensor
Möbius band
model of an axiomatic system
model Riemannian manifolds
monodromy theorem
for local isometries
for paths
Morse index theorem
multilinear
over


multiplicity of conjugacy
Munkres, James
musical isomorphisms
commute with covariant derivatives
Myers's theorem
Myers, Sumner B.
Myers–Steenrod theorem
N
 -manifold
-manifold
 -torus
-torus
flat metric on
nabla
Nash embedding theorem
Nash, John
natural coordinates on the tangent bundle
naturality
of geodesics
of the exponential map
of the Levi-Civita connection
of the Lie bracket
negative definite
negatively oriented basis
Neumann eigenvalue
nilpotent Lie group
noncollinear
nondegenerate
 -tensor
-tensor
 -tensor
-tensor
nondegenerate bilinear form
nondegenerate
 -tuple of vector fields
-tuple of vector fields
 -tuple of vector fields
-tuple of vector fields
nondegenerate subspace
nonvanishing vector field
norm
on a vector space
on an inner product space
pseudo-Riemannian
normal bundle
pseudo-Riemannian
normal connection
normal coordinates
polar
pseudo-Riemannian
Riemannian
normal covering map
normal exponential map
normal Jacobi field
normal neighborhood
of a point
of a submanifold
normal projection
normal space
normal variation
normal vector
outward-pointing
normal vector field
along a curve
O
O'Neill's formula
one-parameter family of curves
one-parameter subgroup
one-sided velocity vectors
open geodesic ball
open map
open Möbius band
orbit
orbit space
order of conjugacy
ordered basis
ordinary differential equation
linear
ordinary vertex
orientable manifold
orientation
and coordinates
and
 -forms
-forms
 -forms
-forms
continuous
induced
of a boundary
of a curved polygon
of a hypersurface
of a manifold
of


orientation covering
orientation form
orientation-preserving
orientation-reversing
oriented basis
oriented coordinate chart
oriented manifold
orthochronous Lorentz group
orthogonal complement
orthogonal group
special
orthogonal vectors
orthonormal basis
standard order for
orthonormal frame
for pseudo-Riemannian metric
orthonormal vectors
osculating circle
outward-pointing normal
outward-pointing vector field
overdetermined system
P
parallel frame
parallel lines
parallel tensor field
parallel transport
along admissible curve
determines the connection
parallel vector field
parametrization
by arc length
graph
of a submanifold
parametrized curve
partition of an interval
partition of unity
path
path class
path-homotopic
path homotopy
path-lifting property
Perelman, Grigori
Pfaffian
piecewise regular curve segment
piecewise smooth vector field
pinching theorems
plane curve
plane curve classification theorem
plane section
Poincaré ball
Poincaré disk
Poincaré half-space
point reflection
pointwise conformal metrics
pointwise
 -pinched
-pinched
 -pinched
-pinched
pointwise pullback
polar coordinates
polar Fermi coordinates
polar normal coordinates
polarization identity
polygon
curved
geodesic
polynomial growth
positive density
positively oriented basis
positively oriented curved polygon
positively oriented
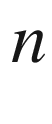 -form
-form
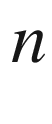 -form
-form
Preissman's theorem
Preissman, Alexandre
principal curvature comparison theorem
principal curvatures
principal directions
product metric
warped
product of paths
product rule
for connections
for divergence operator
for Euclidean connection
product, direct
projection
central
hyperbolic stereographic
normal
of a vector bundle
stereographic
tangential
projective plane
projective space
complex
real
proper group action
proper map
proper variation
proper vector field along a curve
properly embedded
pseudo-Euclidean space
pseudo-Riemannian geodesics
pseudo-Riemannian metric
pseudo-Riemannian normal coordinates
pseudo-Riemannian submanifold
pseudohyperbolic space
pseudosphere
pullback
of a connection
of a density
of an exterior derivative
pointwise
pullback orientation
pushforward of a vector field
Q
quadratic form
quotient manifold theorem
quotient map
R
Radó, Tibor
radial distance function
for a point
for a submanifold
radial geodesics
are minimizing
radial vector field
for a point
for a submanifold
raising an index
rank
constant
of a smooth map
of a tensor
of a vector bundle
rank theorem
equivariant
global
Rauch comparison theorem
ray in a Riemannian manifold
real projective space
regular coordinate ball
regular curve
regular domain
regular level set
regular point of a smooth map
regular value of a smooth map
related vector fields
relativity
general
special
reparametrization
backward
forward
of an admissible curve
representation
of a Lie algebra
of a Lie group
rescaling lemma
restricted exponential map
restricted holonomy
Riccati comparison theorem
matrix
Riccati equation
Riccati, Jacopo
Ricci curvature
geometric interpretation of
Ricci decomposition of the curvature tensor
Ricci flow
Ricci identities
Ricci tensor
geometric interpretation of
Riemann curvature endomorphism
Riemann curvature tensor
Riemann, Bernhard
Riemannian connection
Riemannian covering
Riemannian density
Riemannian distance
isometry invariance of
on a disconnected manifold
Riemannian geodesics
Riemannian isometry
Riemannian manifold
with boundary
Riemannian metric
existence of
Riemannian normal coordinates
Riemannian submanifold
of a pseudo-Riemannian manifold
Riemannian submersion
Riemannian symmetric space
locally
Riemannian volume form
is parallel
right action
right-invariant metric
right-invariant vector field
right translation
rigid motion
rotation index
of a curved polygon
rotation index theorem
for a curved polygon
rough section
round metric
S
SSS theorem
scalar curvature
geometric interpretation of
scalar product
scalar product space
scalar second fundamental form
Schoen, Richard
Schouten tensor
Schur's lemma
secant angle function
second Bianchi identity
second covariant derivative
second fundamental form
geometric interpretation of
scalar
second structure equation
second variation formula
section
of a submersion
of a vector bundle
smooth
sectional curvature
constant
determines the curvature tensor
of Euclidean space
of hyperbolic spaces
of spheres
segment, curve
self-dual
semi-Riemannian metric
semicolon between indices
semidirect product
semigeodesic coordinates
shape operator
sharp (
 )
)
 )
)
sheets of a covering
side of a curved polygon
side-side-side theorem
sign conventions for curvature tensor
sign of a permutation
signature of symmetric bilinear form
signed curvature
of curved polygon
simple closed curve
simply connected space
covering of
single elliptic geometry
singular Riemannian metric
slice coordinates
boundary
smooth atlas
smooth chart
smooth coordinate ball
smooth coordinate chart
smooth coordinate domain
smooth covering map
smooth curve
smooth group action
smooth manifold
with boundary
smooth manifold structure
smooth map
smooth structure
smooth subbundle
smoothly compatible
solvable Lie group
soul theorem
space form
Euclidean
hyperbolic
spherical
special linear group
special orthogonal group
special relativity
special unitary group
spectral theorem
speed of a curve
sphere
Berger
distance function
geodesic
is locally conformally flat
principal curvatures of
round
sectional curvature
volume of
sphere theorem
differentiable
spherical coordinates
spherical space form
splitting theorem
standard basis of


standard coordinates on
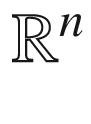
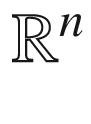
standard order for orthonormal basis
standard orientation of


standard smooth structure
star operator
star-shaped
Steenrod, Norman E.
stereographic projection
hyperbolic
is a conformal diffeomorphism
Stiefel manifold
Stokes orientation
Stokes's theorem
stress-energy tensor
strictly
 -pinched
-pinched
 -pinched
-pinched
structure equation
first
second
sub-Riemannian metric
subalgebra, Lie
subbundle
subgroup, Lie
subinterval of a partition
submanifold
embedded
immersed
pseudo-Riemannian
Riemannian
tangent space to
with boundary
submersion
Riemannian
subordinate to a cover
summation convention
support
of a function
of a section of a vector bundle
surface of
revolution
geodesics
Sylvester's law of inertia
symmetric connection
symmetric group
symmetric product
symmetric space
irreducible
locally
symmetric tensor
symmetries
of Euclidean space
of hyperbolic spaces
of spheres
of the curvature tensor
symmetrization
symmetry lemma
symplectic form
Synge's theorem
Synge, John L.
T
tangent angle function
tangent bundle
tangent covector
tangent cut locus
tangent space
to a submanifold
tangent to a submanifold
tangent vector
tangential acceleration
tangential connection
tangential directional derivative
tangential projection
tangential vector field along a curve
tensor
alternating
contravariant
covariant
mixed
on a manifold
symmetric
tensor bundle
tensor characterization lemma
tensor field
along a curve
tensor product
Theorema Egregium
Thurston geometrization conjecture
topological manifold
with boundary
torsion
 -forms
-forms
 -forms
-forms
torsion element of a group
torsion-free group
torsion tensor
torus
flat metric on
 -dimensional
-dimensional
total covariant derivative
commutes with musical isomorphisms
components of
total curvature theorem
total scalar curvature functional
total space of a vector bundle
totally geodesic
trace
of a tensor
of an endomorphism
with respect to


traceless Ricci tensor
transition function
transition map
transitive group action
on fibers
translation, left and right
transport, parallel
transverse curve
transverse Jacobi field
triangle
Euclidean
ideal
triangulation
trivial free homotopy class
tubular neighborhood
two-point boundary problem
U
Umlaufsatz
uniform tubular neighborhood
uniformization theorem
for compact surfaces
uniformly
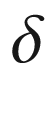 -normal
-normal
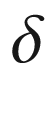 -normal
-normal
uniformly normal
unique lifting property
uniqueness of constant-curvature metrics
unit-speed curve
unit tangent bundle
unit tangent vector field
unitary group
special
universal anti-de Sitter space
universal covering manifold
upper half-plane
upper half-space
upper indices on coordinates
V
vacuum Einstein field equation
variation
first
normal
of a curve
proper
second
through geodesics
variation field
variational equation
variations, calculus of
vector bundle
section of
subbundle
zero section
vector field
along a curve
along a family of curves
canonical form for
commuting
coordinate
Lie algebra of
nonvanishing
normal, along a curve
piecewise smooth
proper
tangential, along a curve
vector, tangent
velocity
vertex
cusp
flat
of a curve
ordinary
vertical action
vertical index position
vertical tangent space
vertical vector field
volume
of a ball
of a Riemannian manifold
of a sphere
volume comparison theorem
Bishop–Gromov
Günther
volume form
von Mangoldt, Hans Carl Friedrich
W
Warner, Frank
warped product
wedge product
Alt convention
determinant convention
Weingarten equation
for a hypersurface
Weingarten map
Weyl–Schouten theorem
Weyl tensor
conformal invariance of
Wilking, Burkhard
Wolf, Joseph
Y
Yamabe equation
Yamabe problem
Z
zero section